Numerical Modelling of High-frequency Internal Waves Generated

by River Discharge in Coastal Ocean

I. K. Marchevsky

1,2 a

, A. A. Osadchiev

3 b

and A. Y. Popov

1 c

Bauman Moscow State Technical University, 5, 2-ya Baumanskaya Str., Moscow, Russia

Ivannikov Institute for System Programming of the RAS, 25, Alexander Solzhenitsyn st., Moscow, Russia

Shirshov Institute of Oceanology, Russian Academy of Sciences, 36 Nahimovskiy Prospekt, Moscow, Russia

Keywords: River Plume, Internal Waves, Coastal Ocean, Small River, Numerical Modelling, Lagrangian–Eulerian

Method.

Abstract: A method for numerical simulation of internal waves generation by discharges of small and rapid rivers

flowing into a coastal sea is proposed. The method is based on PFEM-2 (Particle Finite Element Method, 2

version) and utilizes particles to simulate convection as well as transfer salinity. Main simplifying

assumptions and the mathematical model are presented for this problem. The numerical scheme is split into

predictor (particles motion) and corrector (finite element method solution) steps. The resulting method is

expected to be efficient in terms of mesh fineness and length of simulation time.

1 INTRODUCTION

Satellite imagery detects internal waves with short

wavelength (<100 m) that are generated in the areas

adjacent to estuaries of small rivers and propagate

offshore within river plumes (Fig. 1). This process is

regularly observed in mountainous coastal areas, in

particular, the Ring of Fire (the Pacific coasts of

Mexico, Peru, and Chile; Taiwan, New Guinea, New

Zealand), in Western Balkans, Western Caucasus.

A mechanism of generation of these internal

waves by discharges of small and rapid rivers

inflowing to coastal sea was recently described by

Osadchiev (2018). Friction between river runoff at

high velocity and the subjacent sea of one order of

magnitude lower velocity causes abrupt deceleration

of a freshened flow and increase of its depth, i.e., a

hydraulic jump is formed. Transition from

supercritical to subcritical flow conditions effectively

transforms kinetic energy of river flow to potential

energy and induces generation of high-frequency (65

– 90 s) internal waves. These internal waves

propagate off a river mouth at a stratified layer

between a buoyant river plume and subjacent ambient

sea with phase speed equal to 0.45 – 0.65 m/s and

https://orcid.org/0000-0003-4899-4828

https://orcid.org/0000-0002-6659-0934

https://orcid.org/0000-0002-2744-4889

dissipate within the plume or at its lateral border.

These internal waves increase turbulence and mixing

at this layer and, therefore, influence structure and

dynamics of the river plume.

The process of generation of internal waves by

river discharge described above was reported and

analyzed for small river plumes located off the

northeastern coast of the Black Sea (Osadchiev,

2018). It was shown that river runoff forms a

hydraulic jump and generates internal waves under

certain conditions defined by properties of a river

flow, ambient sea water, and a local topography. In

particular, a river current has to be fast enough to

form a supercritical freshened flow in vicinity of a

river mouth. On the other hand, kinetic energy of a

freshened flow has to be low enough to be inhibited

by friction with ambient sea along a strongly stratified

bottom boundary of a river plume. This condition is

satisfied if river discharge rate is low, i.e., river is

rapid but small.

Despite a certain progress in study of high-

frequency internal waves referred above, many

aspects of their generation, propagation, and

dissipation remain unaddressed. In particular,

emerging of internal waves with a certain period is

384

Marchevsky, I., Osadchiev, A. and Popov, A.

Numerical Modelling of High-frequency Internal Waves Generated by River Discharge in Coastal Ocean.

DOI: 10.5220/0007840203840387

In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 384-387

ISBN: 978-989-758-371-1

Figure 1: Sentinel-2 ocean color composite from 28 December 2017 indicating internal waves generated by small rivers along

the northeastern coast of New Guinea.

presumed to be caused by oscillation of a quasi-

stationary hydraulic jump. However, the exact

background physical mechanism is largely unknown

and requires a detailed study. Thorough description

of this mechanism will reveal dependence of

parameters of internal waves (frequency, phase

speed, wavelength) on external conditions (river

inflow velocity, river plume height, salinity and

vertical stratification, salinity of ambient sea, etc.).

These dependences are crucial for evaluation of

wave-induced turbulence and mixing intensity in

bottom and lateral frontal zones of a river plume that

govern its structure and mixing dynamics (Osadchiev

and Korshenko, 2017; Osadchiev and Sedakov,

2019). In this study we apply a novel Eulerian-

Lagrangian approach to reveal these issues. Based on

results of numerical experiments we present new

insights into the processes describe above.

2 GOVERNING EQUATIONS

For numerical simulation of such phenomenon the

following simplifying assumptions can be taken into

account (Milne-Thomson, 2011):

1) the water is incompressible, so the velocity field

is divergence-free:

0u  

;

(1)

2) the temperature of the water is considered to be

constant, its density



depends only on the

salinity

(in per mille), we confine the

approximate dependency to linear term

  



(2)

3) where



is the density of fresh water (at

0S 

0.65





kg/m

for salt water;

4) the Boussinesq-type approximation is considered

in order to take into account the buoyancy-driven

flow which arises due to the density difference

caused by non-uniform salinity distribution:

()

u u p u g S







       



(3)

where

is the pressure field,



is the kinematic

viscosity coefficient, which we assume to be constant

(







/s for the water);

is the gravity

acceleration;

5) the salinity distribution in general case is

described by the convection-diffusion equation

u S D S



    



(4)

where

is the diffusivity coefficient; for saline

solution it weakly depends on concentration and can

Numerical Modelling of High-frequency Internal Waves Generated by River Discharge in Coastal Ocean

385

be considered equal to

1.1 10D





/s. The latter

means that the Schmidt number





(5)

which defines the ratio of momentum diffusivity

(kinematic viscosity) and mass diffusivity, has the

order of

, so the salinity diffusion process can be

neglected. As the result, we have the equation for

salinity

dS S

dt t



   



(6)

which means that salinity is being transferred along

the velocity streamlines as a passive impurity.

3 COMPUTATIONAL DOMAIN

AND BOUNDARY CONDITIONS

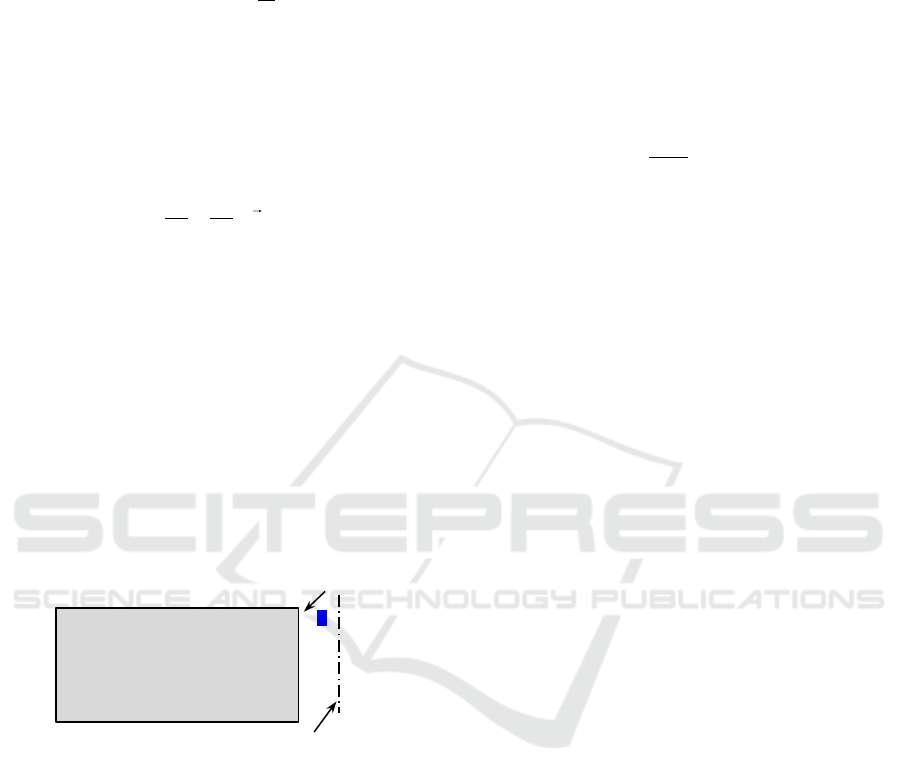
Preliminary numerical simulation can be provided for

2D and 3D axisymmetric (a semicircular sector is

considered) cases. It seems reasonable to consider a

rectangular computational domain shown in the

Fig. 2.

Figure 2: Computational domain.

The boundary conditions on the computation domain

boundaries are the following:

Inlet: given values of the velocity and salinity which

refer to the fresh water from the river.

Wall: zero velocity and zero gradient of salinity and

pressure.

Outlet: mixed boundary condition: а) zero gradient

of velocity and salinity if normal component of

velocity is directed outside the flow domain, b) given

value of the total pressure and given value of salinity,

which refers to the salt water in the sea, when normal

component of velocity is directed inside the flow

domain.

Surface: it is assumed that the surface is flat which

means that the surface waves are not simulated;

normal (vertical) velocity is zero, pressure is equal to

a fixed value which refers to atmospheric pressure,

shear stress is equal to zero. Surface waves can still

be simulated in a more precise simulation, that would

require description of the water surface position and

the Boussinesq boundary conditions consideration on

the free surface. However, even in this case the

surface tension effect should be neglected because the

Weber number







has the order of

10 ...10

4 NUMERICAL METHOD

The described problem can be solved numerically by

using, for example, finite volume method,

implemented in a number of computational codes.

However, the flow in the considered case is

convection-dominated, it means that the convective

term in the Navier–Stokes equation is prevalent over

all other terms: pressure gradient and viscous

diffusion. Moreover, the salinity distribution

evolution is considered as pure convective transport,

as it was mentioned above. It means that the precision

of approximation of the convective terms is much

more crucial than of the pressure and diffusive ones.

The computational domain can be rather large (in

comparison to the size of the river outlet), and

physical time in simulation also should be long

enough to obtain a quasi-steady regime of flow.

Such requirements make it reasonable to use

hybrid Lagrangian–Eulerian methods for numerical

simulation. PFEM-2 (particle finite element method,

the 2-nd version; Idelsohn, Onate and Del Pin, 2004,

as well as Idelsohn et al., 2013) seems to be the most

suitable among them. Its main features are the

following:

1) Particles, which move along the streamlines of

the velocity field, are introduced in order to

approximate the convective term in the Navier–

Stokes equation. These particles are ‘immaterial’, i.e.

they do not transfer the mass and other intrinsic

properties except of marker of the phase (for

multiphase flows). In the considered problem, it

seems to be convenient to consider salinity as the

other property transferred by the particles.

2) Fixed mesh, which can be rather coarse, is

introduced in the flow domain for finite-element

approximation of the other terms – pressure gradient,

viscous term and buoyancy term.

inlet

surface

wall

axis position for

axisymmetric case

outlet

ONM-CozD 2019 - Special Session on Observations and Numerical Modeling of the Coastal Ocean Zone Dynamics

386

3) Interpolation technique is used in order to

transmit velocities and salinity from the particles to

mesh nodes and vice versa.

So each time step is split into two stages. The first

one is predictor, which consists of the particles

motion phase. Note that the step size can be rather

high (CFL number is allowed to be more than 1),

while for particles motion simulation it is normally

split into sub-steps in order to provide CFL not more

than 0.10…0.15. At the same time, the velocity field

is considered to be known at the mesh nodes from the

previous time step, so its finite element reconstruction

and Euler (or Runge–Kutta) explicit method for

particles motion integration make this operation not

time-consuming and easy to parallelize.

After the particles motion sub-steps have been

performed, the velocity and salinity values, having

been transferred with the particles, should be

projected onto mesh nodes. Now the convection

(predictor) stage is finished.

The correction stage consists of solution of the

equation

p u g S







     



(7)

where the initial value is known from the prediction

step. This equation no longer contains the convection

term, which is highly sensitive to numerical

approximation. Implicit finite element scheme is

used, both monolithic and coupled strategies

(including fractional step approach) can be used for

calculation of new values of

and

. The velocity

field

should satisfy the incompressibility

equation (1) while this property is broken for the

velocity field after ‘predictor’ stage.

5 CONCLUSIONS

The proposed method is expected to be an efficient

means of simulation of a mechanism of generation of

internal waves by discharges of small and rapid rivers

inflowing to coastal sea. The heavy use of particles

makes computation possible on rather coarse meshes

as well as long periods of simulation time, which is

required to reach a quasi-steady state. Current

implementation has been provided for 2D and

axisymmetric problems but can be further developed

for solution of fully 3D simulation cases.

ACKNOWLEDGEMENTS

This research was funded by the Ministry of Science

and Education of Russia, theme 0149-2019-0003

(collecting and processing of satellite data) and the

Russian Science Foundation, research project 18-17-

00156 (study of river plumes).

REFERENCES

Osadchiev, A. A., 2018. Small mountainous rivers generate

high-frequency internal waves in coastal ocean.

Scientific Reports, 8, 16609.

Osadchiev, A. A., Korshenko, E. A., 2017. Small river

plumes off the north-eastern coast of the Black Sea

under average climatic and flooding discharge

conditions. Ocean Science, 13, 465-482.

Osadchiev, A. A., Sedakov, R. O., 2019. Spreading

dynamics of small river plumes off the northeastern

coast of the Black Sea observed by Landsat 8 and

Sentinel

Milne-Thomson, L.M., 2011. Theoretical Hydrodynamics,

Dover Books on Physics, Mineola, 5

edition.

Idelsohn, S.R., Onate, E., Del Pin, F., 2004. The particle

finite element method: a powerful tool to solve

incompressible flows with free-surfaces and breaking

waves. International Journal for Numerical Methods in

Engineering, 61, 964-989.

Idelsohn, S.R., Nigro, N.M., Gimenez J.M., Rossi, R.,

Marti, J.M., 2013. A fast and accurate method to solve

the incompressible Navier-Stokes equations.

Engineering Computations, 30/2, 197-222.

Numerical Modelling of High-frequency Internal Waves Generated by River Discharge in Coastal Ocean

387