
ANFIS based IMC PID Controller for Permanent Magnet DC Motor
M. Alasvandi
1
, S. Z. Moussavi
2
, E. Morad
3
and E. Rasouli
4
1
Department of Electrical Engineering, Islamic Azad University Central Tehran Branch, Tehran, Iran
2
Electrical and Computer Engineering Faculty, Shahid Rajaee Teacher Training University, Tehran, Iran
3
Department of Electrical Engineering, Sciences and Research Branch, Islamic Azad University, Tehran, Iran
4
Department of Electrical Engineering, Amirkabir University of Technology, Tehran, Iran
Keywords: Speed Control, ANFIS, IMC, PID, PMDC Motor.
Abstract: Permanent Magnet Direct Current (PMDC) motors are widely used in industrial application and PID
controllers are usually applied to improve performance characteristics of PMDC motor. There are different
methods for setting up PID parameters that one of them has been called Internal Model Control (IMC) which
is used parameter to modify performance characteristics of system. Sometimes setting up IMC PID
parameters are hard so in this paper, ANFIS is used to add proper values with IMC PID coefficients. The
proposed controller used ANFIS based coefficient modifier because it can train easily and help system to
achieve desired performance characteristics. The proposed system used the fuzzy system that is extracted
from training ANFIS system with desired data to improve PMDC motor performance. In this paper IMC
based controller is compared with proposed strategy and simulation results shows that proposed control
system have acceptable characteristic in different situation such as no-load, applied-load, changing reference
speed and it is effective methods to control system in noisy condition.
1 INTRODUCTION
The speed and position control of PMDC motor are
very important because PMDC motor widely has
been exploiting in industrail and proving ground due
to simplicity, low cost and efficiency (Medewar and
Munje, 2015, Angalaeswari et al., 2016). PMDC
motors have uncertain and nonlinear characteristics
so different control methods are applied to improve
their perfomance which is sorted into three main
categories:
1. Classic PID, PI, P controllers (Sreekala and
Sivasubramanian, 2011).
2. Modern control system (Moussavi et al., 2012, Liu
et al., 2014).
3. Intelligent control system (Sharifian et al., 2011,
Wei, 2011, Blessy and Murugan, 2014, Choi et al.,
2015).
The PID controllers have been utilizing to control
different industrial processes from past to present and
control researchers have been trying to find the best
choices for PID coefficients (K
p
, K
i
, K
d
) for various
process models, simultaneously (Subramanyam et al.,
2012). The many different researches are have been
doing to find effective methods for setting up
coefficients of PID controller and IMC which is based
on rboust control procedure is one of them. The
process model is embedded into control system in
IMC based control method and a tunable parameter is
used to ehnance controller performance (Nasir and
Singh, 2015).
On the other hand, researchers try to introduce
control method based on human ability such as
learning and decision making for example fuzzy
system and neural network. Finally, Jyh-Shing Roger
Jang proposed intelligent system based on
combinition of fuzzy and neural network in 1993 that
has been called ANFIS (Jang, 1993). ANFIS applies
learning ability of neural network to creat
membership function parameters of fuzzy system. In
fact, ANFIS uses advantages of neural network and
fuzzy systems simultaneously.
In this paper, IMC and ANFIS are used to
proposed new control strategy which ANFIS based
controller find the best parameter to add with
coefficients of IMC PID controller ( K
p
, K
i
, K
d
) to
improve perfomance characteristics of PMDC motor.
Description of PMDC motor structure is given in
section 2, then concept of IMC PID is explained in
section 3. ANFIS is briefly described in section 4 and
Alasvandi, M., Moussavi, S., Morad, E. and Rasouli, E.
ANFIS based IMC PID Controller for Permanent Magnet DC Motor.
DOI: 10.5220/0007840402350242
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 235-242
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
235
the proposed controller is introduced in section 5. The
simulation results are considered in section 6. Finally,
proposed strategy and simulation results are
summarized in section 7.
2 PERMANENT MAGNET DC
MOTORS
The proposed control method is designed to improve
characteristics of PMDC motor so dynamic model
should be investigated.
The state-space equations are extracted from both
the electrical circuit and mechanical equations of
motion (Shahgholian and Shafaghi, 2010):
1
(1)
1
(2)
The PMDC motor parameters are summarized in
Table 1 (Moussavi et al., 2012, Shahgholian and
Shafaghi, 2010).
Table 1: PMDC motor parameters.
Symbol Description
ω
M
Rotor s
p
ee
d
i
A
Motor current
B
M
Viscous friction constant
J
M
Inertia of roto
r
T
L
Load torque
R
A
Armature resistance
L
A
Armature inductance
K
T
back electromotive force (emf) constant or
tor
q
ue constant
U
T
A
pp
lied volta
g
e to moto
r
T
E
Electroma
g
netic tor
q
ue
u
b
Back emf
If the motor current and rotor speed are chosen as
state variables, the state-space equations are
described as below (Moussavi et al., 2012):
1
0
0
1
(3)
01
00
(4)
The equations (3) and (4) are converted to transfer
function model as follow (Moussavi et al., 2012):
ω
K
(5)
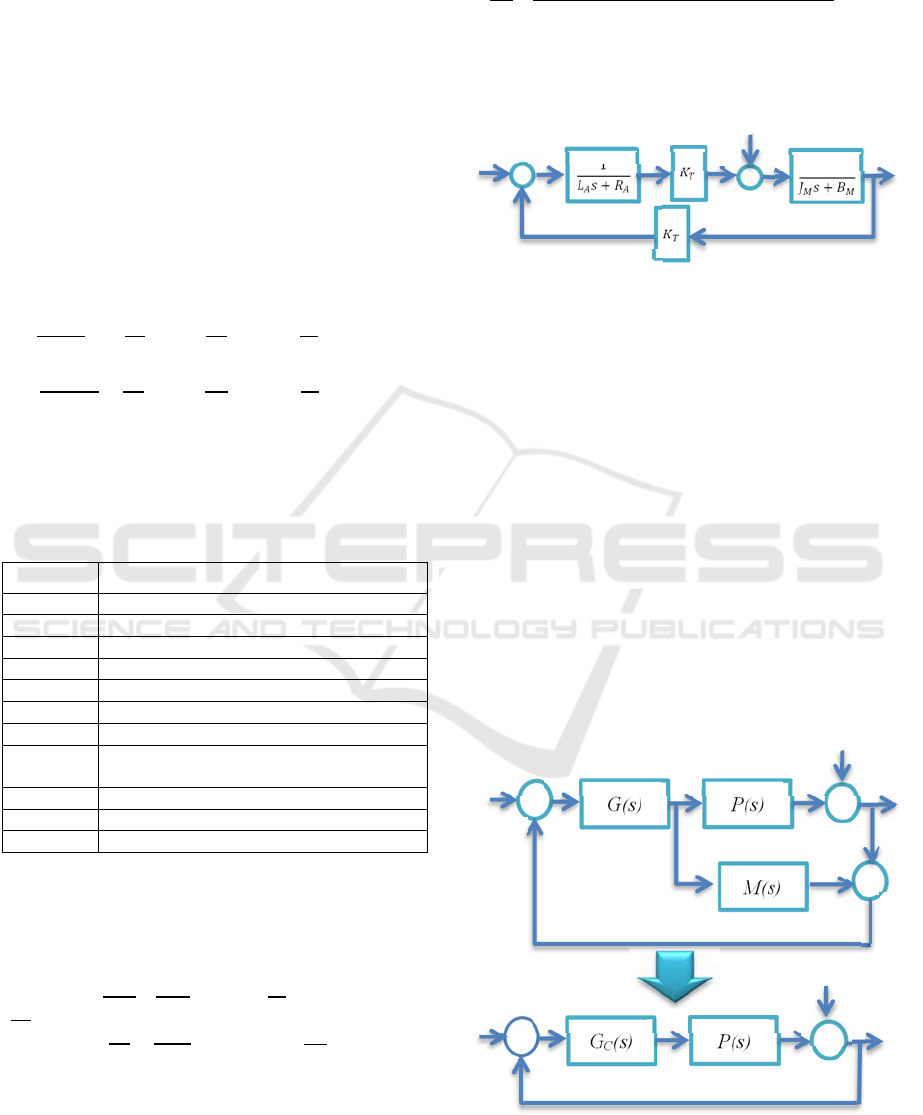
The simplified
block diagram of
PMDC motor is
shown in Figure 1.
Figure 1: PMDC Motor.
3 INTERNAL MODEL CONTROL
The effective conventional control method for closed
loop system is called PID controller that simplicity of
structure and easy implementation are main
advantages of them. PID controller has three main
parameter (K
p
, K
i
, K
d
). K
p
is proportion coefficient
which is applied to increases or to decreases the value
of the output. K
i
is called integral time and it is
applied to reduce the steady-state error of the system.
The other parameter is derivative time (K
d
) which
rises the value of output slightly fast to improve
transient response (Chen and Chang, 2018). Different
methods such as Ziegler–Nichols, Chien–Hrones–
Reswick and Internal Model Control are used to
adjust PID controller parameters.
Figure 2: Equivalent the IMC to general control structure.
1
1
G(s)
P(s)
M(s)
G
C
(s)
P(s)
r
d
u
y
p
y
m
_
+
d
r
_
+
y
p
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
236
Equivalent the typical internal model structure to
a single loop PID control structure is as Figure 2,
Where P(s) is the actual process, M(s) refer to the
model of the process, and G(s) is the IMC primary
controller, u refer to output of internal model
controller, r, y and d refer to the input, the output and
load disturbances, respectively, and Gc(s) is the
controller which can get the result of internal model
controlling structure after varying equivalently. The
IMC controller is designed as below (Naik and
P.Srikanth, 2011):
(6)
Where
is the realizable factor (Naik and
P.Srikanth, 2011).
1
1
1
(7)
Consider the plant model M(s) as the PMDC
motor transfer function then (Naik and P.Srikanth,
2011):
K
(8)
Substitute equation (8) in equation (7) and IMC-
PID tuning parameters are given as (Naik and
P.Srikanth, 2011):
(9)
4 ANFIS CONTROLLER
ANFIS is most effective and important neuro-fuzzy
system that was introduced by Jyh-Shing Roger Jang
in 1993(Jang, 1993). ANFIS is the best combination
of fuzzy controller (FC) and neural network (NN)
which is applied human learning ability of neural
network to provide membership functions and rules
of fuzzy system(Simon and Geetha, 2013). ANFIS
rules and structure are explained as below:
Rule 1: If x is A
1
and y is B
1
then f
1
=p
1
x+ q
1
y + r
1
Rule 2: If x is A
2
and y is B
2
then f
2
=p
2
x+ q
2
y + r
2
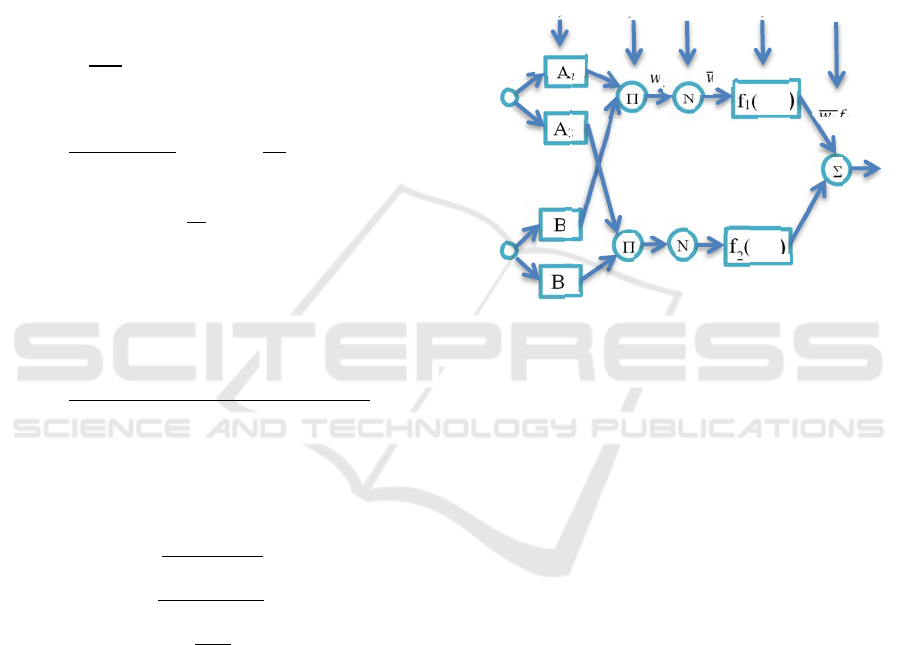
ANFIS architecture is shown in Figure 3. The
process of every ANFIS layer is summarized as
below (Chen and Chang, 2018):
Layer 1: Calculate the correct value for the
parameters of the membership function.
Layer 2: Determine the value of firing strength.
Layer 3: Calculate for normalizing the firing strength.
Layer 4: Offer the result rules of the FIS.
Layer 5: Sum up all inputs to express the overall
output
Figure 3: Equivalent ANFIS.
The proposed control system is introduced in next
section.
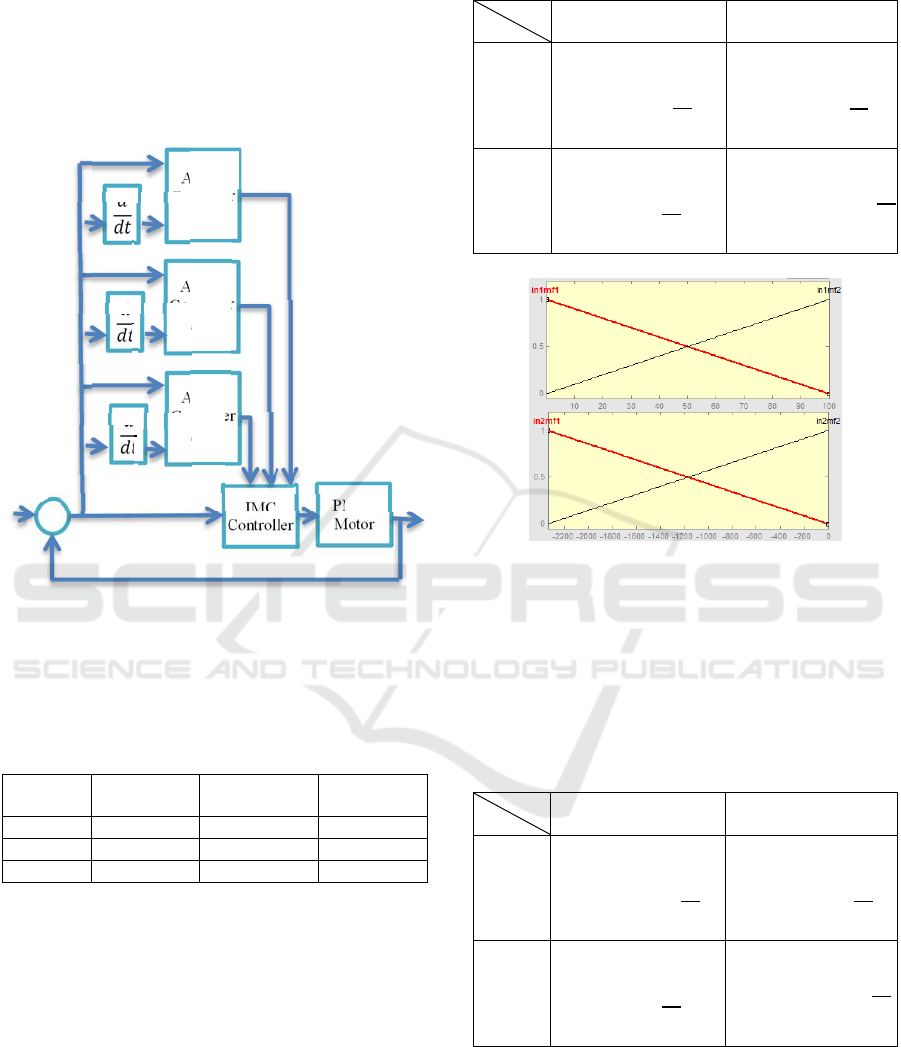
5 PROPOSED CONTROLLER
The proposed method is designed based on IMC PID
and ANFIS controllers to obtain more reasonable
performance characteristics. The equation (9) is used
to obtain coefficients of IMC PID controller then
three ANFIS controller applied to extracted proper
values of (∆K
p
, ∆K
i
, ∆K
d
). The coefficients of
ANFIS and IMC PID controllers have been added to
improve performance characteristics of PMDC
motor. The block diagram of proposed controller is
shown in Figure 4.
Figure 4 shows that each ANFIS controller is
multi input and single output; therefore three ANFIS
controllers are needed. 4001 input-output pairs are
applied for training, checking and testing each of
ANFIS controllers. The (∆K
p
, ∆K
i
, ∆K
d
) are
determined according to the error and derivation of
error.
The input membership functions of ANFIS
controllers are shown in Figures 5, 6 and 7.
A
1
A
2
B
1
B
2
N
N
f
1
(x,y)
f
2
(x,y)
x
y
f
Layer1
Layer2
Layer3
Layer4 Layer5
ANFIS based IMC PID Controller for Permanent Magnet DC Motor
237
Two triangle input membership functions and
four linear output membership functions are used in
ANFIS controllers. The grid partition is applied to
generate fuzzy inference system also optimization is
done by hybrid method. The type and number of input
membership functions effect on the training, checking
and testing errors.
Figure 4: Proposed controller.
Training, checking and testing errors of ANFIS
controllers are shown in Table 2.
Table 2: Training, checking and testing errors of ANFIS
controllers.
ANFIS
controlle
r
Training Error Checking Error Testing Error
∆
K
p
0.0035849 0.0035722 0.0035763
∆
K
i
0.0015141 0.0015139 0.0015181
∆
K
d
4.221×10
-5
4.2191×10
-5
4.2076×10
-5
The values of (∆K
p
, ∆K
i
, ∆K
d
) are determinate
based on error and derivation of error that are shown
in Figure 4. The surfaces of three controllers have
smooth changes so there are not any suddenly
variations in (∆K
p
, ∆K
i
, ∆K
d
) according to (e and
de/dt).
Table 3: Fuzzy rules of ∆K
p
ANFIS controller.
de
e
In 2 mf1 In2mf2
In1mf1
out1mf1
0.01371e
0.001193
de
dt
1.11310
out1mf2
6.186e
0.001413
de
dt
0.001474
In1mf2
out1mf3
0.03644e
0.2659
de
dt
0.0002273
out1mf4
6.249e0.2658
de
dt
0.1243
Figure 5: Input membership function of ∆K
p
controller.
The membership functions and fuzzy rules of ∆K
p
controller are shown in Figure 5 and Table 4,
respectively. Every input have two membership
functions so four linear rules describe all possible
conditions.In this manner, ∆K
i
and
∆K
d
fuzzy
controllers have same property.
Table 4: Fuzzy rules of ∆K
i
ANFIS controller.
de
e
In 2 mf1 In2mf2
In1mf1
out1mf1
0.05659e
0.0007924
de
dt
5.15810
out1mf2
21.79e
0.0004134
de
dt
0.0007318
In1mf2
out1mf3
0.02298e
0.9302
de
dt
0.0007956
out1mf4
21.77 0.9303
de
dt
0.4356
ANFIS
Controller
K
p
ANFIS
Controller
K
i
ANFIS
Controller
K
d
IMC
Controller
PMDC
Motor
Error
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
238

Figure 6: Input membership function of ∆K
i
controller.
The number and shape of membership functions
effect on performance of ANFIS controllers so
changing number or shape of membership function
increase designing error.
Table 5: Fuzzy rules of ∆K
d
ANFIS controller.
de
e
In 2 mf1 In2mf2
In1mf1
out1mf1
4.88810
e
1.45210
de
dt
1.26710
out1mf2
0.1401e
1.51410
de
dt
1.45110
In1mf2
out1mf3
0.0005619e
0.005999
de
dt
5.1310
out1mf4
0.1408e
0.005998
de
dt
0.002809
Figure 7: Input membership function of ∆K
d
controller.
The simulation results that include step response
of PMDC motor in different conditions such as no
load, increasing reference speed, applied load and
noisy load are shown in next section. The
performance characteristics are expressed section 6.
6 SIMULATION RESULTS AND
DISCUSSION
The case study is PMDC motor and parameters are as
follows(Shahgholian and Shafaghi, 2010):
R
A
=7.72 ohm, L
A
= 0.16273 H, K
T
=1.25 Nm,
B
M
=0.003 N.m.s/r and J
M
= 0.0236 kg.m
2
.
At first, the without controller close loop system
is investigated in Figures 8-11.
The without controller system has reasonable rise
time and settling time whereas steady state error is
undesirable and closed loop system has overshoot.
Figure 8: Step response of without controller system (no
load condition).
The new reference speed that equals 120 rad/sec
is applied in t=2 sec and Figure 9 shows that system
cannot receive new reference speed.
Figure 9: Step response of without controller system
(increasing reference speed condition).
Load torque (10 N.m) is applied in t=2 sec. Figure
10 shows that system cannot recovery steady state
speed.
ANFIS based IMC PID Controller for Permanent Magnet DC Motor
239
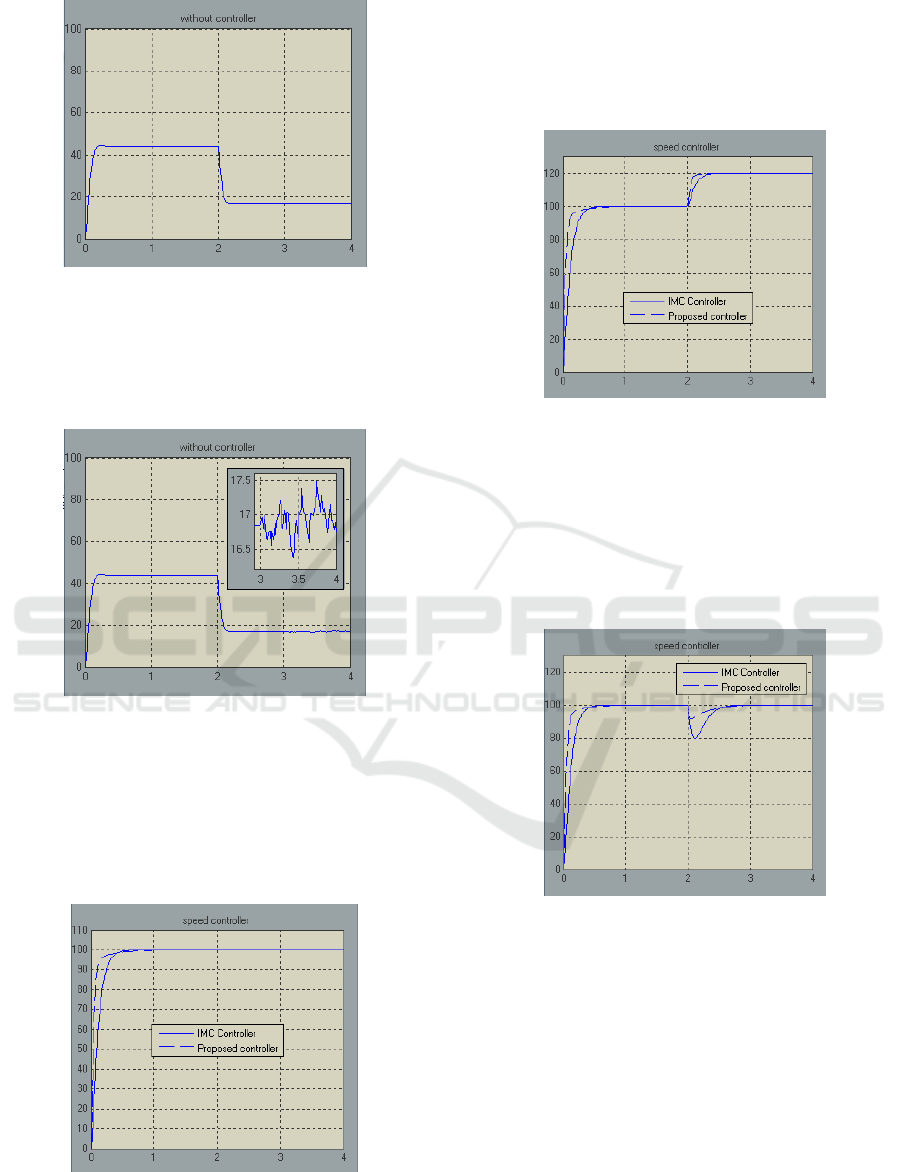
Figure 10: Step response of without controller system
(applied load condition).
The noisy load is applied to system that noise
power equal 0.01w. The undesirable oscillation is
shown in Figure 11.
Figure 11: Step response of without controller system
(applied noisy load condition).
Figure 12 shows that proposed and IMC PID
systems have more reasonable overshoot and steady
state error than without controller system. Moreover,
Figure 12 shows that proposed controller has shorter
rise time and settling time than IMC system.
Figure 12: Step response of control systems (no load
condition).
Figure 13 shows that proposed and IMC PID
systems can attain new reference speed whereas
without controller system doesn't have such
capability. Moreover, proposed controller has the
shortest rise time to reach new reference speed.
Figure 13: Step response of control systems (increasing
reference speed condition).
Figure 14 shows that proposed and IMC PID
systems have better performance characteristics than
without controller system because they can recover
steady state speed. The proposed controller has the
smallest percent minimum speed due to applying load
and the shortest recovery time.
Figure 14: Step response of control systems (applied load
condition).
Figure 15 shows step response of both control
systems in applied noisy load condition. Proposed
controller has the smallest percent oscillations in
applied noisy load condition.
Tables 6-8 show the performance characteristics
of control systems in different conditions. Rise time,
settling time, maximum overshoot and steady state
error are given in Table 6.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
240

Figure 15: Step response of control systems (applied noisy
load condition).
Table 6 shows that proposed controller has the
shortest rise time. Moreover, proposed controller has
more reasonable settling time, maximum overshoot
and steady state error. Without controller has the
shortest settling time whereas rise time, maximum
overshoot and steady state error of without controller
system are undesirable.
Table 6: Performance characteristics of control system in
no load condition.
Method
Rise
Time
(
sec
)
Settling
time
(
sec
)
Maximum
overshoot
(
%
)
Steady
state error
(
%
)
Without
controlle
r
0.1024 0.1637 0.33 55.9186
IMC
controlle
r
0.219 0.3983 0 0
Proposed
controlle
r
0.0892 0.345 0 0
Table 7 shows that without controller system
doesn't have reasonable behaviour in increasing
reference speed whereas proposed controller has the
shortest rise time to achieve new reference speed.
Table 7: Performance characteristics of control system in
increasing reference speed.
Method
Final speed
(
rad/s
)
Rise time
(
s
)
Without controlle
r
------- ---------
IMC controlle
r
120 0.2209
Proposed controlle
r
120 0.0891
Table 8 shows without controller system cannot
recover steady state speed whereas proposed
controller has the shortest recovery time and the
smallest percent minimum speed due to applying load
in applied load condition.
Moreover, Table 8 shows that proposed system
has the smallest percent oscillations in applied noisy
load condition. Tables 7 and 8 show that proposed
controller has shorter rise time and recovery time,
also smaller percent minimum speed due to applying
load and percent oscillations than IMC PID
controller.
Table 8: Performance characteristic of control system in
applied load and noisy load condition.
Method
Applying load
Applied noisy
loa
d
Recovery
time
(s)
Percent
minimum speed
due to applying
load
(%)
Percent
oscillations
(%)
Without
controlle
r
--------- --------------- 6.5475
IMC controller 0.5214 20.2977 1.3846
Proposed
controlle
r
0.4921 8.1908 1.0462
7 CONCLUSIONS
The performance characteristics of PMDC motor in
closed loop system are investigated in different
condition such as No load – Changing reference
speed – applied load – applied noisy load. The
simulation shows that proposed controller has more
reasonable rise time, settling time, overshoot and
steady state error than IMC based controller in no
load condition. Proposed control system has shortest
rise time in increased reference speed condition. The
percent minimum speed due to applying load and
recovery time of proposed controller is more
reasonable than IMC based system in applied load
condition. When noisy load applied to PMDC motor,
proposed control system shows more reasonable
performance characteristic than IMC system. Percent
oscillations of proposed controller and IMC based
system equal 1.0462% and 1.3846%, respectively.
The computation time of Sugeno inference that is
used in ANFIS is shorter than Mamdani fuzzy system.
In the other hand, implementation of proposed
controller because of minimum rule base is so easy.
The simulation results show more reasonable
performance characteristics in different conditions.
ANFIS based IMC PID Controller for Permanent Magnet DC Motor
241

ACKNOWLEDGEMENTS
The Authors thank ISLAMIC AZAD University,
Central Tehran Branch as this work is the result of
master thesis in electrical engineering (MSc Eng.)
with titled "Improvement Performance of Permanent
Magnet Motor by Using Fuzzy Controller" which is
on focus at the Faculty of Engineering.
REFERENCES
Angalaeswari, S., Kumar, A., Kumar, D., and Bhadoriya, S.
(2016). Speed Control of Permanent Magnet (PM)DC
Motor Using Arduino And LabVIEW. International
Conference on Computational Intelligence and
Computing Research. Chennai, India: IEEE.
Blessy, M. S., and Murugan, M. (2014). Modeling and
controlling of BLDC motor based fuzzy logic.
International Conference on Information
Communication and Embedded Systems (pp. 1-6).
Chennai, India: IEEE.
Chen, Y.-H., and Chang, C.-D. (2018). An Intelligent
ANFIS Controller Design for a Mobile Robot.
Proceedings of IEEE International Conference on
Applied System Innovation 2018 (pp. 445-448). Chiba,
Japan: IEEE.
Choi, H. H., Yun, H. M., and Kim, Y. (2015).
Implementation of Evolutionary Fuzzy PID Speed
Controller for PM Synchronous Motor. IEEE
Transactions on Industrial Informatics, 540-547.
Jang, J. (1993). ANFIS: Adaptive-Network-Based Fuzzy
Inference System. IEEE Trans. on System, Man, and
Cybernetics, 665-685.
Liu, Y., China, W., Zhao, J., Xia, M., and Luo, H. (2014).
Model Reference Adaptive Control-Based Speed
Control of Brushless DC Motors With Low-Resolution
Hall-Effect Sensors. IEEE Transactions on Power
Electronics, 1514 - 1522.
Medewar, P. G., and Munje, R. K. (2015). PSO based PID
Controller Tuning for PMDC Motor. International
Conference on Energy Systems and Applications (pp.
522-526). Pune, India: IEEE.
Moussavi, S. Z., Alasvandi, M., and Javadi, S. (2012).
Speed Control of Permanent Magnet DC Motor by
using Combination of Adaptive Controller and Fuzzy
Controller. International Journal of Computer
Applications, 11-15.
Naik, K. A., and P.Srikanth. (2011). Stability Enhancement
of DC Motor using IMC Tuned PID Controller.
International Journal of Advanced Engineering
Sciences and Technologies, 92-96.
Nasir, A. W., and Singh, A. K. (2015). IMC Based
Fractional order Controller for Non-Minimum Phase
System. Annual IEEE India Conference (INDICON)
(pp. 1-6). New Delhi, India: 2015.
Shahgholian, G., and Shafaghi, P. (2010). State Space
Modeling and Eigenvalue Analysis of the Permanent
Magnet DC Motor Drive System. 2010 2nd
International Conference on Electronic Computer
Technology (pp. 63-67). Kuala Lumpur: IEEE.
Sharifian, M., Shafiei, M., Sadeghi, M., and Golestaneh, F.
(2011). Direct Torque Control of Brushless DC Motor
Drives Based on ANFIS Controller with Fuzzy
Supervisory Learning. 2011 International Conference
on Electrical Machines and Systems (pp. 1-6). Beijing:
IEEE.
Simon, R., and Geetha, A. (2013). Comparison on the
performance of Induction motor control using fuzzy
and ANFIS controllers. 2013 IEEE International
Conference ON Emerging Trends in Computing,
Communication and Nanotechnology (pp. 491-495).
Tirunelveli, India: IEEE.
Sreekala, P., and Sivasubramanian, A. (2011). Speed
control of brushless DC motor with PI and fuzzy logic
controller using resonantpole inverter. 2011 IEEE PES
Innovative Smart Grid Technologies (pp. 334-339).
Kollam, Kerala, India: IEEE.
Subramanyam, M., Prasad, K. S., and Rao, P. G. (2012).
Robust Control of Steam Turbine System Speed Using
Improved IMC Tuned PID Controller. Procedia
Engineering, 1450-1456.
Wei, W. (2011). Design of flux-weakening control system
of PMSM based on the fuzzy self-tuning PID controller.
2011 International Conference on Consumer
Electronics, Communications and Networks (pp. 226-
229). XianNing, China: IEEE.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
242
