
A New Certificateless System Construction for Multiple Key Generator
Centers to Secure Device-to-Device Communications
Othmane Nait Hamoud
1,2 a
, Tayeb Kenaza
2 b
and Yacine Challal
1,3 c
1
Ecole Nationale Sup
´
erieure d’Informatique, BP 68M, 16309, Oued-Smar, Alger, Alg
´
erie
2
Ecole Militaire Polytechnique, BP 17 Bordj Elbahri, Alger, Alg
´
erie
3
Sorbonne Universit
´
es, Universit
´
e de Technologie de Compi
`
egne, Heudiasyc UMR CNRS 7253, Compi
`
egne, France
Keywords:
Security, Device-to-Device Communication, Key Management Scheme, Certificateless Public Key
Cryptography, Proximity Services, ProSe.
Abstract:
Device-to-Device (D2D) communication technology comes as one brick among many others in the construc-
tion of the evolving fifth generation system (5G) architecture. The Third Generation Partnership Project
(3GPP) standardized D2D communication technology under the Proximity Services (ProSe) proposal. This
technology allows enabling direct communication between proximate devices without passing through an in-
frastructure network. Security of D2D communications must be assured in all scenarios according to whether
communication control is ensured by the Evolved Packet System (EPS) or the devices themselves. Certificate-
less public key cryptography (CL-PKC) is an interesting solution for securing D2D communications. In this
paper, we propose a new CL-PKC construction to overcome security issues in all scenarios related to D2D
communications and to deal with inherent conflicting security requirements between privacy, anonymity, and
traceability by the use of multiple Key Generator Centers (KGCs). This was considered particularly as re-
sponsibility decentralization between stakeholders to respond the fully mistrust assumption regarding KGCs.
Furthermore, the proposed CL-PKC system can give different networks the opportunity to be compatible and
to work cooperatively.
1 INTRODUCTION
Device-to-Device (D2D) communication is expected
to be one of the main technology components for the
next generation of mobile communication networks
(5G). Proximity Services (ProSe) is the standardiza-
tion of D2D technology. It was introduced for the first
time in Release 12 of the 3GPP specifications (3GPP,
2013) to enhance the capacity and performance of tra-
ditional cellular networks. ProSe allows LTE-A de-
vices to discover each other and to communicate di-
rectly and relies on multiple enhancements to existing
LTE-A standards including new air interface and new
functional elements (3GPP, 2014). Depending on the
degree of implication of a Cellular Network Operator
(CNO) in D2D communications, three typical scenar-
ios and use cases were proposed by 3GPP in (3GPP,
2013), which we illustrate in Figure 1.
a
https://orcid.org/0000-0001-6078-6939
b
https://orcid.org/0000-0002-4240-2978
c
https://orcid.org/0000-0002-9237-6210
Security of D2D communications is a major chal-
lenge since it concerns the security of both radio ac-
cess interface, network infrastructure, devices, and
applications. In the last decade, many solutions have
been proposed in the literature to handle security is-
sues in this new technology (Nait Hamoud et al.,
2018a; Haus et al., 2017; Wang and Yan, 2015). Un-
fortunately, these solutions consider the three typi-
cal scenarios separately and depend on a Trust Third
Party (TTP) which could raise privacy issues in case
of breach of trust. According to our vision, ProSe
application server, which provides authentic con-
tent to ProSe-enabled User Equipment (UE) such as
YouTube’s content or a local social network, would
be owned by the CNO or another third party.
In this paper, we adopt the case where the ProSe
Application server belongs to another operator, called
D2D Server Provider (D2D-SP). This has an advan-
tage in terms of security, especially regarding pri-
vacy issues which gain more attention in the litera-
ture (Haus et al., 2017; Ferrag et al., 2017; Hsu et al.,
2018) due to users’ awareness of their sensitive in-
84
Hamoud, O., Kenaza, T. and Challal, Y.
A New Certificateless System Construction for Multiple Key Generator Centers to Secure Device-to-Device Communications.
DOI: 10.5220/0007841500840095
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 84-95
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Typical scenarios and use-cases in D2D communications.
formation, especially in the context of globalization.
In other words, separating security responsibility be-
tween two entities with opposing interests affords us a
solution to inherent conflicting security requirements
between privacy, anonymity, and traceability which
are being a novel research area in the last years (Sun
et al., 2011; Paja et al., 2013; Alkubaisy, 2017),
and an opportunity to find out other business models
and pricing issues resolution in D2D communications
(Tehrani et al., 2014).
Certificateless public key cryptography (CL-PKC)
has been introduced in (Al-Riyami and Paterson,
2003) as an intermediate public key system between
Public Key Infrastructure (PKI) and Identity based
Public Key Cryptography (ID-PKC) (Shamir, 1984).
Indeed, CL-PKC dispenses with the use of certificates
and does not suffer from the key escrow problem. In
the context of D2D communications, CL-PKC is an
interesting solution to face the majority of security is-
sues in the above typical scenarios.
Recently, a new certificateless Generalized Sign-
cryption (CLGSC) scheme was proposed in (Zhang
et al., 2017) to secure a multi-hop data transmission
protocol in the context of Mobile-Health system. A
few months later, Zhou pointed out in (Zhou, 2018)
that CLGSC scheme is not secure, particularly in
terms of confidentiality. Consequently, he demon-
strated that CLGSC authors’ Robust Security-Aware
D2D-assist data transmission protocol for Mobile-
Health systems is also insecure. Zhao et al. proposed
in (Zhao et al., 2017) a Trustworthy Device Pairing
to secure D2D-enabled Mobile Crowdsourcing Sys-
tems through D2D communications. The proposed
scheme is based on a CL-PKC framework to gener-
ate collaboratively by the Backend Server (BS) and
registering devices, a pair of a private-public key to
each device. However, their TDP does not consider
the replacement of devices’ public keys by BS espe-
cially as it is considered curious. Furthermore, the
device’s trustworthiness can be adjusted by only the
BS after each transaction according to the device be-
havior. Thus, the proposed solution does not consider
the other scenarios. Authors in (Li et al., 2013) pro-
posed a certificateless authentication key agreement
(CL-AKA) protocol to secure Session Initiation Pro-
tocol with different KGCs. However, there is lack of
public key verification mechanism in their solution.
Through this work, we aim to introduce the CL-
PKC in ProSe environment in order to decentralize
authentication procedures and to face inherent secu-
rity requirements’ conflicts, in the sense that neither
the CNO would be able to profile a ProSe-enabled
UE according to its D2D application preferences nor
the D2D-SP should know the ProSe-enabled UE real
identity. Hence, the proposal of a new CL-AKA pro-
tocol that no longer requires CNO’s coverage. Thus,
our contribution through this paper is summarized as
follows. We propose a new construction of a CL-PKC
system in the case of multiple KGCs and make con-
crete this construction by proposing new certifiacte-
less public key encryption (CL-PKE), signature (CL-
PKS), and CL-AKA schemes applied in a ProSe en-
vironment. We show that these schemes are secure
against a stronger adversary. It should be noted that
the main idea of our approach was presented in our
previous work (Nait Hamoud et al., 2018b). How-
ever, more details and rigorous security analysis are
given in this paper.
The remainder of this paper is organized as fol-
lows. Section 2 summarizes the original model of
CL-PKC system (Al-Riyami and Paterson, 2003). In
Section 3, we introduce our system and security mod-
els. The proposed new CL-PKC system construction
and the related schemes are introduced in Section 4.
In section 5 we give security analysis of our schemes.
Finally, a conclusion is presented in Section 6.
A New Certificateless System Construction for Multiple Key Generator Centers to Secure Device-to-Device Communications
85
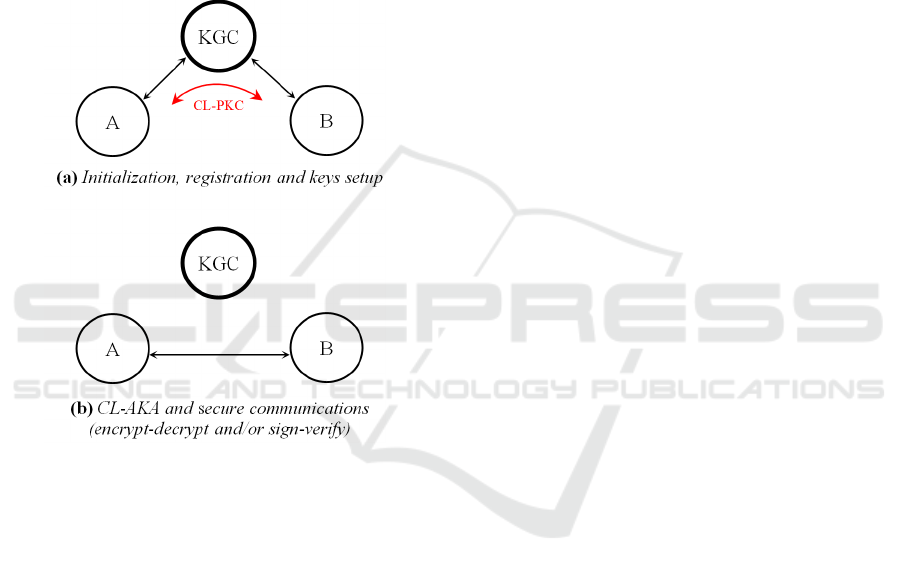
2 CL-PKC: BACKGROUND
Figure 2 shows roughly the main idea of CL-PKC
paradigm (Al-Riyami and Paterson, 2003). Initially, a
CL-PKC system construction is realized through ini-
tialization, registration, and keys setup steps between
three participants: a KGC as a TTP and two commu-
nicating parties A and B (Figure 2a), and thereafter
between only the two communicating parties oppor-
tunistically encountered for authenticated key agree-
ment and secure communications, no matter whether
the KGC is present or not (Figure 2b).
Figure 2: Main idea of a CL-PKC system.
To make concrete their new paradigm, CL-PKC
authors introduced four schemes: CL-PKE, CL-
PKS, CL-AKA, and Hierarchical CL-PKE (HCL-
PKE) schemes. All these schemes are specified
by five common algorithms: Setup, Partial-Private-
Key-Extract, Set-Secret-Value, Set-Private-Key, Set-
Public-Key, and additional algorithms: Encrypt and
Decrypt algorithms in CL-PKE scheme, Sign and Ver-
ify algorithms in CL-PKS scheme. Note that in (Al-
Riyami and Paterson, 2003), authors focus on CL-
PKE showing that a concrete pairing-based CL-PKE
scheme is secure provided that an underlying problem
closely related to the Bilinear Diffie-Hellman Prob-
lem is hard. In the following, we describe briefly the
basic scheme of CL-PKE as shown in Figure 3:
1. Setup: performed by the KGC. It takes as input a
security parameter k and returns the system public
parameters param, the system’s master public key
P
0
and the system’s master private key s.
2. Partial private key extract: for a user A with its
identity ID
A
, the KGC takes params, s and ID
A
as inputs and returns to A, over a confidential and
authentic channel, a partial private key D
A
.
3. Set secret value: a user A takes params, ID
A
and
a random x
A
and outputs its secret value x
A
.
4. Set private key: a user A takes as inputs its partial
private key D
A
, its secret value x
A
and params and
outputs its full private key S
A
.
5. Set public key: a user A takes as inputs its secret
value x
A
and params and outputs its public key
P
A
.
6. Encrypt: a user B, intending to transmit an en-
crypted message to a user A, takes as inputs
params, a message M, A’s public key P
A
and iden-
tity ID
A
and outputs a cipher text C.
7. Decrypt: a user A, receiving an encrypted mes-
sage C, takes as inputs params, C and its private
key S
A
and outputs the message M.
3 SYSTEM AND SECURITY
MODELS
In this section we describe the system model with its
components and the corresponding functions. We de-
scribe also the security model based on the attacker
model.
3.1 System Model
We consider the 3GPP system model which proposed
ProSe as an underlay D2D communications network
of existing LTE-A networks (3GPP, 2014). 3GPP in-
tegrated three specific entities: ProSe Function, ProSe
Application Server and ProSe Application. Figure 4
shows a simplified network architecture for the ProSe
system. But in this system model, we consider that
ProSe function belongs to the CNO while the ProSe
Application Server belongs to a D2D-SP. In the fol-
lowing, we briefly describe these elements.
• ProSe Application is run on ProSe-enabled UE.
• ProSe Function is a logical entity located inside
the Evolved Packet Core (EPC) that belongs to the
CNO. It may provide connections between ProSe
application servers and ProSe-enabled UEs and
acts as a KGC in our new CL-PKC system, and
supports functionalities related to ProSe Applica-
tion server and ProSe-enabled UE Identities (stor-
age, verification, charging, etc.).
SECRYPT 2019 - 16th International Conference on Security and Cryptography
86

Figure 3: Basic scheme of CL-PKE.
• ProSe Application Server is located outside the
EPC and it serves ProSe-enabled UEs requesting
ProSe services. It belongs to the D2D-SP, which
provides authentic content to ProSe-enabled UEs
such as YouTube’s content or a local social net-
work. This content will be shared between other
ProSe-enabled UEs in order to offload cellular
network. The ProSe Application Server acts also
as a KGC in our new CL-PKC system and sup-
ports also functionalities related to ProSe Func-
tion and ProSe-enabled UE Identities (storage,
verification, charging, etc.).
In addition to the existing model, we have
considered a new entity, that we called Regula-
tory Authority (RA) and will detail in Section
4.3. RA supplies the different KGCs with the
appropriate CL-PKC system parameters without a
system wide master key. This is in order to overcome
the malicious but passive KGC problem which we
will detail in Section 3.3.
3.2 Security Requirements
In the following we describe the most important se-
curity requirements that a D2D communications sys-
tem should guarantee while underlining the inherent
conflicting nature of these requirements, particularly
between anonymity, privacy, and traceability:
• Authenticated key agreement (AKA): in order to
secure D2D communications in the three typi-
cal scenarios, especially in the out-of-coverage
scenario, the authentication of any two ProSe-
enabled UE opportunistically encountered in CL-
PKC environment must be carried out based on
public keys presented by each entity.
• Confidentiality: after an AKA is performed be-
tween any two ProSe-enabled UE opportunisti-
cally encountered, their D2D content should be
encrypted by use of a new established symmetric
key.
• Anonymity: refers to the protection of a ProSe-
enabled UE identity to not be linked with other
D2D communication sessions so that a profile
could be defined. It should be noted that ex-
changed data during these sessions are not nec-
essarily encrypted.
• Privacy: through symmetric cryptography, pri-
vacy refers to the ability to keep ProSe-enabled
UE’s sensitive information away from an unau-
thorized entity. It should be noted that ProSe-
enabled UE identity is not necessarily protected.
• Revocability: refers to the ability to reprieve
ProSe-enabled UE’s privilege of a D2D service if
it is detected as malicious or when the commercial
agreement expires.
• Traceability: refers to the ability to keep D2D
communications in check, especially to track the
source of security violation attempts without com-
promising either privacy or anonymity.
3.3 Security Model
In (Al-Riyami and Paterson, 2003), authors adopted
two adversarial models to proof that their CL-PKE
scheme is semantically secure against a fully-adaptive
A New Certificateless System Construction for Multiple Key Generator Centers to Secure Device-to-Device Communications
87
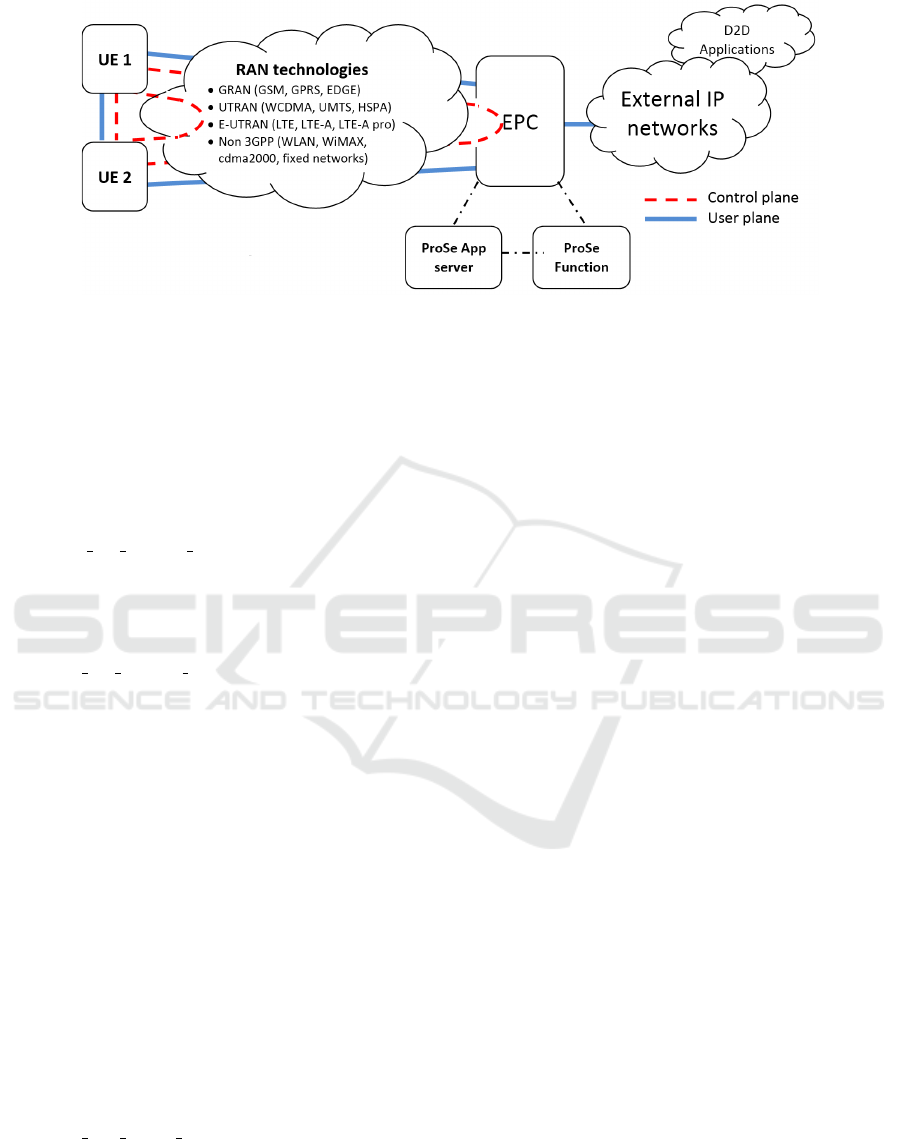
Figure 4: Basic Architecture of the ProSe underlying 3GPP’s EPS.
chosen ciphertext attacker (IND-CCA): Type I adver-
sary which cannot access to the KGC’s master key but
has the ability to replace the public key of all identi-
ties with a value of its choice, and Type II adversary
which can access to the KGC’s master key but may
not replace public keys of the legitimate users. Type
I adversary models an external attacker while Type II
adversary models an internal one. We refer to the later
as curious but passive KGC which might engage in
an adversarial activity such as eavesdropping on ci-
phertexts and making decryption queries.
In 2007, Au et al. proposed for the first
time in (Au et al., 2007) a formal model of
malicious but passive KGC, where the KGC is al-
lowed to generate at the beginning of the system
initialization its master public/secret keys pair mali-
ciously so that it can launch the Type II adversary at-
tack more easily in the later stage of the system by
eavesdropping passively the ciphertexts sent to a user
and trying to decrypt them using its knowledge of the
user partial private key. In their model, the assump-
tion that the KGC is trusted at the beginning of the
setup stage is removed. The KGC may even have al-
ready targeted a particular victim when choosing its
master keys pair.
What if we have a nastier KGC? From our point
of view, if such malicious and curious KGC exists,
nothing can prevent that KGC from being active in
the sense that it is able to replace user’s public keys,
by generating and making available to an illegitimate
user a fake public/private keys pair in order to im-
personate legitimate users. By eliminating any trust
to the KGC, we consider in our security model a
malicious and active KGC which in addition to hav-
ing already been malicious at the beginning of the
setup stage of the system, impersonates a target user
by replacing its public key. That is, the KGC is mali-
cious if it generates its master public/secret keys pair
maliciously in order to derive the user secret value,
and is active if it is able to replace user public key by
generating a fake public/private keys pair for an ille-
gitimate user on behalf of a legitimate user.
Surely, this attack will leave evidence exposing
the KGC’s actions, since detecting two working pub-
lic keys for a legitimate user can only result from the
existence of two partial private keys binding that le-
gitimate user’s identity to these two different public
keys. But in practice, and with the possibility of keys’
revocation, the detection of the existence of such keys
is not obvious especially since the malicious and ac-
tive KGC can temporarily replace an entity’s public
key (whose private key is known) in an attempt to
obtain sensitive information regarding either the user
whose public key has been changed or the user to
whom this encrypted information was sent, and then
resets the true public key. Furthermore, since the very
essence of the introduction of CL-PKC paradigm was
authentication procedures decentralization, hence the
proposal of CL-AKA protocol that no longer requires
infrastructure like that of a PKI, the authentication of
two entities opportunistically encountered in CL-PKC
environment will be carried out based on public keys
presented by each entity.
In order to project the above attacker model to
our system model, neither the CNO nor the D2D-SP
should be trusted. We should consider them as ma-
licious and active KGCs. However, we suppose that
they might not engage in an adversarial activity in a
cooperative way. Thus, we design two attacker mod-
els: insider and outsider attackers. The first one refers
to the CNO or a D2D-SP and the second one refers to
any entity which does not belong to the D2D commu-
nication system.
• Insider attacker: we design our security model
by challenging both the trust between the CNO
and the D2D-SP, and the trust placed by ProSe-
enabled UEs in either the CNO or the D2D-
SP in the sense that, neither CNO would be
SECRYPT 2019 - 16th International Conference on Security and Cryptography
88
able to profile a ProSe-enabled UE according to
its D2D application preferences nor the D2D-SP
should know the real identity of a ProSe-enabled
UE. Thus, insider attacker embodies the well-
known Type II Adversary model but with more
powerful abilities to the point that it becomes
malicious and active KGC.
• Outsider attacker: it embodies the well-known
Type I Adversary model, so other attacks can be
made by UEs which are not ProSe-enabled UEs.
Attackers may compromise both ProSe-enabled UEs
pairing and D2D content. Thus, the potential attacks
that could be conducted by either insider or outsider
attackers are summarized as follows:
1. Eavesdropping attack: typically, it consists in lis-
tening passively the radio channel in order to
get sensitive data. During ProSe-enabled UEs
pairing, this attack could be disastrous for the
key management scheme, since it targets ProSe-
enabled UE’s credentials. On another hand, the
eavesdropper tries to decrypt the encrypted D2D
content.
2. Malicious but passive KGC Attack: it consists
in obtaining the private key of a targeted ProSe-
enabled UE by choosing a generator P and setting
a trapdoor rather than generating a random one
during the establishment of the CL-PKC system
parameters. That chosen P depends on the ProSe-
enabled UE victim’s identity.
3. Signature Forgery Attack: it consists in forging
the D2D content whether during ProSe-enabled
UEs pairing or D2D transactions.
4. Key Compromise Impersonation Attack: it con-
sists in impersonating a legitimate ProSe-enabled
UE B by an attacker to communicate with another
legitimate ProSe-enabled UE A whose long term
private key was learned by that attacker (Li et al.,
2013).
5. Man-In-The-Middle-Attack (MITMA): it consists
in stealthily intercepting and replacing two ProSe-
enabled legitimate UEs’ credentials in order to es-
tablish D2D connections in the middle.
In the next section we detail our new CL-PKC sys-
tem construction for multiple KGCs to secure ProSe.
Considering the presence of multiple KGCs, our ap-
proach is simply the application of the CL-PKE, CL-
PKS, and CL-AKA schemes proposed in (Al-Riyami
and Paterson, 2003), (Huang et al., 2005), and (Li
et al., 2013), respectively, with the appropriate mod-
ifications. Each of the KGCs is assigned by the RA
the same CL-PKC system parameters without a wide
master public key so that it can generate its own pub-
lic/private keys pair. Then, we aggregate these param-
eters so that we define a new logical KGC whose com-
mon public and private keys will be calculated from
KGCs’ public and private keys, respectively. Our pro-
posed CL-PKE and CL-PKS will be detailed in Sec-
tions 4.3, 4.4, and 4.5. As for our CL-AKA, it will be
detailed in Section 4.6.
4 OUR NEW CL-PKC
CONSTRUCTION TO SECURE
D2D COMMUNICATIONS
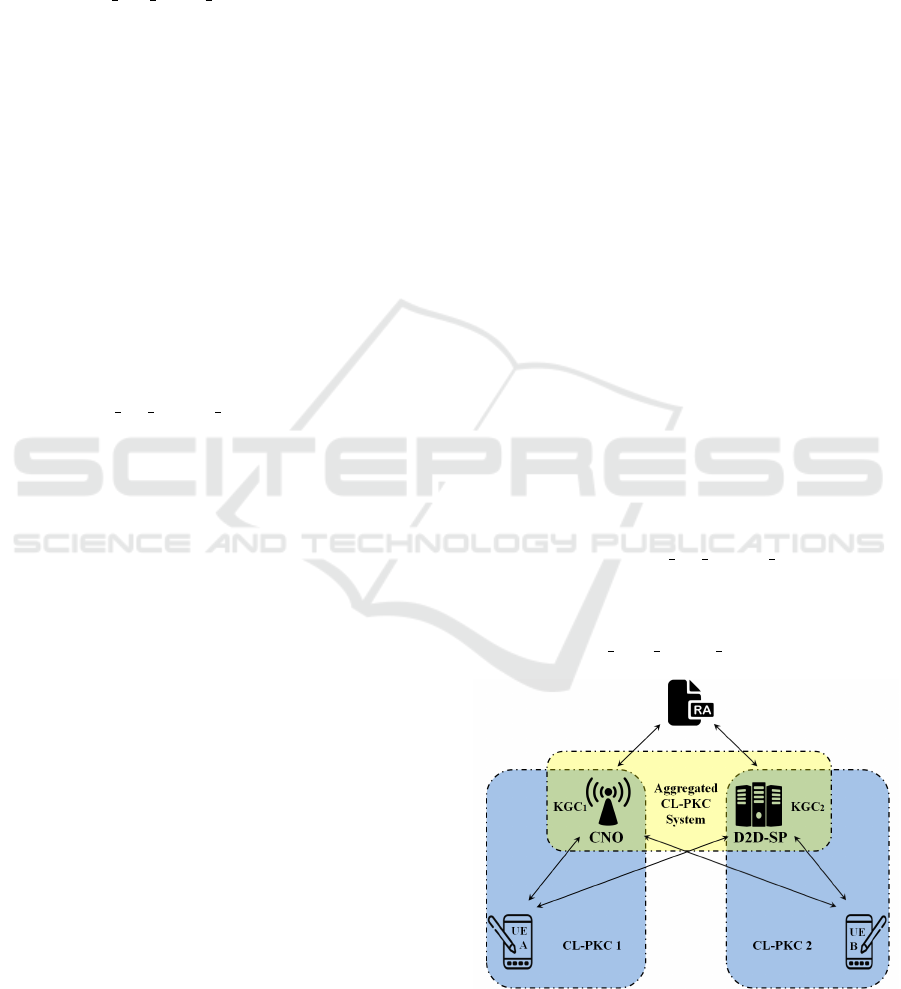
4.1 Overview
Our main idea is to aggregate two CL-PKC systems
parameters into one (Figure 5). This allows, in ad-
dition to struggling security issues in the three typical
scenarios, eliminating the conflicting security require-
ments as mentioned above, particularly, the privacy
against the CNO which should play the role of KGC
1
and anonymity against the D2D-SP which should play
the role of KGC
2
, and to avoid any possible breach
of trust by either KGC
1
or KGC
2
. Furthermore, the
new aggregated CL-PKC system gives different net-
works the opportunity to be compatible and to work
in a cooperative way. On another hand, we have con-
sidered an additional new entity (RA) as a TTP to
overcome the malicious but passive KGC (see Sec-
tion 3.3). Here, the notion of trust concerns only
the CL-PKC system parameters, which are public in
essence, that the RA supplies to the different KGCs
without a system wide master key.
Figure 5: Two CL-PKC system parameters’ aggregation.
A New Certificateless System Construction for Multiple Key Generator Centers to Secure Device-to-Device Communications
89

4.2 Background Definitions
The notations that we use in the rest of the paper are
summarized in Table 1. Let e be a bilinear map. As
mentioned in (Al-Riyami and Paterson, 2003), e will
be derived from either the Weil (Lang, 1987) or Tate
(Frey et al., 1999) pairing on an elliptic curve over a
finite field. Pairing map e’s properties are as follows:
1. Bilinearity: the map e is bilinear if given
Q,W, Z ∈ G
1
, we have e(Q,W + Z) =
e(Q,W).e(Q, Z). As consequence, we have
for any a, b ∈ Z
q
: e(aQ, bW ) = e(Q,W )
ab
=
e(abQ,W) = e(Q, abW ).
2. Non-degeneracy: the map e is non-degenerate if
e(P, P) 6= 1
G2
.
3. Computability: the map e is efficiently com-
putable.
For a more comprehensive description of curves
selection with suitable properties and for a practical
implementation of pairings, we refer to (Galbraith
et al., 2002; Barreto et al., 2002a; Barreto et al.,
2002b).
In the following, we introduce the Bilinear Diffie-
Hellman Problems (BDHP) on which security of our
schemes is based. Given as input < P, aP, bP, cP >∈
G
1
with uniformly random choices of a, b, c ∈ Z
∗
q
:
• Computational BDHP (CBDHP): output
e(P, P)
abc
∈ G
2
.
• Generalized BDHP (GBDHP): output a pair <
Q ∈ G
∗
1
, e(P, Q)
abc
∈ G
2
>.
• Decisional BDHP (DBDHP): given also h ∈ G
2
,
output whether or not h = e(P, P)
abc
.
• Gap BDHP (GapBDHP): given also DBDH or-
acle that is able to decide whether a tuple <
P, aP, bP, cP,h > satisfies h = e(P, P)
abc
or not,
output e(P, P)
abc
.
For further details and a comprehensive descrip-
tion of these mathematical problems, we refer to
(Cheon and Lee, 2002).
4.3 System Initialization
As mentioned in Section 3.1, we consider here an
additional entity, that we call Regulatory Authority
(RA), which is responsible only for generating the
parameters of our CL-PKC system without a master
public key as it was done traditionally, and this to
avoid the malicious
but passive KGC. RA will pro-
vide the different KGCs with the appropriate param-
eters of a CL-PKC system so that they can choose
separately their sub-master public/secret keys pair as
a first step, and then agree on a common public key re-
lated to the new aggregated CL-PKC system, whose
private key could only be defined if they agree to ex-
change their secret keys (which we suppose impossi-
ble since they have conflict of interest).
• Init: This algorithm is executed by RA. Let
G
1
and G
2
be an additive and a multiplica-
tive groups with a large prime order q, respec-
tively. e is a pairing map. Let H
1
, H
2
, H
3
, H
4
and H
5
be cryptographic hash functions. Let
P ∈ G
1
a random generator and S the sig-
nature space. The system parameters are
params =< G
1
, G
2
, e, n, P, H
i
, M , C , S >, where
i ∈ {1, .., 5}. It is worth stressing that a system’s
master public key P
0
is missing at this stage com-
pared to original work (Al-Riyami and Paterson,
2003). It will be calculated later by the different
KGCs based on their public keys sub public keys
and their secret keys sub master keys.
• Setup: This algorithm is executed by the dif-
ferent KGCs: the CNO as KGC
1
and the
D2D-SP as KGC
2
, to agree on the common
public key P
0
. Each of them chooses ran-
domly its sub master key : s
1
and s
2
, respec-
tively (s
1
, s
2
∈ Z
∗
q
). Using params, they calcu-
late their sub public keys : P
01
= s
1
P and P
02
=
s
2
P, respectively. After exchanging their respec-
tive sub public keys, they calculate the common
public key P
0
= P
01
+ P
02
= (s
1
+ s
2
)P = sP
which represents the public key of the new ag-
gregated CL-PKC system parameters. The corre-
sponding logical master key: s = s
1
+ s
2
remains
unknown for both KGCs which publish their
CL-PKC system parameters params
KGC
i
=<
params, P
0i
, P
0
>, respectively, where i = 1, 2.
4.4 Registration
Let ProSe-enabled UE A with identifier ID
A
performs
two registrations to the different KGCs. As a re-
sult, ProSe-enabled UE A sets up two pairs of pub-
lic and private keys: (P
A1
, S
A1
) based on KGC
1
’s
CL-PKC system parameters, and (P
A2
, S
A2
) based on
KGC
2
’s CL-PKC system parameters. Once the public
and private keys are established, ProSe-enabled UE
A aggregates the two public keys into one public key
P
A
= P
A1
+ P
A2
and the two private keys into one pri-
vate key S
A
= S
A1
+S
A2
. In the following, we give the
appropriate algorithms:
• Set-secret-Value: This algorithm is executed by
ProSe-enabled UE A. It takes as inputs A’s iden-
tifier ID
A
∈ {0, 1}
∗
and params
KGC
i
(i = 1, 2).
Then, it outputs x
A
∈ Z
∗
q
as a random secret value.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
90
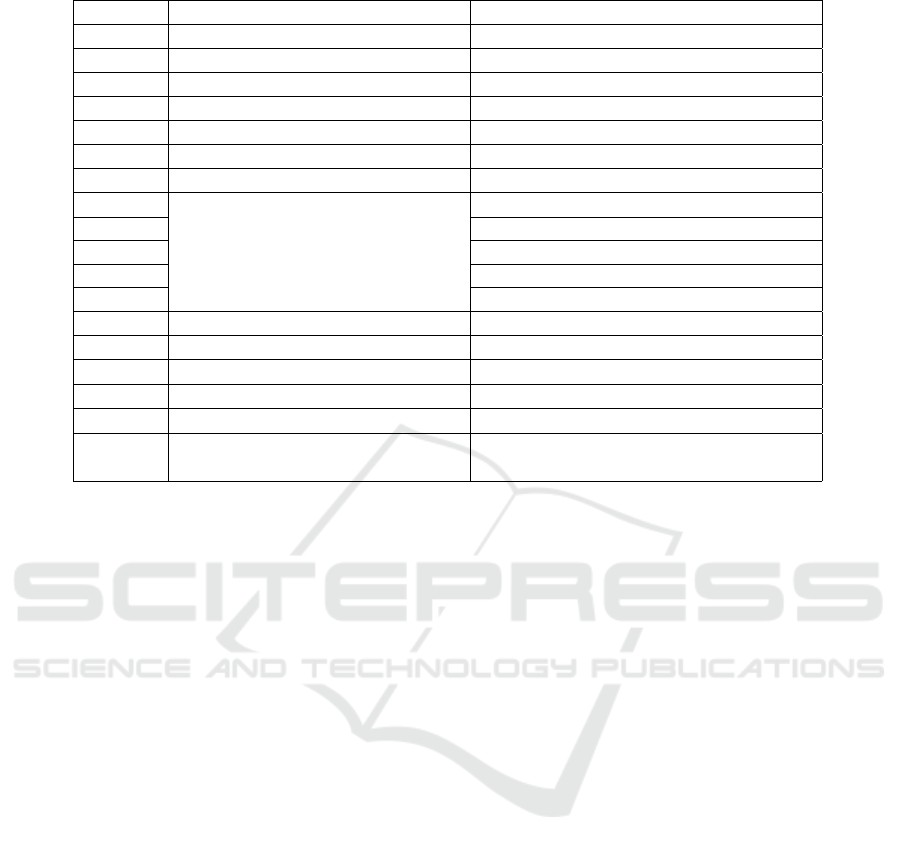
Table 1: Notations and Definitions.
Notation
Meaning Definition
k security parameter
k > 1
q large prime order
-
n bit-length of plain-texts
n ≈ log
2
q
G
1
additive group of order q
-
G
2
multiplicative group of order q
-
e pairing map
e : G
1
× G
1
→ G
2
P a random generator
P ∈ G
1
H
1
cryptographic hash functions
H
1
: {0, 1}
∗
→ G
∗
1
H
2
H
2
: G
2
→ {0, 1}
n
H
3
H
3
: {0, 1}
n
× {0, 1}
n
→ Z
∗
q
H
4
H
4
: {0, 1}
n
→ {0, 1}
n
H
5
H
5
: {0, 1}
∗
× G
2
→ Z
∗
q
M message space
M = {0, 1}
n
C ciphertext space
C = G
1
× {0, 1}
n
S signature space
S = G
1
× Z
∗
q
ID
A
ProSe-enabled UE A’s identifier
ID
A
∈ {0, 1}
∗
x
A
ProSe-enabled UE A’s secret value
x
A
∈ Z
∗
q
params CL-PKC system parameters
params =< G
1
, G
2
, e, n, P, H
i
, M , C , S >
i ∈ {1, .., 5}
• Set-public-Key: This algorithm is executed
by ProSe-enabled UE A. It takes as inputs
params
KGC
i
(i = 1, 2) and A’s secret value x
A
.
Firstly, it checks that the equality P
0
= P
01
+ P
02
holds. If not, it aborts the algorithm. Otherwise,
it calculates A’s sub public keys P
A1
and P
A2
, and
then the ProSe-enabled UE A’s aggregated public
key P
A
=< X
A
,Y
A
> as follows:
P
A1
=< X
A
= x
A
P,Y
A1
= x
A
P
01
= x
A
s
1
P >
P
A2
=< X
A
= x
A
P,Y
A2
= x
A
P
02
= x
A
s
2
P >
P
A
=< X
A
,Y
A1
+Y
A2
>=< X
A
, x
A
(P
01
+ P
02
) >
=< X
A
, x
A
(s
1
+ s
2
)P >=< X
A
, x
A
P
0
>.
• Set-partial-Private-key: This algorithm is exe-
cuted by each KGC
i
(i = 1, 2). It takes as input
ID
A
and outputs A’s sub partial private key D
Ai
=
s
i
Q
A
, where Q
A
= H
1
(ID
A
) ∈ G
∗
1
, and transmits
D
Ai
to A through an authentic and secure channel.
• Set-private-Key: This algorithm is executed by
ProSe-enabled UE A. It takes as inputs: params,
A’s sub partial private keys D
Ai
and A’s secret
value x
A
. Then, it verifies the correctness of these
sub partial private keys by checking if the equality
e(D
Ai
, P) = e(Q
A
, P
0
) holds. If not, it aborts the
algorithm. Otherwise, it computes A’s sub private
keys S
A1
and S
A2
∈ G
∗
1
and then the aggregated
private key S
A
by following these steps:
S
A1
= x
A
D
A1
= x
A
s
1
Q
A
S
A2
= x
A
D
A2
= x
A
s
2
Q
A
S
A
= S
A1
+ S
A2
= x
A
(s
1
+ s
2
)Q
A
= x
A
sQ
A
.
4.5 Main Cryptographic Operations
After the system initialization and the registration
steps, any ProSe-enabled UEs A and B can perform
the following cryptographic operations:
• Encrypt: This algorithm is executed by any
ProSe-enabled UE aiming to send an encrypted
message M for ProSe-enabled UE A with identi-
fier ID
A
∈ {0, 1}
∗
and public key P
A
=< X
A
,Y
A
>.
First, the sender checks the validity of A’s pub-
lic key by verifying that X
A
,Y
A
∈ G
∗
1
and that
the equality e(X
A
, P
0
) = e(Y
A
, P) holds. If not,
it cancels encryption. Second, the sender com-
putes Q
A
= H
1
(ID
A
) ∈ G
∗
1
, and chooses a random
σ ∈ {0, 1}
n
to calculate r = H
3
(σ, M). Finally, it
computes the ciphertext:
C =< U,V,W >
=< rP, σ ⊕ H
2
(e(Q
A
,Y
A
)
r
), M ⊕ H
4
(σ) >.
• Decrypt: This algorithm is executed by ProSe-
enabled UE A. To decrypt an encrypted message
M using its private key S
A
, ProSe-enabled UE A
computes: σ
0
= V ⊕ H
2
(e(S
A
,U)), then computes
the decryption of the ciphertext C as: M
0
= W ⊕
H
4
(σ
0
).
To verify the correctness of M, it sets r
0
=
H
3
(σ
0
, M
0
) and test if equation U = r
0
P holds.
• Sign: This algorithm is executed by ProSe-
enabled UE A aiming to send a signed mes-
sage M using its private key S
A
. First, ProSe-
A New Certificateless System Construction for Multiple Key Generator Centers to Secure Device-to-Device Communications
91

enabled UE A chooses random a ∈ Z
∗
q
, and com-
putes r = e(aP, P) ∈ G
2
. Then it sets v =
H
5
(M, r, e(S
A
, P)) ∈ Z
∗
q
, and computes U = vS
A
+
aP ∈ G
1
. Finally, the algorithm outputs the signa-
ture < U, v >.
• Verify: To verify a signature < U, v > on a mes-
sage M from ProSe-enabled UE A with iden-
tity ID
A
and public key P
A
=< X
A
,Y
A
>, ProSe-
enabled UE B checks the validity of P
A
, and
computes r
0
= e(U, P).e(Q
A
, −Y
A
)
v
. If the equa-
tion v = H(M, r
0
, e(Q
A
,Y
A
)) holds, the signature is
valid.
Notice that Encrypt and Decrypt algorithms are iden-
tical to the provably secure encryption and decryp-
tion algorithms in the FullCL − PKE in (Al-Riyami
and Paterson, 2003), and that Sign and Verify algo-
rithms are also identical to those specified in (Huang
et al., 2005). We did not place any reliance on the CL-
PKS scheme introduced in (Al-Riyami and Paterson,
2003) because of its insecurity as it was pointed out
and proofed in (Huang et al., 2005).
Formally, our CL-PKE and CL-PKS schemes
are specified by the above five common algorithms:
Setup, Partial-Private-Key-Extract, Set-Secret-Value,
Set-Private-Key, Set-Public-Key, and the above four
additional algorithms: Encrypt and Decrypt for the
CL-PKE scheme, and Sign and Verify algorithms for
the CL-PKS scheme.
4.6 User Equipment Pairing
After performing the registration step (Section 4.4),
any two ProSe-enabled UEs opportunistically en-
countered execute our CL-AKA scheme as follows.
Firstly, they exchange their public keys for verifi-
cation and authentication. And after, they establish
common credentials for their secure D2D communi-
cations.
Let ProSe-enabled UEs A and B with their re-
spective pairs of public/private keys < P
A
, S
A
> and
< P
B
, S
B
>, be the intended participants in the pair-
ing step. First, each of them chooses random values
a, b ∈ Z
∗
q
and calculates T
A
= aP and T
B
= bP, respec-
tively. After exchanging their triplets < ID
A
, P
A
, T
A
>
and < ID
B
, P
B
, T
B
>, both of them verify that the
equality e(X
UE
, P
0
) = e(Y
UE
, P) where U E ∈ {A, B}
holds in order to check the validity of each others’
public key. Finally, they may calculate the following
possible symmetric keys:
• K
1
AB
= e(D
A
, X
B
+ T
B
) = K
1
BA
= e(Q
A
, P
0
)
(x
B
+b)
• K
2
AB
= e(Q
B
, P
0
)
(x
A
+a)
= K
2
BA
= e(D
B
, X
A
+ T
A
)
• K
3
AB
= x
A
X
B
= K
3
BA
= x
B
X
A
• K
4
AB
= x
A
T
B
= K
4
BA
= x
B
T
A
• K
5
AB
= aT
B
= K
5
BA
= bT
A
• K
6
AB
= aX
B
= K
6
BA
= bX
A
• K
7
AB
= e(Q
B
,Y
B
)
a
.e(S
A
, T
B
) =
K
7
BA
= e(Q
A
,Y
A
)
b
.e(S
B
, T
A
).
Let k be the session key as in (Li et al., 2013):
k = H
1
(ID
A
|ID
B
|P
A
|P
B
|T
A
|T
B
|K
1
AB
|K
2
AB
|K
4
AB
|K
5
AB
).
5 SECURITY ANALYSIS
In this section, we analyze the different security re-
quirements and prove the resistance of our system
against well known attacks. First, we briefly dis-
cuss the security of FullCL − PKE (Al-Riyami and
Paterson, 2003), CL − PKS (Huang et al., 2005) and
CL − AKA (Li et al., 2013) which are utilized in the
proposed aggregating CL-PKC system. Later, we
discuss how the proposed aggregating CL-PKC sys-
tem achieves our security goals. The FullCL − PKE
(Al-Riyami and Paterson, 2003) and the CL − PKS
(Huang et al., 2005) provide confidentiality (as in-
distinguishability against adaptive chosen ciphertext
attack (IND-CCA)) and unforgeability for encrypted
and signed messages, respectively. These security
requirements are based on the intractability of the
GBDH and ECDH problems, respectively. That is,
it is impossible to expose or forge the full private
key of a ProSe-enabled UE based on the difficulty of
GBDH and ECDH problems, without the knowledge
of both KGC’s sub-master private keys and ProSe-
enabled UE’s secret value. As for CL−AKA (Li et al.,
2013), it is provably secure against a fully adaptive
adversary in the random oracle model, provided that
the underlying problem of Gap BDHP is hard. Fur-
ther details on security proofs are provided in (Al-
Riyami and Paterson, 2003; Huang et al., 2005; Li
et al., 2013).
5.1 Illustrative Scenario of a D2D
Application
Although D2D communications can take advantage
from key management scheme already available in
LTE-A, our solution is proposed independently from
the existing one in order to achieve more and higher
security levels, particularly to avoid any possible
breach of trust by a TTP and to face the inherent con-
flicting security requirements.
Below we give a practical example of a D2D sce-
nario to effectively analyze our new CL-PKC system
construction and the related schemes. Let RA be a
SECRYPT 2019 - 16th International Conference on Security and Cryptography
92

regulatory authority in a country, CNO and D2D-SP
foreign investors in this country such as the CNO
supports ProSe environment and the D2D-SP pro-
vides authentic videos to ProSe-enabled UE such as
YouTube’s content through a set of D2D domain ap-
plications.
The initialization and setup of our CL-PKC sys-
tem is performed by the RA through the execution
of Init algorithm and both the CNO and the D2D-
SP through the execution of Setup algorithm, respec-
tively (Section 4.3). Let A be the real identity of a
UE which aims to benefit from the ProSe and D2D
domain applications. First, it registers to RA in order
to get a pseudo-identity ID
A
. Thereafter, it registers
to both CNO and D2D-SP with that pseudo-identity
through the execution of registration algorithms (Sec-
tion 4.4): Set − secret − value, Set − public − key,
Set − partial − private− key and Set − private− key.
At this point to the registration process, A becomes
a ProSe-enabled UE and can benefit from either the
D2D domain applications and ProSe.
Once the CL-PKC system is established, the D2D-
SP send new authentic videos to ProSe-enabled UEs
so that they can share them with other ProSe-enabled
UEs through D2D communications in order to offload
the cellular network. A’s ProSe-enabled UE download
a new video through the appropriate D2D application
and share it to any other ProSe-enabled UE B oppor-
tunistically encountered. But before that, our CL-
AKA scheme must be performed by the concerned
ProSe-enabled UEs in the pairing step (Section 4.6).
5.2 Resistance against Malicious but
Passive KGC Attack
In our system model (Section 3.1), RA does not pro-
vide the different KGCs a common public key P
0
through its CL-PKC system parameters params as
it was done traditionally. This was considered par-
ticularly as responsibility decentralization in terms
of security between RA and the two KGCs so that
the malicious but passive KGC could not exist. By
eliminating any trust to the different KGCs, we have
avoided this attack by entrusting the generation of
CL-PKC parameters, especially the random generator
P to the RA rather than entrusting it to the KGCs. Of
course, nothing can prevent RA from mounting such
an attack, but we have considered that RA is trustful
and is external from the system (Figure 5).
5.3 Resistance against Malicious and
Active KGC Attack
Firstable, and according to Theorem 1 in (Al-Riyami
and Paterson, 2003), it is trivial to show that our CL-
PKE is IND-CCA secure against standard adversarial
type I and type II models, which follows directly from
the employment of the FullCL − PKE (Al-Riyami
and Paterson, 2003). We are only left with the proof
of our CL-PKE against a malicious-and-active KGC
(CNO or D2D server provider) which, in addition
to replacing the secret values of legitimate ProSe-
enabled UEs with values of its choice, replaces also
the long-term legitimate ProSe-enabled UEs’ public
keys.
Thanks to the aggregation technique of two CL-
PKC system parameters, we have been able to de-
fine another set of aggregated parameters, notably the
master public key of the system whose correspond-
ing master private key is not explicitly defined, hence
not known by both KGCs. This means that even if
both KGCs are malicious-and-active, and may there-
fore engage in a malicious and active KGC attack,
they can not impersonate a legitimate ProSe-enabled
UE. This is mainly because ProSe-enabled UE’s par-
tial private key is dependent on the two KGC master
secrets: D
A
= (s
1
+ s
2
)Q
A
. In other words, it is im-
possible to expose or forge the aggregated master key
s of our CL-PKC system based on the difficulty of
CBDHP, without the knowledge of both KGC’s sub-
master private keys s
1
and s
2
. Of course, nothing
can prevent the two KGCs from exchanging their sub-
master private keys, but this is not obvious especially
in the presence of a conflict of interest between them.
5.4 Resistance against Signature
Forgery Attack
According to Theorem 3 in (Huang et al., 2005), it
is also trivial to show that our CL-PKS is unforge-
able against standard type I adversary model which
follows directly from the employment of CL − PKS
(Huang et al., 2005). We are only left with the proof
of our CL-PKS against a malicious-and-active KGCs.
Here, also thanks to the aggregation technique of two
CL-PKC system parameters, no one of both KGCs
could forge the signature of any ProSe-enabled UE as
it was defined in (Huang et al., 2005).
5.5 Resistance against MITMA
Generally, key agreement protocols suffer from
MITMA which consists in replacing the secret val-
ues of legitimate participants with values of the at-
A New Certificateless System Construction for Multiple Key Generator Centers to Secure Device-to-Device Communications
93

tacker’s choice. As a consequence, an attacker can
impersonate both legitimate participants, and the se-
cret key that was to be secret does not become so. Un-
der a malicious and active KGC, CL-AKA in (Al-
Riyami and Paterson, 2003) and any scheme sharing
the same key structure and generation procedures as
that of (Al-Riyami and Paterson, 2003) are vulnerable
to such an attack even if the pairs of public and private
keys are generated by binding a ProSe-enabled UE’s
public key to its identity. This is possible if a KGC, in
addition to replacing the secret values of legitimate
participants with values of its choice, replaces also
the long-term legitimate participants’ public keys. In
our CL-AKA, a malicious and active KGC cannot
mount such an attack since the aggregated master key
s = s
1
+s
2
is implicitly defined based on the two KGC
master secrets. That is, it is impossible to expose
or forge the aggregated master key s based on the
difficulty of CBDHP, without the knowledge of both
KGC’s sub-master private keys s
1
and s
2
.
Furthermore, according to Theorem 1, 2, 3, and
4 in (Li et al., 2013), our proposed CL-AKA is se-
cure against all known attacks to an authenticated
key agreement protocol providing that the underlying
GapBDHP is hard.
5.6 Key Compromise Impersonation
Attack
Unlike the work of (Li et al., 2013), our CL-AKA
is KCI resistant not only because the attacker cannot
compute K
2
AB
= e(Q
B
, P
0
)
(x
A
+a)
= K
2
BA
= e(D
B
, X
A
+
T
A
) since he/she does not have neither the value a cho-
sen from A nor the value D
B
owned by B, but our CL-
AKA immediately resists KCI attack when checking
the attacker’s public key validity. That is, in (Li et al.,
2013) the public key of an entity A is P
A
= x
A
P, so
there is no way to check and authenticate it. How-
ever in ours the public key P
A
=< X
A
, X
A
>, as in the
original scheme (Al-Riyami and Paterson, 2003), has
two parts X
A
= x
A
P and Y
A
= x
A
sP. The second part
is considered as the KGC’s signature which permits
to any entity to authenticate A by verifying that the
equation e(X
A
, P
0
) = e(Y
A
, P) holds.
5.7 Eliminating Conflicting Security
Requirements
As mentioned in Section 1, a security requirement
conflict can usually arise when anonymity and trace-
ability are simultaneously required of a central au-
thority. In our context, this was solved by decentral-
izing responsibility between multiple entities to re-
spond the fully mistrust assumption regarding a TTP.
Through our system model, RA can play another role
as a registration entity which provides ProSe-enabled
UE A the pseudo-identity ID
A
and keeping its real
identity secret. Thus, in the proposed schemes both
the CNO and the D2D-SP have not access to the A’s
real identity, hence anonymity is guaranteed. How-
ever, this anonymity remains conditional such that
misbehaving entities in the network remain traceable.
This traceability is guaranteed cooperatively by both
the RA on one hand and the CNO and the D2D-SP on
the other hand, this is in order to detect misbehaving
entities through their pseudo-identities. Further secu-
rity mechanisms can be incorporated to the proposed
CL-PKC construction so that the CNO or the D2D-
SP could report security violation to the RA if such
a violation necessitates to reveal the real identity of a
user.
6 CONCLUSION
We proposed in this paper a new CL-PKC system
construction for multiple KGCs to secure D2D com-
munications based on aggregating two KGCs’ sys-
tem parameters into one. This has multiple advan-
tages since the common public key can be calcu-
lated and published by both KGCs while the com-
mon private key remains unknown and implicitly de-
fined. That is, the common private key could be re-
vealed only if the concerned KGCs exchange their
sub-private keys assuming the intractability of CB-
DHP. The main advantage consists in preventing the
CL-PKC system from a stronger adversary which is a
malicious and active KGC. Another advantage con-
sists in giving different networks the opportunity to
be compatible and to work cooperatively. To make
concrete the proposed construction, we proposed also
a new CL-PKE, CL-PKS, and CL-AKA schemes ap-
plied in ProSe environment. The proposed schemes
overcome security issues in all scenarios, particularly
in out o f coverage scenario where any two ProSe-
enabled UEs opportunistically encountered can au-
thenticate each other based on their respective public
keys, Thereafter, they establish a common session key
to encrypt their D2D traffic.
REFERENCES
3GPP (February 2014). Study on architecture enhance-
ments to support proximity services (ProSe) (Rel. 12).
Technical Report (TR) 23.703, 3rd Generation Part-
nership Project (3GPP). V12.0.0.
3GPP (June 2013). Feasibility study for proximity services
SECRYPT 2019 - 16th International Conference on Security and Cryptography
94

(ProSe) (Rel. 12). Technical Report (TR) 22.803, 3rd
Generation Partnership Project (3GPP). V1 2.2.0.
Al-Riyami, S. S. and Paterson, K. G. (2003). Certificateless
public key cryptography. In Advances in Cryptology
- ASIACRYPT 2003, 9th International Conference on
the Theory and Application of Cryptology and Infor-
mation Security, Taipei, Taiwan, November 30 - De-
cember 4, 2003, Proceedings, pages 452–473.
Alkubaisy, D. (2017). A framework managing conflicts
between security and privacy requirements. In 11th
International Conference on Research Challenges in
Information Science, RCIS 2017, Brighton, United
Kingdom, May 10-12, 2017, pages 427–432.
Au, M. H., Mu, Y., Chen, J., Wong, D. S., Liu, J. K., and
Yang, G. (2007). Malicious kgc attacks in certificate-
less cryptography. In Proceedings of the 2Nd ACM
Symposium on Information, Computer and Communi-
cations Security, ASIACCS ’07, pages 302–311, New
York, NY, USA. ACM.
Barreto, P. S. L. M., Kim, H. Y., Lynn, B., and Scott, M.
(2002a). Efficient algorithms for pairing-based cryp-
tosystems. IACR Cryptology ePrint Archive, 2002:8.
Barreto, P. S. L. M., Lynn, B., and Scott, M. (2002b). Con-
structing elliptic curves with prescribed embedding
degrees. In Security in Communication Networks,
Third International Conference, SCN 2002, Amalfi,
Italy, September 11-13, 2002. Revised Papers, pages
257–267.
Cheon, J. H. and Lee, D. H. (2002). Diffie-hellman prob-
lems and bilinear maps. IACR Cryptology ePrint
Archive, 2002:117.
Ferrag, M. A., Maglaras, L., and Ahmim, A. (2017).
Privacy-preserving schemes for ad hoc social net-
works: A survey. IEEE Communications Surveys Tu-
torials, 19(4):3015–3045.
Frey, G., M
¨
uller, M., and R
¨
uck, H. (1999). The tate
pairing and the discrete logarithm applied to elliptic
curve cryptosystems. IEEE Trans. Information The-
ory, 45(5):1717–1719.
Galbraith, S. D., Harrison, K., and Soldera, D. (2002). Im-
plementing the tate pairing. In Algorithmic Number
Theory, 5th International Symposium, ANTS-V, Syd-
ney, Australia, July 7-12, 2002, Proceedings, pages
324–337.
Haus, M., Waqas, M., Ding, A. Y., Li, Y., Tarkoma, S.,
and Ott, J. (2017). Security and privacy in device-to-
device (d2d) communication: A review. IEEE Com-
munications Surveys Tutorials, 19(2):1054–1079.
Hsu, R., Lee, J., Quek, T. Q. S., and Chen, J. (2018). Graad:
Group anonymous and accountable d2d communica-
tion in mobile networks. IEEE Transactions on Infor-
mation Forensics and Security, 13(2):449–464.
Huang, X., Susilo, W., Mu, Y., and Zhang, F. (2005). On
the security of certificateless signature schemes from
asiacrypt 2003. In Cryptology and Network Security,
4th International Conference, CANS 2005, Xiamen,
China, December 14-16, 2005, Proceedings, pages
13–25.
Lang, S. (1987). Elliptic Functions, volume 12. Springer,
New York, NY.
Li, X., Zhang, Y., and Zhang, G. (2013). A new certifi-
cateless authenticated key agreement protocol for SIP
with different kgcs. Security and Communication Net-
works, 6(5):631–643.
Nait Hamoud, O., Kenaza, T., and Challal, Y. (2018a). Se-
curity in device-to-device communications: a survey.
IET Networks, 7(1):14–22.
Nait Hamoud, O., Kenaza, T., and Challal, Y. (2018b).
Towards using multiple KGC for CL-PKC to secure
D2D communications. In 2018 International Confer-
ence on Smart Communications in Network Technolo-
gies (SaCoNeT), pages 283–287.
Paja, E., Dalpiaz, F., and Giorgini, P. (2013). Managing
security requirements conflicts in socio-technical sys-
tems. In Conceptual Modeling - 32th International
Conference, ER 2013, Hong-Kong, China, November
11-13, 2013. Proceedings, pages 270–283.
Shamir, A. (1984). Identity-based cryptosystems and signa-
ture schemes. In Advances in Cryptology, Proceedings
of CRYPTO ’84, Santa Barbara, California, USA, Au-
gust 19-22, 1984, Proceedings, pages 47–53.
Sun, J., Zhang, C., Zhang, Y., and Fang, Y. (2011). Sat: A
security architecture achieving anonymity and trace-
ability in wireless mesh networks. IEEE Transactions
on Dependable and Secure Computing, 8(2):295–307.
Tehrani, M. N., Uysal, M., and Yanikomeroglu, H. (2014).
Device-to-device communication in 5g cellular net-
works: challenges, solutions, and future directions.
IEEE Communications Magazine, 52(5):86–92.
Wang, M. and Yan, Z. (2015). Security in d2d com-
munications: A review. In 2015 IEEE Trust-
com/BigDataSE/ISPA, volume 1, pages 1199–1204.
Zhang, A., Wang, L., Ye, X., and Lin, X. (2017).
Light-weight and robust security-aware d2d-assist
data transmission protocol for mobile-health sys-
tems. IEEE Trans. Information Forensics and Secu-
rity, 12(3):662–675.
Zhao, C., Yang, S., Yang, X., and McCann, J. A. (2017).
Rapid, user-transparent, and trustworthy device pair-
ing for d2d-enabled mobile crowdsourcing. IEEE
Trans. Mob. Comput., 16(7):2008–2022.
Zhou, C. (2018). Comments on “light-weight and robust
security-aware d2d-assist data transmission protocol
for mobile-health systems”. IEEE Transactions on In-
formation Forensics and Security, 13(7):1869–1870.
A New Certificateless System Construction for Multiple Key Generator Centers to Secure Device-to-Device Communications
95
