Quantitative Metrics for Mutation Testing

Amani Ayad

, Imen Marsit

, JiMeng Loh

, Mohamed Nazih Omri

and Ali Mili

1 a

NJIT, Newark NJ, U.S.A.

MARS Laboratory, University of Sousse, Tunisia

Keywords:

Mutation Testing, Software Metrics, Equivalent Mutants, Redundant Mutants, Mutation Score.

Abstract:

Mutant generation is the process of generating several variations of a base program by applying elementary

modiﬁcations to its source code. Mutants are useful only to the extent that they are semantically distinct

from the base program; the problem of identifying and weeding out equivalent mutants is an enduring issue

in mutation testing. In this paper we take a quantitative approach to this problem where we do not focus on

identifying equivalent mutants, but rather on gathering quantitative information about them.

1 EQUIVALENT MUTANTS: AN

ENDURING NUISANCE

Mutation testing is a long-standing technique in soft-

ware testing research, and is ﬁnding its way into ﬁeld

practice; it consists of generating a set of variants of a

base program by applying standard atomic changes

to the source code of the program. In (Papadakis

et al., 2019), Papadakis et al. present a sweeping sur-

vey of mutation testing, starting from its emergence

in the late seventies to the present; they analyze the

evolution of the level of interest in mutation testing,

as reﬂected by the number of publications that ap-

pear in relevant venues. They also survey the various

applications of mutation testing, the tools of mutant

generation, the extensions of the mutation concept to

other software artifacts, and the main technical chal-

lenges of mutation testing. Interestingly, they cite the

problem of equivalent mutants and redundant mutants

(two aspects we will address in this paper) among the

research questions that remain largely unresolved.

Mutants are used for a wide range of purposes

in software testing, and are useful only to the extent

that they are semantically distinct from the base pro-

gram; but it is very common for mutants to be seman-

tically equivalent to the base program, despite being

syntactically distinct. Equivalent mutants are a ma-

jor nuisance in mutation testing because they intro-

duce a signiﬁcant amount of bias in mutation-based

analysis. Consequently, much research has been de-

voted to the identiﬁcation of equivalent mutants in

https://orcid.org/0000-0002-6578-5510

a pool of mutants generated from a base program

by some mutation generation policy (Offut and Pan,

1997; Yao et al., 2014; Inozemtseva and Holmes,

2014; Aadamopoulos et al., 2004; Papadakis et al.,

2014; Schuler and Zeller, 2010; Just et al., 2013b;

Nica and Wotawa, 2012; Delamaro et al., 2001; An-

drews et al., 2005; Namin and Kakarla, 2011; Just

et al., 2014b; Gruen et al., 2009; Just et al., 2013a;

Just et al., 2014a; Kintis et al., 2018; Wang et al.,

2017; Hierons et al., 1999; Carvalho et al., 2018). At

its core, the detection of equivalent mutants consists

in analyzing a base program (say P) and a mutant (say

M) to determine whether P and M are semantically

equivalent, while they are (by construction) syntacti-

cally distinct. This is clearly a very difﬁcult problem,

since it relies on a detailed semantic analysis of P and

M; if we knew how to perform a detailed semantic

analysis of P alone (let alone P and M) we could prob-

ably determine whether P is correct, and do away with

testing altogether. In the absence of a simple, gen-

eral, practical solution, researchers have resorted to

approximate solutions and heuristics. These include,

for example, inferring equivalence from a local analy-

sis of P and M in the neighborhood of the mutation(s);

this produces sufﬁcient but unnecessary conditions,

hence leads to a loss of recall; deﬁnite equivalence re-

quires, inconveniently, that we analyze the programs

in full. Other approaches include overapproximations

and comparison of the programs’ functions (through

slicing) or the programs’ dynamic behavior (through

execution traces); these approaches yield necessary

but insufﬁcient conditions of equivalence, hence lead

to a loss of precision.

Ayad, A., Marsit, I., Loh, J., Omri, M. and Mili, A.

Quantitative Metrics for Mutation Testing.

DOI: 10.5220/0007841800490059

In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 49-59

ISBN: 978-989-758-379-7

It is fair to claim that despite several decades of

research, there is no general, simple, scalable solu-

tion for dealing with equivalent mutants in mutation

testing.

2 A QUANTITATIVE APPROACH

The problem of equivalent mutants takes many forms

in mutation testing, including:

• Mutant Equivalence. When we generate, say 100

mutants of some program P, and we want to check

whether some test data T can detect (kill) all the

mutants, we ought to consider only those mutants

that are not equivalent to P; indeed the mutants

that are semantically equivalent to P cannot be

detected (killed) regardless of how adequate test

data set T is. In this paper we deﬁne a function we

call REM (Ratio of Equivalent Mutants) to capture

the ratio of equivalent mutants that a program P is

prone to generate, for a given mutant generation

policy.

• Mutant Redundancy. Let us assume that out of

the 100 mutants we have generated, we have de-

termined that 80 are not equivalent to P; let us

further assume that test data set T is able to detect

(kill) all 80 mutants. What this tells us about T

depends to a large extent on how many of these

80 mutants are equivalent to each other: at an ex-

treme, if all 80 mutants were semantically equiv-

alent to each other, then all we know about T is

that it was able to distinguish one mutant from P;

at another extreme, if no two mutants were seman-

tically equivalent, then we would know that set T

is able to distinguish as many as 80 distinct mu-

tants from P. Hence it is important to know how

many equivalence classes the set of 80 mutants

has, modulo the relation of semantic equivalence.

In this paper we deﬁne a function we call NEC

(Number of Equivalence Classes) to capture the

number of equivalence classes of the set of mu-

tants modulo semantic equivalence (excluding the

equivalence class of P); and we show how we can

estimate NEC.

• Mutation score. Imagine that we run the 100

mutants we have generated on test data T , and

we ﬁnd that 60 mutants are detected (killed) and

40 are not; it is common to take 0.6 (=60/100)

as the mutation score of T . We argue that this

metric is ﬂawed, for two reasons: ﬁrst, the mu-

tation score ought to be based not on the to-

tal number of generated mutants, but rather on

those that are estimated to be non-equivalent to P

((1 − REM) × 100, in this case); second, the mu-

tation score ought not count the number of indi-

vidual mutants detected, but rather the number of

equivalence classes covered by the detected mu-

tants. Indeed, whenever one mutant is detected

by test data T , all the mutants in the same class

are also detected; at an extreme case, if all 80 mu-

tants form a single equivalence class, and test data

T detects one of them, it automatically detects all

80; to say in such a situation that T detected 80

mutants is misleading; it is more meaningful to

say that T detected one equivalence class (the fact

that the equivalence class in question has 80 ele-

ments is rather insigniﬁcant, if we are interested

to assess the adequacy of T ). Hence we argue

that the mutation score should be deﬁned in terms

of equivalence classes, not in terms of individ-

ual mutants; in this paper, we introduce a metric

to this effect, which we call EMS (Equivalence-

based Mutation Score).

As we shall see in this paper, NEC is deﬁned in terms

of REM, and EMS is deﬁned in terms of NEC; hence

REM plays a pivotal in this study. To gain some in-

sight into how to estimate REM, we ask two related

questions:

• What makes a program prone to generate equiva-

lent mutants?

• Given a base program P and a mutant M, what

may cause the mutant to be equivalent to the base

program?

To answer the ﬁrst question, we make the follow-

ing observation: A program that is prone to gen-

erate equivalent mutants is a program that can con-

tinue performing the same function despite the pres-

ence and sensitization of mutations in its source code.

Now, mutations are supposed to simulate faults in

programs; if we replace ”mutations” by ”faults” in

the above statement we ﬁnd that a program that is

prone to generate equivalent mutants is a program that

can continue perfoming the same function despite the

presence and sensitization of faults in its source code.

This is exactly the characterization of fault tolerant

programs, and we know too well what attribute makes

programs fault tolerant: it is redundancy. Hence if we

can quantify the redundancy of a program, we can use

the redundancy metrics to predict the REM of a pro-

gram.

To answer the second question, we consider the

following circumstances that may cause a mutant to

be equivalent to a base program (using the terminol-

ogy of Laprie et al (Avizienis et al., 2004; Laprie,

1991; Laprie, 2004; Laprie, 1995)).

ICSOFT 2019 - 14th International Conference on Software Technologies

• The mutation is not a fault, i.e. it never generates

a state that is different from the original program;

this arises in trivial circumstances such as when

the mutation applies to dead code, but may also

arise in more common cases, such as, e.g. chang-

ing < onto ≤ when the operands being compared

are never equal (e.g. an array of unique identi-

ﬁers).

• The mutation is a fault, but it causes no error; i.e.

it does cause the generation of a different state,

but the state it generates is correct (as correct as

the state generated by the base program); as an

example, imagine that the mutation causes a list

of items to be visited in a different order from the

original program, but the order is irrelevant.

• The mutation is a fault, it does cause errors, but

the errors do not cause failure. In other words

the mutation causes the generation of an erro-

neous state, but the error is subsequently masked

by downstream code.

• The mutation is a fault, it does cause errors, the

errors do cause failure, but the failure falls within

the tolerance of the equivalence oracle. If the

equivalence oracle does not test for comprehen-

sive equality between the ﬁnal state of P and the

ﬁnal state of M, it is conceivable that M and P are

considered equivalent while their ﬁnal states are

distinct.

3 REDUNDANCY METRICS

In this section, we review some metrics which, we

feel, may be statistically related to the REM of a pro-

gram; these metrics reﬂect various forms of program

redundancy, and they are related with the circum-

stances we cite above for a mutant to be equivalent to

a base program. These metrics are deﬁned by means

of Shannon’s entropy function (Shannon, 1948); we

use the notations H(X), H(X|Y ) and H(X,Y ) to de-

note, respectively, the entropy of random variable X,

the conditional entropy of X given Y , and the joint

entropy of random variables X and Y ; we assume that

the reader is familiar with these concepts, their inter-

pretations, and their properties (Csiszar and Koerner,

2011). For each metric, we brieﬂy present its deﬁni-

tion, its interpretation, how we calculate it, and why

we believe that it is correlated to (because it affects)

the REM of a program. Because the REM is a ratio

that ranges between 0 and 1, we resolve to deﬁne all

our metrics as values between 0 and 1, so as to facili-

tate the derivation of a regression model. For the sake

of simplicity, we compute all entropies under the as-

Table 1: Entropy of Declared State.

Data type Entropy (bits)

bool 1

char 8

int 32

float 64

sumption of equal probability. Under this assumption,

our estimates are in fact upper bounds of the actual

entropy.

3.1 State Redundancy

What we want to represent: When we declare vari-

ables in a program, we do so for the purpose of rep-

resenting the states of the program; for a variety of

reasons, it is very common to ﬁnd that the range of

values that program variables may take is much larger

than the range of values that actual/ feasible program

states may take. We want state redundancy to reﬂect

the gap between the declared state and the actual state

of the program.

How we deﬁne it: If we let S be the declared state

of the program, and σ be the actual state of the pro-

gram, then the state redundancy of the program can be

measured by the difference between their respective

entropies; to normalize it (so that it ranges between

0.0 and 1.0) we divide it by the entropy of the declared

state. Recognizing that the entropy of the actual state

decreases (hence the redundancy increases) as the ex-

ecution of the program proceeds from the initial state

to the ﬁnal state, we deﬁne, in fact two different mea-

sures of state redundancy, one for each state.

Deﬁnition 1. Given a program P whose declared

state (deﬁned by its variable declarations) is S, we

let σ

and σ

be its initial and ﬁnal actual states, we

deﬁne its initial state redundancy and its ﬁnal state re-

dundancy as, respectively:

H(S) − H(σ

)

H(S)

H(S) − H(σ

)

H(S)

How we calculate it: To compute H(S) we use a

table that maps each data type to its width in bits,

As an example, we consider the following program:

void P()

{int year, birthYear, age;

read (year, birthYear);

assert ((2019 <= year <= 2169) // initial

&& (1869 <= birthYear <= 2019));// state

age = year - birthYear; // final state

}

Quantitative Metrics for Mutation Testing

The declared space of this program is deﬁned by

three integer variables, hence H(S) = 96 bits. Its

initial state is deﬁned by two variables (year and

birthYear) that have a range of 151 distinct values and

an integer variable (age) that has free range, hence

H(σ

) = 32 + 2 × log

(151) = 46.48 bits. As for the

ﬁnal state, it is determined fully by the values of year

and birthYear, since age is a function of these two,

hence its entropy is merely: H(σ

) = 2 × log(151) =

14.48 bits. Hence:

96 − 46.48

= 0.516.

96 − 14.48

= 0.85.

Of course, there is more redundancy in the ﬁnal state

than in the initial state.

Why we feel it is correlated to the REM of a pro-

gram: State redundancy reﬂects the amount of dupli-

cation of the information maintained by the program,

or the amount of extra bits of information that are part

of the declared state; the more duplicated bits or un-

used bits are lying around in the program state, the

greater the likelihood that a mutation affects bits that

are not subsequently referenced in the execution of

the program (hence do not affect its outcome).

3.2 Non Injectvity

What we want to represent: A function f is said to be

injective if and only if it maps different inputs onto

different outputs, i.e. x 6= x

⇒ f (x) 6= f (x

). A func-

tion is non-injective if it violates this property; it is

all the more non-injective that it maps a larger set of

distinct inputs onto a common output.

How we deﬁne it: For the purposes of this metric,

we view a program as mapping initial states onto ﬁ-

nal states. One way to quantify non-injectivity is to

use the conditional entropy of the initial state given

the ﬁnal state: this entropy reﬂecte the uncertainty we

have about the initial state given that we know the ﬁ-

nal state; this entropy increases as more initial states

are mapped to the same ﬁnal state; to normalize it, we

divide it by the entropy of the initial state.

Deﬁnition 2. Given a program P on space S, the non-

injectivity of P is denoted by NI and deﬁned by:

NI =

H(σ

|σ

)

H(σ

)

where σ

and σ

are, respectively, the initial and ﬁnal

actual state of P.

Because σ

is a function of σ

, the conditional en-

tropy can be simpliﬁed (Csiszar and Koerner, 2011),

yielding the following formula:

NI =

H(σ

) − H(σ

)

H(σ

)

In (Androutsopoulos et al., 2014), Androutsopoulos

et al. introduce a similar metric, called squeeziness,

which they ﬁnd to be correlated to the probability that

an error arising at some location in a program fails to

propagate to the output.

How we calculate it: We have already discussed

how to compute the entropies of the initial state and

ﬁnal state of a program. As an illustration, we ﬁnd

that the non-injectivity of the program cited in Section

3.1 is:

NI =

H(σ

) − H(σ

)

H(σ

)

46.48 − 14.48

46.48

= 0.69.

Why we feel it is correlated to the REM of a pro-

gram: One of the main sources of mutant equivalence

is the ability of programs to mask errors that have in-

fected the state, by mapping the erroneous state onto

the same ﬁnal state as the correct state. This hap-

pens all the more frequently that the function of the

program is more non-injective; hence non-injectivity

measures exactly the capability of the program to

mask errors caused by the sensitization of mutations.

3.3 Functional Redundancy

What we want to represent: Not all programs can be

faithfully modeled as mappings from initial states to

ﬁnal states, as we do in Section 3.2; sometimes a

more faithful model of a program may be a hetero-

geneous function from some input space X to some

output space Y . Programs exchange information with

their environment through a wide range of channels:

they receive input information (X) through read state-

ments, passed by-value parameters, access to global

variables, etc; and they send output information (Y )

through write statements, passed by-reference param-

eters, return statements, access to global variables,

etc. We want a metric that reﬂects non-injectivity

(hence the potential for masking errors) for this model

of computation.

How we deﬁne it: We let X be the random variable

that represents all the input information used by the

program, and we let Y be the random variable that

represents all the output information that is delivered

by P.

Deﬁnition 3. Given a program P that takes input X

and returns output Y , the functional redundancy of P

is denoted by FR and deﬁned by:

FR =

H(X|Y )

H(X)

ICSOFT 2019 - 14th International Conference on Software Technologies

Because Y is a function of X, we know (Csiszar

and Koerner, 2011) that the conditional entropy

(H(X|Y )) can be written as (H(X )−H(Y )). Also, the

entropy of Y is less than or equal to the entropy of X,

and both are non-negative, hence FR ranges between

0 and 1 (we assume, of course, that H(X) 6= 0).

How we calculate it: The entropy of X is the sum

of the entropies of all the input channels and the en-

tropy of Y is the sum of the entropies of all the output

channels. We consider the following program:

int P(int year, birthyear)

{read (year, birthYear);

assert ((2019 <= year <= 2169)

&& (1869 <= birthYear <= 2019));

age = year - birthYear;

return age;

}

Random variable X is deﬁned by program vari-

ables year and birthYear, hence its entropy is H(X) =

2 × log

(151) = 14.48. Random variable Y is deﬁned

by variable age, whose values range between 0 and

150, hence H(Y ) = log

(151) = 7.24 bits. Hence

FR =

14.48 − 7.24

14.48

= 0.50.

Why we feel it is correlated to the REM of a pro-

gram: Functional redundancy, like non-injectivity, re-

ﬂects the program’s ability to mask errors caused by

mutations; whereas non-injectivity models the pro-

gram as a homogeneous function on its state space,

functional redundancy models it as a heterogeneous

mapping from an input space to an output space.

All the metrics we have discussed so far pertain to

the base program; we refer to them as the program’s

intrinsic metrics. The metric we present in the next

section deals not with the base program, but rather

with the oracle that is used to rule on equivalence.

3.4 Non Determinacy

What we want to represent: Whether two programs

(in particular, a program and a mutant thereof) are

equivalent or not may depend on how thoroughly

we check their behavior. For example, it is possi-

ble that out of three program variables, two represent

the intended function of the programs and the third

is merely an auxiliary variable. In such a case, the

oracle of equivalence ought to check that the relevant

variables have the same value, but ignore the auxiliary

variable.

From this discussion we infer that the equivalence

between a base program P and a mutant M may de-

pend on what oracle is used to compare the output of

P with the output of M, and we are interested to deﬁne

Table 2: Non Determinacy of Sample Oracles.

Ω() H(S

) ND

= x

) ∧ (y

= y

) 0 0

∧(z

= z

)

= x

) ∧ (y

= y

) 32 0.33

= x

) 64 0.66

true 96 1.0

a metric that reﬂects the degree of non-determinacy

of the selected oracle.

We are given a program P on space S and a mu-

tant M on the same space, and we consider an oracle

Ω() on S deﬁned by an equivalence relation on S. We

want the non-determinacy of Ω() to reﬂect how much

uncertainty we have about the output of M for a given

input if we know the output of P for the same input.

Deﬁnition 4. Given a program P and a mutant M

on space S, and given an oracle Ω() deﬁned as an

equivalence relation on S, we let S

and S

be the

random variables that represent the ﬁnal states of P

and M for a common input. The non-determinacy of

Ω() is denoted by ND and deﬁned by:

ND =

H(S

)

H(S

)

Given that Ω() deﬁnes an equivalence class over

S, this metric reﬂects the amount of uncertainty we

have about an element of S if all we know is the equiv-

alence of this element by relation Ω().

How we calculate it: The conditional entropy

H(S

) is really the entropy of the equivalence

classes of S modulo the equivalence relation deﬁned

by Ω(). It represents the amount of uncertainty we

have about an element of S if all we know is its equiv-

alence class; if Ω() is the identity relation then all

equivalence classes are singletons and ND = 0; else

it is the base 2 logarithm of the size of equivalence

classes. As an example, we consider space S deﬁned

by three variables, say x, y, z of type integer, and we

show in the following table a number of possible or-

acles with their respective non-determinacies. For all

these oracles, H(S

) = 3×32 = 96; the only term that

changes is H(S

Why we feel it is correlated to the REM of a pro-

gram: Of course, the weaker the oracle that tests for

equivalence, the more mutants will be found to be

equivalent to the base program.

3.5 A Posteriori Justiﬁcation

In section 2, we had asked two questions: First, what

attribute makes a program prone to generate equiva-

lent mutants; second, under what circumstances can

Quantitative Metrics for Mutation Testing

a mutant behave in a way that is equivalent to a base

program. The metrics we introduced in section 3 an-

swer the ﬁrst question, since they capture different as-

pects of redundancy. In table 3, we discuss why we

feel that the selected metrics answer the second ques-

tion, in the sense that they reﬂect the likelihood of

occurrence of each circumstance that we had identi-

ﬁed.

Table 3: Metrics vs Circumstances of Equivalence.

Metrics Circumstances of Equivalence

Mutation not a Fault

Mutation is a Fault

Causes no Error

FR,NI

Mutation is a Fault

Causes Errors

Errors Masked

Mutation is a Fault

Causes Errors

Errors Propagate

Failure Undetected

3.6 A Java Compiler

In order to automate the calculation of these redun-

dancy metrics, and ensure that our calculations are

applied uniformly, we use compiler generation tech-

nology (ANTLR, http://www.antlr.org/) to parse Java

code and derive these metrics for individual methods

in Java classes. For each method, we must estimate

the following quantities:

• The entropy of the declared space, H(S).

• The entropy of the initial actual space, H(σ

• The entropy of the ﬁnal actual space, H(σ

• The entropy of the input space, H(X).

• The entropy of the output space, H(Y ).

The entropies of the declared space, the input space,

and output space are fairly straightforward; they con-

sist in identifying the relevant variables and adding

their respective entropies, depending on their data

type, as per table 1.

For the entropy of the initial actual space, we are

bound to rely on input from the source code, as we

have no other means to probe the intent of the pro-

grammer (re: how they use declared variables to rep-

resent the actual program state). To this effect, we in-

troduce a special purpose assert statement, which the

engineer may use to specify the precondition of the

method whose REM we want to compute. We pro-

pose the following statement

preassert(<precondition>)

whose semantic deﬁnition is exactly the same as a

normal assert statement, but this one is used specif-

ically to analyze the entropy of the initial actual state.

When the method has an exception call at the begin-

ning as a guard for the method call, then it is straight-

forward to have a preassert() statement immediately

after the exception statement, with the negation of the

condition that triggers the exception. The entropy of

the initial actual state is computed as:

H(σ

) = H(S) − ∆H,

where ∆H is the reduction in entropy represented by

the assertion of the preassert() statement. This

quantity is deﬁned inductively according to the struc-

ture of the assertion, as shown summarily below:

• ∆H(A ∧ B) = ∆H(A) + ∆H(B).

• ∆H(A ∨ B) = max(∆H(A), ∆H(B)).

• ∆H(X == Y ), where X and Y are expressions of

the same type, equals the entropy of the common

type. For example, if x and y are integer variables,

then ∆H(x + 1 == y − 1) is 32 bits.

• ∆H(X < Y ) = ∆H(X <= Y ) = ∆H(X > Y ) =

∆H(X >= Y ) = 1 bit. So for example ∆H(x +1 >

0) = 1 bit, since this equality reduces the range of

possible values of x by half, whose log

is then

reduced by 1.

This is not a perfect solution, but it is adequate for our

purposes.

For the entropy of the ﬁnal actual space, we have

to keep track of dependencies that the program creates

between its variables. We do so using a Boolean ma-

trix (called D, for Dependency), which is initialised to

the identity (T on the diagonal, F outside, to mean that

initially each variable depends only on itself); when-

ever we encounter an assignment statement, of the

form (x=E(y,z,u,v)), we replace the row of x in D

with the logical OR of the rows of all the variables

that appear in expression E. At the end of the pro-

gram we add (i.e. take the logical OR) of all the rows

of the matrix; this yields a vector that indicates which

program variables affect the value of the ﬁnal state

of the program. The sum of the entropies of the se-

lected variables is the entropy of the ﬁnal actual state.

If the assignment statement is embedded within an

if-stement, an if-then-else statement or a while loop,

then the variables that appear in the condition of the

if or while are added to the variables that are on the

right hand side of the assignment, since they affect the

value of the assigned variable.

ICSOFT 2019 - 14th International Conference on Software Technologies

4 A STATISTICAL MODEL

In order to test our assumption that our redundancy

metrics are statistically correlated with the REM of

a program, we have conducted an empirical experi-

ment, whereby we select a set of Java classes from

the Apache Common Mathematics Library and run

our Java compiler to compute the redundancy met-

rics of each method of each class. On the other hand,

we apply a mutant generator to these classes using a

uniform set of standard mutation operators, then we

execute the base program and the mutants on bench-

mark test data sets, and record how many mutants are

killed by the test. Simultaneously, we keep track of

coverage metrics, and exclude from consideration any

method whose line coverage is below 90%. By keep-

ing in our sample only those Java classes for which

line coverage is high (in fact the vast majority reach

100% line coverage) we maximize the likelihood that

mutants that are found to survive after undergoing

the test are equivalent to the base program. Under

this assumption, we use the ratio of surviving mu-

tants of each method over the total number of mu-

tants as the REM of the method. Our data sample

includes about two hundred methods, but when we

exclude those whose size is below 20 LOC we end up

with 66 methods; because we treat individual meth-

ods rather than whole classes, this condition excludes

many small methods. The requirement of anonymity

preclude us from posting this data online, but we may

post it once the requirement is lifted.

We peform a statistical regression using REM as

the dependent variable and the intrinsic redundancy

metrics (i.e. those metrics that pertain to the pro-

gram, not the equivalence oracle) as the independent

variables. We use a logistic model, i.e. a model

such that log(

REM

1−REM

) is a linear combination of

the independent variables. The metric that pertains

to the equivalence oracle (ND) is not part of the

regression analysis, but is integrated in the equation

in such a way that if ND = 0 we obtain the regression

formula involving the intrinsic metrics, and if ND = 1

(extreme case when the oracle tests trivially for true ,

i.e. all the mutants are found to be equivalent) we

want the REM to be 1. The resulting formula is:

REM = ND + (1 − ND)×

(−3.27 + 1.35 × SR

+ 1.26 × FR).

With this equation in place, we can now have a

tool that automatically computes the redundancy met-

rics, then derives the REM using this formula. Figures

1 and 2 show a sample input and output screen for this

tool; not all the functionality alluded to in the input

screen is operational as of the date of writing; for

now, the mutant generators are ﬁxed, and the user

does got have the option to select mutation operators.

5 EQUIVALENCE AND

REDUNDANCY

5.1 Mutant Equivalence

Given a set of M mutants of a base program P, and

given a ratio of equivalent mutants REM, the number

of equivalent mutants is estimated to be M × REM.

Hence we cannot expect any test data set T to kill

more than N = M × (1 − REM) mutants (modulo the

margin of error in the estimation of REM).

5.2 Mutant Redundancy

In (Papadakis et al., 2019), Papadakis et al. raise

the problem of mutant redundancy as the issue where

many mutants may be equivalent among themselves,

hence do not provide test coverage commensurate

with their number. If we have sixty mutants divided

into twelve classes where each class contains ﬁve

equivalent mutants, then we have only twelve distinct

mutants; and if some test data set T kills these sixty

mutants, it should really get credit for twelve mutants

(twelve casualties, so to speak), not sixty, since when-

ever it kills a mutant from one equivalence class, it

automatically kills all the mutants of the same class.

Of course, it is very difﬁcult to determine, in a set

of mutants, which mutants are equivalent and which

are not; but again, the REM enables us to draw some

quantitative data about the level of redundancy in a

pool of mutants.

The REM of the base program is computed us-

ing a regression formula whose independent variables

are the redundancy metrics extracted from the source

code of the program. Since the mutants are gener-

ated from the base program by means of elementary

syntactic changes, it is reasonable to consider that the

mutants have the same REM as the base program. If

we interpret the REM as the probability that any two

mutants are semantically equivalent, then we can esti-

mate the number of equivalence classes by answering

the following question: Given a set of size N, and

given that any two elements of this set have a proba-

bility REM to be in the same equivalence class mod-

ulo some relation EQ, what is the expected number of

equivalence classes of this set modulo EQ?

We denote this number by NEC(N,REM), and we

write it as follows:

Quantitative Metrics for Mutation Testing

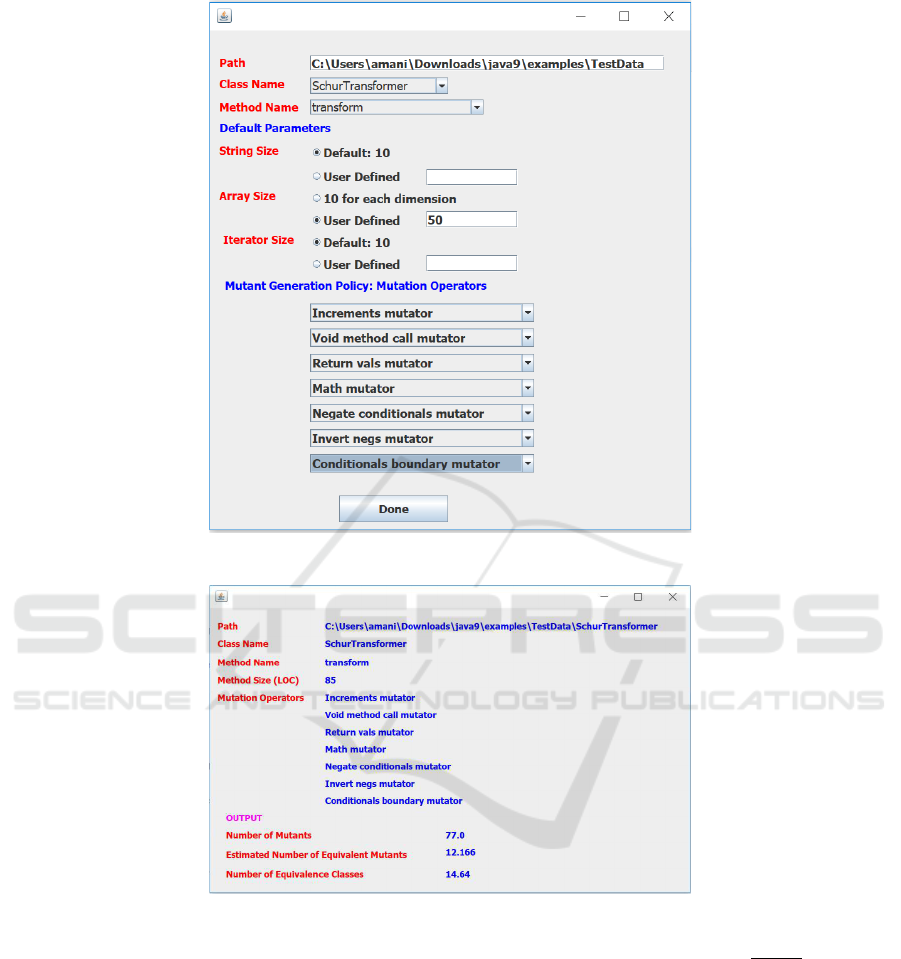
Figure 1: Input Screen.

Figure 2: Output Screen.

NEC(N,REM) =

∑

k=1

k × p(N, REM,k),

where p(N,REM, k) is the probability that a set of N

elements where each pair has probability REM to be

equivalent has k equivalence classes. This probability

satisﬁes the following inductive conditions.

• Basis of Induction. We have two base conditions:

– One Equivalence Class. p(N, REM,1) =

REM

N−1

. This is the probability that all N ele-

ments are equivalent.

– As Many Equivalence Classes as Elements,

or: All Equivalence Classes are Singletons.

p(N, REM,N) = (1 −REM)

N×(N−1)

. This is the

probability that no two elements are equivalent:

every two elements are not equivalent; there are

N × (N − 1) pairs of distinct elements, but be-

cause equivalence is a symmetric relation, we

divide this number by 2 (M

6= M

is the same

event as M

6= M

• Inductive Step. When we add one element to a

set of N − 1 elements, two possibilities may arise:

either this adds one to the number of equivalence

classes (if the new element is equivalent to no

current element of the set); or it maintains the

number of equivalence classes (if the new element

ICSOFT 2019 - 14th International Conference on Software Technologies

is equivalent to one of the existing equivalence

classes). Since these two events are disjoint, the

probability of the disjunction is the sum of the

probabilities of each event. Hence:

p(N, REM,k) = p(N − 1,REM,k)× (1 − (1 −

REM)

+p(N − 1, REM,k − 1) × (1 −

REM)

k−1

The following recursive program computes the

number of equivalence classes of a set of size N

whose elements have probability REM of being

equivalent.

#include <iostream>

#include "math.h"

using namespace std;

double p(int N, int k, double R);

int main ()

{

float R=0.158; int N=65;

float mean = 0.0; float ps=0.0;

for (int k=1; k<=N; k++)

{float prob=p(N,k,R); ps = ps+prob;

mean = mean + k*prob;}

cout<<"ps:"<<ps<<" mean:"<<mean<<endl;

}

double p(int N, int k, double R)

{if (k==1) {return pow(R,N-1);}

else

if (N==k) {return pow(1-R,(k*(k-1))/2);}

else {return p(N-1,k,R)*(1-pow(1-R,k))

+p(N-1,k-1,R)*pow(1-R,k-1);}}

Execution of this program with N = 65 and

REM = 0.158 yields NEC(N,REM) = 14.64, i.e. our

65 mutants represent only about 15 different mutants;

the remaining 50 are redundant.

6 MUTATION SCORE,

REVISITED

The quantiﬁcation of redundancy, discussed in the

previous section, casts a shadow on the traditional

way of measuring the mutation score of a test data

set T : usually, if we execute a set of M mutants on

some test data set T and we ﬁnd that X mutants have

been killed (i.e. shown to be different from the base

program P), we assign to T the mutation score X/M.

This metrics ignores the possibility that several of M

mutants may be equivalent, and several of the X killed

mutants may be equivalent. We argue that this metric

can be improved and made more meaningful, in three

ways:

• Because of the possibility that mutants may be

equivalent to the base program P, the baseline

ought to be the number of non-equivalent mutants,

i.e. N = (1 − REM) × M.

• Because of the possibility that those mutants that

are not equivalent to P may be equivalent amongst

themselves, we ought to focus not on the num-

ber of these mutants, bur rather on the number

of equivalence classes modulo semantic equiva-

lence. This is deﬁned in the previous section as

NEC(N,REM).

• Because of the possibility that the X mutants

killed by test data set T may be equivalent

amongst themselves, we ought to give credit to T

not for the cardinality of X, but rather for the num-

ber of equivalence classes that X may overlap.

We refer to this number as COV (N,K,X), where

K = NEC(N,REM) is the number of equivalence

classes of the set of N mutants modulo equiva-

lence.

To compute COV (N,K,X ), we designate by

,...C

the K equivalence classes, we desig-

nate by f

, for (1 ≤ i ≤ K), the binary functions

that take value 1 if and only if equivalence class

overlaps with (i.e. has a non-empty intersec-

tion with) set X , and value 0 otherwise. Then

COV (N, K,X ) = E(

∑

i=1

K f

). If we assume that all

classes are the same size and that elements of X are

uniformly distributed over the set of mutants, then

this can be written as:

cov(N,K, X) = K × p( f

= 1) = K × (1 − p( f

= 0)),

for an arbitrary i. For the ﬁrst class to be considered,

p( f

= 0) =

K−1

, since each element of X has a

probability

K−1

of not being in class C

; for each sub-

sequent element, the numerator and denominator each

drops by 1. Hence we have the following formula:

COV (N, K,X ) = K × (1 −

K − 1

X−1

∏

i=0

N −

K−1

N − i

The following program computes this function, for

N = 65, K = 15 and X = 50.

#include <iostream>

#include "math.h"

using namespace std;

double cov(int N, int K, int X);

int main ()

{

int N=65; int K=15; int X=50;

cout << "cov: " << cov(N,K,X) << endl;

}

Quantitative Metrics for Mutation Testing

double cov(int N, int K, int X)

{

float prod=1;

for (int i=0; i<K; i++)

{prod = prod *

(N-i/(float)(K-1))/(float)(N-i);}

return K*(1-prod*pow((K-1)/(float)K,X));

}

Execution of this program yields

COV (65,15,50) = 12.55. We propose the fol-

lowing deﬁnition.

Deﬁnition 5. Given a base program P and M mutants

of P, and given a test data set T that has killed X mu-

tants, the mutation score of T is the ratio of equiva-

lence classes covered by X over the total number of

equivalence classes amongst the mutants that are not

equivalent to P.

We denote the mutation score by EMS(M,X). The

following proposition gives an explicit formula of the

mutation score.

Proposition 1. Given a program P and M mutants

of P, and given a test data set T that has killed X mu-

tants, the mutation score of T is given by the following

formula:

EMS(M,X) =

COV (N, NEC(N, REM),X)

NEC(N,REM)

where REM is the ratio of equivalent mutants of P

and N = M(1 − REM) is the number of mutants that

are not equivalent to P.

In the example above, for N = 65, REM = 0.158,

and X = 50 we ﬁnd

EMS(77,50) =

12.55

= 0.84.

7 CONCLUSION

7.1 Summary

In this paper, we argue that the determination of mu-

tant equivalence and mutant redundancy by inspec-

tion and analysis of individual mutants is very expen-

sive and error-prone, at the same time that it is in fact

unnecessary, for most purposes. As a substitute, we

propose to analyze the amount of redundancy that a

program has, in various forms, and we ﬁnd that this

enables us to extract a number of mutation-related

metrics at negligible cost. Central to this quantitative

analysis is the concept of ratio of equivalent mutants,

which measures the probability that any two mutants,

or a mutant and the base program, are semantically

equivalent.

7.2 Assessment and Threats to Validity

A lot of our work rides on the estimation of the REM,

which in turn rides on the estimation of the redun-

dancy metrics, and on the precision/ convergence of

the regression model. This is all the more critical

that the estimate of the number of equivalence classes,

NEC(N,REM), depends a great deal more on REM

than on N. Hence any error that arises in the estima-

tion of REM is likely to greatly affect the precision of

NEC(N,REM); this, in turn, affects the precision of

COV (N, K,X ), and that of EMS(M,X). This puts a

heavy onus on us to double check the way the redun-

dancy metrics are computed.

7.3 Prospects

Our current plan is to reﬁne and upgrade a tool we

are currently developing to automate this quantitative

analysis, and to validate this tool through ﬁeld test-

ing. Also, we want to select a set of mutant genera-

tion policies, and build a separate regression model

for each policy, so that for a given base program,

the calculation of the corresponding REM uses the

regression formula that matches the selected mutant

generation policy. Finally, we have plans to validate

our work empirically, by comparing our estimaates

sof REM against actual values, and by assessing the

precision of our other metrics, such as NEC(N, REM)

and COV (N, K,X).

ACKNOWLEDGEMENTS

This work is partially supported by a grant from NSF,

number DGE1565478.

REFERENCES

Aadamopoulos, K., Harman, M., and Hierons, R. (2004).

How to overcome the equivalent mutant problem and

achieve tailored selective mutation using co-evolution.

In Proceedings, Genetic and Evolutionary Computa-

tion, volume 3103 of LNCS, pages 1338–1349.

Andrews, J., Briand, L., and Labiche, Y. (2005). Is muta-

tion an appropriate tool for testing experiments? In

Proceedings, ICSE.

Androutsopoulos, K., Clark, D., Dan, H., Hierons, R. M.,

and Harman, M. (2014). An analysis of the rela-

tionship between conditional entropy and failed error

propagation in software testing. In Proceedings, ICSE

2014.

ICSOFT 2019 - 14th International Conference on Software Technologies

Avizienis, A., Laprie, J. C., Randell, B., and Landwehr,

C. E. (2004). Basic concepts and taxonomy of de-

pendable and secure computing. IEEE Transactions

on Dependable and Secure Computing, 1(1):11–33.

Carvalho, L., Guimares, M., Fernandes, L., Hajjaji, M. A.,

Gheyi, R., and Thuem, T. (2018). Equivalent mutants

in conﬁgurable systems: An empirical study. In Pro-

ceedings, VAMOS’18, Madrid, Spain.

Csiszar, I. and Koerner, J. (2011). Information Theory:

Coding Theorems for Discrete Memoryless Systems.

Cambridge University Press.

Delamaro, M. E., Maldonado, J. C., and Vincenzi, A. M. R.

(2001). Proteum /im 2.0: An integrated mutation test-

ing environment. In Wong, W. E., editor, Mutation

Testing for the New Century, volume 24, pages 91–

101. Springer Verlag.

Gruen, B., Schuler, D., and Zeller, A. (2009). The impact

of equivalent mutants. In Proceedings, MUTATION

2009, Denver, CO, USA.

Hierons, R., Harman, M., and Danicic, S. (1999). Using

program slicing to assist in the detection of equivalent

mutants. Journal of Software Testing, Veriﬁcation and

Reliability, 9(4).

Inozemtseva, L. and Holmes, R. (2014). Coverage is not

strongly correlated with test suite effectiveness. In

Procedings, 36th International Conference on Soft-

ware Engineering. ACM Press.

Just, R., Ernst, M., and Fraser, G. (2013a). Using state

infection conditions to detect equivalent mutants and

speed up mutation analysis. In Dagstuhl Seminar

13021: Symbolic Methods in Testing, Wadern, Ger-

many.

Just, R., Ernst, M., and Fraser, G. (2014a). Efﬁcient muta-

tion analysis by propagating and partitioning infected

execution states. In Proceedings, ISSTA’14, San Jose,

CA, USA.

Just, R., Ernst, M. D., and Fraser, G. (2013b). Using state

infection conditions to detect equivalent mutants and

sped up mutation analysis. In Proceedings, Dagstuhl

Seminar 13021: Symbolic Methods in Testing.

Just, R., Jalali, D., Inozemtseva, L., Ernst, M., Holmes, R.,

and Fraser, G. (2014b). Are mutants a valid substitute

for real faults in software testing? In Proceedings,

FSE.

Kintis, M., Papadakis, M., Jia, Y., Malveris, N., Y, L. T., and

Harman, M. (2018). Detecting trivial mutant equiva-

lences via compiler optimizations. IEEE Transactions

on Software Engineering, 44(4).

Laprie, J. C. (1991). Dependability: Basic Concepts and

Terminology: in English, French, German, Italian and

Japanese. Springer Verlag, Heidelberg.

Laprie, J. C. (1995). Dependability —its attributes, impair-

ments and means. In Predictably Dependable Com-

puting Systems, pages 1–19. Springer Verlag.

Laprie, J. C. (2004). Dependable computing: Concepts,

challenges, directions. In Proceedings, COMPSAC.

Namin, A. S. and Kakarla, S. (2011). The use of mutation

in testing experiments and its sensitivity to external

threats. In Proceedings, ISSTA.

Nica, S. and Wotawa, F. (2012). Using constraints for equiv-

alent mutant detection. In Andres, C. and Llana, L.,

editors, Second Workshop on Formal methods in the

Development of Software, EPTCS, pages 1–8.

Offut, A. J. and Pan, J. (1997). Automatically detecting

equivalent mutants and infeasible paths. Software

Testing, Veriﬁcation and Reliability, 7(3):165–192.

Papadakis, M., Delamaro, M., and LeTraon, Y. (2014).

Mitigating the effects of equivalent mutants with mu-

tant clasiﬁcation strategies. Science of Computer Pro-

gramming, 95(P3):298–319.

Papadakis, M., Kintis, M., Zhang, J., Jia, Y., Traon, Y. L.,

and Harman, M. (2019). Mutation testing advances:

An analysis and survey. In Advances in Compugters.

Schuler, D. and Zeller, A. (2010). Covering and uncover-

ing equivalent mutants. In Proceedings, International

Conference on Software Testing, Veriﬁcation and Val-

idation, pages 45–54.

Shannon, C. (1948). A mathematical theory of communica-

tion. Bell Syst. Tech. Journal, 27:379–423, 623–656.

Wang, B., Xiong, Y., Shi, Y., Zhang, L., and Hao, D.

(2017). Faster mutation analysis via equivalence mod-

ulo states. In Proceedings, ISSTA’17, Santa Barbara,

CA, USA.

Yao, X., Harman, M., and Jia, Y. (2014). A study of equiv-

alent and stubborn mutation operators using human

analysis of equivalence. In Proceedings, ICSE.

Quantitative Metrics for Mutation Testing