A Spiral Approach to Solve the Routing and Spectrum Assignment

Problem in Ring Topologies for Elastic Optical Networks

Nicolas Jara

, Jesenia Salazar and Reinaldo Vallejos

Department of Electronics, Universidad Tecnica Federico Santa Maria, Valpara

ıso, Chile

Keywords:

Simulation, Elastic Optical Networks, Routing, Spectrum Allocation.

Abstract:

In this paper, we propose a simulation-based strategy to solve the routing and spectrum assignment problem

in elastic optical networks with a static network operation for ring network topologies. First, the proposed

method arrange the network users decreasingly according to their bandwidth demands. Next, we introduce the

Spiral policy to allocate the frequency spectrum. This policy consists of assigning the resources to the user in

a correlative manner, following a spiral, taking advantage of the ring topology. Remark that each user path is

ﬁxed, computed by any shortest path algorithm. We assess the performance and robustness of our model by

comparing the proposal with two optimization models in small rings (5-8 nodes) and with the most referenced

methods found in the literature for larger ring networks (5-50 nodes). The results show that consistently our

method outperforms the ones proposed in the literature, in terms of network cost and fragmentation.

1 INTRODUCTION

Most of the digital data are carried by optical net-

works. The capacity of these networks has grown

vastly over the decades through the appearance of

newer technologies. So far, these networks have been

able to carry out this trafﬁc growth by introducing

several technological improvements. Nevertheless,

researchers have found an impending capacity crunch

in optical communications. It refers to the fact that

the optical ﬁber capacity is not limitless, and said ca-

pacity limit can be reached soon (Ellis et al., 2016;

Waldman, 2018). The foregoing requires an evolution

of current optical architectures to keep up the unceas-

ing growth of the Internet. Since is the base of all our

communication system, any progress means not only

better communication networks but to meaningful so-

cial and economic improvements.

In this context, there are two possible solutions.

First, to install more infrastructure at reaching the

maximum ﬁber capacity. This option is simple but

involves huge investments. Thus, this strategy should

be avoided. Second, ro improve resources manage-

ment in order to efﬁciently use the installed infras-

tructure. This second alternative is the more conve-

nient option today, considering that current networks

do not operate efﬁciently.

https://orcid.org/0000-0003-2495-8929

Currently, the optical network operation is inefﬁ-

cient due some technological features. One of them

is that the frequency spectrum assigned to each com-

munication is ﬁxed, according to the International

Telecommunication Union (ITU) standard. This is

50[GHz] per channel (Iversen Villy, 2002). Nowa-

days, to satisfy said demand growth, the Internet Ser-

vice Providers are rising the bit-rates using this stan-

dard transmission scheme. However, this process in-

volves limitations, due to technical difﬁculties trans-

mitting high bit-rates through long distances (Gerstel

et al., 2012).

To solve the prior problem, a new paradigm

has been proposed, called “Elastic Optical Network”

(EON) (Layec et al., 2013; Gerstel et al., 2012;

Sambo et al., 2012). The EONs allows to ﬂexibly

use the frequency spectrum to attend different traf-

ﬁc needs adaptively, giving only the necessary band-

width to each user. To achieve that, the frequency

spectrum is divided into frequency slots units (FSU)

with a ﬁxed bandwidth associated, and the FSU are

grouped to satisfy the bandwidth required for each

user. This has been an important topic of investiga-

tion for the few last years and, still needs research and

development to be implemented in practice.

The design of elastic optical networks is a hot

topic both at the academic and industrial levels. In

particular, the design of optical networks decomposes

into many different tasks. One of these tasks con-

Jara, N., Salazar, J. and Vallejos, R.

A Spiral Approach to Solve the Routing and Spectrum Assignment Problem in Ring Topologies for Elastic Optical Networks.

DOI: 10.5220/0007842302690276

In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 269-276

ISBN: 978-989-758-381-0

269

sists in assigning a path and a portion of the spectrum

to each network user. This problem is known as the

Routing and Spectrum Allocation (RSA) problem.

The RSA problem consists on ﬁnd, for each user,

a source-destination path, with available spectrum ac-

cording to the user demand. This resource allocation

is subject to the following constraints. First, each FSU

can host one user at the same time; second, the same

FSU allocated to the said user must be available in

all the links on the user path; and in case that the

user requires more than one FSU, the spectrum as-

signed must be consecutive (contiguous). The RSA

problem is crucial in EON planning, however is a NP-

hard (L

opez and Velasco, 2016) problem. Therefore,

in this article, we solve the RSA problem by means of

simulation.

This paper focuses on solving the RSA problem

for ring network topologies. For this end, we design

a strategy based on heuristics and simulation. Each

user path is ﬁxed and computed prior to the network

operation using a shortest path algorithm. To assign

the frequency spectrum to each user, we used the well

known First-Fit policy. However, we introduce the

“Spiral” concept, which seeks to assign the resources

using the ring topology as an advantage, sorting and

allocating the FSU to each user in spiral order. By

doing so, this strategy diminishes the network total

cost and the spectrum fragmentation.

The remainder of this paper is as follows: In Sec-

tion 2 we present the state of art on RSA strategies.

Next, Section 3 presents our proposal to solve said

problem be means of simulation. Section 4 contains

some numerical examples. And ﬁnally, we give some

conclusions and remarks in Section 5.

2 STATE OF ART

To solve the Routing and Spectrum Allocation prob-

lem there are typically 2 scenarios: the static and

dynamic case. On the static case, the resource de-

mands are ﬁxed and well known, hence, the routes

and resources allocated are available to the user per-

manently. In this scenario, the goal is to maximize

the spectrum usage (Talebi et al., 2014a; Meza et al.,

2016). On the other hand, in the dynamic scenario the

users request for resources only when they need to

transmit. These demands can change over time, and

the resources are release after the user ends to send

data. The current optical network operate pseudo-

statically. This is the resources are allocated to the

user during very long periods of time (for instance,

during a contract), which can be considered as perma-

nent on the network operation. Hence, our research is

focused on the static scenario.

One possible method to solve the RSA is by op-

timization. In literature there are several solutions.

However these approaches are highly complex, due to

the space state exponential growth, bringing scalabil-

ity problems and inability to obtain a solution in a rea-

sonable time for real network topologies. The com-

plexity of these models have been widely analyzed in

literature by L

opez and Velazco (2016) (L

opez and

Velasco, 2016), Simmons (2014) (Simmons, 2014) y

Talebi et al. (2014) (Talebi et al., 2014b).

Meza et al. (2016) (Meza et al., 2016) proposed

two optimization models for ring topologies: a pure

ILP model to solve the RSA problem simultaneously

(One Step Approach) and another model composed

by two steps (Two Step Approach) denoted as Short-

est Path Optimal Assignment (SP-OA). The last strat-

egy uses a shortest path heuristic to solve the routing

problem and optimization to solve the spectrum as-

signment. Both schemes show the prior mentioned

difﬁculties, in which both strategies obtain results un-

til 8 and 9 nodes ring topologies, respectively.

The prior discussion reveals that it is necessary to

develop heuristics solution allowing to obtain near op-

timal solutions with scalability to real network topolo-

gies.

The RSA problem is usually solved in two

stages (Wen et al., 2011). First, the route is assigned,

for instance the shortest path. Then, the amount of

FSUs on each link is computed, considering that the

spectrum chosen on all the links on the user path must

be the same (Takagi et al., 2011). Notice that the

previous restriction allows to satisﬁed the wavelength

continuity constraint involved in optical networks.

The standard spectrum allocation (SA) techniques

found in literature are Random-Fit (RF), Most-

Used (MU) and First-Fit (FF) among several varia-

tions (Talebi et al., 2014a). RF assigns the frequency

spectrum randomly, leading to high spectrum frag-

mentation (unused spectrum) (Ahumada et al., 2014).

MU chooses the slots that are most-used in the net-

work. On the other side, FF is the most common and

fastest method used to date. In fact, Abkenar y Rah-

bar (2017) (Shirin Abkenar and Ghaffarpour Rahbar,

2017) shows that most approaches use the First-Fit

scheme. In this scheme the FSUs are considered as a

sequence. When searching for an available FSU, the

search starts on the ﬁrst FSU in the sequence. The

request is accepted if the needed number of contigu-

ous slot is available on all the links belonging to the

predetermined user ﬁxed path. Otherwise, the same

request is send to the next slots on the sequence. The

process continues on the same way, until there are suf-

ﬁcient contiguous FSU available on all the links of

SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

270

the path (Koganti and Sidhu, 2014; Chatterjee et al.,

2013).

As consequence of the SA methods, there is spec-

trum fragmentation over the network frequency spec-

trum (Chatterjee et al., 2015; Christodoulopoulos

et al., 2011). This refers to fact that there might

by some free FSU in the middle area not been used

despite being available on the network. Said phe-

nomenon is important due to the fact it can produce a

meaningful waste of bandwidth, if not properly con-

trolled. Thus one of our objectives is to minimize the

spectrum fragmentation on the network.

In addition, it is also important the order to allo-

cate the resources to the user, affecting the network

capacity required and the spectrum fragmentation, as

pointed out by Simmons (2014) (Simmons, 2014) y

Talebi et al. (2014) (Talebi et al., 2014b), which in-

dicates that a decreasing order of user according to

their bandwidth and length obtains are the more efﬁ-

cient approaches.

3 SIMULATION STRATEGY

This section comprises the main contribution of the

article. First, we explain the model used and the asso-

ciated assumptions. Then, we explain the simulation

strategy to solve the RSA problem.

3.1 Model and Assumptions

We represent the network by a graph G = (N , L),

where N is the set of nodes and L the set of direc-

tional links, with cardinalities |N | = N and |L| = L.

The set of users U ⊂ N

, with cardinality |U| =

U, is composed by all the source-destination pairs.

Each u element contains several values such as:

,bw

i, where s

is the source node, d

the

destination node, bw

is the number of adjacent FSUs

deﬁned per user, considering that i

is the index refer-

encing the ﬁrst frequency spectrum allocated.

User u transmission follows a particular route or

path between its source and its terminal, expressed

by r

, and we denote by R = {r

| c ∈ U} the set

of routes used. These routes are ﬁxed and can be

computed by any algorithm available in the litera-

ture (Dijkstra, 1959; Jara et al., 2017; Koganti and

Sidhu, 2014) prior to network operation. Due to the

fact that the network topologies considered are ring

topologies, we can divide the set R in two subsets.

The subset

−→

R ⊆ R contains the path in clockwise di-

rection, and the subset

←−

R ⊆ R composed by the coun-

terclockwise routes.

In EON, the frequency spectrum is divided in

small frequency segments, denoted as Frequency Slot

Units (FSU). Then, let BW = {bw

|u ∈ U} be the set

of bandwidth requirements measured as a number of

FSU per user u ∈ U.

Let C = {c



| ∈ L} be the set containing the ca-

pacity of each network link  ∈ L, in which the capac-

ity c



is the number of FSU allocated to the link , and

let F = { f

i

|i ≤ c



, ∈ L} be the set of FSU allocated

on each network link, where i is the FSU index and 

the corresponding network link.

3.2 Routing Strategy

The routing problem consists in ﬁnding, for each con-

nection, a route to be followed by the data to be trans-

mitted, while taking into account some spectrum as-

signment scheme, and with the smallest cost possible.

In this paper, the users path are computed ﬁxed, only

one per user, prior the network operation.

In this paper, we consider a ring network topology

with N nodes, in which every user has two possible

routes: clockwise or counterclockwise. The path then

is chosen as the shortest path measured by the num-

ber of hops from source to destination. However, in

the case the ring has a pair number of nodes (par value

of N), the users communicating through the network

diameter, these are the users with a distance equals to

N/2 between the source and destination node, both

clock and counter-clock paths are equal in length. In

these cases, the criteria to assign the routes is to bal-

ance the network links, thus half (or close to half) of

the user will have a clockwise route, and the remain-

ing user will have a counterclockwise path.

In algorithmic form, the procedure can be written

as shown in Figure 1. Symbolically, its execution will

be written R := Routing(U,R ), since its output is the

set of all the users path.

3.3 Spectrum Allocation Strategy

The spectrum assignment (SA) problem consists in

ﬁnding, for each user u ∈ U, the same FSUs available

on all the links in its route. This means, it searches a

number of adjacent slots on each link, using the same

FSU in the whole route. Here we use the First-Fit

spectrum assignment approach since it is simple and

performs adequately in terms of network cost with

a small computational overhead. In a nutshell, the

method orders the different FSU available, and se-

quentially searches until there is one available on the

whole path; if not, the method allocates the user at

the end, after the last FSU allocated on the links in

the user path.

A Spiral Approach to Solve the Routing and Spectrum Assignment Problem in Ring Topologies for Elastic Optical Networks

271

Algorithm 1: Routing.

1: procedure ROUTING(U, R )

2: balance ← 0

3: for all u ∈ U do

4: Calculate routes of minimum length

5: if there is just one result then

6: if r

is clockwise then

−→

R =

−→

R ∪ r

8: else

←−

R =

←−

R ∪ r

10: else

11: if balance > N/2 and N%2 = 0 then

12:

←−

R =

←−

R ∪ r

13: else

14:

−→

R =

−→

R ∪ r

15: balance ← balance + 1

Figure 1: Spiral routing allocation example.

To assign each user we use the First-Fit scheme to

solve the spectrum allocation. However, we use a pre-

deﬁned order to follow the FF allocation. The main

idea of our proposal is to create subsets of users ac-

cording to some given criteria. Then, we follow said

subsets to execute the FF algorithm, taking into ad-

vantage the form of the topology, this means to try to

form rings or a spiral when allocating each user. In

this way giving some order when assigning the fre-

quency spectrum. To illustrate this way of spectrum

allocation in ﬁgure 1 we present a spiral spectrum al-

location. In ﬁgure 1 the circumference surrounding

the ring represents a FSU, and the bigger the circle

radio, the bigger is the FSU index. The arrows on the

ﬁgure indicate both the path and the resource alloca-

tion direction. The order of the user is chosen in a

spiral order, hence the user allocation order is: 1-3,

3-5, 5-2, 2-4, 4-1. Remark that the spiral resource al-

location is obtain since the next user to be allocated

has a source node equal to the destination node of the

prior user in the list.

Let U

⊂ U be the set of user with the same band-

width requirements b = bw, with bw ∈ BW . Thus,

Algorithm 2: DB-SFF.

procedure DB-SFF

R =

for all  ∈ L do



= 0

Routing(U, R );

,...,U

} = Classify(BW, U);

for each U

∈ U do

totalAssigned ← 0

sort(U

)  sort by length, decreasing order

Assign(U

[1])

nextSource ← U

[1].d

while totalAssigned 6= |U

| do

for j ← 0 to |U

| do

if U

[ j].s

= nextSource then

Assign(U

[ j])

nextSource ← U

[ j].d

else if j = |U

| then

nextSource ← nextSource + 1

return U,R ,C

the set of user U is decomposed in subsets U

, each

subset is sorted according to the route length in de-

creasing order. Then, we start to allocate the user

using the subset U

with bigger bandwidth require-

ments, this is the subset U

with b with a higher value.

The spectrum assignment is made following the First-

Fit strategy, but following a Spiral order, as previously

explained. If there is not an user on U

to fulﬁll the

Spiral rule, then the next user to be allocated will be

the next in subset. If all user in U

have been allo-

cated, then we continue with the next U

subset, until

all the network user their spectrum assigned.

The pseudo-code of the procedure can be writ-

ten as shown in Figure 2. The inputs of the simula-

tions are the network topology (G(N ,L)), and the set

of users (U) with its respective bandwidth demands

(BW ). On the other hand, the outputs are the set of

routes (R ) connecting all the user in U, the set of all

the links capacity (C ) measured as number of FSUs,

and the set of FSUs allocated on each network link

(F ).

4 NUMERICAL EXAMPLES

To compare our proposal with other methodologies,

it is necessary to evaluate their performances. The

most important metrics for the RSA problem are: the

cost of the network and the spectrum fragmentation

obtained.

As commonly used (Ramaswami et al., 2009;

Simmons, 2014; Talebi et al., 2014b), in this work

SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

272

Table 1: Table comparing the proposed method (DB-SFF) with both optimization methods proposed in (Meza et al., 2016)

for ring network topologies with bandwidth requirements proportional to the user path length.

Nodes

net

SFR [%] Time [s]

Optimal SP-OA DB-SFF Optimal SP-OA DB-SFF Optimal SP-OA DB-SFF

5 54 54 54 3,70 3,70 7,40 0.375 0,031 0,00057

6 114 118 114 0,00 3,39 0,00 49,23 4,219 0,00074

7 198 198 212 1,01 1,01 7,54 997,5 58,01 0,00092

8 353 372 352 0,28 3,49 0,00 429916 21600 0,00121

9 - - 572 - - 5,59 - - 0,00140

10 - - 657 - - 5,78 - - 0,00177

25 - - 13563 - - 4,96 - - 0,02469

50 - - 100822 - - 2,87 - - 0,21571

the total network cost C

net

is deﬁned as the sum of all

FSU of all network links, that is,

net

∑



(1)

, where c



is the spectrum capacity assigned to link .

This deﬁnition is justiﬁed because the cost of most

components in an optical network is mainly affected

by this parameter. In fact, it determines how many

infrastructure resources are needed to achieve the net-

work operation (Banerjee and Mukherjee, 2000).

As mentioned in the state of art, the non-used FSU

on the network link should be avoided. Thus the spec-

trum fragmentation SFR (percentage) is the sum of all

the fragmented FSU in relation to the network total

cost C

net

. This is

SFR = 100 ·

Number of Non-used FSU

net

. (2)

In case the SFR value obtained is 0, the resource allo-

cation is optimal, thus there are not unused spectrum

portions.

As prior mentioned, First-Fit is the most refer-

enced scheme to solve the spectrum assignment prob-

lem since it is a fast and simple strategy with good

performance. In the text, we called it FF. In conse-

quence, we adopt this approach in all the numerical

examples. However, recall that the Spiral rule to al-

locate the user on the network alters the FF strategy

by deﬁning an speciﬁc order to assign the user on the

network following a spiral o concentric rings order. In

the experiments, we denoted it as SFF.

To judge the methods under several scenarios, we

evaluate them by means of simulation on diverse ring

topologies, having different sizes. For a fair compar-

ison, the procedures considered here use a ﬁxed rout-

ing shortest path (estimated by Dijkstra’s algorithm).

4.1 Comparison with Optimization

Models

First, we compared the results obtained by our pro-

posal (DB-DFF) and the optimization methods pro-

posed by Meza et.al. (Meza et al., 2016), these are

the full optimization method (Optimal) and the Two

Steps Approach denoted as Shortest Path Optimal As-

signment (SP-OA).

Meza et al. (Meza et al., 2016) deﬁned two forms

to deﬁne the users bandwidth requirements, these are:

proportional to the users path length, and inversely

proportional to the users route length. In Tables 1 and

2 we present the results obtained the Optimal, SP-OA

and our DB-SFF, showing the network total cost C

net

spectrum fragmentation SFR and the time needed to

execute the method.

As previously discussed on the state of art section,

due to the RSA problem complexity, both optimiza-

tion methods can be executed on small networks. De-

spite our strategy can be executed in topologies with

50 (and more) nodes, on the Table 1 with propor-

tional bandwidth requirements we can compare our

proposal to optimization only from 5 to 8 node ring

networks, and in the Table 2 with inversely propor-

tional bandwidth requirements we can contrast the

strategies from 5 to 10 node rings.

We can see in Tables 1 and 2 that in some cases

the DB-SFF is able to achieve the optimum solution,

however, in most cases it does not reach said objec-

tive. We can conclude that our proposal achieves re-

sults close to the optimal solution on the studied sce-

narios.

4.2 Comparison with Heuristic Models

In this section we compare the same metrics analyzed

on the previous section (C

net

and SFR) for ring net-

A Spiral Approach to Solve the Routing and Spectrum Assignment Problem in Ring Topologies for Elastic Optical Networks

273

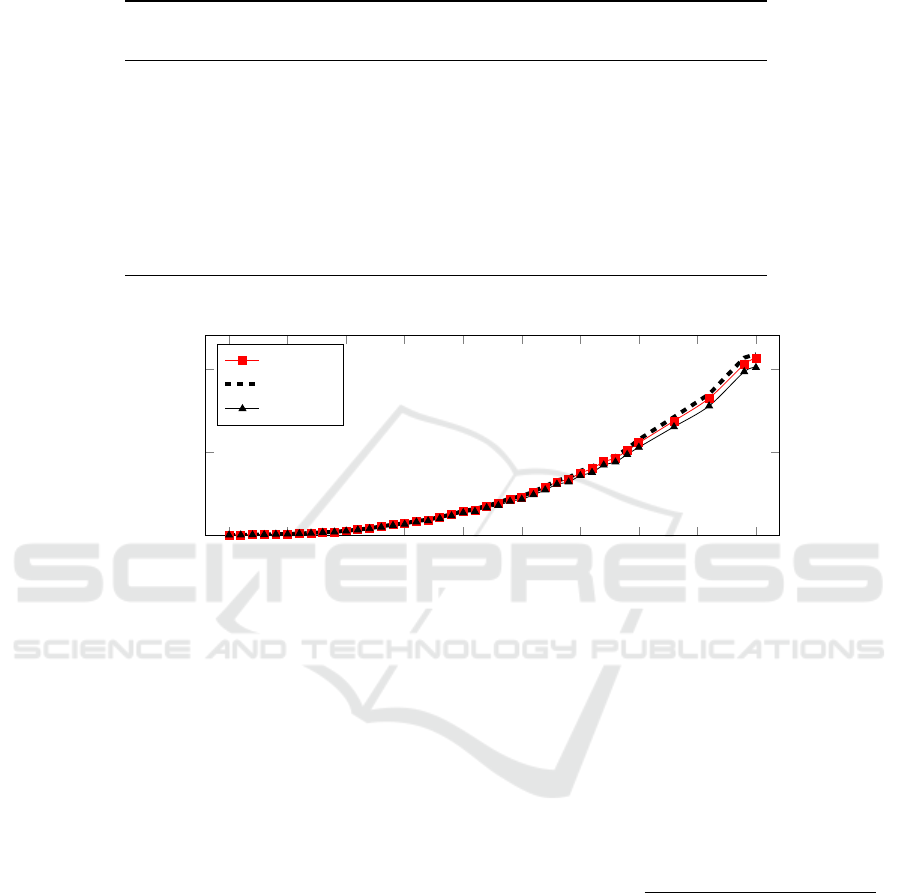
Table 2: Table comparing the proposed method (DB-SFF) with both optimization methods proposed in (Meza et al., 2016)

for ring network topologies with bandwidth requirements inversely proportional to the user path length.

Nodes

net

SFR [%] Time [s]

Optimal SP-OA DB-SFF Optimal SP-OA DB-SFF Optimal SP-OA DB-SFF

5 42 42 44 4,76 4,76 9,09 0.265 0,031 0,00059

6 102 104 102 0,00 1,92 0,00 5.843 5,969 0,00068

7 140 142 159 0,00 1,40 11,95 18,063 0,344 0,00088

8 288 292 316 0,00 1,37 8,86 19,907 202,5 0,00106

9 - 362 412 - 0,55 12,62 - 752,9 0,00129

10 - 646* 718 - 5,88 12,25 - 21600 0,00215

25 - - 7311 - - 9,72 - - 0,01972

50 - - 63238 - - 7,89 - - 0,17934

45 50

0.5

·10

Nodes

net

DL-FF

DB-FF

DB-SFF

Figure 2: C

net

obtained by DB-SFF, DB-FF and DL-SFF on ring topologies between 5 to 50 nodes.

works from 5 to 50 nodes regarding to the best strate-

gies in literature (Simmons, 2014). These are:

Decreasing Bandwidth First Fit (DB-FF): We use

the same routing strategy explained in section 3. The

users are sorted by their bandwidth requirements in

a decreasing order, and sequentially searching for a

spectrum available using the usual First-Fit technique.

Decreasing Length First Fit (DL-FF): Again, we

use the same routing than before. The users are sorted

in decreasing order according to their route length,

and follows the First-Fit scheme to solve the spectrum

allocation.

The methods here presented are executed us-

ing three bandwidth requirements strategies: propor-

tional, inversely proportional to the route length and

arbitrarily, counting 117 scenarios total. Due to lack

of space, only the proportional scenario is presented

in the text.

We can see in Figure 2, the total cost obtained by

all the heuristic method analyzed here (DB-FF, DL-

FF and our proposal DB-SFF) is presented. Despite

the algorithm, the total network cost increases simi-

larly (order N

) as the number of network nodes in-

creases on the ring topologies.

Even though Figure 2 helps us to see the rela-

tion between C

net

and the number of nodes, we can

not clearly visualize the performance of our proposal

against the DB-FF and DL-FF. Thus in Table 3 we il-

lustrate the mean savings (Savings), measured in per-

centage, obtained by our proposal respect to the best

approaches in literature (DB-FF and DL-FF) for the

three bandwidth requirements strategies. The Savings

are obtained according to the following equation:

Savings[%] = 100 ·

net

(Re f )− C

net

(DB − SFF)

net

(Re f )

(3)

where Re f is the method to be compared to.

In Table 3 we can see that DB-SFF presents con-

sistent savings in all cases respect to DB-FF and DL-

FF, obtaining in the worst case scenario mean savings

of 4.83% in all the compared scenarios.

4.2.1 Spectrum Fragmentation

Finally, in this section we analyze the spectrum frag-

mentation obtained by the methods compared in here.

Figure 3 shows the spectrum fragmentation ob-

tained by the DB-SFF, DB-FF and DL-FF for ring

SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

274

45 50

Nodes

SFR

DB-SFF

DB-FF

DL-FF

Figure 3: SFR comparison between DB-SFF and DB-FF according to the number of nodes.

45 50

0.5

·10

Nodes

Fragmented FSU

DL-FF

DB-FF

DB-SFF

Figure 4: Number of empty FSU according to the number of nodes for DB-FF and DB-SFF.

Table 3: Mean C

net

savings obtained by DB-SFF respect the

reference algorithms.

Reference Proportional Arbitrary Inversely

DB-FF 6.92% 6.14% 13.06%

DL-FF 4.83% 7.57% 5.60%

Table 4: Mean SFR obtained by the three algorithms on the

three bandwidth requirements scenarios.

Algorithm Proportional Arbitrary Inversely

DB-SFF 3.96% 7.57% 8.4%

DB-FF 9.24% 9.47% 13.99%

DL-FF 11.03% 13.27% 20.57%

topologies between 5 and 50 nodes for the propor-

tional bandwidth requirements scenario. In Figure 3

is shown that for all network topologies the spectrum

fragmentation of DB-SFF is lower than DB-FF. In

comparison to the DL-FF in Figure 3 there is a tighter

difference. However, except a few cases, our proposal

obtains better results than DL-FF. The prior can be

shown in Table 4 where the mean spectrum fragmen-

tation (SFR) is presented for all the methods and all

the bandwidth requirements strategies previously pre-

sented.

Finally, in Figure 4 we present the total number of

slots fragmented on the network obtained by the three

methods analyzed in this article. It is clear that our

methods obtains much better results in terms of spec-

trum fragmentation than the commonly used RSA so-

lutions, obtaining in the worst-case scenario an 8.4%

percentage of spectrum fragmentation.

5 CONCLUSIONS

In this work, we present a novel method to solve the

crucial problem known as Routing and Spectrum Al-

location. Our method computes: all the users path by

the shortest path algorithm, but balancing the amount

of users on the links; and the amount of slots (fre-

quency spectrum) required by each user following the

First-Fit strategy. However, the order used to allocate

the users is deﬁned in a decreasing order of bandwidth

requirements, using a spiral approach to follow the

users assignment.

The optimization models obtain results only for

small networks, with an execution time prohibitively

high. Hence, we consider the optimal as an ideal,

but no feasible strategy. On the other hand, our

A Spiral Approach to Solve the Routing and Spectrum Assignment Problem in Ring Topologies for Elastic Optical Networks

275

method has results close optimal solutions with ap-

proximately a 6,6% of network fragmentation. More-

over, the proposed method shows better results than

the best strategies from the literature, with savings in

the order of 40% in terms of network fragmentation.

Notice that, for the prior comparison we perform 117

scenarios of simulation for each heuristic method, and

almost a 100% of the results performed better than the

heuristic strategies available in the literature.

Further work would be to solve the RSA prob-

lem on mesh network topologies and considering a

dynamic network operation, adjusting the strategy of

this work to said contexts.

ACKNOWLEDGEMENTS

This work received ﬁnancial support from FONDEF

ID14I10129, CONICYT. This project and institution

is then gratefully acknowledged.

REFERENCES

Ahumada, R., Leiva, A., Alonso, F., Fingerhuth, S., and

Far

ıas, G. (2014). Spectrum Allocation Algorithms

for Elastic DWDM Networks on Dynamic Operation.

IEEE Latin America Transactions, 12(6):1012–1018.

Banerjee, D. and Mukherjee, B. (2000). Wavelength-

routed optical networks: Linear formulation, resource

budgeting tradeoffs, and a reconﬁguration study.

IEEE/ACM Transactions on Networking, 8(5):598–

607.

Chatterjee, B. C., Sarma, N., and Oki, E. (2015). Routing

and Spectrum Allocation in Elastic Optical Networks:

A Tutorial. IEEE Communications Surveys and Tuto-

rials, 17(3).

Chatterjee, B. C., Sarma, N., and Pratim Sahu, P. (2013).

Review and Performance Analysis on Routing and

Wavelength Assignment Approaches for Optical Net-

works. IETE Technical Review, 30(1):12–23.

Christodoulopoulos, K., Tomkos, I., and Varvarigos, E. a.

(2011). Elastic Bandwidth Allocation in Flexible

OFDM- based Optical Networks. Journal of Light-

wave Technology, 29(9):1354 – 1366.

Dijkstra, E. W. (1959). A note on two problems in connec-

tion with graphs. Numerische Mathematik, 1(1):269–

271.

Ellis, A. D., Suibhne, N. M., Saad, D., and Payne, D. N.

(2016). Communication networks beyond the capac-

ity crunch. Philosophical Transactions of the Royal

Society A: Mathematical, Physical and Engineering

Sciences, 374(2062):20150191.

Gerstel, O., Jinno, M., Lord, A., and Yoo, S. J. B. (2012).

Elastic optical networking: a new dawn for the optical

layer? Communications Magazine, IEEE, 50(2):s12–

s20.

Iversen Villy, B. (2002). Teletrafﬁc Engineering Handbook.

Jara, N., Vallejos, R., and Rubino, G. (2017). A method for

joint routing, wavelength dimensioning and fault tol-

erance for any set of simultaneous failures on dynamic

WDM optical networks. Optical Fiber Technology,

38:30–40.

Koganti, R. T. and Sidhu, D. (2014). Analysis of routing

and wavelength assignment in large WDM networks.

In Procedia Computer Science, volume 34, pages 71–

78.

Layec, P., Morea, A., Vacondio, F., Rival, O., and Antona,

J.-C. (2013). Elastic optical networks: The global evo-

lution to software conﬁgurable optical networks. Bell

Labs Technical Journal, 18(3):133–151.

opez, V. and Velasco, L., editors (2016). Elastic Optical

Networks. Optical Networks. Springer International

Publishing, Cham.

Meza, C., Jara, N., Albornoz, V. M., and Vallejos, R. (2016).

Routing and spectrum assignment for elastic, static,

and without conversion optical networks with ring

topology. In 2016 35th International Conference of

the Chilean Computer Science Society (SCCC), pages

1–8.

Ramaswami, R., Sivarajan, K., and Sasaki, G. (2009). Op-

tical Networks: A Practical Perspective, 3rd Edition.

Morgan Kaufmann Publishers Inc., San Francisco,

CA, USA, 3rd edition.

Sambo, N., Castoldi, P., Cugini, F., Bottari, G., and Iovanna,

P. (2012). Toward high-rate and ﬂexible optical net-

works. Communications Magazine, IEEE, 50(5):66–

72.

Shirin Abkenar, F. and Ghaffarpour Rahbar, A. (2017).

Study and Analysis of Routing and Spectrum Al-

location (RSA) and Routing, Modulation and Spec-

trum Allocation (RMSA) Algorithms in Elastic Opti-

cal Networks (EONs).

Simmons, J. M. (2014). Optical Network Design and Plan-

ning. Optical Networks. Springer International Pub-

lishing, Cham.

Takagi, T., Hasegawa, H., Sato, K., Sone, Y., Kozicki, B.,

Hirano, A., and Jinno, M. (2011). Dynamic routing

and frequency slot assignment for elastic optical path

networks that adopt distance adaptive modulation. In

2011 Optical Fiber Communication Conference and

Exposition and the National Fiber Optic Engineers

Conference, number March 2011, pages 1–3.

Talebi, S., Alam, F., Katib, I., Khamis, M., Salama, R., and

Rouskas, G. N. (2014a). Spectrum management tech-

niques for elastic optical networks: A survey. Optical

Switching and Networking, 13:34–48.

Talebi, S., Alam, F., Katib, I., Khamis, M., Salama, R., and

Rouskas, G. N. (2014b). Spectrum management tech-

niques for elastic optical networks: A survey.

Waldman, H. (2018). The Impending Optical Network Ca-

pacity Crunch. Sbfoton Conference, pages 0–3.

Wen, K., Yin, Y., Geisler, D. J., Chang, S., and Yoo, S. J. B.

(2011). Dynamic On-demand Lightpath Provision-

ing Using Spectral Defragmentation in Flexible Band-

width Networks. In 2011 37th European Conference

and Exhibition on Optical Communication, volume 1,

Washington, D.C. OSA.

SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

276