
Test Suite Minimization of Evolving Software Systems:
A Case Study
Amit Goyal
1
, R. K. Shyamasundar
1
, Raoul Jetley
2
, Devina Mohan
2
and Srini Ramaswamy
3
1
Indian Institute of Technology Bombay, Mumbai, India
2
ABB Corporate Research, Bangalore, India
3
ABB Inc., Cleveland, U.S.A.
Keywords:
Minimization, Test Suite Optimization, Regression Testing, EDDL, Greedy, GE, GRE.
Abstract:
Test suite minimization ensures that an optimum set of test cases are selected to provide maximum coverage of
requirements. In this paper, we discuss and evaluate techniques for test suite minimization of evolving software
systems. As a case study, we have used an industrial tool, Static Code Analysis (SCAN) tool for Electronic
Device Description Language (EDDL) as the System Under Test (SUT). We have used standard approaches
including Greedy, Greedy Essential (GE) and Greedy Redundant Essential (GRE) for minimization of the
test suite for a given set of requirements of the SUT. Further, we have proposed and implemented k-coverage
variants of these approaches. The minimized test suite which is obtained as a result reduces testing effort
and time during regression testing. The paper also addresses the need for choosing an appropriate level of
granularity of requirements to efficiently cover all requirements. The paper demonstrates how fine grained
requirements help in finding an optimal test suite to completely address the requirements and also help in
detecting bugs in each version of the software. Finally, the results from different analyses have been presented
and compared and it has been observed that GE heuristics performs the best (run time) under certain conditions.
1 INTRODUCTION
Testing is the process of executing a program with
the intent of finding errors. It helps in reducing the
maintenance cost of the software and accounts for the
maximum percentage of effort among all phases of
the software development life cycle. In an evolving
software, with the introduction of new functionali-
ties (progressive) and bug fixing (corrective), regres-
sion testing comes into the picture which ensures that
changes do not affect the existing software. Fixing
regression errors is much more complex than seeded
errors (B
¨
ohme et al., 2013). Formal verification can
guarantee the absence of errors, but requires clear
specifications and is very effort intensive. Thus, in
practice, regression testing is preferred (B
¨
ohme and
Roychoudhury, 2014). New software development
techniques like component and agile software devel-
opment have led to a substantial increase in the com-
plexity of regression testing (Yoo and Harman, 2012).
Further, with the advent of Internet of Things, there
has been a proliferation in embedded software, which
needs to be tested against many non-functional re-
quirements in addition to the functional requirements.
This again adds up to the complexity of regression
testing. Interaction with the non-deterministic physi-
cal environment also poses a big challenge to the test-
ing of such systems (Banerjee et al., 2016).
In continuously evolving systems, whenever bugs
in a previous version are fixed and the system is re-
built, the naive solution is to run all the test cases
which is very cumbersome and time consuming. As
the software evolves, usually the size of the software
and the number of test cases increase which inflate
the testing effort and it becomes infeasible to run all
the test cases. Thus, it becomes necessary to find the
representative (minimal) set of test cases required to
cover all requirements in an effective manner. As the
software evolves, only the minimized test cases are
checked instead of all existing test cases. This helps
in reducing the testing time, which in turn reduces the
overall time for software development.
Systems that are being designed, need to satisfy
certain set of specified characteristic properties. Some
tools may be designed to check if they satisfy these
properties. One such effort has been the SCAN tool
used for static code analysis of programs written in
EDDL (Mohan and Jetley, 2018). The tool helps in
226
Goyal, A., Shyamasundar, R., Jetley, R., Mohan, D. and Ramaswamy, S.
Test Suite Minimization of Evolving Software Systems: A Case Study.
DOI: 10.5220/0007842502260237
In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 226-237
ISBN: 978-989-758-379-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

debugging and issuing warnings for commonly oc-
curring software errors in EDDL programs. For re-
gression testing of the tool, it is important to find the
minimal test cases from a given test suite to cover all
its requirements. The input here is a set of programs
(test cases), P; a set of patterns of errors to be captured
(requirements), R; the system to be tested (the SCAN
tool) and a mapping between P and R. The result of
the minimal coverage analysis is a set of programs,
p ⊆ P, that are sufficient to cover all the requirements,
r ∈ R . It is useful to find p as in all the future correc-
tive versions of the tool, testing p should be enough to
cover all the requirements. We have adapted and im-
plemented some of the approaches (Greedy, GE and
GRE heuristics) of requirements coverage to perform
a case study on the SCAN tool (Tallam and Gupta,
2006; Chen and Lau, 1996). From a reliability per-
spective, one could say that each property should be
covered at least by two test cases, or k test cases for
some k. To this effect, k-coverage variants of these
heuristics have also been implemented. The value
of k can be chosen based on the resources available
in hand. The effectiveness of all these heuristics has
been demonstrated and evaluated. It has been shown
that if more fine grained requirements are considered,
it leads to better coverage. We shall describe our ap-
proach and our experience in using such heuristics in
the context of the SCAN tool (SUT).
The key contributions of this paper are: (i) appli-
cation of Greedy, GE and GRE heuristics to an in-
dustrial project (ii) proposal of k-coverage variants of
these heuristics (iii) comparison of all these heuristics
on the project (iv) recommendation to use GE heuris-
tics under certain conditions (v) fine grain the require-
ments and its impact on coverage.
The rest of the paper is structured as follows. Sec-
tion 2 gives a background on EDDL, SCAN tool and
various minimization approaches. The approaches
used to find minimal cover for the case study are de-
scribed in Section 3. Implementation and the analy-
ses details are covered in Section 4. Comparison of
the various approaches with respect to each analysis
is done in Section 5. Finally, we conclude in Section
6 along with the future directions.
2 BACKGROUND
2.1 EDDL
Electronic Device Description Language (EDDL) is
a structured and descriptive programming language
for configuration and engineering of digital devices
that conforms to the IEC 61804-3 standard. Since it
is a text based language, it supports cross platform
compatibility and it is independent of control plat-
forms and operating systems. EDDL describes func-
tion blocks, device parameters with their dependen-
cies, along with default and initial values of each de-
vice type. This helps in getting a clear picture of
the device before it is actually present in the system.
EDDL is derived from ANSI C and therefore sup-
ports interactive methods, domain-specific data struc-
tures and nesting among different sections. As EDDL
supports multiple protocols and device types, it pro-
vides consistency and uniformity throughout the sys-
tem and enables manufacturers to create a single en-
gineering environment (IEC-61804-3, 2015).
2.2 SCAN Tool for EDDL
SCAN tool utilizes the concept of static code analy-
sis to detect potential sources of run time errors in the
control code at the compile time itself (Mohan and
Jetley, 2018). It ensures compliance to good program-
ming practices and coding guidelines. It is helpful as
it identifies faults (which can cause system failures
later) at an early stage of development. It can be used
for other domain-specific languages that have similar
structure and characteristics as EDDL (Mandal et al.,
2018). It generates Abstract Syntax Tree (AST) and
Control Flow Graph (CFG) for the control code with
the help of a customized parser (Irony parser) (Irony-
v1.0.0, 2018). AST is used to check syntactic and
pattern based matching while CFG is used for inter-
val domain based data flow analysis to compute range
of all the variables in the code. The tool generates a
.csv file that lists down the errors and warnings with
detailed description, line number and severity level.
A sample EDDL code is shown in the code listing
below. When this program is given as an input to the
SCAN tool, it reports (in a .csv file) syntactic errors
such as duplicate language definition on Line 3 and
use of assignment instead of equals on Line 9. It also
reports potential run time errors such as divide by zero
and arithmetic overflow on Line 11.
1 METHOD Method_Example
2 {
*3 LABEL "Example|en|Sample";
4 DEFINITION
5 {
6 int x, y, z;
7 x=10;
8 y=5;
*9 if(x=10)
10 {
*11 z=x/(x-2*y);
12 }
13 }
14 }
Test Suite Minimization of Evolving Software Systems: A Case Study
227

2.3 Minimization
Regression testing techniques can be classified into
three major categories (Yoo and Harman, 2012):
1. Minimization: Identifies and eliminates redun-
dant test cases from test suite.
2. Selection: Finds a subset of minimized test cases,
required to test changes in the software.
3. Prioritization: Schedules execution order of test
cases to increase early fault detection.
All of them are closely related to each other as
they have similar aims, inputs and solutions.
Test suite minimization can be mapped to minimal
set cover problem and is thus an NP complete prob-
lem. Therefore, most of the existing techniques are
based on heuristics. Horgan and London (1992) ap-
plied linear programming to the minimization prob-
lem. Later, GE and GRE heuristics were applied
which are essentially variations of the greedy algo-
rithm (Chen and Lau, 1996; Papadimitriou and Stei-
glitz, 1998). Offutt et al. (1995) considered several
different orderings of test cases instead of a fixed one
as in greedy approach. Marr
´
e and Bertolino (2003)
considered finding the minimal spanning set over
decision-to-decision graph. Tallam and Gupta (2006)
introduced delayed greedy approach. Jeffrey and
Gupta (2005, 2007) used two testing requirements;
branch coverage and all-uses coverage together which
provided better fault detection capability. The basic
idea is, if a test case is redundant in one but not in
other, even then it is selected. Black et al. (2004)
used bi-criteria approach and applied weighted sum
and integer linear programming to find optimal sub-
sets. Hsu and Orso (2009) considered multi-criteria
test suite minimization using prioritized optimization
and weighted sum approach. Yoo and Harman (2007)
treated the problem of time aware prioritization. Mc-
Master and Memon (2008) proposed minimization
based on call stack coverage. Harder et al. (2003)
used operational abstraction which is formal mathe-
matical description of program behavior and checked
if the removal of a test case changes the detected pro-
gram invariant. Schroeder and Korel (2000) proposed
an approach for black box testing minimization which
identifies for each output variable, the set of inputs
that can affect the output.
Out of all these techniques for test suite mini-
mization; Greedy, GE and GRE heuristics have been
used to find minimal cover of test cases, to cover all
the requirements of an industrial software system, the
SCAN tool.
3 APPROACH
It is proposed to implement Greedy, GE and GRE
heuristics along with their k-coverage variants to find
representative set of test cases to cover all the require-
ments.
3.1 Greedy Heuristics
The greedy approach selects the test case which satis-
fies the maximum number of uncovered requirements.
The approach is described in Algorithm 1 and it takes
the following inputs:
• map - mapping (mxn) between the test cases and
the requirements
• min - minimal test suite (initially {})
• cov - requirements covered by the selected test
cases in min (initially {})
The algorithm first checks if all the requirements
have been covered or not. If yes, it returns the mini-
mal test suite (min). Otherwise, it finds out the num-
ber of uncovered requirements covered by each test
case which is not in min. If none of these test cases
cover any uncovered requirements, then the cover-
age is not possible, the uncovered requirements are
printed and min is returned which covers the require-
ments in cov. Otherwise, the test case which cov-
ers the maximum uncovered requirements is added to
min. Then, all the uncovered requirements covered by
this test case are added to cov. The algorithm again
checks if all the requirements have been covered or
not and the entire procedure is repeated.
Based on time and resources at hand, test team
can also target to find 2-cover which covers all the re-
quirements twice. Similarly, 3, 4, ... k-cover can also
be found. The algorithm for k-coverage is similar to
Algorithm 1. It also takes k as an input which denotes
the required cover. Now, number of times a require-
ment has been covered needs to be tracked and it is
added to cov when it is covered by k test cases in min.
3.2 GE Heuristics
GE heuristics first selects essential test cases which
contain a requirement which is not satisfied by any
another test case and then it selects test cases which
satisfy the maximum number of uncovered require-
ments using greedy approach. The approach is de-
scribed in Algorithm 2 and it takes the same inputs
as taken by Algorithm 1. The algorithm scans each
uncovered requirement and checks if it is satisfied by
only one test case. Such a test case is considered as
ICSOFT 2019 - 14th International Conference on Software Technologies
228

Algorithm 1: Greedy approach.
Input: map, min, cov
Output: min
1 greedy (map, min, cov)
2 {
3 set flag = 0;
4 if !(all requirements ⊆ cov) then
5 set flag = 1;
6 end
7 while flag == 1 do
8 calculate number of uncovered
requirements covered by each test case
/∈ min;
9 if none of the test cases /∈ min cover any
uncovered requirements then
10 print coverage is not possible;
11 print the uncovered requirements;
12 return min;
13 end
14 else
15 add test case covering maximum
uncovered requirements in min;
16 update cov;
17 set flag = 0;
18 if !(all requirements ⊆ cov) then
19 set flag = 1;
20 end
21 end
22 end
23 return min;
24 }
Algorithm 2: GE heuristics.
Input: map, min, cov
Output: min
1 geheuristics (map, min, cov)
2 {
3 for (r = 1; r ≤ n; r + +) do
4 if r /∈ cov and is covered by only one test
case t
m
then
5 add t
m
in min;
6 update cov;
7 end
8 end
9 greedy (map, min, cov);
10 }
an essential test case and it is added to min. All un-
covered requirements which are covered by this test
case are added in cov. Once the scanning is complete,
a call is made to Algorithm 1.
In k-coverage, if a requirement is covered by ex-
actly k test cases then all those test cases are consid-
ered as essential test cases. For implementing k-cover
using GE heuristics, Algorithm 3 is described which
takes four inputs. First three inputs are similar to Al-
gorithm 2 and fourth input is k, which is the desired
cover. For each requirement which is not covered, the
algorithm calculates the number of test cases which
satisfy that requirement and store the test cases in set
choose. If the number is less than k then k-coverage
cannot be found. If it is greater than k, then there is no
essential test case for that requirement and thus algo-
rithm continues for the next requirement. If it is equal
to k, then the test cases in choose which are not in min
are added to min and cov is updated. A requirement
is added to cov when it is covered by k test cases in
min. Finally, the greedy algorithm is run to find the
k-coverage.
Algorithm 3: k-coverage GE heuristics.
Input: map, min, cov, k
Output: min
1 geheuristics (map, min, cov, k)
2 {
3 for (r = 1; r ≤ n; r + +) do
4 if r /∈ cov then
5 set count = 0;
6 set choose = {};
7 set count = number of test cases
covering r;
8 store all such test cases in choose;
9 if count < k then
10 print k-coverage is not possible;
11 end
12 else if count > k then
13 continue;
14 else
15 for each test case t ∈ choose do
16 if t /∈ min then
17 print test case t is an
essential test case;
18 add t to min;
19 update cov;
20 end
21 end
22 end
23 end
24 end
25 greedy (map, min, cov, k);
26 }
3.3 GRE Heuristics
GRE heuristics initially removes the redundant test
cases which satisfy a subset of the requirements sat-
isfied by other test cases and then it selects the essen-
tial test cases. If some requirements are still uncov-
ered, it selects the test cases greedily. Algorithm 4
describes the approach and it takes the same inputs as
taken by Algorithm 1. The algorithm checks whether
a test case t is a subset of another test case s for all
the possible pairs of test cases. If t is found to be a
subset of s then t is added in the redundant set, re-
Test Suite Minimization of Evolving Software Systems: A Case Study
229
moved from the test suite and the map is updated. A
call is made to Algorithm 2 when all the checking is
completed.
In k-coverage, if a test case is found to be a subset
of at least k test cases then the test case is considered
redundant and removed from the test suite. For im-
plementing k-cover using GRE heuristics, Algorithm
5 is described which takes four inputs similar to Algo-
rithm 3. For each test case t, the algorithm calculates
the number of test cases which are its superset. If the
number is greater than or equal to k, t is removed from
the test suite and map is updated accordingly. Finally,
a call is made to Algorithm 3.
Algorithm 4: GRE heuristics.
Input: map, min, cov
Output: min
1 greheuristics (map, min, cov)
2 {
3 for (t = 1; t ≤ m; t + +) do
4 for (s = 1; s ≤m; s + +) do
5 if ((map[t] ⊆ map[s]) && (s 6=
t) && (s /∈ redundant)) then
6 add t in redundant;
7 update map;
8 end
9 end
10 end
11 geheuristics (map, min, cov);
12 }
Algorithm 5: k-coverage GRE heuristics.
Input: map, min, cov, k
Output: min
1 greheuristics (map, min, cov, k)
2 {
3 for (t = 1; t ≤ m; t + +) do
4 set count = 0;
5 for (s = 1; s ≤m; s + +) do
6 if ((map[t] ⊆ map[s]) && (s 6=
t) && (s /∈ redundant)) then
7 count++;
8 end
9 end
10 if count ≥ k then
11 add t in redundant;
12 update map;
13 end
14 end
15 geheuristics (map, min, cov, k);
16 }
3.4 The Overall System
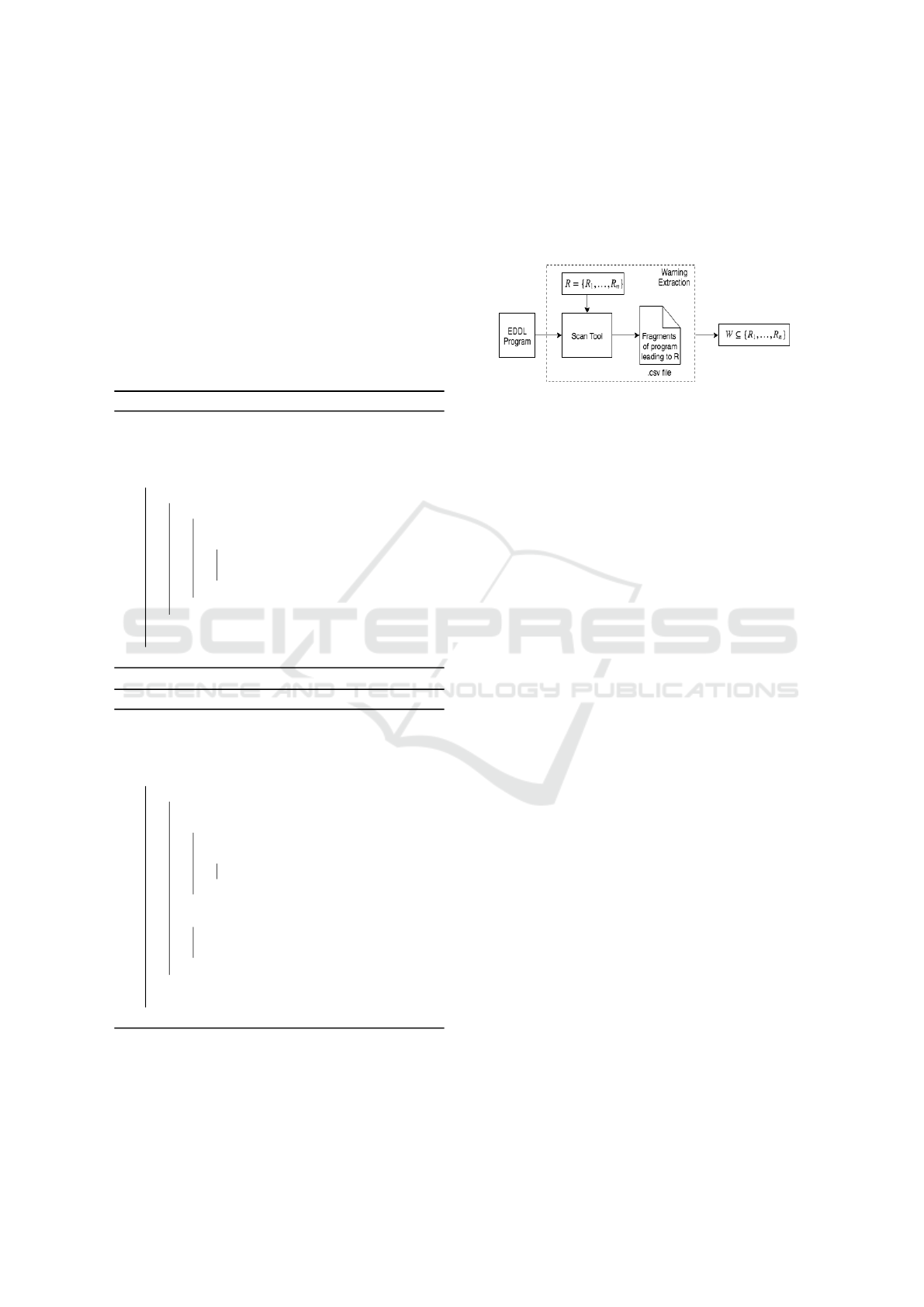
The SCAN tool takes an EDDL program and patterns
of errors (requirements), R to be captured as an input.
It generates a .csv file which contains all the the er-
rors/warnings (subset of R) in the input program with
detailed description, line number and severity level.
During warning extraction, the subset, W of patterns
of errors in R found in the input program is returned
as shown in Figure 1.
Figure 1: Warning extraction.
The overall process as shown in Figure 2 is fol-
lowed. For the requirement coverage of SCAN tool,
a set of EDDL programs/test cases, P are generated
in each analysis. During warning extraction, for each
test case P
i
, a set of warnings, W
i
is generated. Next,
a mapping between test cases, P and requirements, R
is obtained. The mapping is fed to Greedy, GE and
GRE heuristics to obtain a minimal set of programs,
p ⊆ P, which is sufficient to cover all requirements in
R.
4 IMPLEMENTATION
The proposed algorithms have been implemented in
Dev C++ 5.11 on Windows 10. In one of the ver-
sions of the SCAN tool, patterns of errors (require-
ments) listed in Table 1 are covered, based on the
Software Requirements Specification (SRS) docu-
ment provided by domain experts. A brief explana-
tion of these requirements is given later in this sec-
tion.
Initially, in analysis 1, test cases provided by test-
ing team are considered and a mapping is constructed
between the test cases and the requirements as shown
in Table 2 where the rows T1, T2 ... T25 represents
the test cases and the columns 1, 2 ... 21 represents
the requirements R1, R2 ... R21. If a cell entry C
i j
is 1 then test case T
i
leads to error j and 0 if it does
not. The mapping is fed to Greedy, GE and GRE
heuristics and it is found that 8
th
, 14
th
, 18
th
and 19
th
requirements cannot be covered. These requirements
are removed (reported as uncovered requirements to
be taken care in the next version of the tool) in the
refined mapping (having 17 requirements) which is
fed again to the three heuristics. 2-cover is calculated
using k-coverage Greedy, GE and GRE heuristics af-
ter removing requirement 15 (covered by only 1 test
case). Similarly, 3-cover is calculated on further re-
ICSOFT 2019 - 14th International Conference on Software Technologies
230

Figure 2: Overall process.
Table 1: Coarse grained requirements.
No. Requirement
R1 Missing mandatory menus
R2 Unnecessary attributes usage in constructs
R3 Archaic built-ins usage
R4 Redefinition/duplicate definition
R5 Duplicate language definition
R6 Unsupported file format
R7 Enums defined but no value inside
R8 Incorrect variable names
R9 Use of assignment instead of equals
R10 Unused variables
R11 Uninitialized variables
R12 Multiple unit relationships not allowed
R13 String truncation
R14 Implicit cast
R15 Buffer overflow/underflow
R16 Arithmetic overflow/underflow
R17 Divide by zero
R18 Illegal arithmetic function calls
R19 Duplicate identifier
R20 Edit display usage
R21 Cyclic refresh relation
moving requirement 4 (covered by only 2 test cases).
The results are discussed in Section 5 in Table 9.
In analysis 1, test cases 5 and 19 cover most of the
requirements. To do a better analysis, each test case
is designed keeping in consideration the requirement
that is to be met. The obtained mapping given in Table
3 is then used in analysis 2. The results are discussed
in Section 5 in Table 9. k-coverage heuristics return
that 2-cover is not possible for requirements, 3, 4, 9,
15 and 21.
Although in analysis 2, coverage of requirements
is found but still many bugs exist in the system as the
requirements are considered at a very coarse grained
level. In analysis 3, minimal cover is found for fine
grained requirements. For each requirement, a brief
description and sub-requirements considered are enu-
merated below.
• R1: Mandatory menus may be missing in the pro-
gram. Sub-requirements are based on the manda-
tory menus specified by the user. SCAN tool
gives flexibility to the user to customize the list
of mandatory menus.
• R2: Some attributes may not be needed if a vari-
able is not used in a menu. Sub-requirements are
based on unrequired attributes.
• R3: Archaic or deprecated built-ins should not be
used. Sub-requirements are based on the the ar-
chaic built-ins specified by the user.
• R4: Redefinitions inside the import section are
not allowed at multiple levels and the variable be-
ing redefined must not be declared in the same
file. Sub-requirements are based on these two
conditions.
• R5: The language string should not be redefined.
Sub-requirements are based on number of dupli-
cations and their location.
• R6: Usage of unsupported file format should lead
to an error. Sub-requirements are based on user
specified unsupported formats.
• R7: If Enums are defined without any ini-
tialization, a warning should be issued. Sub-
requirements are based on enum types.
• R8: A warning should be issued if undeclared lo-
cal and global variables are used for displaying
their value inside a method. Sub-requirements are
based on the used display function and printing
format.
• R9: Usage of assignment operator inside a con-
ditional expression should be flagged. Sub-
requirements are based on level of nesting of the
if-else construct.
• R10: Declaration of an item that has been defined,
but not used within the scope of the application
must be flagged. Sub-requirements are based on
different types of items.
• R11: If a variable is defined but not initialized
before use, a warning should be issued. Sub-
requirements are based on different types of vari-
ables.
• R12: Multiple unit relationships between vari-
ables should be avoided, as it may lead to loops
and race conditions. Sub-requirements are based
on number of unit relationships.
• R13: Copying a larger string to a smaller string
may result in string truncation which should be
avoided. The assignment can be either be direct
or through another string variable leading to two
sub-requirements.
• R14: When assigning from one data type to an-
other data type, an explicit type cast must be used
to ensure it is done intentionally. To design sub-
requirements, double data type is cast into differ-
ent available data types.
Test Suite Minimization of Evolving Software Systems: A Case Study
231

Table 2: Mapping of test cases and requirements in analysis 1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
T1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T2 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T3 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0
T4 1 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0
T5 1 1 1 0 1 1 1 0 1 1 1 1 0 0 0 1 1 0 0 1 1
T6 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T7 1 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1
T8 1 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1
T9 1 1 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0
T10 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0
T11 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0
T12 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0
T13 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
T14 1 1 0 0 0 1 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0
T15 1 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T16 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T17 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T18 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T19 1 1 1 1 1 1 1 0 1 1 0 1 0 0 0 1 1 0 0 1 1
T20 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0
T21 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0
T22 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0
T23 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0
T24 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
T25 1 1 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0
Table 3: Mapping of test cases and requirements in analysis 2.
1 2 3 4 5 6 7 9 10 11 12 13 15 16 17 20 21
T1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
T2 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0
T3 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
T4 1 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0
T5 1 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0
T6 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0
T7 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0
T9 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0
T10 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
T11 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0
T12 1 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0
T13 1 1 0 0 1 1 1 0 1 1 0 1 0 1 1 1 0
T15 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0
T16 1 0 0 0 0 0 0 0 1 1 0 1 0 1 0 0 0
T17 1 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0
T20 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
T21 1 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0 1
• R15: This may occur when an array tries to ac-
cess an element outside its defined scope. Sub-
requirements are designed based on whether the
overflow or underflow is through an expression or
it is done explicitly.
• R16: Each variable type has fixed amount of
memory associated with it. The computations
may lead to an assignment to a variable, making
it too large or too small, for the variable type to
handle. Sub-requirements are based on different
variable types.
• R17: A run time error may occur if denomi-
nator of a division expression evaluates to zero.
Sub-requirements are based on different patterns
such as explicit division by 0, division by an ex-
pression evaluating to 0, conditional branch lead-
ing/not leading to divide by 0, or an assignment
after divide by 0.
• R18: Arithmetic expressions and functions may
be used with invalid arguments which should be
avoided. For example, arguments of logarithm
function may be negative. Sub-requirements are
based on whether the argument is explicitly spec-
ified, or it is a variable or an expression.
• R19: The use of duplicate identifiers should be
discouraged even when they are not in the same
scope. Sub-requirements are based on identifiers
for different items.
• R20: Usage of EDIT DISPLAY should be
flagged. One sub-requirement is kept for this.
ICSOFT 2019 - 14th International Conference on Software Technologies
232

Table 4: Fine grained requirements.
No. Sub-Requirement No. Sub-Requirement No. Sub-Requirement
R1a device root menu R8c put message-format 3 R14g unsigned short-double
R1b diagnostics root menu R8d display-format 1 R14h unsigned int-double
R1c offline root menu R8e display-format 2 R14i unsigned long-double
R1d process variables root menu R8f display-format 3 R14j unsigned long long-double
R1e root menu R8g acknowledge-format 1 R14k float-double
R1f upload variables R8h acknowledge-format 2 R15a explicit overflow
R1g download variables R8i acknowledge-format 3 R15b explicit underflow
R2a default value R9a if R15c expression overflow
R2b class R9b nesting level 2 R15d expression underflow
R2c help R9c nesting level 3 R16a int/long
R2d label R10a methods R16b short
R3a assign double R10b variables R16c long long
R3b dassign R10c collections R16d char
R3c fassign R10d arrays R16e unsigned char
R3d assign float R10e menus R16f unsigned short
R3e iassign R10f grids R16g unsigned int/long
R3f assign int R10g charts R16h unsigned long long
R3g vassign R10h images R16i float
R3h assign var R11a int R16j double
R3i float value R11b long R17a exp1/0
R3j fvar value R11c short R17b exp1/exp2 where exp2 valuates to 0
R3k int value R11d long long R17c conditional branch leading to divide by 0
R3l ivar value R11e char R17d conditional branch not leading to divide by 0
R3m acknowledge R11f unsigned char R17e assignment after divide by 0
R4a redefinition at multiple levels R11g unsigned short R18a log explicit
R4b redefinition twice R11h unsigned int/long R18b log variable
R5a single label R11i unsigned long long R18c log expression
R5b single help R11j float R19a methods
R5c double label R11k double R19b variables
R5d double help R12a 2 unit relations R19c collections
R5e single label help R12b 3 unit relations R19d arrays
R6a .tiff R13a direct assignment R19e menus
R6b .ppm R13b variable assignment R19f grids
R6c .pgm R14a int-double R19g charts
R6d .heif R14b long-double R19h images
R7a bit enumerated R14c short-double R20a edit display usage
R7b enumerated R14d long long-double R21a cycle of length 2
R8a put message-format 1 R14e char-double R21b cycle of length 3
R8b put message-format 2 R14f unsigned char-double R21c cycle of length 4
• R21: In a refresh relationship, cyclic dependency
can happen which should be avoided, e.g. vari-
able A is refreshed when variable B gets updated
and variable B is refreshed when variable A gets
updated. Sub-requirements are based on length of
the cycle.
A complete list of sub-requirements is given in Ta-
ble 4 where Rαβ represents requirement α and sub-
requirement β. Mapping for analysis 3 in the form
of adjacency list is given in Table 5. It is important
to note that the mapping has been done manually and
the analysis is only complete with respect to SRS and
sub-requirements listed in Table 4. Test case Tαβ
is designed to test requirement Rαβ. In some cases,
Tαβ does not meet Rαβ. One of the reasons is that the
pattern of error in consideration in that requirement is
not handled by the current version of the tool. Also, in
some cases, the user has not selected the pattern in the
rule definition file which defines the patterns of errors
to be detected by the tool. In certain test cases, the
tool hangs, as the underlying parser could not parse
the test case. The uncovered requirements are sum-
marized here:
• assign float requirement under archaic built-ins
usage is not covered since the user has not se-
lected the pattern in the rule definition file.
• double label and double help under duplicate lan-
guage definition are not detected by the current
version.
• All the sub-requirements under incorrect variable
names are not handled by the current version.
• Grids under unused variables are not detected by
the current version.
• Under uninitialized variables; short, char, un-
signed char, unsigned short, unsigned int, long,
long long, unsigned long, unsigned long long and
double are not handled in the current version.
• String truncation for direct assignment is not cap-
tured in the current version.
• Tool hangs in case of explicit buffer underflow as
negative numbers are not parsed in the index of
Test Suite Minimization of Evolving Software Systems: A Case Study
233

Table 5: Mapping of test cases and requirements in analysis 3.
Test Case Requirement Test Case Requirement Test Case Requirement
T1a R1a T8c R2a, R10a, R10b T14g R10a, R14g
T1b R1b T8d R2a, R10a, R10b T14h R10a, R14h
T1c R1c T8e R2a, R10a, R10b T14i R10a, R14i
T1d R1d T8f R2a, R10a, R10b T14j R10a, R14j
T1e R1e T8g R2a, R3m, R10a, R10b T14k R10a, R14k
T1f R1f T8h R2a, R3m, R10a, R10b T15a R10a, R15a
T1g R1g T8i R2a, R3m, R10a, R10b T15b
T2a R2a, R10b T9a R9a, R10a T15c
T2b R2b, R10b T9b R9b, R10a T15d
T2c R2c, R10b T9c R9c,R10a T16a R10a, R16a
T2d R2d, R10b T10a R10a T16b R10a, R16b
T3a R2a, R3a, R10a T10b R10b T16c
T3b R2a, R3b, R10a T10c R10c T16d R10a
T3c R2a, R3c, R10a T10d R10d T16e R10a
T3d R2a, R10a T10e R10e T16f R10a
T3e R2a, R3e, R10a T10f T16g R10a
T3f R2a, R3f, R10a T10g R10g T16h
T3g R2a, R3g, R10a T10h R10h T16i R10a, R16i
T3h R2a, R3h, R10a T11a R10a, R11a T16j
T3i R2a, R3i, R10a T11b R10a T17a R10a, R16a, R17a
T3j R2a, R3j, R10a T11c R10a T17b R10a, R16a, R17b
T3k R2a, R3k, R10a T11d R10a T17c R10a, R16a, R17b, R17c
T3l R2a, R3l, R10a T11e R10a T17d R10a, R16a, R17b, R17d
T3m R3m, R10a T11f R10a T17e R10a
T4a R4a T11g R10a T18a R10a, R18a
T4b R4b, R10b T11h R10a T18b R10a, R18b
T5a R5a, R10g T11i R10a T18c R10a, R18c
T5b R5b, R10g T11j R10a, R11j T19a
T5c R5a, R10g T11k R10a T19b
T5d R5b, R10g T12a R12a T19c
T5e R5a, R5b, R5e, R10g T12b R12b T19d
T6a R6a, R10h T13a R10a T19e
T6b R6b, R10h T13b R10a, R13b T19f
T6c R6c, R10h T14a R10a, R14a T19g
T6d R6d, R10h T14b R10a, R14b T19h
T7a R7a, R10b T14c R10a, R14c T20a R20a
T7b R7b, R10b T14d R10a, R14d T21a R21a
T8a R2a, R10a, R10b T14e R10a, R14e T21b R21b
T8b R2a, R10a, R10b T14f R10a, R14f T21c R21c
the array. Similar behaviour is observed for ex-
pression overflow and underflow as expression in
the index of the array is not parsed.
• Arithmetic overflow is not covered for char, un-
signed char, unsigned short, unsigned int and un-
signed long. Tool hangs on double as C# cannot
parse such big numbers as supported by EDDL. It
also hangs on long long and unsigned long long
variables. The range for unsigned long long and
long long is 20 digits but Irony parser can support
only 19 digits.
• In divide by zero, assignment after divide by zero
is not covered.
• All the requirements under duplicate identifier are
not met. The tool hangs as the identifiers are
stored using a dictionary.
The cover cannot be found in Analysis 3 as many
of the requirements are not met. Appropriate changes
are incorporated in the next version of the tool to re-
solve all the reported errors. Analysis 4 is done on
the new version of the tool and the mapping listed in
Table 6 is obtained. In this analysis, the only require-
ments that can not be covered are arithmetic overflow
for long long, unsigned long long and double. These
are reported as the limitations of the tool. Arithmetic
overflow of long long and unsigned long long can not
be captured as the Irony parser used in the tool for
parsing EDDL files can support only 19 digits. By
taking any number whose value is more than 19 dig-
its, the parser is not able to parse the file and the tool
hangs. Arithmetic overflow of double can not be cap-
tured as C# used for coding the tool does not support
the entire range of double supported by EDDL. The
coverage is found for all the other requirements and
the results are discussed in Section 5 in Table 10. It
is not possible to find the 2-cover, as most of the re-
quirements are met by only one test case.
5 RESULTS
In general it is not possible to grade the coverage pro-
vided by Greedy, GE and GRE heuristics (Yoo and
ICSOFT 2019 - 14th International Conference on Software Technologies
234

Table 6: Mapping of test cases and requirements in analysis 4.
Test Case Requirement Test Case Requirement Test Case Requirement
T1a R1a T8c R2a, R8c, R10a, R10b T14g R10a, R14g
T1b R1b T8d R2a, R8d, R10a, R10b T14h R10a, R14h
T1c R1c T8e R2a, R8e, R10a, R10b T14i R10a, R14i
T1d R1d T8f R2a, R8f, R10a, R10b T14j R10a, R14j
T1e R1e T8g R2a, R3m, R8g, R10a, R10b T14k R10a, R14k
T1f R1f T8h R2a, R3m, R8h, R10a, R10b T15a R10a, R15a
T1g R1g T8i R2a, R3m, R8i, R10a, R10b T15b R10a, R15b
T2a R2a, R10b T9a R9a, R10a T15c R10a, R15c
T2b R2b, R10b T9b R9b, R10a T15d R10a, R15d
T2c R2c, R10b T9c R9c,R10a T16a R10a, R16a
T2d R2d, R10b T10a R10a T16b R10a, R16b
T3a R2a, R3a, R10a T10b R10b T16c
T3b R2a, R3b, R10a T10c R10c T16d R10a, R16d
T3c R2a, R3c, R10a T10d R10d T16e R10a, R16e
T3d R2a, R3d, R10a T10e R10e T16f R10a, R16f
T3e R2a, R3e, R10a T10f R10f T16g R10a, R16g
T3f R2a, R3f, R10a T10g R10g T16h
T3g R2a, R3g, R10a T10h R10h T16i R10a, R16i
T3h R2a, R3h, R10a T11a R10a, R11a T16j
T3i R2a, R3i, R10a T11b R10a, R11b T17a R10a, R16a, R17a
T3j R2a, R3j, R10a T11c R10a, R11c T17b R10a, R16a, R17b
T3k R2a, R3k, R10a T11d R10a, R11d T17c R10a, R16a, R17b, R17c
T3l R2a, R3l, R10a T11e R10a, R11e T17d R10a, R16a, R17b, R17d
T3m R3m, R10a T11f R10a, R11f T17e R10a, R16a, R17b, R17e
T4a R4a T11g R10a, R11g T18a R10a, R18a
T4b R4b, R10b T11h R10a, R11h T18b R10a, R18b
T5a R5a, R10g T11i R10a, R11i T18c R10a, R18c
T5b R5b, R10g T11j R10a, R11j T19a R10a, R19a
T5c R5a, R5c, R10g T11k R10a, R11k T19b R10b, R19b
T5d R5b, R5d, R10g T12a R12a T19c R10c, R19c
T5e R5a, R5b, R5e, R10g T12b R12b T19d R10d, R19d
T6a R6a, R10h T13a R10a, R13a T19e R10e, R19e
T6b R6b, R10h T13b R10a, R13b T19f R10f, R19f
T6c R6c, R10h T14a R10a, R14a T19g R10g, R19g
T6d R6d, R10h T14b R10a, R14b T19h R10h, R19h
T7a R7a, R10b T14c R10a, R14c T20a R20a
T7b R7b, R10b T14d R10a, R14d T21a R21a
T8a R2a, R8a, R10a, R10b T14e R10a, R14e T21b R21b
T8b R2a, R8b, R10a, R10b T14f R10a, R14f T21c R21c
Harman, 2012). Given a set of requirements, a set of
test cases, and a mapping between them, any of the
three heuristics can give better results. For instance,
if we compare GE and GRE, in mapping given in Ta-
ble 7, adopted from Chen and Lau (1995), GE selects
4 test cases and GRE selects 5 test cases.
Table 7: Greedy and GE better than GRE.
1 2 3 4 5 6 7 8 9 10 11
t1 1 1 1 1 1 0 0 0 0 0 0
t2 0 0 0 0 0 1 1 1 0 0 0
t3 0 0 0 0 0 0 0 0 1 1 0
t4 1 1 0 0 0 0 0 0 0 0 1
t5 0 0 0 1 1 1 1 0 0 0 0
t6 0 0 1 0 0 0 0 0 1 0 0
t7 0 0 0 0 0 0 0 0 0 0 1
t8 0 1 0 1 0 0 0 1 0 0 0
t9 0 0 0 0 1 0 0 0 0 1 0
But in mapping given in Table 8 GE selects 3
test cases and GRE selects 2 test cases. To com-
pare Greedy and GRE, in mapping given in Table 7,
Greedy selects 4 test cases and GRE selects 5 test
cases. But in mapping given in Table 8, Greedy se-
lects 3 test cases and GRE selects 2 test cases. To
compare Greedy and GE, if we consider mapping
given in Table 7 and remove t7 from it, in the obtained
mapping, Greedy selects 4 test cases and GE selects
5 test cases. But if we consider mapping given in Ta-
ble 8 and remove t5 from it, in the obtained mapping,
Greedy selects 3 test cases and GE selects 2 test cases.
Thus, any of these heuristics can give better output.
Table 8: GRE better than Greedy and GE.
1 2 3 4
t1 1 0 0 1
t2 1 0 1 0
t3 0 0 1 1
t4 1 1 0 0
t5 0 1 0 0
Considering analysis 1, it can clearly be observed
from Table 9 that for k=1, GE and GRE give better re-
sults than Greedy heuristics while for k=2 and k=3 all
the approaches give similar results. An obvious ob-
servation is that with increasing k, more test cases are
needed to cover the requirements, which also points
towards the convergence of these algorithms. For
analyses 2 and 4, as evident from Table 9 and Table
Test Suite Minimization of Evolving Software Systems: A Case Study
235

Table 9: Results of analysis 1 and analysis 2.
Cover Analysis 1 (k=1) Analysis 1 (k=2) Analysis 1 (k=3) Analysis 2 (k=1)
Uncovered Requirements 8, 14, 18, 19 8, 14, 15, 18, 19 8, 4, 14, 15, 18, 19 8, 14, 18, 19
Approach Test Cases No. Test Cases No. Test Cases No. Test Cases No.
Greedy 5, 9, 15, 21 4 5, 9, 14, 15, 19 5 5, 7, 9, 14, 19, 22, 23, 24 8 3, 4, 9, 13, 15, 21 6
GE 9, 19, 21 3 5, 9, 14, 15, 19 5 5, 7, 9, 14, 19, 22, 23, 24 8 3, 4, 9, 13, 15, 21 6
GRE 9, 19, 21 3 5, 9, 14, 15, 19 5 5, 8, 9, 14, 19, 22, 23, 24 8 3, 4, 9, 13, 15, 21 6
Table 10: Results of analysis 4.
Cover k=1
Uncovered
Requirements
R16c, R16h, R16j
Approach Test Cases No.
Greedy
T1a, T1b, T1c, T1d, T1e, T1f, T1g, T2b,
T2c, T2d, T3a, T3b, T3c, T3d, T3e, T3f,
T3g, T3h, T3i, T3j, T3k, T3l, T4a, T4b,
T5c, T5d, T5e, T6a, T6b, T6c, T6d, T7a,
T7b, T8a, T8b, T8c, T8d, T8e, T8f, T8g,
T8h, T8i, T9a, T9b, T9c, T11a, T11b,
T11c, T11d, T11e, T11f, T11g, T11h,
T11i, T11j, T11k, T12a, T12b, T13a,
T13b, T14a, T14b, T14c, T14d, T14e,
T14f, T14g, T14h, T14i, T14j, T14k,
T15a, T15b, T15c, T15d, T16b, T16d,
T16e, T16f, T16g, T16i, T17a, T17c,
T17d, T17e, T18a, T18b, T18c, T19a,
T19b, T19c, T19d, T19e, T19f, T19g,
T19h, T20a, T21a, T21b, T21c
100
GE Same as Greedy 100
GRE Same as Greedy 100
10 respectively, all approaches output the same num-
ber of test cases to cover the requirements. The early
convergence for k=1 can be attributed to sparsity of
the input matrices and small value of r
overlap
(average
number of test cases which meet a requirement) and a
large number of essential test cases thus leaving very
less alternatives to select.
Figure 3: Run time performance comparison.
Figure 3 presents the run time performance of
Greedy, GE and GRE heuristics in analyses 1 and
2. In analysis 4, Greedy takes 3862.88 µs, GE takes
177.82 µs and GRE takes 2953.98 µs. It can clearly
be observed, in all these analyses, GE performs the
best (GE takes considerably less time than Greedy in
analysis 1 (k=3), analysis 2 and analysis 4 as there
are many essential test cases), followed by Greedy,
and then GRE performs the worst (GRE wastes a
lot of time in pre-processing to remove redundant
test cases). In analysis 4, GRE performs better than
Greedy because its overhead of redundant calculation
is balanced by its essential pass. In software systems,
if r
overlap
is small and many essential test cases exist,
all heuristics will give similar output but run time of
GE will be the least and thus should be preferred.
If more requirements are added, the existing map-
ping can be reused. For this, the mapping of existing
test cases with respect to the new requirements needs
to be filled. Extra test cases to cover them may also
be designed and mapped. Similarly, if a subset of re-
quirements needs to be considered, the existing map
can be reused. The additional requirements and the
corresponding map can simply be removed.
The major limitation of the heuristics used is that
they do not give any weightage to the time required to
run a test case. In future, techniques may be consid-
ered which also focus on the run time of a test case.
6 CONCLUSION
In this paper, Greedy, GE and GRE heuristics have
been successfully used to cover the specified require-
ments (in SRS) of the SUT, the SCAN tool. The mini-
mal cover obtained helps in reducing testing time and
effort while doing regression testing. Existing map-
ping of test cases and requirements can be reused
while adding or removing requirements. k-cover can
be applied if better assurance about coverage is re-
quired at the cost of more testing effort and time.
Learning algorithms can be designed to find an op-
timal value of k. In general, it would be tough to rank
the efficiency of Greedy, GE and GRE heuristics as
they are based on heuristics and none of these is a pre-
cise algorithm. A comparison of output and run time
performance of these heuristics for a given set of test
cases and requirements has been presented for each
analysis done on the SCAN tool. It has been observed
that if r
overlap
is small and there are many essential test
cases, all the heuristics give similar output but GE has
the best run time performance and thus, it is advis-
able to use GE heuristics in such a scenario. Future
work could include an empirical evaluation to find
out the range of r
overlap
and percentage of essential
ICSOFT 2019 - 14th International Conference on Software Technologies
236

test cases. To ensure, all requirements are addressed
properly and covered efficiently, requirements should
be fine grained and then mapped, which in turn also
helps in finding bugs in each version of the SUT.
Efficiency of these heuristics can be tested and
validated on the upcoming versions of the SCAN
tool. Further, these heuristics can be applied on other
evolving software systems, leading to better confi-
dence about behavior and correctness of these sys-
tems. The heuristics can be evaluated for other values
of r
overlap
. Other heuristics such as HGS and multi-
objective optimization can also be evaluated and com-
pared. The test cases designed here might not be cov-
ering entire code of the SUT and thus, code coverage
can be applied using similar techniques. Automated
generation of test cases based on code coverage is
a prominent direction to work upon. Further, tech-
niques which also focus on the time taken to execute
a test case may be considered. Instead of obtaining
the mapping manually, automated generation of map-
ping for a given set of requirements and test cases can
be explored. Dynamic code analysis tools for EDDL
can also be designed in future.
REFERENCES
Banerjee, A., Chattopadhyay, S., and Roychoudhury, A.
(2016). On testing embedded software. Advances in
Computers, 101:121–153.
Black, J., Melachrinoudis, E., and Kaeli, D. (2004). Bi-
criteria models for all-uses test suite reduction. In
Proc. of ICSE, pages 106–115. IEEE.
B
¨
ohme, M., Oliveira, B. C. D. S., and Roychoudhury, A.
(2013). Partition-based regression verification. In
Proc. of ICSE, pages 302–311. IEEE.
B
¨
ohme, M. and Roychoudhury, A. (2014). Corebench:
Studying complexity of regression errors. In Proc. of
ISSTA, pages 105–115. ACM.
Chen, T. and Lau, M. (1995). Heuristics towards the opti-
mization of the size of a test suite. WIT Trans. Info.
Comm., 11.
Chen, T. Y. and Lau, M. F. (1996). Dividing strategies for
the optimization of a test suite. Information Process-
ing Letters, 60(3):135–141.
Harder, M., Mellen, J., and Ernst, M. D. (2003). Improv-
ing test suites via operational abstraction. In Proc. of
ICSE, pages 60–71. IEEE.
Horgan, J. R. and London, S. (1992). A data flow coverage
testing tool for c. In Proc. of Symp. on Assessment of
Quality Softw. Development Tool, pages 2–10. IEEE.
Hsu, H.-Y. and Orso, A. (2009). Mints: A general frame-
work and tool for supporting test-suite minimization.
In Proc. of ICSE, pages 419–429. IEEE.
IEC-61804-3 (2015). Function Blocks for process control
and Electronic Device Description Language, Part 3:
eddl syntax and semantics.
Irony-v1.0.0 (2018). Irony .NET language implemen-
tation kit. Retrieved February 15, 2019, from
http://irony.codeplex.com.
Jeffrey, D. and Gupta, N. (2005). Test suite reduction with
selective redundancy. In Proc. of ICSM, pages 549–
558. IEEE.
Jeffrey, D. and Gupta, N. (2007). Improving fault detec-
tion capability by selectively retaining test cases dur-
ing test suite reduction. IEEE Trans. Softw. Eng.,
33(2):108–123.
Mandal, A., Mohan, D., Jetley, R., Nair, S., and D’Souza,
M. (2018). A generic static analysis framework for
domain-specific languages. In Proc. of IEEE ETFA,
pages 27–34. IEEE.
Marr
´
e, M. and Bertolino, A. (2003). Using spanning
sets for coverage testing. IEEE Trans. Softw. Eng.,
29(11):974–984.
McMaster, S. and Memon, A. (2008). Call-stack coverage
for gui test suite reduction. IEEE Trans. Softw. Eng.,
34(1):99–115.
Mohan, D. and Jetley, R. (2018). Static code analysis for
device description language. In Proc. of Symp. on
AFMSS.
Offutt, J., Pan, J., and Voas, J. M. (1995). Procedures for re-
ducing the size of coverage-based test sets. In Proc. of
Int. Conf. on Testing Computer Software, pages 111–
123. ACM Press New York.
Papadimitriou, C. H. and Steiglitz, K. (1998). Combi-
natorial Optimization: Algorithms and Complexity.
Courier Corporation.
Schroeder, P. J. and Korel, B. (2000). Black-box Test Reduc-
tion Using Input-Output Analysis, volume 25. ACM.
Tallam, S. and Gupta, N. (2006). A concept analysis in-
spired greedy algorithm for test suite minimization.
ACM SIGSOFT Softw. Eng. Notes, 31(1):35–42.
Yoo, S. and Harman, M. (2007). Pareto efficient multi-
objective test case selection. In Proc. of ISSTA, pages
140–150. ACM.
Yoo, S. and Harman, M. (2012). Regression testing mini-
mization, selection and prioritization: a survey. Softw.
Test. Verif. Rel., 22:67–120.
Test Suite Minimization of Evolving Software Systems: A Case Study
237
