
Knowledge Transfer in a Pair of Uniformly Modelled Bayesian Filters
Ladislav Jirsa
1
, Lenka Kukli
ˇ
sov
´
a Pavelkov
´
a
1 a
and Anthony Quinn
1,2 b
1
Institute of Information Theory and Automation, The Czech Academy of Sciences, Prague, Czech Republic
2
Trinity College Dublin, The University of Dublin, Ireland
Keywords:
Fully Probabilistic Design, Bayesian Filtering, Uniform Noise, Knowledge Transfer, Predictor, Orthotopic
Bounds.
Abstract:
The paper presents an optimal Bayesian transfer learning technique applied to a pair of linear state-space
processes driven by uniform state and observation noise processes. Contrary to conventional geometric ap-
proaches to boundedness in filtering problems, a fully Bayesian solution is adopted. This provides an approxi-
mate uniform filtering distribution and associated data predictor by processing the involved bounds via a local
uniform approximation. This Bayesian handling of boundedness provides the opportunity to achieve optimal
Bayesian knowledge transfer between bounded-error filtering nodes. The paper reports excellent rejection of
knowledge below threshold, and positive transfer above threshold. In particular, an informal variant achieves
strong transfer in this latter regime, and the paper discusses the factors which may influence the strength of
this transfer.
1 INTRODUCTION
The problem of data (also known as measurement or
information) fusion is now key in many areas of in-
dustry, driven by the IoT and Industry 4.0 agendas
(Diez-Olivan et al., 2019). Data fusion systems are
required in areas such as sensor networks, robotics,
and video and image processing systems (Khaleghi
et al., 2013). Applications range from health moni-
toring (Vitola et al., 2017) and environmental sensing
(Zou et al., 2017), to cooperative systems for indoor
tracking (Dardari et al., 2015) or urban vehicular lo-
calization (Nassreddine et al., 2010). In all cases, in-
formation about the same quantity of interest (or sev-
eral quantities of interest, related in a specified way)
is acquired by different types of detectors, under dif-
ferent conditions, via multiple experiments and mea-
surement devices. (Lahat et al., 2015) provides an
overview of the main challenges in multimodal data
fusion across various disciplines, while the survey in
(Gravina et al., 2017) discusses clear motivations and
advantages of multi-sensor data fusion.
Diverse approaches to solving data fusion prob-
lems have been proposed in the literature, very of-
ten driven by the specifics of the application, and
it is clear that no universal definition—much less
a
https://orcid.org/0000-0001-5290-2389
b
https://orcid.org/0000-0002-3873-7556
a universal solution—has yet been accepted. Wiener-
type criteria for measurement vector fusion (Will-
ner et al., 1976) have long been available, while di-
rect variants of the Kalman filter have also been pro-
posed for fusion of measurements (Dou et al., 2016)
and states (Yang et al., 2019). Artificial intelligence
(Xiao, 2019), machine learning (Vitola et al., 2017;
Shamshirband et al., 2015; Vapnik and Izmailov,
2017) and expert system approaches (Majumder and
Pratihar, 2018) have all yielded progress in this area.
In the Bayesian framework which we adopt in this
paper, concepts of data, knowledge and information
are all unified via a probabilistic representation, being
typically the distribution of the unknown quantities of
interest, conditioned by data. Each measurement pro-
cess (node or sensor) constructs its local distribution
conditioned on its locally sensed data. The inferred
quantity may be globally shared by all the nodes, or
these may be distinct but related quantities (Azizi and
Quinn, 2018). The task is then one of optimal merg-
ing of these local distributions, a problem closely re-
lated to distributional pooling (Abbas, 2009). An-
other closely related problem is that of knowledge
transfer (Torrey and Shavlik, 2010). Again, in the
Bayesian context of this paper, the requirement is to
transfer probabilistic knowledge (a distribution) from
secondary (i.e. external or source) nodes to a pri-
mary node, to support its inference of the quantity
Jirsa, L., Pavelková, L. and Quinn, A.
Knowledge Transfer in a Pair of Uniformly Modelled Bayesian Filters.
DOI: 10.5220/0007854104990506
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 499-506
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
499

of interest. Optimal Bayesian transfer learning via
Kullback-Leibler divergence (KLD) minimization—
known as fully probabilistic design (FPD) (Quinn
et al., 2016)—is developed in (Quinn et al., 2017),
and specialized to the case of data-predictive transfer
between Kalman filters in (Foley and Quinn, 2018),
(Pape
ˇ
z and Quinn, 2018). In this approach, the sec-
ondary data predictor is transferred to the primary
filtering node via an optimal mean-field-type opera-
tor. This is shown to improve the primary state re-
construction in positive transfer cases, and rejects the
secondary knowledge otherwise. In addition to the
consistency and optimality properties of this Bayesian
transfer learning framework, a key practical advan-
tage here is that the relationship between the primary
and secondary processes does not have to be explicitly
modelled.
In this paper, we address the important prac-
tical context where the involved uncertainties are
bounded. Contemporary examples of sensor networks
with bounded innovations and/or observation pro-
cesses are studied in (Goudjil et al., 2017; He et al.,
2017; Vargas-Melendez et al., 2017). Specifically,
we extend the Bayesian transfer learning technique in
(Quinn et al., 2017) to a pair of linear state-space pro-
cesses driven by uniform state and observation noise
processes. Boundedness in filtering problems is han-
dled via several approaches. Within the Kalman fil-
tering set-up, the state estimates are projected onto
the constraint surface (Fletcher, 2000) or the Gaussian
distribution is truncated (Simon and Simon, 2010).
Using sequential Monte-Carlo sampling methods, the
constraints are respected within the accept/reject steps
of the algorithm, see e.g. (Lang et al., 2007). The
non-probabilistic techniques dealing with “unknown-
but-bounded error” provide an approximate set con-
taining the estimates (Chisci et al., 1996), (Becis-
Aubry et al., 2008). Recently, a fully Bayesian so-
lution has yielded a sequentially uniform filtering dis-
tribution (Pavelkov
´
a and Jirsa, 2018) and associated
data predictor (Jirsa et al., 2019) by processing the
involved bounds via a local uniform approximation
of the state predictor at each filtering step, achiev-
ing a recursive, tractable algorithm. This Bayesian
handling of boundedness now provides the opportu-
nity for optimal Bayesian knowledge transfer between
bounded-error filtering nodes, as set out below.
Throughout the paper, z
t
is the value of a column
vector z at a discrete time instant t ∈ t
?
≡ {1, 2,...,t};
z
t;i
is the i-th entry of z
t
; z(t) ≡ {z
t
,z
t−1
,. . . ,z
1
,z
0
}; z
and z are lower and upper bounds on z, respectively;
≡ means equality by definition, ∝ means equality up
to a constant factor. The symbol f (·|·) denotes a con-
ditional probability density function (pdf); names of
arguments distinguish respective pdfs; no formal dis-
tinction is made between a random variable, its real-
isation and an argument of the pdf. U
z
(z,z) denotes
the uniform pdf of z with the orthotopic support [z, z].
Also, χ(x ∈ x
?
) is the indicator function, i.e. if x ∈ x
?
,
then χ(x ∈ x
?
) = 1, otherwise χ(x ∈ x
?
) = 0.
2 UNIFORMLY MODELLED
BAYESIAN FILTERS:
KNOWLEDGE
REPRESENTATION AND
TRANSFER
We consider a pair of Bayesian filters, and distinguish
between the primary filter (called the target node in
transfer learning (Torrey and Shavlik, 2010) and the
secondary filter (sometimes called the source node),
with all sequences and distributions subscripted by
“s” in the latter case. Each filter processes its local
observation sequence, y
t
and y
s,t
, t ∈ t
?
, respectively,
informative of their local, hidden (state) process, x
t
and x
s,t
, respectively.
In this paper, we adopt linear stochastic state-
space models with known parameters for all four pro-
cesses, each driven by an independent, uniformly-
distributed white noise process of known parameters.
We summarize (isolated) Bayesian filtering for this
class of model in Section 2.1. We briefly review prob-
abilistic knowledge transfer between a pair of general
Bayesian filters in Section 2.2, using the axiomati-
cally optimal FPD principle. Then, in Section 2.3,
we instantiate this FPD-optimal transfer in the current
context of uniformly driven Bayesian filters, recover-
ing a tractable, recursive flow via a local uniform ap-
proximation at each step.
2.1 Bayesian Filtering with Uniformly
Distributed Noise Processes
In the considered Bayesian set up (K
´
arn
´
y et al., 2005),
the system is described by the following pdfs:
prior pdf: f (x
0
) (1)
observation model: f (y
t
|
x
t
)
time evolution model: f (x
t
|
x
t−1
,u
t−1
)
where y
t
is a scalar observable output, u
t
is a known
system input (optional, for generality), and x
t
is an
`-dimensional unobservable system state, t ∈ t
?
.
We assume that (i) hidden process x
t
satisfies the
Markov property, (ii) no direct relationship between
input and output exists in the observation model,
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
500

and (iii) the inputs consist of a known sequence
u
0
,u
1
,. . . ,u
t−1
.
Bayesian sequential state estimation (known as
filtering) consists of the evolution of the posterior
pdf f (x
t
|d(t)) where d(t) is a sequence of observed
data records d
t
= (y
t
,u
t
), t ∈ t
?
. The evolution of
f (x
t
|d(t)) is described by a two-steps recursion that
starts from the prior pdf f (x
0
):
Time Update: f (x
t
|d(t − 1)) =
=
Z
x
?
t−1
f (x
t
|u
t−1
,x
t−1
) f (x
t−1
|d(t − 1))dx
t−1
, (2)
Data Update: f (x
t
|d(t)) =
f (y
t
|x
t
) f (x
t
|d(t − 1))
R
x
?
t
f (y
t
|x
t
) f (x
t
|d(t − 1))dx
t
=
f (y
t
|x
t
) f (x
t
|d(t − 1))
f (y
t
|d(t − 1))
.
(3)
We introduce a linear state space model with a uni-
form noise (LSU model) in the form
f (x
t
|u
t−1
,x
t−1
) = U
x
( ˜x
t
− ρ, ˜x
t
+ ρ)
f (y
t
|x
t
) = U
y
( ˜y
t
− r, ˜y
t
+ r). (4)
where ˜x
t
= Ax
t−1
+ Bu
t−1
, ˜y
t
= Cx
t
, A, B, C are the
known model matrices/vectors of appropriate dimen-
sions, ν
t
∈ (−ρ, ρ) is the uniform state noise with
known parameter ρ, n
t
∈ (−r, r) is the uniform ob-
servation noise with known parameter r.
State estimation of LSU model (4) according to
(2) and (3) leads to a very complex form of poste-
rior pdf. In (Pavelkov
´
a and Jirsa, 2018)
1
, an approxi-
mate Bayesian state estimation of this model (based
on a minimising of Kullback-Leibler divergence of
two pdfs) is proposed. The presented algorithm pro-
vides the evolution of the approximate posterior pdf
f (x
t
|d(t)) that is uniformly distributed on a parallelo-
topic support.
Approximate Time Update. The time update starts
at the time t = 1 with f (x
t−1
|d(t − 1)) = f (x
0
) =
U
x
0
(x
0
,x
0
). Being χ the indicator function, it holds
f (x
t
|d(t − 1)) ≈
`
∏
i=1
χ(m
t;i
− ρ
i
≤ x
t;i
≤ m
t;i
+ ρ
i
)
m
t;i
− m
t;i
+ 2ρ
i
=
=
`
∏
i=1
U
x
t;i
(m
t;i
− ρ
i
,m
t;i
+ ρ
i
) = U
x
t
(m
t
− ρ, m
t
+ ρ),
(5)
1
Note that the paper (Pavelkov
´
a and Jirsa, 2018) con-
tains the typo in the formula (3): the relevant integration
variable should be x
t
instead of x
t−1
.
where m
t
= [m
t;1
,. . . , m
t;`
]
0
, m
t
= [m
t;1
,. . . , m
t;`
]
0
,
m
t;i
=
`
∑
j=1
min(A
i j
x
t−1; j
+ B
i
u
t−1
,A
i j
x
t−1; j
+ B
i
u
t−1
),
(6)
m
t;i
=
`
∑
j=1
max(A
i j
x
t−1; j
+ B
i
u
t−1
,A
i j
x
t−1; j
+ B
i
u
t−1
),
A
i j
means the term on the i-th row and the j-th column
of A.
Approximate Data Update. According to (3), we
process the observation y
t
as y
t
−r ≤ Cx
t
≤ y
t
+r (see
(4)) by the Bayes rule together with the prior (5) from
the time update. The approximate posterior pdf is uni-
formly distributed on a parallelotopic support
f (x
t
|d(t)) ≈ K
t
χ(x
t
≤ M
t
x
t
≤ x
t
), (7)
where K
t
is a normalising constant.
However, the time update (5) in the next step as-
sumes pdf with an orthotopic support. Therefore, the
parallelotope x
t
≤ M
t
x
t
≤ x
t
in (7) is circumscribed by
an orthotope x
t
≤ x
t
≤ x
t
. In this way, we obtain an
approximate “orthotopic” posterior pdf
f (x
t
|d(t)) ≈ U
x
t
(x
t
, x
t
). (8)
The orthotopic bounds x
t
and x
t
are used in the next
time update step (5) for the computation of the terms
m and m (6) and for the computation of point esti-
mates of states ˆx
t
ˆx
t
=
x
t
+ x
t
2
. (9)
Predictive pdf for LSU Model. The data predic-
tor of a linear state-space model is the denominator
of (3), where f (y
t
|x
t
) is given by (4) and f (x
t
|d(t −
1)) is the result of the approximate time update (5).
The approximate uniform predictor as proposed in
(Jirsa et al., 2019) is
f (y
t
|d(t − 1)) ≈
y
t
− y
t
−1
χ
y
t
≤ y
t
≤ y
t
, (10)
where
y
t
= Cs − r (11)
y
t
= Cs + r (12)
for s and s defined so that
s
i
= m
t;i
− ρ
i
, s
i
= m
t;i
+ ρ
i
, if C
i
≥ 0,
s
i
= m
t;i
+ ρ
i
, s
i
= m
t;i
− ρ
i
, if C
i
< 0,
(13)
This predictive pdf is conditioned by m
t
and m
t
considered as statistics, provided the parameters A
and B be known.
Mean value ˆy
t
≡ E[y
t
|d(t − 1)] of (10) is
E[y
t
|d(t − 1)] =
y
t
+ y
t
2
= C
m
t
+ m
t
2
| {z }
E[x
t
|d(t−1)]
. (14)
Knowledge Transfer in a Pair of Uniformly Modelled Bayesian Filters
501

2.2 FPD-optimal Knowledge Transfer
between Bayesian Filters
If knowledge transfer from the secondary to the pri-
mary filter is to be effective (the case known as pos-
itive transfer (Torrey and Shavlik, 2010)), then we
must assume that y
s
(t) is informative of x(t). The core
technical problems to be addressed are (i) that there is
no complete model relating x(t) and x
s
(t), and, there-
fore, (ii) probability calculus (i.e. standard Bayesian
conditioning) does not prescribe the required primary
distribution conditioned on the transferred knowl-
edge. Note that standard Bayesian conditioning yields
the solution only in the case of complete modelling
(Karbalayghareh et al., 2018). However, an insistence
on specification of a complete model of inter-filter de-
pendence may be highly restrictive, and incur model
sensitivity in applications.
Instead, we acknowledge that the required condi-
tional primary state predictor,
˘
f (x
t
|d(t − 1), f
s
), after
transfer of the secondary data predictor, f
s
(y
s
,t
|d
s
(t −
1)) (10), is non-unique. Therefore, we solve the in-
curred decision problem optimally via the fully prob-
abilistic design (FPD) principle (Quinn et al., 2016),
choosing between all cases of
˘
f (x
t
|d(t − 1), f
s
) con-
sistent with the knowledge constraint introduced by
the transfer of f
s
(y
s
,t
|d
s
(t − 1)) (Quinn et al., 2017).
FPD axiomatically prescribes an optimal choice, f
o
,
as a minimizer of the Kullback-Leibler divergence
(KLD) from
˘
f to an ideal distribution, f
I
, chosen by
the designer (K
´
arn
´
y and Kroupa, 2012):
f
o
(x
t
|d(t − 1), f
s
) ≡ arg
˘
f ∈F
minD(
˘
f || f
I
). (15)
Here, the KLD is defined as
D(
˘
f || f
I
) = E
˘
f
h
ln
˘
f
f
I
i
, (16)
and F denotes the set of
˘
f constrained by f
s
(Quinn
et al., 2016),(Quinn et al., 2017). The ideal distribu-
tion is consistently defined as
f
I
(x
t
|d(t − 1)) ≡ f (x
t
|d(t − 1)),
being the state predictor of the isolated primary fil-
ter (5) (i.e. in the absence of any transfer from a sec-
ondary filter). In (Foley and Quinn, 2018), the follow-
ing mean-field operator was shown to satisfy (15), and
so to constitute the FPD-optimal primary state pre-
dictor after the (static) knowledge transfer specified
above:
f
o
(x
t
|d(t − 1), f
s
) ∝ f (x
t
|d(t − 1)) ×
×exp
Z
y
t
f
s
(y
t
|d
s
(t − 1))ln f (y
t
|x
t
)dy
t
. (17)
Note that the optional input u
t
is known and con-
stant. Here, it is not a part of FPD and plays only the
role of a conditioning quantity in d(t − 1).
2.3 FPD-optimal Uniform Knowledge
Transfer
Here, we express the KLD minimiser (17) in the case
of uniform pdfs. The functions appearing in (17) are
f (x
t
|d(t − 1)) ∝ χ (m
t
− ρ ≤ x
t
≤ m
t
+ ρ) (18)
f
s
(y
t
|d
s
(t − 1)) ∝ χ
y
s
,t
≤ y
t
≤ y
s
,t
(19)
f (y
t
|x
t
) ∝ χ (Cx
t
− r ≤ y
t
≤ Cx
t
+ r), (20)
see (5), (10) and (4). Then, the form of (17) is
f
o
(x
t
|d(t − 1), f
s
) ∝ χ(m
t
− ρ ≤ x
t
≤ m
t
+ ρ) ×
×exp
Z
y
t
χ
y
s
,t
≤ y
t
≤ y
s
,t
×
×ln χ (Cx
t
− r ≤ y
t
≤ Cx
t
+ r) dy
t
(21)
The first term in the integral indicates the integration
limits are y
s
,t
and y
s
,t
. The characteristic function in
the logarithm must equal one, which zeroes the expo-
nent and generates an additional constraint for x
t
.
Imposing y
t
∈ (Cx
t
− r,Cx
t
+ r) ∩ (y
s
,t
,y
s
,t
) with
nonempty intersection, we get the constraint for x
t
:
y
s
,t
− r ≤ Cx
t
≤ y
s
,t
+ r. (22)
The constraining inequalities in (22) represent a strip
in the state space. Time update of the target filter
yields an orthotope domain in the state space (Fig-
ure 2). The strip, containing information from the
source filter, and the orthotope then intersect (left side
of Figure 2). This constrained set is the form of the
knowledge transfer between the filters.
However, the data update step requires the prior
pdf to be on the orthotope domain. Therefore, the
constrained set must be circumscribed by another or-
thotope. The orthotope is an intersection of ` per-
pendicular strips. According to (Vicino and Zappa,
1996), all the ` + 1 strips are tightened, i.e. shifted
and/or narrowed, so that distance of their planes is
minimal while their intersection is unchanged (re-
moved redundancy). Then, the tightened ortho-
tope is the domain of the approximate expression of
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
502

f
o
(x
t
|d(t −1), f
s
) as the constrained prior entering the
data update.
Note: The similarity of (22) with the observa-
tion model (4) and their similar processing indicates
similarity of the constraint step and the data update
step. The difference is that the knowledge trans-
fer (22) accepts the interval, i.e. the uniform distri-
bution U
y
(y
s
,t
,y
s
,t
), whereas the data update is sup-
plied with the observed point, y
t
. This point can be
interpreted as the Dirac distribution δ
y
(y − y
t
). In this
distributional sense, both the steps are equivalent.
2.4 Algorithmic Summary
The source and target filters run their state estimation
tasks in parallel. The source filter is run in isolation,
and the data predictor (10) is computed between the
time update and data update steps. Processing of the
source predictor is placed between time update and
data update step in the target filter.
Initialisation:
• Choose final time t > 0, set initial time t = 0
• Set values x
0
, x
0
, u
0
, noises ρ, r, r
s
On-line:
1. Set t = t +1
2. Compute m
t
, m
t
according to (6) for each filter
3. Time update: compute (5) for each filter
4. Compute data predictor of the source filter (10)
5. Knowledge transfer: get the constraining strip
(22) from the source data predictor and process
it to time updated pdf of the target filter ((22)
and below) to transfer knowledge between the
filters (alternatively, use the informal transfer
described later)
6. Get new data u
t
, y
t
, y
s
,t
7. Data update: add the data strip (4) and approx-
imate the obtained support by a parallelotope
(for details see Appendix A.2 in (Pavelkov
´
a and
Jirsa, 2018)) to obtain the resulting form (7)
(alternatively, skip the parallelotope stage and
only tighten the strips, as described in 5.) for
each filter
8. Compute x
t
, x
t
(8) for each filter
9. Compute the point estimate ˆx
t
(9) for the target
filter
10. If t < t, go to 1.
3 EXPERIMENTS
In this section, the simulation experiments demon-
strate the proposed algorithm properties.
3.1 Experiment Setup
We simulate the system studied in (Foley and Quinn,
2018), x
t
∈ R
2
, y
t
∈ R. The known model parameters
are A =
1 1
0 1
, C = [1 0], ρ = 1
(2)
×10
−5
, where
1
(2)
is the unit vector of length 2, r = 10
−3
. B =
0
0
, u
t
= 0, i.e. a system without input/control.
The estimation was run for t = 50 time steps. We in-
vestigate the influence of the observation noise r
s
of
the source filter (20) on estimate precision of the tar-
get filter, quanitified by TNSE (total norm squared-
error) defined as TNSE =
t
∑
t=1
k ˆx
t
− x
t
k
2
, where k · k
is the Euclidean norm. For each combination of the
parameters, the computation was run 2000-times and
the TNSEs were averaged.
Simulated states x
t
, together with the state noise
ρ, are common for both the source and target filters,
whereas the observation noises r and r
s
, contributing
to observed values, differ. This simple setup is suffi-
cient for illustration of the described method.
3.2 Results
-8 -7 -6 -5 -4 -3 -2 -1
log
10
r
s
-5.26
-5.25
-5.24
-5.23
-5.22
-5.21
-5.2
-5.19
log
10
TNSE
FPD transfer, r = 0.001
knowledge transfer
isolated filter
Figure 1: TNSE of the target LSU filter as a function of
the observation noise variance r
s
of the source filter. FPD
transfer.
Figure 1 shows the influence of the source filter
observation noise r
s
on precision of the target filter
through the FPD knowledge transfer. The method re-
jects negative knowledge transfer (unlike in the Gaus-
sian transfer case (Foley and Quinn, 2018)). For
higher values of r
s
, estimate precision coincides with
the isolated target filter (despite fluctuations) and does
not increase. However, decrease of estimation error
for smaller r
s
is not very significant, compared to (Fo-
ley and Quinn, 2018).
Knowledge Transfer in a Pair of Uniformly Modelled Bayesian Filters
503
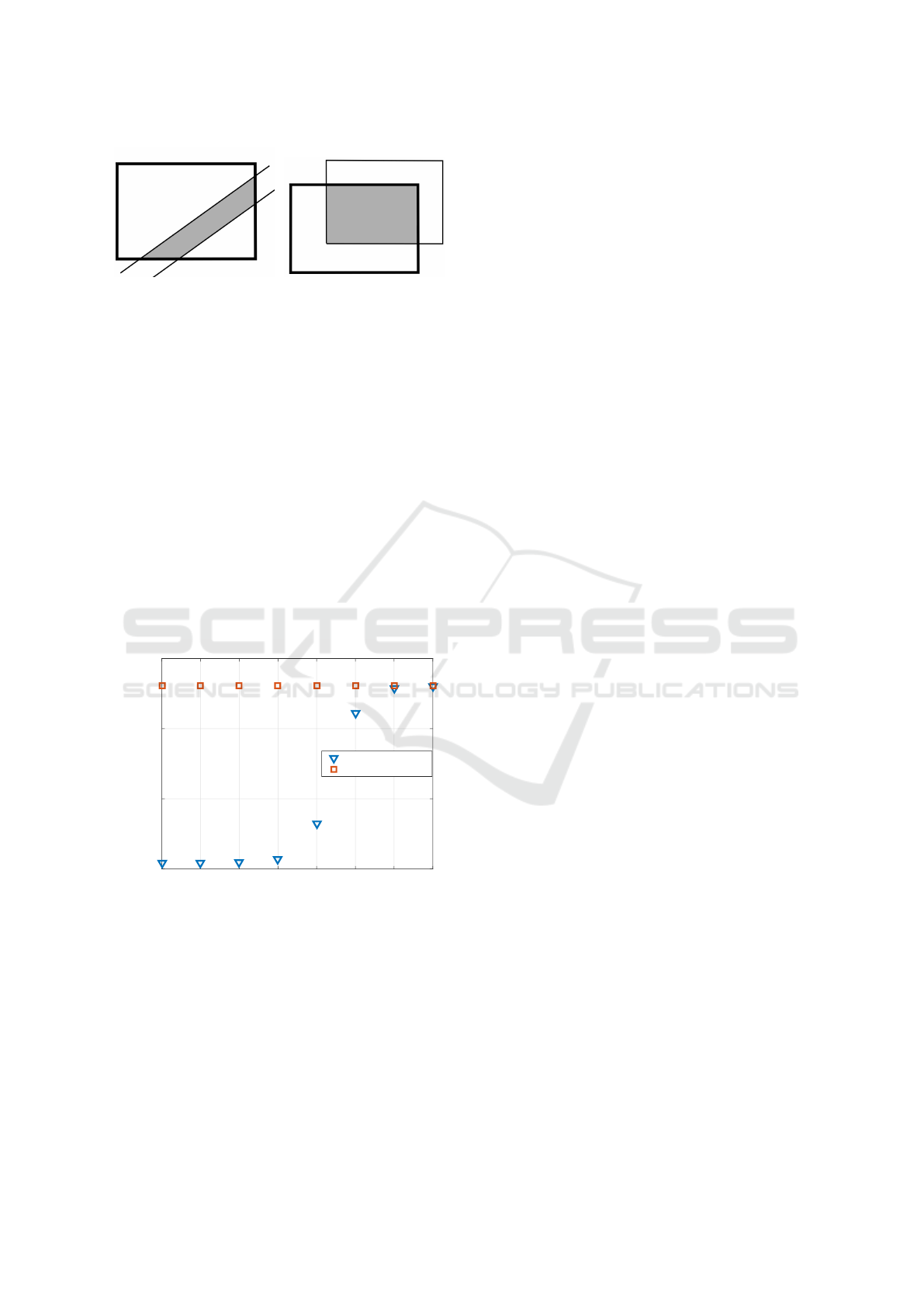
Figure 2: Domain of x
t
. Thick line: target filter, thin line:
transferred set. Left: FPD transfer. Right: informal transfer.
The probable reason for this last point can be il-
lustrated by the left part of Figure 2. The grey area
(the intersection) is to be circumscribed by an ortho-
tope (5). If the strip is too close to the diagonal, the
circumscribing orthotope is similar to the one given
by the time update (if the diagonal is contained in the
strip, the orthotopes are identical). This effect is prob-
ably caused by the fact that orthotopes are too conser-
vative as approximators.
The knowledge transfer acts as a constraint of the
target x
t
set by the source filter. This inspires an infor-
mal transfer, illustrated in the right part of Figure 2.
The idea is to use the intersection of the source and
target time-updated state sets. Although this approach
is not theoretically justified, it seems more suitable for
orthotopic sets. The results of the prediction errors
can be seen in Figure 3, in this informal case. The
-8 -7 -6 -5 -4 -3 -2 -1
log
10
r
s
-6.5
-6
-5.5
-5
log
10
TNSE
Informal transfer, r=0.001
knowledge transfer
isolated filter
Figure 3: TNSE of the target LSU filter as a function of the
observation noise variance r
s
of the source filter. Informal
transfer.
behaviour is qualitatively the same as in the previous
case, but the influence on the target filter precision
is now much more significant in the positive transfer
regime.
It has also been observed that omitting the paral-
lelotope stage in the data update, i.e. involving only
strip tightening as in the FPD-based knowledge trans-
fer, makes no difference in the target state precision.
3.3 Discussion
The isolated LSU filter performance serves as a refer-
ence against which to assess the effect of the knowl-
edge transfer from a source LSU filter to a target one.
A key advantage of the FPD-transfer—apart from its
decision-theoretic optimality—is that the (stochastic)
relationship between the filters does not have to be
specified (in contrast to standard Bayesian transfer
learning techniques (Karbalayghareh et al., 2018)).
This confers robustness on the approach.
Both the FPD and informal transfers of Section 3
exhibit an important property: the ability to reject
the source knowledge in the “below-threshold” case
of inferior-quality data-predictive knowledge transfer
(i.e. where r
s
≥ r). This form of robustness is in con-
trast to FPD transfer between Kalman filters (Gaus-
sian transfer) reported in (Foley and Quinn, 2018),
where r
s
≥ r induces “negative transfer”, decreasing
the target precision in comparison with the isolated
filter. The problem was overcome there by adjust-
ing the transfer to take account of the external pre-
dictive variance. The avoidance of negative trans-
fer in the LSU case is an important finding for the
FPD knowledge transfer mechanism in general, since
it supports a hypothesis—stated in (Foley and Quinn,
2018; Pape
ˇ
z and Quinn, 2018)—that it is a moment-
loss pathology of the Gaussian forms in Kalman fil-
tering that incurred the negative FPD transfer in that
case, and not an intrinsic limitation of the FPD trans-
fer mechanism itself.
On the “above threshold” side (i.e. r
s
< r),
FPD knowledge transfer between LSU filters in-
creases the target precision (Fig. 1)—effecting “pos-
itive transfer”—but this is insignificant compared to
the improvement reported in (Foley and Quinn, 2018).
In contrast, the informal transfer, based on the inter-
section of orthotopes, improves the state estimate pre-
cision strongly (Fig. 3). At threshold (r
s
= r), note
that positive transfer is still achieved in this informal
case. This may be caused by a displacement between
source and target orthotopic domains of the same size
(see the right part of Figure 2).
The weakness of the FPD (i.e. formal) transfer in
the LSU case is probably caused by the fact that or-
thotopes are too conservative as set approximators,
i.e. they approximate the complex polytopic sets too
coarsely (see the diagonal problem described in Fig-
ure 2 (left)). The informal transfer approach (Sec-
tion 3.2) can be suitable for orthotopic approxima-
tions but is not optimal in a Bayesian (FPD) sense. It
may be that this solution does decrease the Kullback-
Leibler divergence (15), (16), but does not give the
minimum (being the FPD solution (17)). However,
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
504

this requires theoretical validation.
In the orthotopically approximated data update
step, the parallelotope stage (7) can be omitted. If so,
the FPD knowledge transfer (Section 2.3) and the data
update involve the same algorithmic flows, as was the
case in (Foley and Quinn, 2018).
4 CONCLUDING REMARKS
The proposed FPD knowledge transfer between LSU
filters has achieved excellent performance, reject-
ing the source data predictor below threshold, while
achieving positive transfer above threshold (particu-
larly in the case of the informal variant). We have
noted in Section 3.3 that the technique is not condi-
tional on an explicit model of interaction between the
filters. It will be interesting in future work to vali-
date further the robustness reported here, by simulat-
ing a richer set of contexts than the one reported in
Section 3, particularly cases of distinct but correlated
state processes.
Future research will also focus on a search for
less conservative approximating sets for the geomet-
ric supports of the uniform approximations adopted
in the time and data update steps of LSU filtering.
The current variant starts with an orthotopic support
within the time update step that is transformed into a
parallelotopic one during the data update step. This is
then circumscribed by an orthotope, to achieve func-
tional closure—and, so, recursion—for the next time
update. It would be less conservative to avoid this
circumscribing approximation, and to recurse within
a parallelotopic support only. However, the compu-
tational overhead of this more complicated setting
needs to be assessed.
In the knowledge transfer step, again, it appears
that it is the conservative nature of the orthotopic ap-
proximation which induces the weakly positive FPD
transfer reported in this paper. Once again, more flex-
ible and so tighter approximating sets—such as par-
allelotopes and zonotopes—will be explored in fu-
ture work. Meanwhile, it will be interesting to find
a formal (FPD) interpretation of the informal pro-
posal which has achieved excellent positive transfer
between the LSU filters (Section 3.2).
In both contexts above, the uniform approxima-
tions on adapted geometric supports are applied lo-
cally at each step of the algorithm, and so it is theo-
retically difficult to assess it convergence after many
steps. In addition, the knowledge transfer is static in
nature (Foley and Quinn, 2018), involving the trans-
fer of the marginal source data predictor at each step.
Progress in this area will require the transfer of dy-
namic (i.e. joint) source knowledge, and a search for a
global approximation of the exact transfer-conditional
target filtering distribution.
ACKNOWLEDGEMENTS
This research has been supported by GA
ˇ
CR grant 18-
15970S.
REFERENCES
Abbas, A. E. (2009). A Kullback-Leibler view of linear and
log-linear pools. Decision Analysis, 6(1):25–37.
Azizi, S. and Quinn, A. (2018). Hierarchical fully proba-
bilistic design for deliberator-based merging in mul-
tiple participant systems. IEEE Transactions on Sys-
tems, Man, and Cybernetics: Systems, 48(4):565–573.
Becis-Aubry, Y., Boutayeb, M., and Darouach, M. (2008).
State estimation in the presence of bounded distur-
bances. Automatica, 44:1867–1873.
Chisci, L., Garulli, A., and Zappa, G. (1996). Recur-
sive state bounding by parallelotopes. Automatica,
32(7):1049–1055.
Dardari, D., Closas, P., and Djuric, P. M. (2015). Indoor
tracking: theory, methods, and technologies. IEEE
Transactions on Vehicular Technology, 64(4):1263–
1278.
Diez-Olivan, A., Ser, J. D., Galar, D., and Sierra, B. (2019).
Data fusion and machine learning for industrial prog-
nosis: trends and perspectives towards industry 4.0.
Information Fusion, 50:92 – 111.
Dou, Y., Ran, C., and Gao, Y. (2016). Weighted mea-
surement fusion Kalman estimator for multisensor de-
scriptor system. International Journal of Sytems Sci-
ence, 47(11):2722–2732.
Fletcher, R. (2000). Practical Methods of Optimization.
John Wiley & Sons.
Foley, C. and Quinn, A. (2018). Fully probabilistic de-
sign for knowledge transfer in a pair of Kalman filters.
IEEE Signal Processing Letters, 25:487–490.
Goudjil, A., Pouliquen, M., Pigeon, E., Gehan, O., and Tar-
gui, B. (2017). Recursive output error identification
algorithm for switched linear systems with bounded
noise. IFAC-PapersOnLine, 50(1):14112–14117.
Gravina, R., Alinia, P., Ghasemzadeh, H., and Fortino, G.
(2017). Multi-sensor fusion in body sensor networks:
state-of-the-art and research challenges. Information
Fusion, 35:68–80.
He, J., Duan, X., Cheng, P., Shi, L., and Cai, L. (2017). Ac-
curate clock synchronization in wireless sensor net-
works with bounded noise. Automatica, 81:350–358.
Jirsa, L., Pavelkov
´
a, L., and Quinn, A. (2019). Approximate
Bayesian prediction using state space model with uni-
form noise. In Gusikhin, O. and Madani, K., editors,
Knowledge Transfer in a Pair of Uniformly Modelled Bayesian Filters
505

Informatics in Control Automation and Robotics, Lec-
ture Notes in Electrical Engineering. Springer. Under
review.
Karbalayghareh, A., Qian, X., and Dougherty, E. R. (2018).
Optimal Bayesian transfer learning. IEEE Transac-
tions on Signal Processing, 66(14):3724–3739.
K
´
arn
´
y, M., B
¨
ohm, J., Guy, T. V., Jirsa, L., Nagy, I., Ne-
doma, P., and Tesa
ˇ
r, L. (2005). Optimized Bayesian
Dynamic Advising: Theory and Algorithms. Springer,
London.
K
´
arn
´
y, M. and Kroupa, T. (2012). Axiomatisation of
fully probabilistic design. Information Sciences,
186(1):105–113.
Khaleghi, B., Khamis, A., Karray, F. O., and Razavi, S. N.
(2013). Multisensor data fusion: a review of the state-
of-the-art. Information Fusion, 14(1):28 – 44.
Lahat, D., Adali, T., and Jutten, C. (2015). Multimodal
data fusion: an overview of methods, challenges, and
prospects. Proceedings of the IEEE, 103(9):1449–
1477.
Lang, L., Chen, W., Bakshi, B. R., Goel, P. K., and Un-
garala, S. (2007). Bayesian estimation via sequential
Monte Carlo sampling — constrained dynamic sys-
tems. Automatica, 43(9):1615–1622.
Majumder, S. and Pratihar, D. K. (2018). Multi-sensors data
fusion through fuzzy clustering and predictive tools.
Expert Systems with Applications, 107:165 – 172.
Nassreddine, G., Abdallah, F., and Denoux, T. (2010). State
estimation using interval analysis and belief-function
theory: application to dynamic vehicle localization.
IEEE Transactions on Systems, Man, and Cybernet-
ics, Part B (Cybernetics), 40(5):1205–1218.
Pape
ˇ
z, M. and Quinn, A. (2018). Dynamic Bayesian knowl-
edge transfer between a pair of Kalman filters. In 2018
28th International Workshop on Machine Learning for
Signal Processing (MLSP), pages 1–6, Aalborg, Den-
mark. IEEE.
Pavelkov
´
a, L. and Jirsa, L. (2018). Approximate recur-
sive Bayesian estimation of state space model with
uniform noise. In Proceedings of the 15th Interna-
tional Conference on Informatics in Control, Automa-
tion and Robotics (ICINCO), pages 388–394, Porto,
Portugal.
Quinn, A., K
´
arn
´
y, M., and Guy, T. (2016). Fully probabilis-
tic design of hierarchical Bayesian models. Informa-
tion Sciences, 369(1):532–547.
Quinn, A., K
´
arn
´
y, M., and Guy, T. V. (2017). Opti-
mal design of priors constrained by external predic-
tors. International Journal of Approximate Reasoning,
84:150–158.
Shamshirband, S., Petkovic, D., Javidnia, H., and Gani, A.
(2015). Sensor data fusion by support vector regres-
sion methodology-a comparative study. IEEE Sensors
Journal, 15(2):850–854.
Simon, D. and Simon, D. L. (2010). Constrained Kalman
filtering via density function truncation for turbofan
engine health estimation. International Journal of
Systems Science, 41:159–171.
Torrey, L. and Shavlik, J. (2010). Transfer learning. In
Handbook of Research on Machine Learning Appli-
cations and Trends: Algorithms, Methods, and Tech-
niques, pages 242–264. IGI Global.
Vapnik, V. and Izmailov, R. (2017). Knowledge transfer
in SVM and neural networks. Annals of Mathematics
and Artificial Intelligence, 81(1-2):3–19.
Vargas-Melendez, L., Boada, B. L., Boada, M. J. L.,
Gauchia, A., and Diaz, V. (2017). Sensor fusion based
on an integrated neural network and probability den-
sity function (PDF) dual Kalman filter for on-line es-
timation of vehicle parameters and states. Sensors,
17(5).
Vicino, A. and Zappa, G. (1996). Sequential approximation
of feasible parameter sets for identification with set
membership uncertainty. IEEE Transactions on Auto-
matic Control, 41(6):774–785.
Vitola, J., Pozo, F., Tibaduiza, D. A., and Anaya, M. (2017).
A sensor data fusion system based on k-nearest neigh-
bor pattern classification for structural health monitor-
ing applications. Sensors, 17(2).
Willner, D., Chang, C., and Dunn, K. (1976). Kalman filter
algorithms for a multi-sensor system. In 1976 IEEE
Conference on Decision and Control including the
15th Symposium on Adaptive Processes, pages 570–
574.
Xiao, F. (2019). Multi-sensor data fusion based on the be-
lief divergence measure of evidences and the belief en-
tropy. Information Fusion, 46:23 – 32.
Yang, C., Yang, Z., and Deng, Z. (2019). Robust weighted
state fusion Kalman estimators for networked systems
with mixed uncertainties. Information Fusion, 45:246
– 265.
Zou, T., Wang, Y., Wang, M., and Lin, S. (2017).
A real-time smooth weighted data fusion algorithm
for greenhouse sensing based on wireless sensor net-
works. Sensors, 17(11).
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
506
