Improving the Convergence of the Periodic QZ Algorithm
Vasile Sima
1 a
and Pascal Gahinet
2 b
1
Modelling, Simulation, Optimization Department, National Institute for Research & Development in Informatics,
Bd. Mares¸al Averescu, Nr. 8–10, Bucharest, Romania
2
MathWorks, 3 Apple Hill Drive, Natick, MA, U.S.A.
Keywords:
Eigenvalue Problem, Hamiltonian Matrix, Numerical Methods, Optimal Control.
Abstract:
The periodic QZ algorithm involved in the structure-preserving skew-Hamiltonian/Hamiltonian algorithm is
investigated. These are key algorithms for many applications in diverse theoretical and practical domains such
as periodic systems, (robust) optimal control, and characterization of dynamical systems. Although in use for
several years, few examples of skew-Hamiltonian/Hamiltonian eigenproblems have been discovered for which
the periodic QZ algorithm either did not converge or required too many iterations to reach the solution. This
paper investigates this rare bad convergence behavior and proposes some modifications of the periodic QZ and
skew-Hamiltonian/Hamiltonian solvers to avoid nonconvergence failures and improve the convergence speed.
The results obtained on a generated set of one million skew-Hamiltonian/Hamiltonian eigenproblems of order
80 show no failures and a significant reduction (sometimes of over 240 times) of the number of iterations.
1 INTRODUCTION
A special, structured eigenvalue problem of much the-
oretical and practical interest is defined by λS − H,
where S is a skew-Hamiltonian matrix, H is a Hamil-
tonian matrix, and λ ∈ C. In the real case, con-
sidered in this paper, often used definitions for such
matrices are (SJ)
T
= −SJ and (HJ)
T
= HJ, where
J :=

0 I
n
−I
n
0

, or
S :=

A D
E A
T

, H :=

C V
W −C
T

, (1)
where A, D, E,C,V,W ∈ R
n×n
, D and E are skew-
symmetric (D = −D
T
, E = −E
T
), V and W are sym-
metric (V = V
T
, W = W
T
), and I
n
is the identity ma-
trix of order n.
The matrix pencil λS − H (or H − λS), defined
above, is skew-Hamiltonian/Hamiltonian (sHH).
These pencils have spectra that are symmetric with
respect to both the real and imaginary axes. But
this symmetry cannot be preserved by general eigen-
solvers such as those in the LAPACK Library (An-
derson et al., 1999) or the eig command from
MATLAB
R

(MathWorks, 2019). For some applica-
tions, including the computation of L
∞
- or H
∞
-norms
a
https://orcid.org/0000-0003-1445-345X
b
https://orcid.org/0000-0002-9485-5127
of linear time-invariant multivariable systems, and so-
lution of algebraic matrix Riccati equations, it is very
important to guarantee the symmetry of the returned
spectra. Ensuring this is possible using structured
eigensolvers such as those implemented in the SLI-
COT Library (Benner et al., 1999) and available in
(MathWorks, 2012) and subsequent releases. The
related theory is exposed, for example, in (Benner
et al., 2002; Benner et al., 2007; Kressner, 2005), and
the basic algorithms are described in (Benner et al.,
2016) and the references therein. The use of these
algorithms for the L
∞
-norms computation and linear-
quadratic and H
∞
optimization is presented in (Ben-
ner et al., 2012a; Benner et al., 2012b; Benner et al.,
2016). The sHH solver is core to the calculation
of the H
∞
-norm, based on (Bruinsma and Steinbuch,
1990), and to nonsmooth minimization of the L
∞
-
norm, which is central to the fixed-order controller
tuning—systune—(Apkarian et al., 2014). The sHH
solver is applied in (Xia et al., 2017) for comput-
ing the R-index of quadratic sector bounds, which of-
fer a characterization of, for instance, dynamical sys-
tems behavior, including passivity, dissipativity, and
input/output gain. The SHH solver also comes into
play in the new “safe” approach in robust control for
finding µ upper bounds for real uncertainty.
The sHH solver uses the periodic QZ algorithm,
sometimes called periodic QR algorithm (Van Loan,
1975; Bojanczyk et al., 1992; Sreedhar and
Sima, V. and Gahinet, P.
Improving the Convergence of the Periodic QZ Algorithm.
DOI: 10.5220/0007876902610268
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 261-268
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
261

Van Dooren, 1994). This algorithm is also indepen-
dently implemented in many applications, for exam-
ple, for periodic linear systems, or for k-cyclic ma-
trices and pencils encountered in the investigation of
Markov chains and the solution of two-point bound-
ary value problems (Bojanczyk et al., 1992).
Although the sHH solver has been in use for sev-
eral years and has been exhaustively tested, some ex-
amples have been recently discovered for which the
underlying periodic QZ solver (pQZ) fails to con-
verge. Such cases are rare events. However, a failure
is very undesirable for applications requiring the full
eigenspectrum, since, in the best situation, only part
of the eigenvalues can be obtained. Therefore, an ef-
fort has been undertaken to investigate the reason for
failures and find a correction. Nonconvergence may
appear because of a too tight tolerance and increasing
it may correct the behavior. However, this may result
in a lower accuracy of the computed eigenvalues.
This paper investigates the pQZ solver failures in
the sHH context and describes the currently adopted
solution to avoid them. Section 2 presents some de-
tails about the algorithms needed for further discus-
sion. Section 3 analyzes a specific failure case. Sec-
tion 4 proposes the solution for forcing convergence
and discusses the obtained results, which illustrate a
much faster convergence than for the previous version
of the solvers. Section 5 summarizes the conclusions.
2 BASIC THEORY AND
UNDERLYING ALGORITHMS
The skew-Hamiltonian/Hamiltonian structure is pre-
served under J-congruence transformations, defined
as λ
e
S −
e
H := JP
T
J
T
(λS − H)P, where P is a non-
singular matrix. The pencils λ
e
S −
e
H and λS − H are
equivalent, that is, they have the same spectrum. For
numerical reasons, P is chosen to be orthogonal so
that the eigenproblem conditioning is also preserved.
Such J-congruence transformations with orthogonal
P are used to reduce the pencil (1) to a condensed
form, which reveals its eigenvalues. A desirable con-
densed form is the skew-Hamiltonian/Hamiltonian
Schur form, also called the structured Schur form,
λ
e
S −
e
H = λ

S
11
S
12
0 S
T
11

−

H
11
H
12
0 −H
T
11

, (2)
where S
11
, H
11
∈ R
n×n
, with S
11
upper triangular and
H
11
in real Schur form. Since the structured Schur
form does not exist in general, the theory makes use
of an embedding of λS −H into an sHH matrix pencil
of double size. Briefly speaking, the sHH algorithm
for computing the eigenvalues of λS − H proceeds as
follows (see (Benner et al., 2013) for more details):
1. Reduce S to skew-Hamiltonian triangular form,
using an orthogonal matrix Q
1
(built from House-
holder transformations and Givens rotations),
S := Q
T
1
SJQ
1
J
T
=

S
11
S
12
0 S
T
11

,
where S
11
is upper triangular. Update H :=
Q
T
1
HJQ
1
J
T
.
2. Set T := S. Reduce H to Hessenberg-triangular
form using orthogonal matrices Q
1
and Q
2
(built
from Givens rotations), which also preserve the
structure of S and T ,
S := Q
T
1
SJQ
1
J
T
=

S
11
S
12
0 S
T
11

,
T := JQ
T
2
J
T
T Q
2
=

T
11
T
12
0 T
T
11

,
H := Q
T
1
HQ
2
=

H
11
H
12
0 H
T
22

,
where S
11
, T
11
, and H
11
are upper triangular and
H
22
is upper Hessenberg.
3. Apply the periodic QZ algorithm to the formal
matrix product H
22
S
−1
11
H
11
T
−1
11
, using orthogonal
matrices V
i
, i = 1 : 4, such that S
11
:= V
T
3
S
11
V
2
,
H
11
:= V
T
3
H
11
V
4
, T
11
:= V
T
1
T
11
V
4
are upper tri-
angular, and H
22
:= V
T
1
H
22
V
2
is upper quasi-
triangular (i.e., it is block upper triangular, with
1 × 1 and 2 × 2 diagonal blocks). MATLAB-style
notation is used for index ranges.
4. Set Λ(S, H) = ±ı
q
Λ(H
22
S
−1
11
H
11
T
−1
11
), where
Λ(·(, ·)) denotes the spectrum of the matrix · (or
of the matrix pencil ·, ·).
Taking symmetry into account, only n eigenvalues
are returned by the solver, namely those with non-
negative imaginary part and those positive, if real.
The remaining eigenvalues have opposite signs. The
matrices S
11
and T
11
in the formal matrix product
H
22
S
−1
11
H
11
T
−1
11
may be singular, meaning that there
are infinite eigenvalues.
1
However, it is assumed
that the original matrix pencil is regular, that is,
det(λS − H) 6≡ 0. Note that the transformed formal
matrix product is similar with the initial matrix prod-
uct at Step 3, that is, they have the same spectrum.
Even if the matrices S
11
and T
11
are nonsingular, eval-
uating the product and calling a standard eigensolver
1
This is the reason of referring to a “formal” matrix
product, since when any of the matrices S
11
or T
11
is sin-
gular, that product does not exist.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
262

is not a good idea in general because of a risk of nu-
merical cancellations, especially for large number of
factors and of ill-conditioned inverses.
This paper investigates in more detail the numeri-
cal behavior of the periodic QZ algorithm at Step 3 in
the context of solving sHH eigenproblems.
Consider now a formal matrix product P,
P =
k
∏
i=1
A
s
i
i
, (3)
where A
i
∈ R
n×n
, and s
i
= ±1, i = 1 : k. The pQZ
algorithm does not evaluate the product but just trans-
forms the factors to reveal the eigenstructure. A nega-
tive exponent s
i
means that the “inverse” of the corre-
sponding factor, A
i
, should be considered. If a factor
with such an exponent is singular, the algorithm will
still provide a solution, revealing one or more infinite
eigenvalues. The pQZ algorithm operates with gen-
eral formal matrix products, where the factors have
no structure. Any such product can be reduced to a
similar one, where one of the factors is upper Hessen-
berg and all other factors are upper triangular. Such a
reduction is described in (Bojanczyk et al., 1992) for
the case with alternating exponents in (3). In the con-
text of this paper, consider that A
h
is upper Hessen-
berg and A
i
are upper triangular, i 6= h. Without loss
of generality it is assumed that s
h
= 1. Otherwise, all
exponents can be virtually multiplied by −1.
2
Since
Λ(P) = Λ

h−1
∏
i=1
A
s
i
i
k
∏
i=h
A
s
i
i

= Λ

k
∏
i=h
A
s
i
i
h−1
∏
i=1
A
s
i
i

,
it can be assumed that h = 1 or h = k. For the
sHH problem described above, h = 1, k = 4, and
s =

1, −1, 1, −1

.
The pQZ algorithm is a generalization of the QZ
algorithm that was treated in, for example, (Golub and
Van Loan, 1996). The essential ingredients are the
same: reduction to a Hessenberg-triangular form, de-
flation, computation of the shifts, and the QZ step.
All transformations applied during the computations
are defined as follows:
e
A
i
:=

Q
T
i
A
i
Q
i⊕1
, if s
i
= 1,
Q
T
i⊕1
A
i
Q
i
, if s
i
= −1,
(4)
where Q
i
, i = 1 : k, are orthogonal matrices (built by
multiplying plane rotations, in the context of this pa-
per), and i ⊕ 1 := mod(i, k) + 1. Using (4) it follows
that
e
A
s
i
i
= Q
T
i
A
s
i
i
Q
i⊕1
. It is easy to verify that the defi-
nitions in (4) preserve similarity between the original
and transformed formal product. Indeed,
e
A
s
1
1
e
A
s
2
2
·· ·
e
A
s
k
k
= Q
T
1
A
s
1
1
A
s
2
2
·· ·A
s
k
k
Q
1
= Q
T
1
PQ
1
.
2
Note that in this case the eigenvalues of the original
product will be the reciprocals of the eigenvalues computed
with opposite exponents.
Two deflation strategies are implemented in the pe-
riodic QZ solver. The first strategy is a “careful”
(or cautious) one, where the convergence criteria are
based on the magnitudes of neighboring elements.
This is the recommended option and it is used by the
sHH solver when calling the periodic QZ algorithm.
The second one is a more “aggressive” strategy, when
elements on the subdiagonal or diagonal are set to
zero as soon as they become smaller in magnitude
than the norm of the corresponding factor times the
relative machine precision, ε
M
. This option is only
recommended if balancing is applied beforehand and
convergence problems are observed.
The processing following a deflation detection is
performed in specific ways for the Hessenberg matrix
and for triangular matrices. More details are given for
the Hessenberg matrix case. The notation a
(i)
pq
denotes
the (p, q) entry of A
i
, also written as A
(i)
when sub-
scripts are needed. For the cautious case, define t =
ε
M
(|a
(1)
j−1, j−1
|+|a
(1)
j, j
|), if t 6= 0, and t = ε
M
kA
(1)
1: j,1: j
k
1
,
otherwise, where k · k
1
refers to the 1-norm of a ma-
trix. If |a
(1)
j, j−1
| ≤ t, then a
(1)
j, j−1
is considered negli-
gible, the Hessenberg matrix is split into two Hes-
senberg submatrices, A
(1)
1: j−1,1: j−1
and A
(1)
j:n, j:n
, and the
eigenvalue problem is solved separately for each of
them, starting with the trailing part. Of course, if
the previous deflation took place at an index l, then
the current subproblem to be solved is defined by the
range of indices j : l. In the “aggressive” deflation
case, the tolerance used is t = ε
M
kA
1
k
F
, where the
subscript F refers to the Frobenius norm. Summa-
rizing, a deflation in the Hessenberg matrix reduces
to partitioning of the problem into subproblems. No
transformations are necessary.
Similar tests are performed for the triangular ma-
trices of the formal matrix product. When there is a
zero diagonal element in a triangular matrix A
i
with
s
i
= 1, about n suitably chosen Givens rotations ap-
plied on each side of each factor will deflate a zero
eigenvalue. Similarly, when there is a zero diagonal
element in a triangular matrix A
i
with s
i
= −1, an in-
finite eigenvalue will be deflated. More details are
given in (Bojanczyk et al., 1992; Kressner, 2001).
The periodic QZ step works with subproblems
where the Hessenberg submatrix is unreduced, that
is, without any zero on the first subdiagonal, and the
triangular submatrices are nonsingular. Starting with
a suitably chosen initial transformation discussed be-
low, new transformations are found and are propa-
gated to all factors via (4) so that the transformed
subproblem preserves its Hessenberg-triangular form.
Each such “sweep” is equivalent to one step of the
standard QR algorithm applied to the formal matrix
Improving the Convergence of the Periodic QZ Algorithm
263

product. According to the theory of the standard
eigenproblem, after a number of QR steps, defla-
tion(s) will occur and the problem decomposes into
smaller subproblems. Normally, the pQZ algorithm
finishes finding all eigenvalues. However, in rare
cases the algorithm may not converge.
The initial transformation is chosen with the aim
of increasing the convergence speed. This is per-
formed using shifts. Assume that the eigenvalues
λ
l+1
, . . . , λ
n
have been determined and an unreduced
nonsingular subproblem has been found, defined by
the range of indices j : l, where initially l = n. The
standard technique for matrices (or matrix pencils) is
to use as shifts the eigenvalues of the block(s) defined
by l − 1 : l, if l > 1, or by l, otherwise. Since the
bottom 2 ×2 part may have complex conjugate eigen-
values, using two shifts simultaneously is necessary
to keep the arithmetic real. Actually, the two shifts
implicitly used are the eigenvalues λ
1
and λ
2
of the
2 × 2 matrix (adapted from (Kressner, 2001))
F :=
"
a
(1)
mm
a
(1)
ml
a
(1)
lm
a
(1)
ll
#
k
∏
i=2
"
a
(i)
mm
a
(i)
ml
0 a
(i)
ll
#
s
i
, (5)
where m = l − 1.
The algorithm annihilates the second and third en-
tries of the first column, P
1
, of the double shift Wilkin-
son polynomial
P
λ
:=

P − λ
1
I
q

P − λ
2
I
q

= P
2
− (λ
1
+ λ
2
)P + λ
1
λ
2
I
q
, (6)
where P denotes the submatrix containing the rows
and columns j : l of P, and q = l − j + 1. Specifically,
two Givens rotations, G
1
and G
2
, are computed such
that

G
1
0
0 I
q−2



1 0 0
0 G
2
0
0 0 I
q−3


P
1
=: U
0
P
1
(7)
is transformed to a multiple of e
1
, the first column
of the identity matrix I
q
. Note that the entries 4 : q
of P
1
are zero by construction. Although this is a
standard procedure for eigensolvers, a brief explana-
tion is useful. The algorithm actually performs two
QR steps with shifts λ
1
and λ
2
. The QR factorization,
P − λ
1
I
q
= Q
a
R
a
, where Q
a
is orthogonal and R
a
up-
per triangular, and the spectrum preserving operation
P
a
:= R
a
Q
a
+ λ
1
I
q
= Q
T
a
PQ
a
define the first QR step. Q
a
is chosen so that P
a
is
upper Hessenberg. Similarly, P
a
− λ
2
I
q
= Q
b
R
b
, and
P
b
:= R
b
Q
b
+ λ
2
I
q
= Q
T
b
P
a
Q
b
= Q
T
b
Q
T
a
PQ
a
Q
b
define the second QR step. Setting Q = Q
a
Q
b
, R =
R
b
R
a
, premultiplying Q
b
R
b
= P
a
− λ
2
I
q
by Q
a
, and
postmultiplying it by R
a
= Q
T
a
(P − λ
1
I
q
), it follows
that
QR =

P − λ
2
I
q

P − λ
1
I
q

= P
λ
is a QR factorization of P
λ
. Moreover, QP
b
= PQ and
P
b
is, without loss of generality, an unreduced Hes-
senberg matrix. But any real unreduced Hessenberg
matrix H := Q
T
PQ, with Q an orthogonal matrix, has
the property that H and Q are uniquely determined
by the first column of Q, see, for instance, (Golub and
Van Loan, 1996). Therefore, if from P one determines
an upper Hessenberg matrix H so that
e
QH = P
e
Q,
where
e
Q is orthogonal and its first column coincides
with that of Q, then
e
Q = Q and H = P
b
. Now, P
λ
can
be triangularized by a product of q − 1 Householder
transformations, U
i
= U
T
i
, i = 1 : q − 1, and the first
column of Q = U
1
U
2
·· ·U
q−1
coincides with that of
U
1
(and with that of U
0
in (7)), which has at most
the first three entries nonzero. Hence, U
1
PU
1
has a
“bump” of extra possibly nonzero entries in the loca-
tions (3,1), (4,1), and (4,2). If U
1
PU
1
is reduced to an
upper Hessenberg matrix H, then H = P
b
.
For numerical reasons, P, F, Λ(F), and P
λ
are not
explicitly computed but a suitable embedding is used.
The previous version of the solver used the embed-
ding proposed in (Kressner, 2001),
P
λ
=

A
1
I
q

k
∏
i=2

A
i
0
0 a
(i)
mm
I
q

s
i
·

−I
q
0
a
(1)
mm
I
q
−a
(1)
lm
I
q

"
−A
1
a
(1)
lm
I
q
a
(1)
ll
I
q
0 a
(1)
mm
I
q
a
(1)
ml
I
q
#
·
k
∏
i=2



A
i
0 0
0 a
(i)
mm
I
q
a
(i)
ml
I
q
0 0 a
(i)
ll
I
q



s
i


I
q
0
I
q


, (8)
where A
i
is the submatrix defined by the rows and
columns j : l of A
i
. By exploiting the structure in (8),
the rotations G
1
and G
2
can be efficiently computed.
Evaluating the embedding (8) indeed gives
P
2
− (λ
1
+ λ
2
)P + λ
1
λ
2
I
q
.
3 CONVERGENCE FAILURE
EXPERIMENT
Although myriads of sHH eigenproblems have been
successfully solved, in recent work a problem was
identified where the pQZ solver, hence also the sHH
solver, failed to converge. Because this event proved
difficult to reproduce across platforms, a small bi-
nary scaling was applied to make the solver fail more
consistently and obtain failure rate statistics for algo-
rithm comparison purposes and further investigations.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
264

This is briefly described below. The start was with a
structured skew-symmetric/symmetric pencil of order
2n = 80 defined by the skew-symmetric matrix N and
symmetric matrix M, given as
N :=

−D A
−A
T
E

, M :=

−V C
C
T
W

. (9)
The (skew-)symmetry of N and M implies that D and
E are skew-symmetric and V and W are symmetric
matrices. By applying a block-column permutation
and sign changes, the pencil λS − H, with S := −NJ
and H := −MJ, is sHH.
Starting from this example, a large number of tests
have been performed. Specifically, randomized small
scaling factors have been used, chosen as 2
r
, with r
randomly taking values in the set {−2, −1, 0, 1, 2}.
Two vectors, S
1
, S
2
, of length 40, with such scaling
factors have been used for each new example, gener-
ated as,
e
A = diag(S
1
)A diag(S
2
);
e
D = diag(S
1
)D diag(S
1
);
e
E = diag(S
2
)E diag(S
2
);
e
C = diag(S
1
)C diag(S
2
);
e
V = diag(S
1
)V diag(S
1
);
e
W = diag(S
2
)W diag(S
2
).
With this scaling, the sHH problems for A, D, E, C,
V , W and
e
A,
e
D,
e
E,
e
C,
e
V ,
e
W have the same eigenval-
ues. Moreover, since all problems generated in this
manner only differ by a small scaling from the origi-
nal problem, the convergence behavior of the periodic
QZ algorithm should be quite similar for all of them.
However, in the first tests with the previous sHH ver-
sion of the solver, there were 42 cases of noncon-
vergence failures in 21095 trials. For such a failure,
the periodic QZ algorithm (called by the sHH solver)
cannot separate a 1 × 1 or 2 × 2 submatrix at the bot-
tom of the current Hessenberg matrix, defined by the
last row and column index l. This means that the l-
th eigenvalue could not be found since the periodic
QZ iteration did not converge. The processed subma-
trix C
1:l,1:l
is still in the upper Hessenberg form (not
necessarily unreduced) and not in full Schur form (at
least, its elements c
l−1,l−2
and c
l,l−1
are not zero).
One approach for solving the convergence prob-
lem is to increase the accepted maximum total num-
ber of iterations. The initial version of the pQZ solver
has this value set to 30n. Such a number is also used
in the LAPACK eigensolvers. However, a larger value
could be used, for example, 60n, taking into account
that a 2n-order eigenproblem is actually solved. Some
statistics for the failure rates for different values of the
number of iterations are shown in Table 1, for exactly
the same problems (generated using the same initial
seed for the MATLAB function rand).
In contrast, using the “aggressive” strategy, con-
vergence was achieved for all nonconverging prob-
lems. This observation suggested that after a fail-
ure with the cautious strategy, in principle, a second
call with the “aggressive” strategy might work. Since
the number of nonconverging examples is very small
compared to the number of tests, the additional com-
putational effort due to the second call of the solver is
negligible.
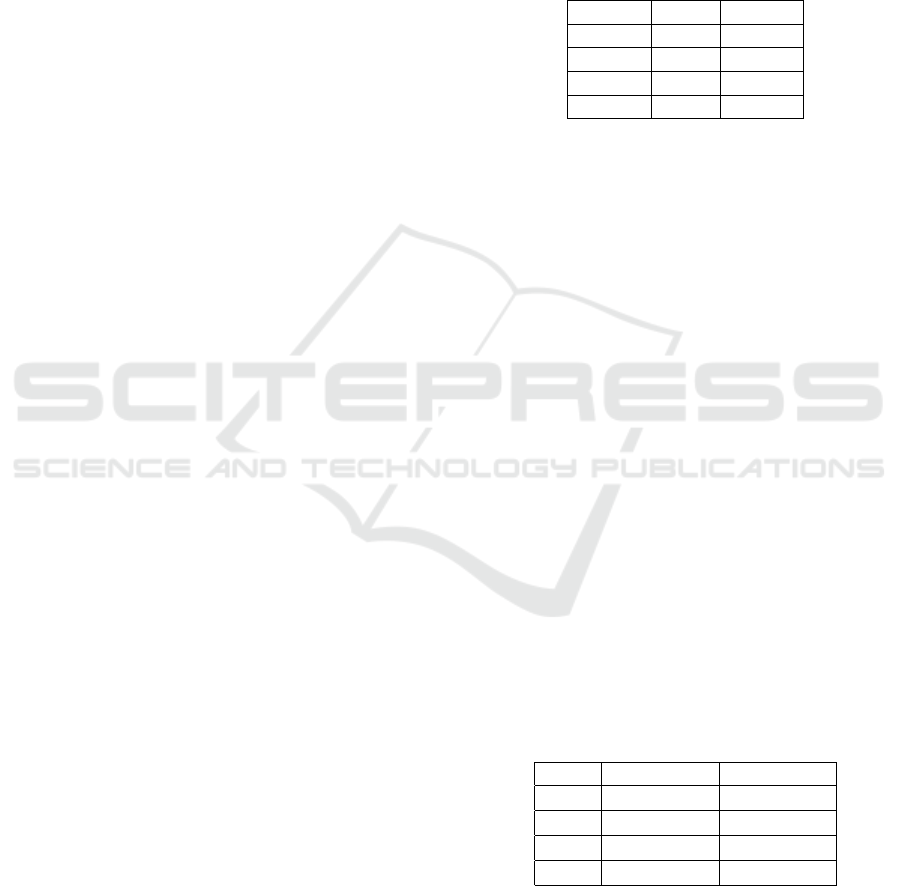
Table 1: Failure rates statistics for several values of the total
number of iterations, maxit, allowed for pQZ algorithm.
runs maxit failures
21095 30n 42
60n 1
100107 60n 17
120n 1
Note that increasing the allowed total number of it-
erations does not practically affect the computational
effort. However, there is no guarantee that all prob-
lems could be solved, no matter how many iterations
are allowed. Based on these remarks, several changes
in the implementation details of the sHH and pQZ
solvers have been evaluated. The simplest and ef-
fective working solution has been to allow for 120n
iterations and make a second call of the pQZ solver
with the “aggressive” option when the first call (with
the “careful” option) returned with an error indicating
nonconvergence. With this modification, there were
only four cases, out of 10
6
scaled problems, when the
first call to the pQZ solver did not converge. For these
cases, convergence occurred with the second call. Ta-
ble 2 shows some error statistics for all these 10
6
runs
with respect to the original problem. The notations
used are as follows: err is the error norm (the Eu-
clidean norm of the vector of differences in the eigen-
values of the original and a scaled problem); rerr is
the relative error norm; max, min, and mean denote
the maximum, minimum, and the mean of all these er-
rors, respectively; norm denotes the Euclidean norm
of the vector of all error norms.
Table 2: Global error statistics for 10
6
runs of the sHH
solver with respect to the original problem.
err rerr
max 3.20 · 10
−11
5.18 · 10
−13
min 8.94 · 10
−14
1.45 · 10
−15
mean 7.36 · 10
−13
1.19 · 10
−14
norm 1.09 · 10
−9
1.77 · 10
−11
The values in Table 2 are very good results. More-
over, with the previous version of the solver there
were about 20-30 fatal failures (meaning nonconver-
gence) for each batch of 10
4
problems, that is, 2000-
3000 failures for a 10
6
problem set.
Improving the Convergence of the Periodic QZ Algorithm
265

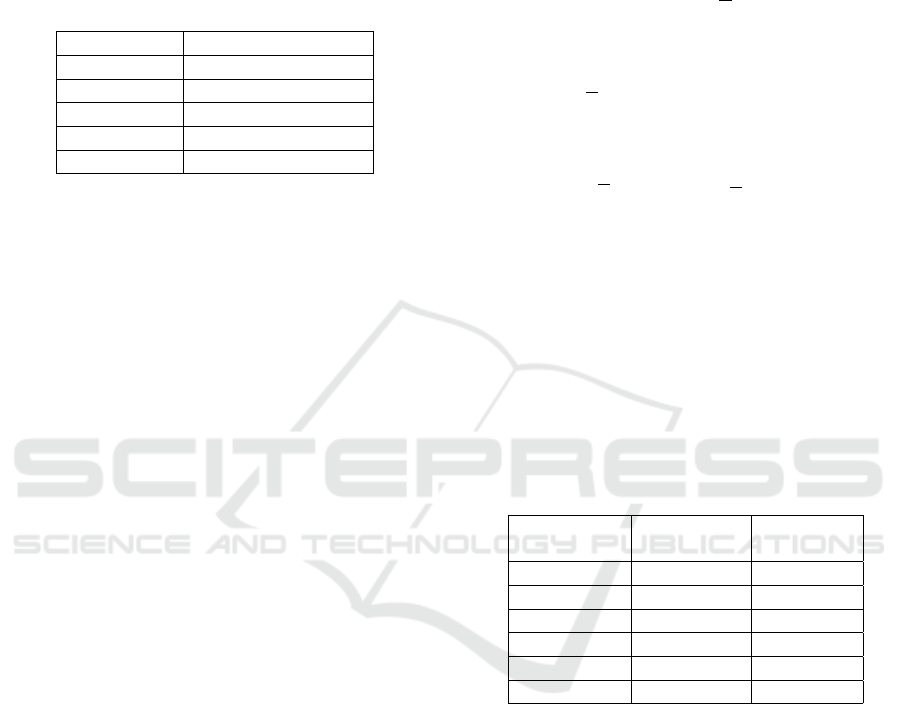
Table 3 shows the number of examples, from a
set of 40004 scaled problems generated as described
above, needing a number of iterations of the periodic
QZ algorithm in various ranges. The only iteration
count that exceeded 3000 was 3090.
Table 3: Histogram data for the number of iterations of the
periodic QZ algorithm for 40004 runs.
Iterations Number of examples
> 3000 1
(2000, 3000 ] 14
(1000, 2000 ] 96
(100, 1000 ] 8,679
≤ 100 31,214
Therefore, less than 100 iterations are needed for al-
most all cases. The mean number is about 108. But
there are about 100 problems that needed more than
30n = 1200 iterations. Even 60n is not sufficiently
large for about a dozen problems.
4 IMPROVING PERIODIC QZ
ALGORITHM
During the tests, it was discovered that the implicit
Wilkinson double shift polynomial used by the peri-
odic QZ solver was not the desired one. Specifically,
the first rows of the matrix F in (5) and of the trailing
2 × 2 submatrix of P
λ
in (6) differ, since the contribu-
tion of the l −2 rows of the factors is not taken into ac-
count, where l is the last row of the currently deflated
subproblem. The influence of the l − 2 rows could
be avoided if the Hessenberg matrix would be the last
factor of the product. But in the implementation of the
sHH solver, the Hessenberg matrix is assumed to be
the first one. Since F is incorrect, the implicitly used
shifts are inaccurate, at least in the first iterations of
the pQZ algorithm for the same subproblem. How-
ever, the shifts become increasingly accurate if and
when the iterative process converges for the current
subproblem. The occasionally observed convergence
difficulties were supposed to be explainable by the use
of possibly poor approximations of the true eigenval-
ues of the trailing 2 × 2 submatrix of the product.
Since the eigenvalues of the formal product P
in (3) with s
1
= 1 are the same as the eigenvalues of

k
∏
i=2
A
s
i
i

A
1
, (10)
it was then necessary to find an appropriate embed-
ding for the product having the Hessenberg matrix A
1
as the last factor and to adapt the solver for this new
setting. Then, the eigenvalues of the trailing 2 × 2
subproblem of the new double shift polynomial will
be indeed correct.
For the formal matrix product in (10) it can be
proven that an embedding of the corresponding P
λ
is
P
λ
=

−I
q
I
q
0

k
∏
i=2



A
i
0 0
0 a
(i)
mm
I
q
a
(i)
ml
I
q
0 0 a
(i)
ll
I
q



s
i
·



A
1
0
a
(1)
mm
I
q
a
(1)
ml
I
q
a
(1)
lm
I
q
a
(1)
ll
I
q



"
−I
q
a
(1)
ll
I
q
0 −a
(1)
lm
I
q
#
·
k
∏
j=2

A
i
0
0 a
(i)
ll
I
q

s
i

A
1
I
q

. (11)
This embedding is used to find the matrix U
0
so that
when premultiplying P
λ
by U
0
, its first column is re-
duced to a multiple of e
1
.
However, the tests with the scaled problems men-
tioned before have shown a behavior similar to that
for the previous version of the solver. Specifically, for
four problems out of 1,010,000, the modified solver
did not converge in 120n = 4800 iterations. The re-
sults are shown in Table 4.
Table 4: Histogram data for the number of iterations of the
modified periodic QZ algorithm for 1,010,000 runs.
Iterations Number of
examples
Percentage
> 4000 8 0.00079
(3000, 4000 ] 45 0.0045
(2000, 3000 ] 373 0.037
(1000, 2000 ] 2,492 0.25
(100, 1000 ] 217,554 21.54
≤ 100 789,528 78.17
Therefore, 99.71% of the problems required less than
1000 iterations. However, 2,245 problems required
more than 30n = 1200 iterations (the usual maximum
number of iterations in a QR-like algorithm), of which
151 problems required more than 60n iterations. The
mean number of iterations is 106, the median is 85,
and the standard deviation is 104.55. The error statis-
tics are identical or slightly better than in Table 2. All
four problems showing nonconvergence actually con-
verged after a second call to the periodic QZ solver
with the “aggressive” strategy.
The irregularity of a nonnegligible number of
problems requiring much more iterations than the
large majority, for a sequence of problems (with iden-
tical eigenvalues) differing only by small, powers of
2, scaling factors, suggested that further investiga-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
266

tion is needed. The nonconverging example encoun-
tered first in the series has been analyzed in detail.
The behavior of the solver for this problem can be
summarized as follows: out of n = 40 eigenvalues to
compute, the last 22 have been found after 61 itera-
tions and the algorithm has further deflated a block
of size 4 in the rows and columns 15:18, which has
two pairs of complex conjugate eigenvalues. Unfor-
tunately, this subproblem could not be split in the re-
maining 4800 − 61 iterations.
The 4×4 nonconverging subproblem was isolated
and analyzed separately. The product of its factors has
eigenvalues 75.74 ± 0.07689ı and 116.84 ± 0.06248ı,
but the eigenvalues of the trailing 2 × 2 (product) sub-
matrix are real, about 75.75 and 116.82. So, the pQZ
solver implicitly assumed these real eigenvalues as
initial shifts. The behavior in the remaining itera-
tions, but the last three ones, was similar. Omitting
these last three iterations, at each other iteration, the
two real eigenvalues belonged to two clusters cen-
tered at 75.74 and 116.84, with standard deviations
about 7.74 · 10
−2
and 3.98 · 10
−2
, respectively. The
problem was solved after 1149 iterations, which is
about three times larger than the default value, that
is, 120 × 4. However, the minimum absolute value of
the (3,2) element during iterations, except for the last
three, was 9.22 · 10
−5
. The last three absolute values
were 6.18· 10
−8
, 5.26· 10
−19
and 0, respectively. The
eigenvalues used as shifts for the last three iterations
were 116.84 ± 0.06248ı.
The main convergence difficulty above seems to
be due to the existence of two consecutive 2 × 2
blocks with small imaginary parts. The implicitly
chosen shifts are taken close to the real parts of
the complex eigenvalues from both blocks. Conse-
quently, it is impossible to force convergence in this
case using such shifts.
This remark suggested how to modify the periodic
QZ solver to force convergence when needed. Specif-
ically, if an eigenvalue (pair) does not converge af-
ter 60 iterations and the order of the current deflated
(hence nonsingular) subproblem is at most six, then
a new routine is called, which computes the eigen-
values of that subproblem using the LAPACK (An-
derson et al., 1999) routine DLAHQR and finds two
rotations making the first column of the real Wilkin-
son double shift polynomial parallel to the first unit
vector. The shifts are chosen as the two eigenvalues
with largest moduli. If there are complex conjugate
eigenvalues, the real eigenvalues, if any, are not con-
sidered. The idea is to force convergence for the 2 ×2
blocks because such blocks may produce convergence
difficulties. Clearly, this strategy evaluates the prod-
uct of the factors, but only for small order subprob-
lems for which there are convergence difficulties. If
the shifts found in this manner are still inaccurate be-
cause of nearly singular submatrices and because of
multiplying the factors, then convergence difficulties
may in principle persist, though this never occurred in
the case study of this paper. For most examples, this
strategy is not invoked at all. A “window” of 60 it-
erations for each new eigenvalue (pair) has been cho-
sen in order to allow the use of exceptional transfor-
mations, as in other eigensolvers. After invoking an
exceptional transformation, a switch is set for calling
the new routine finding the eigenvalues to be used as
shifts. However, this routine is invoked only if con-
vergence does not occur after 30 additional iterations
for the same small order (≤ 6) subproblem. In such
a case, the routine can be called for the next, at most
10, consecutive iterations.
The strategy described above proved to be very
effective for the 10
6
set of scaled problems. All prob-
lems converged and the maximum number of itera-
tions was 204. The second call of the periodic QZ
solver, with the “aggressive” deflation strategy, was
never needed. The error statistics are actually the
same as before (see Table 2) but the convergence is
much faster. Specifically, 99.88% of the problems re-
quire less than 150 iterations, which is much smaller
than 30n = 1200. The mean number of iterations is
90.65, the median value is 85, and the standard devi-
ation is 13.85, again much smaller than for the previ-
ous versions of the periodic QZ algorithm. The sum-
mary of the convergence results is given in Table 5. It
is possible to avoid using exceptional transformations
for small order deflated subproblems, calling the new
routine instead, and further increasing the speed by
using a smaller window size. Experiments with this
approach have resulted in further reduction of the to-
tal number of iterations. The value 4 for the maxi-
mum order of the subproblem has also been used in-
stead of 6 and the behavior has been the same for our
case study. The value 6 has been chosen to possibly
enlarge the domain in which this strategy is effective.
Table 5: Histogram data for the number of iterations of
the latest modification of the periodic QZ algorithm for
1,000,001 runs.
Iterations Number of
examples
Percentage
> 200 2 0.0002
(150, 200 ] 1,233 0.123
(100, 150 ] 219,236 21.92
(75, 100 ] 774,329 77.43
(50, 75 ] 5,201 0.52
The new routine for finding the shifts is called only
Improving the Convergence of the Periodic QZ Algorithm
267

when there are convergence difficulties (after 60 iter-
ations in the current version). Otherwise, and also for
the next eigenvalues, the implicit scheme is used, as
long as it works fast enough. The main difficulty with
the original solver was that the implicitly used eigen-
values have been real approximations of eigenvalues
from two different blocks with complex eigenvalues.
If the real parts of a complex conjugate pair with small
imaginary parts would have been used, the implicit
scheme would be likely to succeed but this was not
the case and too many iterations were required in the
situation described above. Actually, all 10
6
problems
have been solved by allowing around 5500 iterations.
5 CONCLUSIONS
The periodic QZ algorithm involved in the structure-
preserving skew-Hamiltonian/Hamiltonian algorithm
has been investigated. The main algorithmic is-
sues have been presented and the convergence be-
havior has been analyzed for a series of equivalent
skew-Hamiltonian/Hamiltonian eigenproblems of or-
der 80, which differ by small, powers of 2, scaling
factors. In a few cases, the previous version of the
solver did not converge. For other cases the num-
ber of iterations required for convergence varied in a
very large range (from less than 100 till over 5000).
Some modifications of the periodic QZ and skew-
Hamiltonian/Hamiltonian solvers have been proposed
for which there are no failures and the number of iter-
ations did not exceed 204 for the same large set of ex-
amples. These solvers are needed in many domains,
including periodic systems and robust optimal con-
trol.
REFERENCES
Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel,
J., Dongarra, J., Du Croz, J., Greenbaum, A., Ham-
marling, S., McKenney, A., and Sorensen, D. (1999).
LAPACK Users’ Guide: Third Edition. Software · En-
vironments · Tools. SIAM, Philadelphia.
Apkarian, P., Gahinet, P. M., and Buhr, C. (2014). Multi-
model, multi-objective tuning of fixed-structure con-
trollers. In Proceedings 13th European Control Con-
ference (ECC), 24–27 June 2014, Strasbourg, France,
pages 856–861. IEEE.
Benner, P., Byers, R., Losse, P., Mehrmann, V., and
Xu, H. (2007). Numerical solution of real skew-
Hamiltonian/Hamiltonian eigenproblems. Technical
report, Technische Universit
¨
at Chemnitz, Chemnitz.
Benner, P., Byers, R., Mehrmann, V., and Xu, H. (2002).
Numerical computation of deflating subspaces of
skew Hamiltonian/Hamiltonian pencils. SIAM J. Ma-
trix Anal. Appl., 24(1):165–190.
Benner, P., Mehrmann, V., Sima, V., Van Huffel, S., and
Varga, A. (1999). SLICOT — A subroutine library
in systems and control theory. In Datta, B. N., ed-
itor, Applied and Computational Control, Signals,
and Circuits, volume 1, chapter 10, pages 499–539.
Birkh
¨
auser, Boston, MA.
Benner, P., Sima, V., and Voigt, M. (2012a). L
∞
-norm com-
putation for continuous-time descriptor systems us-
ing structured matrix pencils. IEEE Trans. Automat.
Contr., AC-57(1):233–238.
Benner, P., Sima, V., and Voigt, M. (2012b). Robust and
efficient algorithms for L
∞
-norm computations for de-
scriptor systems. In Bendtsen, J. D., editor, 7th IFAC
Symposium on Robust Control Design (ROCOND’12),
pages 189–194. IFAC.
Benner, P., Sima, V., and Voigt, M. (2013). FOR-
TRAN 77 subroutines for the solution of skew-
Hamiltonian/Hamiltonian eigenproblems. Part I: Al-
gorithms and applications. SLICOT Working Note
2013-1.
Benner, P., Sima, V., and Voigt, M. (2016). Al-
gorithm 961: Fortran 77 subroutines for the so-
lution of skew-Hamiltonian/Hamiltonian eigenprob-
lems. ACM Transactions on Mathematical Software
(TOMS), 42(3):1–26.
Bojanczyk, A. W., Golub, G., and Van Dooren, P. (1992).
The periodic Schur decomposition: Algorithms and
applications. In Luk, F. T., editor, Proc. of the SPIE
Conference Advanced Signal Processing Algorithms,
Architectures, and Implementations III, volume 1770,
pages 31–42.
Bruinsma, N. A. and Steinbuch, M. (1990). A fast algo-
rithm to compute the H
∞
-norm of a transfer function.
Systems Control Lett., 14(4):287–293.
Golub, G. H. and Van Loan, C. F. (1996). Matrix Computa-
tions. The Johns Hopkins University Press, Baltimore,
MA, third edition.
Kressner, D. (2001). An efficient and reliable implemen-
tation of the periodic QZ algorithm. In IFAC Pro-
ceedings Volumes (IFAC Workshop on Periodic Con-
trol Systems), volume 34, pages 183–188.
Kressner, D. (2005). Numerical Methods for General and
Structured Eigenvalue Problems, volume 46 of Lec-
ture Notes in Computational Science and Engineer-
ing. Springer-Verlag, Berlin.
MathWorks
R

(2019). MATLAB
R

, Release R2019a,
March 2019.
MathWorks
R

(2012). Control System Toolbox
TM
, Release
R2012a, March 2012.
Sreedhar, J. and Van Dooren, P. (1994). Periodic Schur form
and some matrix equations. In Proceedings of the
Symposium on the Mathematical Theory of Networks
and Systems (MTNS’93), Regensburg, Germany, 2–6
August 1993, volume 1, pages 339–362. John Wiley
& Sons.
Van Loan, C. F. (1975). A general matrix eigenvalue algo-
rithm. SIAM J. Numer. Anal., 12:819–834.
Xia, M., Gahinet, P.M., Abroug, N., and Buhr, C. (2017).
Sector bounds in control design and analysis. In 2017
IEEE 56th Annual Conference on Decision and Con-
trol (CDC), Melbourne, Australia, pages 1169–1174.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
268