
Gray-Box Models for Performance Assessment of Spark Applications
Marco Lattuada
1 a
, Eugenio Gianniti
1 b
, Marjan Hosseini
1
, Danilo Ardagna
1 c
,
Alexandre Maros
2
, Fabricio Murai
2 d
, Ana Paula Couto da Silva
2
and Jussara M. Almeida
2
1
Politecnico di Milano, Italy
2
Universidade Federal de Minas Gerais, Brazil
Keywords:
Spark, Big Data, Machine Learning.
Abstract:
Big data applications are among the most suitable applications to be executed on cluster resources because
of their high requirements of computational power and data storage. Correctly sizing the resources devoted
to their execution does not guarantee they will be executed as expected. Nevertheless, their execution can be
affected by perturbations which can change the expected execution time. Identifying when these types of issue
occurred by comparing their actual execution time with the expected one is mandatory to identify potentially
critical situations and to take the appropriate steps to prevent them. To fulfill this objective, accurate estimates
are necessary. In this paper, machine learning techniques coupled with a posteriori knowledge are exploited
to build performance estimation models. Experimental results show how the models built with the proposed
approach are able to outperform a reference state-of-the-art method (i.e., Ernest method), reducing in some
scenarios the error from the 221.09-167.07% to 13.15-30.58%.
1 INTRODUCTION
Many factors such as multi-tenancy, virtualization
and resource sharing can affect the performance of
federated cloud services and their resources. Mon-
itoring the status of the system during the applica-
tions runs to detect anomalies and perturbations can
be complex and can further degrade the overall per-
formance of the system. If the expected execution
time of the running applications was known a pri-
ori, the identification of perturbed runs would be triv-
ial since it would just be a matter of comparing real
and expected execution time. In most of the scenar-
ios of practical interest, however, even the expected
execution time of running without perturbation can
be unavailable. For this reason, performance mod-
eling is used (Lazowska et al., 1984) to predict the
performance of a real application by abstracting its
behaviour.
Three main approaches have been proposed,
namely, white-box analytical models (AMs), black-
box machine learning (ML) models, and gray-box
a
https://orcid.org/0000-0003-0062-6049
b
https://orcid.org/0000-0002-5647-4024
c
https://orcid.org/0000-0003-4224-927X
d
https://orcid.org/0000-0003-4487-6381
ML models. AMs require the knowledge of the sys-
tem internals, which is not always available and typ-
ically relies on some simplifying assumptions at the
expense of losing accuracy (Lazowska et al., 1984).
On the other side, black-box models (Didona and Ro-
mano, 2015) based on ML try to learn from data and
make predictions without a detailed knowledge of the
system. Finally, gray-box models combine aspects
of the two approaches and consist of black-box mod-
els enriched with a set of features which better cap-
ture the behaviour of the applications under analysis.
ML models require a training phase in which they
use experimental data coming from different work-
loads and configurations. In order to obtain these ini-
tial data, it is necessary to run a set of experiments
which is costly and time consuming. Moreover, since
ML models are usually characterized by a wide set
of hyper-parameters, which influence their accuracy,
training should be done with hyper-parameter tuning
to achieve the best possible results. Therefore, the
training phase might take a long time. However, once
trained, the prediction of ML models is very fast and
usually very accurate. This is why ML models are re-
cently becoming popular in studying the performance
of large systems (Ataie et al., 2016).
In this paper, five classic ML models for regres-
sion are considered: `
1
-regularized Linear Regression
Lattuada, M., Gianniti, E., Hosseini, M., Ardagna, D., Maros, A., Murai, F., Couto da Silva, A. and Almeida, J.
Gray-Box Models for Performance Assessment of Spark Applications.
DOI: 10.5220/0007877806090618
In Proceedings of the 9th International Conference on Cloud Computing and Services Science (CLOSER 2019), pages 609-618
ISBN: 978-989-758-365-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
609

(LASSO), Neural Network, Decision Tree, Random
Forests, and Support Vector Regression. A ML li-
brary was also developed in order to automate the
training and evaluation of ML models and their hyper-
parameter tuning. We focus on assessing Spark appli-
cations performance, i.e., evaluate the execution time
measured for an application with respect to the ex-
pected one. Since the analysis is performed at the
end of applications execution, a posteriori knowledge
about them can be exploited. Examples of such type
of information are number of tasks, maximum and av-
erage task execution time, shuffle time and number of
bytes transmitted among the stages. To prove the gen-
erality of the proposed approach, a heterogeneous set
of applications including Spark SQL-based applica-
tions and ML benchmarks was considered.
The results of our experiments showed that there
is no single ML model which always performs well
or which always outperforms the others. According
to the initial application profiling data available in
the training set and the application data size, differ-
ent ML models provide significantly different accu-
racy. Therefore, it is very important to have a library
to automate the training and hyper-parameter tuning
process. In this way, different scenarios can be effec-
tively investigated.
The rest of the paper is organized as follows.
Section 2 presents the related work while Section 3
presents the evaluated performance models. The ex-
perimental setup is introduced in Section 4 and the
obtained results are presented in Section 5. Finally,
the conclusions are drawn in Section 6.
2 RELATED WORK
The performance analysis and prediction of big data
applications running on the cloud can be tackled from
different perspectives. The most traditional ones rely
on analytical models (Nelson and Tantawi, 1988;
Mak and Lundstrom, 1990; Tripathi and Liang, 2000;
Ardagna et al., 2018) and simulation (Bertoli et al.,
2009; Wang and Khan, 2015). Yet, recent stud-
ies have employed supervised machine learning mod-
els for performance prediction (Venkataraman et al.,
2016; Mustafa et al., 2018; Pan et al., 2017; Alipour-
fard et al., 2017), which is the focus of this paper.
One such example is a regression model proposed by
the Spark creators (Venkataraman et al., 2016). The
model uses a reduced set of features, which are func-
tions of the data set size and of the number of cores.
The estimation of the model parameters was based on
non-negative least squares.
Mustafa et al. (Mustafa et al., 2018) proposed a
prediction platform for Spark SQL queries and ma-
chine learning applications, which, similarly to our
gray box models, also exploits features related to each
stage of the Spark application. This implies the exis-
tence of previous knowledge of the application pro-
file. However, some of these features (e.g., numbers
of nonShuffledRead, shuffledReadRecords and input-
Partitions
1
) are at a lower level compared to ours, and
thus require a finer-grained analysis of the Spark log
to be computed. The authors reported prediction er-
rors of 10% for SQL queries and about 25% for ma-
chine learning jobs. As we will show, our approach
achieves better accuracy, and our experimental de-
sign considers more recent Spark workloads, includ-
ing deep learning use cases.
CherryPick (Alipourfard et al., 2017) is a sys-
tem that leverages Bayesian optimization to find near-
optimal cloud configurations that minimize cloud us-
age costs for MapReduce and Spark applications. Un-
like other studies, the goal was not to accurately pre-
dict applications performance, but rather design a
model that is accurate enough to distinguish the best
configuration from the rest. Similar ideas were also
exploited in the design of Hemingway (Pan et al.,
2017), which embeds the Ernest model and is special-
ized in the identification of the optimal cluster config-
uration for Spark MLlib based applications.
In a related, but different direction, Nguyen et al.
(Nguyen et al., 2018) proposed a strategy to generate
training data to fit a performance model. The model is
meant to be used for predicting which Spark settings
yield the smallest application execution time (i.e., ca-
pacity planning). In contrast, we here compare alter-
native ML models and feature sets in the task of pre-
dicting the performance of an application running on
a given configuration.
3 ML MODELS FOR ASSESSING
THE PERFORMANCE OF
SPARK APPLICATIONS
This section presents the input features and the tech-
niques used to build the proposed regression models,
comparing them to the considered reference, model
Ernest (Venkataraman et al., 2016). The performance
models, which are built by means of Machine Learn-
ing (ML) techniques, consist of functions that relate
application characteristics, infrastructure settings, and
profiling information to the expected application exe-
cution time. The purpose of these models in the con-
1
https://spark.apache.org/docs/latest/rdd-programming-
guide.html
IWFCC 2019 - Special Session on Federation in Cloud and Container Infrastructures
610

sidered context is to assess the trustworthiness and the
absence of perturbations of the infrastructure w.r.t. the
execution performance. More precisely, the aim is to
determine whether an application run was affected by
performance degradation due to resource contention.
This task, which will be referred as Performance As-
sessment is of paramount importance in cloud man-
agement to verify that the resource allocation and iso-
lation did not lead, because of multiple applications
interference, to performance degradation. A second
possible task can be the capacity planning, i.e., to de-
termine the minimum amount of resources that must
be allocated so that the execution time is smaller than
a given limit. Differently from the first task, the sec-
ond cannot rely on a posteriori knowledge and it will
not be considered in the rest of the paper.
The type of data available for fitting the ML mod-
els depends on: (i) the application and (ii) the in-
frastructure settings. In this paper, three possible
classes of Spark applications are considered: SQL
based workloads, traditional machine learning algo-
rithms, and SparkDL (Deep Learning pipelines for
Spark).
3.1 Models Overview
Five classic ML models for regression are considered:
`
1
-regularized Linear Regression (LASSO), Neural
Network, Decision Tree, Random Forests, and Sup-
port Vector Regression. A short description of each
model is provided below.
• Linear regression (LR) assumes a linear relation-
ship between features and the outcome. This
model is typically fit using variants of the least
squares method. The `
1
-regularized and `
2
-
regularized Linear Regression are respectively
known as LASSO, and Ridge Regression. It is
possible to force all coefficients associated with
features to be positive by fitting the data using the
non-negative least squares (NNLS) method. In
this paper, LASSO is considered which also helps
in reducing the number of features by frequently
setting weights to zero
2
. The NNLS method is
used by the reference method (Ernest (Venkatara-
man et al., 2016)).
• Decision tree (DT) is a model represented a
rooted, binary tree, composed of internal and leaf
nodes. Each internal node represents a test based
on the value of a feature. Leaf nodes aggregate
training data that satisfy the tests encoded by the
respective path. Algorithms used for constructing
such a tree include ID3 (Iterative Dichotomiser),
2
https://web.stanford.edu/∼hastie/ElemStatLearn/
C4.5 (a successor of ID3) and CART (Classifica-
tion and Regression trees). Given a set of feature
values, a prediction is made by applying succes-
sive tests until a leaf is reached. The prediction
combines the outcome values associated with that
leaf.
• Random forest (RF) is an ensemble method,
which builds a collection of decision trees, to get
more accurate and less variable results. Each tree
is constructed by a random selection of features.
The predicted outcome is obtained by averaging
the predictions of all trees. Both fitting and pre-
diction are efficient (computationally simple) for
this method.
• Neural network (NN) is a model represented by
a set of connected input/output units (nodes) in
which each connection has a weight associated
with it. The network consists of an input layer,
one or more hidden layers and an output layer.
The inputs are given to the input layer, then
weighted and fed to the second layer which is a
hidden layer. The outputs of a hidden layer can
be given to another hidden layer or to the output
layer. Finally, the output layer gives the predic-
tion of the network for the given inputs. During
the network training, the difference between pre-
dicted value and true value (error) will be prop-
agated backward by apportioning them to each
node’s weights according to the amount of this er-
ror the node accounts for. This algorithm is called
backpropagation.
• Support vector regression (SVR) is a two step
model derived from support vector machines.
First step aims at addressing non-linearities: a
non-linear function is used to map original data
in a high dimensional feature space. In the second
step, hyper-planes are used to describe the linear
functions between points in the created space and
the metric to be estimated.
Linear regression was chosen because of its readabil-
ity and its usage in the Ernest models. Decision trees
and random forests while still partially interpretable,
are also able to describe non-linear relationships in
the data. Last, support vector regression and neural
networks are able to capture quite complex relation-
ships between applications characteristics and their
execution time.
3.2 Features Overview
Table 1 shows the features used by the considered
models. Two sets of features can be identified: fea-
tures which are available a priori and features which
Gray-Box Models for Performance Assessment of Spark Applications
611

Table 1: Features used in models for performance assessment.
Type of Knowledge Features
A Priori
- Ratio of data size to number of cores
- Log of number of cores
- Data size
- Number of cores
- Number of TensorFlow cores (SparkDL only)
A Posteriori
- number of tasks
- max/avg time over tasks
- max/avg shuffle time
- max/avg number of bytes transmitted between stages
- number of executor cores
- inverse of number of executor cores
A Posteriori (SparkDL)
- individual TensorFlow calls execution time
- inverse of total number of cores
are only available a posteriori. The former set is
composed of features which are derived by the Ernest
model and exploit information which is available be-
fore running the applications (more precisely, the
number of cores and the input data size) . The latter
set is composed of features which are associated with
the Spark DAG (directed acyclic graph), which repre-
sents the sequence of stages executed by Spark when
running an application
3
. This type of information can
be easily extracted from applications logs after their
completion. In general, since the DAG is specific to
each application run, the relationship between these
metrics and running time only holds for the same
DAG. To be able to achieve this, a fixed DAG struc-
ture was needed, at least across different number of
cores. In particular, for each stage, the extracted in-
formation is: the number of tasks, the maximum and
average execution time of the tasks, the maximum and
the average shuffle time, the maximum and average
number of bytes transmitted among the stages. For
SparkDL, not only the cores assigned to Spark execu-
tors, but also the TensorFlow execution time and the
inverse of total number of cores available in the clus-
ter are included as features.
It is worth noting that full information (i.e., in-
cluding a posteriori knowledge) can be used since
built models are used to assess the performance of the
applications and not to predict it.
4 EXPERIMENTAL SETTINGS
This section presents and details the experimental
setup adopted in all the experiments performed to col-
lect the results presented in this paper. This section
first describe the applications used as workloads in
our experiments (Section 4.1) and the considered tar-
3
https://data-flair.training/blogs/dag-in-apache-spark/
get platforms on which applications were run (Sec-
tion 4.2). How the data were split into training and
test sets is described in Section 4.3, while the model
parametrization is presented in Section 4.4. Finally
the metrics adopted to evaluate the models are de-
scribed in Section 4.5.
4.1 Applications Workloads
To verify the generality of the proposed approach,
three different types of applications are considered,
which are representatives of different types of work-
loads:
• Query26, an interactive query from the TPC-DS
industry benchmark
4
representative of SQL-like
workload, which includes a small number of tasks
and stages (i.e., 10). It was run for various input
data set sizes: 250 GB, 750 GB, and 1000 GB.
• K-means, a ML benchmark from Sparkbench
5
.
K-means is the core of many ML applications
(clustering is an unsupervised learning technique,
which, however, is used very frequently to per-
form preliminary data set analyses even if in
the following classification techniques are consid-
ered). It was run for Spark dataframes with 100
features, with values uniformly distributed in the
[0,1] range and the number of rows varying in 5,
10, 15 and 20 million. The DAG was the same
across all runs and for all the data sizes, contain-
ing 15 stages.
• Image classification, a benchmark for image pro-
cessing internally developed and based on the
SparkDL library
6
. The developed application is
based on the novel deep learning pipelines which
4
http://www.tpc.org/tpcds
5
https://codait.github.io/spark-bench
6
https://databricks.github.io/spark-deep-learning/site/
index.html
IWFCC 2019 - Special Session on Federation in Cloud and Container Infrastructures
612

makes possible to develop high-level deep learn-
ing applications on Spark. In particular, this
framework supports transfer learning, one of the
most popular approaches used in the deep learn-
ing when the data set for training is small (Csurka,
2017), which enables to use pre-trained models on
different tasks. In particular, the application we
developed is a binary image classification using
InceptionV3 as featurizer and linear SVM as clas-
sifier. The number of images in the input varied in
1000, 1500 and 2500 while the number of stages
is 8. As anticipated in Section 3.2, this bench-
mark is characterized by additional features and,
hence, is the most complex of the three consid-
ered workloads. SparkDL heavily relies on Ten-
sorFlow which affects the application completion
times. When SparkDL runs, the number of cores
allocated to Spark workers can be limited, but
spark-submit parameters cannot control the num-
ber of cores for TensorFlow, which uses all the
cores available in the cluster. For this reason,
also the TensorFlow number of cores (which cor-
responds to the number of cores available in the
cluster) and its inverse are included in the set of
used features.
4.2 Hosting Platforms
Applications were run on two platforms, Microsoft
Azure and a private IBM Power8 cluster, which are
representatives of different computing environments.
As a public cloud, Microsoft Azure is potentially af-
fected by resource contention. Thus, application ex-
ecutions might experience more variability. In con-
trast, IBM Power8 was fully dedicated to run the con-
sidered benchmarks without any other concurrent ac-
tivity (thus with no resource contention).
Query 26 and SparkDL were executed on Mi-
crosoft Azure using the HDInsight service with work-
ers based on 6 D13v2 virtual machines (VMs), each
with 8 CPU cores and 56 GB of memory running
Spark 2.2.0 on Linux. SparkDL application requires,
in addition, that TensorFlow and Keras are available
on the Spark cluster: versions 1.4.0 and 2.1.5 were
used, respectively. The executors memory was set to
10 GB. K-means was run on a Power8 deployment
that includes Hortonworks distribution 2.6, same as
Microsoft Azure, with 4 VMs, each with 12 cores and
58 GB of RAM, for a total of 48 CPU cores available
for Spark workers, plus a master node with 4 cores
and 48 GB of RAM. The executors memory, in this
case, was set to 4GB.
For Query 26 and K-means, experiments were run
varying the number of Spark cores between 6 and
44 cores (step of 2), repeating the execution with
the same configuration 6 times. For SparkDL, the
number of cores was varied between 2 and 48 (step
of 2), repeating each experiment with the same con-
figuration (i.e., the number of images and cores) 5
times. By considering different workloads, hosting
platforms and setup configurations, we build a rich
set of scenarios to test our prediction models.
4.3 Train and Test Sets Settings
Table 2: Workload data sizes in different scenarios.
Workload
Core Interpolation Data Extrapolation
Training Test Training Test
Query 26 [GB] 750 750 250, 750 1000
K-means [Rows] 15 15 5, 10, 15 20
SparkDL [Images] 1500 1500 1000, 1500 2000
To evaluate the ML models accuracy and analyze their
interpolation and extrapolation capabilities, the data
are split into training and test sets according to the
data size and by considering different cores configu-
ration. For each workload, in particular, two different
types of scenarios are considered, which are summa-
rized in Table 2
• core interpolation scenarios: only runs with the
same dataset size are considered (reported in Ta-
ble 2). Figure 1 shows the various scenarios (y-
axis) built for each workload based on different
splits of the data into training and test sets: in each
row (case number), blue boxes represent configu-
rations for which the data were used as part of the
training set (and cross-validation) and red crosses
indicate configurations used as part of the test
set
7
.
• data size extrapolation scenarios: the runs with
the largest dataset size (spanning across all avail-
able cores configurations) are put in the test set
while the runs with the other dataset sizes in
the training data, as shown in the two rightmost
columns of Table 2.
In the first class of scenarios, the cases were de-
signed such that larger case numbers are associated
with harder predictions, as there training data include
samples from a smaller range of experiments w.r.t. the
number of cores. For example, for both Query 26 and
K-means, scenario C1 is built by alternating configu-
rations in the sequence of the number of cores (x-axis)
as training and test data. For Query 26, data from ex-
periments with the number of cores equal to 6, 10,
. . . , 40 and 44 are put in the training data (blue boxes)
7
The experiments with Query 26 on 20 cores were re-
moved because of anomalies (see Figure 1a).
Gray-Box Models for Performance Assessment of Spark Applications
613

(a) Query 26 (b) K-means (c) SparkDL
Figure 1: Core interpolation scenario: train-test split in each case for Query 26, K-means and SparkDL.
while the remaining samples are included in the test
set (red cross). The gap between the number of cores
of consecutive configurations included in the training
data is gradually incremented. The gap in cases 4,
5, 6, and 7 was varied to assess its impact on model
accuracy. Since there is a large difference in the appli-
cation completion time in the runs where the number
of cores is small, the data for the smallest number of
cores were always included in the training set. For
SparkDL, the process was the same but limiting the
number of cases to three.
Even in the second class of scenarios, the train-
ing sets are further reduced by removing runs with
some configurations of number of cores according to
the same schema presented for core interpolation. By
doing so, in these experiments the core interpolation
and the data size extrapolation capabilities are evalu-
ated at the same time. In other words, the data size
extrapolation differ from the core interpolation sce-
narios because: (i) the dataset sizes in training and
test sets are no longer the same, (ii) the test set also
includes observations where the number of cores is
the same as in some observations of the training set
(but again with different dataset sizes).
4.4 Hyper-parameter Tuning
Each of the model described in Section 3.1 is char-
acterized by a set of hyper-parameters which can be
tuned to improve the accuracy of the models. Cor-
rectly sizing the design space on them is a critical
task, since a too narrow solution space can exclude
good solutions, while on the contrary a too wide solu-
tions space can lengthen too much the model selection
process. The hyper-parameters and the values which
were considered in this work are listed in Table 3. An
inhouse Python library was developed on the top of
PyTorch 0.4.0
8
(for neural network training) and of
scikit-learn 0.19.1
9
(for all the other techniques) to
explore their different values. For every algorithm,
the Mean Squared Error (MSE) integrated with hold-
8
https://pytorch.org
9
https://scikit-learn.org
out cross-validation was used to select the values that
led to the best model.
To further prevent over-fitting, a regularization
term is added to LR (Linear Regression) and NN
(Neural Network). For LR, LASSO was chosen pro-
viding `
1
-norm. The use of intercept and the penalty
constant α are the set of available hyper-parameters
and are shown in Table 3 For the NN algorithm, the
Table 3: Hyper-parameters for ML techniques.
Linear Regression
Hyper-Parameter Values
Penalty α 0.001, 0.01, 0.05, 0.1, 0.5, 1.0, 5.0, 10.0
Fit intercept True, False
Neural Network
Hyper-Parameter Values
# Layers n 1, 2, 3
# Perceptrons/Layer all combinations in [3,4,5]
n
Activation Functions sigmoid, ReLU, tanh
`
2
Penalty 0.0001, 0.001, 0.01, 0.05, 0.1
Learning Rate 0.001, 0.01, 0.1
β
1
0.7, 0.8, 0.9
# Minibatches 1
Optimizer Adam, SGD
Decision Tree & Random Forest
Hyper-Parameter Decision Tree Random Forest
Max Depth 3, 5, 10, No Limit 3, 10, 20, No Limit
Max Features auto, sqrt, log auto, sqrt, log
Min samples to split 2.0 2.0
Min samples per leaf 1%, 5%, 10%, 20%, 30% 1, 2, 4
Criterion MSE, fMSE, MAE MSE, MAE
# Trees NA 5, 10, 50, 100
SVR
Hyper-Parameter Values
C 0.001, 0.01, 0.1, 1, 10, 50, 75
ε 0.05, 0.1, 0.2, 0.3, 0.5
γ 1e-7, 1e-4, 0.001, 0.01, 0.1, 1
Kernel linear, rbf, polynomial, sigmoid
Degree 2, 3, 5, 7
`
2
penalty Frobenius norm (Golub and Van Loan,
1996) was used. Also rectified linear unit function
ReLU was selected in general as the best activation
function. In all cases, the training data size was not
large; therefore, we set the number of minibatches
to 1 in order to consume the whole input at once.
The main hyper-parameter considered to evaluate the
performance was the optimizer. Adam and Stochastic
Gradient Descent (SGD) were evaluated as possible
candidates.
The former was selected as our experiments
showed that it converges much faster than the latter.
The number of epochs was set to 10,000. DT and RF
share many hyper-parameters and their values, there-
IWFCC 2019 - Special Session on Federation in Cloud and Container Infrastructures
614

fore, are grouped in Table 3. Max Depth is the max-
imum depth of the tree which is specified to avoid
over-fitting. Max Features is used to select the num-
ber of available features to consider when searching
for the best split. A value of auto implies a maxi-
mum number of features equal to the total number of
features. Values of sqrt and log imply a maximum
equal to the square root and the base-2 logarithm of
the number of features, respectively. Minimum Sam-
ples to Split/per Leaf is used for setting, respectively,
the minimum number of samples required to split a
node and the minimum percentage/number of sam-
ples required to be a leaf. Criterion is the function
used to measure the quality of a split: MSE stands for
mean square error (minimizes `
2
loss), fMSE stands
for mean squared error with Friedman’s improvement
score for potential splits and, last, MAE stands for
mean absolute error (minimizes `
1
loss). Parameter
number of trees, the number of trees in the forest, only
applies to RF. A range of values is explored to analyze
diminishing return effects on the error. Finally, con-
cerning the SVR hyper-parameters, the degree is used
only with the polynomial kernel while the gamma pa-
rameter is valid only for polynomial, rbf and sigmoid
kernel. In the case of this regression technique, differ-
ent types of kernels are tried to observe which would
capture better the behavior of the application time ac-
cording to the number of cores.
4.5 Performance Metrics
To be able to compare the performance results of
different methods, the mean absolute percent error
(MAPE) of the response time assessment was used,
as it is more widely used in the performance liter-
ature (Lazowska et al., 1984) than MSE (used for
hyper-parameter tuning). Moreover, the results across
different experiments can be easily integrated even
if they have very different execution times. Indeed,
MAPE measures the relative error (in absolute terms)
of the prediction with respect to the true response
times, i.e.,
MAPE =
100%
N
N
∑
k=1
y
k
− ˆy
k
y
k
(1)
where
• N is the number of data points.
• y
k
is the response time measured on the opera-
tional system.
• ˆy
k
is the predicted response time from the learnt
model.
For each setup, 10 runs were executed for the LR,
DT and RF algorithms, and the average MAPE across
all 10 runs was computed and reported. For NN,
which has much longer training times, we performed
a single run (i.e., random train-test split).
5 EXPERIMENTAL RESULTS
In this section, the prediction results for each work-
load on each sets of scenarios (i.e., core interpolation
and data extrapolation) are presented. For each set,
this section reports the results in terms of MAPE for
each case described in Section 4.3 for each of the ML
technique described in Section 3.1 (LR, NN, DT, RF,
and SVR) comparing them with the reference model
(Ernest).
5.1 Query 26 Results
Table 4 and Table 5 show the MAPE results for core
interpolation and data extrapolation scenarios, respec-
tively, for Query 26. It is worth noting that in both
the sets of scenarios, Ernest method is quite accurate
(worst error is 8.02%) and outperforms gray box mod-
els since the features it exploits are better able to cap-
ture the characteristics of the application in terms of
performance. Moreover, there is no significant differ-
ences in its accuracy across different cases, showing
that even with few observations it is possible to obtain
good fits.
Analyzing the results of the gray-box models,
there is no ML technique which always outperforms
the other, but LR and NN are the best choices depend-
ing on the particular scenario.
Table 4: MAPE (%) of execution time estimates on Power8
for Query 26 in core interpolation scenario (fixed data size
of 750 GB for all data sets).
Ernest
Gray Box
DT LR NN RF SVR
C1 1.50 9.64 4.46 7.10 6.71 7.35
C2 1.64 9.92 8.82 5.57 12.32 20.53
C3 1.71 16.12 6.23 4.24 15.31 10.25
C4 1.66 27.05 10.62 6.09 14.37 16.92
C5 1.59 25.54 42.08 6.23 44.60 39.74
C6 1.70 11.39 35.80 6.75 41.44 68.95
Even if they are not able to achieve the same accuracy
of the Ernest method, the worst result (32.29% on C4
of data extrapolation scenario) still allows to assess
the performance of the run application
5.2 K-means Results
Table 6 and Table 7 present the result obtained by
Ernest and by the ML techniques on K-means. Dif-
Gray-Box Models for Performance Assessment of Spark Applications
615
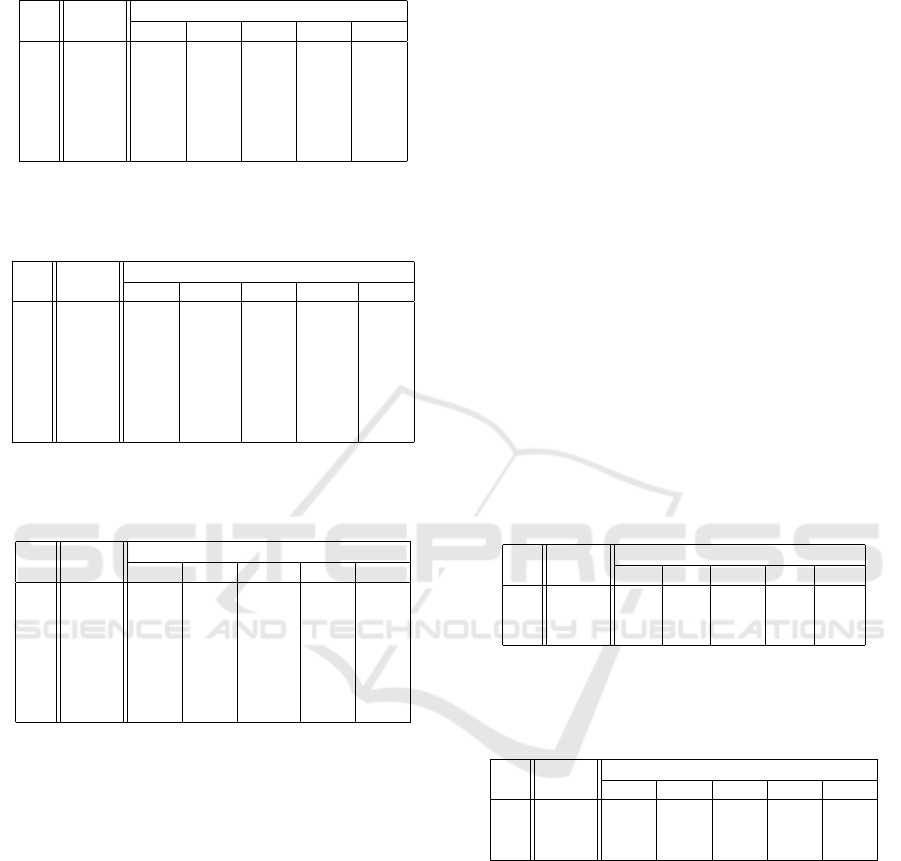
Table 5: MAPE (%) of execution time estimates on Power8
for Query 26 in data extrapolation scenario (250 GB,
750GB for training and 1000GB for testing).
Ernest
Gray Box
DT LR NN RF SVR
C1 7.49 37.13 32.91 10.23 44.16 38.08
C2 7.44 35.01 27.26 36.07 40.66 32.30
C3 7.31 32.39 36.36 20.18 47.46 38.74
C4 7.26 32.75 32.29 48.80 46.29 32.31
C5 7.59 41.93 12.41 21.90 31.50 18.11
C6 8.02 38.45 24.05 19.91 32.22 29.22
Table 6: MAPE (%) of execution time estimates on Power8
for K-means in core interpolation scenario (15M points for
training and 15M points for test).
Ernest
Gray Box
DT LR NN RF SVR
C1 126.69 17.27 74.04 11.99 105.31 28.09
C2 148.10 21.41 83.33 10.27 112.77 29.13
C3 161.35 46.46 122.07 47.30 67.58 36.14
C4 176.52 49.66 143.33 47.60 81.70 24.47
C5 187.00 31.20 273.19 29.88 99.74 84.00
C6 159.88 21.90 166.57 26.66 59.40 66.75
C7 178.08 31.59 159.44 47.65 102.96 38.74
Table 7: MAPE (%) of execution time estimates on Power8
for K-means in data extrapolation scenario (5M, 10M, and
15M points for training and 20M points for test).
Ernest
Gray Box
DT LR NN RF SVR
C1 167.07 26.47 20.24 59.50 26.07 16.04
C2 183.09 26.31 13.15 91.60 29.19 18.63
C3 200.83 37.28 31.86 131.54 33.47 30.58
C4 204.42 69.61 24.24 453.67 32.08 18.67
C5 221.09 26.89 26.86 16.01 39.72 25.29
C6 206.59 21.19 37.72 37.39 29.61 34.16
C7 208.37 29.44 43.14 145.81 30.21 24.06
ferently from the previous workload, the reference
model here is not able to correctly describe the ex-
pected performance of the considered application. In
the best case, the estimation error is 126.69% while
in the worst case it reaches up to 221.09%. On the
contrary, the errors of the best considered ML tech-
nique in each scenario are significantly smaller. In
the worst case, C3 of core interpolation, the error of
the best technique (i.e., SVR) is 36.14% Even for this
workload, there is no ML technique which always
performs better than all the other in all the consid-
ered scenario. Indeed, all the techniques but RF are
the best choice in at least one combination of case-
scenario.
5.3 SparkDL Results
Finally, results for SparkDL are shown in Table 8 and
Table 9 for the core interpolation and data extrapola-
tion scenarios. Even if the predictions by the Ernest
method for this workload are better than for the pre-
vious, it still outperformed by other ML techniques.
In the core interpolation scenario the difference is not
so relevant since the error of the Ernest prediction is
in the range 5.71-10.48% while the error of the best
ML technique is in the range 3.70-4.66%. As for pre-
vious workloads, there is not an absolute best tech-
nique: NN, SVR, LR get the best results in each of
the three cases.
On the contrary, the data extrapolation for
SparkDL results to be a harder scenario to be ad-
dressed by the Ernest method with MAPE in the range
36.81-43.49%. Proposed models produce a signifi-
cantly smaller error (range is 9.90-10.04%). Even in
this last scenario there is not a unique winner: LR is
the best technique for C1 and C2 while the best C3
model is built by NN.
Table 8: MAPE (%) of execution time estimates on Mi-
crosoft Azure for SparkDL in core interpolation scenario
(1500 images for training and 1500 images for testing).
Ernest
Gray Box
DT LR NN RF SVR
C1 10.48 5.16 5.60 3.84 5.87 4.12
C2 6.30 5.67 9.47 11.32 5.56 4.66
C3 5.71 6.40 3.70 5.07 8.29 4.96
Table 9: MAPE (%) of execution time estimates on Mi-
crosoft Azure for SparkDL in data extrapolation scenario
(1000 and 1500 images for training and 2500 images for
testing).
Ernest
Gray Box
DT LR NN RF SVR
C1 43.49 33.10 10.73 25.04 36.72 27.82
C2 37.39 34.94 10.04 17.64 35.47 32.13
C3 36.81 32.19 14.76 9.90 35.75 32.97
5.4 Discussion
The previous sections presented the results of the ref-
erence model and of the ML models for each ana-
lyzed workload and scenario. The Ernest models per-
form best (MAPE smaller than 8.02%) in the simplest
considered scenario (i.e., Query 26 both in core in-
terpolation and data extrapolation). In the SparkDL
core interpolation scenario, Ernest models still per-
form well despite not being the best models. In con-
trast, in the other scenarios, the large MAPE values
(up to 187%) make the models unsuitable for produc-
IWFCC 2019 - Special Session on Federation in Cloud and Container Infrastructures
616

tion environments, thus justifying the necessity of in-
troducing new techniques to be effectively exploited.
From the results previously presented, it can be
noticed that there is not a unique ML technique which
outperforms all the others in every situation. More-
over, even by limiting to a single type of scenar-
ios there is not a single winner. On the contrary, a
slight change in the composition of the training set
and of the test set (i.e., considering different cases)
may change which is the technique which performs
best. For example, in the data extrapolation scenario
for K-means the best technique is SVR for C1, C3,
C4, and C7, LR for C2, NN for C5 and DT for C6.
The comparison between the best gray box models
and the reference Ernest model leads to two different
situations. In scenarios where applications are char-
acterized by regularity (i.e., Query 26 and SparkDL
with fixed data size), Ernest yields very good results
with MAPE values smaller than 11%, whereas the
best gray box model generally achieves worse perfor-
mance (MAPE of best models is in the range 3.84-
42.29%). Yet, in the remaining scenarios, which are
characterized by a larger variability in the application
execution times, the best gray box model outperforms
the Ernest model by a large margin. The MAPE range
of the latter is 36.81-187.0% while the largest error of
the best gray box model is only 31.59% (C of core in-
terpolation with K-means). However, recall that gray
box models use DAG-related features which are not
available for the test instance at prediction time (a pri-
ori), but they can be used as they are only to assess the
performance of the analyzed applications.
6 CONCLUSIONS AND FUTURE
WORK
In this paper, the accuracy of alternative supervised
machine learning techniques to assess the perfor-
mance of Spark applications has been analysed. Our
aim is to train models able at identifying perturba-
tions which affect the execution time of production
applications. Experimental results on a rich set of dif-
ferent scenarios demonstrated that the proposed gray
black box models are able to achieve relevant accu-
racy in different scenarios with different workloads.
Moreover, in complex scenarios (i.e., data extrapola-
tion in complex applications) where the Ernest refer-
ence model fails (error up to 187%), the largest er-
ror of the best gray-box model is 31.59%. However,
results show how there is no ML technique which
always outperforms the others, hence different tech-
niques have to be evaluated in each scenario to choose
the best model. As future work, the study of the
performance of Spark applications running on GPU-
based clusters is foreseen. Moreover, the use of the
models to identify resource contention on production
systems will be also considered.
ACKNOWLEDGEMENTS
This work has been partially supported by the project
ATMOSPHERE (https://atmosphere-eubrazil.eu),
funded by the Brazilian Ministry of Science, Technol-
ogy and Innovation (Project 51119 - MCTI/RNP 4th
Coordinated Call) and by the European Commission
under the Cooperation Programme, Horizon 2020
(grant agreement no 777154).
REFERENCES
Alipourfard, O., Liu, H. H., Chen, J., Venkataraman, S., Yu,
M., and Zhang, M. (2017). Cherrypick: Adaptively
unearthing the best cloud configurations for big data
analytics. In NSDI 2017 Proc., pages 469–482.
Ardagna, D., Barbierato, E., Evangelinou, A., Gianniti,
E., Gribaudo, M., Pinto, T. B. M., Guimar
˜
aes, A.,
Couto da Silva, A. P., and Almeida, J. M. (2018). Per-
formance prediction of cloud-based big data applica-
tions. In ICPE ’18, pages 192–199.
Ataie, E., Gianniti, E., Ardagna, D., and Movaghar,
A. (2016). A combined analytical modeling ma-
chine learning approach for performance prediction of
mapreduce jobs in cloud environment. In SYNASC
2016, Timisoara, Romania, September 24-27, 2016,
pages 431–439.
Bertoli, M., Casale, G., and Serazzi, G. (2009). JMT: per-
formance engineering tools for system modeling. SIG-
METRICS Performance Evaluation Review, 36(4):10–
15.
Csurka, G. (2017). Domain adaptation for visual applica-
tions: A comprehensive survey.
Didona, D. and Romano, P. (2015). Using analytical models
to bootstrap machine learning performance predictors.
In 21st IEEE International Conference on Parallel
and Distributed Systems, ICPADS 2015, Melbourne,
Australia, December 14-17, 2015, pages 405–413.
Golub, G. H. and Van Loan, C. F. (1996). Matrix Com-
putations. The Johns Hopkins University Press, third
edition.
Lazowska, E. D., Zahorjan, J., Graham, G. S., and Sev-
cik, K. C. (1984). Quantitative System Performance.
Prentice-Hall.
Mak, V. and Lundstrom, S. (1990). Predicting performance
of parallel computations. IEEE Trans. on Parallel &
Distributed Systems, 1(undefined):257–270.
Mustafa, S., Elghandour, I., and Ismail, M. A. (2018). A
machine learning approach for predicting execution
time of spark jobs. Alexandria Engineering Journal,
57(4):3767 – 3778.
Gray-Box Models for Performance Assessment of Spark Applications
617

Nelson, R. D. and Tantawi, A. N. (1988). Approxi-
mate analysis of fork/join synchronization in parallel
queues. IEEE Trans. Computers, 37(6):739–743.
Nguyen, N., Khan, M. M. H., and Wang, K. (2018). To-
wards automatic tuning of apache spark configuration.
In CLOUD, pages 417–425.
Pan, X., Venkataraman, S., Tai, Z., and Gonzalez, J. (2017).
Hemingway: Modeling distributed optimization algo-
rithms. CoRR, abs/1702.05865.
Tripathi, S. K. and Liang, D.-R. (2000). On performance
prediction of parallel computations with precedent
constraints. IEEE Trans. on Parallel & Distr. Systems,
11:491–508.
Venkataraman, S., Yang, Z., Franklin, M., Recht, B., and
Stoica, I. (2016). Ernest: Efficient performance pre-
diction for large-scale advanced analytics. In 13th
USENIX Symposium on Networked Systems Design
and Implementation, pages 363–378.
Wang, K. and Khan, M. M. H. (2015). Performance predic-
tion for apache spark platform. In HPCC-CSS-ICESS
2015 Proc., pages 166–173.
IWFCC 2019 - Special Session on Federation in Cloud and Container Infrastructures
618
