Real Time Financial Risk Monitoring as a Data-intensive Application

Petra Ristau and Lukas Krain

JRC Capital Management & Research GmbH, Kurfürstendamm 186, 10707 Berlin, Germany

Keywords: Financial Risk Measures, Value-at-Risk, Expected Shortfall, Monte-Carlo Simulations.

Abstract: This paper will examine the possibility of real-time risk calculations within the financial services industry.

Due to regulatory standards, this paper will focus mainly on the calculations of value-at-risk (VaR) and

expected shortfall (ES). Their computation currently requires simplified theory in order to be done within

real-time. This demonstrates a real-world disadvantage to investment professionals since they need to

comply with regulatory requirements when doing real-time decisions without knowing the accurate risk

numbers at any one time. Within the CloudDBAppliance project, we designed an architecture that shall

make real-time risk monitoring possible using cloud computing and a fast analytical processing platform.

1 INTRODUCTION

The financial services industry is heavily dependent

on risk simulations and calculations. This is even

more true in todays world since financial markets

change their behavior quicker and more drastically.

Regulatory entities, such as the German BaFin,

require finacial service providers to submit risk

figures such as value-at-risk (VaR) and may require

the submition of expected shortfall (ES) in the near

future. Due to their high complexity, it is common

practice to compute these figures in overnight batch

processes. Therefore, in between, investment

professionals need to estimate the according risk

measures and complete the decision-making process

without a clear understanding of their current

posistions. This presents an issue since the trader

opens and closes positions due to his perceived risk-

return profile. However, he does not know the

effects of his trade on the entirety of the trading

portfolios and the effects will only be calculated

overnight. In a worst-case scenario, the trader opens

a position on day t, the risk department computes at

night that the risk is too large to be kept in the books

and requires the trader to liquidate at a loss the next

morning.

The complexity of the risk calculations arises

from a Mont-Carlo simulation. In order to complete

this simulation, numerous statistics about financial

products need to be estimated which adds to the

computational requirements.

Although financial service providers face

different types of risks, we will focus only on market

risk, that is, the risk of falling investment values.

The remainder of the paper is structured as follows:

The next chapter introduces into the risk evaluation

task and discusses its computational complexity,

section 3 deals with requirements analysis while

section 4 introduces the platform architecture and

section 5 presents conclusions.

2 EXPLANATION OF RISK

FIGURES

In this chapter, we will have a look at how to

interpret a given VaR or ES figure and list all data

that is needed to do the calculations.

2.1 Value-at-Risk and Expected

Shortfall

According to modern portfolio theory (Elton et al.,

2014) the cross-correlations between financial

product’s prices have a big effect on the entire

portfolio value. This is why investment professionals

try to diversify risk by including uncorrelated or

even negatively correlated instruments into their

portfolio. This however, does not give the portfolio

manager an idea of possible losses beyond

deviations from the expected return. This is what

VaR does. VaR is technically a percentile of the loss

660

Ristau, P. and Krain, L.

Real Time Financial Risk Monitoring as a Data-intensive Application.

DOI: 10.5220/0007905706600665

In Proceedings of the 9th International Conference on Cloud Computing and Services Science (CLOSER 2019), pages 660-665

ISBN: 978-989-758-365-0

distribution (Krokhmal et al., 2001) of an asset and

as such, VaR is a function of the asset returns, a

time-interval and a confidence level. VaR is stated in

a way such as “The 10-day, 99% VaR is equal to

72%”. Such a statement would mean that the risk

manager is 99% confident that the portfolio will not

lose more that 72% of its value within the next 10

days. ES gives an estimation of the loss given that

the loss exceeds the VaR. Continuing the above

example, an ES of 98% would be interpreted as

“Given that the loss is greater than 72%, the

expected value for the loss is 98%”. The ES can also

be translated as “There is a 1% chance of an event

that yields an expected return of -98%”.

2.2 Required Data

In order to calculate the VaR, we need an

appropriate length of price history. The variance-

covariance matrix needs to be calculated and a few

parameters need to be chosen i.e. which simulation

technique (Monte-Carlo-Simulation or historical

simulation), the number of simulations and which

distribution defines the given data best (in the case

of the Monte-Carlo-Simulation). The last factor, the

underlying distribution, can be estimated using the

historical data as well.

2.3 Mathematical Derivation of Value

at Risk and Expected Shortfall

In this article we will not discuss the selection of the

most appropriate method and the problematic of the

normal distribution assumption and refer to (Jorion,

2006) and (Embrecht et al., 2005). We decided to

exclude the parametric approach and instead use a

quantile function/distributional approach. We have

to simulate return data and then deduct information

from the simulated distributions. While Engle,

Manganelli (Engle and Manganelli, 2001) state VaR

as the solution to

















,

where 



is the loss at time t, 



is all the collected

information at the time prior to the calculation and

theta is the desired confidence level, Ziegel (2013)

describes VaR as the solution of











inf∈|









,

with 



being the cumulative distribution function of

the return distribution.

Assuming that we managed to compute the VaR

number for a given return distribution, we can easily

compute the ES using a simple mean over all

simulated returns that breach the VaR figure.

Therefore, the ES is given by





∈



|



,

where 



is used as described above.

As already discussed, there are two main

simulation methods for generating the returns, from

which the quantile functions can start. Because the

historical simulation takes the actual past price

history for scenario building, it is heavily dependent

on the assumption that the training data is

representative for the underlying asset’s overall

returns. In the crucial case of stress scenarios that

never happened before it will thus underestimate the

risk.

This problem is solved by the Monte-Carlo

simulation, which estimates the underlying

distribution and generates thousands of simulated

future scenario based on it. The quantile functions

then calculate the risk figures based on the

distribution of the future scenarios. The academic

literature tends to link the Student’s t-distribution to

capital market returns (Harris, 2017), so the risk

manager has been given a hint about which

distribution to use.

2.4 Calculation Efficiency

Next, we will look at the runtime of a VaR

calculation based on a Monte-Carlo simulation. We

will see where the trade-off between speed and

accuracy of the calculation arises.

The first factor to consider when talking about

the runtime of a VaR calculation is the size of the

training data. As discussed above we only need the

asset returns for the calculations. The length of the

training data and the number of assets within the

portfolio increase the size of the training data

linearly. Obviously, a portfolio with x assets and a

training data set of the most recent T asset returns

has  data points. The training data can be

represented in a matrix

∶

,



,

where  and 1, and 

,



,

is the return of

asset x at time t.

The next factor to consider is the variance-

covariance matrix. If our portfolio includes x assets,

the variance-covariance matrix will be -

dimensional and therefore, it has 



entries with the

single asset’s variance on the main diagonal and the

covariance of asset i and j in the i-th row and j-th

column. Obviously, the variance-covariance matrix

is symmetrical, since the covariance function is

Real Time Financial Risk Monitoring as a Data-intensive Application

661

symmetrical. With 



entries in a symmetrical

matrix we need to calculate 



/2 entries,

which grows quadratically with an additional asset

in the portfolio. Next, we look at the necessary

number of computations for the variance and

covariance. Using the regular formula for the two

statistics, we get





,



∶

,











∗

,







and





 ∶ 

,













,

where  is the expectation operator and 



,



are the

returns of two assets within the portfolio. The

expectation operator requires linear runtime over the

length of the training data. If the training data has

length T, then the variance requires 2





calculations. The covariance requires 4





calculation because two different variables are

observed. This leads to a computational effort of

  1



∗

4





2





for the entire variance-covariance matrix using the

standard equations and a brute force approach for

calculating them.

The next step in calculating the VaR is

estimation of the underlying distribution.

Independently from the chosen distribution the

simulation of a vector

̃



which is the generated returns of the simulated

future of length n. If the returns in the training data

are daily returns then the simulated future of length

n would be appropriate for a n-day VaR. This

procedure needs to be repeated multiple times for a

simulation. The sum of each individual vector ̃ is

the overall return of the portfolio over the required

time-period. Any function of the ones shown above

can be used to calculate the required percentile of

the sums of the ̃.

This calculation requires a lot of computational

runtime, mainly due to the quadratic growth of the

variance-covariance matrix and the generation of the

multivariate distribution. Furthermore, the number

of simulated random vectors ̃ should be very high.

In fact, even though the size of the training data has

an optimum unequal to the maximum, the number of

simulated portfolio returns will always increase the

accuracy of the VaR figure. An increased number of

simulated return vectors however, increases the

computational requirements as well. Yet, the

computations of all ̃ is the same and in fact, need to

be independent from each other (that is, the

generation of one random return vector must not

depend on the generation of another random return

vector). Therefore, a parallel computation of the

random return vectors will decrease the runtime in a

very efficient manner because the calculations of the

random return vectors can the distributed to all

processors equally. Furthermore, there exist efficient

parallel algorithms to compute the variance and the

covariance much more efficiently.

3 REQUIREMENTS ANALYSIS

The real-time risk monitoring for investment

banking use case shall implement a risk assessment

application that does, on the one hand, comply with

regulatory requirements of the financial supervisory

authorities, and on the other hand, speeds up the risk

valuation. That is, it can be used intraday not only

for regularly or ad-hoc queries, but even for pre-

trade analysis of potentially new trades before the

traders actually give the order.

3.1 Use Case Analysis

Two types of human actors will interact with the risk

monitoring platform:

The Risk Controller will have access on all use

cases, i.e. the calculation of risk measures (VaR and

ES) as well as the corresponding sensitivities. The

pre-trade analysis may be triggered by the Risk

Controller as well as by the Trader who has just

detected an investment opportunity and would like

to evaluate the portfolio risk as if the new trade was

already carried out. This is what the ‘what-if’

analysis will compute.

Figure 1: Risk monitoring use case diagram.

The other two actors depicted in the above

diagram represent the pricing engine and the

ADITCA 2019 - Special Session on Appliances for Data-Intensive and Time Critical Applications

662

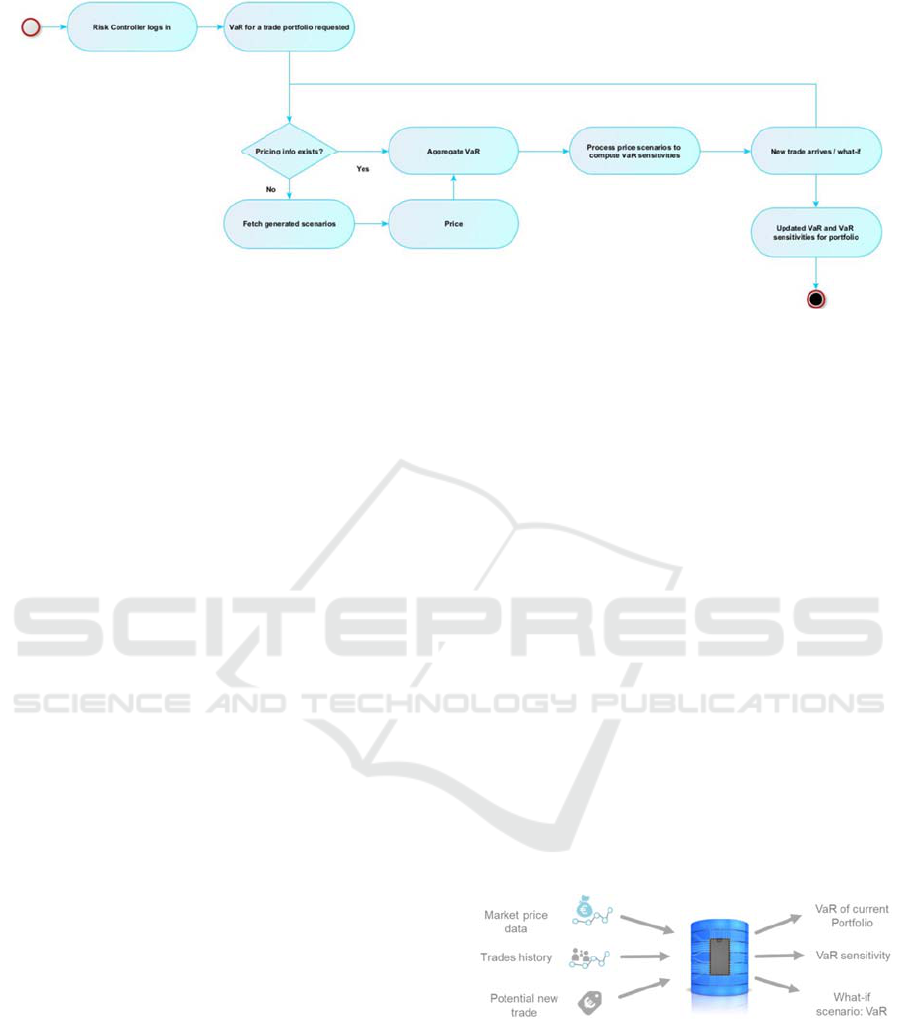
Figure 3: Activity diagram.

scenario engine that carry out the calculations as

described in section 2, but can be replaced by

instances using other calculation approaches.

While the scenario engine contains simulated

risk factors the pricing engine is a program that

makes real time price calculations based on real time

market data.

3.2 Input and Output Streams

The basis for every risk evaluation is the trade

history, consisting of string variables identifying the

currently open positions and past closed positions, in

combination with the history of market price data.

The result is a time series of numeric returns of the

portfolio that will serve as input for the pricing

engine that will generate a sufficient number of

pricing scenarios in order to put the risk valuation on

a profound basis. The resulting returns are deducted

from the price data input, which is a time series of

the most recent bid and ask prices. Due to the real-

time character of the data, each position within the

portfolio will generate new numeric data every tick,

i.e. every time a new price for the security is

available. The pricing engine will average all prices

within one second in order to generate an evenly

spaced data-stream. In case of no price change

within a one-second period, the most recent price

will be used. The input and output streams depicted

in figure 2 below consist of:

Open Positions: The basis for every risk evaluation

is the trade history, consisting of currently open

positions and past closed positions, in combination

with the history of market price data. All currently

open positions and their relative amount held form

the portfolio. The relative amount held is stored as

numeric data and will be called ‘weight of the

position’. The result is a time series of returns of the

portfolio that will serve as input for the pricing

engine that will generate a sufficient number of

pricing scenarios in order to put the risk valuation on

a profound basis. We estimate ‘sufficient’ to be no

less than 20.000 scenarios in regular financial

market times but much higher numbers during

stressed scenarios reaching 100.000 scenarios and

more. The estimate of 20.000 scenarios follows from

analyses of the stability of the risk calculation.

Potential New Trade: In order to provide also pre-

trade analysis, the trader may enter the position

he/she may intend to enter and may start a what-if

analysis that evaluates the changes of the risk

measure that would be caused by this additional

trade.

On the output side we receive the risk measures

VaR and ES for the current portfolio together with

their sensitivities to a range of parameters.

In case that a pre-trade analysis was triggered the

output will consist of the newly calculated risk

measures VaR and ES for the expanded portfolio

(what-if-scenario VaR).

Figure 2: Inputs and Outputs.

3.3 Activity Diagram

The sequence of operations is rather straightforward,

as can be seen from figure 3 above. From the login

of the risk controller or trader up to the calculation

of the VaR and ES risk measures the internal task

sequence depends on the availability of pricing

Real Time Financial Risk Monitoring as a Data-intensive Application

663

information. If pricing scenarios exist, the risk

measures VaR and ES can be calculated directly.

Otherwise, a sufficient number of price scenarios

has to be generated and fetched. Subsequently, the

related sensitivities are computed with respect to a

given set of parameters. If a new pre-trade analysis

is requested, the risk measure of the existing

portfolio has to be updated in the same way, before

the additional trade will be added and the new risk

measures are calculated incrementally.

4 PLATFORM ARCHITECTURE

In the real-time risk monitoring use case, we aim to

develop a solution capable of doing highly non-

linear financial risk computation on a large portfolio

of trades changing in real-time (new trades coming

in, what-if scenarios, etc.). The goal is to utilize in-

memory capabilities of the solution to avoid

expensive brute-force re-computations and make it

possible to both compute risks much faster but also

to allow marginal computations of risk for new

incoming transactions. The risk monitoring

application is designed to use fast analytical and

streaming processing capabilities of third-party

systems, i.e. the Big Data Analytics Engine, the

Operational DB and the Streaming Analytics Engine

shown in figure 4 below.

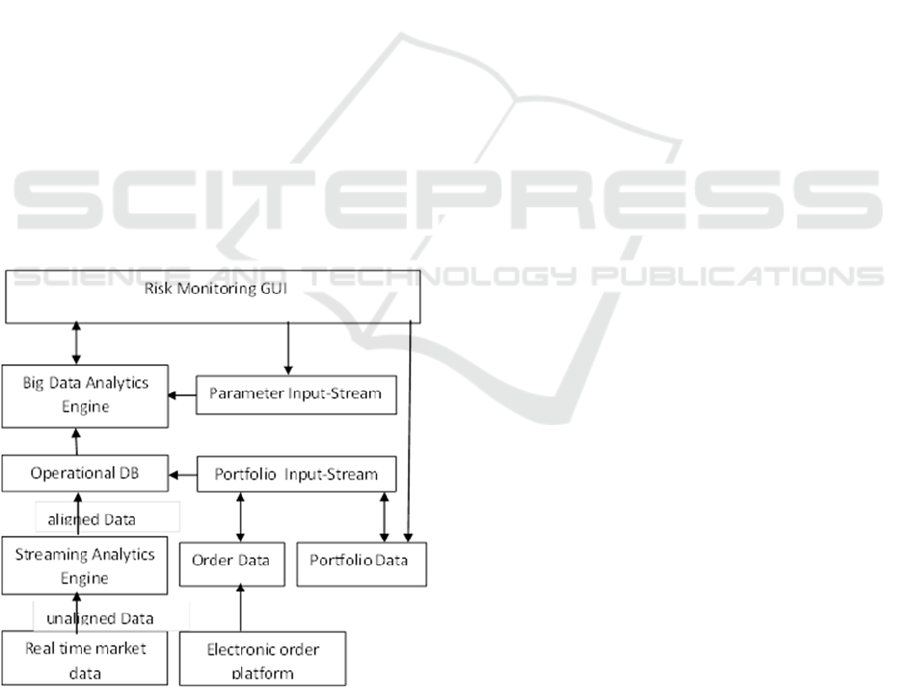
Figure 4: Use case architecture and data flow.

The input data streams are located at the bottom

of the diagram. The real time market data is one

high frequency data stream of financial price data

for stocks, bonds, futures, currencies, etc. as offered

by numerous providers like Bloomberg, Reuters, or

Metastock. The task of the streaming analytics

engine is to filter only those assets that are contained

in the current portfolio and to align all incoming data

into streams with synchronous time stamps (e.g. on

1 second basis). This is a prerequisite for the

calculation of the variance-covariance matrix.

The aligned data is then stored in the

operational data base and immediately passed

through into the Big Data Analytics Engine. The

Analytics Engine can be configured via a GUI

where also the results are presented to the user.

Concerning the second type of input, the trade

history, we can distinguish between order data and

portfolio data. The order data consists of all trades

and is derived directly from the electronic order

platform. Each broker offers a dedicated order

platform where traders enter the new trades that are

then instantaneously forwarded to the account held

by the broker. The portfolio data is entered by the

risk manager directly from the GUI and contains

information about the asset allocation of the

portfolio.

The Portfolio Input-Steam is an API dedicated

to the storage of the order and portfolio data in the

data base.

Finally, the Parameter Input-Stream is fed

from the GUI and contains all parameters for the

scenario generation that usually remain fixed, but

might be subject to change in the case that the risk

controller needs to make adjustments.

5 CONCLUSION

The presented risk monitoring use case is a data-

intensive application in a critical infrastructure. It

does not require many different functionalities, but

focusses on a central aspect in the daily risk

management procedures of banks and financial

institutes.

The challenge of the application lies in the

computational complexity of the calculation of the

risk measures. This is where it will exploit the

capabilities of the underlying existing big data and

streaming analytics platforms. Using the projects’

platforms, it will be possible to calculate risk figures

in real-time and therefore prevent the trader from

entering into trades that yield a harmful risk

structure.

The chosen architecture design is kept modular

and will allow for the replacement of single

components, either on the side of data base or

ADITCA 2019 - Special Session on Appliances for Data-Intensive and Time Critical Applications

664

analytical platform, but also with respect to the data

sources like the real time market data feed or

electronic order platform by simply replacing the

interface. This will keep the design sustainable and

open for future extensions of requirements.

ACKNOWLEDGEMENTS

This project has received funding from the European

Union’s Horizon 2020 research and innovation

programme under grant agreement No. 732051. The

authors acknowledge consortium members support

in the described work and efforts in the

implementation of the platform components.

REFERENCES

Elton, E., Gruber, M., Brown, S., Goetzmann, W., 2014.

Modern Portfolio Theory and Investment Analysis.

John Wiley & Sons, 9

edition.

Embrechts, P., Frey, R., McNeil, A., 2005. Quantitative

risk management: Concepts, techniques and tools.

Princeton university press: Princeton, Vol. 3.

Harris, D.E., 2017. The Distribution of Returns. Journal of

Mathematical Finance, 7, 769-804.

Jorion, P. 2006. Value at risk: the new benchmark for

controlling market risk. Chicago: IRWIN, 3

edition.

Krokhmal, P., Palmquist, J., Uryasev, S. 2002. Portfolio

Optimization with conditional Value-at-Risk Objective

and Constraints. Journal of risk 4, 43-68.

anganelli, S., Engle, R., 2001. Working paper. Value

risk models in finance. European Central Bank

Working Paper Series. Available at SSRN:

https://ssrn.com/abstract=356220.

Ziegel, J., 2013. Coherence and Elicitibility. Mathematical

Finance 26.4, 901-918.

Real Time Financial Risk Monitoring as a Data-intensive Application

665