Numerical Simulation of Internal Wave Attractors in Horizontally

Elongated Domains with Sloping Boundaries

Ilias Sibgatullin

1,2,3

, Xu Xiulin

, Evgeny Ermanuyk

, Daniil Ryazanov

1,3

and Kirill Vatutin

1,3

Ivannikov Institute for System Programming, Russian Academy of Sciences, Moscow, Russia

Shirshov Institute of Oceanology, Russian Academy of Sciences, Moscow, Russia

Moscow Lomonosov State University, Moscow, Russia

Lavrentyev Institute of Hydrodynamics, Russian Academy of Sciences, Novosibirsk, Russia

Keywords:

Internal Waves, Inertial Waves, Mixing, Wave Turbulence.

Abstract:

Global tides create continuous input of mechanical energy to the ocean, and produce inertia-gravity waves

which change the processes of vertical mixing, affect background stratiﬁcation, create mean and zonal cur-

rents. Internal and inertial wave attractors may arise in natural ocean and coastal topography, and due to

energy accumulation they produce turbulence or increase turbulence intensity even for moderate values of the

input energy. Previous studies of internal wave attractors at a laboratory scale were concerned mostly with

basins of comparable vertical and horizontal dimensions, while in ocean we typically deal with horizontally

elongated geometries and low ratios between the tidal and buoyancy frequencies. In this work we describe

laminar and turbulent regimes of internal wave attractors in domains with large aspect ratio subject to forcing

at low non-dimensional frequency.

1 INTRODUCTION

A large amount of energy is constantly injected into

interior of the Ocean due to interaction of barotropic

tides with the bottom topography. As a result the

inertia-gravity waves radiate from generation sites,

producing signiﬁcant effects on the vertical mixing

and stratiﬁcation (Morozov, 1995; Dauxois et al.,

2018). In addition, inertia-gravity wave motion

resulting from tides can produce mean and zonal

ﬂows (Winters, 2015; Manders and Maas, 2004; Har-

lander and Maas, 2007). Inertia and gravity waves

possess a very peculiar dispersion relation, which for

certain frequency deﬁnes only the direction of wave

propagation with respect to gravity or angular veloc-

ity vector. It was shown theoretically, experimentally

and numerically, that in closed basins with sloping

boundaries there may exist an attracting geometrical

structure in physical space, a wave attractor. The the-

ory of wave attractors in ideal ﬂuids is well elabo-

rated now, and in (Maas et al., 1997) one can see a

diagram illustrating a rich variety of internal wave-

ray patterns in a closed domain as function of two pa-

rameters, governing the geometry of the domain and

the wave-ray slopes. While this diagram is very use-

ful to identify the domains of parameters correspond-

ing to strong energy focusing in ideal ﬂuid, it is not

fully relevant to real ﬂuids, with effects due to vis-

cosity and wave turbulence included. Previous works

(Brouzet et al., 2016b; Brouzet et al., 2016a; Brouzet

et al., 2017) considered trapezoidal geometry of the

ﬂuid domain, with comparable vertical and horizontal

dimensions. Transition to nonlinear wave turbulence

was studied in details, and scaling laws were investi-

gated for such a geometric setup.

In the present paper we show some numerical

results for internal wave attractors in a horizontally

elongated domain at low ratio between forcing and

buoyancy frequency, which is closer to typical situa-

tions in oceanology applications.

2 MATHEMATICAL MODEL

The subject of this study is the internal wave dynam-

ics in a closed domain with one border inclined with

respect to the vertical. Such a geometry can naturally

occur near ridges, coastal areas, continental slopes

and so on. We perform Direct Numerical Simulations

366

Sibgatullin, I., Xiulin, X., Ermanuyk, E., Ryazanov, D. and Vatutin, K.

Numerical Simulation of Internal Wave Attractors in Horizontally Elongated Domains with Sloping Boundaries.

DOI: 10.5220/0007909203660370

In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 366-370

ISBN: 978-989-758-371-1

within the framework of a mathematical model con-

sisting of Navier – Stokes equations coupled to trans-

port and diffusion of salt and continuity equations,

and the boundary conditions given below:

∂~v

∂t

+ (~v,∇)~v = −∇

˜p

+ ν∆~v + ρ

~g; (1)

∂ρ

∂t

+ (~v,∇)ρ

= λ

∆ρ

, div(~v) = 0, (2)

where ~v – velocity; ρ = ρ

+ ρ

– density; ρ

– min-

imal density; ρ

– salt density; ˜p - pressure ρ

; ν –

kinematic viscosity; λ

– coefﬁcient of salt diffusion.

We consider a continuously stratiﬁed initial state

with constant buoyancy frequency

N(z) =

−

ρ(z)

dρ(z)

We prescribe the no-slip condition at all rigid

boundaries except for one boundary where we apply

a speciﬁc harmonic forcing. In the case of rotating

ﬂuid, different types of such forcing are introduced in

(Sibgatullin et al., 2017), which describes for the ﬁrst

time the laminar and weakly turbulent inertial wave

regimes in an annular frustum. In the case of strati-

ﬁed ﬂuid, the boundary conditions and external forc-

ing closely mimicking the experimental ones are de-

scribed in (Brouzet et al., 2016b).

Figure 1: Internal wave attractors for two geometries, hav-

ing opposite slopes of the right boundary with respect to the

gravity direction. Vertical component of velocity is shown

with color. The energy ﬂows in opposite directions in left

and right conﬁgurations, otherwise the dynamics is similar.

Figure 1 presents the sketch of the generic geomer-

ical setup used in analytical, numerical and experi-

mental studies of the wave attractors. The ﬂuid is

conﬁned inside a trapezoidal prism, with two bases

of the trapeze perpendicular to gravity, the left wall

being vertical and the right wall tilted by a certain

angle α. The ﬁrst attempts to model wave attractors

assumed two-dimensionality of the ﬂow (Grisouard

et al., 2008). This assumption allowed a fully rel-

evant qualitative simulation of wave attractors, with

relatively poor quantitative agreement between nu-

merical and experimental results. Later, the ﬁrst fully

3D DNS greatly improved the quantitative agreement

between experiments and simulations both in linear

and non-linear regimes, and showed the signiﬁcance

of the dissipation at the lateral walls of the ﬂuid do-

main (Brouzet et al., 2016b; Brouzet et al., 2016a;

Beckebanze et al., 2018). Interestingly, numerical

simulations of wave attractors generated by a span-

wise localized wave maker in the otherwise two-

dimensional setup demonstarted a strong qualitative

trend toward two-dimensionality of wave motion, but

with speciﬁc non-uniform energy distribution in span-

wise direction and signiﬁcant effects due to the lateral

walls (Pillet et al., 2018).

Figure 2: α = 60

◦

, a=0.02 cm, horizontal and vertical com-

ponents of velocity.

Substituting the solution in form of monochromatic

travelling waves into linearised Euler equations de-

scribing the motion of a uniformly stratiﬁed ideal

ﬂuid, one can obtain the following dispersion relation:

= N

sin

(θ), (3)

where ω

– wave frequency. It can be seen that the

dispersion relation admits the propagation of waves

in form of oblique wave beams, but does not contain

any length scale. In many practical problems a qual-

itative description of wave patterns can be obtained

by neglecting the width of wave beams and consid-

ering the propagation of wave rays. The problem of

wave-ray billiard in the geometric setup presented in

Figure 1 can be re-scaled by introducing two quan-

tities d and τ, d being the parameter responsible for

the slope (with the limiting values −1 and +1 cor-

responding to triangular and rectangular geometry),

and τ =





− 1 being the parameter respon-

sible for the forcing frequency. In ideal ﬂuid, a di-

Numerical Simulation of Internal Wave Attractors in Horizontally Elongated Domains with Sloping Boundaries

367

agram of Lyapunov exponents of internal wave rays

(Maas et al., 1997) characterises the wave regimes,

and show the domains of strong convergence toward

attractors. However, in real world viscosity and wave

turbulence come into play, adding a rich variety of

linear and non-linear regimes.

In numerical simulations of linear regimes one

needs to resolve the boundary layers at rigid bound-

aries, and the structure of the attractor beams, which

appear in form of oblique viscous shear layers. In

simulations of strongly nonlinear regimes, one needs

to resolve the small-scale patterns resulting from a

cascade of wave-wave interactions. In a density-

stratiﬁed ﬂuid the numerical simulations are com-

plicated by necessity to resolve the diffusion of the

stratifying agent, and at high values of the Prandtl-

Schmidt number the small-scale structures appear,

which greatly complicate the interaction of the waves

beams of the attractors with the walls (Sibgatullin and

Kalugin, 2016). In direct numerical simulations de-

scribed in the present paper we use the spectral ele-

ment method, which proves to be highly efﬁcient for

this type of problems (Brouzet et al., 2016b; Brouzet

et al., 2016a; Beckebanze et al., 2018).

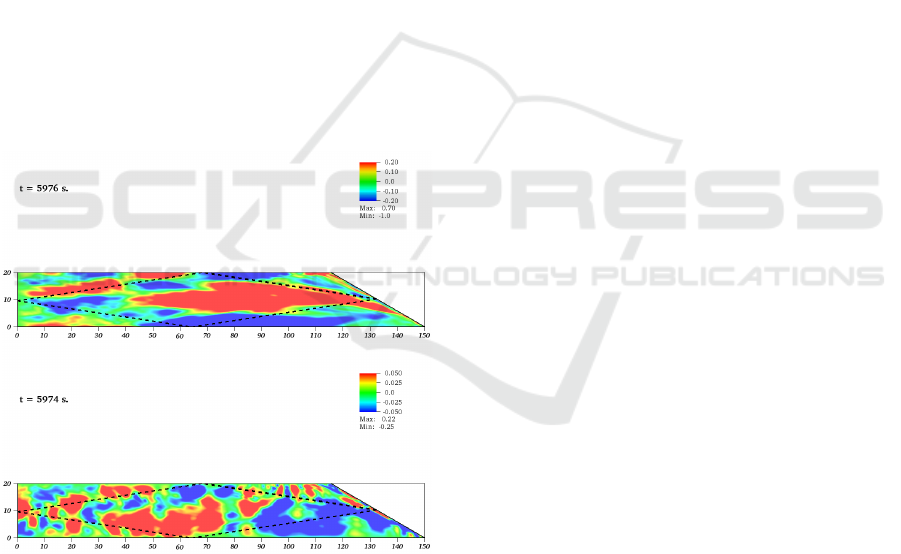
Figure 3: α = 60

◦

, a=0.05 cm, horizontal and vertical com-

ponents of velocity.

3 NUMERICAL RESULTS

Many previous studies on dynamics of internal wave

attractors used the trapezoidal geometry depicted in

Figure 1 (Mass et al., 1997; Scolan et al., 2013;

Brouzet et al., 2016b; Brouzet et al., 2016a; Becke-

banze et al., 2018; Brouzet et al., 2017; Dauxois et al.,

2017), where the largest base of the trapezium varied

between 30 to 150 cm and the ﬂuid depth was about

2/3 of the largest base. The angle of the slope with the

gravity was typically about 30

◦

. The external forcing

was realized by moving vertical boundary of the ﬂuid

volume or by oscillating the tank ﬁlled with the den-

sity stratiﬁed water.

Signiﬁcant change of aspect (depth-to-length) ra-

tio of the geometrical setup may introduce new dy-

namical effects in the behaviour of the system at lam-

inar and turbulent regimes. Of particular interest is the

horizontally elongated geometry, which is relevant to

typical applications in oceanography.

In the following, the tidal forcing is simulated in

a highly simpliﬁed way by imposing small-amplitude

oscillations of the largest base of the trapezium L in

the following form:

ξ = asin(2πx/L)sin(ω

We take the length of the domain L = 150 cm and

the depth is H = 20 cm. The value of the buoyancy

frequency is N = 1 rad/s. The kinematic viscosity of

the ﬂuid is taken to be ν = 0.002 cm

/s, ﬁve times

smaller than the viscosity of water. The global Stokes

number, which can be introduced as St = H

N/ν

is 2 · 10

. In the present paper we are mostly con-

cerned with the qualitative effects observed in hori-

zontally elongated domains. Therefore we perform

two-dimensional simulations.

Figure 2 shows the horizontal and vertical com-

ponents of velocity ﬁeld at small forcing amplitude

a = 0.02 cm. The narrow wave beams are localized

in the vicinity of the theoretical sceleton of the at-

tractor given by solution of the wave-ray billiard and

marked with a black dashed line. One can identify

the presence of nonlinear effects, in particular, wave

beams at double frequency 2ω

emitted at the points

of reﬂection of the primary wave beam. Note that the

possibility of super-harmonic effects is an important

feature of the horizontally elongated setup. In pre-

vious studies of wave turbulence in internal wave at-

tractors (Scolan et al., 2013; Brouzet et al., 2016b;

Brouzet et al., 2016a) the typical non-dimensional

forcing frequency was ω

/N > 0.5. Therefore the

super-harmonics could exist only in form of evanes-

cent waves. The present study considers a more real-

istic case where the super-harmonic waves are prop-

agative.

Figure 3 shows the horizontal and vertical compo-

nents of the velocity ﬁeld for the forcing amplitude

a = 0.05 cm (i.e. only 2.5 times larger than in the

case shown in Figure 2). Note that the forcing am-

plitude remains very small compared to the size of

the ﬂuid domain: a/L is about 3 · 10

−4

. The wave

pattern now is completely different: we can see at

the same time the small-scale structures located in

ONM-CozD 2019 - Special Session on Observations and Numerical Modeling of the Coastal Ocean Zone Dynamics

368

the upper right corner, and the large-scale structures

in the bulk of the domain. This observation sug-

gests the existence of the inverse cascade resulting

from the complex turbulent wave motion. This qual-

itative consideration is to be conﬁrmed by a careful

Fourier-Hilbert analysis being performed at present

time. Importantly, the observed snapshot bears no re-

semblance to a classic pattern of internal wave attrac-

tor. Therefore, at high energy input into the system

the fact that a particular geometry admits the exis-

tence of wave attractors may be completely hidden by

wave turbulence although the concentration of energy

at the attractor is at the origin of the observed energy

cascade. This is particularly important for interpreta-

tion of oceanographic measurements which typically

deal rather with the large-scale patterns seen Figure 3

than with the narrow-beam patterns presented in Fig-

ure 2. Establishing the link between the two patterns

may signiﬁcantly enrich our understanding of the un-

derlying nonlinear dynamics. Broad numerical calcu-

lations are now under way, focused at the analysis of

the spectra of the wave motions in space and time and

other characteristics of wave turbulence in different

areas of horizontally elongated ﬂuid domains.

4 CONCLUSIONS

This communication describes the peculiarities of in-

ternal wave turbulence in horizontally elongated con-

ﬁned ﬂuid domains with one sloping wall. The wave

attractors in such a geometry typically have a lower

amplitude threshold corresponding to onset of wave

turbulence as compared to conventional setups where

length and depth of the ﬂuid domain are comparable.

The most important result of this study consists in

revealing the inverse cascade. We consider the time-

evolution of the internal wave regime from the state

of rest toward formation of the attractor and transition

to a fully developed wave turbulence via a cascade of

wave-wave interactions. In the regime of wave turbu-

lence we observe the small scale structures to merge

and form larger structures. This result may explain

in particular why internal wave attractors are hard to

detect in natural conditions: we see here that they ini-

tially act as a source of wave turbulence, but after-

wards they are hidden behind the large scale turbu-

lence arising due to development of the inverse cas-

cade.

ACKNOWLEDGEMENTS

This research was supported by the Russian

Ministry of Education and Science (Agreement

14.616.21.0075, Project ID RFMEFI61617X0075).

The computations are performed using the equipment

of the shared research facilities of HPC computing re-

sources at Lomonosov Moscow State University.

REFERENCES

Beckebanze, F., Brouzet, C., Sibgatullin, I. N., and Maas,

L. R. M. (2018). Damping of quasi-two-dimensional

internal wave attractors by rigid-wall friction. Journal

of Fluid Mechanics, 841:614–635.

Brouzet, C., Ermanyuk, E., Joubaud, S., Sibgatullin, I., and

Dauxois, T. (2016a). Energy cascade in internal-wave

attractors. EPL (Europhysics Letters), 113(4):44001.

Brouzet, C., Sibgatullin, I., Scolan, H., Ermanyuk, E., and

Dauxois, T. (2016b). Internal wave attractors exam-

ined using laboratory experiments and 3d numerical

simulations. Journal of Fluid Mechanics, 793:109–

131.

Brouzet, C., Sibgatullin, I. N., Ermanyuk, E. V., Joubaud,

S., and Dauxois, T. (2017). Scale effects in internal

wave attractors. Phys. Rev. Fluids, 2:114803.

Dauxois, T., Brouzet, C., Ermanyuk, E., Joubaud, S.,

Tourneau, D. L., and Sibgatullin, I. (2017). Energy

cascade in internal wave attractors. Procedia IUTAM,

20:120 – 127. 24th International Congress of Theo-

retical and Applied Mechanics.

Dauxois, T., Ermanyuk, E., Brouzet, C., Joubaud, S., and

Sibgatullin, I. (2018). Abyssal Mixing in the Labora-

tory, pages 221–237. Springer International Publish-

ing, Cham.

Grisouard, N., Staquet, C., and Pairaud, I. (2008). Numeri-

cal simulation of a two-dimensional internal wave at-

tractor. Journal of Fluid Mechanics, 614:1.

Harlander, U. and Maas, L. R. M. (2007). Internal boundary

layers in a well-mixed equatorial atmosphere/ocean.

Dynamics of Atmospheres and Oceans, 44:1–28.

Maas, L. R. M., Benielli, D., Sommeria, J., and Lam, F.-

P. A. (1997). Observation of an internal wave attractor

in a conﬁned, stably stratiﬁed ﬂuid. Nature, 388:557–

561.

Manders, A. M. M. and Maas, L. R. M. (2004). On the

three-dimensional structure of the inertial wave ﬁeld

in a rectangular basin with one sloping boundary.

Fluid Dynamics Research, 35(1):1.

Mass, L., Benielli, D., Sommeria, J., and Lam, F.-P. A.

(1997). Observation of an internal wave attrac-

tor in a conﬁned, stably stratiﬁed ﬂuid. Nature,

388(6642):557.

Morozov, E. G. (1995). Semidiurnal internal wave global

ﬁeld. Deep Sea Research Part I: Oceanographic Re-

search Papers, 42(1):135 – 148.

Pillet, G., Ermanyuk, E. V., Maas, L. R. M., Sibgatullin,

I. N., and Dauxois, T. (2018). Internal wave attractors

Numerical Simulation of Internal Wave Attractors in Horizontally Elongated Domains with Sloping Boundaries

369

in three-dimensional geometries: trapping by oblique

reﬂection. Journal of Fluid Mechanics, 845:203–225.

Scolan, H., Ermanyuk, E., and Dauxois, T. (2013). Non-

linear fate of internal wave attractors. Physical review

letters, 110(23):234501.

Sibgatullin, I., Ermanyuk, E., Maas, L., Xu, X., and

Dauxois, T. (2017). Direct numerical simulation of

three-dimensional inertial wave attractors. In 2017

Ivannikov ISPRAS Open Conference (ISPRAS), pages

137–143.

Sibgatullin, I. and Kalugin, M. (2016). High-resolution

simulation of internal waves attractors and impact

of interaction of high amplitude internal waves with

walls on dynamics of waves attractors. ECCOMAS

Congress 2016 - Proceedings of the 7th European

Congress on Computational Methods in Applied Sci-

ences and Engineering, 4:7130–7137.

Winters, K. B. (2015). Tidally-forced ﬂow in a rotating,

stratiﬁed, shoaling basin. Ocean Modelling, 90:72–

81.

ONM-CozD 2019 - Special Session on Observations and Numerical Modeling of the Coastal Ocean Zone Dynamics

370