
Advanced Multi-neural System for Cuff-less Blood Pressure
Estimation through Nonlinear HC-features
Francesco Rundo
1a
, Alessandro Ortis
2b
, Sebastiano Battiato
2c
and Sabrina Conoci
1d
1
STMicroelectronics, ADG Group – Central R&D, Str. Primosole, 50, 95121 Catania CT, Italy
2
Dipartimento di Matematica e Informatica, Università Degli Studi di Catania, Viale A. Doria 6, 95125 - Catania, Italy
Keywords: Blood Pressure Estimation, PPG, ECG.
Abstract: Blood Pressure (BP) is one of the most important physiological indicator that can provide useful information
in the medical field. BP is usually measured by a sphygmomanometer device, which is composed by a cuff
and a mechanical manometer. In this paper, a novel algorithmic approach to accurately estimate both systolic
and diastolic blood pressure is presented. This algorithm exploits the PhotoPlethysmoGraphy (PPG) signal
pattern acquired by non-invasive and cuff-less Physio-Probe (PP) silicon-based SiPM device. The PPG data
are then processed with ad-hoc bio-inspired mathematical model which estimates both systolic and diastolic
pressure values. We compared our results with those measured using a classical sphygmomanometer device
and encouraging results of about 97% accuracy were achieved.
1 INTRODUCTION
The classical medical method to measure Blood
Pressure (BP) is the use of the stethoscope. Recent
cuff-based digital devices approaches are invasive,
costly and do not allow continuous monitoring.
Innovative methods try to estimate BP by analyzing
the waves produced upon the heart dynamic along the
arteries. In (Kurylyak, 2013) a non-invasive
continuous BP estimation approach based on
Artificial Neural Networks (ANNs) is proposed. The
ANN is trained with 21 input parameters extracted
from PPG signals. In (Yan, 2006) the authors
described a new set of PPG hand-crafted features
exhibiting encouraging results. The paper reported in
(Gu, 2008) proposes an estimation of BP by means of
new calibration parameters related to the dicrotic
notch of the processed PPG waveform. The papers in
(Teng, 2003) and in (Fortino, 2010) provide detailed
surveys on the methodologies proposed in the
literature for estimating BP from PPG signals.
However, all these methodologies present the
disadvantage that are based on PTT (Pulse Transit
Time) calculation, which requires the sampling of
a
https://orcid.org/0000-0003-1766-3065
b
https://orcid.org/0000-0003-3461-4679
c
https://orcid.org/0000-0001-6127-2470
d
https://orcid.org/0000-0002-5874-7284
both ECG (ElectroCardioGraphy) and PPG signals.
Additionally, specific HW (PPG/ECG) sensors and
SW (data extraction (PTT, PWV)) are needed.
Finally, those methods may involve high
computational costs against a reduced accuracy
and/or an estimation capability limited to a common
pressure range (70/110 - 80/120 mmHg).
In this paper, a novel algorithmic approach to
accurately estimate both Systolic and Diastolic blood
pressure (SBP, DBP) is presented. This algorithm
analyzes the PPG signal acquired by non-invasive and
cuff-less silicon photomultiplier sensor (SiPM),
which can be installed in a commercial medical
device or in a simply mobile phone.
2 THE PROPOSED BLOOD
PRESSURE ESTIMATION
SYSTEM
PPG signal is becoming increasingly popular in
extracting cardiovascular information since it is
sampled
with non-invasive optical technologies
Rundo, F., Ortis, A., Battiato, S. and Conoci, S.
Advanced Multi-neural System for Cuff-less Blood Pressure Estimation through Nonlinear HC-features.
DOI: 10.5220/0007909403210325
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 321-325
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
321

Figure 1: (a) BP estimation pipeline; (b) PPG and derivatives for hand crafted features.
(Vinciguerra, 2017). This signal has a great potential
for the assessment of vascular diseases related to
aging, hypertension, and atherosclerosis, providing
information on arterial stiffness and elasticity
(Oreggia, 2015).
To achieve the above reported cardiovascular
information, a robust PPG signal without artifacts is
mandatory. In particular, a compliant PPG waveform
must comprise systolic peak (SP), dicrotic notch
(DN) and diastolic peak (DP). In our previous works
(Rundo, 2018) (Mazzillo, 2018) we presented a PPG
pattern recognition pipeline allowing to achieve high
robust PPG compliant waveform. The obtained PPG
signal is herein furtherly processed to achieve a
reliable BP estimation. The pipeline we used is
reported in Figure 1(a). It includes a Mathematical
Analysis System block, presented in (Rundo, 2018)
and (Mazzillo, 2018), receiving compliant PPG
signals as input. The output of this block is then
learned by two layer of Neural Network (NN)
providing both SBP and DBP output signals.
a) Mathematical Analysis System Block. This block is
able to calculate a set of 18 features on the compliant
PPG waveform and on the first and second (time)
derivatives (Fig. 1 (b)). The following equations F
1
to F
18
are exemplary of how such first act of
processing can be performed in the proposed
approach:
ln
1
(1)
ln
1
(2)
ln
1
(3)
(4)
(5)
(6)
ln
1
(7)
ln
1
(8)
ln
1
(9)
(10)
(11)
SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications
322

(12)
ln
1
(13)
ln
1
(14)
ln
1
(15)
(16)
(17)
(18)
where:
ln is (natural) logarithm; N
PPG
are the PPF waveform
samples over a period of the PPG signal; suffixes sys,
dia and dic are the systolic, diastolic and dicrotic
phases of the PPG signal identified as the portions a–
b, a1–b1, a2–b2 (systolic), b–d, b1–d1,b2–d2
(dicrotic), c–e, c1-e1 and c2–e2 (diastolic) in the
diagrams (PPG and its first derivative and second
derivative) of Figure 1(b); L
i
x
indicates the length of
sub-curve of PPG waveform, for the systolic,
diastolic and dicrotic phases sys, dia and dic,
respectively and with i=1. N
PPG
; in the same way,
L
i
x(∂PPG/∂t) represents the length of the sub-curve
of the first derivative of the PPG signal, and L
i
x
(∂
2
PPG/∂t
2
) represents the length of the sub-curve of
the second derivative of the PPG signal, again for sys,
dia and dic, respectively. For the first and second
derivative of PPG signal, the Simpson rule can be
adopted for computing the length of the curve
(Matthews, 2004); - σ
x
denotes standard deviation for
variable L
i
x.
The F
1
– F
18
features have been properly designed
with the aim to have an exhaustive and analytical
description of the shape of the PPG waveform.
Indeed, beside common statistical indices described
by features F
1
, F
4
, F
10
and F
16
, we considered specific
features based on the first and second derivative of
the waveform aimed to point out the peculiarities
related to the directions and the inflection points of
the PPG waveform, respectively.
b) Neural Systems 1 and 2. The F
1
– F
18
features are
fed into the Artificial Neural Network (ANN) blocks
to perform further processing to correlate the PPG
signal with real SBP (systolic) and DBP (diastolic) to
achieve a reliable model for BP estimation. Training
values are derived from a set of measurements
performed on 30 patients in which BP was measured
by conventional sphygmomanometer concurrently
with the PPG signal. The first ANN (Neural System
1) is a Multi-Layer Perceptron (MLP) with a modified
Polak-Ribiere back-propagation learning algorithm
(Fletcher, 1964) (Hagan, 1996). This ANN performs
a preliminary reconstruction of the blood pressure of
a subject both for systolic (SBP) and diastolic (DBP)
values, providing an estimation denoted as f
1
(*) and
f
2
(*) for SBP and DBP respectively. The second ANN
is an advanced modified version of the SOM Motor
Map (Ortis, 2013), able to complete such a
reconstruction of both SBP and DBP values by
detecting a second estimation or component K
1
(*) and
K
2
(*).
Below are reported the mathematical models used
in the ANN layers:
,
(19)
,
(20)
Consequently, the pressure values
SBPrec/DBPrec comprise a non-linear portion (f1/f2)
and a linear portion (K
1
/K
2
).
Concerning the SOM Motor Map NN, the
following equations describe the typical “Winner
Take All” algorithm used for clustering the described
input hand crafted PPG features:
,
,
,1
,
,
,
∙,,∙
,
,
,
1
(21)
,
,
,1
,
,
,
∙,,∙
,
,
,
1
(22)
where (x
min
,y
min
) represents the coordinates of the
neurons which minimize the Euclidian distance
between the input weights and the related hand
crafted input vector while “ ” and “ ,,”
represents the learning rate and neighborhood
function (gaussian) of the WTA algorithm. This
winner neuron produces the related output per
following equation:
Advanced Multi-neural System for Cuff-less Blood Pressure Estimation through Nonlinear HC-features
323
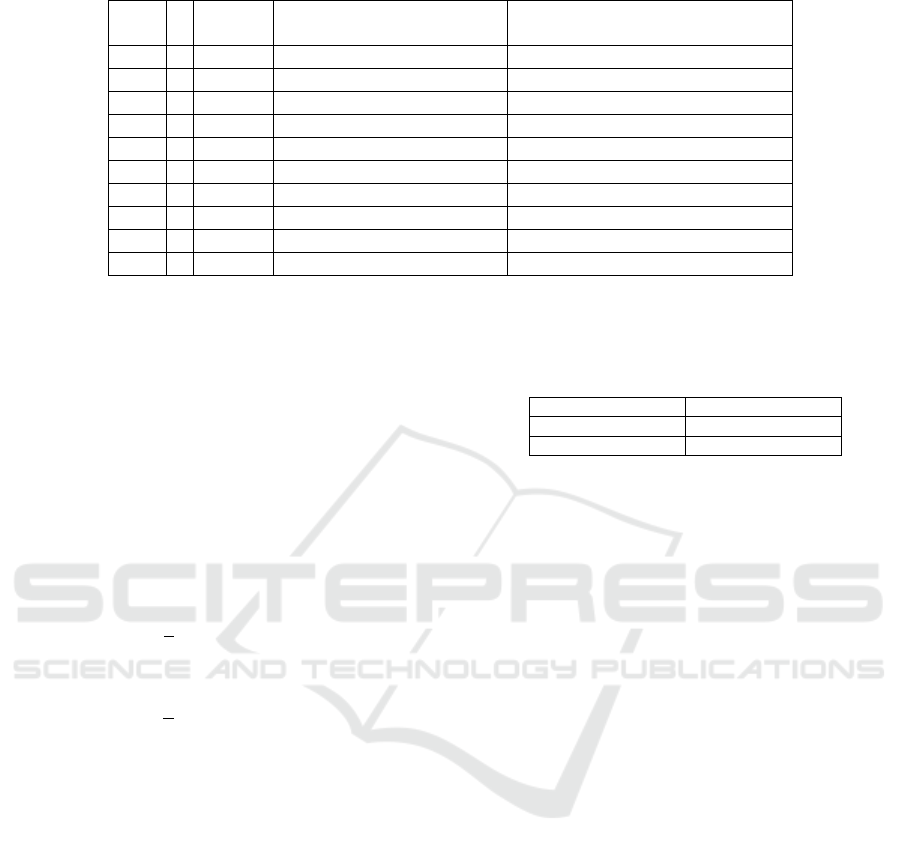
Table 1: DBP and SBP Results.
Patient
Number
Age Pathologies Actual Blood Pressure (DBP/SBP)Estimated Blood Pressure (DBP
rec
/SBP
rec
)
1 32 No 85/123 83.21/121.11
2 24 No 80/120 79.22/122.53
3 53 Yes 85/125 83.98/123.24
4 65 Yes 90/135 91.09/132.99
5 46 No 70/120 68.92/119.87
6 33 No 80/115 78.81/115.09
7 21 No 70/105 69.04/104.98
8 52 Yes 90/130 89.01/132.21
9 25 No 80/130 78.99/131.09
10 58 No 85/130 83.93/129.91
,
,
,1
,
,
,
∙,,
∙
,
,
,
(23)
,
,
,1
,
,
,
∙,,
∙
,
,
,
)
(24)
We compute the following learning errors:
1
1
2
1
1
(25)
1
1
2
1
1
(26)
If the above error functions are progressive
decreasing (i.e., the conditions in Equation (27) and
Equation (28) are satisfied), the related weights
update will be confirmed and then we have Equation
(29) and Equation (39). Otherwise, both input and
output weight updates will be discarded.
1
(27)
1
(28)
,
,
,1
,
(29)
,
,
,1
,
(30)
3 RESULTS
This study was conducted in accordance with the
Helsinki Declaration of 1975. All patients provided
written informed consent before enrollment. The
study was approved by the Ethical Committee
Catania 1 (Authorization No. 113/2018/PO).
Table 2: Average errors of the proposed algorithm.
Blood Pressure Average Error
DBP 2.718 mmHg
SBP 2.853 mmHg
We engaged 30 patients having different genders
(male and female), ages (between 20 and 70 years
old) and pathologies (we collected healthy subjects
and sick ones with different issues such as cardiac
problems, hypertension, diabetes, etc.).
Table 1 and Table 2 show SBP and DBP values
and the average error the obtained by the proposed
approach, respectively. The average error for both
estimation (SBP and DBP) is less than 3 mmHg
corresponding to about 10/15 % of real measure. This
is an acceptable result from a medical point of view
and with respects to prior state of the art above
mentioned.
4 CONCLUSIONS
In this paper we proposed a novel algorithmic for
non-invasive cuff-less BP estimation, easily
embedded in several kind of devices from mobile to
portable medical systems. This algorithm takes the
PhotoPlethysmoGraphy (PPG) signal as input,
acquired by miniaturized silicon photomultiplier
SiPM devices. The PPG data are processed with ad-
hoc bio-inspired mathematical model which
estimates both systolic and diastolic pressure values.
We compared our results with the measures obtained
by using a classical sphygmomanometer device,
achieving a mean accuracy of 97%. Hence, the
performances achieved by the proposed method are
suitable for clinical use.
SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications
324

Future works aim to improve better the estimation
increasing the training set number and the type of
neural system we used. Further efforts will be also
devoted to the extension of the experiments, by a
comparative evaluation among a set of state-of-the-
art methods on a proper large-scale benchmark
dataset.
REFERENCES
Kurylyak, Y., Lamonaca, F., and Grimaldi, D. (2013, May).
A neural network-based method for continuous blood
pressure estimation from a PPG signal. In 2013 IEEE
International instrumentation and measurement
technology conference (I2MTC) (pp. 280-283). IEEE.
Y Yan, Y. S., and Y. T. Zhang. "Noninvasive estimation of
blood pressure using photoplethysmographic signals in
the period domain." 2005 IEEE Engineering in
Medicine and Biology 27th Annual Conference. IEEE,
2006.
Gu, W. B., C. C. Y. Poon, and Y. T. Zhang. "A novel
parameter from PPG dicrotic notch for estimation of
systolic blood pressure using pulse transit time." 2008
5th International Summer School and Symposium on
Medical Devices and Biosensors. IEEE, 2008.
Teng, X. F., and Y. T. Zhang. "Continuous and noninvasive
estimation of arterial blood pressure using a
photoplethysmographic approach." Proceedings of the
25th Annual International Conference of the IEEE
Engineering in Medicine and Biology Society (IEEE
Cat. No. 03CH37439). Vol. 4. IEEE, 2003.
Fortino, G., and Giampà, V. (2010, April). PPG-based
methods for non-invasive and continuous blood
pressure measurement: an overview and development
issues in body sensor networks. In 2010 IEEE
International Workshop on Medical Measurements and
Applications (pp. 10-13). IEEE.
Vinciguerra, V., Ambra, E., Maddiona, L., Oliveri, S.,
Romeo, M. F., Mazzillo, M., Rundo, F., and Fallica, G.
(2017, September). Progresses towards a processing
pipeline in photoplethysmogram (PPG) based on
SiPMs. In 2017 European Conference on Circuit
Theory and Design (ECCTD) (pp. 1-5). IEEE.
Oreggia, D., Guarino, S., Parisi, A., Pernice, R., Adamo, G.,
Mistretta, L., Di Buono, P., Fallica, G., Cino, C. and
Busacca, A.. Physiological parameters measurements
in a cardiac cycle via a combo PPG-ECG system.
Proceedings of the AEIT International Annual
Conference, 2015; pp. 1-6;
Rundo, F., Conoci, S., Ortis, A., Battiato, S. “An Advanced
Bio-Inspired PhotoPlethysmoGraphy (PPG) and ECG
Pattern Recognition System for Medical Assessment”.
Sensors 2018, 18, 405.
Mazzillo, M., Maddiona, L., Rundo, F., Sciuto, A.,
Libertino, S., Lombardo, S., and Fallica, G. (2018).
Characterization of SiPMs with NIR long-pass
interferential and plastic filters. IEEE Photonics
Journal, 10(3), 1-12.
Matthews, John H. (2004). "Simpson's 3/8 Rule for
Numerical Integration". Numerical Analysis -
Numerical Methods Project. California State
University, Fullerton. Archived from the original on 4
December 2008. Retrieved 11 November 2008.
Fletcher, Reeves, and Colin M. Reeves. "Function
minimization by conjugate gradients." The computer
journal 7.2 (1964): 149-154.
Hagan, M. T., Demuth, H. B., Beale, M. H., & De Jesús, O.
(1996). Neural network design (Vol. 20). Boston: Pws
Pub.
Ortis A., Rundo F., Di Giore G., Battiato S. (2013)
Adaptive Compression of Stereoscopic Images. In:
Petrosino A. (eds) Image Analysis and Processing –
ICIAP 2013. ICIAP 2013. Lecture Notes in Computer
Science, vol 8156. Springer, Berlin, Heidelberg.
Advanced Multi-neural System for Cuff-less Blood Pressure Estimation through Nonlinear HC-features
325
