
A Generic Control Framework for Mobile Robots Edge Following
Mathieu Deremetz
1 a
, Adrian Couvent
1 b
, Roland Lenain
1 c
, Benoit Thuilot
2
and Christophe Cariou
1 d
1
Universit
´
e Clermont Auvergne, Irstea, UR TSCF, Centre de Clermont-Ferrand,
9 avenue Blaise Pascal CS 20085, F-63178 Aubi
`
ere, France
2
Universit
´
e Clermont Auvergne, CNRS, SIGMA Clermont, Institut Pascal, F-63000 Clermont-Ferrand, France
christophe.cariou@irstea.fr
Keywords:
Wheeled Robots, Field and Agriculture Robots, Edge Tracking.
Abstract:
In this paper, the problem associated with accurate control for mobile robots following an edge is addressed
thanks to a backstepping control. In particular, the control of the angular speed (control input) is investigated
through the derivation of a new backstepping control by gathering derivatives regarding to time and to the
curvilinear abscissa in a single framework. This new reference then allows both time and distance convergence
of the robot states towards a trajectory computed with points given by a Lidar only. This permits to address
the control of different kinds of robots (skid-steering, car like, four-wheel-steering) in a common framework
and to consider independently the speed regulation, the lateral and the longitudinal controls. The control
proposed here allows an accurate and reactive path tracking even if the environment is complex and narrow.
The efficiency of the approach is investigated through full scale experiments in various conditions.
1 INTRODUCTION
Mobile robotics has raised as a promising solution to
help people in everyday life and has been the subject
of a lot of significant advances. The progress achieved
on autonomous cars (Marmoiton and Slade, 2016) is
one of the best examples, since first commercial so-
lutions are about to be marketed. Human transporta-
tion is not the sole application area which may benefit
from autonomous mobile robots and numerous social
needs may be addressed thanks to this topic (Berger-
man et al., 2016). This is particularly the case in envi-
ronment and agriculture areas, where painful and dan-
gerous works have to be achieved. As a result, the use
of robots able to act autonomously to pull an imple-
ment or to carry out heavy loads may permit, among
others, the reduction of the hardness of work or the
limitation of the operator exposition to risks (Black-
more, 2016).
In this context, the autonomous motion task of-
ten consists in trajectory following, which has been
deeply studied in the literature (Samson et al., 2016).
a
https://orcid.org/0000-0002-1239-0320
b
https://orcid.org/0000-0002-3453-1358
c
https://orcid.org/0000-0003-0348-8673
d
https://orcid.org/0000-0002-7343-7452
In open area, this can be easily achieved using a GPS
sensors, offering permanently an absolute localization
for the robot navigation (Cariou et al., 2010). Never-
theless, this sensor appears to be expensive and not al-
ways applicable, especially in vineyard or orchard ap-
plications. The height of the vegetation in these con-
texts may indeed lead to a bad reception of satellite
signals. Moreover, since agricultural tasks have to be
done with respect to crops, the regulation of the robot
motion with respect to vegetation must be favoured.
As a result, alternative approaches have been pro-
posed, often based on artificial vision such as consid-
ered in (Cherubini and Chaumette, 2013), in (Tour-
rette et al., 2017), or in (Astrand and Baerveldt, 2005)
for agricultural applications, or based on a Lidar, such
as achieved in (Bayar et al., 2015). As soon as a lo-
cal positioning is available, different control laws can
then be applied (such as derived in (D’Andr
´
ea-Novel
et al., 1995), or (Lenain et al., 2017)). Nevertheless,
such approaches do not explicitly compute the an-
gular orientation and are therefor not suitable when
moving autonomously in narrow spaces, such as en-
countered for instance in vineyard, or when achiev-
ing harsh manoeuvres. Another approach introduced
in (Deremetz et al., 2017) allows to control the abso-
lute orientation of the robot with respect to the global
104
Deremetz, M., Couvent, A., Lenain, R., Thuilot, B. and Cariou, C.
A Generic Control Framework for Mobile Robots Edge Following.
DOI: 10.5220/0007915501040113
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 104-113
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

frame, but this latter is not available in the considered
applications.
In this paper, an alternative approach of the tra-
jectory tracking to follow an edge is proposed. It
is based on a backstepping control, allowing to con-
sider independently longitudinal and lateral controls
and separate the position and the orientation servo-
ing of the robot. This permits to improve the control
of the robot orientation to improve manoeuvrability
and avoid the collision with the structure to be fol-
lowed. This control is generic and developed for sev-
eral kinds of robots: skid-steering, car-like mobile,
or four-wheel steering robots. In the latter case, the
backstepping approach is enhanced in order to regu-
late the actual orientation of the robot in order to opti-
mize the work of an on-boarded implement (which is
important for agricultural tasks, such as spraying) as
well as the manoeuvrability.
This paper is decomposed as follows. First, the
kinematic model of a mobile robot with respect to an
edge is recalled. Based on this generic modelling,
the proposed backstepping control approach is de-
tailed. Then additive features to improve manoeu-
vrability and safety are presented. Finally, the effi-
ciency of the proposed control architecture is investi-
gated through full scale experiments in various condi-
tions, using several kinds of robots.
2 MODELLING
2.1 Assumptions and Notations
In this paper, the objective is to follow a structure,
using an edge detector, thanks to a mobile robot. For
that purpose, a control strategy based on the trajectory
tracking point of view may be considered, as classi-
cally investigated in (Samson et al., 2016). In this
point of view, a four-wheel-steering robot can be de-
scribed as a bicycle such as depicted in Fig 1. The
robot is reduced to two wheels, one for the front axle
with a steering angle denoted as δ
F
, and one for the
rear axle, with an angle denoted δ
R
.
The position of the robot is defined with respect to
the detected structure Γ to be followed (considered as
a trajectory), with a lateral error y, also called track-
ing error, and a curvilinear abscissa s (i.e. the dis-
tance achieved along the trajectory). Let us denote by
˜
θ, the difference between the orientation of the robot
and the direction of the tangent to Γ at the curvilin-
ear abscissa s. The curvature of the trajectory to be
followed at the curvilinear abscissa s is denoted by
c(s). With these notations the objective of the struc-
ture following strategy is to ensure the convergence
Figure 1: Modelling of the mobile robot w.r.t. the detected
structure Γ.
of the lateral deviation y to some desired set point y
d
,
at a desired speed v
d
. As it will be pointed out in the
following, even if a four-wheel-steering robot is pre-
sented in this section, the proposed control strategy is
also derived for a skid-steering robot or a car-like mo-
bile robot (with only an inactive rear steering δ
R
= 0).
The state vector associated to this framework may be
defined as follows:
X =
s
y
˜
θ
. (1)
2.2 Motion Equations
Based on the notations introduced previously and ac-
cording to (Samson et al., 2016), one can obtain the
derivative of the state vector X with respect to time,
which constitutes the evolution model for the path
tracking problem.
˙
X =
˙s =
v cos (
˜
θ + δ
R
)
1 − y c(s)
˙y = v sin(
˜
θ + δ
R
)
˙
˜
θ = u
θ
−
c(s)v cos(
˜
θ + δ
R
)
1 − y c(s)
. (2)
The variable u
θ
denotes the yaw rate of the robot,
which is directly a control variable for a skid steering
robot. For a four-wheel-steering robot, this variable
depends on the values of the steering angles, which
are the actual control variables. The relation between
u
θ
and these steering angles can be defined by the fol-
lowing relationship:
u
θ
= v cos(δ
R
)
tan(δ
F
) − tan(δ
R
)
L
, (3)
with L denoting the robot wheelbase. For a car-like
mobile robot, the model (2)-(3) still stands by impos-
ing a null rear steering angle (δ
R
= 0).
A Generic Control Framework for Mobile Robots Edge Following
105

In this paper, another objective is to follow a struc-
ture relying on the travelled distance of the robot (that
is to say independently from the robot’s speed). As
a result, the model (2) can be rewritten according to
derivatives w.r.t. the curvilinear abscissa s instead of
w.r.t. time. Let us define by X
0
=
dX
ds
, the derivatives
of the variable X w.r.t. s. From (2) it can be expressed
as:
X
0
=
s
0
= 1
y
0
= (1 − y c(s))tan(
˜
θ + δ
R
)
˜
θ
0
= u
θ
1 − y c(s)
v cos(
˜
θ + δ
R
)
− c(s)
. (4)
The expression (4) exists for the last equation (yaw
motion) if the longitudinal velocity v is not null. This
assumption is not a limitation in the following since
the synthesis of the control avoids this singularity.
3 PROPOSED CONTROL
ARCHITECTURE
The control strategy proposed in this paper is based
on a backstepping approach, which is summarized in
Fig. 2. Using this principle, this control scheme can
be adapted to several kinds of mobile robots using the
same paradigm. Thanks to a detection algorithm, a
reference trajectory is obtained and the state vector
X may be known. In particular, the lateral deviation
is measured and can be compared to the desired one
y
d
. The resulting error between these two values is
then used to compute a desired orientation, allowing
the robot to reach the desired lateral deviation under a
desired distance. Thus, this orientation is used as a set
point to compute a control law for the angular speed.
For a skid-steering robot, this is directly the control
imposed to the robot. For a four-wheel-steering robot,
this permits to deduce the front steering angle.
Figure 2: Synopsis of the proposed control architecture.
The desired orientation also permits to regulate
the speed of the robot and the rear steering angle for
a 4 wheel driven (4WD) robot:
• For a skid-steered robot, since the robot can turn
on itself, the velocity is controlled independently
from the yaw rate, in order to improve the tracking
accuracy and avoid collision.
• For a four-wheel-steering robot, the yaw rate can
not be controlled regardless of the longitudinal ve-
locity. Nevertheless, the rear steering angle can be
actuated to improve the convergence of the robot
or to control the actual orientation of the robot
w.r.t. to the structure to be followed, impacting
the convergence of the lateral error.
These different steps are detailed hereafter.
3.1 Computation of the Target Value of
the Angular Deviation
From a control point of view, the objective of the
structure following is to ensure the convergence of the
lateral deviation y to some desired set point y
d
, sup-
posed to be constant ˙y
d
= 0. Let us consider the error
e
y
= y − y
d
, to be regulated to zero after a settling dis-
tance. Using the second equation of the model (4),
one can write the derivative of this error with respect
to the curvilinear abscissa:
e
0
y
= αtan(
˜
θ
2
)
, (5)
with α = (1 − y c(s)) and
˜
θ
2
=
˜
θ + δ
R
. Let us con-
sider tan
˜
θ
2
as an intermediate control variable. One
can note that if we impose for this variable the expres-
sion (6)
tan
˜
θ
d
=
k
y
e
y
α
, (6)
the dynamic of the error (5) becomes:
e
0
y
= k
y
e
y
, (7)
where k
y
is a negative scalar that specifies the settling
distance for the convergence of the lateral deviation
of the robot to the desired lateral deviation y
d
.
The virtual control value (6) of
˜
θ
d
then constitutes
a set point to be reached by
˜
θ
2
(reduced to the actual
orientation
˜
θ in the case of skid-steering or car-like
robots). For that purpose, let us consider the error
defined as:
e
˜
θ
= tan
˜
θ
2
− tan
˜
θ
d
, (8)
representative of the orientation error of the robot
with respect to the desired orientation. The design
of control laws ensuring the convergence of this error
depends on the considered robot and is addressed in
the two next sections.
3.2 Control Law Design for
Skid-steering Robots
Since a skid-steering robot can turn on itself, the ori-
entation of the robot may be regulated without taking
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
106

the longitudinal speed into account. As a result, one
can consider the time derivative of the error (8) de-
rived from the model (2), with δ
R
= 0:
˙e
˜
θ
=
1
cos
2
˜
θ
u
θ
−
c(s)v cos
˜
θ
α
. (9)
This expression is obtained by considering that the
time derivative of the desired orientation may be ne-
glected with respect to the reactivity of the angular
speed regulation (i.e.
˙
˜
θ
d
≈ 0).
The convergence of the error e
˜
θ
to zero may be ob-
tained by considering for the controlled angular speed
of the robot, the control law (10) such that:
u
θ
= k
˜
θ
e
˜
θ
cos
2
˜
θ +
c(s)v cos
˜
θ
α
. (10)
This expression indeed imposes the condition (11) for
the derivative of the angular error, where k
˜
θ
is a nega-
tive scalar that specifies the settling time of error dy-
namics.
˙e
˜
θ
= k
˜
θ
e
˜
θ
. (11)
In this control, the assumption
˙
˜
θ
d
= 0, may be en-
sured by choosing |k
˜
θ
| |k
y
˙s| ensuring that the ori-
entation of the robot reaches the desired orientation
fast enough.
The global stability of this two-steps backstepping
control law may indeed be checked by considering the
Lyapunov function candidate:
V =
1
2
k
˜
θ
k
y
α
2
˙s
e
2
y
+
1
2
tan
2
˜
θ
. (12)
When considering that curvilinear velocity is strictly
positive, and slow varying (as well as α),It’s time
derivative can be expressed as:
˙
V =
k
˜
θ
k
y
α
2
˙s
˙e
y
e
y
+
˙
˜
θ
cos
2
˜
θ
tan
˜
θ
. (13)
Considering that ˙e
y
= e
0
y
˙s, and expressions (5) for e
0
y
and (2) for
˙
˜
θ, this derivative becomes.
˙
V =
k
˜
θ
k
y
α
tan
˜
θe
y
+
u
θ
−
c(s)v cos
˜
θ
α
cos
2
˜
θ
tan
˜
θ
. (14)
Finally by introducing the control law (10) in (14)
leads to the following expression for the derivative of
the function V :
˙
V = k
˜
θ
tan
2
˜
θ
. (15)
which is negative and null if and only if
˜
θ = 0.
Based on the fact that the function V defined
by (12) is Lyapunov, one can deduce that the robot
controlled using (10) is exponentially stable and en-
sures the convergence of e
y
to zero (i.e, the robot con-
verge to its desired set point). The definition of the
function V exists providing that ˙s > 0 (i.e. the robot
goes ahead along the trajectory). When the robot
stops, it can of course not converge to the desired set
points. Nevertheless, the control law (10) can still be
applied and the robot can turn on itself to reach the
condition (6), and be oriented to reach the trajectory
after a desired distance.
3.3 Control Law Design for the Front
Steering Axle of Car-like or 4WD
Robots
Since these two kinds of robots cannot turn when their
longitudinal speed is null, the derivative of e
˜
θ
is de-
rived this time from model (4) expressed with respect
to the curvilinear abscissa. Relying on expression (3)
and model (4), one can derive:
e
0
˜
θ
= cos(δ
R
)α
tan(δ
F
) − tan(δ
R
)
L cos
3
(
˜
θ
2
)
−
c(s)
cos
2
(
˜
θ
2
)
.
(16)
Once more, this expression is obtained by considering
that
˜
θ
d
is slow-varying w.r.t. the achieved distance
(
˜
θ
0
d
≈ 0) compared to the yaw dynamics imposed to
the robot. The convergence of this error to zero may
then be imposed considering the control law (17) for
the front steering angle:
δ
F
= arctan
tan(δ
R
) +
L cos
3
(
˜
θ
2
)
α cosδ
R
k
˜
θ
e
˜
θ
+
c(s)
cos
2
(
˜
θ
2
)
.
(17)
Since control law (17) indeed leads to the follow-
ing expression for the error dynamics:
e
0
˜
θ
= k
˜
θ
e
˜
θ
, (18)
where k
˜
θ
is a negative scalar that specifies the set-
tling distance of the convergence of e
˜
θ
to zero. In
order for this settling distance to be shorter than the
settling distance imposed on lateral error e
y
, the con-
dition —k
˜
θ
| |k
y
| has to be satisfied
The global stability of this two-steps backsteeping
control can be established by straightforwardly deriv-
ing twice e
y
w.r.t. the curvilinear distance and then
injecting control law (17). One can indeed obtain:
e
00
y
= k
˜
θ
e
0
y
− k
˜
θ
k
y
e
y
. (19)
This condition ensures the convergence of e
y
to zero
as soon as k
˜
θ
and k
y
are negative.
If the robot is a car-like robot, then the expres-
sion (17) has to be directly applied with δ
R
= 0. For
a four-wheel-steering robot, this control law may be
computed providing that δ
R
is known, which is nor-
mally ensured, since this variable is also controlled.
An expression for this last control variable is detailed
in the following section.
A Generic Control Framework for Mobile Robots Edge Following
107
3.4 Control Law Design for the Rear
Steering Axle of 4WD Robots
In the previous section, an expression for the front
steering angle has been defined in order to impose
that
˜
θ
2
converges to some desired
˜
θ
d
. Nevertheless,
the actual orientation of the robot stays uncontrolled
and clearly relies on the rear steering angle. In steady
state phases, since e
˜
θ
converges to zero, one indeed
has:
˜
θ →
˜
θ
d
− δ
R
. (20)
To go further, one can then control the rear steering
angle to regulate the actual robot orientation to some
desired orientation
˜
θ
r
. For that purpose, let us de-
fine the error e
r
= tan
˜
θ − tan
˜
θ
r
. By properly tuning
the gain of the forthcoming control law, the derivative
w.r.t. s of the rear steering angle δ
R
can be neglected.
The derivative w.r.t. s of the error e
r
can then be writ-
ten as:
e
0
r
= e
0
˜
θ
e
0
r
= k
˜
θ
(tan(
˜
θ + δ
R
) − tan
˜
θ
d
)
. (21)
In view of this expression, the control law (22) can be
defined for the rear steering angle.
δ
R
= arctan
k
r
e
r
k
˜
θ
+ tan
˜
θ
d
−
˜
θ . (22)
This control law indeed provides the error dynamics
defined by the following differential equation:
e
0
r
= k
r
e
r
. (23)
This ensures, providing that k
r
is a negative scalar,
that the angular deviation
˜
θ converges to the desired
one
˜
θ
r
. This latter desired orientation may be defined
at the user convenience. For instance one can set
˜
θ
r
=
0, to ensure that the robot is parallel to the structure, or
˜
θ
r
=
˜
θ
d
to increase the manoeuvrability. In practice,
it would be best to define
˜
θ
r
as a function such that:
˜
θ
r
=
0 if |
˜
θ
d
| <
˜
θ
th
,
˜
θ
d
if |
˜
θ
d
| >
˜
θ
th
,
(24)
where
˜
θ
th
is a positive angle corresponding to the
threshold where the robot behaviour changes (i.e. par-
allel to the structure or manoeuvrability increase).
With this choice, if the robot is far from the desired
distance, the rear steering angle helps the robot to
converge to the set point, and if the robot is close to
the desired position, the rear steering angle ensures
that the robot is parallel to the structure. This is im-
portant when considering agricultural tasks, such as
spraying, since the on-boarded implement must have
a defined orientation. A commutation function may
be used instead of the switch proposed by (24). A
threshold of 15
◦
is settled in this paper.
4 VELOCITY CONTROL AND
COLLISION AVOIDANCE
In order to avoid collisions with the structure, a limi-
tation of the desired orientation
˜
θ
d
is introduced, de-
pending on the robot size (track and wheelbase). It is
here possible since the first step of the proposed back-
stepping control design consists precisely in defin-
ing a desired orientation. Finally, since skid-steering
robots are able to turn on themselves, a dedicated
speed regulation law is proposed in order to enable a
structure following including very small radii of cur-
vature.
4.1 Limitation of the Robot Orientation
In Fig. 3, one can observe that when regulating a de-
sired lateral distance, the front of the robot may touch
the structure when this latter proposes important cur-
vatures.
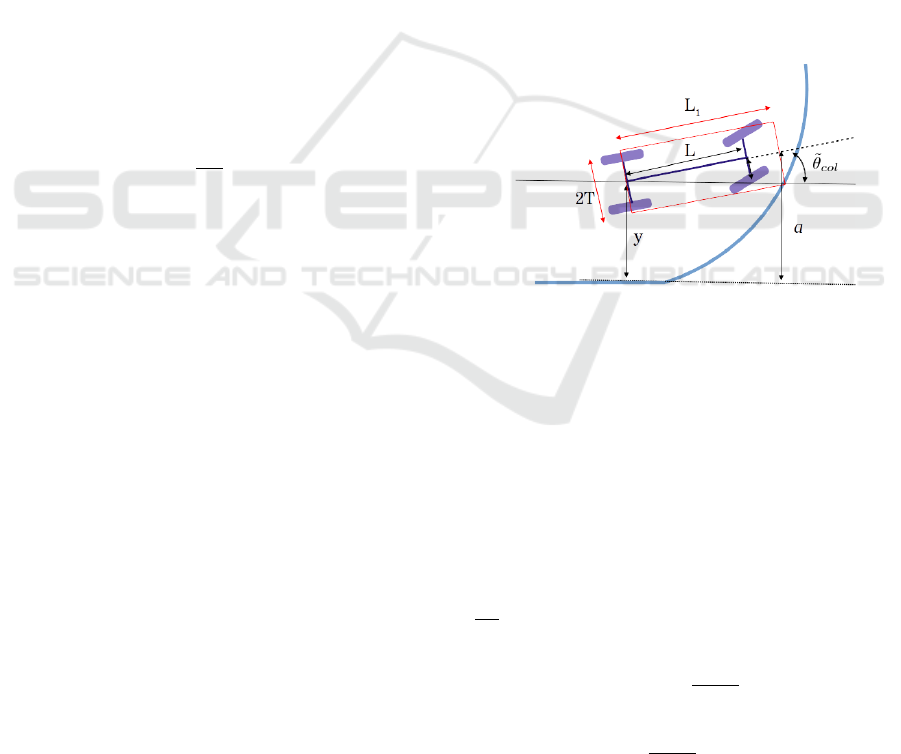
Figure 3: Case of collision while the robot is well regulated.
In such a configuration, the robot must overstep
the nominal regulation laws and turn in order to avoid
collisions. It is possible to compute the maximal ad-
missible orientation of the robot to avoid the collision.
This angle, denoted
˜
θ
col
, may be geometrically de-
fined by:
y = a + T + L
1
sin
˜
θ
col
, (25)
with T the half-track of the robot and a the distance
between the tangent at the trajectory and the impact
point. If we consider that the trajectory is locally cir-
cular (such as suggested in Fig. 3), with a radius of
1
c(s)
, this distance a may be approximated by the fol-
lowing expression:
a =
1−cosγ
c(s)
, (26)
with γ = arctan(L
1
c(s)). The expression (25) exists
under the condition |
y−V −a
L
1
| < 1, which means that
the front of the robot stays on the good side of the
structure, which is assumed to be the case in practice.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
108

Figure 4: Case of collision on the right and the left.
Since the structure to be followed can be located
on the right or on the left of the robot,
˜
θ
col
has two
possible values denoted
˜
θ
col
right
and
˜
θ
col
le f t
, depend-
ing on the side where the structure is, as depicted in
Fig. 4. As soon as these two limits are known, an ad-
vantage of the proposed backstepping approach lies
in the fact that the desired orientation of the robot
˜
θ
d
,
computed by the control law (6) can be bounded. In
the following, the limits are computed in real time and
the targeted orientation is defined such as:
˜
θ =
ξ if
˜
θ
col
right
< ξ <
˜
θ
col
le f t
,
˜
θ
col
le f t
if ξ >
˜
θ
col
le f t
,
˜
θ
col
right
if ξ <
˜
θ
col
right
,
(27)
with ξ = arctan
k
y
e
y
α
− δ
R
, such as defined by (6).
4.2 Limitation of the Robot Speed
In order to ensure an accurate edge tracking, it is rel-
evant to take the actuator settling time into account.
Indeed, the major consequences of this parameter are
overshoots on the tracking error. To limit this phe-
nomenon, it has been chosen to link the linear speed
of the robot with its angular deviation with respect to
the edge (i.e. v = f (
˜
θ −
˜
θ
d
) = f (e
˜
θ
)). A profile, such
as the one illustrated in Fig. 5 can be considered. This
permits to adjust the linear speed of the robot when a
tricky and narrow edge following appears.
Figure 5: Dependency between the linear speed and the
robot angular deviation.
Indeed, this profile is defined thanks to two pa-
rameters: the maximum linear speed of the robot v
max
and a threshold in the orientation error e
˜
θ
chosen in
advance. As long as the absolute value of the error is
lower than a threshold, the linear speed of the robot is
positive. It decreases when the orientation error e
˜
θ
ap-
proaches the threshold angle and is null beyond. This
is applied on a skid-steering robot, since it can turn on
itself, and then resume its motion to ensure a relevant
structure following.
5 EXPERIMENTAL RESULTS
5.1 Experimental Testbed
The proposed control framework has been tested on
two robots in two different conditions, depicted in
Fig. 6:
• a skid-steering mobile robot, moving in indoor
conditions, and following several kinds of struc-
ture (box, wall, shelves), such as depicted in
Fig. 6(a). It is a 25kg electric robot with a wheel-
base of 0.6m. The Lidar is setlled at 0.8m from
the rear wheel;
• a four-wheel-steering mobile robot moving in off-
road conditions, following a row of trees (see
Fig. 6(b)). This is a 520kg robot with a 1.2m-
wheelbase. The Lidar is situated at 1.8m from the
middle of the rear axle.
Both of the robot are equipped with a Sick-LMS laser.
The structures to be followed, quite different, are de-
picted by red lines in Fig. 6, reflecting some harsh
curvature in indoor conditions and an almost straight
line structure in outdoor conditions. The running di-
rection is depicted by the pink arrow.
Figure 6: Robots during the experiments: (a) indoor skid-
steering mobile robot (b) outdoor four-wheel-steering mo-
bile robot.
The structures are detected relying on the algo-
rithm described in Figure 7. It permits to obtain a
relevant and smooth trajectory in both indoor and out-
door environments.
A Generic Control Framework for Mobile Robots Edge Following
109

Figure 7: Algorithm to estimate surrounding structures.
5.2 Skid-steering Robot in Indoor
Conditions
The first experiment proposed in this paper consists
in an indoor structure following by the skid-steering
mobile robot shown in Fig. 6(a). During this test, the
robot follows a box on the right and then a box on the
left (from A to B), it then follows a large door (from B
to C), and shelf legs arranged in circle (from C to D).
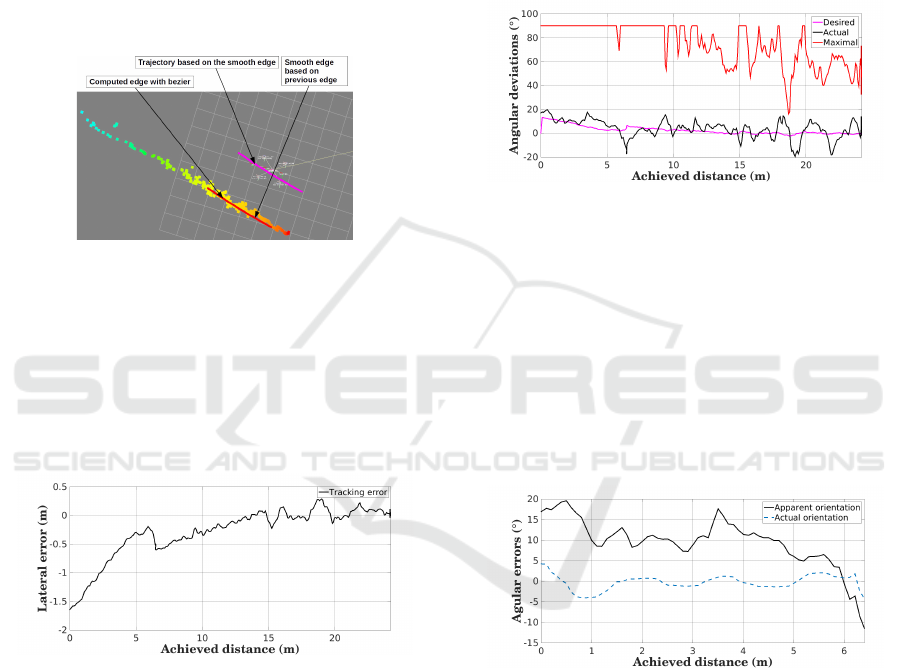
Fig. 8 shows a snapshot of the structure detection and
the trajectory generated when the robot is following
the structure from C to D.
Figure 8: Trajectory generation during the structure follow-
ing in indoor conditions between C and D.
One can see in Fig. 8 the laser impact points on the
shelf legs in green, the points of interest generated in
white and the computed trajectory in red, using a sec-
ond order polynomial curve fitting. The objective is
to follow the various structures with a desired lateral
deviation y
d
of 1m. The results related to the track-
ing error e
y
during this first experiment are depicted
in Fig. 9. In this figure, one can see that when the
trajectory is achievable, the error converges and stays
around 0, with an accuracy of few centimeters.
This is especially the case when the robot is fol-
Figure 9: Result of the tracking error during the indoor ex-
periment.
lowing the part between C and D, since the curvature
stays quite low. In contrast, one can see important
deviations:
• at curvilinear abscissa 1m, when the robot
switches from the box on the right to the one on
the left;
• around points B and C, when the robot has to fol-
low high curvatures.
At these points, a discontinuity in the edge occurs. As
a result, these errors are linked to the modification of
the shape to be followed and can then be viewed as an
initial error, canceled after the robot has moved.
Moreover, when the robot faces high curvatures, there
is a risk of collisions and the desired orientation
˜
θ
d
is
bounded by
˜
θ
col
right
, as it is shown in Fig. 10. In this
figure, the desired orientation
˜
θ
d
is reported in ma-
genta and compared with the actual one
˜
θ in blue. The
minimal admissible orientation
˜
θ
col
right
is reported in
red (maximal in terms of absolute value). One can
then see that at each large deviation (just after points
B and C), when the robot has to achieve an almost
90
◦
turn, the minimal value bounds the desired value
to avoid collisions. As a result, the tracking error is
not correctly regulated since the minimal value is im-
posed instead of the one required to reach the desired
lateral deviation y
d
. The same phenomenon can be
observed around curvilinear abscissa 9m. Elsewhere,
the minimal acceptable value stays far from the de-
sired one and may reach 90
◦
, which is the default
value.
Achieved distance (m)
0 2 4 6 8 10 12
Angular error (°)
-100
-50
0
50
Minimal
Actual
Desired
A
B
C
D
Figure 10: Desired, actual, and minimal orientations during
the indoor experiment.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
110
5.3 4WS Robot in Outdoor Conditions
The second experiment proposed in this paper con-
sists in an outdoor structure following by a four-
wheel-steering robot. Here, the objective is to follow
a row of trees such as depicted in Fig. 6(b), with a
desired distance of 1.5m and the robot parallel to this
structure (i.e.
˜
θ
r
= 0). In these conditions, the struc-
ture is almost straight. As it can be seen in Fig. 11,
the trajectory generated (in red) is indeed nearly con-
sidered as a straight line, even if the impact points of
the laser (in yellow) are quite noisy.
Figure 11: Trajectory generation during the structure fol-
lowing in outdoor conditions.
Thanks to the generation of the trajectory, the
robot is able to follow accurately the row of trees,
as illustrated by the tracking error shown in Fig. 12.
One can see that after the initialization phase, the er-
ror converges to zero and remains then close to this
value. One can also notice that the obtained accuraccy
is in the order of few centimetres.
Figure 12: Result of the tracking error during the outdoor
experiment.
This convergence is obtained thanks to the de-
sired orientation control proposed in this paper. The
desired orientation
˜
θ
d
is illustrated in Fig.13 in ma-
genta. The maximal admissible angle (the robot fol-
lows on the left), depicted in red in this figure, stays
far from the desired orientation, and does not disturb
in this case the accuracy of the tracking. One can
nevertheless see that this maximal orientation logi-
cally decreases, as soon as the robot comes closer
and closer from the actual structure. Since the de-
sired distance has been set to 1.5m (y
d
=1.5m) and
the half-track of the robot is equal to 0.6m, the robot
rear left wheel could collide the trees if the lateral er-
ror reaches 0.9m. This can be illustrated at curvilinear
18m, where the maximal admissible angle is close to
the actual one, as depicted in Fig. 13.
The desired orientation is compared to the orien-
tation
˜
θ
2
=
˜
θ + δ
R
which is the variable actually con-
trolled for a 4WS robot (as detailed in section 3.3)
and illustrated in black. Despite some disturbances,
one can see a good correlation that allows to obtain
the satisfactory lateral position regulation illustrated
in Fig. 12.
Figure 13: Desired, actual, and maximal orientations dur-
ing the outdoor experiment.
It can also be verified that the rear steering law
allows to keep the robot parallel to the structure, as
desired (since
˜
θ
r
= 0). This can be particularly em-
phasized when focusing on the initialization phase of
the tracking (before the settling distance of 6m has
been reached). Fig. 14 compares the orientation
˜
θ
2
,
in black, and the actual one
˜
θ in blue, from 0m to 6m.
Since the desired orientation
˜
θ
d
stays below 15
◦
, the
desired actual angle
˜
θ
r
is null, as figured out by the
relationship (24).
Figure 14: Comparison between
˜
θ
2
and the actual orienta-
tion
˜
θ.
Thanks to control laws (22), the actual orientation
˜
θ, whose initial value is 5
◦
converges and stays close
to zero, while the rear steering angle permits to con-
verge to a null tracking error. This point is particularly
important when considering agricultural tasks.
6 CONCLUSION
In this paper, a generic control algorithm for track-
ing accurately a structure at a desired distance is pro-
posed, based on an edge detection by a Lidar. It per-
A Generic Control Framework for Mobile Robots Edge Following
111

mits to address in a common framework, several kinds
of mobile robots, thanks to a backstepping approach.
A desired orientation is first computed, allowing the
robot to converge to the desired distance from the
structure to be followed, whatever its configuration
(skid-steering, car-like, or four-wheel-steering). This
is achieved using the derivative with respect to curvi-
linear distance, in order to have a behaviour which
is independent from the velocity. Beyond the con-
vergence of the lateral error, this first step also per-
mits to detect and avoid collisions, by considering
the minimal and maximal admissible orientation, in-
side the motion control framework. Moreover, this
desired orientation is also used to compute a speed
limitation for skid-steering mobile robots, allowing
to achieve harsh manoeuvres. The second step con-
sists in the regulation of the orientation of the robot
to the desired one computed in the first step. For
skid-steering robots, this is achieved relying on a
model with derivatives w.r.t. time, allowing them
to rotate even with a null longitudinal speed in or-
der to enhance the manoeuvrability. For four-wheel-
steering mobile robots (and consequently car-like mo-
bile robots), a strategy based on the curvilinear ab-
scissa is proposed, adding two steps in the approach.
The front steering angle is first controlled to impose
that the orientation
˜
θ
2
(robot orientation increased by
the rear steering angle) converges to the desired one
and next the rear steering angle regulates the actual
robot orientation to increase the manoeuvrability or to
ensure the parallelism of the robot with respect to the
structure to be followed, depending on the situation.
Such an approach permits to regulate independently
the position and the orientation of the robot.
The effectiveness of the proposed algorithm has
been investigated through full scale experiments,
showing its robustness and efficiency in various con-
ditions, with different kinds of structures to be fol-
lowed (indoor furnitures and vegetations) and with
several kinds of robots. In particular, this algo-
rithm has been successfully tested on a 25-kg skid-
steering robot and on a 520-kg four-wheel-steering
robot, showing the generality of the proposed con-
trol law(s). This opens the way to achieve fully au-
tonomous agricultural tasks, especially in orchard or
vineyard, for spraying application. A new robot, able
to carry out an automated sprayer is indeed under de-
velopment to test such an approach in fully working
conditions.
ACKNOWLEDGMENT
This work has been sponsored by the French Na-
tional Research Agency under the grant number
ANR-14-CE27-0004 attributed to Adap2E project
(adap2e.irstea.fr). It has also been sponsored by
the French government research program ”Investisse-
ments d’Avenir” through the IDEX-ISITE initiative
16-IDEX-0001 (CAP 20-25), the IMobS3 Labora-
tory of Excellence (ANR-10-LABX-16-01) and the
RobotEx Equipment of Excellence (ANR-10-EQPX-
44). This research was also financed by the European
Union through the Regional Competitiveness and
Employment program -2014-2020- (ERDF – AURA
region) and by the AURA region.
REFERENCES
Astrand, B. and Baerveldt, A.-J. (2005). A vision based
row-following system for agricultural field machinery.
Mechatronics, 15(2):251 – 269.
Bayar, G., Bergerman, M., Koku, A. B., and Konukseven,
E. I. (2015). Localization and control of an au-
tonomous orchard vehicle. Computers and Electron-
ics in Agriculture, 115:118 – 128.
Bergerman, M., Billingsley, J., Reid, J., and Van Henten,
E. (2016). Robotics in Agriculture and Forestry. In
Springer Handbook of Robotics, pages 1463–1492.
Springer International Publishing.
Blackmore, S. (2016). Towards robotic agriculture. In SPIE
Commercial+ Scientific Sensing and Imaging, pages
986603–986603. International Society for Optics and
Photonics.
Cariou, C., Lenain, R., Thuilot, B., and Martinet, P. (2010).
Autonomous maneuver of a farm vehicle with a trailed
implement: motion planner and lateral-longitudinal
controllers. In IEEE International Conference on,
Robotics and Automation (ICRA), pages 3819–3824.
Cherubini, A. and Chaumette, F. (2013). Visual naviga-
tion of a mobile robot with laser-based collision avoid-
ance. The International Journal of Robotics Research,
32(2):189–205.
D’Andr
´
ea-Novel, B., Campion, G., and Bastin, G. (1995).
Control of nonholonomic wheeled mobile robots by
state feedback linearization. The International journal
of robotics research, 14(6):543–559.
Deremetz, M., Lenain, R., Couvent, A., Cariou, C., and
Thuilot, B. (2017). Path tracking of a four-wheel steer-
ing mobile robot: A robust off-road parallel steering
strategy. In European Conference on Mobile Robots
(ECMR), pages 1–7.
Lenain, R., Deremetz, M., Braconnier, J.-B., Thuilot, B.,
and Rousseau, V. (2017). Robust sideslip angles ob-
server for accurate off-road path tracking control. Ad-
vanced Robotics, 31(9):453–467.
Marmoiton, F. and Slade, M. (2016). Toward Smart Au-
tonomous Cars. In Intelligent Transportation Systems:
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
112

From Good Practices to Standards, pages 84–109.
CRC Press.
Samson, C., Morin, P., and Lenain, R. (2016). Modeling
and control of wheeled mobile robots. In Springer
Handbook of Robotics, pages 1235–1266. Springer.
Tourrette, T., Lenain, R., Rouveure, R., and Solatges, T.
(2017). Tracking footprints for agricultural applica-
tions: a low cost lidar approach. In IEEE/RSJ Interna-
tional Conference on Intelligent Robots and Systems:
Agri-Food Robotics Workshop.
A Generic Control Framework for Mobile Robots Edge Following
113
