
Improved Dempster-Shafer Sensor Fusion using Distance Function and
Evidence Weighted Penalty: Application in Object Detection
Nazmuzzaman Khan and Sohel Anwar
Mechanical and Energy Engineering Department, Indiana University-Purdue University Indianapolis, Indiana, U.S.A.
Keywords: Sensor Data Fusion, Object Detection, Dempster-Shafer Theory, Conflicting Evidence.
Abstract:
Dempster-Shafer (DS) combination method can deal with the uncertainty and inconsistency of multi-sensor
data fusion and widely used in data fusion, fault detection, pattern recognition, and supplier selection. The
original DS theory has limitations such as its inability to handle conflicting data properly which can result into
inaccuracy in the output of a multi-sensor data fusion process. To eliminate such limitations of the original
DS theory, a novel method is proposed in this paper that uses distance function to measure the credibility of
each sensor and uses weighted penalty of faulty sensor evidence to create maximum evidence for the correct
detection. A detailed example for object detection with conflicting sensor input is presented which showcases
all the steps of the proposed method. A numerical simulation is used to show that the proposed method
effectively eliminates the limitations of original DS combination rule and offers an improvement over the
current state-of-the-art models.
1 INTRODUCTION
In 1960’s Arthur P. Dempster introduced a new
concept – ‘upper and lower probabilities’ (Demp-
ster, 2008) which included uncertainty in probability.
Later in 1970’s Shafer renamed upper and lower prob-
abilities to degree of belief and renamed the theory
“Mathematical theory of evidence” (Shafer, 1976).
Which is currently known as Dempster-Shafer (DS)
theory of evidence. Fundamental to DS theory is
the representation of uncertain knowledge in the form
of Basic Probability Assignment (BPA). The direct
consequence is that, while the actual probability of
an individual state may be unknown, it’s minimum
and maximum values are specified. The belief in the
‘unknown’ state reflects the weakness of the knowl-
edge. It is considered as generalizations of Bayes
theory as probabilities/mass are assigned to multiple
possible events as opposed to mutually exclusive sin-
gletons in Bayes. Within the framework of DS the-
ory information obtained from multiple sources are
represented by degree of belief/mass function. Then
they are fused using Dempster’s rule of combination.
Hence, DS theory is a multi-source data fusion tech-
nique to capture more reliable single output combin-
ing several input source (Hafeez, 2011). DS informa-
tion fusion theory has been applied in pattern recog-
nition (Denoeux, 1995; Ma et al., 2016; Denoeux,
2000), decision making and classification (Hafeez,
2011; Deng and Jiang, 2018; Luo, 1993; Basti
`
ere,
1998; Beynon et al., 2000), optimization (Chen and
Rao, 1998; Kang et al., 2018), risk and fault detection
(Jiang et al., 2016a; Xiao, 2017), quality measure-
ment/supplier selection (Sadiq and Rodriguez, 2005;
Liu et al., 2018).
A multi-sensor system has two distinct advantages
over a single sensor system when used with proper
fusion algorithm:
1. A single sensor may provide faulty, erroneous re-
sults and there is no way to modify that other than
changing the sensor. A multi-sensor system pro-
vides results with diverse accuracy. With the help
of proper fusion algorithm faulty sensor can be
easily detected.
2. Multi-sensor system receives information with
wide variety and characteristics. Thus, it helps to
create a more robust system with less interference.
But to use DS sensor fusion algorithm for robust
application, we have to overcome the fuse paradox
presented by Zadeh (Zadeh, 1986). Existing modified
methods are divided mainly into three categories:
1. Method 1: Modification of combination equations
in DS theory.
664
Khan, N. and Anwar, S.
Improved Dempster-Shafer Sensor Fusion using Distance Function and Evidence Weighted Penalty: Application in Object Detection.
DOI: 10.5220/0007917106640671
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 664-671
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2. Method 2: Revision of original evidence before
combination.
3. Method 3: Hybrid technique combining both
modification of DS rule and original evidence.
Method 1: Smet’s rule (Smets, 2000) is essentially
the Dempster rule applied in Smets’ Transferable Be-
lief Model. Smet believed that conflict is caused by
incompleteness of frame of discernment. So Smet
moved mass of conflict directly to empty set as an
unknown proposition. In Yager’s rule (Yager, 1987),
the mass associated with conflict is directly given to
universal set, which enlarges the degree of ignorance.
Yager’s rule provide the same results when conflict is
zero. Although these two methods solve the conflict
situation theoretically, the uncertainty of the system
still exists. Bicheng et al. (Li et al., 2001) mod-
ified Yager’s rule and conflicting probability of the
evidences are distributed to every proposition based
on average support. Inagaki (Inagaki, 1991) defined
a continuous parametrized class of combination op-
erations which subsumes both Dempster’s rule and
Yager’s rule. Zhang (Zhang, 1994) pointed out that
DS rule fails to take into account the focal element
intersection. He presented the ‘two-frame’ represen-
tation of DS theory where he measures focal element
intersections based on cardinality. But all these meth-
ods sometimes violate the theoretical properties of DS
combination rule like commutativity and associativ-
ity.
Method 2: Chen et al. (Chen et al., 2013) used tri-
angular functions to set a fuzzy model for each sensor.
Assuming each sensor output is gaussian, BPA was
determined from the sensor outputs using the fuzzy
model. Then the raw BPA was weighted using the
credibility of each BPA before fusing. Sun (Sun et al.,
2013) also used fuzzy membership function to con-
vert sensor value to fuzzy value. Support degree was
calculated using an error distance function. If sensor
output is not gaussian, then fuzzy set methods can’t
be applied. Instead of distance function, an entropy
function (Deng entropy (Deng, 2015)) was used to
calculate the credibility of evidence in (Jiang et al.,
2016a). This was inspired by Murphy’s method (Mur-
phy, 1998), which used an average of BPAs. Mur-
phy’s method had first convergence rate but failed to
consider the relation between focal elements. Jiang
(Jiang et al., 2016b) used an entropy function to mea-
sure the weight of the evidence to modify them be-
fore applying to DS rule. Later Xiao (Xiao, 2018) ap-
plied belief divergence to measure the credibility of
evidence, which increased the fusion results slightly.
Murphy’s method is the simplest to implement and
most of the methods within this type is inspired by
his method. Most of the other methods are over com-
plicated compared to Murphy’s and may not always
be useful for real time application. But they do not
modify the original DS combination rule and the com-
mutative and associative properties remain intact.
Method 3: Through the comparison between two
kinds of conflict resolutions, it is easy to see the un-
derlying logic of two methods. Method 1 cancel the
normalization step in DS theory and redistribute the
conflict with different measure. Method 2 consider
the essential differences propositions of each sensor
in multi-sensor systems and solve the conflict by mod-
ifying the original evidence. If method 1 and 2 is
combined, then the inherent paradoxes of DS rule are
solved. Building on this idea, Lin (Lin et al., 2016)
and Ye Fang (Ye et al., 2017; Ye et al., 2018) pub-
lished several new improvements of original DS com-
bination rule. They improve the fusion results but of-
ten too complicated and over-engineered to apply for
real-time use. These methods also loose commuta-
tive and associative properties of DS rule. Also, the
amount of improvement of fused results may not be
necessary for some specific application.
In this paper, we propose a novel combination
method to solve the fusion of multi-sensor conflicting
information by using credibility transformation which
measures credibility from sensor data and also consid-
ers operator ‘experience’. We firstly revised the orig-
inal evidence of each sensor by multiplying it with
sensor accuracy. Sensor accuracy can be implemented
using operator’s extensive knowledge of the system or
to optimize the correct fused result. Then we revise
the original evidence separately by the introduction of
Euclidean distance function. This distance function
creates credibility for each sensor which redistributes
the conflicting mass. After the redistribution of con-
flicting information, the multi-sensor system obtains
an accurate and effective fusion result.
2 THEORETICAL BACKGROUND
2.1 Frame of Discernment
The frame of discernment contains M mutually exclu-
sive and exhaustive hypotheses:
Θ =
{
θ
1
,θ
2
,.....,θ
M
}
(1)
The representation of uncertainties in the DS theory is
similar to that in conventional probability theory and
involves assigning probabilities to the space Θ. How-
ever, the DS theory has one significant new feature: it
allows the probability to be assigned to subsets of Θ
Improved Dempster-Shafer Sensor Fusion using Distance Function and Evidence Weighted Penalty: Application in Object Detection
665

as well as the individual element θ
i
. Accordingly, we
can derive the power set 2
θ
of DS theory:
2
θ
=
{
φ,
{
θ
1
}
,
{
θ
2
}
,.....,
{
θ
1
,θ
M
}
,Θ
}
(2)
Where φ is empty set. It is clearly seen in (2) that the
power set 2
θ
has 2
M
propositions. Any subset except
singleton of possible values means their union, for ex-
ample,
{
θ
1
,θ
2
,θ
3
}
= θ
1
∪ θ
2
∪ θ3. Complete proba-
bility assignment to power set is called basic proba-
bility assignment (BPA).
2.2 Basic Probability Assignment (BPA)
/ Mass Function
Evidences in DS theory are acquired by multi-sensor
information. Mass function (mass) is a function, m =
2
Θ
→ [0,1] that satisfies (3) and (4):
m(φ) = 0 (3)
∑
[m(θ)∀θ ∈ 2
Θ
] = 1 (4)
Elements of power set having m(θ) > 0 is called
focal elements. This can be explained with the
help of simple example: Let the three objects to
be detected be, Θ = {a, b, c}. Powerset 2
Θ
= 2
3
=
{φ,a,b,c,{a,b},{a,c},{b,c},{a,b,c}}.
Example, from a sensor or by an expert follow-
ing mass values are assigned, m(a) = 0.2, m(b) = 0.3,
m(a,b) = 0.4, m(a,b,c) = 0.1. The above four subsets
are called focal elements.
2.3 Dempster-Shafer Rule of
Combination
The purpose of data fusion is to summarize and sim-
plify information rationally obtained from indepen-
dent and multiple sources. It emphasizes on the agree-
ment between multiple sources and ignores all the
conflicting evidence through normalization. the DS
combination rule of two evidences m
1
and m
2
is de-
fined:
m
1−2
(A) =
∑
B
T
C=A
{m
1
(B).m
1
(C)}
1 − K
(5)
K =
∑
B
T
C=φ
{m
1
(B).m
1
(C)} (6)
when A 6= φ and m(φ) = 0 and K is the degree of
conflict in two sources of evidences.
The denominator (1-K) is a normalization factor,
which helps aggregation by completely ignoring the
conflicting evidence and is calculated by adding up
the products of BPA’s of all sets where intersection
is null. DS combination rule in (5) conforms to both
commutative law and associate law.
3 PROPOSED IMPROVEMENT
TO DS COMBINATION RULE
VIA EVIDENCE-BASED
SENSOR FUSION IN OBJECT
DETECTION
We present the proposed improvement of the DS com-
bination rule using a specific example. Here we want
to detect three different kinds of weed (Ragweed, Pig-
weed and Cocklebur), which are very common in corn
fields. But the improved theory can be applied to
other detection level sensor fusions as well. The sen-
sors used in detecting the weeds are:
3D Lidar: It provides very accurate 3D point cloud
of surrounding. Weeds can be scanned as a 3D point
cloud data. Scanned point cloud data could be used
to train a neural-network to detect the weeds using
real-time scans. But this process is computationally
very expensive as the hardware must process a huge
amount of 3D point cloud data in in real-time.
2D Lidar, Radar, Ultrasonic: A 2D lidar pro-
vides a scan of a plane which can be used to detect
width/height of a specific object. Radar provides dis-
tance of an object as a state vector. Ultrasonic sen-
sors provide distance of an object but with a shorter
range than Radar. All of the above-mentioned sen-
sors provide useful information if the objects we want
to detect have different shape/size and speed. Cars
and trucks have different shape. Cars and pedes-
trian/bicycle have different speeds. These sensors will
provide useful information for autonomous vehicle
application. Weeds on the other hand are mostly of
same size and shape (other than very intricate differ-
ences in leaf shape) and stationary. Thus these sensors
less likely to provide useful information for weed de-
tection.
RGB Camera: Weed images can be used to train a
deep neural-network to detect weeds with a reason-
able accuracy. Different positioning of cameras can
discern certain distinct shapes of weed leaves. These
cameras are inexpensive and their accuracy is measur-
able.
RGB-D Camera: Depth information can provide ad-
ditional features to increase detection accuracy. They
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
666

are reasonably cheap and accuracy is measurable.
How well they work on outside environment depends
on hardware quality. We therefore will focus on the
RGB or RGB-D cameras as the sensor of choice for
this application.
3.1 Improved Dempster-Shafer Rule of
Combination
Problem statement: Let’s assume, we have set up 3
sensors to detect weed from real time video feed. Sen-
sor 1 and 2 are RGB camera and Sensor 3 is RGB-D
camera. We consider the following detection for a
specific frame from continuous video feed:
Table 1: Sensor output of detected weed.
sensors Ragweed Pigweed Cocklebur
sensor 1: m
1
0.7 0.2 0.1
sensor 2: m
2
0.05 0.9 0.05
sensor 3: m
3
0.8 0.1 0.1
If evidences agreed with one another, then we
could have used the original DS rule to combine these
evidences. But here sensor 2 is clearly at fault as it is
disagreeing with sensor 1 and 3 for Ragweed.
Solution: This could have been solved using the
methods in section 1. But method 1 (modification of
combination equations in DS theory) and method 3
(hybrid technique combining both modification of DS
rule and original evidence) both loses the associative
and commutative property of DS combination rule.
We argue that keeping these two properties are more
important than getting a slight improvement in accu-
racy in fused results. These two properties will help to
keep the overall hardware system modular (plug and
play). We would be able to plug in new sensors or re-
move faulty sensors without changing anything major
in software. We propose the following method to im-
prove the original DS rule for conflicting information.
Step 1: Build a multi sensor information matrix.
M =
m
1
(H
1
) m
1
(H
2
) ··· m
1
(H
M
)
m
2
(H
1
) m
2
(H
2
) ··· m
2
(H
M
)
.
.
.
.
.
.
.
.
.
.
.
.
m
N
(H
1
) m
N
(H
2
) · · · m
N
(H
M
)
=
0.7 0.2 0.1
0.05 0.9 0.05
0.8 0.1 0.1
Step 2: Penalize weighted evidence. One of the ad-
vantages of DS rule is to express domain knowledge
as credibility factor. We can penalize the weight of ev-
idence of the faulty sensor to maximize correct fused
result. Evidence should be adjusted according to their
credibility following this formula:
m(A)
ad justed
= m(A) ∗ α
α = evidence weight of each sensor
For the following calculations we assume α = 1
for all three sensors.
Step 3: Measure the relative distance between evi-
dences. Several distance function can be used to mea-
sure the relative distance. They all have their own
advantages and disadvantages regarding runtime and
accuracy (Chen et al., 2017). We have used Euclidean
distance function:
D(m
i
,m
j
) =
s
M
∑
t=1
m
i
(H
t
) − m
j
(H
t
)
2
=
d(m
1
,m
1
) d(m
1
,m
2
) d(m
1
,m
3
)
d(m
2
,m
1
) d(m
2
,m
2
) d(m
2
,m
3
)
d(m
3
,m
1
) d(m
3
,m
2
) d(m
3
,m
3
)
=
0 0.9565 0.1414
0.9565 0 0.7511
0.1414 0.7511 0
d(m
1
,m
2
) =
p
(|0.7–0.05|
2
+ |0.2–0.9|
2
+
|0.1–0.05|
2
) = 0.9565
Because sensor 2 disagrees with sensor 1 and 3,
d(m
1
,m
2
) and d(m
2
,m
3
) is larger than d(m
1
,m
3
).
Step 4: Create similarity matrix.
sim(m
i
,m
j
) = I − D(m
i
,m
j
)
=
1 0.0435 0.8586
0.0435 1 0.2489
0.8586 0.2489 1
Step 5: Create Supplementary matrix or vector.
sup(m
i
,m
j
) =
∑
N
j=1and j6=i
sim(m
i
,m
j
) =
0.9021
0.2924
1.1075
Step 6: Create credibility matrix or vector.
crd(m
i
) =
sup(m
i
)
∑
N
i=1
sup(m
i
)
=
0.3919
0.127
0.4811
Here, sensor 2 has the lowest credibility. Between
sensor 1 and 3, sensor 3 showed higher evidence for
Improved Dempster-Shafer Sensor Fusion using Distance Function and Evidence Weighted Penalty: Application in Object Detection
667
Ragweed (which is true detection). As a result, sensor
3 has higher credibility than sensor 1.
Step 7: Modify the original evidence.
m(A) =
∑
N
i=1
m
i
(A).crd(m
i
)
m{Ragweed} = 0.7 * 0.3919 + 0.05 * 0.127 + 0.8
* 0.4811 = 0.6655
m{Pigweed} = 0.2 * 0.3919 + 0.9 * 0.127 + 0.1 *
0.4811 = 0.2419
m{Cocklebur} = 0.1 * 0.3919 + 0.05 * 0.127 + 0.1
* 0.4811 = 0.0943
After normalizing,
m{Ragweed} = 0.6644
m{Pigweed} = 0.2415
m{Cocklebur} = 0.0941
Table 2: Modified evidence.
sensors Ragweed Pigweed Cocklebur
sensor 1: m
1
0.6644 0.2415 0.0941
sensor 2: m
2
0.6644 0.2415 0.0941
sensor 3: m
3
0.6644 0.2415 0.0941
Figure 1: Increasing the number of sensors increases fused
detection accuracy (m(A)).
Fusing the evidences of 3 sensors (from table 4):
m
123
(Ragweed) = 0.5796/0.6064 = 0.9506
m
123
(Pigweed) = 0.0276/0.6064 = 0.0455
m
123
(Cocklebur) = 0.0016/0.6064 = 0.0026
Clearly the proposed method overcomes the inherent
paradoxes of original DS rule and detected Ragweed
with 95.06 % accuracy after fusing the results. On the
other hand, if we have used the original evidences,
the results would have been:
m
123
(Ragweed)
original
= 0.59
m
123
(Pigweed)
original
= 0.38
m
123
(Cocklebur)
original
= 0.03
Which provides higher confidence on pigweed.
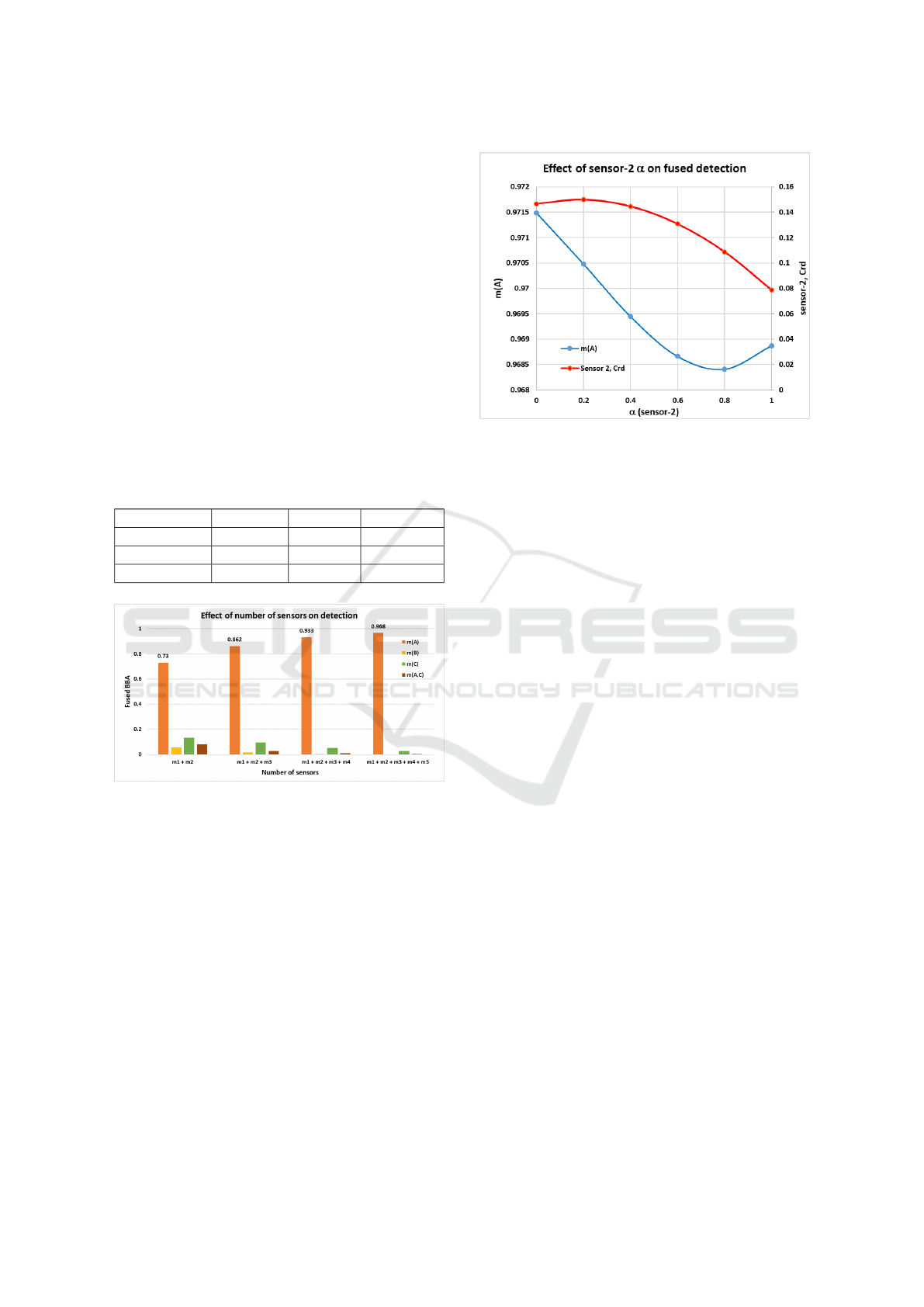
Figure 2: Effect of sensor 2 evidence weight (α) value
on fused detection accuracy (m(A)) and credibility (step 6:
crd(m
i
)).
4 SIMULATION RESULTS AND
ANALYSIS
The following example is used to further analyze and
compare the proposed method. Let us consider a
multi-sensor-based target recognition problem asso-
ciated with the sensor reports that are collected from
five different types of sensors. These sensor reports
which are modeled as the BBAs are given in Table
5 (Xiao, 2019), where the frame of discernment Θ
that consists of three potential objects is given by
Θ = {A, B,C}. Last column of Table 5 also contains
the credibility values of each sensor from step 6 of
proposed method. Sensors are providing conflicting
information. A is the correctly detected object, m(A)
should have the highest value after fusion. Sensor
2 (evidence m
2
) is providing conflicting information
with respect to other 4 sensors. Mass value m
2
(A) is
zero for sensor 2.
Figure 1. shows how evidence of A, m(A) in-
creased with increasing number of sensors. It is inter-
esting to see that fused result of m1 ⊕ m
2
providing
high evidence of A. This shows the underlying mech-
anism of the improved algorithm. Because original
evidences are modified before applying fusion algo-
rithm, conflicting sensor doesn’t affect the final fused
evidence at any stages of fusion. It also shows in-
creasing the number of consistent sensors increases
the possibility of correct detection. Figure 2. shows
how the evidence weight (step 2: α) of the conflict-
ing sensor (sensor 2) affects the overall fused result.
The proposed algorithm calculates the credibility of a
sensor (step 6: Crd) from its evidences, which is pre-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
668

Table 3: Fusion of sensor 1 and 2 using Eq. (5) and (6).
sensors m
1
(Rag) = 0.6644 m
1
(Pig) = 0.2415 m
1
(Cockle) = 0.0941
m
2
(Rag) = 0.6644 m
1−2
(Rag) = 0.4414 m
1−2
(φ) = 0.1605 m
1−2
(φ) = 0.0625
m
2
(Pig) = 0.2415 m
1−2
(φ) = 0.1605 m
1−2
(Pig) = 0.0583 m
1−2
(φ) = 0.0227
m
2
(Cockle) = 0.0941 m
1−2
(φ) = 0.0625 m
1−2
(φ) = 0.0227 m
1−2
(Cockle) = 0.0088
K =
∑
φ = 0.1605 + 0.0625 + 0.1605 + 0.0227 + .0625 + .0227 = 0.4914; 1 – K = 0.5086
Table 4: Fusion of sensor 1, 2 and 3.
sensors m
3
(Rag) = 0.6644 m
3
(Pig) = 0.2415 m
3
(Cockle) = 0.0941
m
1
2(Rag) = 0.8678 m
1−2−3
(Rag) = 0.5765 m
1−2−3
(φ) = 0.2095 m
1−2−3
(φ) = 0.0186
m
1
2(Pig) = 0.1146 m
1−2−3
(φ) = 0.0761 m
1−2−3
(Pig) = 0.0276 m
1−2−3
(φ) = 0.0107
m
1
2(Cockle) = 0.0173 m
1−2−3
(φ) = 0.0115 m
1−2−3
(φ) = 0.0042 m
1−2−3
(Cockle) = 0.0016
K =
∑
φ =0.2095 + 0.0186 + 0.0761 + .0107 + .0115 + .0042 = 0.3936; 1 – K = 0.6064
Table 5: The BBA for a multi-sensor object recognition.
BBA {A} {B} {C} {A,C} Credibility (step 6)
sensor 1: m
1
0.41 0.29 0.30 0 0.195
sensor 2: m
2
0 0.9 0.1 0 0.078
sensor 3: m
3
0.58 0.07 0 0.35 0.239
sensor 4: m
4
0.55 0.1 0 0.35 0.243
sensor 5: m
5
0.6 0.1 0 0.3 0.242
Table 6: Combination results of the evidences in terms of different combination rules.
Methods {A} {B} {C} {A,C}
Dempster (Shafer, 1976) 0 0.142 0.8578 0
Murphy (Murphy, 1998) 0.962 0.021 0.0138 0.0032
Deng (Deng, 2015) 0.982 0.0039 0.0107 0.0034
Zhang (Zhang and Deng, 2017) 0.982 0.0034 0.0115 0.0032
Xiao (Xiao, 2019) 0.9905 0.0002 0.0061 0.0043
Proposed 0.9715 0.0003 0.025 0.0031
sented at the final column of Table 5. If the sensor has
conflicting evidence, the algorithm calculates lowest
credibility of that sensor. But if we penalize the evi-
dences of the conflicting sensor with a weight lower
than 1, credibility of that sensor goes up. Because
conflict of evidence goes down. As a result, as α goes
down, Crd goes up for sensor 2 to a certain limit.
In other words, by penalizing the evidences of the
faulty sensor, we are decreasing the faulty evidence
and increasing the sensor’s credibility. Fused evi-
dence m
12345
(A) has the highest value for α = 0. So,
the algorithm will calculate highest evidence value of
correctly detected object, when we set α = 0 for the
sensor with lowest credibility.
From Table 5, it can be observed that the evi-
dence m
2
conflicts highly with other evidences. The
fusion of the results are obtained by different com-
bination approaches and are presented in Table 6. As
shown in Table 6, Dempster’s combination rule gener-
ates counterintuitive result and recognizes the object
C as the target, even though the other four evidences
support the target A. Whereas the methods proposed
by Murphy, Deng, Zhang, Xiao and the proposed
method present reasonable results and recognize the
target A. The proposed method achieved better re-
sults compared to Dempster-Shafer and Murphy’s
method. Although the proposed method achieved
slightly lower accuracy compared to Xiao, Deng and
Zhang’s method However, the proposed method is
computationally less expensive and requires less steps
when compared with these methods. The proposed
method also successfully eliminates all the limitations
of original DS method indicated by Zadeh.
5 CONCLUSIONS
Since conflicting information may occur in multi-
sensor systems, robust multi-sensor fusion is needed
to achieve reliable and accurate information in such
a system. In this paper, a novel method for multi-
sensor data fusion is proposed by considering both of
the credibility degree between the evidences and pe-
nalizing the evidence of faulty sensor. The proposed
Improved Dempster-Shafer Sensor Fusion using Distance Function and Evidence Weighted Penalty: Application in Object Detection
669

method consists of two main rules. Firstly, an Eu-
clidean distance was proposed to measure the distance
between the bodies of the evidences; then, the credi-
bility degree of the evidences is calculated. Secondly,
a weighted evidence value is given to all the sensors.
By assigning the evidence weight value to a small
number to a sensor deemed less reliable (the sensor
with lowest credibility), highest detection accuracy is
achieved. Modified evidences are fused by applying
the Dempster’s combination rule. A detailed example
for weed detection from an autonomous robot with
conflicting sensor input is presented which showcases
all the steps of the proposed method. A numerical
simulation is used to show that the proposed method
is comparably effective while offering a more compu-
tationally feasible algorithm than other related meth-
ods to handle the conflicting evidence combination
problem under multi-sensor environment
REFERENCES
Basti
`
ere, A. (1998). Methods for multisensor classifica-
tion of airborne targets integrating evidence theory.
Aerospace Science and Technology, 2(6):401–411.
Beynon, M., Curry, B., and Morgan, P. (2000). The
dempster–shafer theory of evidence: an alternative ap-
proach to multicriteria decision modelling. Omega,
28(1):37–50.
Chen, J., Ye, F., and Jiang, T. (2017). Numerical analyses
of modified ds combination methods based on differ-
ent distance functions. In 2017 Progress in Electro-
magnetics Research Symposium-Fall (PIERS-FALL),
pages 2169–2175. IEEE.
Chen, L. and Rao, S. (1998). A modified dempster-shafer
theory for multicriteria optimization. Engineering op-
timization, 30(3-4):177–201.
Chen, S., Deng, Y., and Wu, J. (2013). Fuzzy sensor fusion
based on evidence theory and its application. Applied
Artificial Intelligence, 27(3):235–248.
Dempster, A. P. (2008). Upper and lower probabilities in-
duced by a multivalued mapping. In Classic Works
of the Dempster-Shafer Theory of Belief Functions,
pages 57–72. Springer.
Deng, X. and Jiang, W. (2018). An evidential axiomatic
design approach for decision making using the evalu-
ation of belief structure satisfaction to uncertain target
values. International Journal of Intelligent Systems,
33(1):15–32.
Deng, Y. (2015). Deng entropy: a generalized shannon en-
tropy to measure uncertainty. viXra 1502.0222.
Denoeux, T. (1995). A k-nearest neighbor classification rule
based on dempster-shafer theory. IEEE transactions
on systems, man, and cybernetics, 25(5):804–813.
Denoeux, T. (2000). A neural network classifier based on
dempster-shafer theory. IEEE Transactions on Sys-
tems, Man, and Cybernetics-Part A: Systems and Hu-
mans, 30(2):131–150.
Hafeez, M. (2011). Application of dempster shafer theory
to assess the status of sealed fire in a cole mine.
Inagaki, T. (1991). Interdependence between safety-control
policy and multiple-sensor schemes via dempster-
shafer theory. IEEE Transactions on Reliability,
40(2):182–188.
Jiang, W., Wei, B., Xie, C., and Zhou, D. (2016a).
An evidential sensor fusion method in fault di-
agnosis. Advances in Mechanical Engineering,
8(3):1687814016641820.
Jiang, W., Zhuang, M., Qin, X., and Tang, Y. (2016b). Con-
flicting evidence combination based on uncertainty
measure and distance of evidence. SpringerPlus,
5(1):1217.
Kang, B., Chhipi-Shrestha, G., Deng, Y., Mori, J., Hewage,
K., and Sadiq, R. (2018). Development of a pre-
dictive model for clostridium difficile infection inci-
dence in hospitals using gaussian mixture model and
dempster–shafer theory. Stochastic Environmental Re-
search and Risk Assessment, 32(6):1743–1758.
Li, B., Wang, B., Wei, J., Huang, Y., and Guo, Z. (2001).
Efficient combination rule of evidence theory. In Ob-
ject Detection, Classification, and Tracking Technolo-
gies, volume 4554, pages 237–241. International So-
ciety for Optics and Photonics.
Lin, Y., Wang, C., Ma, C., Dou, Z., and Ma, X. (2016).
A new combination method for multisensor con-
flict information. The Journal of Supercomputing,
72(7):2874–2890.
Liu, T., Deng, Y., and Chan, F. (2018). Evidential supplier
selection based on dematel and game theory. Interna-
tional Journal of Fuzzy Systems, 20(4):1321–1333.
Luo, W. (1993). Imprecise probability and decision in
civil engineering: Dempster-Shafer theory and appli-
cation. PhD thesis, University of British Columbia.
Ma, J., Liu, W., Miller, P., and Zhou, H. (2016). An eviden-
tial fusion approach for gender profiling. Information
Sciences, 333:10–20.
Murphy, R. R. (1998). Dempster-shafer theory for sensor
fusion in autonomous mobile robots. IEEE Transac-
tions on Robotics and Automation, 14(2):197–206.
Sadiq, R. and Rodriguez, M. J. (2005). Interpreting drink-
ing water quality in the distribution system using
dempster–shafer theory of evidence. Chemosphere,
59(2):177–188.
Shafer, G. (1976). A mathematical theory of evidence, vol-
ume 42. Princeton university press.
Smets, P. (2000). Data fusion in the transferable belief
model. In Proceedings of the third international con-
ference on information fusion, volume 1, pages PS21–
PS33. IEEE.
Sun, S., Gao, J., Chen, M., Xu, B., and Ding, Z. (2013).
Fs-ds based multi-sensor data fusion. Journal of Soft-
ware, 8(5):1157–1162.
Xiao, F. (2017). A novel evidence theory and fuzzy pref-
erence approach-based multi-sensor data fusion tech-
nique for fault diagnosis. Sensors, 17(11):2504.
Xiao, F. (2018). An improved method for combining con-
flicting evidences based on the similarity measure
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
670

and belief function entropy. International Journal of
Fuzzy Systems, 20(4):1256–1266.
Xiao, F. (2019). Multi-sensor data fusion based on the be-
lief divergence measure of evidences and the belief en-
tropy. Information Fusion, 46:23–32.
Yager, R. R. (1987). On the dempster-shafer framework
and new combination rules. Information sciences,
41(2):93–137.
Ye, F., Chen, J., and Li, Y. (2017). Improvement of ds evi-
dence theory for multi-sensor conflicting information.
Symmetry, 9(5):69.
Ye, F., Chen, J., and Tian, Y. (2018). A robust ds combina-
tion method based on evidence correction and conflict
redistribution. Journal of Sensors, 2018.
Zadeh, L. A. (1986). A simple view of the dempster-shafer
theory of evidence and its implication for the rule of
combination. AI magazine, 7(2):85–85.
Zhang, J. and Deng, Y. (2017). A method to determine ba-
sic probability assignment in the open world and its
application in data fusion and classification. Applied
Intelligence, 46(4):934–951.
Zhang, L. (1994). Representation, independence, and com-
bination of evidence in the dempster-shafer theory. In
Advances in the Dempster-Shafer theory of evidence,
pages 51–69. John Wiley & Sons, Inc.
Improved Dempster-Shafer Sensor Fusion using Distance Function and Evidence Weighted Penalty: Application in Object Detection
671
