
Comparative Analysis of Store Clustering Techniques in the Retail
Industry
Kanika Agarwal, Prateek Jain and Mamta Rajnayak
Accenture Digital, Accenture Private Solution Limited., India
Keywords: Store Clustering, Self Organizing Maps, Gaussian Mixture Matrix, Fuzzy C-means.
Abstract: Many offline retailers in European Markets are currently exploring different store designs to address local
demands and to gain a competitive edge. There has been a significant demand in this industry to use analytics
as a key pillar to take store-centric informed strategic decisions. The main objective of this case study is to
propose a robust store clustering mechanism which will help the business to understand their stores better and
frame store-centric marketing strategies with an aim to maximize their revenues. This paper evaluates four
advance analytics-based clustering techniques namely: Hierarchical clustering, Self Organizing Maps,
Gaussian Mixture Matrix, and Fuzzy C-means These techniques are used for clustering offline stores of a
global retailer across four European markets. The results from these four techniques are compared and
presented in this paper.
1 INTRODUCTION
Over the last decade, there has been a steady growth
in the European retail market. Retailers have designed
different store designs across the markets to cater to
local customer preferences and to gain competitive
advantage. There has been a significant demand for
analytics in the market to drift from traditional
descriptive to more of a predictive/prescriptive
approach.
According to a report by Neilsen, there has been a
shift in the convenience store’s transaction and
purchase patterns. The store visit has increased,
however, spending per visit has decreased. There has
been a change in customer lifestyle, for instance,
people prefer fresh and healthy products nowadays.
Availability of contactless payment method, self-
checkouts also have a positive impact on store
footfall. Analyzing these factors would help the
retailer in maximizing profit and optimizing
inventory.
The retailers are concerned with the following
business problems.
1. How are the various stores performing? Which
stores have the maximum potential to grow?
2. What is the customer footfall? What is the
average spending per transaction?
3. What kinds of products are purchased the
most? Is it tobacco, coffee, grocery or any
other category?
4. What are the top performing manufacturers
and brands?
5. What type of customers visits the stores? What
are their preferences?
6. How much is the store responsive to
promotion such as discount coupons, meal
deal offers etc.?
7. How accessible is the store? Is parking facility
available or is the store well connected?
8. What is the store firmographics: store size,
store layout, store design?
This paper is designed to address these business
problems and propose a strategic point of view to
retailers with an end objective to be more profitable
and competitive in the market.
The retailer considered in this paper is operational
in many European countries such as Germany,
Netherland, Austria, Poland, United Kingdom,
Switzerland etc. It has more than 5000 store outlets
and millions of customer base across all the
geographies. It offers a wide range of product
portfolio: groceries, tobacco, drinks, fast food,
packaged food etc. This retail organisation wants to
leverage power of analytics and better understand
their retail store business with an aim to stay ahead of
Agarwal, K., Jain, P. and Rajnayak, M.
Comparative Analysis of Store Clustering Techniques in the Retail Industry.
DOI: 10.5220/0007917500650073
In Proceedings of the 8th International Conference on Data Science, Technology and Applications (DATA 2019), pages 65-73
ISBN: 978-989-758-377-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
65

its peers. To achieve this aim, it is important for this
organisation to better understand the markets in
which they are operating and have a personalised
local view of the retail stores within these markets.
Hence, store segmentation is proposed to cater to
these business requirements. Given the complexity of
data and market dynamics, it is imperative to apply
some sophisticated clustering techniques which
would address the limitations of traditional
techniques like K-mean and agglomerative
clustering.
This paper proposes the use of advance machine
learning techniques like Self Organizing Maps
(SOM), Gaussian Mixture Models (GMM), Fuzzy C-
means (FCM) for clustering offline stores of different
European markets. The results of these techniques are
also compared with results of legacy clustering
technique like hierarchical to prepare a comparative
analysis for each market.
This paper is structured as follows. Section 2
presents the related literature available in this domain.
Section 3 describes the different data sources,
variables and techniques used in the analysis. Section
4 presents the comparative results of the techniques
applied across different markets and the paper is
concluded in Section 5.
2 RELATED WORKS
Various algorithms have been proposed by
researchers relating to clustering applications for
retailers in the literature and results from clustering
have been presented.
Researchers have classified internet retail sites for
an e-commerce company. 35 observable internet
retail store’s attributes are used, and hierarchical
clustering technique is applied to classify store into
five distinct web catalog interface categories:
superstores, promotional stores, plain sales stores,
one-page stores, and product listings. The classified
online stores differ primarily on the three dimensions:
size, service offerings, and interface quality (Spiller
and Lohse, 2015).
Researchers analyze the data of a supermarket
chain which has 73 stores in Turkey. Data related to
stores such as store size, number of competitors
nearby, trade area demographics like distribution of
population by age, marital status are used for
conducting the segmentation. Hierarchical clustering
is applied, and effective target marketing strategy is
designed for each store segment (Bilgic, Kantardzic,
and Cakir, 2015).
Researchers have applied artificial neural
networks (ANNs) as an alternative means of
segmenting customers in retail space. Hopfield–
Kagmar (HK) clustering algorithm, an ANN
technique based on Hopfield networks, is compared
with K-means clustering algorithms. Purchase
behavior such as the total number of orders, days
since first purchase, the number of credit cards etc is
used for profiling the customers. The results indicate
that ANNs could be more useful to retailers for
segmentation because they provide more
homogeneous segmentation solution than K-means
clustering algorithms and are less sensitive to initial
starting conditions (Boone and Roehm, 2002).
Researchers have applied clustering techniques
namely K-means clustering, Mountain clustering, and
Subtractive clustering on the dataset for medical
diagnosis of heart disease. It is observed that K-means
overperformed in cases where many dimensions are
present. Mountain clustering is suitable only for
problems with two or three dimensions (Hammouda
and Karray, 2002).
Most of the papers have applied hard clustering
techniques like K-means and hierarchical. Most of
them have been used for customer segmentation
rather than for store segmentation. Even if there is
some research in the store segmentation space, it is
predominantly focused on online channel than the
traditional offline channel. To add further, the
attributes used for store clustering are mostly related
to firmographics, customer demographics or
competitor information. In this paper, store clustering
is performed for a retail organisation. Attributes
related to purchase pattern, transaction pattern,
customer behaviour, store dimensions are used for
clustering. Both hard clustering technique such as
hierarchical clustering and soft clustering techniques
such as Self Organizing Maps (SOM), Gaussian
Mixture Models (GMM), Fuzzy C-means (FCM) are
applied for clustering stores for four different
European markets. A comparative study on the results
derived from these different techniques for different
markets has been presented in this paper.
3 DATA AND METHODLOGY
The retailer considered is a UK based multinational
organization offering convenience retail services to
.consumers. The company operates through various
channels. Some of the stores are owned and operated
by the company itself, however, there are some which
are owned and operated by a franchise or a dealer.
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
66
In this paper, data is analyzed for four different
European markets. The time frame considered for the
analysis is one year. The data sources used are
transaction data, product data, store data, loyalty data,
and competitor’s data. In transaction data, attributes
like transaction date, sales, quantity etc. are captured.
Attributes like product description, category
description, brand etc. are captured in the product
dataset. Dimensions like store size, location,
operating channel etc. are recorded in the store data.
Information related to purchase behavior of the
customers using the loyalty card, methods of
payments, discounts, point redemption etc. are
captured in the loyalty data. Competitor’s data
included the competitor’s pricing attributes. All the
datasets together have millions of transactions
encapsulating close to a hundred raw variables.
Table 1: Description of some of the variables captured in
the dataset.
Variable name Data type Description
Transaction id Varchar
Unique id associated
with each transaction.
Transaction
date
Time
stamp
Time at which
transaction is recorded.
Product id Varchar
Unique id the product
purchased.
Store id Varchar
Unique id of the store in
which the product is
sold.
Sales Numeric
Sales value of the
product.
Quantity Numeric
Quantity in which
product is sold.
Product
description
Varchar
Description of the
product sold.
Category
description
Varchar
Description of the
category the product
belonged to such as
tobacco, drinks etc.
Operating
channel
Varchar
Flag to identify id the
store owned by
company or not.
Location Varchar
Indicate if the store is
located centrally or if it
is in countryside.
3.1 Data Wrangling
To perform store clustering, the data must be
represented at a store level. So, after collating the
datasets, all the variables are rolled at a store level.
Depending on the nature of the variable, aggregation
methods like sum, count, max, min are applied. For
example, in the case of sales and quantity sum is
taken, however, in the case of transactions, a distinct
count is calculated. Many derived variables like
spending per category, average price, sales
corresponding to different months, week of the day
and time of the day are created. This led to the
creation of around 400 variables for each store. These
set of variables provide a holistic view of stores and
capture dimensions related to demographics,
firmographics, transaction pattern, purchase pattern
etc
In order to ensure that quality data is used for
clustering, a cleansing procedure is applied. The
process is as followed.
1. A univariate analysis is conducted to calculate
the percentile distributions (0.01, 0.05,
0.1,0.25, 0.5, 0.75, 0,9 ,0.95 ,0.99), count of
missing values etc.
2. As per the nature of the variable, missing value
imputation techniques like replacement with
mean/median/mode etc. are applied.
3. Variables with significant missing values are
excluded from the analysis.
4. Variables that showed less variability are also
removed.
5. The last step is the outlier treatment.
Depending on the distribution of the variable
the treatment is conducted. For some variables
95
th
percentile value is used to replace the
outlier at the upper end and similarly for
others, some other threshold is applied.
All the stores are not considered for analysis.
Only the stores that are owned by the company and
that are operational for more than 80% of the time
period are taken into account.
Conducting clustering on 400 variables is neither
efficient nor feasible. So, the next process is the
selection of relevant variables. To do this, the variable
clustering technique is applied. The package
ClustofVar in R is used for the same. Hierarchical
clustering technique is applied to club variables
strongly related to each other. The algorithm is
explained in detail in the section3.2.4. There is only
one difference, here the algorithm is applied to group
variables and in section 3.2.4 it is applied to group
stores. Once the variables are grouped into clusters, a
loading is attached to each variable. From each cluster
some variables are selected based on the loading
value and business inputs. Around 30 variables are
shortlisted to be used in the final clustering process.
Comparative Analysis of Store Clustering Techniques in the Retail Industry
67

3.2 Clustering Techniques
There are two kinds of clustering techniques: hard
clustering and soft clustering. In case of hard
clustering a data point belongs to only one cluster
However, in case of soft clustering, a data point has
the probability of belonging to all the clusters. K-
means and Hierarchical clustering fall under the hard
clustering classification while Self Organizing Maps
(SOM), Gaussian Mixture Models (GMM), Fuzzy C-
means (FCM) are a part of soft clustering
classification.
In this section, the hard clustering technique:
Hierarchical and soft clustering techniques: SOM,
GMM, FCM are explained in detail.
3.2.1 Self Organizing Maps
This is a type of artificial neural network which works
on the principle of reducing high dimensional data
into low dimensional space. The technique maintains
the spatial relationship between the data. The process
followed by SOM is as follows.
1. The very first step is the specification of grid
space as hexagonal or rectangular. For
example, grid space for 6 clusters could be
2x3, 1x6, 6x1 or 3x2. In figure1, it is
rectangular 2x3.
2. Once the grid is selected, each cluster/node in
the grid is assigned a random weight. The
dimension of a node is equivalent to the
number of variables in the data. For example,
in figure2, Node1 has 3 weight dimensions
corresponding to 3 variables (X
1
, X
2
, X
3
) in the
data.
3. For each iteration, an observation is randomly
selected, and a distance metric is calculated
with respect to all the nodes as shown in
figure2.
4. The cluster with the minimum distance is
assigned to the observation.
5. As this happens, the whole grid moves closer
to the observations, as shown in figure3. The
movement is dependent on the learning rate
specified in the model.
6. Weights of the nodes are adjusted.
7. This completes an iteration for one
observation (Step 3-6).
8. In the next iteration, again one observation is
selected to pass through the above steps.
9. The process is repeated iteratively till all the
observations are assigned a cluster and a
convergence criterion is achieved.
The equation used for updating weight is as
follows.
1
(1)
where t is time step, W(t) is the weight at time t,
L is the leaning rate factor at time t, θ(t) is
neighbourhood function at time t.
The fine-tuning parameters for SOM are the cluster
number, the dimension of grid space, the learning rate
which determines the rate at which the node’s weights
are updated. For the analysis, the Kohonen package
in R is used. SOM is one of the techniques which is
very powerful when it comes to visualization of the
clusters across different dimensions.
Figure 1: This figure shows the grid 2x3 (on the left) and
the set of observations (on the right). (Source mentioned in
the references section).
Figure 2: This figure shows the calculation of distance for
observation with 3 dimensions. (Source mentioned in the
references section).
Figure 3: This figure shows how the grid moves when a
cluster is assigned to observation. (Source mentioned in the
references section).
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
68

3.2.2 Gaussian Mixture Models (GMM)
This technique is a probabilistic approach to
clustering. GMM is a mixture of K Gaussian
component that means it is a weighted average of K
Gaussian (normal) distribution. The technique is
based on the Expectation Maximisation algorithm.
The technique works in the following way.
1. For each cluster, a mean and standard
deviation value is allocated. In figure4, there
are two clusters which have a normal
distribution with mean and standard deviation
as (µ
a,
σ
a )
,( µ
b
,σ
b) .
2. Then for each observation, the probability of
belonging to these 2 clusters is calculated
using equation2. In figure 5, the two different
colors per observation show the probability
attached to the corresponding distribution.
3. Using these probabilities, the mean and
standard deviation of the clusters are re-
estimated as shown in equation4 and
equation5.
4. The process keeps on repeating until
convergence is achieved. Figure 6 shows how
the final distribution changes over various
iterations.
Figure 4: This figure shows the initial distribution of two
clusters. (Source mentioned in the references section).
Figure 5: This figure shows the probability assigned to each
observation based on the parameters of the distribution.
(Source mentioned in the references section).
Figure 6: This figure shows the result after multiple
iterations. (Source mentioned in the references section).
The equations used in GMM are as follows.
⁄
⁄
⁄
(2)
exp
(3)
μ
⋯
⋯
(4)
⋯
⋯
(5)
Here x
i
is the ith observation, µ
b
is the mean of the
second cluster, σ
b
is the standard deviation of the
second cluster.
The optimal number of clusters is chosen based
on the Akaike Information Criterion and the Bayes
Information Criterion. Mclust package in R is used
for conducting the exercise.
3.2.3 Fuzzy C-Means (FCM)
This technique is like K-means, however, here every
observation has a degree of belonging to all the
clusters. The process for clustering is as follows.
1. Cluster centers are created randomly based on
the number of clusters.
2. Euclidean distance between the observations
and cluster centroids is calculated in this step.
3. Then, the membership matrix is generated,
using equation 6.
4. After this, the centroids are updated using
equation 7.
5. The last two steps are repeated until the
convergence criterion, as shown in equation 8
is achieved. The value of epsilon should be
between 0 and 1.
Comparative Analysis of Store Clustering Techniques in the Retail Industry
69

The equations are as follows.
∑
||
||
||
||
(6)
∑
∑
(7)
(8)
Where Uij
= membership of the ith data to the jth
cluster, m = fuzziness exponent, C = number of
clusters, c
j
= jth cluster centre , x
i
= ith observation ,
N = number of observations.
The fine-tuning parameters here are the number of
clusters and the fuzziness exponent “m” whose value
should be greater than one. For this exercise, fclust
package in R is applied.
3.2.4 Hierarchical Clustering
In hierarchical clustering, the bottom up clustering
approach is applied. The process applied is as
follows.
1. Each observation is considered as a single
cluster.
2. Then the distance between every pair of
observation is calculated and stored in a
distance matrix. The distance between cluster
can be calculated using complete linkage,
average linkage etc.
3. Pair closest to each other are merged together
and as a result, the number of clusters is
reduced by 1 in each step.
4. Step 2 and 3 are repeated until all the points
are a part of one big cluster.
At the end of the process, a dendrogram is created
as shown in figure7. This helps to identify the optimal
number of clusters. The package hclust in R is used
for the analysis.
Figure 7: This figure shows a dendrogram. The line depicts
the point at which dendrogram is cut.
4 IMPLEMENTATION AND
RESULTS
In section 3, the clustering modelling exercise is
discussed. This section describes the different steps
that are performed after the clustering modelling task
is completed.
4.1 Validation
Several iterations are performed, and many
parameters are considered to get the final iteration.
Some of the validation steps are as follows.
1. The number of clusters formed is decided
based on statistical as well as business inputs.
Some of the statistical techniques that are used
to identify the optimal set of clusters are
dendrograms, heatmaps etc. The number of
clusters formed lied in the range of 3-5
depending on the market and technique.
2. The minimum number of stores per cluster is
set to be at least 30.
3. The following parameters across iterations are
compared.
Table 1: Metrics compared.
Hierarchical Dunn Index, Silhoutte
coefficient
SOM Neighbour distance, Training
Progress
GMM Akaike Information Criterion,
Bayes Information Criterion
FCM Coefficient of Variation
4 All the clusters formed have some distinct
features that would ensure that stores within a
cluster are homogeneous and stores across
clusters are heterogeneous.
4.2 Profiling
There are two levels of profiling that are performed
during this exercise.
1. Basic profiling: In this, all the modelling vari-
ables that are used for clustering are considered
and their variations across the clusters are
captured. If the variables are numerical then
mean is considered and if the variables are
categorical then the frequency is considered.
2. Advance Profiling: In this, other variables
apart from modelling variables that are
relevant to the business are considered and
their variations across the clusters are captured
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
70
in a similar way as described for basic
profiling. This helped in personifying the
clusters and capturing all the differentiated
attributes for each cluster. For instance, as
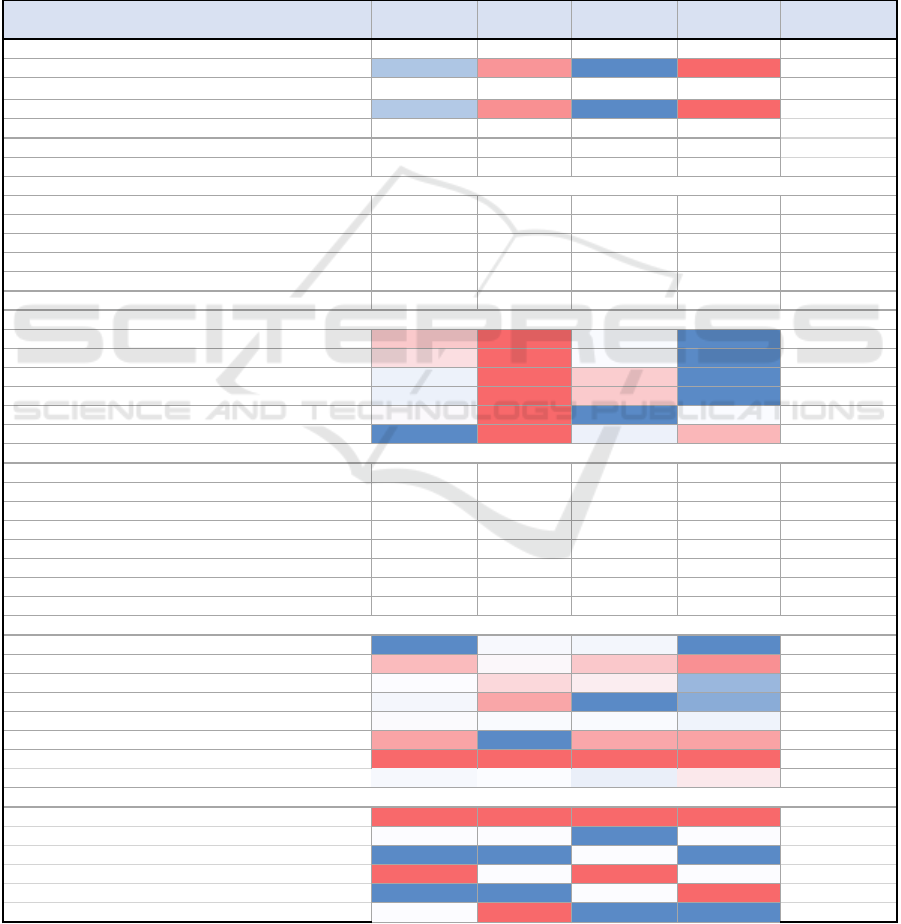
shown in figure 8, cluster 3 has the maximum
sales whereas cluster 4 has the minimum sales.
Cluster 1 has the maximum numbers of stores
and because of that, they have the maximum
number of the customer base as well. Spending
per transaction is another attribute that is used
to differentiate clusters. The spending per
transaction in cluster 1 is higher as compared to
others. Also, each cluster is dominant in at least
one of the categories. For example, category 1
has the maximum sales share for cluster 1
where as category6 is dominant in cluster 2.
This insight would help the category managers,
in better understanding and designing of the
strategies/promotions. Distribution of different
store designs within a cluster is also captured.
For instance, the stores of cluster 4 and 3,
majorly have Z layout whereas cluster 2 and 1
have mostly layout Y. This information helped
in better understanding of store attributes.
Figure 8: This figure shows the store profiling for one market using GMM.
KPIs Cluster1 Cluster2 Cluster3 Cluster4
Average
Value
Number of Sites 88 47 110 38 283
Share of Sites, % 31% 17% 39% 13%
Total Sales 2,518 m 968 m 3,449 m 681 m 1,904 m
Sales Share 33% 13% 45% 9%
Customer Count 501,200 230,345 631,134 239,234 400,478
Loyal Transactions/Overall Transactions (%) 44% 74% 56% 63%
Points Redeemed/Points Issue (%) 56% 61% 54% 72%
Transactions (Per Store) 165,130 157,152 173,600 335,215 178,514
Transactions (Per Month/Per Store) 14,056 13,125 14,524 28,338 15,025
Sales (Per Store) 3,602,804 2,643,445 3,139,645 5,792,097 3,369,966
Sales (Per Month/Per Store) 305,429 220,771 262,638 489,562 283,424
Units Per Transaction 2.5 2.2 2.9 2.5 2.6
Sales Per Transaction 21.8 16.8 18.1 17.3 18.9
Transactions (Per Store) 93 88 97 188
Transactions (Per Month/Per Store) 94 87 97 189
Sales (Per Store) 107 78 93 172
Sales (Per Month/Per Store) 108 78 93 173
Units Per Transaction 95 83 11
0
95
Sales Per Transaction 116 89 96 92
Category 1 111,565 16,992 20,806 107,820 64,296
Category 2 13,415 14,314 11,891 18,195 14,454
Category 3 21,930 11,645 15,668 83,616 33,215
Category 4 26,609 7,242 79,306 89,497 50,664
Category 5 21,669 16,307 18,651 50,751 26,844
Category 6 10,386 78,652 8,474 22,911 30,106
Category 7 2,713 1,842 2,025 7,974 3,638
Category 8 25,314 15,156 24,258 40,784 26,378
Category 1 48% 10% 11% 26%
Category 2 6% 9% 7% 4%
Category 3 9% 7% 9% 20%
Category 4 11% 4% 44% 21%
Category 5 9% 10% 10% 12%
Category 6 4% 49% 5% 5%
Category 7 1% 1% 1% 2%
Category 8 11% 9% 13% 10%
Store Size -Small 31% 25% 23% 23%
Store Size -Medium 34% 29% 44% 34%
Store Size -Large 35% 46% 33% 43%
Store Layout -X 23% 27% 25% 35%
Store Layout -Y 41% 50% 35% 24%
Store Layout -Z 36% 23% 40% 41%
Store KPIs
KPIs Per Store & Per Store/Month, Absolute Values
KPIs Per Store & Per Store/Month, Indices
Category Average Sales Per Site/Per Month
Category Average Sales Per Site/Per Month, % Share
Comparative Analysis of Store Clustering Techniques in the Retail Industry
71

Figure 9: This shows the quarterly migration from all the techniques across all the markets.
4.3 Business Recommendations
The profiling helped in providing business
recommendations related to the following business
problems.
1. Identifying the key categories for the stores in
order to make a strategic decision. Category 4
is dominant in cluster 3 indicating the stores
belonging to cluster 3 should focus more on
category4.
2. For each cluster, an index can be created using
dimensions like average spend per transaction,
average units per transaction etc. These index
scores can then be leveraged to identify the
categories for each cluster which have the
maximum potential to grow.
3. Identifying the top performing stores. Cluster
3 has the maximum sales share but per store
sales is maximum for cluster 4 indicating that
cluster 4 stores on average performed better
than others.
4. Customer preferences are captured across
stores. For instance, cluster 2 has the
maximum number of Loyalty customers
followed by cluster 4. However, the Loyal
customer points redemption is the most in
cluster 4 which means promotions are most
effective for cluster 4 stores.
5. Understanding store firmographics to
optimize product portfolio. Cluster 1 has
mostly small size stores whereas cluster 3 has
medium type stores and cluster 2 / 4 are mostly
made up of large stores. This information
would help in space optimization planning for
each cluster type.
4.4 Scoring
The clustering techniques used above are
unsupervised learning algorithms, this essentially
means that there is no dependent variable in the
modelling exercise. In case, a new store is entering
a market then these algorithms cannot be applied to
classify the new store among one of the existing
clusters. To overcome this, machine learning
techniques such as Random Forest/Support Vector
Machines are applied. Here, the independent
variables are chosen out of the set of clustering
modelling variables and the dependent variable is
cluster mapping of each store. Hence, this is the
classic use case of multinomial classification. Once,
the prediction model is built, this model is further
used to score on the existing/new stores at a set
frequency (Quarterly/Semi-Annually/Annually).
Market Quarters Q2 '17 - Q3 '17 Q3 '17 - Q4 '17 Q4 '17 - Q1 '18 Q1 '18 - Q2 '18 Average
Hierarchical
11.8% 13.6% 11.0% 8.5%
11%
FCM
14.3% 15.8% 7.4% 11.0%
12%
GMM
12.2% 12.9% 7.8% 8.8%
10%
SOM
10.4% 10.0% 6.4% 4.2%
8%
Hierarchical
7.8% 10.9% 7.8% 9.3%
9%
FCM
3.9% 5.6% 7.4% 8.4%
6%
GMM
2.8% 5.5% 6.8% 8.8%
6%
SOM
4.2% 3.9% 4.6% 4.2%
4%
Hierarchical
7.6% 7.2% 4.9% 4.9%
6%
FCM
3.4% 5.1% 6.9% 6.8%
6%
GMM
2.3% 3.2% 3.6% 4.0%
3%
SOM
3.7% 3.4% 4.1% 3.7%
4%
Hierarchical
2.1% 1.5% 1.1% 3.8%
2%
FCM
3.5% 1.6% 1.1% 2.9%
2%
GMM
2.6% 3.5% 4.5% 3.4%
4%
SOM
4.2% 1.7% 1.7% 3.3%
3%
1
2
3
4
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
72

4.5 Migration
To check the robustness of the model, migration
across quarters is calculated. For this, store level data
is prepared for 5 quarters. Stores belonging to the
quarters are scored using the prediction model built at
the earlier stage. For example, each store of Q2 and
Q3 of 2017 are scored (allocated a cluster). Then
migration is calculated across quarters. Migration is
the number of stores which have changed cluster
across the two quarters divided by the total number of
common stores across the two quarters. As shown in
figure 9, in market 1, the migration from Q2’17 to
Q3’17 using Hierarchical clustering is 11.8%. This
mean for 11.8% of the stores the cluster allotment
changed when the quarter changed from Q2 to Q3.
Lower migration implies that the model is robust.
Hence, quarterly migration is considered as one of the
most important criteria for choosing the best
technique.
As shown in figure 9, SOM performed the best for
market 1 and market 2 with an average migration
across quarters of about 7.8% and 4.2% respectively.
GMM is the best technique for market 3 with the
average migration of 3.3%. Hierarchical clustering
performed the best for market 4 with the average
migration of 2.1%, however, the results from fuzzy
logic are close. Different techniques performed
differently in each market.
5 CONCLUSIONS
The paper considers four clustering techniques
namely: Hierarchal Clustering, Self Organizing
Maps (SOM), Gaussian Mixture Matrix (GMM) and
Fuzzy C-means(FCM). The techniques are applied to
the retail database to cluster the stores with similar
profile together. Each technique has a different
approach to clustering. The main parameter for the
retailer to measure the effectiveness of the cluster is
quarterly migration. It is noticed that no technique is
the best for all the markets. SOM performed better in
two markets, however, GMM and Hierarchical
outperformed the other techniques in one market
each. So, it is concluded that it is difficult to
generalize one technique to be the best suited for store
clustering exercise. The data and the features
determine which technique is to be applied. From this
exercise, it is recommended different clustering
techniques should be performed and one with the best
results should be finally selected.
ACKNOWLEDGEMENTS
The authors would like to thank three reviewers who
assisted in reviewing the content and improving the
quality of the paper.
REFERENCES
Bilgic E., Kantardzic M. and Cakir O. (2015). Retail Store
Segmentation for Target Marketing.
Spiller, P. and Lohse, G. (1997). A classification of internet
retail stores. International Journal of Electronic
Commerce, 2(2), pp.29-56.
Boone, D. and Roehm, M. (2002). Retail segmentation
using artificial neural networks. International Journal
of Research in Marketing. 19(3), pp287-301.
Hammouda, K. and Karray, F. (2002). A comparative study
of data clustering techniques. Tools of Intelligent
Systems Design.
Laverenko, V. (2014). EM algorithm: how it works.[
image]. Available at https://www.youtube.com/
watch?v=REypj2sy_5U&t=338s
Alogobean.com, (2017). Self Organizing Maps Tutorials.
[image] Available at: https://www.superdatascience.
com/blogs/the-ultimate-guide-to-self-organizing-
maps-soms
Superdatascience.com, (2018). The Ultimate Guide to Self
Organizing Maps. [image]. Available at: https://
algobeans.com/2017/11/02/self-organizing-map/
Chavent, M., Kuentz, V., Liquet, B., Saracco, J. (2011).
ClustofVar: An R package for clustering of variables.
Journal of Statistical Software, 55(2)
Watkins, M. (2014). The rise of modern convenience store
in Europe. Available at: https://www.nielsen.com/
eu/en/insights/reports/2014/the-rise-of-the-modern-
convenience-store-in-europe.html
Comparative Analysis of Store Clustering Techniques in the Retail Industry
73
