
DABSTERS: Distributed Authorities using Blind Signature to Effect
Robust Security in e-Voting
Marwa Chaieb
1
, Mirko Koscina
2,5
, Souheib Yousfi
3
, Pascal Lafourcade
4
and Riadh Robbana
3
1
Faculty of Sciences of Tunis, University Tunis El-Manar, Tunis, Tunisia
2
D
´
epartement d’Informatique,
´
Ecole Normale Sup
´
erieure, Paris, France
3
LIP2, National Institute of Applied Science and Technology, University of Carthage, Tunis, Tunisia
4
LIMOS, University Clermont Auvergne, CNRS UMR6158, Aubi
`
ere, France
5
Be-Studys, Geneva, Switzerland
Keywords:
e-Voting, Blind Signature, Fully-decentralized, Permissioned Blockchain.
Abstract:
Creating an online electronic voting system that meets all legal requirements of election organizers and vot-
ers has constituted a real challenge for a long period of time. Permissioned Blockchains (also called Private
Blockchains) are a cutting-edge invention, introduced as a security breakthrough for many existing and emerg-
ing technologies. One potential application of private Blockchain concerns e-voting systems. We propose a
fully-decentralized e-voting system based on permissioned Blockchain, called DABSTERS in e-voting. Our
system uses a blinded signature consensus algorithm, which is a modified version of Practical Byzantine Fault
Tolerance (PBFT), to preserve voter’s privacy. Our protocol ensures several security properties: voter’s eligi-
bility, vote integrity, vote secrecy, fairness, receipt freeness, individual and universal verifiability.
1 INTRODUCTION
Blockchain technology is a distributed, immutable
and public ledger that ensures transparency, decen-
tralization, irreversibility, and non-repudiation prop-
erties. The first Blockchain implementation is Bit-
coin (Nakamoto, 2008), which corresponds to a per-
missionless architecture, where everybody can anony-
mously join the network. In 2014, Vitalik Buterin pro-
posed a second permissionless Blockchain implemen-
tation called Ethereum (Buterin, 2014). Ethereum
combines the traditional idea of the distributed ledger
with smart contracts built on the top of a virtual
machine. However, the advantages of Blockchain
come with significant drawbacks such as an unbear-
able computational complexity and limited scalabil-
ity. But its most important weakness is the efficiency
of the mechanism used to avoid the misbehavior of
dishonest miners. Thus, for every new block, it is re-
quired to follow a consensus mechanism to agree on
the next block to be appended to the chain, such as
Proof-of-Work (PoW) and Proof-of-Stake (PoS) used
respectively in Bitcoin and Ethereum. In these con-
sensus mechanisms, miners collect the transactions,
validate them and organize them in a block. Once
a miner has successfully passed the selection mecha-
nism imposed by the consensus algorithm to propose
a new block, the selected miner broadcasts the block
to the network to be validated by the rest of miners
and then to be added to the chain. Dishonest min-
ers can modify transactions data before storing them
on the blocks. This issue gets worse especially if the
exchanged data are sensitive or important. It is the
case of e-voting systems where exchanged data are
votes. Dishonest miners can invalidate elections by
modifying these transactions. Moreover, permission-
less Blockchains are not suitable to manage tailored
business rules, like special data access restrictions and
user profiling. These special requirements can be ad-
dressed by using permissioned Blockchain. Thus, we
can rely on private Blockchain not just for the im-
mutability of the system but also on the users’ man-
agement for sensitive services like e-voting. Hence,
our aim is to design a fully distributed secure archi-
tecture for electronic voting systems.
Our contributions are:
• A new architecture of trust for e-voting sys-
tems. This architecture is based on permissioned
Blockchain and on a blind consensus which pro-
vides voter’s privacy and vote’s integrity.
• A secure and fully distributed e-voting protocol,
called DABSTERS in e-voting for Distributed Au-
thorities using Blind Signature To Effect Robust
Security, based on our propounded architecture.
228
Chaieb, M., Koscina, M., Yousfi, S., Lafourcade, P. and Robbana, R.
DABSTERS: Distributed Authorities using Blind Signature to Effect Robust Security in e-Voting.
DOI: 10.5220/0007917702280235
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 228-235
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

DABSTERS in e-voting satisfies the following secu-
rity properties. Eligibility: Only registered voters
can vote, and nobody can submit more votes than al-
lowed. Fairness: No preliminary results that could
influence other voters’ decisions are made available.
Robustness: The protocol can tolerate misbehaving
voters. Integrity: Is the assurance of the accuracy
and consistency of votes. Individual Verifiability:
Each voter can check whether his vote was counted
correctly. Universal Verifiability: Anybody can ver-
ify that the announced result corresponds to the sum
of all votes. Vote-Privacy: The votes are kept pri-
vate. This can also be modeled as an unlinkability
between the voter and his vote. Receipt-Freeness:
A voter cannot generate a receipt to prove to a third
party which candidate has voted for.
Related Work: We study various voting systems
based on Blockchain technology and we resume their
security properties in Table 1.
Open Vote Network (McCorry et al., 2017): It is a
self-tallying, boardroom scale e-voting protocol im-
plemented as a smart contract in Ethereum. Open
Vote Network ensures votes privacy since votes are
encrypted before being cast. This protocol is self tal-
lying so it is universally verifiable and ensures indi-
vidual verifiability thanks to the use of Blockchain.
However, it suffers from several security issues. For
example, it supports only elections with two options
(yes or no) and with a maximum of 50 voters due to
the mathematical tools that they used and to the gas
limit for blocks imposed by Ethereum. Additionally,
this protocol does not provide any mechanism to en-
sure coercion resistance and needs to trust the elec-
tion administrator to ensure voter’s eligibility. Open
Vote Network is not resistant to the misbehavior of
a dishonest miners who can invalidate the election by
modifying voters’ transactions before storing them on
blocks. A dishonest voter can also invalidate the elec-
tion by sending an invalid vote.
TIVI (Smartmatic, 2016): It is an online voting
solution based on biometric authentication, designed
by the company Smartmatic. It checks the elector’s
identity via a selfie using facial recognition technol-
ogy. TIVI ensures several security properties such as
voters’ eligibility since it provides different authen-
tication techniques and votes secrecy so long as the
encryption remains uncompromised. It provides also
voters’ privacy thanks to its mixing phase and offers
the possibility to follow votes by the mean of a QR
code stored during voting phase and checked later via
a smartphone application. However, this system does
not provide any mechanism to protect voters from
coercion or to ensure receipt-freeness. Additionally,
TIVI uses the Ethereum Blockchain as a ballot box
so it is not resistant to misbehaving miners that could
invalidate the election by modifying votes before stor-
ing them on the election Blockchain.
Follow My Vote (Followmyvote, 2012): It is
an online voting protocol that uses the Ethereum
Blockchain as a ballot box. A trusted authority au-
thenticates eligible voters and provides them with
pass-phrases needed in case of changing their votes
in the future. Voters can watch the election progress
in real time as votes are cast. Follow My Vote re-
spects a limited number of security properties. It in-
cludes an authentication phase which ensures voters’
eligibility. It allows voters to locate their votes, and
check that they are both present and correct using
their voters’ IDs. Nevertheless, this voting system re-
quires a trusted authority to ensure votes confidential-
ity and hide the correspondence between the voters’
real identities and their voting keys. If this authority is
corrupted, votes are no longer anonymous. Votes se-
crecy is not verified because votes are cast without be-
ing encrypted. Moreover, the ability to change votes,
coupled with the ability to observe the election in real
time compromise fairness property. This system is not
coercion resistance, a coercer can force a voter to vote
in a certain way and check his submission later using
his pass-phrase. FMV is not universally verifiable be-
cause there is no way to verify that the votes present
in the election final result are cast by eligible voters.
Verify-Your-Vote: a Verifiable Blockchain-based
Online Voting Protocol (Chaieb et al., 2018): It is an
online electronic voting protocol that uses Ethereum
Blockchain as a bulletin board. It is based on a variety
of cryptographic primitives, namely Elliptic Curve
Cryptography, pairings and Identity Based Encryp-
tion.
The combination of security properties in this pro-
tocol has numerous advantages. As shown in Table 1,
it ensures voter’s privacy because the Blockchain is
characterized by the anonymity of its transactions. It
also ensures fairness, individual and universal veri-
fiability thanks to the ballot structure that includes
counter-values and to the homomorphism property of
pairings. However, VYV suffers from acknowledged
weaknesses where the honesty of human being is in-
volved especially in the registration phase and the ar-
chitecture of the system. A first problem is that the
registration phase is centralized. A unique authority,
which is the registration agent, is responsible for ver-
ifying the eligibility of voters and registering them. A
dishonest agent can register persons who do not have
the right to vote. Thus, ineligible voters, who are pro-
vided by valid authentication parameters, can access
the Blockchain and participate in the election. A sec-
ond problem is inherent in the use of Ethereum be-
DABSTERS: Distributed Authorities using Blind Signature to Effect Robust Security in e-Voting
229

cause each transaction sent by the protocol entities in
the Blockchain passes through miners who validate it,
put it in the current block and execute the consensus
algorithm. Again in VYV, any dishonest miner in the
election Blockchain can modify transactions before
storing them on blocks. This risk constitutes a real is-
sue if dishonest miners modify eligible voters’ trans-
actions during the voting phase. These transactions
contain encrypted votes. If they change their values,
tallying authorities (TAs) will not be able to decrypt
them. As a result, TAs count only votes that were
not modified by dishonest miners during the voting
phase. The other votes will be discarded, thus, some
eligible voters may have their choices not counted in
the election final tally. Therefore, dishonest miners
cause false election result.
DABSTERS in e-voting comes with significant
improvements to address the weaknesses of (Chaieb
et al., 2018). It proposes a new architecture of trust,
based on permissioned Blockchain and blind signa-
ture. It also proposes a distributed registration phase
and adds a validation phase, where all parties can
check the validity of registered voters list and have
the right to reject it if they detect a dishonest behavior
from the RA.
Outline: In the next section, we give an overview of
the PBFT and the blinded signature consensus algo-
rithms. Then in Section 3, we describe our proposed
e-voting protocol, DABSTERS in e-voting, give its
different entities and phases, and give an overview of
our ballot structure. The conclusion is a summary of
DABSTERS in e-voting protocol and a proposal for
ongoing evaluation of its performance.
2 BACKGROUND
We give a definition of the Okamoto-Schnorr blind
signature (Okamoto, 1992), before using it in a PBFT
based consensus.
Blind Signature: Let p and q be two large primes
with q|p − 1. Let G be a cyclic group of prime
order q, and g and h be generators of G. Let H :
{0, 1}
∗
→ Z
q
be a cryptographic hash function.
Key Generation: Let (r, s)
r
←− Z
q
and y = g
r
h
s
be the
A’s private and public key, respectively.
Blind Signature Protocol: 1. A chooses (t, u)
r
←−
Z
q
, computes a = g
t
h
u
, and sends a to the user.
2. The user chooses (β, γ, δ)
r
←− Z
q
and computes
the blind version of a as α = ag
−β
h
−γ
y
δ
, and
ε = H(M, α). Then calculates e = ε − δ mod q,
and sends e to the A.
3. A computes S = u − es mod q and R = t − er
mod q, sends (S, R) to the user.
4. The user calculates ρ = R − β mod q and σ =
S − γ mod q.
Verification: Given a message M ∈ {0, 1}
∗
and a sig-
nature (ρ, σ, ε), we have α = g
ρ
h
σ
y
ε
mod p.
The Okamoto-Schnorr blind signature scheme is
suitable with a private Blockchain architecture due
to the blinding process that can be performed by
the same authority responsible of the enrollment pro-
cess. We use BlindSign(M,(β,σ, γ), y) and Verify-
BlindSign(M,(ρ, δ, ε), y) to blind sign and to verify
the blinded signature, respectively using Okamoto-
Schnorr, where M corresponds to the message to be
signed, (β, σ, γ) to the secret values randomly cho-
sen, (ρ, δ, ε) to the blinded signature; and y to the
RA’s public key. The result obtained from the func-
tion BlindSign corresponds to the blinded signature
(ρ, σ, ε). On the other hand, the function VerifyBlind-
Sign returns a response valid or invalid.
PBFT: Now, considering a permissioned Practical
Byzantine Fault Tolerance (PBFT) based consensus
protocol like the one introduced in Hyperledger Fab-
ric (Androulaki et al., 2018). In this protocol, the dig-
ital signature is used as a user authentication method
without protecting the user privacy. Hence, for a pri-
vacy preserving consensus protocol, we need to add
the following properties to the PBFT based consen-
sus algorithm:
• A voter V
i
sends a newly signed transaction to the
registration authority (RA) which is responsible
for the enrollment of voters.
• V
i
’s signature is validated only by the RA.
• The RA anonymises the identity of V
i
.
• The RA signs the transaction sent by V
i
to the net-
work.
• All the node of the transactions validation process
can validate the RA’s signature.
• The RA signature cannot be duplicated.
Now, to keep the privacy of the voter and peers in-
volved in the transactional process, we need to hide
his/her ID and make his/her signature blind. As pre-
sented in (Koscina et al., 2018), to address the issue
related to the digital signature, we replace the sign-
ing mechanism used in the original protocol by the
Okamoto-Schnorr blind signature scheme. In order
to maintain the consistency and liveness that the pro-
tocol has, we keep the transactional flow. However,
the steps are modified in order to accept the new blind
signature scheme to authenticate the clients and peers.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
230

Table 1: Security properties of VYV, OVN, TIVI, FMV and DABSTERS in e-voting.
VYV OVN TIVI FMV DABSTERS
Eligibility Trusted authority Trusted admin X Trusted authority X
Fairness X X X X X
Robustness X X X X X
Integrity X X X X X
Individual verifiability X X X X X
Universal verifiability X X X X X
Vote-Privacy X X X X X
Receipt-freeness X X X X X
Coercion resistance X X X X X
3 DESCRIPTION OF DABSTERS
IN e-VOTING
Our protocol uses the same ballot structure as (Chaieb
et al., 2018), illustrated in Figure 1, and proposes a
totally different architecture for the system.
Ballot number BN
Pseudo Candidate’s Choice Counter-value
”ID C
j
” ”name name
j
” ”CV
BN,name
j
,k
”
0 Paul CV
BN,name
0
,0
1 Nico CV
BN,name
1
,1
2 Joel CV
BN,name
2
,2
Figure 1: Ballot structure (P. Udaya and Teague, 2007).
It is based on a PBFT based consensus proto-
col (Androulaki et al., 2018) and on a blinded signa-
ture consensus protocol, called BlindCons (Koscina
et al., 2018). It eliminates the risk of invalidating the
election because of dishonest miners who modify the
transactions before storing them on blocks. We also
propose a distributed enrollment phase to reduce the
need to trust election agents and impose the publica-
tion of the list of eligible registered voters at the end
of the enrollment phase. This list is auditable and
verifiable by all parties during the validation phase.
Our scheme unfolds in 5 stages. It starts with an en-
rollment phase in which registration authorities (RAs)
verify the eligibility of voters by verifying the exis-
tence of their names and their identity card numbers in
a list published beforehand and containing the names
of all persons who have the right to vote. Then, all
eligible voters are registered and provided with cre-
dentials. Enrollment phase is offline. At the end of
this phase, RAs construct a list containing the names
of all registered eligible voters and their ID card num-
bers. This list can be rejected or published on the elec-
tion Blockchain during the validation phase. Once the
list is validated, we move to the third stage which is
voting phase. Each eligible voter (V
i
) initiates a trans-
action in which he writes his encrypted vote, signs
the transaction using his credential and sends it to the
RAs to check his signature and blind it. Then, the
voter sends the transaction with the blinded signature
and his anonymous ID (his credential) to the consen-
sus peers to be validated and stored, anonymously, in
the election Blockchain. After validating and storing
all votes in our Blockchain, tallying authorities (TAs)
read these encrypted votes from the network, decrypt
them, and proceed to the tally. The final stage is the
verification phase. During this phase, voters make
sure that their votes has been considered correctly and
check the accuracy of the tally. The individual verifia-
bility is ensured thanks to the counter-values included
in each ballot and the universal verification is ensured
thanks to the homomorphism property of pairings.
Except the enrollment phase, all the phases of our pro-
tocol are on-chain. Therefore, we call the PBFT based
consensus protocol with each transaction initiated by
authorities and BlindCons with each transaction initi-
ated by eligible voters because we don’t need to hide
the identity of our authorities but we need to ensure
voter’s privacy. In the following, we give a detailed
description of the role of our protocol stakeholder, its
phases and the two consensus.
3.1 Protocol Stakeholder
DABSTERS in e-voting involves three main entities:
• Registration Authorities (RAs): they verify the el-
igibility of every person wishing to register to the
election and provide only eligible voters by their
credentials which are constructed by cooperation
between all RAs.
• Eligible Voters (V): every eligible voter (V
i
) has
the right to vote more than once before the end of
the voting phase and only his last vote is counted.
Voters have the possibility to verify that their
votes are cast as intended and counted as cast dur-
ing the verification phase. Also, they can check
the accuracy of the election final result but they
are not obliged to participate to the verification
phase (they can vote and go).
DABSTERS: Distributed Authorities using Blind Signature to Effect Robust Security in e-Voting
231

• Tallying Authorities (TAs): the protocol includes
as many tallying authorities as candidates. They
construct n ballots, where n is the number of reg-
istered voters, thus every voter has a unique ballot
which is different from the other ballots, before
the voting phase, encrypt and send them to vot-
ers during the voting phase, decrypt votes and cal-
culate the election final result during the tallying
phase and publish the different values that allow
voters to check the accuracy of the count during
the verification phase.
DABSTERS in e-voting also involves observers and
election organizers who have the right to host the
Blockchain peers to ensure the correctness of the ex-
ecution of the protocol.
3.2 Protocol Stages
Our solution includes the following phases:
3.2.1 Enrollment Phase
Every person who has the right to vote and desires
to do so, physically goes to the nearest registration
station. He provides his national identity card to the
RAs, who verify his eligibility by checking if his
name and ID card number exists in a list, previously
published, contains all persons that are able to partic-
ipate in the election. If he is an eligible voter, the RAs
save the number of his ID card and provide him with
a credential that allows him to participate in the vot-
ing process. Voters’ credentials are calculated using
elliptic curve cryptography and have this form:
Credential
V
i
= S
M
· H
1
(ID
V
i
) where:
• S
M
= S
1
·S
2
. . . S
R
is a secret master key calculated
by cooperation between all RAs. Each registra-
tion authority participates with its secret fragment
S
r
; r ∈ {1 . . . R},
• H
1
is an hash function defined as follows: H
1
:
{0, 1}
∗
→ G
1
; G
1
an additive cyclic group of order
prime number q,
• ID
V
i
is the number of the ID card of the voter V
i
.
3.2.2 Validation Phase
After registering all eligible voters, RAs create a list
containing the names and the identity card numbers
of all registered voters. This list should be viewable
and verifiable by voters, election organizers and ob-
servers. Thus, RAs send this list in a transaction
on our election Blockchain. This transaction passes
through the five steps of the PBFT based consensus
protocol to be validated if the list is correct or rejected
if the list contains names of ineligible voters.
• Step 1: Transaction Initiation. RAs generate the
list of eligible voters to be validated by the net-
work. The list is sent to a submitter peer (SP).
In the case of an offline or misbehaving SP, RAs
send the transaction to the next one. The structure
of the message is as follow:
< SUBMIT,ID
RA
, List, T xPayload, σ
RA
> where:
– ID
RA
: is the ID of the registration authorities,
– W rite(List): is the operation invoked by the
RAs to be executed by the network. It consists
of writing the list of eligible voters and their ID
card numbers in the Blockchain,
– List: is the payload of the submitted transac-
tion, which is the list of registered voters to be
published on the Blockchain,
– σ
RA
: is the signature of the RAs,
– retryFlag: is a boolean variable to identify
whether to retry the submission of the transac-
tion in case of the transaction fails.
• Step 2: Transaction Proposal. The SP receives
the transaction and verifies the RAs’ signature.
Then prepares a transaction proposal to be sent
to the endorsing peers (EP). EP are composed
of some voters, election organizers and observers
who desire to host the Blockchain peers. Transac-
tion proposal has the following form:
< PROPOSAL, m
RA
, Trans
prop
> where:
– m
RA
= (ID
RA
,Write(List), List, σ
RA
)
– Trans
prop
= (SP,W rite(List), List, StateU pdate,
VerDep):
∗ StateUpdate corresponds to the state ma-
chine after simulating locally the operation
coming in Write(List).
∗ VerDep is the version dependency associated
to the variable to be created or modified. It is
used to keep the consistency of the variables
across the different machine state version.
• Step 3: Transaction Endorsement. Each EP
verifies the signature of the RAs σ
RA
coming in
m
RA
and checks that the list of eligible voters in
m
RA
and Trans
prop
is the same. Then, each EP
verifies the eligibility of all names and ID card
numbers included in the list. If they are all valid,
the EP generates a transaction valid message to
be sent to the SP. This transaction includes the
following values: < T RANSACT ION − VALID,
T x
ID
, σ
EP
> where:
– T x
ID
is the transaction ID,
– σ
EP
is the signature of the endorser peer.
But if the list includes names of ineligible
voters, the EP generates a transaction in-
valid message, which has the following form:
< T RANSACT ION − INVALID, T x
ID
, Error,
InvalidList, σ
EP
> where:
SECRYPT 2019 - 16th International Conference on Security and Cryptography
232

– Error: can has the following values:
∗ INCORRECT-STATE: when the endorser
tries to validate the transaction with a differ-
ent local version of the Blockchain than the
one coming in the transaction proposal.
∗ INCORRECT-VERSION: when the version
of the variable where the list will be recorded
differs from the one referred in the transaction
proposal.
∗ REJECTED: for any other reason.
– InvalidList: is the list of ineligible names that
were included in the list sent by the RAs.
• Step 4: Broadcasting to Consensus. The SP
waits for the response from the EP. When it re-
ceives enough Transaction Valid messages ade-
quately signed, the peer stores the endorsing sig-
natures into packaged called endorsement. Once
the transaction is considered endorsed, the peer
invokes the consensus services by using broad-
cast(blob), where blob = (Trans
prop
, endorse-
ment). The number of responses and endorsement
to consider the transaction proposal as endorsed is
equal to 50% + 1 of the total number of endorser
peers. If the transaction has failed to collect the
enough endorsements, it abandons this transaction
and notifies the RAs.
• Step 5: Commitment. Once the SP broadcasts
the transaction to consensus, the ordering services
(Or) put it into the current block, which will be
sent to all peers once built. Finally, if the transac-
tion was not validated, the RAs are informed by
the SP.
In the case of an invalid list, the registration au-
thorities have to correct the list and restart the vali-
dation phase. We move to the next phase (which is
the voting phase) only when we obtain a valid list of
registered voters.
3.2.3 Voting Phase
Two entities participate during this phase:
• The TAs who have constructed ballots before
the beginning of the voting phase. To construct
a ballot, TAs calculate, locally, the unique bal-
lot number BN = {g, D}
PK
TA
, the offset value
o f f set = H(g) mod m and the counter-values
CV
BN,name
j
,k
= e(Q
name j
, S
k
· Q
BN
), where g is a
generator of G an additive cyclic group of order
a prime number, D is a random number, PK
TA
is TAs’ public key, m is the number of candi-
dates, e(., .) is the pairing function, S
k
is the se-
cret key of the tallying authority TA
k
, Q
name j
=
H
1
(name
j
) and Q
BN
= H
1
(BN) are two points
of the elliptic curve E. Then, TAs choose, ran-
domly, a blank ballot for each voter, encrypt it
with the voter’s public key and transmit it to the
corresponding voter via the Blockchain. Ballots
are sent encrypted because they contain secret in-
formation like the BN, the o f f set and counter-
values. To send encrypted ballots to voters via the
Blockchain, TAs interact with the PBFT consen-
sus peers. These interactions unfold in five steps,
the same steps as those presented in section 3.2.2,
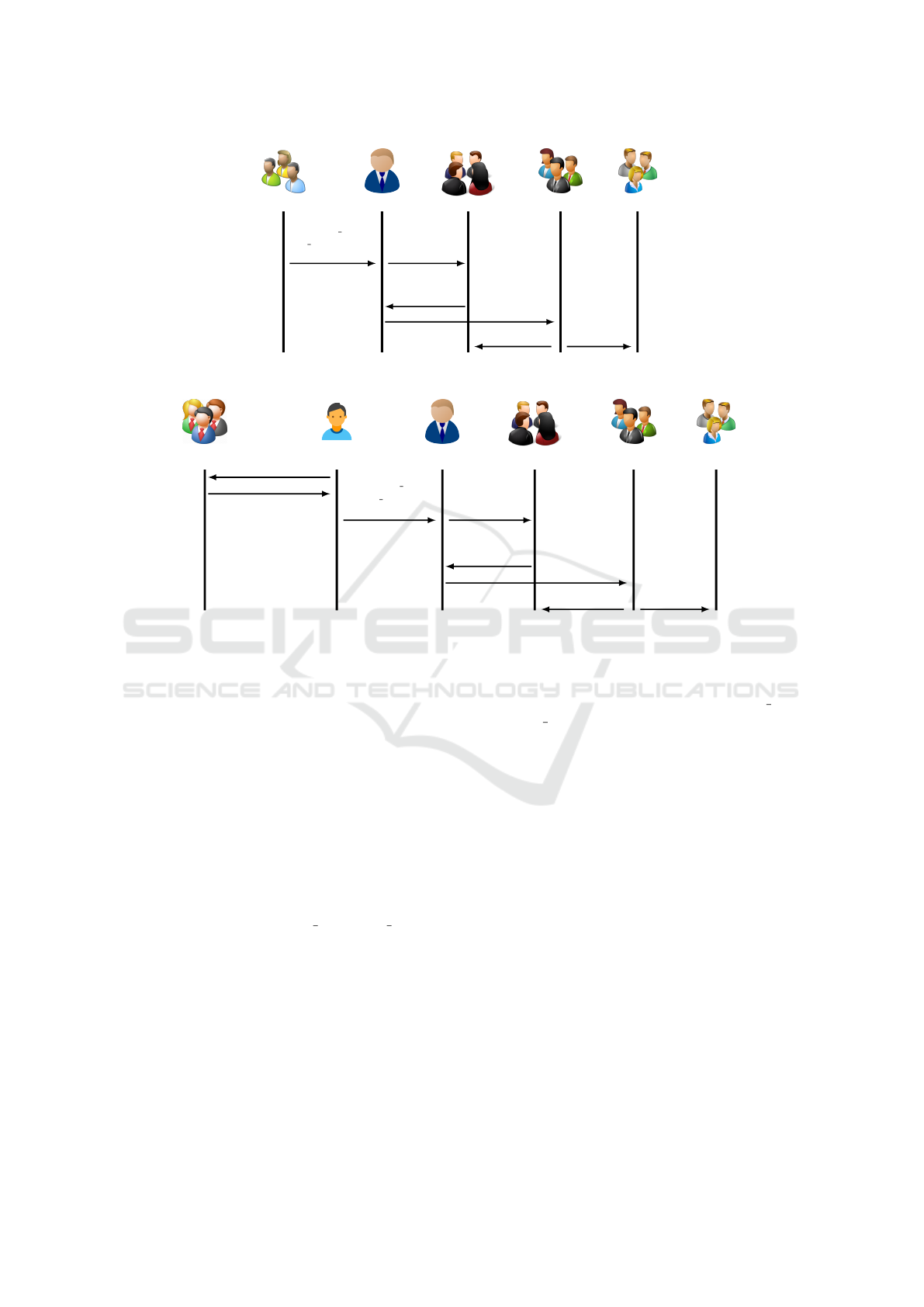
and described in Figure 2.
1. Transaction Initiation. TAs initiate a transac-
tion and send it to a SP. The transaction con-
tains their ID (ID
TA
), the list of encrypted bal-
lots, the transaction payload, their signature
(σ
TA
) and the value of the variable retryFlag.
2. Transaction Proposal. SP verifies the
TAs signature and prepares a transaction
proposal Trans
prop
= (SP,Write(Enc Ballot),
Enc Ballot, stateU pdate,VerDep) to be sent
to the EP with the TAs message m
TA
=
(ID
TA
,Write(Enc Ballot), Enc Ballot, σ
TA
)
3. Transaction Endorsement. EP verifies σ
TA
coming in m
TA
, simulates the transaction pro-
posal and validates that the stateU pdate and
verDep are correct. If the validation process is
successful, the endorser peer generates a trans-
action valid message to be sent to the SP.
4. Broadcasting to Consensus. When the SP
receives a number of Transaction Valid mes-
sage equals to 50% + 1 of the total num-
ber of endorser peers, adequately signed, he
stores the endorsing signatures into an endorse-
ment package and invokes the consensus ser-
vices by using broadcast(blob); wher blob =
(Trans
prop
, endorsement).
5. Commitment. Ordering services (Or) add
the transaction to a block. Once the Or col-
lects enough endorsed transactions to construct
a block, he broadcasts the new block to all
other peers. A block has the following form:
B = ([tx
1
,tx
2
, . . . ,tx
k
];h) where h corresponds
to the hash value of the previous block.
• Every eligible voter retrieves his ballot, decrypts
it using his secret key and encrypts his vote by
voting then sends it in a transaction through the
Blockchain. To encrypt his vote, the voter uses the
Identity Based Encryption and encrypts his ballot
number BN with Q
C
j
= H
1
(C
j
) where C
j
is the
pseudo ID of the chosen candidate. Thus, each en-
crypted vote has the following form: Enc Vote =
{BN}
Q
C
j
.
To be read from the Blockchain or be written on it,
voters’ transactions pass through the blinded sig-
nature consensus. We model in Figure 3 the steps
through which a transaction of an eligible voter
DABSTERS: Distributed Authorities using Blind Signature to Effect Robust Security in e-Voting
233
TAs
SP
EP
SUBMIT, ID
TA
,
Write(Enc Ballot),
Enc Ballot, σ
TA
,
retryFlag
Or
PROPOSAL, m
TA
,
Trans
prop
P
TRANSACTION
-VALID, Tx
id
,σ
ep
broadcast(blob)
B = ([T x
1
, T x
2
,
. . . , T x
k
], h)
B = ([T x
1
, T x
2
,
. . . , T x
k
], h)
Figure 2: Interaction between TAs and peers.
RAs
V
BlindSign(M, (β, γ, δ), y)
SP
(ρ, σ, ε)
EP
SUBMIT, Credential
V
i
,
Write(Enc vote),
Enc vote,
retryFlag, (ρ, σ, ε)
Or
PROPOSAL,
m
V
i
, trans
prop
P
TRANSACTION
-VALID, Tx
id
,
σ
ep
broadcast(blob)
B = ([T x
1
, T x
2
,
. . . , T x
k
], h)
B = ([T x
1
, T x
2
,
. . . , T x
k
], h)
Figure 3: Interactions between eligible voter and BlindCons peers.
passes. We take the example of a transaction con-
taining an encrypted vote.
During the interactions between TAs and peers,
we use the digital signature as user authentica-
tion method without protecting the TAs privacy
because we do not need to hide the identity of our
protocol authorities. However, when it comes to
interactions between voters and peers, we need to
preserve voters’ privacy by blinding their signa-
tures. The privacy preserving consensus adds two
steps:
i) The signature of each eligible voter is blinded
automatically after the vote is cast by the func-
tion BlindSign(M, (β, γ, δ), PK
RA
), where M =
(Credential
V
i
||W rite(Enc Vote)||Enc vote,
retryFlag) is the message to be signed, (β, γ , δ)
are secret values randomly chosen by the voter
and PK
RA
is the public key of the RAs.
ii) RAs blind the signature of each eligible voter
by providing him the tuple (R, S) to construct
his blinded signature (ρ, σ, ε) to be used during
his interactions with the peers.
The other steps are the same as the PBFT based
consensus, but instead of sending their signatures,
the voters send their blinded signatures provided
by the RAs.
1. Initiating Transaction:
<SUBMIT, Credential
V
i
, W rite(Enc Vote),
Enc vote, retryFlag, (ρ, σ, ε) >
2. Transaction Proposal:
<PROPOSAL,m
V
i
,trans
prop
>
3. Transaction Endorsement:
< TRANSACTION-VALID, T x
id
, σ
ep
>
4. Broadcasting to Consensus: broadcast(blob)
5. Commitment: B = ([T x
1
, T x
2
, . . . , T x
k
], h)
The voters who intend to verify that their votes
were properly counted must memorize the counter-
values that correspond to their chosen candidates be-
fore casting their votes.
3.2.4 Tallying Phase
After all votes have been cast, TAs proceed to the
tally. We have as many TAs as candidates. Each tally-
ing authority TA
k
is responsible for counting the num-
ber of votes for a specific pseudo ID C
j
: for exam-
ple the first tallying authority TA
1
decrypts, with its
secret key S
1
· Q
C
1
, all bulletins that were encrypted
with the public key Q
C
1
(certainly these ballots con-
tain votes for candidates with C
j
= 0). TA
k
starts by
initiating a transaction to read encrypted votes from
SECRYPT 2019 - 16th International Conference on Security and Cryptography
234

the Blockchain. This transaction passes through the
five steps of the PBFT based consensus. Then, it de-
crypts the votes with its secret key S
k
that were en-
crypted with Q
C
j
in order to reveal the bulletin num-
ber BN. Then, it reconstructs the ballot, identifies
the chosen candidate, and added to the correspond-
ing counter. At the end of this phase, TA
k
publishes
the count for each candidate using the following for-
mula: σ
k,name
j
=
l
j
∑
i=1
S
k
· Q
BN
i
where l
j
is the number
of votes received by the candidate j, S
k
is the private
key of the tallying authority k, Q
BN
i
= H
1
(BN
i
) and
BN
i
is the ballot number of the vote i that corresponds
to the candidate with name name
j
.
3.2.5 Verification Phase
This phase allows voters to check that their votes were
counted as cast and that the election final result corre-
sponds to the sum of all eligible votes. It includes two
sub-phases. During the first one, TAs calculate the list
of chosen counter-values from each ballot number and
the name of the chosen candidate, and publish this list
on the Blockchain. Each eligible voter can read this
list and verify the existence of his counter-value to
be sure that his vote was counted correctly. The sec-
ond sub-phase uses the homomorphism of pairings to
check the accuracy of the tally. Using the published
counts and the reconstructed counter-values, we can
verify that the announced result corresponds to the
sum of all eligible votes, as follows:
l
∏
i=1
CV
BN
i
=
m
∏
k=1
m
∏
j=1
l
j
∏
i=1
CV
BN
i,name
j
,k
=
m
∏
k=1
m
∏
j=1
l
j
∏
i=1
e(Q
name
j
, S
k
· Q
BN
i
)
=
m
∏
k=1
m
∏
j=1
e(Q
name
j
,
l
j
∑
i=1
S
k
· Q
BN
i
)
=
m
∏
k=1
m
∏
j=1
e(Q
name
j
, σ
k,name
j
) (1)
Where l =
m
∑
j=1
l
j
is the total number of votes. These
equalities use the bilinear property of pairing:
l
j
∏
i=1
e(Q
name
j
, S
k
· Q
BN
i
) = e(Q
name
j
,
l
j
∑
i=1
S
k
· Q
BN
i
)
4 CONCLUSION
We proposed a fully decentralized e-voting sys-
tem that combines several security properties, called
DABSTERS in e-voting. It uses a new architecture
that allows enhancement of the security of e-voting
systems and guarantees the trustworthiness required
by voters and election organizers. It is designed to be
implemented on private Blockchains and uses a new
blinded signature consensus algorithm to guarantee
vote integrity and voter’s privacy due to the unlink-
ability property that the blinded signature has. Future
work will be dedicated to evaluating the performance
and the scalability of this protocol.
ACKNOWLEDGEMENTS
This paper is supported by European Union’s Horizon
2020 research and innovation programme under grant
agreement No 780121, project PTwist.
REFERENCES
Androulaki, E., Barger, A., Bortnikov, V., Cachin, C.,
Christidis, K., Caro, A. D., Enyeart, D., Ferris, C.,
Laventman, G., Manevich, Y., et al. (2018). Hyper-
ledger fabric: a distributed operating system for per-
missioned blockchains. In Proceedings of the Thir-
teenth EuroSys Conference, EuroSys 2018, Porto, Por-
tugal, April 23-26, 2018, pages 30:1–30:15. ACM.
Buterin, V. (2014). A next generation smart contract & de-
centralized application platform.
Chaieb, M., Yousfi, S., Lafourcade, P., and Robbana, R.
(2018). Verify-your-vote: A verifiable blockchain-
based online voting protocol. In Themistocleous, M.
and da Cunha, P. R., editors, Information Systems -
15th European, Mediterranean, and Middle Eastern
Conference, EMCIS, 2018, Proceedings, volume 341
of Lecture Notes in Business Information Processing,
pages 16–30. Springer.
Followmyvote (2012). Follow my vote. https://
followmyvote.com/.
Koscina, M., Lafourcade, P., Manset, D., and Naccache, D.
(2018). Blindcons: A consensus algorithm for pri-
vacy preserving private blockchains. Technical report,
LIMOS. http://sancy.univ-bpclermont.fr/
∼
lafourcade/
BlindCons.pdf.
McCorry, P., Shahandashti, S. F., and Hao, F. (2017). A
smart contract for boardroom voting with maximum
voter privacy. In FC 2017, volume 10322. Springer.
Nakamoto, S. (November 2008). Bitcoin: A peer-to-peer
electronic cash system.
Okamoto, T. (1992). Provably secure and practical identifi-
cation schemes and corresponding signature schemes.
In Crypto 92, pages 31–53. Springer.
P. Udaya, S. N. and Teague, V. (2007). A secure electronic
voting scheme using identity based public key cryp-
tography. In Proceedings of SAR-SSI 2007, Annecy,
France, June 12-16, 2007.
Smartmatic (2016). Tivi. http://www.smartmatic.com/
voting/online-voting-tivi/.
DABSTERS: Distributed Authorities using Blind Signature to Effect Robust Security in e-Voting
235
