
Secure Intersection with MapReduce
Radu Ciucanu
1
, Matthieu Giraud
2
, Pascal Lafourcarde
2
and Lihua Ye
3
1
INSA Centre Val de Loire, Univ. Orl
´
eans, LIFO EA 4022, Bourges, France
2
LIMOS, UMR 6158, Universit
´
e Clermont Auvergne, Aubi
`
ere, France
3
Harbin Institute of Technology, China
Keywords:
Intersection, Database, Privacy, Security, MapReduce.
Abstract:
Relation intersection is a fundamental problem, which becomes non-trivial when the relations to be intersected
are too large to fit on a single machine. Hence, a natural approach is to design parallel algorithms that are
executed on a cluster of machines rented from a public cloud provider. Intersection of relations becomes even
more difficult when each relation belongs to a different data owner that wants to protect her data privacy. We
consider the popular MapReduce paradigm for outsourcing data and computations to a semi-honest public
cloud. Our main contribution is the SI protocol (for Secure Intersection) that allows to securely compute the
intersection of an arbitrary number of relations, each of them being encrypted by its owner. The user allowed
to query the intersection result has only to decrypt the result sent by the public cloud. SI does not leak (to the
public cloud or to the user) any information on tuples that are not in the final relation intersection result, even
if the public cloud and the user collude i.e., they share all their private information. We prove the security of
SI and provide an empirical evaluation showing its efficiency.
1 INTRODUCTION
The outsourcing of data and computation to the
cloud is a frequent scenario in modern applications.
While many cloud service providers with an impor-
tant amount of data storage and of power computation
(e.g., Google Cloud Platform, Amazon Web Services,
Microsoft Azure) are available for a reasonable price,
they do not usually address the fundamental problem
of protecting the privacy of users’ data.
We consider the problem of intersection of an ar-
bitrary number of relations, each of them belonging
to a different data owner. We rely on the popular
MapReduce (Dean and Ghemawat, 2004) paradigm
for outsourcing data and computations to a semi-
honest public cloud. Our goal is to compute the re-
lations’ intersection while preserving the data privacy
of each of the data owners. We develop a protocol
based on public-key cryptography where each par-
ticipant encrypts and sends their respective relation
on the public cloud. The public cloud cannot learn
neither the input nor the output data, but may learn
only the number of tuples in the intersection. At the
end of the computation, the public cloud sends the
result to the final user, who only has to decrypt the
received data. Moreover, if the public cloud and the
user collude, i.e., the public cloud knows the user’s
private key, then they cannot learn other information
than the intersection result. Secure intersection has a
lot of applications such that privacy-preserving data
mining (Aggarwal and Yu, 2008), homeland secu-
rity (Cristofaro and Tsudik, 2010), human genome re-
search (Baldi et al., 2011), Botnet detection (Nagaraja
et al., 2010), social networks (Mezzour et al., 2009),
and location sharing (Narayanan et al., 2011).
1.1 Intersection with MapReduce
A protocol to compute the intersection between two
relations with MapReduce is presented in Chapter 2
of (Leskovec et al., 2014). We note that intersection
between relations can be viewed as intersection be-
tween sets where elements of these sets correspond
to the tuples of relations having the same schema. In
Chapter 2 of (Leskovec et al., 2014), the public cloud
receives two relations from their respective owner. A
collection of cloud nodes has chunks of these two re-
lations. The Map function creates for each tuple t a
key-value pair (t,t) where key and value are equal to
the tuple. Then, the key-value pairs are grouped by
key, i.e., key-value pairs output by the map phase that
have the same key are sent to the same reducer (i.e.,
236
Ciucanu, R., Giraud, M., Lafourcarde, P. and Ye, L.
Secure Intersection with MapReduce.
DOI: 10.5220/0007918902360243
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 236-243
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the application of the Reduce function to a single key
and its associated values). For each key, the Reduce
function checks if the considered key is associated to
two values. If it is the case, i.e., tuple t is present
in both relations, then the public cloud produces and
sends the pair (−,t) to the user. The dash value “−”
corresponds to the empty value, we use it to be con-
sistent with the key-value result form required by the
MapReduce paradigm. Hence, all tuples received by
the user correspond to the tuples that are in both rela-
tions. However, the key is irrelevant at the end of the
protocol, hence we often omit to write it. We illustrate
this approach with the following example considering
three relations.
Example: We consider three relations: NSA,
GCHQ, and Mossad. Each relation is owned by their
respective data owner. These three relations have the
same schema composed of only one attribute, namely
“Suspect’s ID”. They are defined as follows: NSA =
{F654,U840, X098}, GCHQ = {F654, M349,P027},
and Mossad = {F654,M349,U840}. An external user,
called Interpol, wants to receive the intersection of
these three relations denoted Interpol. We illus-
trate the execution of intersection computation with
MapReduce for this setting in Figure 1. First, each
data owner outsources their respective relation into
the public cloud. Then, the public cloud runs the
map function on each relation and sends the output to
the master controller in order to sort key-value pairs
by key. Then, the master controller sends key-value
pairs sharing the same key to the same reducer. In
our example, we obtain 5 reducers since there are 5
different suspect’s identities. The reducer associated
to the key F654 has three values since the identity
F654 is present in the three relations NSA, GCHQ,
and Mossad. The reducer associated to the key M349
has two values since the identity M349 is only present
in relations GCHQ and Mossad. Other reducers are
associated to only one value since the corresponding
suspect’s identity is present in only one relation. For
each reducer, the public cloud runs the reduce func-
tion and sends the tuple (−, ID) to the user if the sus-
pect’s identity ID is present is the three relations, else
the public cloud sends nothing. In our example, we
observe that the user Interpol only receives the pair
(−,F654) since the suspect’s identity F654 is present
in the three relations NSA, GCHQ, and Mossad.
1.2 Problem Statement
We assume n + 2 parties: n data owners, the public
cloud, and the external user (simply referred as user
in the following). Each data owner is trusted (i.e.,
they dutifully follow the protocol and do not collude
with other party) and outsources a relation R
i
, with
i ∈ J1,nK, to the public cloud, denoted C . We denote
by R
i
the owner of the relation R
i
for i ∈ J1,nK. A
user, denoted U, and who does not know the individ-
ual relations R
i
is authorized to query the intersection
of these n relations.
We assume that the public cloud is semi-
honest (Lindell, 2017), i.e., it executes dutifully the
computation task but tries to learn the maximum of
information on relations R
i
and on their intersection.
In the original protocol (Leskovec et al., 2014), tuples
of each relation are not encrypted, hence the public
cloud learns all the content of each relation and the
result of the intersection that it sends to the user as
illustrated in Figure 1. To preserve data owners’ pri-
vacy, the cloud should not learn any plain input data,
contrary to what happens for the original protocol.
Moreover, we assume that the public cloud can
collude with the user, i.e., they share all their respec-
tive private information. We want that the user that
queried the intersection of these n relations may learn
nothing else than the intersection of the n relations,
even in case of collusion with the public cloud.
1.3 Contributions
We revisit the standard protocol for the computa-
tion of intersection with MapReduce (Leskovec et al.,
2014) and propose a new protocol called SI (for Se-
cure Intersection) that satisfies our aforementioned
problem statement. More precisely:
• Our protocol SI guarantees that the user who
queries the intersection of the n relations learns
only the final result. Moreover, the public cloud
does not learn information about the input data
that belongs to the data owners, it learns only the
cardinal of each relation and of the intersection.
SI also satisfies the problem setting in the pres-
ence of collusion between the user and the public
cloud. The security proof of our protocol is given
in the extended version available online
1
.
• To show the practical scalability of SI, we present
experimental results using the MapReduce open-
source implementation Apache Hadoop 3.2.0.
• Our protocol SI is efficient from both computa-
tion and communication points of view. The over-
head for the computation complexity is linear in
the number of tuples by relation while the com-
munication complexity is the same as in the stan-
dard protocol (Leskovec et al., 2014). Our tech-
nique is based on classical cryptographic tools
such that pseudo-random function, asymmetric
1
https://hal.archives-ouvertes.fr/hal-02129141
Secure Intersection with MapReduce
237

Data owners
Relations
NSA
GCHQ
Mossad
Map
NSA
GCHQ
Mossad
Master Controller
Public cloud
Key F654
Values
F654
F654
F654
Key M349
Values
M349
M349
Key P027
Value P027
Key U840
Value U840
Key X098
Value X098
Reduce
User
Relation Interpol
(−,F654)
Figure 1: Example of intersection with MapReduce between three relations.
Protocol Comp. cost Com. cost
Standard 2nN (n + 1)N
SI
C
E
· N
(n + 1)N+C
f
· (3n − 2)
+C
⊕
· (2N · (n − 2))
Figure 2: Trade-offs between computation and communica-
tion costs for our secure protocol SI vs the standard MapRe-
duce protocol. Let N = max(|R
1
|,. .. ,|R
n
|). Let C
f
(resp.
C
E
, C
⊕
) be the computation cost of a pseudo-random func-
tion evaluation (resp. asymmetric encryption, xor opera-
tion).
and one-time-pad encryptions. We summarize in
Figure 2 the trade-offs between computation and
communication costs for our secure protocol SI vs
the standard MapReduce protocol computing the
intersection of n ≥ 2 relations. In our communica-
tion cost analysis, we measure the total size of the
data that is emitted from a map or reduce node.
1.4 Related Work
As previously mentioned, a relation can be seen as
a set where tuples are set’s elements. Private Set
Intersection (PSI) refers to the cryptographic prim-
itive where two parties compute the intersection of
their respective sets such that minimal information
is revealed during the process. It was introduced by
Freedman et al. (Freedman et al., 2004). The aim of
such a primitive is to allow the two parties to learn
the elements common to both sets and nothing else.
Such primitives where neither party has any advan-
tage over the other and where all parties know the
intersection are called mutual PSI (Cristofaro et al.,
2010). On the contrary, primitives where only one
party learns the intersection of the two sets while the
other learns nothing are called one-way PSI (Cristo-
faro et al., 2010). Contrary to these approaches, our
protocol SI does not reveal any information on the in-
tersection to the data owner. Only the user knows the
intersection.
The seminal work (Freedman et al., 2004) uses
two-party computation and partial homomorphic en-
cryption allowing two owners to securely compute
the intersection of two sets. The proposed protocol
is proven against semi-honest adversaries in the stan-
dard model and also proven for a malicious adversary
in random oracle model. Authors consider one client
and one server, each of them owning a secret dataset
where the client sends polynomial coefficients associ-
ated to her dataset in an encrypted way to the server.
At the end of the protocol the server knows which ele-
ments are shared with the server while the later learns
nothing. In our protocol SI, we consider an arbitrary
number of clients owning different relations and using
a semi-honest public cloud to send the intersection of
the relations to the user.
Following this work, (Hazay and Nissim, 2010)
proposed an improved construction considering the
presence of a malicious adversaries in the standard
model. Contrary to us, the complexity of this con-
struction still remains not linear in the number of el-
ements in sets. (Cristofaro et al., 2010), and (Kissner
and Song, 2005) proposed protocols for mutual PSI
with linear complexity while in our protocol the user
does not have any set to intersect. The scheme pro-
posed by (Cristofaro et al., 2010) considers a mali-
cious adversary using zero-knowledge proofs. Their
scheme requires that the user performs computations
at the beginning and at the end of the protocol while
SECRYPT 2019 - 16th International Conference on Security and Cryptography
238

she has only to decrypt the final result in our protocol.
In the scheme of (Kissner and Song, 2005), each data
owner learns the result of the intersection. In this pa-
per, we consider semi-honest adversary and prove the
security of our protocol in the random oracle model.
As remarked above, the intersection computed by our
protocol is only known by the user and not by the data
owners and the public cloud.
More recently, Hazay and Venkitasubrama-
niam (Hazay and Venkitasubramaniam, 2017) pro-
posed a protocol considering a star topology between
data owners where a designated party first learns the
encrypted cross intersection with other parties, then
deduces the outcome. In our protocol, we consider a
different topology where a public cloud receives en-
crypted sets to intersect and sends the outcome to the
user. In (Kolesnikov et al., 2017), the authors pro-
posed a protocol based on oblivious programmable
PRF (OPPRF) where each party has to compute a
share of zero for each set’s element in a coordinate
way. The outcome is obtained by a centralized data
owner considering only OPPRF evaluations that are
equal to zero. In our protocol, the user that queries
the intersection is not a data owner, moreover, data
owners just have to share PRF secret keys and no to
perform secret sharing computation.
Outline. We introduce the needed cryptographic
tools in Section 2. We recall the standard MapReduce
set intersection protocol and present our secure proto-
col SI in Section 3. Before to conclude, we present in
Section 4 experimental evaluations of SI protocol.
2 CRYPTOGRAPHIC TOOLS
We recall definitions of public-key encryption scheme
and of pseudo-random function used in SI.
Definition 1 (Public-key encryption). Let η be a se-
curity parameter. A public-key encryption (PKE)
scheme consists of three algorithms.
• The randomized key generation algorithm G takes
the security parameter to return a public/secret
key pair (pk, sk).
• The encryption algorithm E takes a public key pk
and a plaintext m to return a ciphertext c. We de-
note by E(pk, m) the encryption of m.
• The deterministic decryption algorithm D takes a
secret key sk and a ciphertext c to return a corre-
sponding plaintext m or a special symbol ⊥ indi-
cating that the ciphertext was invalid. We denote
by D(sk,c) the decryption of c.
Definition 2 (Pseudo-random function). Let η be a
security parameter. A pseudo-random function (PRF)
F is a deterministic algorithm that has two inputs:
k ∈ {0, 1}
`(η)
(where `(·) is a polynomial function),
and x ∈ X . Its output is y := F(k,x) ∈ Y . We said
that F is defined over ({0,1}
`(η)
,X ,Y ).
In the rest of the paper, we assume that data of par-
ticipants are included in X , and the size of Y is larger
enough to avoid collisions. Moreover, we denote by
f
k
(·) = F(k,·) an instance of F.
3 MAPREDUCE INTERSECTION
We consider n ≥ 2 data owners, each of them owning
a relation. These n relations have the same schema
and are denoted R
1
,. . . , R
n
. We first recall in Sec-
tion 3.1 the standard MapReduce protocol to perform
the intersection of n relations, i.e., a simple general-
ization of the binary protocol presented in Chapter 2
of (Leskovec et al., 2014). This protocol obviously
does not verify privacy properties of our problem set-
ting since the public cloud learns all tuples of each
relation sent by the respective data owner, and the in-
tersection of these n relations sent to the user. Then
we present in Section 3.2 our secure protocol denoted
SI that computes the intersection of n relations using
MapReduce. We prove that contrary to the standard
protocol, SI guarantees that the public cloud learns
only cardinals of relations R
i
for i ∈ J1, nK. Moreover,
if the public cloud and the user collude, then they
learn the intersection of these n relations that the user
still knows, and cardinals of relations R
i
for i ∈ J1, nK
that the public cloud still knows, and nothing else.
3.1 Standard MapReduce Intersection
In the standard protocol (Leskovec et al., 2014), the
Map function creates for each tuple t of each relation
R
i
, with i ∈ J1,nK, a key-value pair where the key and
the value are equal to the tuple t. For a key t, the as-
sociated reducer receives a list of tuples t. Hence, if
a tuple t is only present in one relation, the reducer
receives a collection only composed of one tuple t.
On the contrary, if a tuple t
0
is present in all the n re-
lations, the reducer receives a collection of n tuples
equal to t
0
. If a key t is associated to a collection
of n tuples t, then the Reduce function produces the
key-value pair (−,t) and sends it to the user. Other-
wise, it produces nothing. All key-value pairs out-
putted by the Reduce function constitute the result
of the intersection of the n relations. We present the
standard protocol computing the intersection protocol
with MapReduce in Figure 3.
Secure Intersection with MapReduce
239

Map function:
// key: id of a chunk of R
i
// value: collection of tuples t ∈ R
i
foreach t ∈ R
i
do
emit (t,t).
Reduce function:
// key: tuple t ∈ ∪
n
i=1
R
i
// values: collection of tuples t
L = [ ]
foreach v ∈ values do
L ← L ∪ {v}
if |L| = n then
emit (−,t).
Figure 3: MapReduce protocol to compute the intersection
of n relations.
We now consider a semi-honest public cloud per-
forming the intersection of n relations with MapRe-
duce. In such a scenario, the public cloud learns all
the content of each relation along with the intersec-
tion of these n relations.
3.2 Secure MapReduce Intersection
In order to compute intersection with MapReduce in a
privacy-preserving way between n ≥ 2 relations, our
protocol uses pseudo-random function, asymmetric
and one-time encryptions. We denote by F a secure
pseudo-random function defined over (K , X ,Y ) and
by Π = (G,E,D) an IND-CPA asymmetric encryp-
tion scheme. We also assume that the length of val-
ues outputted by the pseudo-random function is equal
to the length of ciphertext outputted by the asymmet-
ric encryption scheme. In practice, we can use the
Advanced Encryption Standard (AES) (Daemen and
Rijmen, 2002) with the Cipher Block Chaining mode
on padded message in order to obtain a ciphertext of
the same length than the ciphertext obtained with the
asymmetric encryption.
Preprocessing of our Secure Protocol SI. Before
outsourcing their relation to the public cloud, data
owners perform a key setup and a preprocessing on
their respective relation R
i
to obtain a protected re-
lation denoted R
∗
i
. We present the key setup and the
preprocessing phase in Figure 4.
First, we need a secret key k
1
∈ X that is shared
between the n data owners. Moreover we need n − 1
other secret keys k
i
∈ K (for 2 ≤ i ≤ n) such that
k
i
6= k
j
for i 6= j. Key k
i
with i ≥ 2 is shared between
the owner of relation R
1
and the owner of relation R
i
.
Hence, the owner of relation R
1
has a set of secret
keys equals to {k
1
,k
2
,. . . , k
n
} while the owner of re-
lation R
i
(for 2 ≤ i ≤ n) has a set of secret keys equals
to {k
1
,k
i
}. We note that the choice of owner of rela-
tion R
1
knowing all the secret keys is arbitrary, and we
call the associated relation, i.e., R
1
, the main relation.
Preprocessing:
// input: relation R
i
with i ∈ J1,nK
// outputs: protected relation R
∗
i
for 1 ≤ i ≤ n do k
i
$
← K ;
R
∗
i
←
/
0;
if i = 1 then
foreach t ∈ R
1
do
R
∗
1
← R
∗
1
∪ {( f
k
1
(t),(E(pk,t) ⊕
n
j=2
f
k
j
(t)))}
else
foreach t ∈ R
i
do
R
∗
i
← R
∗
i
∪ {( f
k
1
(t),( f
k
i
(t)))}
return R
∗
i
.
Figure 4: Preprocessing of our secure protocol SI run by
each data owner.
The aim of this preprocessing is to protect owners’
data in order to avoid the public cloud to learn tuples
of each relation and the result of the intersection sent
to the user. Moreover, this preprocessing is in agree-
ment with the MapReduce paradigm. Indeed, each
protected relation R
∗
i
is composed of tuples under the
key-value pair form.
First of all, each key of pairs of R
∗
i
is a pseudo-
random evaluation of a tuple using the secret key k
1
known by each data owner. Since a pseudo-random
function is deterministic, equal tuples share the same
value of key. Hence, the map phase sends these key-
value pairs to the same reducer as expected.
Moreover, each value of key-value pairs of the
protected relation R
∗
1
is equal to the encryption of
the tuple using the asymmetric encryption scheme Π
with the user public key pk xored by n − 1 pseudo-
random evaluations of the tuple using secret keys
k
2
,. . . , k
n
. More precisely, for each tuple t ∈ R
1
, the
preprocessing computes the key-value pair equals to
( f
k
1
(t),E(pk,t) ⊕
n
j=2
f
k
j
(t)). Hence, when the pub-
lic cloud receives such key-value pairs and colludes
with the user, it cannot learn the value of tuples since
the asymmetric encryption is protected by pseudo-
random evaluations, and secret keys k
1
,. . . , k
n
are not
known by the public cloud.
Map and Reduce Phases of SI Protocol. The pre-
processing presented in Figure 4 outputs an encrypted
relation whose tuples are of the key-value pair form.
Hence, once the public cloud receives the n encrypted
SECRYPT 2019 - 16th International Conference on Security and Cryptography
240

relations R
∗
i
(for i ∈ J1,nK) from the data owners, it
runs the Map function that is simply the identity func-
tion.
After the grouping by key, the Reduce function
checks if the current key f
k
1
(t), for t ∈ ∪
N
i=1
R
i
, is as-
sociated to a list of n values. If that is the case, it
means that the n relations contain the tuple associ-
ated to the current key. Then the Reduce function uses
these n values to perform an exclusive or, and obtains
the asymmetric encryption of the tuple E(pk,t) due
the property of the exclusive or.
Finally, the Reduce function produces the key-
value pair (−,E(pk,t)) and sends it to the user. The
output of the Reduce function is in a key-value form
to be consistent with the MapReduce paradigm since
at the end of the SI protocol keys are irrelevant. All
key-value pairs outputted by the Reduce function con-
stitute the intersection of the n relations. The user has
only to decrypt each value of key-value pair using her
secret key in order to obtain the intersection in plain
form. Our protocol SI is described in Figure 5.
Map function:
// key: id of a chunk of R
∗
i
with i ∈ J1,nK
// values: collection of ( f
k
1
(t),E(pk,t) ⊕
n
j=2
f
k
j
(t))
// or ( f
k
1
(t), f
k
j
(t)) with j ∈ J2,nK
foreach (k, v) ∈ values do
emit (k,v)
Reduce function:
// key: f
k
1
(t) such that t ∈ ∪
n
i=1
R
i
// values: collection of E(pk,t) ⊕
n
j=2
f
k
j
(t) or
f
k
j
(t) // with j ∈ J2,nK
L ← [ ]
foreach v ∈ values do
L ← L ∪ {v}
if |L| = n then
E(pk,t) ← E(pk,t) ⊕
n
j=2
f
k
j
(t) ⊕
n
j=2
f
k
j
(t)
emit (−, E (pk,t))
Figure 5: Map and Reduce functions of SI.
Example. We illustrate our SI protocol following
the example presented in Section 1. First, we perform
the preprocessing on relations: NSA, GCHQ, and
Mossad. We consider relation NSA as the main
relation. The three data owners share the secret key
k
1
, data owners of relations NSA and GCHQ share a
secret key k
2
, and data owners of relations NSA and
Mossad share a secret key k
3
. Hence, after the pre-
processing phase, we obtain three protected relations
denoted NSA
∗
, GCHQ
∗
, and Mossad
∗
: NSA
∗
has
tuples ( f
k
1
(F65),E (pk, F65) ⊕ f
k
2
(F65) ⊕ f
k
3
(F65)),
( f
k
1
(U84),E (pk, U84) ⊕ f
k
2
(U84) ⊕ f
k
3
(U84)), and
( f
k
1
(X09),E (pk, X09) ⊕ f
k
2
(X09) ⊕ f
k
3
(X09));
GCHQ
∗
has tuples ( f
k
1
(F65), f
k
2
(F65)),
( f
k
1
(M34), f
k
2
(M34)), ( f
k
1
(P02), f
k
2
(P02)); Mossad
∗
has tuples ( f
k
1
(F65), f
k
3
(F65)), ( f
k
1
(M34), f
k
3
(M34)),
( f
k
1
(U84), f
k
3
(U84)). We illustrate the execution of
intersection computation with MapReduce using our
secure protocol SI in Figure 6.
Proof of Correctness. We say that the protocol SI is
correct if for n ≥ 2 relations R
1
,R
2
,. . . R
n
, SI returns
the correct intersection of the n ≥ 2 relations, i.e., the
encrypted relation composed of pairs (−,E (pk,t))
such that t ∈ R, where R := ∩
n
i=1
R
i
.
Lemma 1. Assume that the pseudo-random function
family F perfectly emulates a random oracle, then
protocol SI is correct.
Proof. Let R
1
,R
2
,. . . R
n
be n relations. Let
R
∗
1
,R
∗
2
,. . . R
∗
n
be the corresponding encrypted relations
computed by the preprocessing phase of SI. We set
R := ∩
n
i=1
R
i
.
For each t ∈ R, there exists a key-value pair in rela-
tion R
∗
1
of the form ( f
k
1
(t),E(pk,t) ⊕
n
i=2
f
k
i
(t)), and
a key-value pair in relation R
∗
j
, with 2 ≤ j ≤ n, of
the form ( f
k
1
(t), f
k
j
(t)). Following the MapReduce
paradigm, the n values are sent to the same reducer
that sums the corresponding values. Thus, for each
key f
k
1
(t), with t ∈ R, we obtain:
E(pk,t) ⊕
n
i=2
f
k
i
(t) ⊕
n
i=2
f
k
i
(t) = E(pk,t) .
Hence, for each t ∈ R, reducer associated to the key
f
k
1
(t) emits the pair (−,E(pk,t)) to the user. More-
over, for each t ∈
∪
n
i=1
R
i
\R, the reducer associated
to the key f
k
1
(t) does not output the pair (−,E(pk,t))
since it is associated to less than n values. Finally,
SI produces pairs (−,E(pk,t)) such that t ∈ R corre-
sponding to the intersection of relations R
1
,R
2
,. . . , R
n
which concludes the proof.
4 EXPERIMENTAL RESULTS
We present an experimental comparison between
the standard MapReduce set intersection proto-
col (Leskovec et al., 2014), and our secure protocol
SI. We run two types of experiments, where we vary
two different parameters: the number of tuples per re-
lation for a fixed number of 2 relations, and the num-
ber of intersected relations.
Secure Intersection with MapReduce
241
Data owners
Relations
NSA
∗
GCHQ
∗
Mossad
∗
Map
NSA
∗
GCHQ
∗
Mossad
∗
Master Controller
Public cloud
Key f
k
1
(F65)
Values
E(pk,F65) ⊕
3
j=2
f
k
j
(F65)
f
k
2
(F65)
f
k
3
(F65)
Key f
k
1
(M34)
Values
f
k
2
(M34)
f
k
3
(M34)
Key f
k
1
(P02)
Value f
k
2
(P02)
Key f
k
1
(U84)
Value f
k
3
(U84)
Key f
k
1
(X09)
Value E(pk,X09) ⊕
3
j=2
f
k
j
(X09)
Reduce
User
Relation Interpol
(−,F65)
Figure 6: Example of intersection with MapReduce between three relations using our secure protocol SI.
Settings. We have done all computations on a clus-
ter running Ubuntu Server 16.04 LTS with Hadoop
3.2.0 using Java 1.8.0. We use the Hadoop streaming
utility and implement the Map and Reduce functions
in Golang 1.6.2. The cluster is composed of one mas-
ter node and of ten slave nodes. Each node has four
CPU cadenced to 2.4 GHz, 80 GB of disk, and 8 GB
of RAM.
According to our SI protocol, we use as pseudo-
random function the Advanced Encryption Standard
(AES) symmetric encryption scheme in Cipher Block
Chaining (CBC) encryption mode with a key size of
128 bits. For the purpose of our protocol, the initial
vector is fixed and common to all data owners. For
the asymmetric encryption scheme, we use the RSA-
OAEP scheme with a key size of 2048 bits and SHA-
256 as hash function.
For each experiment, we report average CPU
times over 8 runs. Since the cluster environment is
not isolated from other machines of the netword, we
do not give measures for the communication cost.
Varying the Number of Tuples. In the experiment
on the number of tuples, we consider two relations
of the same schema composed of only one attribute.
These two relations have the same cardinal C and
share C/2 elements. Tuples of the first relation consist
in all integers from 1 to C, while tuples of the second
relation consist in all integers from C/2 to C +C/2.
We run the original protocol (Leskovec et al., 2014)
and our secure protocol SI on couples of relations of
cardinal 500,000 to 3, 000, 000, by step of 250, 000.
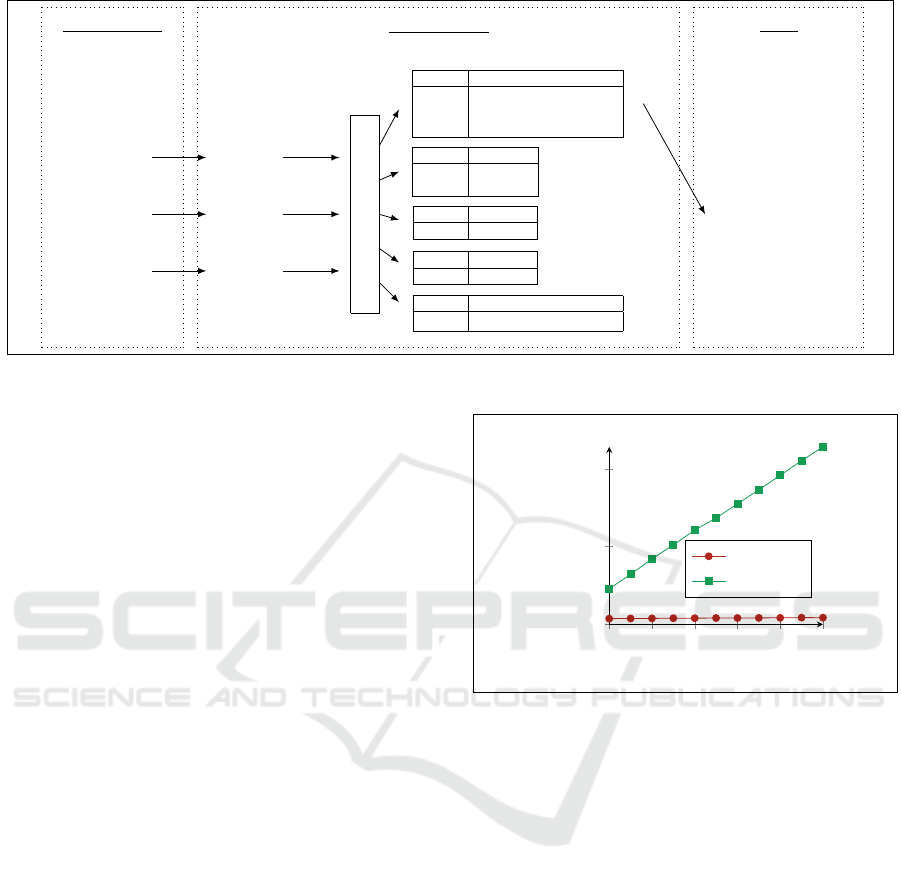
We remark in Figure 7 that the computation com-
plexity of our secure protocol is linear as determined
in the complexity study (cf. Figure 2).
0.5
1
1.5
2
2.5
3
0
1,000
2,000
Number of tuples (in millions).
CPU time (in seconds).
Standard
SI
Figure 7: CPU time vs the number of tuples for the Standard
and SI protocols to compute the intersection between two
relations.
Varying the Number of Intersected Relations. In
the experiment on the number of intersected relations,
we consider intersection between different number of
relations of the same schema composed of only one
attribute. We start by computing the intersection of 2
relations to finish with the intersection of 10 relations.
In each case, relations have 500,000 tuples and shares
250,000 tuples. In practice, for the intersection of
2 ≤ n ≤ 10 relations, tuples of the first relation consist
in integers from 1 to 500,000, and tuples of the i-th
relation, with 2 ≤ i ≤ n, consist in integers from 1 to
250,000 and integers from i · 250, 000 + 1 to (i + 1) ·
250,000.
We compare the standard protocol (Leskovec
et al., 2014) and our secure protocol SI for the ex-
periment on the number of intersected relations. As
shown in Figure 8, the computation complexity of our
secure protocol is linear as determined in the com-
plexity study (cf. Figure 2). We observe that the com-
putation complexity is less compare to the experiment
SECRYPT 2019 - 16th International Conference on Security and Cryptography
242

2 3 4
5 6
7 8 9 10
0
200
400
Number of tuples (in millions).
CPU time (in seconds).
Standard
SI
Figure 8: CPU time of the experiment on the number of
intersected relation on the original protocol(Leskovec et al.,
2014) and of our secure protocol SI.
on the number of tuples. Indeed, when we run the SI
protocols with 10 relations of 500, 000 tuples (i.e., a
total of 5,000, 000 tuples), the CPU time is approx-
imately equals to 550 seconds while the CPU time
for the intersection of 2 relations of 2 millions (i.e.,
a total of 4, 000, 000 tuples) is approximately equals
to 1,500 seconds. This is due to number of common
elements of each relation. In the case of the inter-
section of 10 relations (each composed of 500,000
tuples), relations share 250,000 while in the case of
the intersection of the 2 relations (each composed of
2,000, 000 tuples), relations share 1, 000, 000 tuples.
Hence, the Reduce function has to performs a large
number of exclusive or on 2048-bits strings.
5 CONCLUSION
We have presented an efficient privacy-preserving
protocol using the MapReduce paradigm to compute
the intersection between an arbitrary number of re-
lations. In fact, in the standard protocol (Leskovec
et al., 2014), the public cloud performing the compu-
tation learns all tuples of the data owners along the in-
tersection result that it sends to the user. In our proto-
col SI, the public cloud cannot learn such information
on the input sets. Moreover, if the cloud and the user
collude, then they cannot learn more than the result of
the intersection. If no such a collusion exists, then the
public cloud only learns cardinals of the relations sent
by the data owner, and the cardinal of their intersec-
tion. We have compared the standard and our secure
approach SI with respect to three fundamental criteria:
computation cost, communication cost, and privacy
guarantees. We also implemented SI with the Hadoop
framework and presented empirical results showing
the scalability of SI.
Looking forward to future work, we plan to study
secure set intersection with MapReduce while consid-
ering a malicious public cloud, i.e., the public cloud
can perform any operations on data that it process.
REFERENCES
Aggarwal, C. C. and Yu, P. S. (2008). A general survey
of privacy-preserving data mining models and algo-
rithms. In Privacy-Preserving Data Mining.
Baldi, P., Baronio, R., Cristofaro, E. D., Gasti, P., and
Tsudik, G. (2011). Countering GATTACA: effi-
cient and secure testing of fully-sequenced human
genomes. In CCS.
Cristofaro, E. D., Kim, J., and Tsudik, G. (2010). Linear-
Complexity Private Set Intersection Protocols Secure
in Malicious Model. In ASIACRYPT.
Cristofaro, E. D. and Tsudik, G. (2010). Practical private
set intersection protocols with linear complexity. In
FC.
Daemen, J. and Rijmen, V. (2002). The Design of Rijn-
dael: AES. Information Security and Cryptography.
Springer.
Dean, J. and Ghemawat, S. (2004). Mapreduce: Simplified
data processing on large clusters. In OSDI.
Freedman, M. J., Nissim, K., and Pinkas, B. (2004). Effi-
cient Private Matching and Set Intersection. In EU-
ROCRYPT.
Hazay, C. and Nissim, K. (2010). Efficient Set Operations
in the Presence of Malicious Adversaries. In PKC.
Hazay, C. and Venkitasubramaniam, M. (2017). Scalable
multi-party private set-intersection. In PKC.
Kissner, L. and Song, D. X. (2005). Privacy-preserving set
operations. In CRYPTO.
Kolesnikov, V., Matania, N., Pinkas, B., Rosulek, M., and
Trieu, N. (2017). Practical multi-party private set in-
tersection from symmetric-key techniques. In CCS.
Leskovec, J., Rajaraman, A., and Ullman, J. D. (2014). Min-
ing of Massive Datasets, 2nd Ed. Cambridge Univer-
sity Press.
Lindell, Y. (2017). How to simulate it - A tutorial on the
simulation proof technique. In Tutorials on the Foun-
dations of Cryptography.
Mezzour, G., Perrig, A., Gligor, V. D., and Papadimitratos,
P. (2009). Privacy-preserving relationship path dis-
covery in social networks. In CANS.
Nagaraja, S., Mittal, P., Hong, C., Caesar, M., and Borisov,
N. (2010). Botgrep: Finding P2P bots with structured
graph analysis. In USENIX.
Narayanan, A., Thiagarajan, N., Lakhani, M., Hamburg,
M., and Boneh, D. (2011). Location privacy via pri-
vate proximity testing. In NDSS.
Secure Intersection with MapReduce
243
