BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable

Encryption with Fine-grained Multi-delegation & Break-The-Glass

Access Control

Mukti Padhya

1 a

and Devesh C. Jinwala

Department of Computer Engineering, Sardar Vallabhbhai National Institute of Technology (SVNIT), Surat, India

Department of Computer Science and Engineering, Indian Institute of Technology, Jammu, India

Keywords:

Searchable Encryption, Data Sharing, Data Retrieval, Cloud Server, Multi-keyword Search, Multi-delegation,

Revocation, Break-The-Glass Access.

Abstract:

Delegation is the technique of sharing the available rights from the delegator to the delegatee for the purpose

data sharing. The Key Aggregate Searchable Encryption (KASE) scheme supports delegation of search rights

for any set of ciphertexts using a key of constant-size. However, three critical issues still need to be consid-

ered. Firstly, the existing KASE schemes only discuss delegation of rights from the data owner to other user.

However, if a subject receiving a delegation cannot perform time-critical task on the shared data, it becomes

necessary for the delegatee to further delegate their received rights to another user. Secondly, the existing

delegation mechanisms tend to rely on manual processes initiated by end-users. If no authorized user exists

to perform (or to delegate) a time-critical task, in such exceptional case, we require mechanism that ﬂexi-

bly handles emergency situations by breaking or by controlled overriding of the standard access permissions.

Thirdly, the access of user in the system changes dynamically and it requires KASE to support user revocation

securely while not affecting the legitimate users’ access to the shared ﬁles. To address all of the above issues,

we propose Revocable KASE with Break-The-Glass access control (BTG-RKASE) to provide (i)ﬁne-grained

multi-delegation of available rights from the delegatee to another user,(ii)break-the-glass access mechanism

when no authorized user exists to perform (or to delegate) a time-critical task,(iii)revocation of delegated rights

(even in case of multi-delegation). The security and empirical analysis shows that BTG-RKASE performs bet-

ter than the existing KASE schemes.

1 INTRODUCTION

The cryptography-based access control (Sandhu et al.,

1996; Sahai et al., 2005) is designed to prevent

unauthorized access of data stored on the untrusted

cloud server. However, in some exceptional situa-

tions the tight access policies of traditional access

control schemes (such as Role-Based Access Control

(RBAC) (Sandhu et al., 1996), Attribute-Based Ac-

cess Control (ABAC) (Sahai et al., 2005)) prevent the

data accessibility. Let us consider the following ex-

ample from a healthcare application to clarify the is-

sues we aim to address in this paper.

The E-Healthcare Record (EHR) storage system

allows patients to store their health-related informa-

tion on the cloud server. The EHR records contain

the patient’s personal information and his health in-

https://orcid.org/0000-0002-0498-4188

formation such as the patient’s blood pressure, heart-

beats etc. However, the privacy and conﬁdentiality

of that patient’s medical records cannot be neglected.

Therefore, to prevent unauthorized access of medical

records, patient (Alice) use cryptography-based ac-

cess control and deﬁne access policy for the health

records (Figure 1a). For example, the access policy

(Doctor =’Bob’ and Hospital=’ABC’) or Lab=’XYZ’

allows doctor Bob from ’ABC’ hospital or manager

of ’XYZ’ laboratory to access Alice’s data. Suppose,

Bob is away from work for some particular reason,

such as sickness or on holiday, who has the right to ac-

cess Alice’s medical records in order to evaluate and

treat her appropriately? As per the access policy de-

ﬁned by Alice, other doctors or nurses from the emer-

gency ward can not access Alice’s medical record. If

we consider the sickness of the patient, data accessi-

bility is needed to give timely treatment, at the same

time we cannot ignore the privacy of patient’s med-

Padhya, M. and Jinwala, D.

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass Access Control.

DOI: 10.5220/0007919901090124

In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 109-124

ISBN: 978-989-758-378-0

109

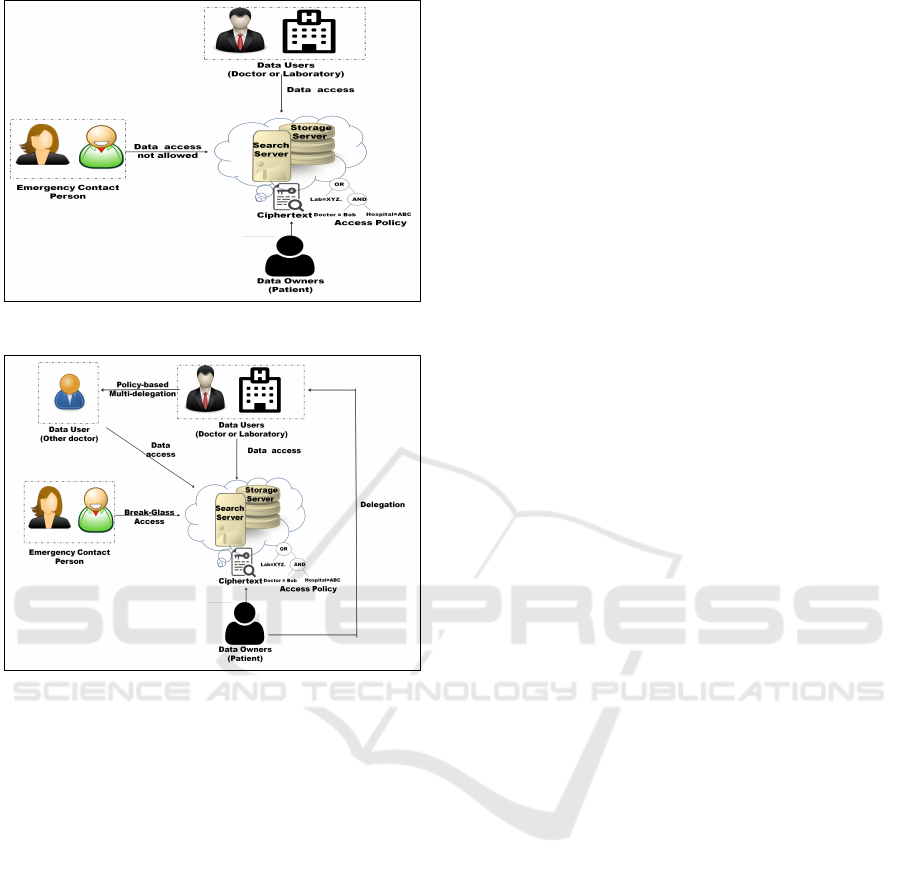
(a) Traditional approach of access control using the existing cryptography-

based schemes (Sandhu et al., 1996; Sahai et al., 2005)

(b) The proposed approach using ﬁne-grained multi-delegation and break-

the-glass access control

Figure 1: Access control and data security in EHR System.

ical record and information? The question is, how

can we design an access control model to provide pri-

vacy, conﬁdentiality and availability at the same time?

The possible solution to provide ﬂexible access con-

trol and also maintaining data security is delegation of

rights over Alice’s medical records from Bob to other

doctor.

Delegation mechanism (Crampton and Khamb-

hammettu, 2008; Schaad and Moffett, 2002) allow

subjects to transfer their available rights (data access

and search), roles, tasks, or duties to another subject.

Subsequently, a subject receiving a delegation (the

delegatee) will act on behalf of the delegating sub-

ject (the delegator). Recent attempts at Key Aggre-

gate Searchable Encryption (KASE) (Cui et al., 2016)

allows a data owner to delegate keyword search rights

on a set S of ﬁles. KASE inherits the property of Key

Aggregate Encryption (KAE) (Chu et al., 2014), i.e.,

to delegate search rights on |S| number of ﬁles, the

data owner is required to share a single aggregate key

with a user. In addition, a user is required to sub-

mit a single aggregate trapdoor (instead of a group of

trapdoors) to the cloud to perform a keyword search

across |S| number of shared ﬁles. However, the limi-

tation of the existing delegation schemes (Chu et al.,

2014; Banu, 2015; Dang et al., 2016; Mahalle and

Pawade, ; Patranabis et al., 2015; Cui et al., 2016; Li

et al., 2016; Li et al., 2018; Zhou et al., 2018; Pad-

hya and Jinwala, 2018) is that they only discuss del-

egation of rights from the data owner to other user.

On the other hand, if a subject receiving a delegation

cannot perform time-critical task on the shared data,

it becomes necessary to further delegate the received

rights from the delegatee to another user. We deﬁne

such transitive delegation of rights from the delegatee

to another user a multi-delegation. For example, in

above discussed scenario of EHR system Alice can

delegate search and access rights of her records to

Bob using the existing delegation schemes (Chu et al.,

2014; Banu, 2015; Dang et al., 2016; Mahalle and

Pawade, ; Patranabis et al., 2015; Cui et al., 2016; Li

et al., 2016; Li et al., 2018; Zhou et al., 2018; Pad-

hya and Jinwala, 2018). However, multi-delegation

from Bob to other doctors is not possible in the ex-

isting delegation schemes. In the existing delegation

schemes (Chu et al., 2014; Banu, 2015; Dang et al.,

2016; Mahalle and Pawade, ; Patranabis et al., 2015;

Cui et al., 2016; Li et al., 2016; Li et al., 2018; Zhou

et al., 2018; Padhya and Jinwala, 2018), the possi-

ble way to do multi-delegation is that the delegatee

can share his received key having rights for dataset

S with other users. However, this solution is infea-

sible and insecure in case of delegatee wants to share

selected dataset S

⊂ S with other user. Further, multi-

delegation can temporarily change the access control

state so as to allow a subject to use another subject’s

privileges. It may be possible that the data owner does

not want to reveal his data to any user other than the

delegatee.

Furthermore, in the critical system such as health-

care industry and disaster management, even if the

set of authorized entities are unavailable, the task on

the shared dataset is expected to be done in reason-

able time. In the healthcare industry, patients are ex-

pected to be treated in reasonable time. In case of

Bob delegates his rights over Alice’s medical records

to John and John meets medical emergency, then how

to access the patient’s data?. Therefore, we solicit the

answer to an interesting research question as how to

handle exceptional situation when no authorized user

exists to perform (or to delegate) a time-critical task?

Motivated by use cases from the disaster management

domain, the break-the-glass principle (Joint, 2004)

was introduced as one approach to ﬂexibly handle

emergency situations by breaking or overriding the

SECRYPT 2019 - 16th International Conference on Security and Cryptography

110

standard access permissions in a controlled manner.

In essence, break-the-glass policies (Ferreira et al.,

2006; Ardagna et al., 2008; Ardagna et al., 2010;

Marinovic et al., 2011) allow a subject to perform an

action under certain conditions (e.g., life-threatening

situation of patient) even though he/she was not pre-

viously authorized to do so. Usually, such override

accesses are monitored and documented for later re-

views and audits.

However, the break-glass policies do not take into

account the existence or availability of authorized

users. In essence, a break-glass policy extend the set

of authorized accesses for the duration of emergency

and possibly allowing a unauthorized user to access

the data (or resource), even though authorized sub-

jects are available. It is difﬁcult to address the above

violations in an access control policy for the health-

care application because an overly loose policy might

permit access to inappropriate users, but an overly

tight policy might prevent access from the appropriate

users. A potential research direction would be to ﬁnd

ways to the controlled overriding of access control re-

strictions.

Envisioning these speciﬁc requirements in KASE,

we present a KASE scheme with ﬁne-grained multi-

delegation and break-the-glass access policy. A no-

tion of subject availability is also introduced, and the

proposed scheme allows searchable group data shar-

ing, ﬂexible access control and data security in the

following ways (Figure 1b): in normal situations, the

authorized user with the delegated key can access and

search over the shared dataset, provided ciphertext

class is within the range of aggregate key. For the

ﬁne-grained multi-delegation, if the attributes of the

delegatee satisfy the hidden access policy (deﬁned

by the data owner), the delegatee can delegate his

received rights to another user. In exceptional situ-

ation (when the authorized users are not available),

the break-glass access mechanism allow timely ac-

cess to the data, provided the attributes of the user

satisfy the break-the-glass policy. Additionally, the

proposed scheme also allows revocation of delegated

rights even in case of multi-delegation. The revoca-

tion refers to the process of taking away the delegated

privileges. If the receiver of delegated rights leaves

the system, or if the data is used differently than the

data owner agreed, then data owner or delegator re-

quires to revoke the delegated rights. Additionally,

the revocation in the proposed scheme does not af-

fects the non-revoked users, as they do not require

to update their corresponding delegated keys, which

greatly reduces the expensive cost of key update and

the overhead of key delegate authority.

1.1 Related Work

The KASE scheme (Cui et al., 2016), derives its roots

from the seminal work on Key Aggregate Encryption

(KAE) by Chu et.al. (Chu et al., 2014). In KASE, a

data owner delegates search rights on a dataset using

an aggregate key and the user can search over shared

data by submitting a single aggregate trapdoor to the

cloud. Despite the advantage of the secure delegation

of search rights using a constant size key, KASE (Cui

et al., 2016; Li et al., 2016; Li et al., 2018; Zhou et al.,

2018; Padhya and Jinwala, 2018) also brings the se-

curity issues and challenges.

The KASE schemes proposed in (Cui et al., 2016;

Zhou et al., 2018) do not support searching over

multi-owner data using a single key of constant size.

Therefore, Li et al. (Li et al., 2016) propose KASE

to support multi-owner search using a single trapdoor

and also provide veriﬁcation of search results using

an aggregate key. However, security proof against

chosen keyword attack is not discussed for the KASE

schemes (Cui et al., 2016; Li et al., 2016). Moreover,

the existing KASE schemes (Cui et al., 2016; Li et al.,

2016) do not provide data and trapdoor privacy, as dis-

cussed in (Kiayias et al., 2016). Zhou et al. show the

possible insider attack on the KASE (Cui et al., 2016)

scheme in (Zhou et al., 2018). Further, the KASE

(Cui et al., 2016; Li et al., 2016) schemes consider the

security assumption of Bilinear Difﬁe-Hellman Expo-

nent (BDHE). However, SDH or its variants such as

the BDHE do not guarantee the security for speciﬁc

parameters, as discussed in (Cheon, 2006). In (Pad-

hya and Jinwala, 2018), the authors proposed KASE

that supports search over multi-owner data using a

single aggregate key and also overcomes other secu-

rity issues of the existing KASE schemes (Cui et al.,

2016; Li et al., 2016; Li et al., 2018). However,

the KASE scheme proposed in (Padhya and Jinwala,

2018) does not supports conjunctive keyword search

and key leakage resiliency. In (Zhou et al., 2018),

the authors consider Industrial IoT (IIoT) applications

and propose a KASE scheme in the ﬁle-centric frame-

work for IIoT applications. However, this approach

suffers from low performance. In this scheme, each

user’s public key has 3n + 1 elements and secret has

n + 3 elements. Here, n is the maximum number of

documents held by a data owner.

In the existing KASE (Cui et al., 2016; Li et al.,

2016; Li et al., 2018; Zhou et al., 2018; Padhya

and Jinwala, 2018) schemes if the delegatee needs to

share his received rights on the shared dataset with

another user, then he must carry out the following

steps (Figure 2a): (i) ﬁrst download the selected data,

(ii) retrieve the plaintext through decryption, (iii) re-

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass

Access Control

111

(a) Traditional approach using the existing KASE (Cui et al., 2016; Li et al., 2016; Li et al., 2018; Zhou et al., 2018; Padhya and Jinwala,

2018) schemes

(b) The proposed approach

Figure 2: Multi-Delegation.

encrypt the selected dataset using his own keys (iv)

outsource the re-encrypted data to the cloud server,

and (v) share the keys with the user (to whom the dele-

gatee wants to delegate his received rights). However,

this solution seems secure but such retrieval, as well

as the re-encryption process, become infeasible for

real-time use. Another possible solution to do multi-

delegation in the existing KASE (Cui et al., 2016; Li

et al., 2016; Li et al., 2018; Zhou et al., 2018; Padhya

and Jinwala, 2018) schemes is as follows: the dele-

gate can ask the data owner to generate a new aggre-

gate key k

agg

for selected dataset S

= {1,..,n

} and

share it with the user. However, this solution requires

both data owner and the delegatee to be involved in

the delegation process and later on it may result in

the tedious task for the data owner. Additionally, the

delegatee cannot directly share his aggregate key k

agg

having search rights for dataset S with other users.

Therefore, to minimize the overhead required for

multi-delegation (especially the expensive cost of re-

encryption of selected dataset) at the user sides, a bet-

ter approach is to outsource the computation of re-

encryption to the third party. We observe that Proxy

Re-Encryption (PRE) (Blaze et al., 1998) can solve

the issue of multi-delegation of rights with minimal

required overhead at user sides. PRE allows an un-

trusted proxy to re-encrypt a ciphertext from being en-

crypted under one key to another key, without learn-

ing anything about the underlying plaintext. Further-

more, the re-encrypted ciphertext can be decrypted

by the delegatee using his own key (Figure 2b). In

the proposed scheme, if the attributes of the delega-

tee satisfy the hidden access policy (deﬁned by the

data owner), the delegatee can further delegate their

received rights to other user(s) by requesting a proxy

server to re-encrypt the selected data from the shared

dataset.

To the best of our knowledge, ours is the ﬁrst

KASE scheme that meets all the following require-

ments all together viz.: ﬁne-grained multi-delegation,

break-the-glass access control, revocation and pri-

vacy preservation simultaneously.

1.2 Our Contributions

The characteristics and contributions of the BTG-

RKASE are as follows:

• Fine-grained multi-delegation: The proposal al-

lows a data owner to delegate access and search

rights of any set of ciphertexts by sharing an ag-

gregate key with the delegatee. In addition, BTG-

RKASE support transitive delegation of rights

from the delegatee to other user(s) in a ﬁne-

grained manner. Further, the expensive computa-

tion of re-encryption required for multi-delegation

is outsourced to proxy server.

• Break-the-glass access control: In exceptional sit-

uation (when the authorized users are not avail-

able), the break-glass access mechanism allow

timely access to the data, provided the attributes

of the user satisfy the break-the-glass policy.

• Revocation in multi-delegation: The subject who

delegated the rights remains accountable for the

SECRYPT 2019 - 16th International Conference on Security and Cryptography

112

outcome of the delegated privileges. Therefore,

the proposed scheme allows the data owner and

the delegator (in case of multi-delegation) to re-

voke any user’s delegated rights in case delegatee

behaves maliciously or leaves the system.

• Multi-keyword Search. We enhance the existing

KASE schemes and improve its query expressive-

ness by supporting multi-keyword search over the

shared dataset using a trapdoor of constant size.

• Privacy preservation: The proposed BTG-

RKASE scheme preserves the privacy, as the hid-

den access policy deﬁned by the data owner, the

attribute token, keyword ciphertext and the query

trapdoor do not reveal any information about re-

lated attributes or keywords.

• Improve Query Performance. The proposed

KASE scheme allows searching over the shared

dataset S using a single trapdoor Tr, that a query

requester submits to the cloud server. The exiting

KASE schemes (Cui et al., 2016; Li et al., 2016;

Li et al., 2018; Zhou et al., 2018) require |S| num-

ber of trapdoor to search over shared dataset S,

as the existing KASE schemes generate adjusted

trapdoors Tr

to search over doc

for each l ∈ S

using the given trapdoor Tr.

1.3 Outline of the Paper

The rest of the paper is organized as follows: The pre-

liminaries are given in Section 2. The system archi-

tecture and security model are deﬁned in Section 3.

We give a concrete construction of the proposed BTG-

RKASE scheme in Section 4. The security analysis of

the BTG-RKASE is discussed in Section 5. The em-

pirical evaluation of the proposed scheme is discussed

in Section 6. Conclusion and future extensions are

provided in Section 7. References are at the end.

2 PRELIMINARIES

In this section, we introduce computational problems,

hardness assumptions and notations used throughout

this paper. We rely on the standard deﬁnitions used

for security of cryptographic schemes.

2.1 Computational Assumption

Deﬁnition 1 DDH Assumption: The DDH prob-

lem in group G of prime order p (according to

the security parameter) is a problem for input of

a tuple (g,g

,R) where, a, b,c ∈ Z

be cho-

sen at random and g be a generator of G,then to

Table 1: Notations used in the proposed BTG-RKASE

scheme.

Term Meaning

λ Security parameter

n Number of documents held by a data owner

B Bilinear map group system

SP System parameter

doc

document

PubK Public parameters

pk Public key

msk Master secret key

sk Secret key

Break-glass key of document doc

Encrypted break-glass key of document doc

rk re-encryption key

SK Attribute token

Attr Set of user’s attributes used to generate attribute token SK

l Index of document or ﬁle

S Subset S ⊆ {1, .....,n} contains the indices of documents

KS Keyword space that involves m different keywords in the system

keyword

i, j

value of keyword w

from it’s N

different possible values

−→

Q Set of query keywords attached with the query trapdoor Tr

−−→

KW Set of keywords attached with the ciphertext C

−−→

M Message or Plaintext

C Ciphertext

−−→

Keyword ciphertext

Data ciphertext

Public information related to ciphertext of l

document

i.e. parameters C

and C

Re-encrypted ciphertext

Access policy attached with ciphertext C

and deﬁned by data owner

BT G

Break-the-glass access policy attached with ciphertext C

and deﬁned by data owner

agg

Aggregate key

Tr Trapdoor used to search query keyword(s) within set

−→

R Search result

Revocation list of l

document

The set of revoked users’ identity for l

document

User id of query requester

Π Multiplicative notation

att

Set of all possible values for attribute att

atr

i, j

value of attribute att

in the set AV

att

Available

The status of availability of user having id U

(Available = 1, Not available =0)

decide whether R= g

abc

or not. An algorithm A

has advantage ε in solving DDH problem in G if

Adv

DDH

(A):=|Pr[A(g,g

abc

) = 0]−

Pr[A(g,g

,R) = 0]| ≥ ε(κ). We say that the

DDH assumption holds in G if no Probabilistic Poly-

nomial Time (PPT) algorithm has an advantage of at

least ε in solving the DDH problem in G.

2.2 Notations

The list of notations used throughout the paper is

given in the Table 1.

3 SYSTEM ARCHITECTURE

AND SECURITY MODEL

In this section we present the formal deﬁnition of the

proposed BTG-RKASE scheme and formalize a secu-

rity model for it.

3.1 Framework

The proposed BTG-RKASE scheme is an ensemble

of randomized polynomial-time algorithms, as dis-

cussed further, here. The data owner ﬁrst sets up an

account on the cloud server and establishes the public

system parameter via Setup(). At the time of register-

ing in the system, the Trusted Authority (TA) assigns

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass

Access Control

113

a unique id to the user. TA manages users in the sys-

tem and it is fully trusted by entities in the system.

The data owner generates a public, secret and master-

secret keys via Keygen(). The data owner securely

send secret key to the TA. The TA constructs attribute

token via AttrGen(). Messages can be encrypted via

Encrypt() algorithm. The data owner generates key

for break-the-glass access via KeyGen BTG(). To

delegate the search and access rights to a speciﬁc sub-

set of data classes, the data owner uses the master-

secret to generate a constant size aggregate key via

Extract(). The generated key can be passed to dele-

gatees securely (via secure e-mails or secure device).

The data owner or delegator can take away the del-

egated privileges via Revocation() algorithm. For

multi-delegation of received data rights, the delega-

tee can generate re-encryption key via ReKeygen()

algorithm. The generated key can be passed to proxy

server, using which the proxy server can re-encrypt

the requested set of data via ReEncrypt(). Finally,

any user with an aggregate key can search over shared

dataset by generating query trapdoor via Trapdoor-

Gen(). On receiving the query trapdoor from the user,

the cloud server runs the Test() algorithm to retrieve

matching documents and send it further to the query

requester. The user can access the ciphertext via De-

crypt() algorithm, provided ciphertext class is within

the range of aggregate key. For the break-the-glass ac-

cess, the user run BTG Access() algorithm, provided

the attributes of the user satisfy the break-the-glass

policy.

Furthermore, in the following discussion of the

proposed scheme, the keyword space contains m dif-

ferent keywords, i.e., KS = {w

,....,w

}. Each

keyword w

contains N

possible values and w

i, j

rep-

resents the j

value of keyword w

. Let assume

that there are total X users in the system and U =

,...,U

} is a set of all users’ identities. There-

fore, each cloud user can be uniquely identiﬁed by

his assigned identity U

∈ U. Additionally, U

⊂ U

represents the set of revoked users’ identities for l

document, where U

∈ U

represents an identity of

user whose delegated rights needs to be revoked over

document. The revocation list U

may be empty,

which means there is no user needs to be revoked for

document.

• SP ←Setup(1

, n): Takes as input the security pa-

rameter λ and the number of documents held by a

data owner n. Outputs the public system param-

eters SP, which is omitted from the input of the

other algorithms for brevity.

• (pk, sk,msk) ←KeyGen(): Outputs a public, se-

cret and master-secret key pair (pk, sk,msk) for a

data owner registering in the system.

• SK ←AttrGen(sk,Attr): Takes as input the secret

key sk and the set of attributes Attr of user. Out-

puts the attribute token SK.

• C

←Encrypt(pk,sk,l,M,KW, A): Takes as input

the the public key pk, secret key sk, document in-

dex l, message M, set of related keyword(s) KW ,

and the hidden access policy A. Outputs the corre-

sponding ciphertext C

= (δ

), where

is data-ciphertext, C

keyword-ciphertext, δ

public information, C

ciphertext with the hidden

access policy.

• BK

←KeyGen

BTG(sk, msk,l,BT G): , Takes as

input the master-secret key msk, secret key sk,

document index l, and the break-the-glass policy

BT G. Generates a break-glass key K

for docu-

ment doc

and then encrypt it using given break-

the-glass policy BT G. The algorithm outputs en-

crypted key BK

. If user’s attribute token SK satis-

ﬁes break-glass policy BT G then user can recover

break-glass key K

to access document doc

• k

agg

←Extract(msk, S): Takes as input the master-

secret key msk of data owner and subset of data

classes S ⊆ {1,2, ...,n}. Outputs the aggregate

key k

agg

which aggregates the search and access

rights of all encrypted messages within set S.

• RL ←Revocation(U

,msk,l): Takes as input the

set of revoked users’ identities U

, master-secret

key msk, and document index l. Outputs the revo-

cation list RL

= (RL

,RL

• rk←ReKeygen(pk, pk

): Takes as input the pub-

lic key pk of data owner and public key pk

of del-

egatee (who wants to delegate his received rights

further to other user(s)). The algorithm generates

re-encryption key rk.

• (C

|∀l ∈ S

) ←ReEncrypt(rk, SK, S

): Takes as

input the re-encryption key rk, the attribute token

SK and set S

of encrypted documents’ indices.

Outputs re-encrypted ciphertexts C

iff SK  A

∀l ∈ S

• Tr ←TrapdoorGen(k

agg

−→

Q ): Takes as input an

aggregate key k

agg

and a set of query keywords

−→

Q . Outputs a single trapdoor Tr.

• R ←Test(Tr, S,l,U

): Takes as input a query

trapdoor Tr, a set of shared documents’ indices

S, document index l, and identity of the query re-

quester U

∈ U. If U

is not the revoked user

and l ∈ S, Test algorithm returns the search result

R ∈ {0,1} by following the rules shown below:

R =

(

1,If

−→

Q 

−−→

0,Otherwise

Otherwise, the algorithm returns NULL.

SECRYPT 2019 - 16th International Conference on Security and Cryptography

114

• M ←Decrypt(k

agg

, S,l, C

): Takes as input the

ciphertext C

, the data class l, and the aggregate

key k

agg

corresponding to the set S. The algorithm

outputs the decrypted result M if l ∈ S.

• M ←BTG Access(SK,l, U

): Takes as input the

attribute token SK, an identity of the query re-

quester U

, and the data class l. The algorithm

outputs the decrypted result M iff SK  BTG

and

is not the revoked user.

3.2 Security Model

We consider the cloud servers and data users to be

honest but curious, i.e., they follow the given proto-

cols honestly, but try to get some additional informa-

tion beyond their authorization. However, the capac-

ity of the data user in the system is limited by both

storage space and computing power. Moreover, com-

munication channels involving the server are assumed

to be insecure.

It is required that the ciphertext does not reveal

any information about the corresponding keyword(s)

to an adversary. We prove this claim by the secu-

rity of Indistinguishability against Chosen Keyword

Attack (IND-CKA) model. Moreover, given a valid

search token, the adversary can only gain information

whether the search is successful by Indistinguisha-

bility against Keyword Guessing Attack (IND-KGA)

model. We use the static corruption model, that means

the set of corrupted users has to be deﬁned in the ini-

tialization phase. In addition, the adversary is not al-

lowed to ask for re-encryption key from uncorrupted

users to corrupted users or vice versa. We introduce

the games between an attack algorithm A and a chal-

lenger, both of whom are given input of n, the to-

tal number of documents. In the following games,

F(L, T ) is a binary relation, where L is the set of at-

tributes labeled with user’s attribute token SK and T

is the hidden access policy attached with ciphertext.

F(L, T ) = 1, if the attributes in L satisfy the access

policy speciﬁed in T i.e. L  T ; else, F(L,T ) = 0.

3.2.1 IND-CKA Model

Init Phase. The adversary A selects a set of cor-

rupted users denoted by CoList sends it to the chal-

lenger. The adversary also commits two ciphertext

access policies T

∗

and T

∗

and challenge index i

for

which he wishes to be challenged upon.

Setup. The challenger runs Setup(1

,n) to generate

system parameters. The setup algorithm also deﬁnes

a keyword space ks and attribute set AT T R.

Query Phase 1. The adversary A adaptively queries

,...., q

to following oracles and oracle answers in

polynomial time.

• Uncorrupted Key Generation Oracle O

: Out-

puts a new key pair (pk,sk,msk) ←Keygen() and

give pk to A.

• Corrupted Key Generation Oracle O

msk

: Gen-

erates (pk, sk,msk) ←Keygen() and issues key

pair (pk,sk,msk) to A

• Attribute Token Generation Oracle O

: The

adversary is allowed to request for polynomially

bounded number of attribute token on attributes L

with the restriction that F(L, T

∗

) = F(L,T

∗

) = 1

or F(L, T

∗

) = F(L,T

∗

) = 0

• Aggregate Key Generation Oracle O

agg

: On

giving input of (msk, S) by the adversary, where

msk is master secret key corresponding to pk and

pk is from O

msk

, then oracle returns an aggregate

key k

agg

← Extract(msk,S). The restriction is that

an adversary can not ask for the aggregate key for

challenge index, i.e., if i

∈ S, then O

agg

returns

null.

• Re-encryption Key Generation Oracle O

: On

giving input of (pk, pk

) by the adversary, where

pk, pk

are from O

or O

msk

, then oracle gen-

erates re-encryption key rk ←ReKeygen(pk, pk

Here, one constraint is required that both the pub-

lic key pk, pk

are either corrupted or both are un-

corrupted, i.e. pk and pk

both are from O

msk

. The adversary is not allowed to ask for

re-encryption key from uncorrupted users to cor-

rupted users or vice versa.

• Re-encryption Oracle O

: On giving in-

put of (rk,S

), where re-encryption key

rk ←ReKeygen(pk, pk

) and pk, pk

are from

or O

msk

, then oracle generates re-encrypted

ciphertext (C

|∀l ∈ S

) ←ReEncrypt(rk,SK,S

)

• Trapdoor Generation Oracle O

: It runs

Tr ←TrapdoorGen(k

agg

−→

Q ), and returns the trap-

door Tr for

−→

Q to A.

• Test Oracle O

test

: On giving input of trapdoor

Tr, set S and document index l ∈ S, the chal-

lenger checks k

agg

corresponding to set S occurs

in table T

agg

, if yes, the oracle returns output of

Test(Tr,S,l,U

) to the adversary. Otherwise, it

returns null.

Challenge Phase.

The attacker A sends the challenger two equal length

set of keywords

−−→

;

−−→

on which it wishes to be

challenged along with an index i

, a message M from

message space, a public key pk, secret key sk, and

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass

Access Control

115

the challenge access policy T

∗

and T

∗

. Here, the

restriction is that if for any attribute token gener-

ated by oracle O

in Phase 1 on an attribute list L,

F(L, T

∗

) = F(L,T

∗

) = 1 then

−−→

. Addi-

tionally, the attacker had not previously asked for the

query trapdoor corresponding to keywords

−−→

;

−−→

to the oracle O

and pk is from the O

. The

challenger chooses β randomly from {0,1} and runs

Encrypt(pk,sk,i

,M,

−−→

∗

) and returns keyword

ciphertext C

∗

to the adversary.

Query Phase 2. Identical to that in phase 1., the ad-

versary asks for more queries q

n+1

,....., q

except the

following oracles:

• Trapdoor Generation Oracle O

: On giving in-

put of (k

agg

−→

Q ) by the adversary, the challenger

answers same as that in phase 1, except the fol-

lowing cases:

– The adversary had previously ask for the trap-

door corresponding to a set of keywords

−−→

–

−→

Q =

−−→

−→

Q =

−−→

If one of the above condition holds, then chal-

lenger returns null.

• Test Oracle O

test

: On input of Test(Tr,S,l,U

if i

= l or i

∈ S, then the challenger returns null.

Otherwise the challenger responds as that in phase

Guess. The adversary A outputs its guess β

∈ {0,1}

for β and wins the game if β = β

The advantage of the adversary in this game is de-

ﬁned as ADV

BTG-RKASE

A,K

= |Pr[β = β

]−

|, where the

probability is taken over the random bits used by the

challenger and the adversary.

Deﬁnition 2 (IND-CKA Security): We say that the

proposed BTG-RKASE scheme hold the privacy for

keyword if ADV

BTG-RKASE

A,K

is negligible with respect

to the security parameter for any polynomial time ad-

versary.

3.2.2 IND-KGA Model

Init Phase. The adversary A selects a set of cor-

rupted users denoted by CoList sends it to the chal-

lenger. The adversary also commits two set of query

keywords

−→

and

−→

and challenge index i

for which

he wishes to be challenged upon.

Setup. The challenger runs Setup(1

,n) to generate

system parameters. The setup algorithm also deﬁnes

a keyword space ks and attribute set AT T R.

Query Phase 1. The adversary A adaptively queries

,...., q

to oracles and oracle answers in polynomial

time. The oracles are identical to that in the IND-

CKA security model except the following:

• Ciphertext Generation Oracle O

: The attacker

A sends the challenger set of keywords

−−→

KW along

with an index l, a message M from message

space, a public key pk, secret key sk, and ac-

cess policy A. If l 6= i

, then the challenger runs

Encrypt(pk,sk,l,M,

−−→

KW ,A) and returns ciphertext

to the adversary.

Challenge Phase. The attacker A sends the chal-

lenger two equal length set of keywords

−→

;

−→

which it wishes to be challenged along with an index

, and an aggregate key k

c−agg

corresponding to a set

S which includes an index i

. Here, the restriction

is that the attacker had not previously asked for the

ciphertext corresponding to keywords

−→

;

−→

to the

oracle O

. The challenger chooses β randomly from

{0,1} and runs TrapdoorGen(k

c−agg

−→

) and returns

query trapdoor Tr

∗

to the adversary.

Query Phase 2. Identical to that in phase 1, the adver-

sary asks for more queries q

n+1

,....., q

except that

• The adversary A cannot ask for the aggregate key

corresponding to a set S which includes an index

• Ciphertext query on keyword set

−→

under

challenge index i

is not allowed

Guess. The adversary A outputs its guess β

∈ {0,1}

for β and wins the game if β = β

The advantage of the adversary in this game is de-

ﬁned as ADV

BT G−RKASE

A,KG

= |Pr[β = β

]−

|, where the

probability is taken over the random bits used by the

challenger and the adversary.

Deﬁnition 3 (IND-KGA Security): We say that the

proposed BTG − RKASE method hold the privacy for

trapdoor if ADV

BT G−RKASE

A,KG

is negligible with respect

to the security parameter for any polynomial time ad-

versary.

3.3 Availability of Subjects

The proposed scheme BTG-RKASE makes break-

the-glass access decisions based on the availability

of subjects. The deﬁnition of availability will be

application-speciﬁc. In the context of a hospital,

a doctor may have access to the patient’s data, but

may not be physically present in the hospital and un-

able to respond to any emergency situation of his pa-

tient. In the military setting, availability may simply

be whether the corresponding user is still alive and

present on battleﬁeld.

SECRYPT 2019 - 16th International Conference on Security and Cryptography

116

To identify a set of available authorized subjects at

request evaluation time, the proposed scheme main-

tain a set denoted by Au

⊂ U represents the set of

users’ identities who has access right for document

doc

, where Au

∈ Au

represents an identity of the

delegatee who has received the access rights over l

document. The proposed scheme achieves the set Au

updating through the cloud servers to save the com-

putational overhead of data owner. In case of multi-

delegation, the user who further delegates his avail-

able rights for doc

, updates the set Au

. Further-

more, the proposed scheme also use one more nota-

tion Available

to represent the status of availability

of user having id U

. If Available

= 1, user hav-

ing id U

is available, otherwise he is not available

(Available

= 0). Therefore, if Available

= 0|∀Au

∈

, then break-the-glass access on doc

is possible,

provided user’s attributes satisfy the break-the-glass

policy

4 THE PROPOSED METHOD:

BTG-RKASE

In this section, we discuss the construction of the

proposed scheme. The attribute space to deﬁne ac-

cess policy A is ATT R = {att

,att

,.., att

}. Assume

att

={av

,av

,...av

} be the set of all possible val-

ues of attribute att

, where η

denotes the maximum

number of values for i

attribute. Here, av

attr

i, j

rep-

resents the j

value of attribute attr

. The other no-

tations used in the forthcoming discussion are already

introduced in Section 2. The detailed construction of

the proposed BTG-RKASE scheme is as follows:

1. Setup (1

, n): The data owner runs this algo-

rithm and publish the system parameters SP = (B,

PubK,H

). In the following discussion, bilin-

ear map group system B=(p,G,G

,e(., .)), where

p is the order of G and 2

≤ p ≤ 2

λ+1

. g is a gen-

erator of group G. n is the number of documents

D= (doc

, doc

, ..., doc

) that belongs to a data

owner. The random element α ∈ Z

. Algorithm 1

gives a formal description of Setup operation.

2 Keygen: The data owner runs this algorithm to

generate a key pair (pk,sk,msk)

pk = v= g

; sk = ρ; msk = γ, where γ∈ Z

and

ρ∈ Z

Algorithm 1: Setup (1

, n) → SP.

1: B=(p, G,G

,e(., .))

2: PubK ← (g, g

, ..,g

n+2

, ...,g

)

3: g

← g

∈ G| ∀l ∈ {1,2,..,n, n + 2,...,2n}

4: Select two one-way, collision resistant hash func-

tions H

: {0, 1}

∗

× {0,1}

∗

→ G, H

: {0, 1}

∗

{0,1}

∗

→ G

5: SP ← (B, PubK,H

)

6: ks ←

{0,1}

∗

3 AttrGen(sk, Attr) : The attribute token genera-

tion algorithms takes as input the secret key sk,

a set Attr of attributes and generates a attribute to-

ken of constant size. Algorithm 2 gives a formal

description of AttrGen operation:

Algorithm 2: AttrGen(sk,Attr) → SK.

1: Select r ∈

2: S

← g

3: for all av

attr

i, j

∈ Attr do

4: S

← g

(Π(H

(av

attr

i, j

)))

5: Return SK =< S

4 Encrypt(pk,sk,l,M,

−−→

KW ,A): The data owner

gives public key, secret key sk, message M, docu-

ment index l, keywords set

−−→

KW , and access policy

A as input. The data owner generates the cipher-

text by following the steps as shown in Algorithm

3. Algorithm 3 gives a formal description of En-

crypt operation.

Algorithm 3: Encrypt (pk, sk,l, M, KW, A) → C

1: Select t ∈ Z

2: if l ∈ {1,2,...,n} then

3: C

← g

4: C

← (v · g

)

5: C

= C

−−→

← Π(H

i, j

))

|∀w

i, j

∈

−−→

6: C

= C

← M · e(g

)

|M ∈ G

7: for all av

attr

i, j

∈ A do

8: C

= (Π(H

(av

attr

i, j

)))

9: C

= l · e(g

)

10: C

= (C

)

11: C

= (δ

−−→

) = (C

)

12: Data owner stores ciphertext C

on the cloud

server.

5. KeyGen BTG(sk, msk,l,BT G): The data owner

generates the break-glass key by following the

steps as shown in Algorithm 4. Algorithm 4 gives

a formal description of KeyGen BTG operation.

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass

Access Control

117

Algorithm 4: KeyGen BTG(sk,msk, l,BT G) → BK

1: Select β ∈ Z

2: if l ∈ {1,2,...,n} then

3: K

← g

4: bk

= g

5: for all av

attr

i, j

∈ BT G do

6: bk

= (Π(H

(av

attr

i, j

)))

7: bk

= K

· e(g

)

8: BK

← (bk

,bk

)

6. Extract (msk,S): For any subset S ⊆ {1,...,n}

which contains all the indices of document sets,

the algorithm outputs aggregate key k

agg

by com-

puting:

agg

= Π

j∈S

The data owner securely sends k

agg

and a set S to

the user, to delegate the keyword search and data

access rights of the ciphertexts within set S.

7. Revocation(U

,msk,l): The algorithm outputs re-

vocation list RL

for document l, on giving input

of master-secret key and a set of revoked users’

identities U

whose delegate rights needs to be

revoked over document doc

. The l

document

must not be either accessed or searched by any

user U

∈ U

. The cloud server checks the user’s

authorization using RL

at the time of receiving

any request for document l (such as access or

search request). Algorithm 4 gives a formal de-

scription of Revocation operation.

Algorithm 5: Revocation(U

,msk,l) → RL

1: Select r ∈ Z

2: RL

← g

rγ

3: RL

←(Π

∈U

)

4: RL

← (RL

,RL

)

5: Data owner stores revocation list RL

on the cloud

server.

8. ReKeygen(pk, pk

): This algorithm outputs re-

encryption key rk by computing:

rk = pk

/pk = g

9. ReEncrypt(rk,SK,S

): On receiving the re-

encryption request from DU, proxy server ﬁrst

matches user attribute token SK with the hidden

access policy A

|∀l ∈ S

deﬁned by the data owner.

If the attribute token SK satisﬁes the access policy

, then the cloud server re-encrypt C

using the

re-encryption key rk and calculates re-encrypted

ciphertext C

by following the steps as shown in

Algorithm 6. Algorithm 6 gives a formal descrip-

tion of ReEncrypt operation.

Algorithm 6: ReEncrypt (rk, SK,S

) → C

|∀l ∈ S

1: for all l ∈ S

2: Y

←

·e(S

)

e(C

)

3:  If SK  A

, then Y

= l otherwise it gets

any random value which indicates SK 2 A

4: if Y

= l then

5: C

← C

∗ rk

6: C

← C

, C

← C

7: C

← C

, C

← C

8: Stores the ciphertext C

on the cloud server

10. TrapdoorGen(k

agg

−→

Q ): The user who wants to

perform the keyword search over the shared data,

runs this algorithm and generates a single aggre-

gate trapdoor Tr. If the set S of documents are in

the range of an aggregate key k

agg

, then the user

having trapdoor Tr can search over any document

in the range of set S. Algorithm 7 gives a formal

description of TrapdoorGen() operation.

Algorithm 7: TrapdoorGen(k

agg

, Q)→ Tr.

1: Select b ∈ Z

2: Tr

← {k

agg

· Π(H(w

i, j

))

}

i, j

∈

−→

3: Tr

← g

4: Tr ←(Tr

,Tr

)

5: The user submits (Tr,S) to the cloud server.

11. Test (Tr, S,l,U

): To check if document doc

contains query keyword(s) within set

−→

Q or not,

the cloud server follows steps as shown in Al-

gorithm 8. Algorithm 8 gives a formal descrip-

tion of Test operation. In the following discussion

∈ U is an identity of query requester and U

is a set of revoked users’ identities corresponding

to list RL

12. Decrypt (k

agg

,S,l,C

): If l /∈ S, Decrypt algorithm

outputs NULL. Otherwise, returns the output:

M = C

e(k

agg

pub

, C

) /e(pub

, C

)

e(pub

, C

)

{pub

}

l∈S

= {Π

j∈S

j+l

}

l∈S

{pub

}

l∈S

= {Π

j∈S, j6=l

n+1− j+l

}

l∈S

pub

= Π

j∈S

pub

= Π

j∈S

n+1− j+l

For efﬁciency consideration, the parameters

({pub

, pub

}

l∈S

, pub

) for the set S is

computed only once.

SECRYPT 2019 - 16th International Conference on Security and Cryptography

118

Algorithm 8: Test (Tr,S,l,U

)→ R ∈ {0,1}.

1: if Revoked(U

,RL

,l) 6= 1 then

2: if l ∈ S then

3: pub

= Π

j∈S

j+l

4: pub

= Π

j∈S

5: R = e(Tr

· pub

) / e(pub

)

e(C

,Tr

)

6: if R = 1 then

7: Add doc

to the search result list

8: Return R

9: if l /∈ S then

10: Return Failure

11: if Revoked(U

,RL

,l) = 1 then

12: Return Failure

13: FUNCTION Revoked(U

,RL

,l)

14: pub

← Π

∈U

6=U

15: Y ← e(RL

)/e(U

· pub

,RL

)

16: Return Y

13. BTG Access(SK,l, U

): On giving input of the

attribute token SK, identity of query requester

, and the data class l, the cloud server follows

steps as shown in Algorithm 9. Algorithm 9 gives

a formal description of BTG Access operation.

Algorithm 9: BTGAccess(SK,l, U

)→ M.

1: if Revoked(U

,RL

,l) 6= 1 then

2: if Available

= 0|∀Au

∈ Au

then

3: Take the attribute token SK = (S

) of

user U

and match SK with the break-glass pol-

icy of l

document BTG

4: if SK  BTG

then

5: K

←

·e(S

,bk

)

e(bk

)

6: Using K

user U

can access C

7: M = C

e(K

pub

, C

)

/e(pub

, C

) e(pub

, C

)

8:  Here, while computing parameters

(pub

, pub

), the set S contains only

one element, i.e., l itself.

9: elseReturn Failure

10: if Revoked(U

,RL

,l) = 1 then

11: Return Failure

12: FUNCTION Revoked(U

,RL

,l)

13: pub

← Π

∈U

6=U

14: Return Y ← e(RL

)/e(U

· pub

,RL

)

4.1 Analysis of the BTG-RKASE

The correctness of Test algorithm can be realized as

follows:

If the query requester U

is revoked user, then

= e(RL

)/e(U

· pub

,RL

)

= e((Π

∈U

)

γr

)/e(U

·Π

∈U

6=U

γr

) = 1

Therefor, if identity of query requester is within

set of revoked users then Test algorithm outputs fail-

ure. Then, user is no longer permitted to search on the

document.

Now, consider the case U

/∈ U

, i.e., query re-

quester is not the revoked user. If the user’s query

trapdoor Tr matches with the keyword ciphertext

−−→

, then Test algorithm outputs:

e(Tr

· pub

) / e(pub

) e(C

,Tr

)

e(Tr

· pub

)

e(pub

) e(C

,Tr

)

e(k

agg

· Π(H(w

i, j

))

· Π

j∈S

j+l

)

e(Π

j∈S

,(v · g

)

) e(Π(H(w

i, j

))

)

e(k

agg

) e(Π(H(w

i, j

))

) e(Π

j∈S

j+l

)

e(Π

j∈S

γt

) e(Π

j∈S

) e(Π(H(w

i, j

))

)

= 1

The correctness of BTG Access algorithm can be

realized as follows:

If the user’s attribute token SK satisﬁes the

break-glass policy BT G of the document doc

, then

BTG Access algorithm outputs

· e(S

,bk

)

e(bk

)

· e(g,g)

βρ

e(g

,(Π(H

(av

attr

i, j

)))

)

e(g

(Π(H

(av

attr

i, j

)))

)

= K

Using K

user can access document doc

BTG Access outputs as follows:

e(K

pub

, C

) /e(pub

, C

) e(pub

)

e(g

· Π

j∈S

j+l

· Π

j∈S, j6=l

n+1− j+l

)

e(Π

j∈S

,(v · g

)

) e(Π

j∈S

n+1− j+l

)

e(g

) e(Π

j∈S

j+l

) e(Π

j∈S, j6=l

n+1− j+l

)

e(Π

j∈S

γt

) e(Π

j∈S

) e(Π

j∈S

n+1− j+l

)

M e(g

)

e(Π

j∈S

n+1− j+l

)

e(g

n+1

)

e(Π

j∈S

n+1− j+l

)

M e(g

)

e(g

)

= M

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass

Access Control

119

5 SECURITY ANALYSIS

Theorem 1. If the decisional DDH assumption hold

in (G,G

), then the proposed BTG-RKASE scheme

preserves the keyword privacy in the random oracle

model.

Proof.

We consider a challenger C , a simulator S I M

and a polynomial-time adversary A. We assume

that the adversary A has a non-negligible advantage

ε(l) to break the privacy of our scheme. Then, we

can construct simulator SI M that breaks the de-

cisional DDH problem ς= (g, g

, g

, R) with

the probability Pr|Abreaks decisional DDH| ≥ 1/2 +

ε(1−(q

test

dec

)·τ−Pr|Abreaks break-the-glass policy|

2e·q

Here, q

test

are the number of queries to

re-encryption oracle, test oracle, and trapdoor gener-

ation oracle, respectively. τ is the maximum prob-

ability that any given signature veriﬁcation token is

output by G and it is assumed to be very negligible.

Moreover, Pr|Abreaks break-the-glass policy| is also

very negligible as per our assumption.

On DDH input (g,g

,R), simulator S I M

aims to decide if R = g

abc

The challenger C generates a,b,c,z ∈

, bilin-

ear groups G,G

with prime order p and the mapping

G × G → G

. g is a generator of group G. The chal-

lenger C computes X as follows:

R =

(

abc

,(X = 0)

,(X = 1)

The challenger gives instance (g, g

, g

, R)∈

to simulator SI M .

SI M interacts with A (SIM simulates the C for

A) and starts the simulation as follows.

Init Phase. The adversary A selects a set of cor-

rupted users denoted by CoList sends it to the chal-

lenger. The adversary also commits two ciphertext

access policies T

∗

and T

∗

and challenge index i

for

which he wishes to be challenged upon.

Setup. The simulator SI M generates system param-

eters SP=(g, g

,.. . ,g

n+2

,. ..,g

Here, g

= (g

)

∈ G for l = {1,2,.. .,n,n +

2,. ..,2n}.

Moreover, S I M simulates the hash oracles for

keyword and attribute as follows:

• O

: Given a keyword w

, having value w

i, j

, the

hash function proceeds as follows:

– If w

i, j

has not been queried before, then S I M

toss a random coin c

∈ {0,1} with the proba-

bility that Pr|c

= 0| = 1/(q

+ 1), where q

very large number. We require that q

should

be larger than the number of oracle queries

for O

agg

test

. If c

= 0, then selects

f ∈ Z

and computes T

∗

i, j

= (g

)

. Other-

wise, computes T

∗

i, j

= (g

)

. Add the tuple

< w

i, j

∗

i, j

> to table T

and return T

∗

i, j

– Otherwise, retrieve T

∗

i, j

from table T

with re-

spect to w

i, j

and return T

∗

i, j

• O

: Given a attribute value av

attr

i, j

, it proceeds

as follows:

– If av

attr

i, j

has not been queried before, then toss

a random coin c

∈ {0, 1}. If c

= 0, then selects

a random value h ∈

and computes T

attr

i, j

= (g

)

. Otherwise, computes T

attr

i, j

= (g

)

Add the tuple < attr,c

i, j

attr

i, j

> to table

attr

and return T

attr

– Otherwise, retrieve T

attr

i, j

from table T

attr

with

respect to attr and return T

attr

i, j

Query Phase 1. The simulator SI M constructs

following oracles and adversary A can adaptively

queries q

,...., q

to these oracles in polynomial for

multiple times.

• Uncorrupted Key Generation Oracle O

: On

input an index i, if corrupted

= 1, then S I M sets

public-key pk

= v =g

where γ

∈

; otherwise,

SI M computes pk

= v =(g

)

. Finally, S I M

records the tuple < pk

,γ

,corrupted

> in table

and responds A with pk

and sk

= ρ

where

∈

. Table T

is used to records the outputs

of O

and O

msk

and these records will be used in

other oracles to response the queries.

• Corrupted Key Generation Oracle O

msk

: On

input of pk

, S I M checks whether pk

oc-

curs in T

, if not, SI M terminates. Other-

wise, if corrupted

= 0, SI M terminates. If

corrupted

= 1, S I M responds A with (pk

,msk

= γ

,sk

= ρ

), and records the tuple <

,γ

,corrupted

> in table T

• Attribute Token Generation Oracle O

Whenever A makes its i

attribute token gen-

eration query for the set L

of attributes such

that F(L

∗

) = F(L

∗

) = 1 or F(L

∗

) =

F(L

∗

) = 0, i.e., F(L

∗

) = F(L

∗

Speciﬁcally, A is allowed to issue a valid attribute

token generation query which can satisfy chal-

lenge access policy, with the restriction that the to-

ken should satisfy both the challenge access struc-

ture T

∗

and T

∗

. The simulator S I M selects a

random values r

∈

and computes the attribute

token as follows:

SECRYPT 2019 - 16th International Conference on Security and Cryptography

120

SK =< S

>= < g

(Π(H

(av

attr

j,k

)))

|∀av

attr

j,k

∈ L

• Aggregate Key Generation Oracle O

agg

: On

giving input of (msk

,S) by the adversary,where

msk

is master secret key corresponding to pk

the simulator checks that key pair (pk

,msk

) oc-

curs in table T

, if not, S I M reports failure and

terminates. Otherwise, it returns an aggregate

key k

agg

← Extract(msk

,S) and add the tuple

< k

agg

,msk

,S > in table T

agg

. The adversary A

cannot ask for the aggregate key corresponding to

a set S that includes an index i

• Re-encryption Key Generation Oracle O

: On

giving input of (pk

, pk

) by the adversary, S I M

checks whether pk

, pk

occur in T

,if not, S I M

terminates. Otherwise SI M does the following

operations:

– If corrupted

= corrupted

, SI M responds A

with pk

/pk

– If corrupted

6= corrupted

, SI M aborts

• Re-encryption Oracle O

: On giving in-

put of (rk,S

), where re-encryption key

rk ←ReKeygen(pk, pk

), SI M checks whether

, pk

occur in T

and pk, pk

are from O

msk

,if not, S I M terminates. Otherwise, SIM

performs as following:

– If corrupted

= corrupted

, SI M responds A

with re-encrypted ciphertext (C

|∀l ∈ S

) ←

ReEncrypt(rk,SK, S

)

– If corrupted

6= corrupted

, SI M aborts

• Trapdoor Generation Oracle O

: On input

agg

−→

Q ), the simulator proceeds as follows:

– It queries O

∀w

j,k

∈

−→

Q and obtain

j,k

∗

j,k

)

– If corrupted

= 1, set trapdoor Tr ←

TrapdoorGen(k

agg

−→

Q )

– If corrupted

= 0 ∧ c

= 1, set trapdoor Tr ←

TrapdoorGen(k

agg

−→

Q )

– Otherwise, report failure and terminate.

• Test Oracle O

test

: On giving input of (Tr ←

TrapdoorGen(k

agg

−→

Q ),S,l), S I M checks k

agg

occurs in table T

agg

, if yes, SI M returns output

of Test(Tr,S,l,U

) to the adversary. Otherwise,

SI M returns null.

Challenge Phase. The attacker A sends the chal-

lenger two equal length set of keywords

−−→

;

−−→

on which it wishes to be challenged along with an in-

dex i

, a message M from message space, a public

key pk

∗

, secret key sk, and the challenge access pol-

icy T

∗

and T

∗

. Here, the restriction is that if for any

attribute token generated in Phase 1 on an attribute list

L, F(L, T

∗

) = F(L,T

∗

) = 1 then

−−→

. If pk

∗

is not in table T

or corrupted

∗

= 1, then simulator

SI M terminates. If H

(

−−→

) = 1 and H

(

−−→

) = 1,

then the simulator returns ’failure’ and aborts. Other-

wise, the simulator S I M chooses d ∈ {0,1} as fol-

lows:

• If H

(

−−→

) = 1 and H

(

−−→

) = 0, then set d = 1

• If H

(

−−→

) = 0 and H

(

−−→

) = 1, then set d = 0

• otherwise, let d ←

{0,1}

The challenger runs

Encrypt(pk,sk,i

,M,

−−→

∗

) and returns ciphertext

∗

to the adversary.

The Challenger C sets t = a and computes cipher-

text for

−−→

and access policy T

∗

as follows:

∗

= g

; C

∗

= (v · g

)

∗

= C

−−→

= Π(H

i, j

))

|∀w

i, j

∈

−−→

∗

= C

= M e(g

, g

)

∗

= Π(H

(av

attr

i, j

)))

|∀attr

i, j

∈ T

∗

= i

· e(g

)

Query Phase 2. Same as Phase 1, the adversary asks

for more queries q

n+1

,....., q

except the following

oracles:

• Trapdoor Generation Oracle O

: On giving in-

put of (k

agg

−→

Q ) by the adversary, the challenger

answers same as that in phase 1, except the fol-

lowing cases:

– The adversary had previously ask for the trap-

door corresponding to a set of keywords

−−→

–

−→

Q =

−−→

−→

Q =

−−→

If one of the above condition holds, then chal-

lenger returns null.

• Test Oracle O

test

: On input of Test(Tr,S,l,U

if i

= l or i

∈ S, then the challenger returns null.

Otherwise the challenger responds as that in phase

Guess. The adversary A outputs its guess d

∈ {0,1}

for d.

If d

= d , then SI M outputs X

= 0 . If d

6= d ,

then SI M outputs X

= 1.

This completes the simulation.

If S I M does not report failure and it receives

DDH instances as input, the challenge ciphertext is

a valid encryption of (pk

∗

,M,

−−→

∗

) and A

guesses d

= d with the advantage l. If SI M does

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass

Access Control

121

not receives DDH instances as input, the challenge

ciphertext does not contain information about

−−→

since keyword ciphertext is uniformly distributed in

and independent of d. The adversary A guesses

= d with exactly 1/2 probability.

We analyze the probability that the simulator does

not report failure or abort during the simulation.

When A asks for trapdoor to oracle O

, it

happens H

(kv

j,k

) = 0 for some keyword w

j,k

and it makes simulator to respond with failure.

The probability that the simulator SI M aborts is

Pr[H

(kv

j,k

) = 0]= 1/(q

+ 1). Therefore, as A

makes at most q

oracle queries, the probability of

the simulator not reporting failure and aborting is

(1 − 1/(q

+ 1))

≥ 1/e

The only situation that SIM reports failure

during challenge phase is that H

(

−−→

) = 1 and

(

−−→

) = 1. Since Pr[H

(

−−→

) = 0]= 1/(q

1) for d ∈ {0, 1} and the values of H

(

−−→

) and

(

−−→

) are independent of A. Furthermore, these

two values are independent of each other. Hence, we

have

Pr|H

(

−−→

) = 1∧ H

(

−−→

) = 1| = (1 −1/(q

1))

≤ 1 − 1/q

Hence, the probability that the simulator has no

failure state is at least 1/q

Therefore, the simulator simulates without failure

with the probability at least 1/e + 1/q

Let us analyze the advantage of the simulator solv-

ing DDH problem on condition that the simulation

completes perfectly.

Based on this, there will be two cases as follows:

case(i): if X = 0, then Z = g

abc

and hence challenge

ciphertext is a correct ciphertext of keyword

−−→

Then, the probability of A guessing correctly d = d

is 1/2 + ε.

case(ii): if X = 1, then the challenge ciphertext is in-

dependent of

−−→

and

−−→

, so that A can not ob-

tain any information of d. Then, the probability of A

guessing correctly d = d

is 1/2.

From (i) and (ii), it follows that SI M ’s advantage

in this DDH game can be computed as:

(

+ ε) +

Therefore, if the A has a non-negligible advan-

tage ε in the above game then we can build a simula-

tor (SI M ) which can break the DDH problem with

non negligible quantity = (

)

, which is an in-

tractable problem. 

Theorem 2. If the decisional DDH assumption hold

in (G,G

), then the proposed BTG-RKASE scheme

preserves the trapdoor privacy in the random oracle

model.

Proof. The proof of Theorem 2 is similar to the proof

of Theorem 1.

6 EMPIRICAL EVALUATION

In this section, we evaluate and analyze the compu-

tational cost of different algorithms of the proposed

scheme.

6.1 Implementation Details

In order to evaluate the performance, we implement

the prototype of our scheme and conduct the ex-

periments using Java Pairing Based Cryptographic

(JPBC) library (De Caro and Iovino, 2011). We con-

ducted experiments as follows: client implementa-

tions were executed in a personal computer with 64

bit Intel(R) Core(TM) i5 -7200U CPU @ 2.50 GHz

with Windows10 OS; server implementations were

deployed in the Amazon AWS cloud, using an EC2

M5 large instance. Communications were performed

on a 10MB/s connection, with 26.932ms round-trip

time. We used the ofﬁcial Medicare.gov Hospital

Compare datasets provided by the Centers for Medi-

care and Medicaid Services (Hos, 2019). Each doc-

ument is ﬁxed to 10 KB with random words cho-

sen from a dictionary and the query is also contain-

ing some random keywords. We use Type A pairing

for evaluation and it is the fastest (symmetric) pairing

among all types of curves. Type A pairings are con-

structed on the curve y

= x

+ x over the ﬁeld F

for

some prime q = 3 mod 4.

6.2 Experimental Results

The time cost of Setup() is linear in the maximum

number of documents belonging to the data owner

(Figure 3a). Figure 3b shows the computational cost

of KeyGen() approximate to a constant. The com-

putational cost of AttrGen() is linear in number of

attributes, as shown in Figure 3c. The results given

in Figure 3d and Figure 3e show that the compu-

tational overhead of Encrypt() is linear in the num-

ber of keywords to be attached with the ciphertext

and number of attributes in the access policy. Fig-

ure 3f show that the computational overhead of Key-

Gen BTG() is linear in the number of attributes in

the break-glass policy. Figure 3g shows the compu-

tational time of Extract() is linear in the number of

shared documents. The computational cost of Revo-

cation() is linear in the number of revoked users, as

SECRYPT 2019 - 16th International Conference on Security and Cryptography

122

(a) Time cost of Setup() (b) Time cost of KeyGen() (c) Time cost of AttrGen() (d) Time cost of Encrypt()

based on number of keywords

(e) Time cost of Encrypt()

based on number of attributes

in access policy

(f) Time cost of Key-

Gen BTG() based on number

of attributes in break-glass

policy

(g) Time cost of Extract() (h) Time cost of Revocation() (i) Time cost of TrapdoorGen() (j) Time cost of ReKeygen()

(k) Time cost of ReEncrypt() (l) Time cost of Test() based on

number of keywords

(m) Time cost of Test() based

on number of shared docu-

ments

(n) Time cost of Decrypt() (o) Time cost of BTG Access()

Figure 3: The computational cost of BTG-RKASE algorithms().

shown in Figure 3h. Figure 3i shows the computa-

tional time of TrapdoorGen() is linear in the number

of keywords within search query set. Figure 3j shows

the computational time of ReKeygen() approximate

to a constant. Figure 3k shows that the computational

time of ReEncrypt() is linear in number of documents

to be re-encrypted. The execution time of Test() is lin-

ear in the number of shared documents (Figure 3m),

whereas in case of multi-keyword search the compu-

tational time of Test() remains constant with respect

to the number of keywords in the query set (Figure3l).

Figure 3n show that the cost of decryption is in linear

with the number of documents. Figure 3o show the

computational time of veriﬁcation of break-the-glass

policy is constant as it require only 2 pairing opera-

tions, independent of number of attributes.

7 CONCLUSIONS AND FUTURE

EXTENSION

The main contribution of this paper is to provide a

mechanism which can handle emergency situations

where no authorized user exists to perform (or to dele-

gate) a time-critical task. The proposed BTG-RKASE

system supports three ways for searchable group data

sharing and accessing encrypted dataset: delegation,

policy-based ﬁne-grained multi-delegation and break-

the-glass access. In normal situations, the authorized

user with the delegated key can access the shared

dataset, provided ciphertext class is within the range

of aggregate key. In ﬁne-grained multi-delegation

mode, if the attributes of the delegatee satisfy the hid-

den access policy (deﬁned by the data owner), the

delegatee can delegate his received rights to another

user. The expensive computation of re-encryption

required for multi-delegation is outsourced to proxy

server without compromising the data conﬁdentiality.

In exceptional situation (when the authorized users

are not available), the break-glass access mechanism

allow timely access to the data, provided the attributes

of the user satisfy the break-the-glass policy. The

proposed scheme also allows revocation of delegated

rights even in case of multi-delegation. The other con-

tribution of the proposed approach is that it supports

multi-keyword search over the shared dataset using a

BTG-RKASE: Privacy Preserving Revocable Key Aggregate Searchable Encryption with Fine-grained Multi-delegation Break-The-Glass

Access Control

123

single trapdoor (instead of multiple trapdoors). Our

performance evaluation and simulation results indi-

cated that the proposed method is efﬁcient and secure.

In future, we plan to design an trust and risk-based

auto-delegation mechanism which can respond auto-

matically to the absence of appropriately authorized

users, after ﬁnding the legitimacy of the user (based

on trust and risk value) for emergency access.

ACKNOWLEDGMENTS

The second author acknowledges the support received

from Indian Institute of Technology Jammu under the

Faculty Professional Development Grant and the ﬁrst

author acknowledges the Visveswaraya PhD Support

Scheme at Sardar Vallabhbhai National Institute of

Technology, Surat.

REFERENCES

(2019). Hospital compare. available at

https://data.medicare.gov/data/hospital-compare,

accessed on February 13, 2019.

Ardagna, C. A., Di Vimercati, S. D. C., Foresti, S., Grandi-

son, T. W., Jajodia, S., and Samarati, P. (2010). Access

control for smarter healthcare using policy spaces.

Computers & Security, 29(8):848–858.

Ardagna, C. A., di Vimercati, S. D. C., Grandison, T., Ja-

jodia, S., and Samarati, P. (2008). Regulating excep-

tions in healthcare using policy spaces. In IFIP An-

nual Conference on Data and Applications Security

and Privacy, pages 254–267. Springer.

Banu, A. S. (2015). Efﬁcient data sharing in cloud medium

with key aggregate cryptosystem. Networking and

Communication Engineering, 7(3):118–121.

Blaze, M., Bleumer, G., and Strauss, M. (1998). Divertible

protocols and atomic proxy cryptography. Advances

in Cryptology—EUROCRYPT’98, pages 127–144.

Cheon, J. H. (2006). Security analysis of the strong difﬁe-

hellman problem. In Advances in Cryptology - EU-

ROCRYPT 2006, pages 1–11. Springer Berlin Heidel-

berg.

Chu, C.-K., Chow, S. S., Tzeng, W.-G., Zhou, J., and Deng,

R. H. (2014). Key-aggregate cryptosystem for scal-

able data sharing in cloud storage. IEEE transactions

on parallel and distributed systems, 25(2):468–477.

Crampton, J. and Khambhammettu, H. (2008). On delega-

tion and workﬂow execution models. In Proceedings

of the 2008 ACM symposium on Applied computing,

pages 2137–2144. ACM.

Cui, B., Liu, Z., and Wang, L. (2016). Key-aggregate

searchable encryption (kase) for group data sharing

via cloud storage. IEEE Transactions on computers,

65(8):2374–2385.

Dang, H., Chong, Y. L., Brun, F., and Chang, E.-C. (2016).

Practical and scalable sharing of encrypted data in

cloud storage with key aggregation. In Proceedings

of the 4th ACM Workshop on Information Hiding and

Multimedia Security, pages 69–80. ACM.

De Caro, A. and Iovino, V. (2011). jpbc: Java pairing

based cryptography. In Computers and communica-

tions (ISCC), 2011 IEEE Symposium on, pages 850–

855. IEEE.

Ferreira, A., Cruz-Correia, R., Antunes, L., Farinha, P.,

Oliveira-Palhares, E., Chadwick, D. W., and Costa-

Pereira, A. (2006). How to break access control in

a controlled manner. In Computer-Based Medical

Systems, 2006. CBMS 2006. 19th IEEE International

Symposium on, pages 847–854. IEEE.

Joint, N. (2004). Break-glass: An approach to granting

emergency access to healthcare systems. COCIR/JIRA

Security And Privacy Committee (SPC).

Kiayias, A., Oksuz, O., Russell, A., Tang, Q., and Wang, B.

(2016). Efﬁcient encrypted keyword search for multi-

user data sharing. In European Symposium on Re-

search in Computer Security, volume NA, pages 173–

195. Springer.

Li, T., Liu, Z., Jia, C., Fu, Z., and Li, J. (2018). Key-

aggregate searchable encryption under multi-owner

setting for group data sharing in the cloud. Interna-

tional Journal of Web and Grid Services, 14(1):21–43.

Li, T., Liu, Z., Li, P., Jia, C., Jiang, Z. L., and Li, J. (2016).

Veriﬁable searchable encryption with aggregate keys

for data sharing in outsourcing storage. In Informa-

tion Security and Privacy, pages 153–169. Springer

International Publishing.

Mahalle, R. V. and Pawade, P. P. A review of secure data

sharing in cloud using key aggregate cryptosystem

and decoy technology. International Journal of Sci-

ence and Research (IJSR), 3.

Marinovic, S., Craven, R., Ma, J., and Dulay, N. (2011).

Rumpole: a ﬂexible break-glass access control model.

In Proceedings of the 16th ACM symposium on Access

control models and technologies, pages 73–82. ACM.

Padhya, M. and Jinwala, D. (2018). Mulkase - a novel

approach for key aggregate searchable encryption for

multi-owner data. Frontiers of Information Technol-

ogy Electronic Engineering, -1(-1).

Patranabis, S., Shrivastava, Y., and Mukhopadhyay, D.

(2015). Dynamic key-aggregate cryptosystem on el-

liptic curves for online data sharing. In Interna-

tional Conference in Cryptology in India, pages 25–

44. Springer.

Sahai, A., Waters, B., et al. (2005). Fuzzy identity-based

encryption. In Eurocrypt, volume 3494, pages 457–

473. Springer.

Sandhu, R. S., Coyne, E. J., Feinstein, H. L., and Youman,

C. E. (1996). Role-based access control models. Com-

puter, 29(2):38–47.

Schaad, A. and Moffett, J. D. (2002). Delegation of obli-

gations. In Policies for Distributed Systems and Net-

works, 2002. Proceedings. Third International Work-

shop on, pages 25–35. IEEE.

Zhou, R., Zhang, X., Du, X., Wang, X., Yang, G., and

Guizani, M. (2018). File-centric multi-key aggregate

keyword searchable encryption for industrial internet

of things. IEEE Transactions on Industrial Informat-

ics.

SECRYPT 2019 - 16th International Conference on Security and Cryptography

124