
Middle Point Reduction of the Chain-recurrent Set
Carlos Arg
´
aez
1 a
, Peter Giesl
2 b
and Sigurdur Freyr Hafstein
1 c
1
Science Institute, University of Iceland, Dunhagi 5, 107 Reykjav
´
ık, Iceland
2
Department of Mathematics, University of Sussex, Falmer, BN1 9QH, U.K.
Keywords:
Lyapunov Functions, Chain-recurrent Set, Programming, Algorithm, Mathematics, Dynamical Systems.
Abstract:
Describing dynamical systems requires capability to isolate periodic behaviour. In Lyapunov’s theory, the
qualitative behaviour of a dynamical system given by a differential equation can be described by a scalar
function that decreases along solutions: the Complete Lyapunov Function. The chain-recurrent set will pro-
duce constant values of an associated complete Lyapunov function and zero values of its orbital derivative.
Recently, we have managed to isolate the chain-recurrent set of different dynamical systems in 2- and 3- di-
mensions. An overestimation, however, is always obtained. In this paper, we present a method to reduce such
overestimation based on geometrical middle points for 2-dimensional systems.
1 INTRODUCTION
The study of dynamical systems offers different
methodologies to approach time-evolving phenomena
expressed as ordinary differential equations. Several
disciplines find in its semantics a powerful descriptive
language and in its results, useful tools to obtain solu-
tions. From a geometrical point of view, a dynam-
ical system describes the time-evolution of a point
in a state-space or geometrical manifold. Practically,
time-evolving phenomena can often be described as
a time-autonomous system of differential equations
given by the expression (1),
˙
x = f(x), (1)
where x ∈ R
n
and n ∈ N. Furthermore, while seen
as function of its components, f : R
n
→ R
n
is a vec-
tor field while
˙
x represents the derivative against time.
Systems like (1), in which f(x) does not explicitly de-
pend on the time t, are called autonomous. However,
the solutions to (1) lead to time-dependent solutions
unless f(x) is identically zero.
The methodology to study and describe the be-
haviour of dynamical systems can vary. Since an ana-
lytical solution is only available in the simplest cases,
one could attempt to solve numerically the differen-
tial equation system (1) for a large collection of ini-
a
https://orcid.org/0000-0002-0455-8015
b
https://orcid.org/0000-0003-1421-6980
c
https://orcid.org/0000-0003-0073-2765
tial conditions. That would indeed describe the sys-
tem but only under a copious effort and would require
to find a solution curve S
t
ξ, defined as S
t
ξ := x(t) for
numerous initial condition x(0) = ξ ∈ R
n
.
Computing the invariant manifolds which form
the boundaries of the attractors’ basins of attraction
(Krauskopf et al., 2005) is also a well-known method-
ology along with set oriented methods (Dellnitz and
Junge, 2002) or the cell mapping approach (Hsu,
1987). All these methods require large computational
effort.
When the stability of a dynamical system is of in-
terest, one could turn to what today is known as Lya-
punov’s second method for stability. This was pro-
posed by Aleksandr Lyapunov (Lyapunov, 1992) in
1893 and consists in constructing a scalar function,
nowadays known as a Lyapunov function. It is built
around an equilibrium point, or more generally an at-
tractor of the dynamical system. The explicit solution
to the differential equation is not required.
The equilibrium points are the zeros of the right-
hand side, i.e. points x
0
with f(x
0
) = 0, implying that
any solution taking it as an initial condition is an equi-
librium, i.e. will not change in time for it is a constant
solution. An attractor, however, is a set whose neigh-
bourhood’s points will provide solutions that tend to
the attractor as time grows.
An equilibrium point is called stable if close
points produce close-remaining solutions. It is called
attractive if all adjacent solutions will tend to it as
time grows. That means that for an attractive equi-
Argáez, C., Giesl, P. and Hafstein, S.
Middle Point Reduction of the Chain-recurrent Set.
DOI: 10.5220/0007920601410152
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 141-152
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
141

librium x
0
one can find a ball B
δ
(x
0
), with δ > 0 such
that kS
t
x −x
0
k → 0,t → ∞ for all x ∈ B
δ
(x
0
).
The attractivity and stability are two different con-
cepts and do not imply one another, however, when
both occur, then we talk about an asymptotically sta-
ble equilibrium.
Solutions could also have the possibility of com-
ing back to a given point after a certain time T . A set
of points in which the behaviour of a dynamical sys-
tem will repeat after a certain time T , i.e. is recurrent,
is a called a periodic orbit.
A Lyapunov function is an auxiliary scalar-valued
function whose domain is a subset of the state-space,
and which is strictly decreasing along all solution tra-
jectories in a neighbourhood of an attractor, such as
an asymptotically stable equilibrium point or periodic
orbit. Furthermore, it attains its minimum on the at-
tractor.
This is the classical definition of a strict Lyapunov
function and it can be understood in the physical word
using a simple paragon, i.e. a system with dissipative
energy.
However, this function is only defined in the
neighbourhood of one attractor and serves to describe
the set of points whose solutions converge to the it:
the basin of attraction.
For a long time it was hard to obtain a Lyapunov
function for a given dynamical system. If the system
under analysis is linear, it is possible to obtain a clas-
sical Lyapunov function relatively easily. However, if
the system is not linear then, in general, one could not
hope to be able to obtain a Lyapunov function easily.
An extension defined on the whole state space, a
complete Lyapunov function, was introduced in (Con-
ley, 1978; Conley, 1988; Hurley, 1995; Hurley, 1998).
A complete Lyapunov function characterizes the
complete qualitative behaviour of the dynamical sys-
tem on the whole phase space and not just in a neigh-
bourhood of one particular attractor. Therefore, it al-
lows to describe the different basins of attraction for
the different attractors the dynamical system could
have. It divides the state-space into two disjoint ar-
eas: The first is the gradient-like flow, where the sys-
tem’s trajectories flow through. The second is where
infinitesimal perturbations can make the system recur-
rent. These two areas describe fundamentally differ-
ent behaviours.
The regions in which the system is recurrent is
usually referred to as the chain-recurrent set.
An ε-trajectory is arbitrarily close to a true sys-
tem’s solution and a point in the chain-recurrent set
is recurrent or almost recurrent; for a precise defi-
nition see, e.g. (Conley, 1978). The dynamics out-
side of the chain-recurrent set are similar to a gra-
dient system, i.e. a system (1) where the right-hand
side f(x) is given by the gradient ∇U (x) of a function
U : R
n
→ R.
Definition 1.1 (Complete Lyapunov Function). Let us
consider an autonomous system of differential equa-
tions described by,
˙
x = f(x), x ∈R
n
A complete Lyapunov function is a continuous
scalar function, V : R
n
→ R that:
• Is constant in each chain-transitive component of
the chain-recurrent set
• Decreases strictly along solution trajectories in
other places
These conditions imply that, if V is differentiable,
its time-derivative should be zero or decreasing:
dV (x)
dt
= ∇V (x) ·
dx
dt
= ∇V (x) ·
˙
x = ∇V (x) ·f(x) ≤ 0.
This quantity is called orbital derivative.
Conley (Conley, 1978) gave the first mathematical
existence proof for complete Lyapunov functions of a
dynamical system defined on a compact metric space.
Hurley (Hurley, 1998) extended these results to sepa-
rable metric spaces. More recent results are found in
(Fathi and Pageault, 2019; Bernhard and Suhr, 2018).
In this paper we use a computationally efficient
algorithm to compute a complete Lyapunov function
using Radial Basis Functions, which was introduced
for classical Lyapunov functions in (Giesl, 2007). It
has been developed in (Arg
´
aez et al., 2017; Arg
´
aez
et al., 2018b; Arg
´
aez et al., 2018c; Giesl et al., 2018;
Arg
´
aez et al., 2018a).
The general idea is to approximate a “solution”
to the ill-posed problem V
0
(x) = −1, where V
0
(x) =
∇V (x) ·f(x) is the derivative along solutions of the
ODE, i.e. the orbital derivative. This approximation
is inspired by the fact that the orbital derivative has to
be negative everywhere except in areas in which the
system has recurrent behaviour.
A function v is computed using Radial Basis Func-
tions, a mesh-free collocation technique, such that
v
0
(x) = −1 is fulfilled at all points x in a finite set
of collocation points X.
The discretized problem of computing v is well-
posed and possesses a unique solution. However, the
computed function v cannot fulfil the PDE V
0
(x) =
−1 at all points of the chain-recurrent set, such as an
equilibrium or a periodic orbit. This is the key com-
ponent to locate the chain-recurrent set with our gen-
eral algorithms; we use the area where v fails to ful-
fil the PDE to determine the chain-recurrent set. The
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
142

points in this set have vanishing values over the orbital
derivative.
However, points in the neighbourhood of the
chain-recurrent set, tend to have an orbital deriva-
tive near zero. That causes an overestimation of the
chain-recurrent set. There have been systematic ap-
proaches to solve of this problem. First, in (Arg
´
aez
et al., 2018b) it was observed that for systems, in
which the speed varies greatly along solutions, the or-
bital derivative can vary greatly. This caused a con-
siderable overestimation of the chain-recurrent set. A
normalization condition was introduced to homoge-
nize the speed at all points of the system. Later in
Section 2 this step will be further explained.
Second, in (Arg
´
aez et al., 2019b), an effort was
made to understand the importance of a clustering
algorithm to classify different orbits and equilibria.
That was introduced firstly as a test over circular or-
bits only. Based on the geometrical constraints, toler-
ance radii were defined to reduce the overestimation
of the chain-recurrent set. The general idea is sum-
marized as follows:
• Obtain an approximation to the chain-recurrent
set
• For each circular orbit in the chain-recurrent set
with radius r, define two new radii, r
max
and r
min
,
then
r
1
= r
min
+ 0.52 ∗(r
max
−r
min
)
r
2
= r
max
−0.52 ∗(r
max
−r
min
)
• Remove from the chain-recurrent set all points
with Euclidian norm r 6∈ [r
2
,r
1
]
Obvious limitations arise with this approach as it
only works with circular shapes, but it showed greatly
improved results for adequate systems.
Later in (Arg
´
aez et al., 2019a), an algorithm ca-
pable of decomposing the chain-recurrent set into its
connected components was presented. That was done
regardless of the shapes of the components.
Now, a large chain-recurrent set containing equi-
libria and orbits of different shapes, would be classi-
fied in subsets. However, no algorithm to reduce the
overestimation was given in that work.
Now, in this paper we will propose a reduction
algorithm capable of reducing the overestimation of
the chain-recurrent set. The idea for the reduction
is based on exploiting the geometrical properties of
the collocation grid used to compute the Lyapunov
function. That means that we compute middle points
of different cleverly-chosen sections of the chain-
recurrent set. The union of these middle points is used
as a reduced estimation of the chain-recurrent set.
In Section 2 a brief description of how to com-
pute a complete Lyapunov function is given. Then in
Section 3 the novel algorithm to reduce the overesti-
mation is explained. In Section 4 examples of its ap-
plication are given, which are discussed in Section 5.
Section 6 analyses the computation cost of this algo-
rithm and finally Section 7 will summarize the results
of this work.
2 CONSTRUCTION OF
COMPLETE LYAPUNOV
FUNCTIONS
2.1 Mesh-free Collocation
Radial Basis Functions (RBF) are a powerful method-
ology to construct complete Lyapunov functions
when posed as a generalized interpolation problem
(Wendland, 1998)
They are real-valued functions whose evaluation
depends only on the distance from the origin. Com-
mon examples of RBFs are Gaussians and multi-
quadrics.
In this work, we use Wendland functions as RBF,
which are compactly supported and positive definite
functions (Wendland, 1998). They have the advantage
of being expressed as algebraic polynomials on their
compact support.
Further, the corresponding Reproducing Kernel
Hilbert Space H is norm-equivalent to a Sobolev
space.
2.2 Wendland Functions
The general form of a Wendland function is ψ(x) :=
ψ
l,k
(ckxk), where c > 0 determines the size of the
compact support and k ∈ N is a smoothness param-
eter. For our application the parameter l is fixed as
l = b
n
2
c+ k + 1. The Reproducing Kernel Hilbert
Space corresponding to ψ
l,k
contains the same func-
tions as the Sobolev space W
k+(n+1)/2
2
(R
n
) and the
spaces are norm equivalent.
The functions ψ
l,k
are defined by the recursion:
For l ∈ N and k ∈ N
0
, we define
ψ
l,0
(r) = (1 −r)
l
+
,
ψ
l,k+1
(r) =
R
1
r
tψ
l,k
(t)dt
(2)
for r ∈ R
+
0
, where x
+
= x for x ≥ 0 and x
+
= 0 for
x < 0.
Middle Point Reduction of the Chain-recurrent Set
143
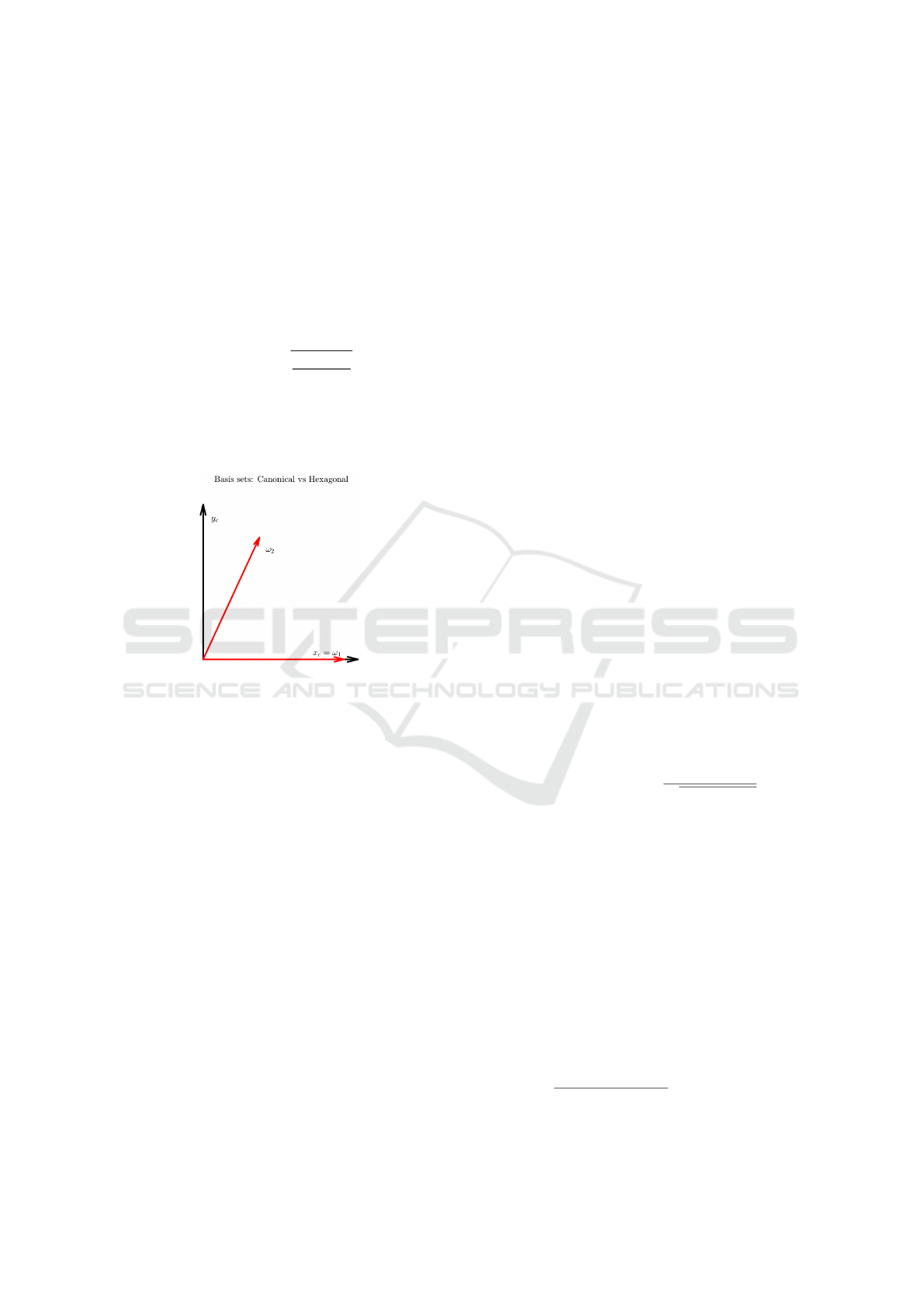
2.3 Collocation Points
As collocation points, we use a subset, X =
{x
1
,.. . ,x
N
} ⊂ R
n
, of a hexagonal grid with fineness-
parameter α
Hexa-basis
∈R
+
constructed according to the
equation:
{
α
Hexa-basis
∑
n
k=1
i
k
ω
k
: i
k
∈ Z
}
,
ω
k
=
∑
k−1
j=1
ε
j
e
j
+ (k + 1)ε
k
e
k
and ε
k
=
r
1
2k(k + 1)
.
(3)
Here e
j
is the usual jth unit vector.
These basis vectors are shown in red colour in Fig-
ure 1 in R
2
, while the canonical vectors are shown in
black.
Figure 1: Black: Canonical basis. Red: Hexagonal basis
set.
Although any scattered points could be used as
collocation points, the hexagonal grid has been shown
to minimize the condition numbers of the collocation
matrices for a fixed fill distance, i.e. a measure of the
density of the collocation grid (Iske, 1998).
Since f(x) = 0 for all equilibria x, we remove all
equilibria from the set of collocation points X; not do-
ing so would cause the collocation matrix to be singu-
lar.
The first approximation v to a complete Lyapunov
function is then given by the function that satisfies
the PDE v
0
(x) = −1 at all collocation points and is
norm minimal in the corresponding Reproducing Ker-
nel Hilbert space H.
In later iterations we solve v
0
(x) = r
j
for different
r
j
≤ 0, determined by previous approximations.
Practically, we compute v by solving a system of
N linear equations, where N is the number of colloca-
tion points.
The explicit formulas for v and its orbital deriva-
tive are
v(x) =
∑
N
j=1
β
j
hx
j
−x, f(x
j
)iψ
1
(kx −x
j
k),
v
0
(x) =
∑
N
j=1
β
j
h
−ψ
1
(kx −x
j
k)hf(x),f(x
j
)i
+ψ
2
(kx −x
j
k)hx −x
j
,f(x)i
·hx
j
−x, f(x
j
)i
i
,
where ψ
1
,ψ
2
are functions computed from the Wend-
land function ψ
l,k
used, h·,·i denotes the standard
scalar product and k· k the Euclidean norm in R
n
,
β ∈ R
N
is the solution to Aβ = r, r
j
= r(x
j
) and A
is the N ×N matrix with entries
a
i j
= ψ
2
(kx
i
−x
j
k)hx
i
−x
j
,f(x
i
)ihx
j
−x
i
,f(x
j
)i (4)
−ψ
1
(kx
i
−x
j
k)hf(x
i
),f(x
j
)i
for i 6= j and
a
ii
= −ψ
1
(0)kf(x
i
)k
2
.
More detailed explanations on this construction are
given in (Giesl, 2007, Chapter 3).
If no collocation point x
j
is an equilibrium for the
system, i.e. f(x
j
) 6= 0 for all j, then the matrix A is
positive definite and the system of equations Aβ = r
has a unique solution.
The last assertion will hold true independently of
whether the underlying discretized PDE has a solu-
tion or not, while error estimates are obviously only
available if the PDE has a solution.
Note that in the context of RBF, a positive definite
function ψ refers to the matrix (ψ(kx
i
−x
j
k))
i, j
being
positive definite for X = {x
1
,x
2
,.. . ,x
N
}, where x
i
6=
x
j
if i 6= j.
As explained in (1), in (Arg
´
aez et al., 2018b) we
introduced an “almost” normalized approach, i.e., the
original dynamical system (1) was substituted by
˙
x =
ˆ
f(x), where
ˆ
f(x) =
f(x)
p
δ
2
+ kf(x)k
2
(5)
with a small parameter δ > 0. This normalization al-
ready reduces significantly the overestimation of the
chain-recurrent set.
2.4 Evaluation Grid
After we have solved the PDE numerically, i.e. forced
V
0
(x
j
) = −r
j
at every collocation point x
j
, we use an
evaluation grid Y
x
j
around each collocation point x
j
to evaluate the results.
Placing all evaluation points aligned to the flow
of the ODE system, as introduced in (Arg
´
aez et al.,
2018c; Arg
´
aez et al., 2018a), has proved successful.
The formula for the evaluation grid is
Y
x
j
=
(
x
j
±
r ·k ·α
Hexa-basis
·
ˆ
f(x
j
)
mk
ˆ
f(x
j
)k
: k ∈ {1, .. ., m}
)
,
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
144

where α
Hexa-basis
is the parameter used to build the
hexagonal grid defined above, r ∈ (0,1) is the ratio
up to which the evaluation points will be placed and
m ∈N denotes the number of points in the evaluation
grid that will be placed on both sides of the colloca-
tion points aligned to the flow.
Using this evaluation grid means that there will
not be any evaluated points to provide information
about the dynamical system other than in the direction
of the flow. However, this evaluation grid avoids ex-
ponential growth of evaluation points as the system’s
dimension becomes higher and the results are usually
good, i.e. enough information about the dynamics is
gained.
We start by computing the approximate solution
v
0
to V
0
(x) = −1 with collocation points X. As we
have previously done in (Arg
´
aez et al., 2017; Arg
´
aez
et al., 2018b), we define a tolerance parameter −1 <
γ ≤ 0. In each step i of the iteration we mark a col-
location point x
j
as being in the chain-recurrent set
(x
j
∈ X
0
) if there is at least one point y ∈ Y
x
j
such
that v
0
i
(y) > γ. The points for which the condition
v
0
i
(y) ≤ γ holds for all y ∈ Y
x
j
are considered to be-
long to the gradient-like flow (x
j
∈ X
−
).
As has been done in (Arg
´
aez et al., 2018c), in this
paper we replace the right-hand side −1 by the aver-
age of the values v
0
i
(y) over the evaluation grid y ∈Y
x
j
at each collocation point x
j
for averages that are neg-
ative. In cases in which the average is positive we use
0. In formulas, we calculate the approximate solution
v
i+1
of V
0
(x
j
) = ˜r
j
with
˜r
j
=
1
2m
∑
y∈Y
x
j
v
0
i
(y)
−
,
where x
−
= min(0,x). We will refer to this as the
“non-scaled” version.
However, this approach can lead to a continuous
decrease of “energy” over the iterations.
Recall that the original value of the orbital deriva-
tive condition in the first iteration is −1, but the new
value is obtained by averaging and bounding by 0.
This can cause it to converge to zero and thus force the
total “energy” of the Lyapunov function to decrease.
To avoid this, we scale the condition of the orbital
derivative after the first iteration onwards so that the
sum of all r
j
over all collocation points is constant
for all iterations; we will refer to this as the “scaled”
method.
Our algorithm to compute complete Lyapunov
functions and classify the chain-recurrent set can be
summarized as follows:
1. Create the set of collocation points X and compute
the approximate solution v
0
to V
0
(x) = −1; set i = 0
2. For each collocation point x
j
, compute v
0
i
(y) for
all y ∈ Y
x
j
: if v
0
i
(y) > γ for a point y ∈ Y
x
j
, then
x
j
∈X
0
, otherwise x
j
∈X
−
, where γ ≤ 0 is a cho-
sen critical value
3. Define ˜r
j
=
1
2m
∑
y∈Y
x
j
v
0
i
(y)
−
4. Define r
j
=
N
∑
N
l=1
|˜r
l
|
˜r
j
,
5. Compute the approximate solution v
i+1
to
V
0
(x
j
) = r
j
for j = 1, . ..,N; this is the scaled
version, while approximating the solution of
V
0
(x
j
) = ˜r
j
would be the non-scaled version
6. Set i → i + 1 and repeat steps 2. to 5. until no
more points are added to X
0
.
Note that the sets X
0
and X
−
may change at each step
of the algorithm.
3 MIDDLE POINT REDUCTION
3.1 Middle Point Algorithm
Once we have obtained our approximations X
0
and
X
−
to the chain-recurrent and gradient-like flow re-
spectively, we want to classify the points X
0
in the
chain-recurrent set into its different connected com-
ponents, e.g. different orbits and equilibria.
The way of doing it follows the algorithm ex-
plained in (Arg
´
aez et al., 2019a).
A brief description is given below:
Algorithm 3.1: Once the chain-recurrent set is obtained.
1. Measure all distances from the origin to the dif-
ferent failing points
2. Sort all points in an increasing order according to
their distance from the origin
3. Measure the difference in radii-length between
every two consecutive points. Gaps are consid-
ered to happen when difference in distance is
greater than α
Hexa-basis
for two consecutive points
4. All points before the first gap are considered to
be a part of the first set of connected components.
Between the first and the second gap, all points
are considered to be part of the second set of con-
nected component, etc. After we have found all
gaps, the last one of them and the longest radius
length define the last set of connected components
5. Each set of component is decomposed into its
connected components
Middle Point Reduction of the Chain-recurrent Set
145

Let us point out that the chain-recurrent set is
given by the points in the collocation grid that failed
the approximation.
Therefore, they will all be aligned to the basis set
of vectors of the hexagonal grid, see Figure 2.
For each point in this classification of the chain-
recurrent set, we will build two groups. One will con-
sist of all its neighbours and neighbours of its neigh-
bours, etc., aligned to the first basis vector. The sec-
ond will consist of all its neighbours and neighbours
of its neighbours, etc., aligned to the second basis vec-
tor.
Figure 2: Points in the collocation grid aligned to the hexag-
onal basis set. Distance between two consecutive points is
α
Hexa−basis
.
Given a point x
c
in a sub-classification of the
chain-recurrent set, a way of obtaining the most di-
rect neighbours in a direction of a vector ω
k
in the
hexagonal basis (3) is to “walk” positively and neg-
atively in the sense of that direction, with steps of
size α
Hexa−basis
. That is, consider the points x
c
+
jα
Hexa−basis
ω
k
for integer j. Then, the neighbours of
its neighbours will be found with the “next step”, etc.
When a next pth-step is given and no point is found,
then the search in that direction’s sense is stopped.
The total search of neighbours for that point stops
when both direction’s senses, the positive and the
negative, reach a point that was not originally in the
chain-recurrent set. Then, the new sub-classification
group continues with another point.
Once we have grouped all the points in the sub-
classification of chain-recurrent set, then each indi-
vidual group is organized by its different distances be-
tween points. The two most far-apart points in each
group are the boundaries of that group in that direc-
tion. These two points give, in that particular direc-
tion, the middle point that we are looking for to obtain
the reduction.
We consider that the reduced chain-recurrent set
is the total union of the middle points for each point’s
group in both directions.
Let us recall that the middle point of two points
(x
1
,y
1
) and (x
2
,y
2
) is given by,
x
m
=
x
1
+ x
2
2
, y
m
=
y
1
+ y
2
2
(6)
Single points in the orbit will be themselves after
the reduction as they are, themselves, their middle-
points. For one dimensional chain-recurrent set, the
algorithm is listed bellow.
Begin
1) Construct the Lyapunov function and its orbital
derivative;
2) Obtain the chain-recurrent set;
3) Divide it into its connected components
4) For each point in the chain-recurrent set build a
group of adjacent collocation points in direction ω
1
and one in direction ω
2
5) Identify groups that are equal 6) Find the extreme
points in each group and replace the points in the
group by the middle point
7) The reduced chain-recurrent set is the collection of
all middle points
8) Merge all groups aligned with ω
2
into a another set
of groups
9) For each group apply the middle points formula 10)
The reduced chain-recurrent set is the collection of all
middle points
End.
4 RESULTS
4.1 Two Periodic Orbits
We consider system (1) with right-hand side
f(x,y) =
−x(x
2
+ y
2
−1/4)(x
2
+ y
2
−1) −y
−y(x
2
+ y
2
−1/4)(x
2
+ y
2
−1) + x
.
(7)
This system has an asymptotically stable equilibrium
at the origin. Moreover, the system has two periodic
circular orbits: an asymptotically stable periodic orbit
at Ω
1
= {(x,y) ∈ R
2
| x
2
+ y
2
= 1} and a repelling
periodic orbit at Ω
2
= {(x, y) ∈ R
2
| x
2
+ y
2
= 1/4}.
To compute the complete Lyapunov function with
our method we used the Wendland function ψ
5,3
. The
collocation points were set in a region [−1.5,1.5] ×
[−1.5,1.5] ⊂ R
2
and we used a hexagonal grid (3)
with α
Hexa−basis
= 0.0162. The evaluation grid was
computed with the directional grid (6) with parameter
m = 50.
We computed this example with the almost-
normalized method
˙
x =
ˆ
f(x) with δ
2
= 10
−8
and γ =
−0.8.
Figure 4 shows the complete Lyapunov function
and its orbital derivative computed using 3 iterations.
The two orbits with radii 1/2 and 1 can clearly be
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
146
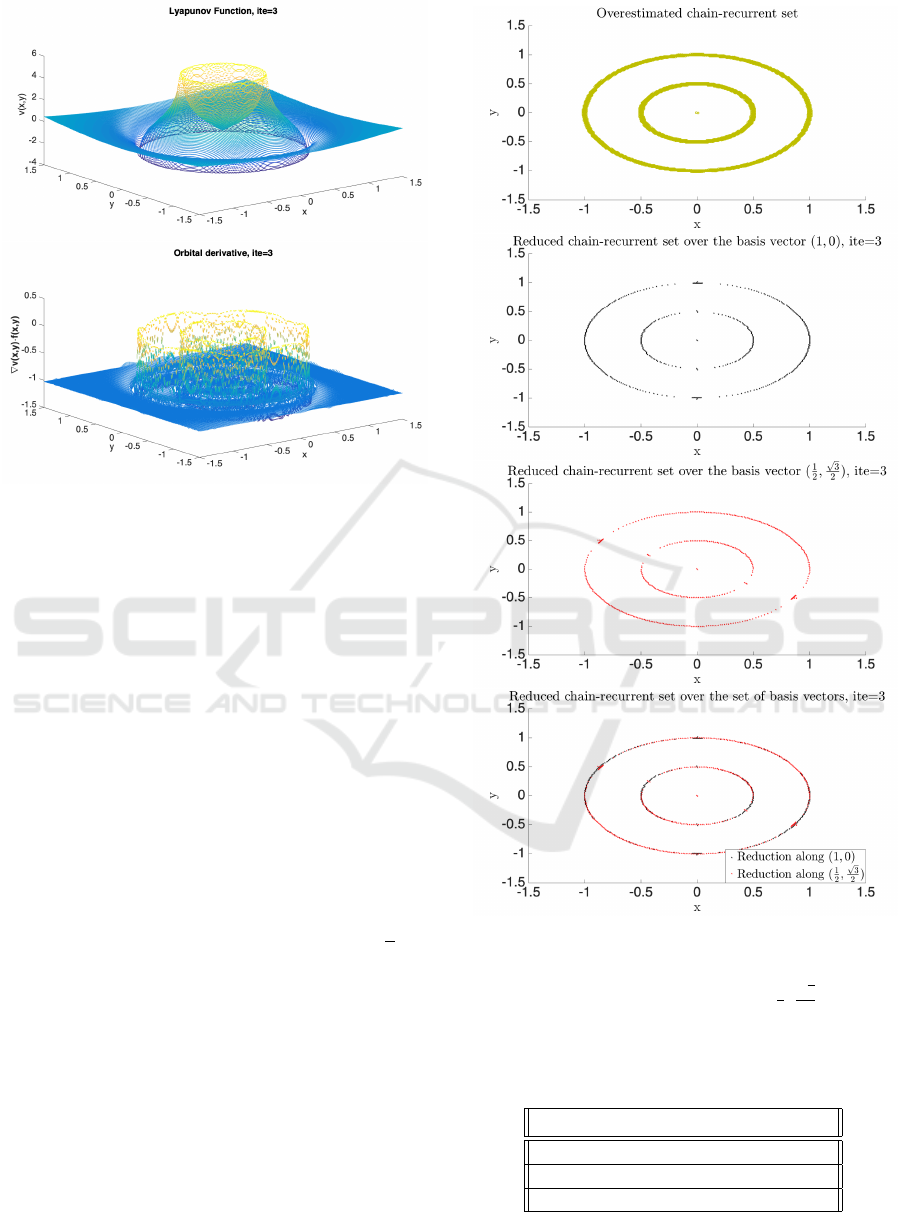
Figure 3: Upper: Complete Lyapunov function for system
7. Lower: Orbital derivative for system 7.
identified. The first one is a repeller and the second is
attractive. We see that beyond the second orbit with
radius 1, the behaviour of the Lyapunov function is
well behaved and its orbital derivative whose value
approximated −1 nicely. However, at the orbits and
close to the equilibrium at zero, we can see that the
orbital derivative fails the approximation. The collo-
cation points associated to the failing point are shown
in the last figure of Figure 3 in dark-yellow colour.
That is our approximation to the chain-recurrent set.
The middle-point reduced the chain-recurrent set over
the vector basis (1,0) is shown in the upper figure of
3. The two dots representing the equilibrium point at
the origin, the middle point reduction, are the same as
the original ones before reduction. They did not have
neighbours within a α
Hexa−basis
distance. As such,
the middle-up figure shows the middle-point reduced
chain-recurrent set over the vector basis (1/2,
√
3/2),
Figure 3. It is interesting to notice that in different
directions there will be different areas without points.
It is the union of both groups, lowest figure in Figure
3, that gives the total reduction.
The final reduction is shown over the first over-
estimated chain-recurrent set at the bottom of Figure
3. Let us show in numbers what the reduction means,
Table 1.
Table (1) shows the number of elements in the
chain-recurrent set in both cases: The non-reduced
and the reduced one. As can be seen, the number
of elements after the reduction can be a half of the
amount of numbers before the reduction.
Figure 4: Upper: Overestimated chain-recurrent set with
γ = 0.8. Middle up: Middle point reduction over the hexag-
onal basis vector (1, 0). Middle down: Middle point re-
duction over the hexagonal basis vector
1
2
,
√
3
2
. Bottom:
Both reductions. All figures for system (7).
Table 1: Difference in the total amount of points per section
of the chain-recurrent set for example (7).
Section Before After
Equilibrium point 2 2
Orbit r = 1/2 612 256
Orbit r = 1 1062 512
Middle Point Reduction of the Chain-recurrent Set
147
4.2 Van der Pol Oscillator
˙x
˙y
= f(x, y) =
y
(1 −x
2
)y −x
. (8)
For computing the complete Lyapunov function as-
sociated to system (8), we set α
Hexa-basis
= 0.043 over
the area defined by [−4,4]
2
⊂ R
2
. The Wendland
function parameters used are (l, k,c) = (4,2,1), the
critical value γ = −0.5, and δ
2
= 10
−8
. The evalua-
tion grid was computed with the directional grid with
m = 10. The complete Lyapunov function at the ini-
tial iteration and the orbital derivative over the chain-
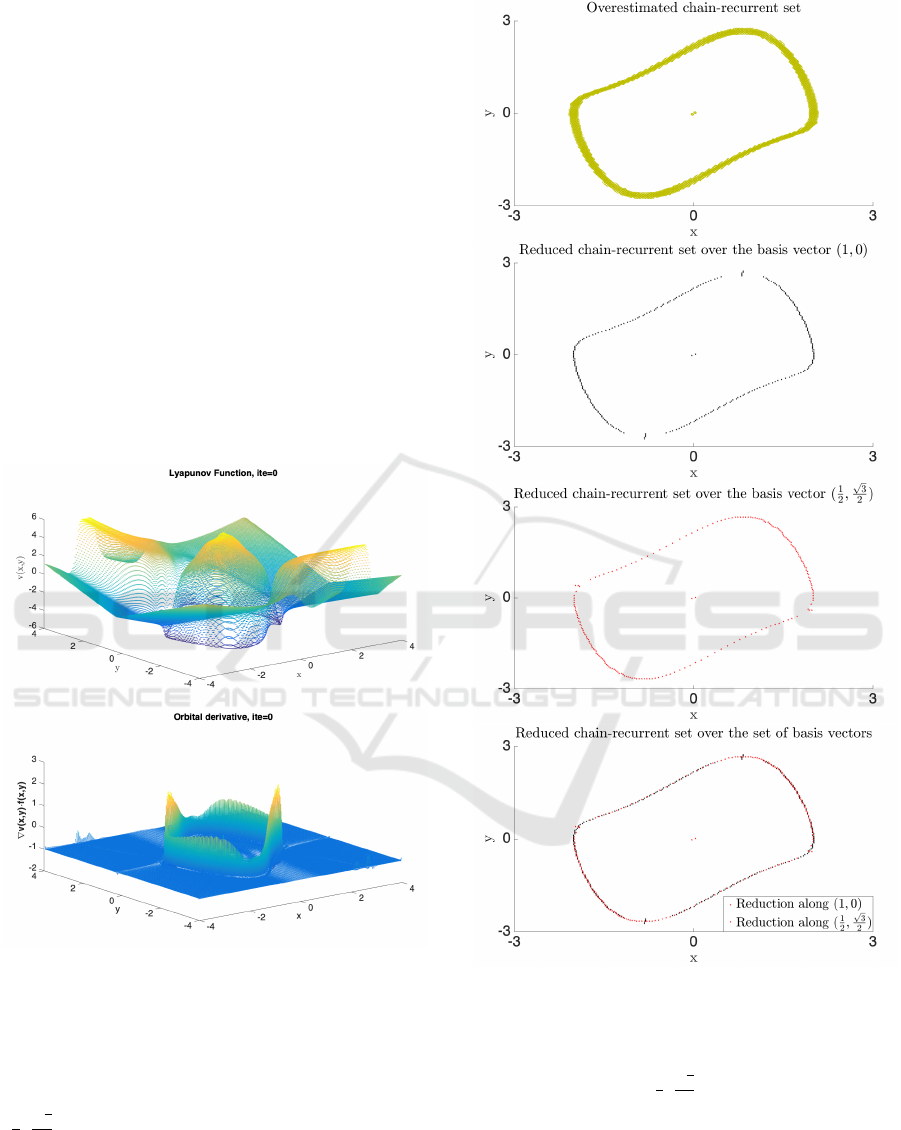
recurrent set is shown in Figure 5.
As can be seen, the Lyapunov function has a re-
peller at the origin and it has a non-circular but still
symmetric orbit around the origin. Away from the
orbit, the orbital derivative satisfies the condition −1
nicely but again the approximation fails in the orbit,
the repeller and the points nearby.
Figure 5: Upper: Complete Lyapunov function for system
8. Lower: Orbital derivative for system (8).
Our approximated chain-recurrent set is shown
in the last figure of Figure 5 in dark-yellow colour.
Again the upper figure shows the reduction along
(1,0) and middle-upper figures the reduction along
(
1
2
,
√
3
2
). The total middle-point reduction is again
shown in figure middle-lower of Figure 6. The re-
duction becomes clear when seen over the original
estimation of the chain-recurrent set, lower figure in
Figure 6.
Figure 6: This figure shows both the overestimation and
the reductions. It is divided in four subfigures. Upper:
Overestimated chain-recurrent set with γ = 0.043. Middle
up: Middle point reduction over the hexagonal basis vec-
tor (1,0). Middle down: Middle point reduction over the
hexagonal basis vector
1
2
,
√
3
2
Bottom: Both reductions.
All figures for system (8).
In Table 2 the reduction is quantified. The table shows
that the number of elements is reduced to circa a third
of its original overestimated value.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
148
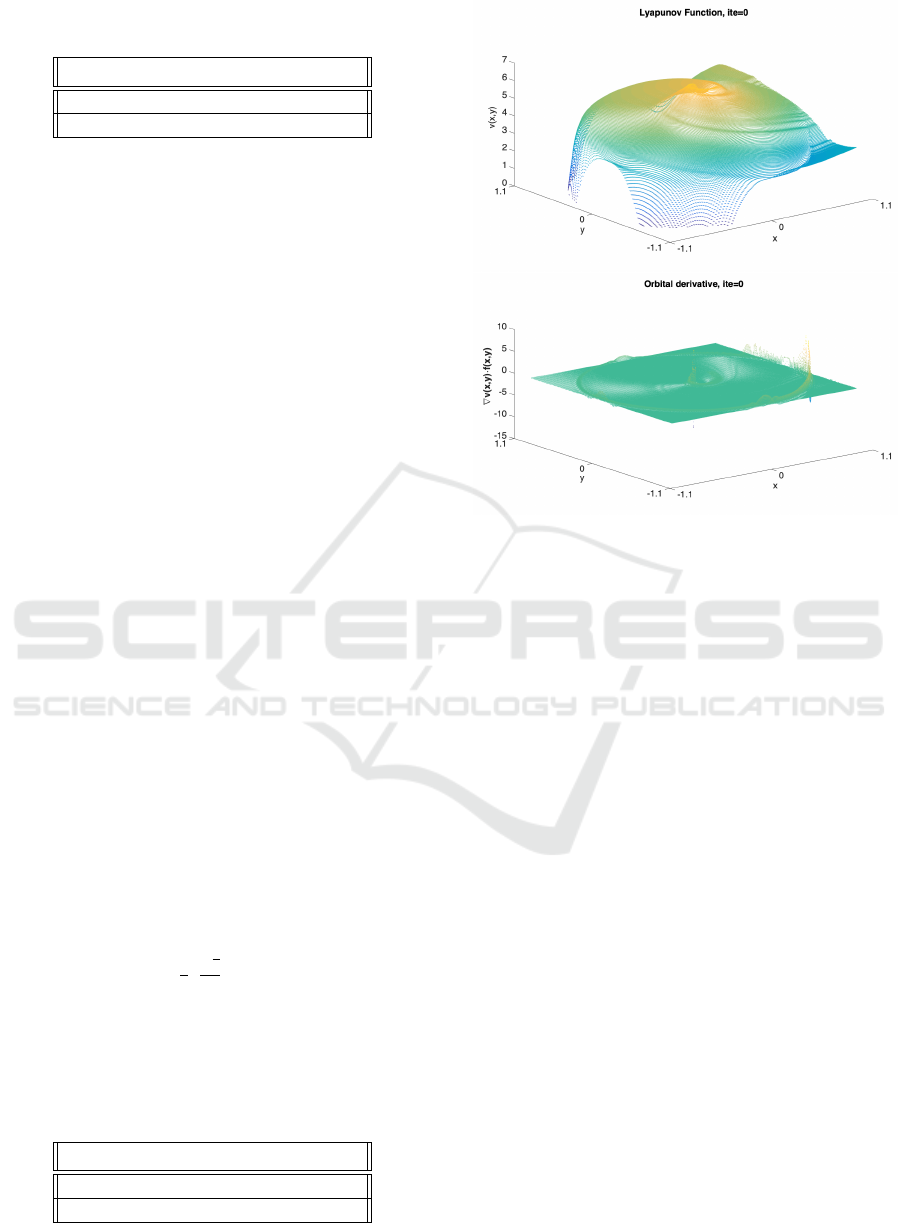
Table 2: Difference in the total amount of points per section
of the chain-recurrent set for example (8).
Section Before After
Equilibrium point 2 2
Limiting orbit 1212 444
4.3 Homoclinic Orbit
As in (Arg
´
aez et al., 2017), we also consider here the
following example
˙x
˙y
= f(x, y) (9)
=
x(1 −x
2
−y
2
) −y((x −1)
2
+ (x
2
+ y
2
−1)
2
)
y(1 −x
2
−y
2
) + x((x −1)
2
+ (x
2
+ y
2
−1)
2
)
.
The origin is an unstable focus and the system has
an asymptotically stable homoclinic orbit at a cir-
cle centred at the origin and with radius 1, con-
necting the equilibrium (1,0) with itself. We used
the Wendland function ψ
4,2
for our computations.
Our collocation points were defined in the region
[−1.1,1.1] ×[−1.1, 1.1] ⊂ R
2
with a hexagonal grid
(3) with α
Hexa−basis
= 0.011. In this example, we have
used the normalized method, i.e. we replaced f by
ˆ
f as
in (5) with δ
2
= 10
−8
, and we used γ = −0.75. As
before, the evaluation grid was computed with the di-
rectional grid with m = 10. The complete Lyapunov
function and its orbital derivative are shown in Figure
7.
The Lyapunov function has a maximum at the ori-
gin which is a repelling equilibrium point. The orbit
can be seen at radius 1. The orbital derivative condi-
tion approximates very well the condition −1 every-
where except in the orbit and in the origin. The ap-
proximated chain-recurrent set is shown at the lower
figure of Figure 7 in dark-yellow colour. Figure 8 has
four subfigures. The upper figure shows the overes-
timation. The middle-upper one is the middle-point
reduction over (1,0). The middle-lower is the middle-
point reduction over
1
2
,
√
3
2
. The lowest is the union
of both.
Let us show in numbers what the reduction means,
table 3.
Table 3: Difference in the total amount of points per section
of the chain-recurrent set for problem 9.
Section Before After
Equilibrium point 255 86
Homoclinic orbit 1579 941
Figure 7: Upper: Complete Lyapunov function for system
9. Lower: Orbital derivative for system 9. This figures
where obtain after just one iteration.
5 DISCUSSION
Let us discuss the results by analysing first the ho-
moclinic orbit example. The orbit has a circumfer-
ence of radius r = 1. The α
Hexa-basis
parameter for
that problem was set to be α
Hexa-basis
= 0.011. That
would let us assume that the total amount of colloca-
tion points that should be given in the orbit is the total
perimeter divided by α
Hexa-basis
, that is: P/α
Hexa-basis
=
2πr/0.011 = 571 points. In that calculation P rep-
resents the perimeter of the orbit. The first overes-
timated approximation we obtained had 1579 on the
orbit with radius r = 1, so it was 276% overestimated.
The middle point reduction gave 165% overestima-
tion. So, 111% less.
One could think that these new results happen to
be overestimated as well. However, this is not the
case. They are in fact good results because the middle
point reduction is placing points over the orbit where
collocation points where not even defined. That is,
between two different collocation points. Figure 9
shows this in a pedagogical way:
Figure 9 shows middle-point reductions in be-
tween different collocation points. So, the distance
between two consecutive points in the reduction is
now, α
Hexa-basis
/2 = 0.0055. In the ideal case in which
all points were placed equidistantly that would make
Middle Point Reduction of the Chain-recurrent Set
149
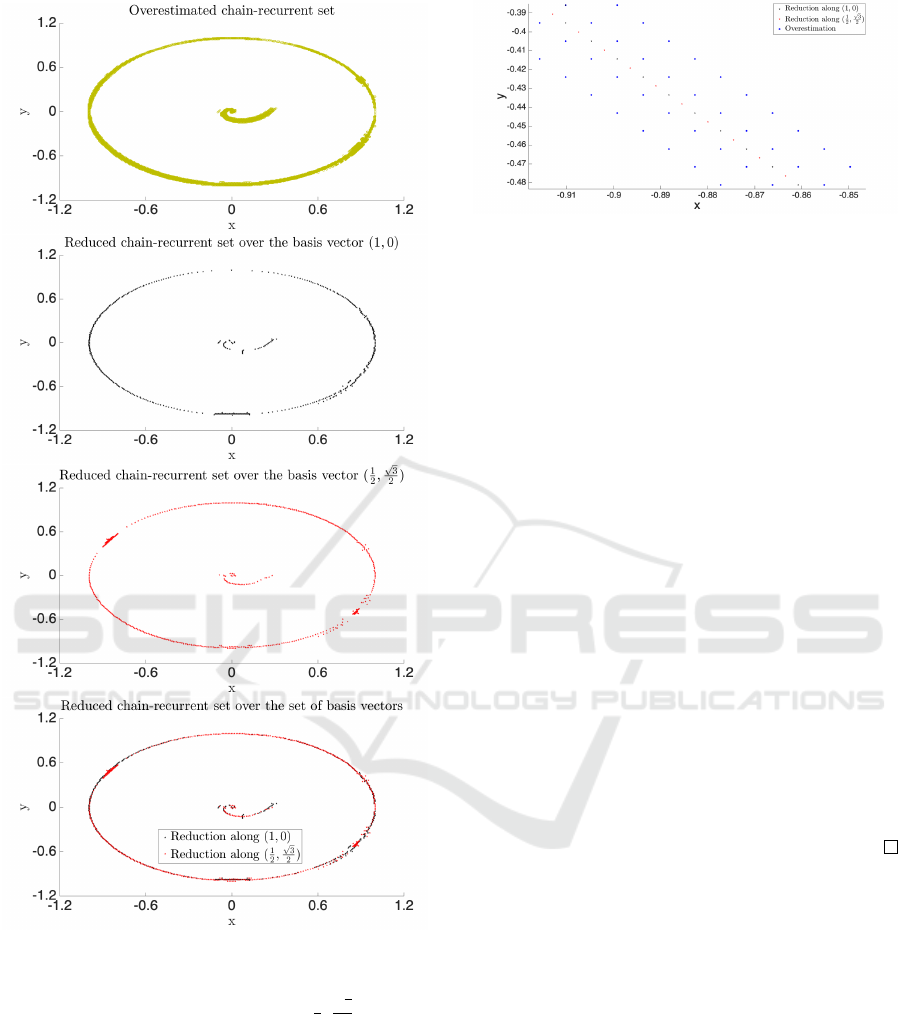
Figure 8: Upper: Overestimated chain-recurrent set with
γ = −0.75. Middle up: Middle point reduction over the
hexagonal basis vector (1,0). Middle down: Middle point
reduction over the hexagonal basis vector
1
2
,
√
3
2
Bottom:
Both reductions. All figures for example (9).
a total number of P/α
Hexa-basis
= 2πr/0.0055 = 1142
points. However, not all points in the middle point
reduction are placed equidistantly.
Now, the equilibrium point is overestimated with
86 points. That is because the chain-recurrent set
approximation failed from the beginning with 255
points. That makes a reduction of over 70%.
Similar analysis can be made for examples (7) and
Figure 9: Middle point reductions seen around the colloca-
tion points.
(8). However, in these last cases, the equilibrium
point is better estimated.
These results lead us to enunciate the following
lemma.
Lemma 5.1 (Middle point reduction). Under the
middle-point reduction to a closed orbit of a Lya-
punov function constructed with the algorithm de-
scribed in Sec. 2. The cardinality of elements in the
reduction will be bounded below by P
o
/α
Hexa-basis
.
Where P
o
> 1 is the perimeter of the closed orbit
and α
Hexa-basis
< 1 is the parameter to build collocation
grid.
Proof. Given the geometric conditions used to build
the collocation points, the reduced points can be as
much as α
Hexa-basis
apart. That will only happen if all
the middle points reductions give a point that already
belong to the collocation grid. If on the other hand,
the middle point reduction gives only new points, then
by construction the new points will be placed between
elements of the collocation grid and again, they will
be apart by α
Hexa-basis
.
Therefore, the total amount of points in the reduc-
tion will be always bounded below by P
o
/α
Hexa-basis
.
6 OBSERVATIONS
In (Arg
´
aez et al., 2019c), we made a large analysis of
the cost of computing an approximation to a complete
Lyapunov function with our method using I iterations.
That analysis is carried out under the big-oh approach.
It was proven that our computation is as expen-
sive as O(N
3
+ IN
2
nm) where N is the total number
of collocation points, n is the dimension of the prob-
lem and m the total amount of points to be evaluated
in the evaluation grid.
Generating the different groups aligned to the dif-
ferent vector basis set is built with two for-loops per
orbit. However, the total amount of failing points, µ,
i.e. points in the chain-recurrent set, is much lower
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
150

than N. So, a for-loop is carried to all points in the
chain-recurrent set, per each point, p steps are given
in both directions of the basis set. Finally, each new
point is checked to belong to the chain-recurrent set.
So, the total cost is µ
2
p with p < µ < N. Therefore,
the total cost of constructing the complete Lyapunov
function remains O(N
3
+ IN
2
nm).
It is to be pointed out that the example 8 is actually
an example arising from engineering. It represents the
limiting cycles in electrical circuits built with vacuum
tubes. Therefore this is a real-life application of our
methodology.
7 CONCLUSIONS
We have introduced an algorithm capable of reduc-
ing the overestimation of the chain-recurrent set. This
algorithm is based on exploring the geometrical con-
straints used to construct the complete Lyapunov
function in the first place. Grouping the elements of
the chain-recurrent subsets (or orbits) into different
small groups of points aligned to the hexagonal basis
vectors allowed us to obtain the corresponding middle
points. The new points obtained over the orbit can be
added to the collocation points for further iterations
and constraints. However, that will be done in future
work.
An important observation to be made is that al-
though the elements of the different groups are always
elements of the hexagonal collocation grid, the mid-
dle points might not be part of it. However, it was
to be expected that the continuous orbit would pass
through the spaces between two consecutive colloca-
tion points. That enlightens the fact that the denser
the collocation points grid is, the better the results.
Furthermore, since we know that these points have
zero orbital derivative, one could now re-build the
complete Lyapunov function with the right condition
on that particular set without forcing extra points to be
zero; optimizing our new approximation to the com-
plete Lyapunov function.
However, a remaining problem to solve is an
equivalent algorithm capable to work in higher di-
mensions.
Finally, our method has been applied to a real-
world application problem arising from electrical en-
gineering, as our results for equation (8) shows.
ACKNOWLEDGEMENTS
The first author in this paper is supported by the Ice-
landic Research Fund (Rann
´
ıs) grant number 163074-
052, Complete Lyapunov functions: Efficient numer-
ical computation.
REFERENCES
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2017). Analysing
dynamical systems towards computing complete Lya-
punov functions. In Proceedings of the 7th In-
ternational Conference on Simulation and Modeling
Methodologies, Technologies and Applications (SI-
MULTECH), pages 134–144. Madrid, Spain.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2018a). Computation
of complete Lyapunov functions for three-dimensional
systems. In Proceedings IEEE Conference on Deci-
sion and Control (CDC), 2018, pages 4059–4064. Mi-
ami Beach, FL, USA.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2018b). Compu-
tational approach for complete Lyapunov functions.
In Dynamical Systems in Theoretical Perspective.
Springer Proceedings in Mathematics & Statistics. ed.
Awrejcewicz J. (eds)., volume 248.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2018c). Iterative
construction of complete Lyapunov functions. In Pro-
ceedings of the 8th International Conference on Sim-
ulation and Modeling Methodologies, Technologies
and Applications (SIMULTECH). Porto, Portugal.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2019a). Clustering
algorithm for generalized recurrences using complete
Lyapunov functions. In International Conference on
Informatics in Control, ICINCO. SUBMITTED.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2019b). Improved
estimation of the chain-recurrent set. In ECC 2019,
Naples.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2019c). Iterative
construction of complete lyapunov functions: Analysis
of algorithm efficiency. In Springer. SUBMITTED.
Bernhard, P. and Suhr, S. (2018). Lyapounov functions of
closed cone fields: From Conley theory to time func-
tions. Commun. Math. Phys., 359:467–498.
Conley, C. (1978). Isolated Invariant Sets and the Morse In-
dex. CBMS Regional Conference Series no. 38. Amer-
ican Mathematical Society.
Conley, C. (1988). The gradient structure of a flow I. Er-
godic Theory Dynam. Systems, 8:11–26.
Dellnitz, M. and Junge, O. (2002). Set oriented numeri-
cal methods for dynamical systems. In Handbook of
dynamical systems, Vol. 2, pages 221–264. North-
Holland, Amsterdam.
Fathi, A. and Pageault, P. (2019). Smoothing Lyapunov
functions. Trans. Amer. Math. Soc., 371:1677–1700.
Giesl, P. (2007). Construction of Global Lyapunov Func-
tions Using Radial Basis Functions. Lecture Notes in
Math. 1904, Springer.
Giesl, P., Arg
´
aez, C., Hafstein, S., and Wendland, H. (2018).
Construction of a complete Lyapunov function using
quadratic programming. In Proceedings of the 15th
International Conference on Informatics in Control,
Automation and Robotics (ICINCO). SIMULTECH
2018, Porto.
Middle Point Reduction of the Chain-recurrent Set
151

Hsu, C. S. (1987). Cell-to-cell mapping, volume 64 of Ap-
plied Mathematical Sciences. Springer-Verlag, New
York.
Hurley, M. (1995). Chain recurrence, semiflows, and gra-
dients. J Dyn Diff Equat, 7(3):437–456.
Hurley, M. (1998). Lyapunov functions and attractors in
arbitrary metric spaces. Proc. Amer. Math. Soc.,
126:245–256.
Iske, A. (1998). Perfect centre placement for radial basis
function methods. Technical Report TUM-M9809, TU
Munich, Germany.
Krauskopf, B., Osinga, H., Doedel, E. J., Henderson, M.,
Guckenheimer, J., Vladimirsky, A., Dellnitz, M., and
Junge, O. (2005). A survey of methods for computing
(un)stable manifolds of vector fields. Internat. J. Bifur.
Chaos Appl. Sci. Engrg., 15(3):763–791.
Lyapunov, A. M. (1992). The general problem of the sta-
bility of motion. Internat. J. Control, 55(3):521–790.
Translated by A. T. Fuller from
´
Edouard Davaux’s
French translation (1907) of the 1892 Russian orig-
inal.
Wendland, H. (1998). Error estimates for interpolation by
compactly supported Radial Basis Functions of mini-
mal degree. J. Approx. Theory, 93:258–272.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
152
