Large Deviations in Discrete-time Systems with Control Signal Delay
Nina Vunder
a
, Natalia Dudarenko
b
and Valery Grigoriev
c
Faculty of Control Systems and Robotics, ITMO University, 49 Kronverksky Pr., Saint Petersburg, Russia
Keywords: Deviation, Peak Effect, Linear Control Systems, Delay, Discrete Systems, Eigenvectors, Modal Control,
Condition Number, Norms.
Abstract: The paper considers a problem of deviations (peak effect) in the free motion of linear discrete stable systems
with a control signal delay. The problem consists in structure of eigenvectors of the state matrix. The control
signal delay adds additional order to a discrete-time model and leads to the variation of eigenvectors structure
and deviation increasing in the free motion of the system. A tracking discrete-time system is a subject of the
research. An approach to the modal control law design taking into account the value of delay and the deviation
is suggested in the paper. It is proposed to assess the upper bound of peaking processes in the system with the
condition number of an eigenvectors matrix. The results are supported by an example.
1 INTRODUCTION
Large deviation problem in the free motion of a linear
system is investigated for a long time (Feldbaum,
1948), (Izmailov, 1978). Firstly, the relationship
between the large deviations of the motion of a
system and its poles was observed. Then, the problem
of large deviations for systems with observers were
investigated (Polotskij, 1981). The large deviations
problem in cascade control systems was considered
also (Sussman and Kokotovic, 1991), where the result
of R.N. Izmailov was generalized to obtain
estimations of the deviations for the outputs.
Recently, the estimation of the deviations for the
case of large and small values of the poles were
obtained using the linear matrix inequalities
technique (Polyak and Smirnov, 2016) and the state-
space approach (Vunder et al., 2015, 2016). Thus, it
is found that not only the multiplicity of eigenvalues
(Vunder et al., 2015, 2016), but also the output
method of control signal can cause significant
deviations of norm of a free-motion state vector of the
discrete-time system ((Whidborne and McKernan,
2007), (Vunder and Ushakov, 2016), (Halikias et al.,
2010), (Francis and Glover, 1978), (Kimura, 1981)).
However, little number of publications is
published on the deviations assessments for discrete-
a
https://orcid.org/0000-0003-1201-4816
b
https://orcid.org/0000-0002-3553-0584
c
https://orcid.org/0000-0001-8374-1899
time systems. Therefore, the aim of this paper is to
propose deviations estimations for the discrete-time
system with the control system delay and design a
modal control law taking into account the value of the
delay and the deviation. The results of the paper can
be useful for the stabilization problems solution like
a stabilization problem for planes (Polyak at al.,
2015) or switching systems (Liberzon, 2003).
The paper is laid out as follows. Firstly, the
deviation assessments in discrete-time systems
without control signal delay are presented. Then, the
case of discrete-time systems with control signal
delay is described and a modal control law taking into
account the value of delay and the deviation is
proposed. Thereafter, the example of a discrete-time
plant is presented. The paper is finished with some
concluding remarks.
2 DEVIATIONS IN
DISCRETE-TIME SYSTEMS
WITHOUT CONTROL SIGNAL
DELAY
Any discrete-time control system is a composition of
following parts: digital controller, a digital-to-analog
Vunder, N., Dudarenko, N. and Grigoriev, V.
Large Deviations in Discrete-time Systems with Control Signal Delay.
DOI: 10.5220/0007920702810288
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 281-288
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
281

converter, and a continuous-time plant. In order to
obtain a single mathematical description of this
composition, processes are studied at the time
instances
tkt
, where
k
is positive integer, it is
called the discrete time;
t

is the sample time. This
means that the discrete-time plant is said to be
discrete time sampling from continuous-time state
and output variables under a piecewise-constant
control signal with the duration
t . Note that a
control signal from the digital controller can output
both without and with delay

. This fact gives rise to
two discrete-time representations of the continuous-
time plant.
Consider a linear continuous-time plant










0
;0
t
xt Axt But x xt

 

,




yt Cxt
,
(1)
where
,,
nr m
x
Ru Ry R
are state vector, input
vector, output vector respectively;
,
nn
AR


nr
BR

 ,
mn
CR


are state matrix, input matrix,
output matrix. If the control of plant (1) for
tkt


is realized without delay, then it can be represented as
follows
    
,1ut uk k t t k t
(2)
Combining (1) and (2), from (Zadeh and Desoer,
2008), we get following discrete-time model










0
1;0
k
xk Axk Buk x xk

  
,



yk Cxk
,
(3)
where


argktkt
is discrete time;
t

is
sample time;


dim dim
A
A
,



dim dimBB
,


dim dim ;CC

exp
A
At
,


1
,BAIAB


C С
.
Analytically, control (2) can be written as






g
uk Kgk Kxk
,
(4)
where
m
g
R
is an external input;
,
rm rn
g
K
RKR


are the feed forward matrix, the
feedback matrix respectively. Combining (4) and (3),
we get discrete-time closed-loop system
    
 
  
0
1;0
,
k
xk Fxk Ggk x xk
yk Cxk
kgkyk


  









(5)
where
F
ABK


,
g
GBK
,
(6)


k 
is a tracking error. Eigenvalues and
eigenvectors of the state matrix
F is given by






arg det 0 :
,
Im 0, ; , 1, ;
i
iij
IF
F
ij ni j








  






(7)
;1,
iii
F
in  
.
(8)
If the external input is not available to direct
measurement, then control (4) is presented as





  
,
gr
uk Kgk Kxk K k Kxk


(9)
where






1
1
1
arg
,
,
yg
gg
ry
KK
KK CIFBKI
CI F B
KKKC





 



r
K
is feedback matrix for a part of the state vector
components.
Block diagram representation of system (5) with
control (9) is shown in figure 1.
Β
Α


y
k
C

x
k

1xk


uk
r
K
K



g
k



k 

1
Z
Figure 1: Block diagram of system without control delay.
Note also that the modification of control in form
(9) does not change the mathematical representation
of system (5).
Let us single out the autonomous component in the
discrete-time system (5)




1;0.xk Fxk x
(10)
The solution of equation (10) takes the form




0.
k
xk Fx
(11)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
282

For the state matrix
F
the following condition
satisfies
M
FM
,
(12)
where
 


exp exp ; 1,
ii
tdiag ti n      
:;1,
ii iii
M
row M F i n



 is a square
matrix whose columns are the n linearly independent
eigenvectors of
F . Using (11) and (12), we get
M
F
M
kk

,
(13)
Now, combining (11) and (13), we obtain
  
1
00
kk
xk Fx M M x


.
(14)
From (14) it follows
  

01
00 ,
kk k
x
x
kFx Fx F

 
(15)
where

is any consistent norm here and elsewhere.
Let us form an upper bound of (15)
 




 
1
1
max
0
0
;1, 0
0,
k
k
k
i
k
xk M M x
MMx
С Mdiag i nx
CM x


 
 




(16)
where


1
С MMM


is condition number
(Gantmacher, 2000), (Golub and Van Loan, 2012) of
the matrix
M
;
max

is a maximum eigenvalue of the
matrix
F
that satisfies conditions


max max
Im 0, 0  . Thus, by


01x  , we have
the upper bound




max
01
sup
k
x
xk CM



.
(17)
From (17) the following properties have to be
considered:
1. The condition number


С M
of the eigenvectors
matrix
M
determines quality of processes in the
system on free motion norm.
2. If eigenvalues are orthogonal to each other, then the
condition number


С M
is equal to one. As a result,
processes in the system (5) start from the point


0x
and then decrease monotonic.
3. If even one pair of close to collinear eigenvectors
exists, then the condition number


С M
can be
sufficiently large. Processes in the system (5) start
from the point


0x
too but then there can appear
significant deviation of free motion trajectory. In this
case the upper bound



sup
x
k start from the
point






00С Mx x
.
3 DEVIATIONS IN
DISCRETE-TIME SYSTEMS
WITH CONTROL SIGNAL
DELAY
The case of a discrete-time system with the control
signal delay is characterized by the increased
dimension of the matrices and modification of
eigenvector structure of the state matrix.
If the control


ut
of plant (1) for
tkt


realizes with delay
t



, then it can be represented
as follows (Grigoriev et al., 1983)



  
1, ;
,1.
uk k t t k t
ut
uk k t t k t






 




(18)
Combining (18) and (1), we get following
discrete-time model (Grigoriev et al., 1983) of plant







 


1
11
,
x
kxk uk uk
yk Cxk
  


(19)
where






1
1
1
,
.
Ie
eI
 
 

   

  




(20)
Block diagram representation of model (19) is
shown in figure 2.


Β



1
Β
Α


yk
C


x
k


1xk


uk


k


1k




1uk

1
Z
1
Z
Figure 2: Block diagram of plant with control delay.
Let us introduce an additional state vector

,
then, by figure 2, we get a following discrete-time
model
Large Deviations in Discrete-time Systems with Control Signal Delay
283









   
1
1
1
1
00
;,
xk
xk
k
xk
B
AB
uk
k
I
Ax k Bu k y k Cx k

 













 








(21)
where



1
;;0
00
B
AB
ABCC
I













,
(22)
 
ru dimdim

.
It should be noted, it is recommended to take the
discrete interval
t

. At the same time, the
discrete interval is limited as
t
by the
Nyquist–Shannon–Kotelnikov theorem, where

 is
a system bandwidth. If it is impossible to take the
discrete interval
t

due to the theorem, then the
order of the discrete model (19) increases by more
than 1. This case is not considered in the paper.
Consider two cases.
The first case is called
“unpredictable delay” (or unaccounted delay). The
control is given by (4), but on account of the
modification of plant model (21), (22) the discrete-
time system takes the form














 
0
1;0;
,
k
x к FxkGgkx xk
yk Cxk

  



 



(23)
where

 


1
,
0
,0.
g
g
AB K B
F
K
BK
GCC
K



















(24)
Block diagram representation of system (23) with
control (9) is shown in figure 3.


Β


1
Β
Α


y
k
C


x
k

1xk


uk


k


1k

1uk

r
K
K


g
k



k


1
Z
1
Z
Figure 3: Block diagram of system with unpredictable delay
in control.
Free motion of system (23) can be represented by
 


 
1
00
k
k
x к FxMMx



 

.
(25)
From (25) it follows
 





1
max
0
00,
k
kk
xk F x
MMx CM x


 



  



(26)
where


CM

is condition number of a




11nn


-matrix
M

;





arg ; 1, 1
iiii
MrowM F M M i n 




is
eigenvectors matrix of state matrix
F

;





max
max arg 0 ; 1, 1
i
i
IF i n 




.
As a result, the upper bound of free motion of system
(23) takes the following form






max
01
sup
k
x
xk CM







.
(27)
It should be noted that a change of condition
number


CM

happens even by 0

 although
eigenvalues set of the matrix



0FF  

is
increased a zero eigenvalue
n1
0 



. Let us show
that. Consider the matrix


0F


0
0
0
ABK
F
K










.
(28)
Obviously, by property (Gantmacher, 2000) of a
block-triangular matrix, the eigenvalues set of matrix
(28) consists of the eigenvalues set of the matrix




;1,
ii
F
ABK i n     

and
n1
0 



.
For eigenvectors
i


of the matrix


0F

the following
condition satisfies
 


000
iii ii
FFI  


 

.
(29)
The eigenvector
i


belongs to null space N



0
i
F
I




of a characteristic matrix



0
i
F
I




. Null space implementation for each eigenvalue
i


,
including
n1
0 



, which corresponds a nonzero
eigenvector. Eigenvectors
i


correspond to


;1,
ii
in  

but they don’t preserve components
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
284

of eigenvectors
i

. As a result, the condition number


CM

significant changes even by 0

 .
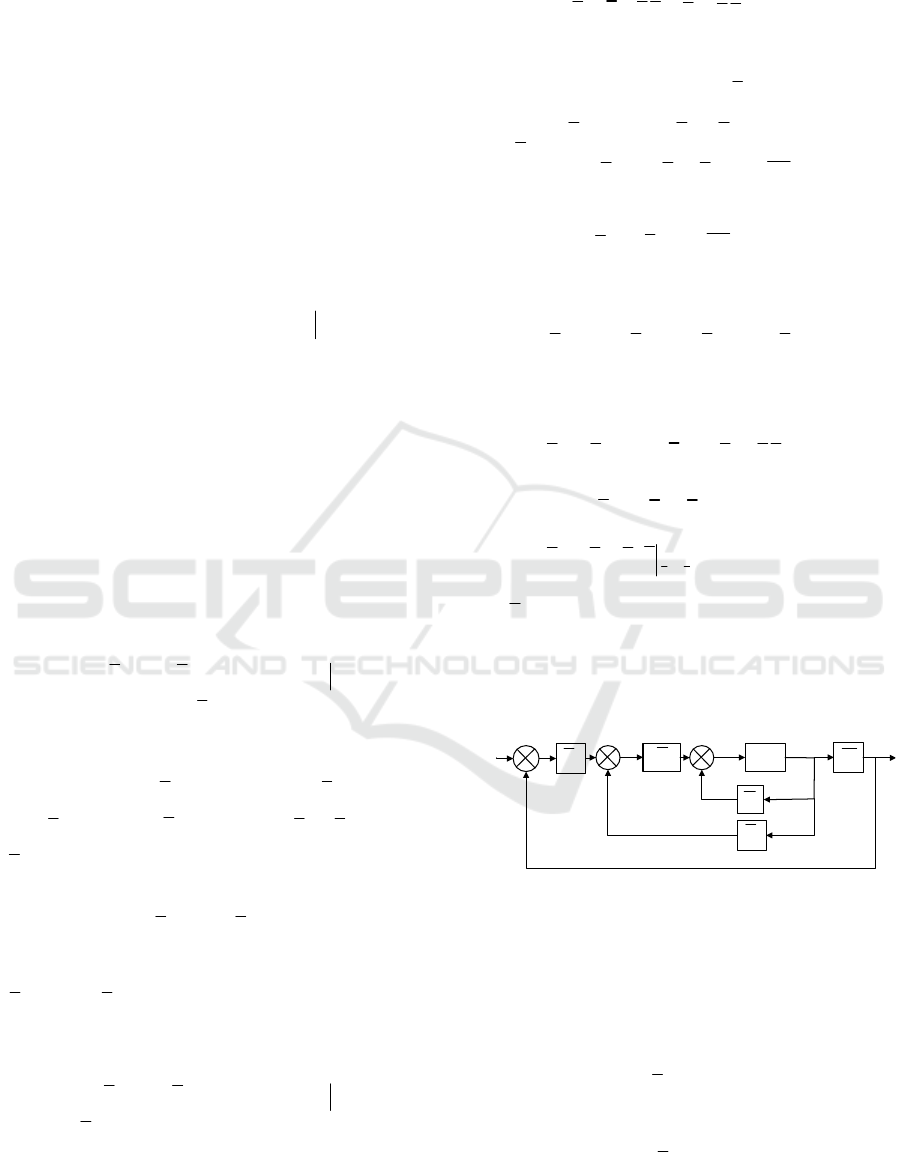
The second case is called “predictable delay” (or
accounted delay). The control of plant (21) takes the
form
   
  
.
gx
xr
uk Kgk Kxk K k
K
kKxkK k




 
 




(30)
Combining (21) and (30), we get following
discrete-time closed-loop system
     
 
0
1;0;
.
k
xk Fxk Ggk x xk
yk Cxk

  





 


(31)
where

  


1
,
,0.
x
x
g
g
AB K B B K
F
KK
BK
GCC
K
































(32)
Control law (30) is formed such that an
eigenvalues set of matrix

F



consists of
eigenvalues set of matrix
F (6) and an eigenvalue
n1




. The eigenvalue
n1




is taken to much less than
,1,
i
in 
.
Block diagram representation of system (31) with
control (30) is shown in figure 4.


Β



1
Β
Α


yk
C


xk


1xk


uk

k

1k

1uk
x
K

K


K



g
k

K


1
Z

1
Z

Figure 4: Block diagram of system with predictable delay
in control.
Free motion of system (31) can be represented
 


 
1
00
k
k
x к FxMMx 




 
.
(33)
From (33) it follows
 






1
max
0
00
k
kk
xk F x
MMx CM x


 




  

  



(34)
where


CM


is condition number of a




11nn


-matrix
M


;





arg ; 1, 1
iiii
MrowM F M M i n 






is
eigenvectors matrix of state matrix
F


;





max
max arg 0 ; 1, 1
i
i
IF i n 






. As
a result, the upper bound of free motion of system (30)
takes the following form






max
01
sup
k
x
xk CM









.
(35)
4 EXAMPLE
Consider discrete-time plant (3) for
0.01st
with
matrices
10.01
01
A







;
0.0001
0.01
B




;


10C 
.
Design modal control law for discrete-time
systems with and without delay gives the following.
1. Assume the required quality indicators of the
closed loop system are provided by assigning the
following eigenvalues




12
0.9802; 0.9048F    
, that corresponds to
the eigenvalues




12
2; 10F   
for the
continuous-time analog of the plant. The satisfactory
eigenvalues are achieved by the modal control with
the feedback matrix


18.84 11.4K 
.
Then, the
state matrix of the close loop system (10) is obtained
as
0.999 0.0094
0.1884 0.886
F








with the eigenvectors
12
0.4472 0.0995
;
0.8944 0.995


 


 


 
, and the condition
number of eigenvectors matrix






12
,5.434С MC  
. Norm (15) of free
motion of the system (10) is shown in figure 5.
Large Deviations in Discrete-time Systems with Control Signal Delay
285

Figure 5: Norm

x
t
of free motion of the system(10).
The condition number


С M
is much greater
than one. Thus, there is a deviation of free motion
trajectories from a monotone decreasing curve.
2. The case of “unpredictable delay”. If the control

ut
of plant (1) for
0.01tktk s
is realized
with delay
0.5 tt

, then we get the discrete-
time system (23) with the same feedback matrix
K
and the following state matrix:

 
 
 
1
0
1 18.84 0.5 1.5 0.01 11.4 0.5 1.5 0.5
18.84 1 11.4 .
18.84 11.4 0
AB K B
F
K
tt ttt
tt






      


 










Here, the eigenvalues and eigenvectors are
derived as



12 3
0.9801; 0.8987; 0.0644 ,F   
 

   
123
0.2179 0.0089 0
0.4352 ; 0.0933 ; 0.0057
0.8735 0.9956 1










. The
condition number of eigenvectors matrix is


123
, , 70.674С MC 



 

. Norm of free
motion of the system (23) is shown in figure 6.
Figure 6: Norm

x
t
of free motion of the system (23).
The condition number


С M

is sufficiently
large. Thus, there is significant deviation of free
motion trajectories from a monotone decreasing
curve.
3. The case of “predictable delay”. Assume system
(31) is realized with the control law (18). The third
eigenvalue is assigned as
3
0.8187  


. Then the
feedback matrix

3.4157 2.247 0.715K 


provides the state matrix

0.5 0.005
10.010
0.0171 0.9888 0.0086
3.4157 2.2468 0.715
t
F

















,
with eigenvalues





123
0.9802; 0.9048; 0.8187 ,F   
 

 

   
eigenvectors
123
0.2192 0.0102 0.0026
0.4363 ; 0.0996 ; 0.05 ,
0.8727 0.995 0.9987


  

  
  

  

  


  
 
 

and the condition number of eigenvectors matrix




123
, , 131.9С MC 




 

 

. Norm of free
motion of this system is shown in figure 7a.
If we take another third eigenvalue, that is close to
1, then the feedback matrix

0.1875 0.3014 0.8766K 


provides the state
matrix

0.5 0.005
10.010
0.0009 0.9985 0.0094
0.1875 0.3014 0.8766
t
F

















with eigenvalues





123
0.9802; 0.9048; 0.99 ,F   
 

 

   
and
eigenvectors
123
0.2192 0.0102 0.5783
0.4363 ; 0.0996 ; 0.5769
0.8727 0.995 0.5769



  

  
  

  

  


  
 
 
of
the system (31). In this case the condition number of
eigenvectors matrix is




123
,, 17.5787С MC 




 

 

. Norm of free
motion of this system is shown in figure 7b.
From received curves it follows that the greater
modulus of eigenvalue
3



is, the smaller condition
number


С M


. This indicates a damping of the
deviation.
012
t= tk
0
5
10
15
20
||x(t)|
|
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
286

a
b
Figure 7: Norm


x
t
of free motion of the system (31)
with different values of the third eigenvalue.
5 CONCLUSIONS
Stable discrete-time systems with control signal delay
were considered in the paper and the problem of large
deviations in the free motion of the systems was
investigated. The upper bound of peaking processes
in the system was estimated with the condition
number of its eigenvectors matrix. The modal control
law was designed taking into account the delay and
the deviation. It was shown relationship between the
delay and the eigenvectors structure, and the value of
the deviations in the free motion of the discrete-time
system. Modification of the additional eigenvalue due
to the control signal delay gives opportunity to affect
the deviation and reduce it. The level of the deviation
reducing depends on requirements to dynamic quality
indicators of the researched system.
In future, it is supposed to expand the results of
the paper to the case of stabilization and control
discrete-time systems by observers with unknown
initial conditions.
ACKNOWLEDGEMENTS
This work was financially supported by Government
of Russian Federation, Grant 08-
08 and by the
Ministry of Education and Science of Russian
Federation, goszadanie no. 8.8885.2017/8.9.
REFERENCES
Sussman, H., Kokotovic, P., 1991. The peaking
phenomenon and the global stabilization of nonlinear
systems. In IEEE Transactions on Automatic Control.
Polotskij, V., 1981. Estimation of the state of single-output
linear systems by means of observers. In Automation
and Remote Control (In Russian).
Izmailov, R., 1987. The peak effect in stationary linear
systems with scalar inputs and outputs. In Automation
and Remote Control (In Russian).
Feldbaum, A., 1948. On the distribution of roots of
characteristic equations of control systems. In
Avtomatika i Telemekhanika (In Russian).
Vunder, N., A., Ushakov, A., V., Nuyya, O., S., Peshcherov,
R., O., 2016. Free motion of sequence of similar
aperiodic blocks // In ICUMT’16, 8th International
Congress on Ultra Modern Telecommunications and
Control Systems and Workshops.
Vunder, N., A., Ushakov, A.,V., 2015. On the features of
the trajectories of autonomous discrete systems
generated by a multiplicity factor of eigenvalues of state
matrices. In IEEE International Symposium on
Intelligent Control.
Whidborne, J., F., McKernan, J., 2007. On the
minimization of maximum transient energy growth In
IEEE Transactions on Automatic Control.
Polyak, B., T., Tremba, A., A., Khlebnikov, M., V.,
Shcherbakov P., S., Smirnov, G., V., 2015. Large
deviations in linear control systems with nonzero initial
conditions In Automation and Remote Control.
Liberzon, D., 2003. Switching in Systems and Control,
Boston: Birkhauser.
Polyak, B., T., Smirnov, G., V., 2016. Large deviations for
non-zero initial conditions in linear systems In
Automatica.
Vunder, N., A., Ushakov, A., V., 2016. Peaks Emergence
Conditions in Free Movement Trajectories of Linear
Stable Systems In ICINCO’16, 13th International
Conference on Informatics in Control, Automation and
Robotics, Doctoral Consortium.
Halikias, G., Papageorgiou, A., Karcanias, N., 2010. Non-
overshooting stabilization via state and output
feedback. In International Journal of Control.
Francis, B., A., Glover, K., 1978. Bounded Peaking in the
Optimal Linear Regulator with Cheap Control In IEEE
Transactions on Automatic Control.
Kimura, H., 1981. A New Approach to the Perfect
Regulation and the Bounded Peaking in Linear
Multivariable Control Systems In IEEE Transactions
on Automatic Control.
Zadeh, L., A., Desoer C., A., 2008. Linear system theory:
the state space approach, New York: Dover
Publications. New York, 4th edition.
Gantmacher, F., R., 2000. The Theory of Matrices, American
Mathematical Society. Providence, Rhode Island.
Golub, G., H., Van Loan, C., F., 2012. Matrix
Computations, Johns Hopkins University Press.
Baltimore and London, 4th edition.
012
t= tk
0
5
10
15
20
||x(t)||
Large Deviations in Discrete-time Systems with Control Signal Delay
287

Grigoriev, V., V., Drozdov, V., N., Lavrentiev, V., V.,
Ushakov, A., V., 1983. Synthesis of discrete regulators
by computer, Mashinostroenie. Leningrad (In Russian).
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
288