
Control Strategies for an Octopus-like Soft Manipulator
Simone Cacace
1
, Anna Chiara Lai
2 a
and Paola Loreti
2
1
Dipartimento di Matematica e Fisica, Universit
`
a degli Studi Roma Tre, Largo S. Murialdo, 1,
00154 Rome, Italy
2
Dipartimento di Scienze di Base e Applicate per l’Ingegneria, Sapienza Universit
`
a di Roma, Via A. Scarpa, 16, 00161
Rome, Italy
Keywords:
Soft Manipulators, Octopus Arm, Control Strategies.
Abstract:
We investigate a reachability control problem for a soft manipulator inspired to an octopus arm. Cases mod-
elling mechanical breakdowns of the actuators are treated in detail: we explicitly characterize the equilibria,
and we provide numerical simulations of optimal control strategies.
1 INTRODUCTION
In this paper we investigate a control theoretical
framework for a soft manipulator model, and we
present related numerical simulations. Our model al-
lows to deal with the case in which only a portion
of the manipulator is controlled, while the remain-
ing part of the device is driven by internal reaction
forces only. This scenario includes mechanical break-
downs, or a voluntary deactivation for energy saving
purposes: its investigation is one of the main novel-
ties also with respect to (Cacace et al., 2018), where
the model is originally introduced.
Soft manipulators attracted the interest of re-
searchers due to their ability to adapt to constrained
enviroments, and their potential suitability for human-
robot interactions (Rus and Tolley, 2015; Laschi and
Cianchetti, 2014). Starting from the first works on
hyper-redundant manipulators (Chirikjian and Bur-
dick, 1990; Chirikjian and Burdick, 1995), the chal-
lenging motion planning of tentacle-like soft manipu-
lators was attacked by several points of view: among
many others, we refer to (Jones and Walker, 2006) for
the study of the kinematics, to (Kazakidi et al., 2015;
Kang et al., 2011) for a discrete dynamical model, to
(Lai and Loreti, 2014; Lai and Loreti, 2012; Lai et al.,
2014) for a number theoretic approach, and to (Thu-
ruthel et al., 2016) for a machine learning implemen-
tation. To the best of our knowledge, the approach in
the present paper, based on optimal control theory of
PDEs (see for instance (Tr
¨
oltzsch, 2010)), appears to
the be new.
a
https://orcid.org/0000-0003-2096-6753
Our device is modelled as an inextensible elastic
string with curvature constraints (i.e. the device can-
not bend over a fixed threshold), and whose curvature
is pointwise forced by a control term, modelling an
angular elastic internal force. The resulting dynam-
ics is an evolutive controlled non-linear fourth order
partial differential equation, generalizing the classical
Euler-Bernoulli equation. At this stage of our inves-
tigation, we adopt some simplifications in the model
–we are dealing with a theoretical object, a fully re-
sponsive, noise free planar manipulator with infinite
degrees of freedom– but this allows us to go into the
deep in the optimization process, by providing opti-
mal open loop controls for a reachability problem.
The paper is organized as follows. In Section 2
we introduce our model in full generality and we dis-
cuss some particular parameter settings. In Section
3 we investigate the problem of steering the tip of
the manipulator to a target point, while minimizing
a quadratic cost on the controls and the kinetic energy
at final time of the manipulator. Section 4 contains
some numerical simulations and finally in Section 5
we draw our conclusions.
2 A CONTROL MODEL FOR A
SOFT MANIPULATOR
Our goal is to describe the dynamics of a soft manip-
ulator encompassing the following features:
- inextensibility: the manipulator can bend but not
stretch longitudinally.
82
Cacace, S., Lai, A. and Loreti, P.
Control Strategies for an Octopus-like Soft Manipulator.
DOI: 10.5220/0007921700820090
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 82-90
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: Exact constraint equations and related elastic po-
tentials derived from penalty method. The functions ν and
µ represent non-uniform elastic constants.
Constraint Constraint Penalization
equation elastic potential
Inextensibility |q
s
| = 1 None
Curvature |q
ss
| ≤ ω ν(|q
ss
|
2
− ω
2
)
2
+
Control q
s
× q
ss
= ωu µ (ωu − q
s
× q
ss
)
2
- bending moment: the soft structure of the device
resists to bending via an angular elastic potential.
- bending constraint: the manipulator cannot bend
over a fixed threshold
- bending control: a time-varying, internal angular
elastic force is applied in order to pointwise force
the bending of the device.
From a morphological point of view, we regard the
manipulator as a three-dimensional body with an
axial symmetry, a non-uniform thickness and a fixed
endpoint. In what follows we build up a system
of PDEs modelling the evolution of the curve on
the plane representing the symmetry axis. From a
physical point of view, such an axis is modelled as an
inextensible string, whose mass represents the mass
of the whole manipulator. Also bending constraints
(and controls) of the manipulator are projected on
the axis: they are identified by suitably weighted
curvature constraints. For instance, the bending
constraint is translated into forcing the curvature of
the axis under a fixed (non-uniform) threshold ω; the
bending control is translated into forcing the signed
curvature to the quantity ωu, where u ∈ [−1,1] is
the control map. The relation between the original
three-dimensional problem and the projected one
is further discussed in Section 2.1 below. In what
follows, we focus on the symmetry axis evolu-
tion. The unknowns of our problem are the curve
q(s,t) : [0,1] × R
+
→ R
2
parametrizing the symmetry
axis of the manipulator in arclength coordinates, and
the associated inextensibility multiplier σ(s,t) ∈ R.
We denote by q
s
, q
ss
, q
tt
partial derivatives in
space and time respectively. The quantity |q
ss
|
represents the curvature of q, whereas the product
q
s
× q
ss
:= q
s
· q
⊥
ss
represents the signed curvature,
where the symbol q
⊥
ss
denotes the counter-clockwise
orthogonal vector to q
ss
. With these notations, we
summarize the constraints described above in Table
1. Note that also the bending moment allows for a de-
scription in terms of curvature constraints: imposing
the constraint |q
ss
| = 0 by penalty method yields the
elastic potential ε|q
ss
|
2
, for some elastic (constant in
time) function ε(s). We then consider the Lagrangian
L(q,σ) :=
Z
1
0
1
2
ρ|q
t
|
2
−
1
2
σ(|q
s
|
2
− 1)
−
1
4
ν
|q
ss
|
2
− ω
2
2
+
−
1
2
ε|q
ss
|
2
−
1
2
µ(ωu − q
s
× q
ss
)
2
ds ,
(1)
whose integral terms respectively represent the ki-
netic energy (ρ is the mass density), the exact inex-
tensibility constraint (σ is the Lagrange multiplier),
the curvature constraint, the bending moment, and the
curvature control. Equation of motions are then de-
rived via the least action principle – see (Cacace et al.,
2018). They result in the following system:
ρq
tt
=
σq
s
− Hq
⊥
ss
s
−
Gq
ss
+ Hq
⊥
s
ss
|q
s
|
2
= 1
(2)
for (s,t) ∈ (0,1) × (0, T ). The map G :=
G[q,ν,ε, ω] = ε + ν
|q
ss
|
2
− ω
2
+
encompasses the
bending moment and the curvature constraint –
(·)
+
denotes the positive part. The map H :=
H[q,µ,u,ω] = µ (ωu − q
s
× q
ss
) represents the control
term. Equation (2) is completed with suitable initial
data, and with the following boundary conditions for
t ∈ (0, T ):
- fixed endpoint conditions:
(
q(0,t) = (0,0),
q
s
(0,t) = −(0,1)
- free endpoint conditions:
q
ss
(1,t) = 0 (zero bending moment)
q
sss
(1,t) = 0 (zero shear stress)
σ(1,t) = 0 (zero tension boundary).
Note that the fixed endpoint conditions are a mod-
elling choice, while the free endpoint conditions
follow from the stationarity conditions for the La-
grangian L.
For technical details on the derivation of the equa-
tions we refer to (Cacace et al., 2018).
2.1 Model Parameter Settings
We propose a parameter tuning in order to encompass,
in the one-dimensional model, the morphology of the
original three-dimensional manipulator. The key mor-
phological assumptions on the manipulator are the
following: axial symmetry and uniform mass density
ρ
v
. In particular, we assume that in its position at rest
(i.e. when its symmetry axis has uniformly zero cur-
vature) the manipulator is a solid of rotation, gener-
ated by the function d(s), s ∈ [0, 1]; we call Ω(s) the
Control Strategies for an Octopus-like Soft Manipulator
83

circle of radius d(s) representing the cross section of
the manipulator at the point s ∈ [0, 1] of its axis. Note
that d measures the thickness of the manipulator: in
octopus arm shaped manipulators, d is a decreasing
function. Choosing ρ(s) := πρ
v
d(s)
2
corresponds to
concentrate the mass of Ω(s) on its barycentre.
In our model, bending the manipulator determines
a compression/dilatation of the soft, elastic material
composing its body, for which we assume an uniform
yield point, i.e., the pointwise elastic forces must be
uniformly bounded by some F
max
in order to avoid
inelastic deformations. Now, due to the axial symme-
try, for every s ∈ [0,1], the maximal angular elastic
force in Ω(s) is attained on its boundary and it reads
F(s) = e|q
ss
|d(s), where e is the elastic constant of
the material. Therefore the constraint F(s) ≤ F
max
is
equivalent to the curvature constraint |q
ss
| ≤ ω, where
we set ω(s) = F
max
/(ed(s)).
2.1.1 On Mass Distributions with Exponential
Decay
In our numerical simulations, we assume ρ to have
an exponential decay. By the arguments above, this
choice is consistent with the case of three dimensional
structures whose thickness decays exponentially, and
it can be viewed as an interpolation of self-similar,
discrete structures (Lai et al., 2016a). In turn, self-
similarity assumption has several advantages from
both a practical and theoretical point of view. In-
deed, asking for a manipulator to be self-similar sim-
ply means to be composed by identical, rescaled mod-
ules. From a geometrical point of view, self-similarity
is a powerful assumption allowing, via fractal geome-
try techniques (Lai, 2012), for a detailed investigation
of inverse kinematics of the manipulator, see for in-
stance (Lai et al., 2016b).
2.2 Control Parameter Settings
We now show how to set the control parameters to
model a mechanical breakdown of the actuators.
We recall that the controlled elastic potential is
U[q,µ,u,ω] :=
1
2
µ(ωu − q
s
× q
ss
)
2
.
and the associated elastic force is
F[q,µ, u, ω] := −(Hq
⊥
ss
)
s
− (Hq
⊥
s
)
ss
where H = µ(ωu − q
s
× q
ss
). Clearly, to choose µ ≡ 0
is equivalent to neglect F, and it yields the uncon-
trolled dynamics:
ρq
tt
= (σq
s
)
s
− (Gq
ss
)
ss
. (3)
More generally, to set µ(s) = 0 for s ∈ [s
1
,s
2
] means
that the portion of q between [s
1
,s
2
] is uncontrolled:
it evolves according to (3) with (time dependent, con-
trolled) boundary conditions in q(s
1
,t) and q(s
2
,t).
We conclude with some remarks on how the con-
trol deactivation affects the equilibria of the system.
A general formula for the equilibria of (2) is provided
in (Cacace et al., 2018): if µ(1) = µ
s
(1) = 0, then the
signed curvature κ := q
s
×q
ss
of the (unique) equilib-
rium q of (2) is proportional to µ, precisely it satisfies
κ(s) = µ(s)
ω(s)u(s)
µ(s) + ε(s)
s ∈ (0,1).
In particular for µ ≡ 0 the equilibrium is given by
q(s,t) ≡ (0, −s) for all (s,t) ∈ [0, 1] × (0, T ). More
generally, if q is uncontrolled in [s
1
,s
2
], i.e., µ(s) = 0
for all s ∈ [s
1
,s
2
], then |q
ss
| = |κ(s)| = 0, that is the
corresponding portion of the device at the equilibrium
is arranged in a straight line.
3 THE REACHABILITY
OPTIMAL CONTROL
PROBLEM
In this section we address the problem of steering
the tip of the device –i.e., q(1,t)– to a target point
q
∗
∈ R
2
, using controls that optimize accuracy, steadi-
ness and energy consumption. In the framework of
optimal control theory, this problem can be restated
as a constrained minimization of a cost functional in-
volving:
- the tip-target distance: we want the tip to reach
and remain close to the target;
- a quadratic cost on the controls, that is we want to
force the device –precisely, its symmetry axis– to
bend as least as possible.
- the kinetic energy of the whole manipulator at fi-
nal time.
More formally, given q
∗
∈ R
2
and T, τ > 0, we want
to minimize the functional
J (q,u) =
1
2τ
Z
T
0
|q(1,t)− q
∗
|
2
dt
+
1
2
Z
T
0
Z
1
0
u
2
ds dt
+
1
2
Z
1
0
ρ(s)|q
t
(s,T )|
2
ds,
(4)
among all the controls u : [0,1] × [0, T ] → [−1, 1], and
subject to the symmetry axis dynamics (2). The first
two terms in J account respectively for the tip-target
distance and the quadratic cost on the controls, during
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
84

all the evolution, whereas the last term corresponds to
the kinetic energy at the final time T.
In what follows we give the first order optimality
conditions for this control problem, that is we write
a system of PDEs, called the adjoint system, whose
unknowns are the stationary points (q,σ,u) of J (sub-
ject to the symmetry axis dynamics), and the related
multipliers ( ¯q,
¯
σ) called the adjoint states. Roughly
speaking, if a control u
∗
is optimal, then the adjoint
system admits a solution of the form (q,σ,u
∗
, ¯q,
¯
σ).
The adjoint system is composed by a variational in-
equality for the optimal control and four PDEs: two
of them describe the evolution of the adjoint states,
and two of them are simply the dynamics the system
is subject to, i.e., the equations of motion of the sym-
metry axis (2). Following (Cacace et al., 2018), the
adjoint states equations are:
ρ ¯q
tt
=
σ ¯q
s
− H ¯q
⊥
ss
s
−
G ¯q
ss
+ H ¯q
⊥
s
ss
+
¯
σq
s
−
¯
Hq
⊥
ss
s
−
¯
Gq
ss
+
¯
Hq
⊥
s
ss
¯q
s
· q
s
= 0
(5)
for (s,t) ∈ (0,1) × (0,T ), where
- the maps G and H are defined in Section 2.
- the maps
¯
G and
¯
H are the linearisations of G and
H, respectively. In particular
¯
G[q, ¯q, ν, ω] = g[q, ν,ω]q
ss
· ¯q
ss
,
¯
H[q, ¯q,µ] = µ ( ¯q
s
× q
ss
+ q
s
× ¯q
ss
) ,
where g[q, ν, ω] = 2ν1(|q
ss
|
2
−ω
2
) and 1(·) stands
for the Heaviside function, i.e. 1(x) = 1 for x ≥ 0
and 1(x) = 0 otherwise.
System (5) is completed with the following final and
boundary conditions, derived as well from the opti-
mality conditions:
- final conditions:
¯q(s,T ) = −q
t
(s,T ), ¯q
t
(s,T ) = 0
for s ∈ (0, 1). We point out that initial conditions
for q are replaced in the adjoint system with final
conditions for ¯q: this is a quite fair consequence of
the fact that the optimization process takes into ac-
count the dynamics on the whole timeline (0,T ).
- fixed endpoint boundary conditions:
¯q(0,t) = 0, ¯q
s
(0,t) = 0
for t ∈ (0,T ) – remark the symmetry with the
fixed endpoint conditions on q;
- free endpoint boundary conditions:
¯q
ss
(1,t) = 0
¯q
sss
(1,t) =
1
τε
(q − q
∗
) · q
⊥
s
q
⊥
s
(1,t)
¯
σ(1,t) = −
1
τ
(q − q
∗
) · q
s
(1,t)
for t ∈ (0,T ). Note that we recover the zero bend-
ing moment condition, as for the free endpoint of
q. On the other hand, as one may expect, both the
shear stress condition on ¯q and the adjoint tension
boundary condition on
¯
σ are affected by the fact
that the system is forced towards the target q
∗
.
Finally, the variational inequality for the control is
Z
T
0
Z
1
0
(u + ω
¯
H[q, ¯q])(v − u)dsdt ≥ 0 . (6)
for every v : [0,1] × [0,T ] → [−1, 1], which provides,
in a weak sense, the variation of the functional J with
respect to u, subject to the constraint |u| ≤ 1.
4 NUMERICAL SIMULATIONS
The optimal control problem discussed in Section 3
is approached in two phases. At a first stage we look
at a stationary optimal control problem, involving the
equilibria of the system (2). Then such stationary so-
lutions are used as initial guess for the original dy-
namic optimal control problem, i.e., for the numerical
solution of the system composed by (2), (5) and (6).
4.1 Stationary Optimal Control
Problem
First of all we remark that if (q, σ) is an equilib-
rium for the symmetry axis equation (2) and if µ(1) =
µ
s
(1) = 0, then q is the solution of the following sec-
ond order ODE:
q
ss
=
µω
µ + ε
uq
⊥
s
in (0,1)
|q
s
|
2
= 1 in (0,1)
q(0) = (0,0)
q
s
(0) = −(0,1).
(7)
The stationary optimal control problem is the follow-
ing
min
1
2
Z
1
0
u
2
ds +
1
2τ
|q(1) − q
∗
|
2
, (8)
subject to (7) and to |u| ≤ 1. Note that the above cost
functional is the stationary version of J : a quadratic
cost on the controls and a tip-target distance are still
involved, whereas time integrals and time-dependent
terms as the kinetic energy are clearly neglected. Us-
ing the first two equations of (7), we have |q
ss
| =
¯
ω|u|,
where
¯
ω := µω/(µ + ε). Therefore we can get rid of
the dependence from u in (7) and look for the solu-
Control Strategies for an Octopus-like Soft Manipulator
85
Table 2: Global parameter settings.
Parameter description Setting
mass distribution ρ(s) = exp(−s)
bending moment ε(s) = 10
−3
(1 − 0.9s)
curvature constraint ν(s) = 10
−3
(1 − 0.09s)
penalty
curvature control µ(s) = (1 − s)e
−0.1
s
2
1−s
2
penalty
curvature constraint ω(s) = 3π(1 + s
2
)
target point q
∗
= (0.3563,−0.4423)
target penalty τ = 10
−4
Discretization step ∆
s
= 0.05
Table 3: Control deactivation settings related to µ
I
.
Test Control deactivation region
Test 1 I =
/
0
Test 2 I = [0.35, 0.65]
Test 3 I = [0.25, 0.4] ∪ [0.6,0.75]
tions of the following Euler elastica’s like problem:
min
1
2
Z
(0,1)\I
1
¯
ω
2
|q
ss
|
2
ds +
1
2τ
|q(1) − q
∗
|
2
subject to
|q
s
|
2
= 1 in (0,1)
|q
ss
| ≤
¯
ω in (0,1)
q(0) = (0,0)
q
s
(0) = −(0,−1),
(9)
where we set I := {s ∈ (0, 1) | µ(s) = 0}. In other
words we are looking for the curve q –with length
1 and curvature bounded by
¯
ω– minimizing the total
curvature and the distance of its tip from q
∗
. Dot-
multiplying by q
⊥
s
both sides of the first equation of
(7), we obtain that the optimal control for the original
stationary problem (8) is then given by
u(s) =
(
q
ss
(s)·q
⊥
s
(s)
¯
ω(s)
if µ(s) 6= 0,
0 otherwise.
(10)
Note that in (Cacace et al., 2018) we assumed µ >
0 in (0,1). Here we also consider the case µ(s) =
0. As a matter of fact, for µ(s) = 0, the dynamics
and its equilibria are independent from u(s): it can be
arbitrarily chosen. The particular choice u(s) = 0 in
I allows the cost functional (8) to be consistent also
with the case of uncontrolled regions.
To numerically solve (9) we encompass the con-
straints |q
s
| = 1 and |q
ss
| ≤
¯
ω via an augmented La-
grangian method, and we discretize it with a finite dif-
ference scheme. The non-linear terms of the resulting
discrete system of equations are treated via a quasi
Newton’s method. Parameters settings are reported in
Table 2.
-0.6
-0.4
-0.2
0
0.2
-0.4 -0.2 0 0.2 0.4 0.6
(a)
-20
-15
-10
-5
0
5
10
15
20
0 0.2 0.4 0.6 0.8 1
(b)
Figure 1: In (a) the solution q of Test 1, in (b) the related
signed curvature κ(s) (bold line) and curvature constraints
±
¯
ω (thin lines).
We investigate the problem in three scenarios, see
Table 3: in the first we assume that µ is positive in
(0,1), in the second and third experiment we neglect
µ in some sub-intervals of (0,1). The latter cases rep-
resent situations in which we cannot control a portion
of the device – see Section 2.2. In particular, for a
given I ⊂ (0,1), we employ the following curvature
control penalty parameter
µ
I
(s) =
(
0 if s ∈ I
µ(s) otherwise.
In Figure 1 we report the results of Test 1 –see
Table 3. In Figure 2 and 3 we show the results of Test
2 and Test 3, respectively. In these cases the controls
are in-actuated in a subset of (0,1): the corresponding
regions are depicted in red. The particular choice of
q
∗
allows for it to be reached in all these three cases,
but clearly, with different optimal solutions.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
86

-0.6
-0.4
-0.2
0
0.2
-0.4 -0.2 0 0.2 0.4 0.6
(a)
-20
-15
-10
-5
0
5
10
15
20
0 0.2 0.4 0.6 0.8 1
(b)
Figure 2: In (a) the solution q of Test 2, in (b) the related
signed curvature κ(s) (bold line) and curvature constraints
±
¯
ω (thin lines).
4.2 Dynamic Optimal Control Problem
We address the minimization of the cost functional J
subject to a dissipative version of the dynamical sys-
tem (2):
ρq
tt
=
σq
s
− Hq
⊥
ss
s
−
Gq
ss
+ Hq
⊥
s
ss
− βq
t
− γq
sssst
.
(11)
In particular, the term −βq
t
represents an environ-
mental viscous friction proportional to the velocity;
the term −γq
sssst
an internal viscous friction, propor-
tional to the change in time of the curvature. This
implies that if we plug in (11) the optimal stationary
(constant in time) control u given in Equation (10),
then the system converges as T → +∞ to the optimal
stationary equilibrium q described in Section 4.1 - see
Equation (7). Here we look for time-varying optimal
controls, i.e., for solutions u
∗
of the dynamic optimal
control problem described in Section 3. The adjoint
-0.6
-0.4
-0.2
0
0.2
-0.4 -0.2 0 0.2 0.4 0.6
(a)
-20
-15
-10
-5
0
5
10
15
20
0 0.2 0.4 0.6 0.8 1
(b)
Figure 3: In (a) the solution q of Test 3, in (b) the related
signed curvature κ(s) (bold line) and curvature constraints
±
¯
ω (thin lines).
Table 4: Dynamic parameter settings.
Parameter description Setting
Environmental friction β(s) = β(s) := 2 − s
Internal friction γ(s) := 10
−6
(2 − s)
Final time T = 2
Time discretization step ∆
t
= 0.001
states equations in the dissipative version read:
ρ ¯q
tt
=
σ ¯q
s
− H ¯q
⊥
ss
s
−
G ¯q
ss
+ H ¯q
⊥
s
ss
+
¯
σq
s
−
¯
Hq
⊥
ss
s
−
¯
Gq
ss
+
¯
Hq
⊥
s
ss
+β ¯q
t
+ γ ¯q
sssst
¯q
s
· q
s
= 0
(12)
for (s,t) ∈ (0,1) × (0,T ).
The adjoint system composed by (11), (12) and
(6) can be discretized using a standard finite differ-
ence scheme in space-time, then solved by an adjoint-
based gradient descent method. The key idea is the
following: starting from an initial guess u given by the
Control Strategies for an Octopus-like Soft Manipulator
87

0
100
200
300
400
500
600
0 0.5 1 1.5 2
(a)
0
100
200
300
400
500
600
0 0.5 1 1.5 2
(b)
Figure 4: Time evolution of target energy J
q
∗
for the static
(a) and dynamic (b) optimal control.
stationary optimal control, we first solve the equation
of motion (11) forward in time. Then the solution-
control triplet (q, σ,u) is plugged into (12) which is
solved backward in time. Finally, we use the vector
(q,σ, u, ¯q,
¯
σ) in (6) to update the value of the u. The
procedure is iterated up to convergence on the control.
We assume that µ(s) = 0 in a subinterval I =
[0.35,0.65] of (0,1) – this choice corresponding to
Test 2 in Section 4.1, see Table 3 and Figure 1. In
other words, we are modelling the scenario in which
approximately one third of the central actuators of the
device are out of order. The parameters related to
the dynamical aspects, in particular those involved by
friction forces and time discretization are reported in
Table 4. The other parameters are set as in Section
4.1, see Table 2.
We compare the performances of optimal station-
ary and dynamic controls in terms of the evolution
of the three components of our integral cost: the
tip-target distance, the control energy and the kinetic
energy.
In Figure 4 we plot the function
J
q
∗
(t) := |q(1,t)− q
∗
|
2
representing the tip-target distance at time t ∈ [0,2],
in both cases of statically and dynamically optimized
controls. More precisely, in Figure 4(a) we plugged in
the system (11) a constant in time control u
s
, that we
call static optimal control, given by the solution of the
stationary control problem (8). We then considered
the resulting trajectory q(s,t) and measured the tip-
target distance J
q
∗
(t). In Figure 4(b) we see the tip-
target distance of the trajectory q obtained by numer-
ically solving the adjoint system, that is the trajectory
corresponding to a time-dependent optimal control u
d
that we call in the sequel dynamic optimal control.
In agreement with the theoretical setting, in particu-
lar with the strong dependence of the cost functional
J on the tip-target distance (see also the value for the
weight τ in Table 2), the dynamical optimization pro-
cess yields, up to some oscillations, a much lower
J
q
∗
(t) than the stationary case. We also remark the
damping of the oscillations of J
q
∗
(t) in the dynamical
case: this confirms that the dynamical optimization
process tends to reach and stay close to the target as
soon as possible.
In Figure 5 we plot the function
J
u
(t) :=
Z
1
0
u
2
(t)ds
representing the quadratic cost on the controls at time
t ∈ [0,2]. In the case of static controls, J
u
s
(t) is con-
stant by construction. The dynamic optimal controls
J
u
d
(t) are on average smaller than J
u
s
(t): this implies
that the dynamical optimization process actually re-
duces the total cost of the controls
Z
T
0
J
u
(t)dt
with respect to the stationary optimization. Also note
that the dynamic optimal control u
d
yields a large
variation of its cost J
u
d
(t) at the beginning of the evo-
lution, while stabilizing it around the static control
cost J
u
s
(t) in a second time. This implies that the op-
timization process tends to concentrate the variation
of controls at the beginning, while the second part of
the evolution is demanded to small adjustments, con-
firming what we already remarked by looking at the
tip-target distance evolution.
Finally, in Figure 5 we plot the function
J
v
(t) :=
1
2
Z
1
0
ρ(s)|q
t
(s,t)|
2
ds
representing the kinetic energy of the whole axis at
time t ∈ [0,2] in the cases of stationary and dynamic
optimal controls. Note that the evolutions of the J
v
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
88
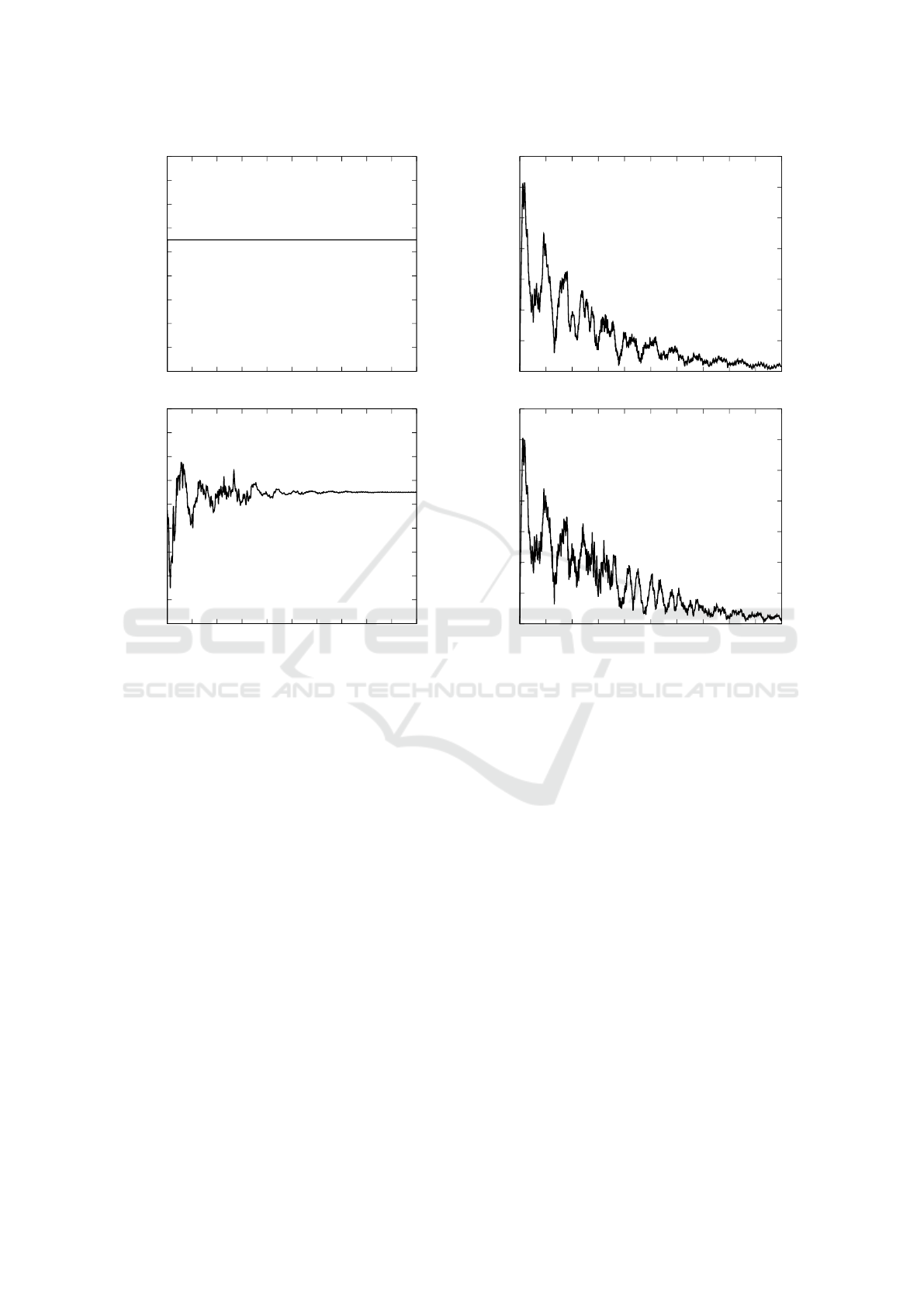
0.0705
0.071
0.0715
0.072
0.0725
0.073
0.0735
0.074
0.0745
0.075
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
(a)
0.0705
0.071
0.0715
0.072
0.0725
0.073
0.0735
0.074
0.0745
0.075
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
(b)
Figure 5: Time evolution of control energy J
u
for the sta-
tionary (a) and dynamic (b) optimal control.
are comparable, but at final time T , dynamical opti-
mal controls yield a kinetic energy J
v
(T ) lower than
the one associated to the stationary optimal controls.
This is consistent with the fact that the cost functional
J depends only on the kinetic energy at final time.
Finally note that, since the system is converging to
an equilibrium due to frictional forces, J
v
(t) → 0 as
t → +∞: it is then reasonable to expect a larger time
frame to improve the performances of the kinetic en-
ergy in both dynamic and stationary cases. For the
dynamically controlled case only, steadiness can also
be traded with accuracy by increasing the weight of
the term J
v
(T ) in the functional J .
5 CONCLUSIONS
In this paper we addressed the optimal control of a
planar soft manipulator, modelled as an inextensible
elastic string with non-uniform mass, curvature con-
straints and curvature controls. Parameters are set in
order to encompass in the one-dimensional model the
0
0.5
1
1.5
2
2.5
3
3.5
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
(a)
0
0.5
1
1.5
2
2.5
3
3.5
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
(b)
Figure 6: Time evolution of kinetic energy J
v
for the static
(a) and dynamic (b) optimal control.
morphology of a three-dimensional manipulator. We
looked in particular to the case in which a part of the
device is uncontrolled and, consequently, driven only
by internal reaction forces. Optimal open loop con-
trols are obtained via a constrained minimization of
a cost functional in both the stationary and dynamic
case. Numerical simulations are provided in the spe-
cial case of partially actuated controls. They agree
with the theoretical control model.
A challenging open question is to find alterna-
tive, not necessarily open loop, optimal strategies.
Then we plan to investigate other optimization tech-
niques, such as model predictive feedbacks and ma-
chine learning algorithms.
REFERENCES
Cacace, S., Lai, A. C., and Loreti, P. (2018). Modeling
and Optimal Control of an Octopus Tentacle. arXiv
e-prints, page arXiv:1811.08229.
Chirikjian, G. S. and Burdick, J. W. (1990). An obstacle
avoidance algorithm for hyper-redundant manipula-
Control Strategies for an Octopus-like Soft Manipulator
89

tors. In Proceedings., IEEE International Conference
on Robotics and Automation, pages 625–631. IEEE.
Chirikjian, G. S. and Burdick, J. W. (1995). The kinematics
of hyper-redundant robot locomotion. IEEE transac-
tions on robotics and automation, 11(6):781–793.
Jones, B. A. and Walker, I. D. (2006). Kinematics for mul-
tisection continuum robots. IEEE Transactions on
Robotics, 22(1):43–55.
Kang, R., Kazakidi, A., Guglielmino, E., Branson, D. T.,
Tsakiris, D. P., Ekaterinaris, J. A., and Caldwell,
D. G. (2011). Dynamic model of a hyper-redundant,
octopus-like manipulator for underwater applications.
In Intelligent Robots and Systems (IROS), 2011
IEEE/RSJ International Conference on, pages 4054–
4059. IEEE.
Kazakidi, A., Tsakiris, D. P., Angelidis, D., Sotiropoulos,
F., and Ekaterinaris, J. A. (2015). Cfd study of aquatic
thrust generation by an octopus-like arm under intense
prescribed deformations. 115:54–65.
Lai, A. C. (2012). Geometrical aspects of expansions
in complex bases. Acta Mathematica Hungarica,
136(4):275–300.
Lai, A. C. and Loreti, P. (2012). Discrete asymptotic reach-
ability via expansions in non-integer bases. In 2012 9-
th international conference on informatics in control,
automation and robotics (ICINCO), volume 2, pages
360–365. IEEE.
Lai, A. C. and Loreti, P. (2014). Robot’s hand and expan-
sions in non-integer bases. Discrete Mathematics &
Theoretical Computer Science, 16(1).
Lai, A. C., Loreti, P., and Vellucci, P. (2014). A model for
robotic hand based on fibonacci sequence. In 2014
11th International Conference on Informatics in Con-
trol, Automation and Robotics (ICINCO), volume 2,
pages 577–584. IEEE.
Lai, A. C., Loreti, P., and Vellucci, P. (2016a). A continuous
fibonacci model for robotic octopus arm. In 2016 Eu-
ropean Modelling Symposium (EMS), pages 99–103.
IEEE.
Lai, A. C., Loreti, P., and Vellucci, P. (2016b). A fibonacci
control system with application to hyper-redundant
manipulators. Mathematics of Control, Signals, and
Systems, 28(2):15.
Laschi, C. and Cianchetti, M. (2014). Soft robotics: new
perspectives for robot bodyware and control. Frontiers
in bioengineering and biotechnology, 2:3.
Rus, D. and Tolley, M. T. (2015). Design, fabrication and
control of soft robots. Nature, 521(7553):467–475.
Thuruthel, T., Falotico, E., Cianchetti, M., Renda, F., and
Laschi, C. (2016). Learning global inverse statics so-
lution for a redundant soft robot. In Proceedings of
the 13th International Conference on Informatics in
Control, Automation and Robotics, volume 2, pages
303–310.
Tr
¨
oltzsch, F. (2010). Optimal control of partial differential
equations: theory, methods, and applications, volume
112. American Mathematical Soc.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
90
