Finite Control Augmented with Fuzzy Logic for Automotive Air-spring
Suspension System
Mohamed Essam Shalabi
1
, Haitham El-Hussieny
2
, A. A. Abouelsoud
3
and Ahmed M. R. Fath Elbab
1,4
1
Mechatronics and Robotics Engineering Department, Egypt-Japan University for Science and Technology,
Alexandria, Egypt
2
Electrical Engineering Department, Faculty of Engineering (Shoubra), Benha University, Cairo, Egypt
3
Electronics and Communication Department, Cairo University, Cairo, Egypt
4
On leave from Mechanical Eng. Department, Assiut University, Egypt
Keywords:
Air Suspension, Vibration Isolation, Fuzzy Control.
Abstract:
This paper investigates the spring stiffness control of air suspension systems working under different oper-
ating conditions of road profile frequencies and amplitudes. Usually changing the stiffness of the air spring
involves variations of the enclosed air pressure by pumping air into or out of the air chamber, or by changing
its volume. Since, changing spring stiffness through controlling its pressure consumes power and is not instan-
taneous, controlling the stiffness through finite volume control is merged with a PI-like Fuzzy Logic Control
(PI-FLC) in this paper. This is achieved by connecting the air spring volume to two additional unequal vol-
umes. By controlling the total spring volumes through ON-OFF switching valves, four different stiffness
settings are available, and one can achieve an improved performance of air suspension system. A nonlinear
quarter-car model is used to evaluate the proposed approach while a Genetic Algorithm (GA) optimization
is applied to estimate the PI-FLC optimal gains and the finite levels for switching the spring volumes. Nu-
merical simulations results demonstrate the performance of the proposed control under different road profile.
The vehicle body acceleration decreases by a value that reaches 4 cm/s2 which means improving the passen-
ger ride comfort as well as maintaining the passenger safety. This in turns encourages the implementation
of the proposed approach on an actual vehicle air suspension in the near future to further verify the system
performance.
1 INTRODUCTION
Nowadays, many manufacturers are using pneumatic
suspension for their vehicle as it is known for its low
transmissibility coefficient. The load capacity for the
air spring depends on the air pressure inside the spring
and its effective area. The vehicle suspension system
function is to carry the vehicle weight, isolate the ve-
hicle body from road unevenness and to maintain the
road-wheel contact. So, the design of the suspension
system is responsible for ride quality and stability.
A conflict between ride quality and handling is ex-
ist, where soft suspension is required for better ride
quality, while a stiff suspension is required for good
handling behavior (Wong, 2008).
Presthus (Presthus, 2002) proposed a new model
for simulation of the air spring behavior of railway
train. The model is three- dimensional and consists
of two parts, describing vertical and horizontal be-
havior. The air spring model is implemented in the
vehicle dynamic simulation program GENSYS and
the results were consistent with the experimental data.
Gavriloski et. al. (Gavriloski et al., 2014) proposed
a frequency dependent mathematical model for air
spring stiffness which enables the application in mod-
els with no need to experimental work.
Nieto et. al. (Nieto et al., 2011) developed an
adaptive pneumatic suspension system based on ex-
citation frequency. A control strategy is proposed to
avoid undesirable resonant frequencies. The control
procedure is based on the pre-knowledge of incoming
vibration and an efficient prediction technique is used
when the incoming frequency is unknown. An ex-
perimental estimation of air spring characteristics in
Shalabi, M., El-Hussieny, H., Abouelsoud, A. and Fath Elbab, A.
Finite Control Augmented with Fuzzy Logic for Automotive Air-spring Suspension System.
DOI: 10.5220/0007922002890294
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 289-294
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
289

active vibration control system is proposed in (Ballo,
2001) and then the results were compared with theo-
retical considerations estimation.
Bedarff and Pelz (Bedarff and Pelz, ) developed
an active and integrated suspension system capable
of changing its stiffness. This is done by changing
the load carrying area. They choose double acting air
spring bellow with adjustable piston segments.
Zepeng et. al. (Zepeng et al., 2017) tried to
solve the overshoot phenomena found in electric ve-
hicle. This is done by applying fuzzy control to elec-
trically controlled air suspension (ECAS). This work
is done theoretically and verified using AMESim.
It was found that the fuzzy control can solve the
overshoot problem. Miriji and Arockia (Mirji and
Arockia, 2014) applied a fuzzy logic control to half-
car suspension model using Matlab. The half car
suspension (four-degree of freedom) model was es-
tablished and the equations of motion were derived.
Fuzzy logic and PID control for suspension model
were achieved using Matlab. The results showed that
the fuzzy control resulted in more improvement in
stability than PID control. Omar and Ozkan (Omar
and
¨
Ozkan, 2015) applied Linear Quadratic Regu-
lator (LQR) method to study the effect of in-wheel
electric motors mass on the active suspension sys-
tem performance. Their study showed that there was
a bad effect of increasing the unsprung mass due to
the addition of in-wheel motor to the system on the
road holding and ride comfort. Another disadvan-
tage was a higher actuator force was needed to work
in the suspension system with in-wheel motor com-
pared to the same system without IWM. Gohari and
Tahmasebi (Gohari and Tahmasebi, 2015) designed
neuro-active force control (AFC) technique and ap-
plied in active seat suspension system. The con-
troller used is PID which controls the actuator and
the force generated from the actuator was then mea-
sured. The estimated mass was estimated using Arti-
ficial Neural Network (ANN). The results of simula-
tion demonstrated that neuro-AFC scheme improves
the performance of control system compared to the
uncontrolled and PID controller counterpart. Gokul
and Malar presented a new design for air suspension
using LQR control strategy which is applied on air
suspension dynamic model, then the performance was
checked on shaker table. A comparative study is done
between the proposed control system and PID con-
trol system under different operating conditions and
it was found the system performance is improved us-
ing LQR control strategy(S. and K., 2019). From the
above paragraphs, it is divided into two main sections.
The first is developing the air spring dynamic model
to use it in a simulation for suspension system. The
second is developing techniques to improve the per-
formance of vehicle suspension such as variable area
air spring, excitation frequency preknowledge, Apply
fuzzy logic control or neuro active force control.
The motivation of this work is to develop an au-
tomotive suspension system with variable stiffness
for the conflicting requirements of ride and handling.
This paper is concerned with the control of air-spring
suspension using PI-like Fuzzy Logic with control al-
gorithm responsible for changing the air volume to
vary the spring stiffness through using two unequal
volumes.
This paper is organized as follows: the mathe-
matical model of the air-spring suspension system is
developed in Section II. The proposed finite control
augmented with PI-like FLC is discussed in details in
Section III, while the applied Genetic Algorithm opti-
mization is highlighted in Section IV. The simulation
results are presented and discussed in Section V. Fi-
nally, Section VI is the conclusion.
2 MATHEMATICAL MODEL
The stiffness, K of the air spring is defined as the in-
cremental force, dF per incremental deflection, dz.
The force can be calculated by gauge pressure p
g
in-
side the spring multiplied by the effective area, A
e
.
F = p
g
A
e
(1)
K =
dF
dz
=
d(p
g
A
e
)
dz
= A
e
d p
g
dz
+ p
g
dA
e
dz
(2)
Neglecting the change in the effective area, we obtain:
K = A
e
d p
g
dz
(3)
To calculate the change of pressure inside the spring,
polytrophic process is assumed (Gavriloski et al.,
2014).
pV
n
= constant (4)
Where p is pressure, V is the volume and n is poly-
trophic coefficient. By differentiation:
d(p
g
V
n
)
dz
= p
g
nV
n−1
dV
dz
+V
n
d p
g
dz
= 0 (5)
Since the cross-section area is considered constant,
the rate of change of volume per unit deflection is
the effective area but with negative sign. This is be-
cause decreasing the volume increases the deflection
and vice versa.
dV
dz
= −A
e
(6)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
290

d p
g
dz
=
p
g
nA
e
V
(7)
Hence,
K =
p
g
nA
2
e
V
(8)
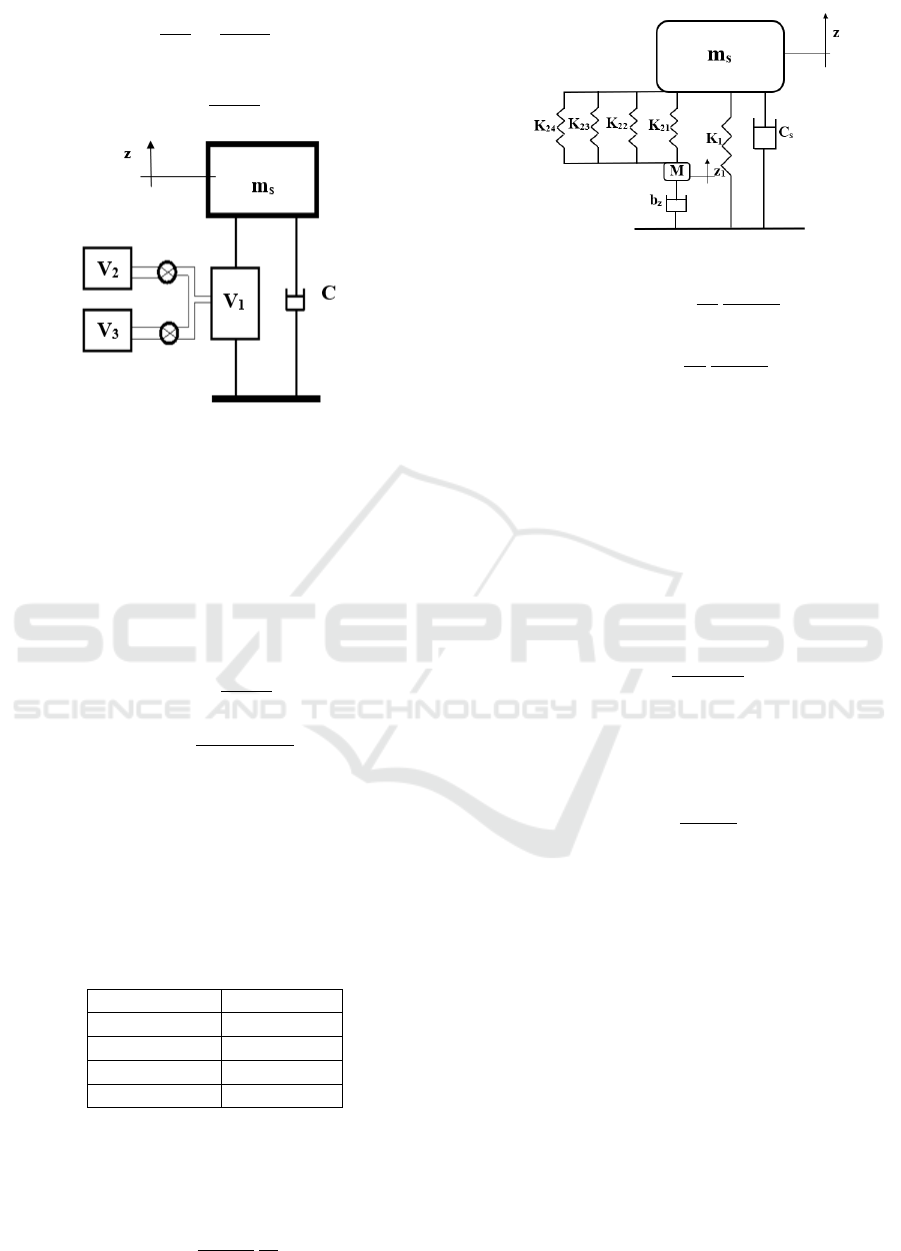
Figure 1: Proposed schematic diagram for the air volume
connected to two additional volumes via ON/OFF valves.
The air spring stiffness is inversely proportional
to the air volume. The stiffness value is controlled
by connecting two unequal auxiliary volumes V
2
and
V
3
(V
3
> V
2
) to the main air volume V
1
in successions
through ON/OFF valves, as shown in Fig. 1. When
the two valves are closed, the effective volume is V
1
(minimum volume), so that the effective stiffness will
be maximum as given:
K
max
=
p
g
nA
2
e
V
1
(9)
K
min
=
p
g
nA
2
e
V
1
+V
2
+V
3
(10)
The dynamic model shown in Fig. 2 consists of
two springs K
1
and K
2
in which they have four values
K
11
and K
21
, K
12
and K
22
, K
13
and K
23
or K
14
and K
24
according to volume connection described in Table. 1.
The mass M represents the moving air inside the pipe
and viscous damper b
z
which represents the viscous
damping inside the pipe.
Table 1: Stiffness with volumes configuration.
K
2
V
K
11
AND K
21
V
1
K
12
AND K
22
V
1
+V
2
K
13
AND K
23
V
1
+V
3
K
14
AND K
24
V
1
+V
2
+V
3
The equation of motion (Gavriloski et al., 2014)
for the model in Figure 2 is:
M ¨z
1
= (z − z
1
)K
2
− b
z
| ˙z
1
| ˙z
1
(11)
Where
K
2
=
p
g
nA
2
e
V
1
+V
r
V
r
V
1
(12)
Figure 2: Dynamic model of the air spring.
b
z
= 0.5ρk
t
A
p
(
A
e
A
p
V
r
V
r
+V
1
)
3
(13)
M = ρA
p
l
p
(
A
e
A
p
V
r
V
r
+V
1
)
2
(14)
Where:
z
1
: air displacement inside the pipe
V
1
: air bag volume
V
r
: reservoir volume (0, V2, V3, V2+V3)
ρ: air density
k
t
: total pressure drop in the pipeline
A
p
: pipe area
l
p
: pipe length
And the equivalent air suspension stiffness, K
s
equation will be:
K
s
=
RMS(F
z
)
RMS(z)
(15)
Where, F
z
‘ is the total force on the sprung mass:
F
z
= p
g
A
e
+ K
1
z + K
2
(z − z
1
) (16)
K
1
=
p
g
nA
2
e
V
1
+V
r
(17)
The system is merged in two degree of freedom
model (DOF) as shown in Fig. 3. The excitation input
for the system is z
0
where K
s
,C
s
represent the variable
stiffness of the air spring and the damping coefficient
of the air suspension, respectively, while K
tr
and C
tr
represent the tire stiffness and damping coefficient.
The model parameters are:
m
s
: Sprung mass, kg
m
us
: Unsprung mass, kg
K
s
: air spring stiffness, N/m
K
tr
: Tire radial stiffness, N/m
C
s
: Suspension damping coefficient, Ns/m
C
tr
: Tire equivalent damping coefficient, Ns/m
z: Sprung mass vertical amplitude, mm
z
2
: Unsprung mass vertical amplitude, mm
z
0
: Road vertical excitation amplitude, mm
The system is modeled as 3-DOF with excitation
input z
0
. The equations of motion of the model shown
Finite Control Augmented with Fuzzy Logic for Automotive Air-spring Suspension System
291

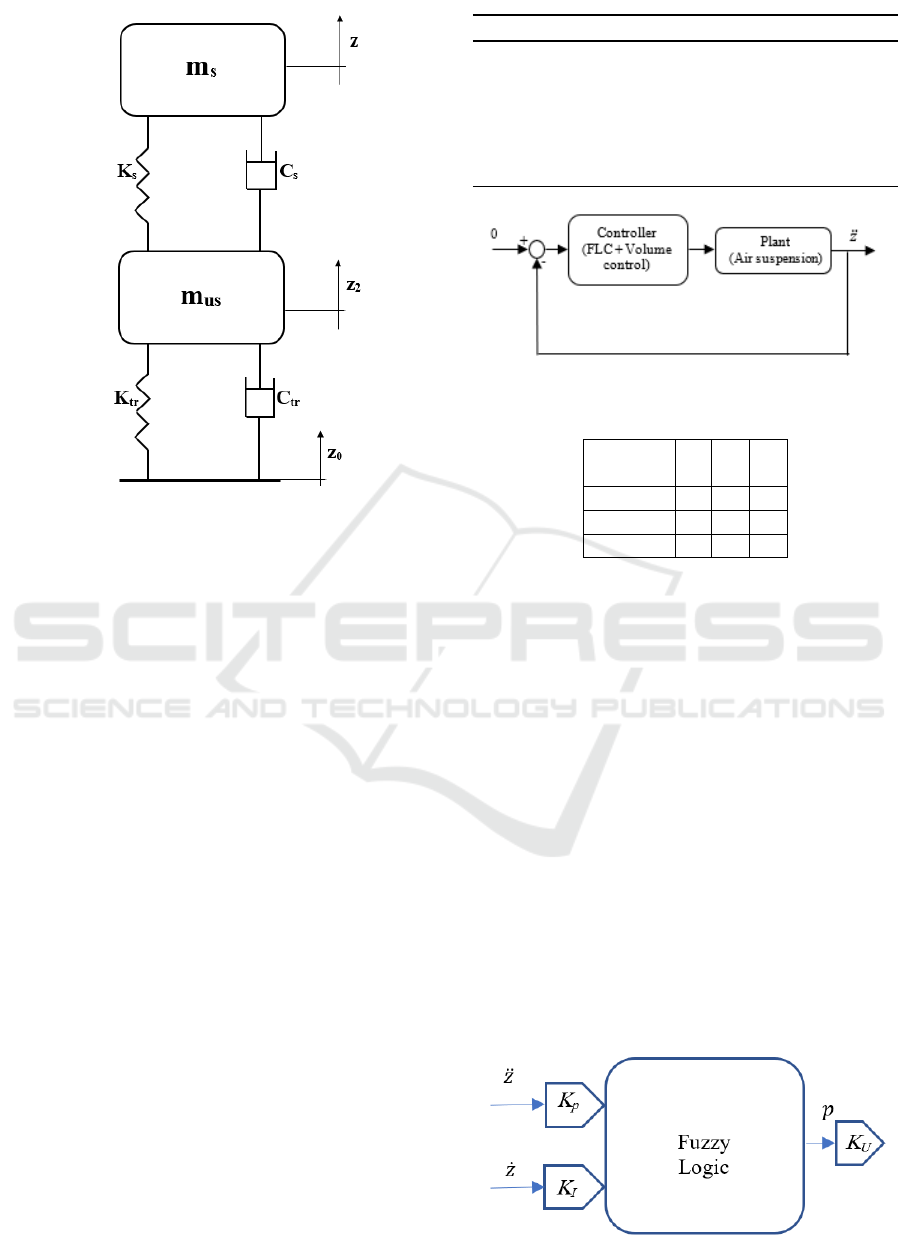
Figure 3: Quarter car air suspension model.
in Fig. 3 are:
For sprung mass
m
s
¨z +C
s
(˙z − ˙z
2
) + K
s
(z − z
2
) = 0 (18)
For unsprung mass
m
us
¨z
2
+C
s
( ˙z
2
− ˙z) + K
s
(z
2
− z)
+C
tr
( ˙z
2
− ˙z
0
) + K
tr
(z
2
− z
0
) = 0
(19)
3 FINITE CONTROL
AUGMENTED WITH FUZZY
LOGIC
The proposed control is applied where there are four
different settings as described before. The default is
all volumes (V
1
,V
2
,V
3
) are connected for minimum
stiffness for better comfort. Until the unsprung mass
displacement z
2
increases gradually to the excitation
amplitude, the volume will decrease to V
1
by closing
off the valves to increase the spring stiffness. The
control algorithm is given in Algorithm 1.
A block diagram shows the schematic diagram for
the control system shown in Figure 4. Since K
s
de-
pends on the pressure p
g
of the air spring as well as
the volume, a Mamdani PI like-fuzzy logic control
(Figure 5) for incremental change ∆p
g
is applied with
three linguistic fuzzy input sets for acceleration ¨z and
velocity ˙z positive P, zero Z, negative N. The linguis-
tic output fuzzy sets for ∆p
g
are the same as the input.
Figure 6 shows the membership of the fuzzy set of the
input and outputs and Table. 2 shows the rule base.
Algorithm 1: Control Algorithm.
if z
2
<= Threshold 1 (l
1
) then
Connect V
2
+V
3
to V
1
else if Threshold 1 < z
2
<= Threshold 2 (l
2
) then
Connect V
3
to V
1
else
Disconnect V
2
and V
3
from V
1
end if
Figure 4: Block diagram for the control system.
Table 2: Fuzzy rule base.
H
H
H
H
H
˙z
¨z
P Z N
P P P Z
Z P Z N
N Z N N
4 GENETIC OPTIMIZATION
As explained before, the fuzzy system has two input
and one output on which each input or output has a
gain. We need to know the optimum value for these
gains K
p
, K
I
and K
u
. As well as, the thresholds of
the volumes control algorithm l
1
, l
2
and l
3
. Genetic
algorithm optimization technique is applied to find the
set of optimal gains and threshold levels method. The
objective function J for the optimization is chosen as
follow:
J = minӨz
2
(20)
The objective is minimizing the sum of squared
sprung mass acceleration measured over the total time
by minimizing the suspension stiffness, Ks as de-
scribed before while limiting the unsprung mass dis-
placement z
2
to a value not more than the road excita-
tion amplitude to ensure tire road holding. Since the
Figure 5: Fuzzy logic Schematic diagram.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
292

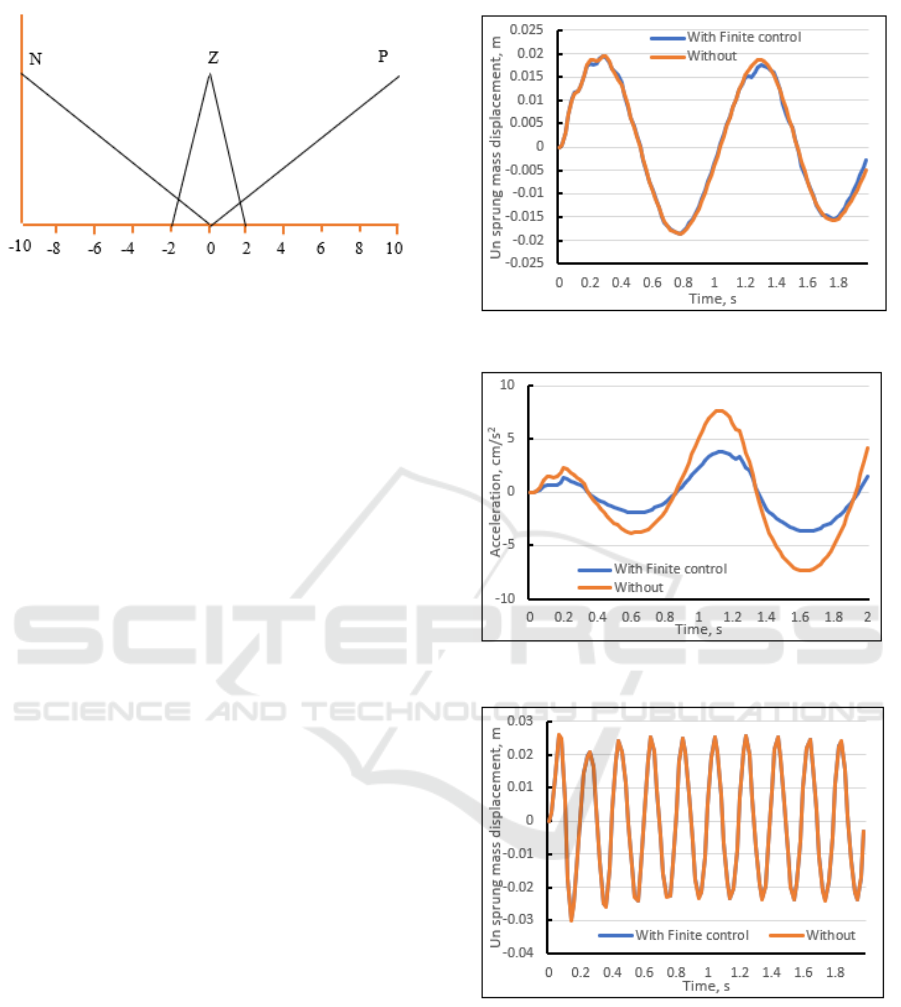
Figure 6: Member ship of the fuzzy sets for inputs and out-
puts.
threshold levels are arranged in sequence, i.e. l
1
<
l
2
< l
3
, the following inequality constraint is added to
the GA problem.

1 −1 0
0 1 −1



l
1
l
2
l
3


<

0
0

5 SIMULATION RESULTS
The two-DOF air suspension system is modeled and
simulated using Matlab R2017a and a function stiff
was created which depends on frequency, air volume
and pressure to calculate the stiffness at different con-
ditions which is then used to calculate the transmissi-
bility ratio for the sprung and the unsprung mass. The
system is modeled at different operating conditions of
amplitudes and frequencies.
The values of the control gains and thresholds
levels K
e
, K
de
, K
u
, l
1
, l
2
and l
3
are 13.866, 30.528,
540.552, 0.73, 0.782 and 0.783 respectively.
Figures 7 and 8 show the vertical amplitude of the
unsprung mass and the vehicle body acceleration with
the proposed finite control versus the one without fi-
nite control for an input excitation of 2 cm amplitude
and 1 Hz frequency.
The figures show that implementing the proposed
strategy reduces the sprung mass acceleration by a
value that reaches 4 cm/s
2
while ensuring the vehicle
safety as shown in Figure 7 which leads to improving
the ride comfort.
Figures 9 and 10 show the unsprung mass vertical
displacement and the vehicle body acceleration under
excitation of 2 cm and 5 Hz frequency.
From the above figures, it can be found that the
unsprung mass displacement curves coincide over
each other. While for acceleration at 5 Hz, the pro-
posed control reduces the transmissibility with a value
reaches 3 cm/s
2
. The system is not able to decrease
Figure 7: Unsprung mass vertical displacement with time.
Figure 8: The vehicle body acceleration versus time.
Figure 9: Unsprung mass vertical displacement with time
under excitation of 2 cm amplitude and 5 Hz frequency.
the unsprung displacement at high frequencies but
still have the benefit of improving comfort perfor-
mance.
Finite Control Augmented with Fuzzy Logic for Automotive Air-spring Suspension System
293

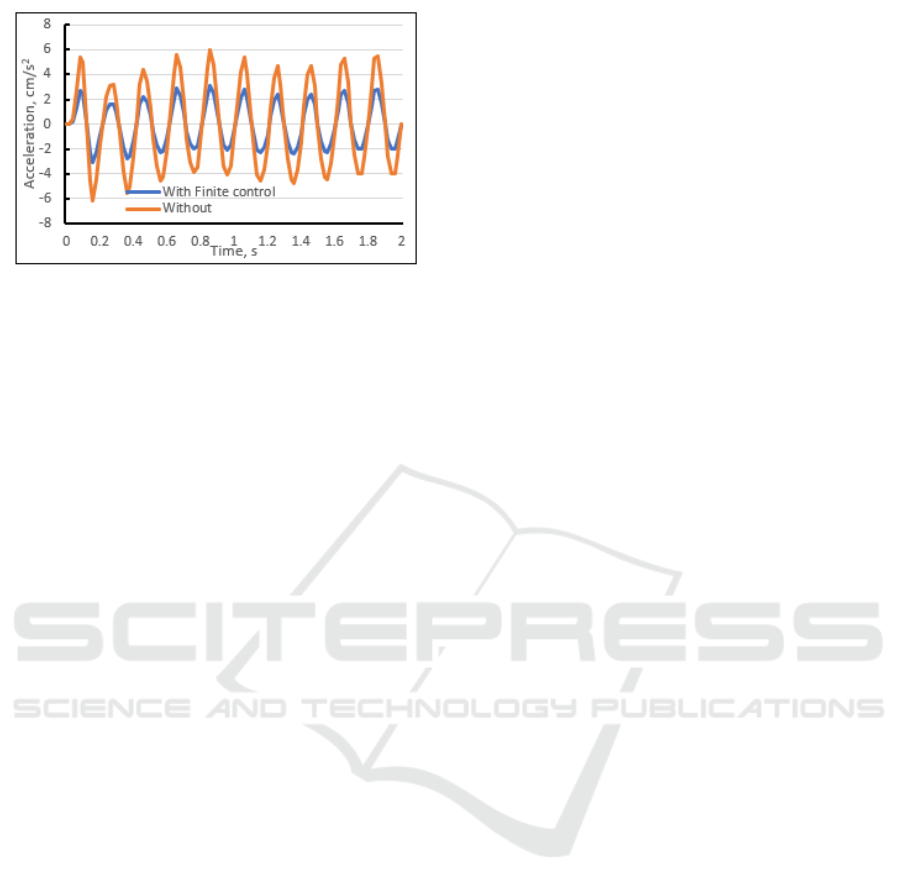
Figure 10: The vehicle body acceleration versus time under
excitation of 2 cm amplitude and 5 Hz frequency.
6 CONCLUSION
A control strategy is proposed in this work in order
to improve ride and safety by using additional vol-
umes connected to the air spring and switching be-
tween them. The control strategy is merged with a
PI like fuzzy control that control the pressure inside
the air spring. The control parameters are estimated
using Genetic algorithm. It was found that implemen-
tation of the proposed strategy improves the compro-
mise between ride and handling behavior especially
over a wide range of frequency.
The vehicle body acceleration decreases by a
value that reaches 4 cm/s
2
which means improving the
passenger ride comfort as well maintain the passen-
ger safety. In future, we could compare our proposed
approach with the Inverse Optimal Control (IOC) ap-
proach (El-Hussieny et al., 2015) found in the litera-
ture.
REFERENCES
Ballo, I. (2001). Properties of air spring as a force generator
in active vibration control systems. Vehicle System
Dynamics, 35(1):67–72.
Bedarff, D.-I. T. and Pelz, I. P. Development of an active
and integrated suspension system.
El-Hussieny, H., Assal, S. F., Abouelsoud, A., Megahed,
S. M., and Ogasawara, T. (2015). Incremental learn-
ing of reach-to-grasp behavior: A pso-based inverse
optimal control approach. In 2015 7th International
Conference of Soft Computing and Pattern Recogni-
tion (SoCPaR), pages 129–135. IEEE.
Gavriloski, V., Jovanova, J., Tasevski, G., and Djidrov, M.
(2014). Development of a new air spring dynamic
model. FME Transactions, 42(4):305–310.
Gohari, M. and Tahmasebi, M. (2015). Active off-road seat
suspension system using intelligent active force con-
trol. Journal of Low Frequency Noise, Vibration and
Active Control, 34(4):475–489.
Mirji, S. and Arockia, A. (2014). Fuzzy logic control for
half car suspension system using matlab. Interna-
tional Journal of Engineering Research & Technology
(IJERT), 3(3).
Nieto, A., Morales, A., Trapero, J., Chicharro, J., and Pin-
tado, P. (2011). An adaptive pneumatic suspension
based on the estimation of the excitation frequency.
Journal of sound and vibration, 330(9):1891–1903.
Omar, A. A. A. and
¨
Ozkan, B. (2015). Evaluation of effect
of in-wheel electric motors mass on the active suspen-
sion system performance using linear quadratic regu-
lator control method. Evaluation, 4(1).
Presthus, M. (2002). Derivation of air spring model param-
eters for train simulation.
S., G. P. and K., M. M. (2019). A contemporary adaptive air
suspension using lqr control for passenger vehicles.
ISA Transactions.
Wong, J. Y. (2008). Theory of ground vehicles. John Wiley
& Sons.
Zepeng, G., Jinrui, N., Lian, L., and Xiaolin, X. (2017).
Research on air suspension control system based on
fuzzy control. Energy Procedia, 105:2653–2659.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
294