Nonparametric System Identification Matlab Toolbox
Grzegorz Mzyk
a
Department of Electronics, Wrocaw University of Science and Technology, W. Wyspiaskiego 27, 50-370 Wrocaw, Poland
Keywords:
System Identification, Nonparametric Estimation, Kernel Regression, Orthogonal Expansion, Hammerstein
System, Wiener System.
Abstract:
In the paper the first version of Nonparametric System Identification Matlab Toolbox is presented. It is based
on theoretical results concerning nonparametric identification method, achieved for the last four decades. The
library includes both standard (kernel based or orthogonal expansion based) nonparametric methods and recent
algorithms including combined (parametric-nonparametric) algorithms. Hammerstein and Wiener models and
their serial connections are considered. Nonparametric estimates, usually run as a preliminary steps, play
supporting role in the main procedure of estimating system parameters by the least squares method. Multi-
level (hybrid) structure of algorithms, i.e. combining both parametric and nonparametric approaches allows
to decompose the problem of identification of interconnected complex system into simpler local subproblems.
Moreover, asymptotic consistency of all estimates was formally proved, even under existence of random and
correlated noise.
1 INTRODUCTION
1.1 History
The need of having accurate models of relationships is
of crucial meaning for decision making, system iden-
tification, forecasting, designing of optimal control,
system identification, pattern recognition, simulation
and many others. For ages, people wanted to explain
the nature of real relationships to improve efficiency
of production and organization, increase the level of
safety or to forecast the future and adapt to changing
conditions. Formally, the paper by Gauss ((Gauss and
Davis, 1857)), from 19th century, which introduces
the least squares method is treated as initiation of the
field. In general, building models is based on two kind
of knowledge:
• parametric, a priori, usually provided by experts
or determined by laws of physics, i.e., we are
given the formula with finite and known number
of unknown parameters,
• nonparameric, i.e., the set of input-output data
collected in the experiment (learning sequence).
As we feel intuitively, thanks to parametric knowl-
edge we can significantly narrow the class of poten-
a
https://orcid.org/0000-0002-1701-5095
tial relationships taken into consideration, and conse-
quently speed up the convergence rapidly. Neverthe-
less the risk of false parametric assumption cannot be
neglected. If the assumed formula is not correct, the
non-zero approximation error appears, which cannot
be reduced even when the number of measurements
tends to infinity.
Traditional approaches assumed linear dynamic
models as the simplest (rough) approximation of the
real system. If they turned out insufficient, the poly-
nomial or bilinear models were applied. Assuming
smoothness of nonlinear characteristics the Volterra
kernel expansion approach has been proposed ((Boyd
et al., 1984)). Nevertheless, the computational com-
plexity of algorithms was not rewarding, owing to
large number of parameters needed to be estimated,
particularly for long-memory systems with irregular
nonlinearities. Moreover, the theoretical analysis of
statistical properties of the parametric estimates is rel-
atively difficult in general case. As an alternative to
Volterra representation, the concept of block-oriented
models was proposed in 1960’s ((Narendra and Gall-
man, 1966)). The system is modelled by intercon-
nections of simple components of two types – linear
dynamics and static nonlinearities. The most popular
structures in this class are Hammerstein and Wiener
models (see (Pintelon and Schoukens, 2004) and (Giri
and Bai, 2010)).
Mzyk, G.
Nonparametric System Identification Matlab Toolbox.
DOI: 10.5220/0007922306910698
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 691-698
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
691

In parallel, the theory of nonparametric regres-
sion function estimation was developed ((Nadaraya,
1964), (Stone, 1982), (Cristobal et al., 1987), (H
¨
ardle,
1990), (Wand and Jones, 1995), (Efromovich, 1999),
(Gyorfi et al., 2002), (Ruppert et al., 2003)). First
attempts to nonparametric identification of dynamic
systems were made by Greblicki and Pawlak in
1980’s (see e.g. (Greblicki and Pawlak, 1986)). The
theory was developed towards relaxation of assump-
tion concerning nonlinearities and restrictions im-
posed on the input process ((Hasiewicz et al., 2005),
(Pawlak et al., 2007), (Greblicki and Pawlak, 2008),
(Bai, 2010), (Rochdi et al., 2010), (
´
Sliwi
´
nski, 2013)).
The proposed algorithms recover true characteristics
and are free of approximation error. Nevertheless,
since they are based on measurements only (neglect
risky prior knowledge about parametric representa-
tion), the rate of convergence is relatively slower and
the obtained results are satisfactory only asymptoti-
cally.
Recent approaches to system identification tries
to combine both parametric and nonparametric algo-
rithms to inherit advantages of both philosophies, i.e.
to achieve accurate estimates for moderate number of
measurements and guarantee asymptotic consistency,
when the number of data grows large. The idea was
introduced in (Hasiewicz and Mzyk, 2004) and con-
tinued in (Hasiewicz and Mzyk, 2009), (Greblicki and
Mzyk, 2009), (Mzyk, 2014) and (Mzyk and Wachel,
2017). In general, the nonparametric pilot kernel esti-
mate supports least squares method in the sense that it
censors the data to allow for decomposition of inter-
connected system identification task into simple (lo-
cal) subproblems.
1.2 Paper Organization
The paper starts from recalling standard nonparamet-
ric estimates of probability density function (Section
2) and of the regression function (Section 3). Both
kernel based and orthogonal expansion methods are
reminded. Next, in Section 4, nonparametric algo-
rithms are applied for identification of nonlinear static
characteristic in Hammerstein system. Also the cross-
correlation method is presented for nonparametric
identification of linear dynamic element in Ham-
merstein system. Finally, the combined parametric-
nonparametric method is shown, in which, kernel or
orthogonal algorithms recover inaccessible interac-
tion signal for independent modeling of individual
blocks by the least squares. In Section 5, Wiener
system identification problem is considered. It is
relatively more difficult comparing to Hammerstein
system, owing to correlated excitation of the nonlin-
ear static component. Firstly, the traditional cross-
correlation based method is shown under assump-
tion of Gaussian excitation, and next, more sophisti-
cated algorithms, based on input censoring or deriva-
tive estimation are shown. Finally, the multi-level
(hybrid) strategies, elaborated for sandwich L-N-
L (Wiener-Hammerstein) and N-L-N (Hammerstein-
Wiener) systems are presented in sections 6 and 7, re-
spectively. General information about Nonparametric
System Identification Toolbox can be found in Section
8. Our goal is to provide the ready to use identifica-
tion tools in accessible form, based on the theoretical
results of nonparametric estimates, elaborated in the
team over the last three decades.
2 ESTIMATION OF
PROBABILITY DENSITY
FUNCTION
Let us assume that we are given the sequence of N re-
alizations
{
u
k
}
N
k=1
of random variable u, and we need
to recover the probability density function f (u), with-
out any prior assumptions concerning its parametric
form.
2.1 Kernel Method
The kernel estimate of the probability density func-
tion has the form
b
f (u) =
1
Nh
N
∑
k=1
K

u
k
−u
h

, (1)
where K () is a kernel function, e.g.
K (v) =

1, as
|
v
|
≤
1
2
0, otherwise
, (2)
which selects measurements from neighbourhood of
the point u, and h = h (N) is a bandwidth parameter
(radius of selection). It can be show that for N → ∞,
in all continuity points u it holds that
h(N) → 0 =⇒ E
b
f (u) → f (u), (3)
Nh(N) → ∞ =⇒ var
b
f (u) → 0, (4)
i.e., the
b
f (u) → f (u) in the mean squared sense, if
both (3) and (4) are fulfilled.
2.2 Orthogonal Expansion Method
Alternatively, assuming that f (u) is square integrable,
i.e. f (u) ⊂ L
2
, and using any complete set of or-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
692

thonormal basis functions
{
ϕ
i
(u)
}
∞
i=0
, it can be rep-
resented as follows
f (u) =
∞
∑
i=1
a
i
ϕ
i
(u), (5)
where
a
i
= f (u) ◦ϕ
i
(u) =
Z
D
f (u)ϕ
i
(u)du = Eϕ
i
(u). (6)
The set D in (6) is specific for the orthonormal ba-
sis
{
ϕ
i
(u)
}
∞
i=0
used in the identification algorithm.
The most popular are trigonometric series, orthogo-
nal polynomials (Laguerre, Lagrange, Hermite), or
wavelets. The unknown coefficients a
i
’s can be re-
covered from experimental data
{
u
k
}
N
k=1
, as sample
means
b
a
i
=
1
N
N
∑
k=1
ϕ
i
(u
k
), (7)
and owing to Parseval equality, arbitrary accuracy of
the approximate
b
f (u) =
Q
∑
i=1
b
a
i
ϕ
i
(u) (8)
can be achieved, using appropriately selected scale
(cut-off level) Q. In general, asymptotic consistency,
i.e. the convergence
b
f (u) → f (u) in the mean square
sense is guaranteed as Q(N) → ∞ and
Q(N)
N
→ 0, as
N → ∞.
3 ESTIMATION OF REGRESSION
FUNCTION
In this section we consider the problem of nonpara-
metric estimation of nonlinear characteristic µ () of
the static system, with noise-corrupted output
y
k
= µ (u
k
) + z
k
. (9)
Assuming that the noise z
k
is zero mean, Ez
k
= 0, has
finite variance, var<∞, and is independent of the exci-
tation u
k
, it can easily be shown that the input-output
regression function is equivalent to characteristic µ (),
i.e.
R(u) = E
{
y
k
|u
k
= u
}
= µ(u). (10)
For all points u such that f (u) > 0 one can write
R(u) =
g(u)
f (u)
, (11)
where g(u) = R (u) f (u) = µ (u) f (u).
3.1 Kernel Method
Since the noise-free output µ (u
k
) is not accessible
for measurement, assuming continuity of µ (u) in the
point u, the natural idea in nonparametric estima-
tion of g(u) is to use selected measurements y
k
’s, for
which respective inputs u
k
’s belong to the neighbour-
hood of u,
b
g(u) =
1
Nh
N
∑
k=1
y
k
K

u
k
−u
h

. (12)
It leads to kernel regression function estimate of the
form
b
R(u) =
b
g(u)
b
f (u)
=
∑
N
k=1
y
k
K

u
k
−u
h

∑
N
k=1
K

u
k
−u
h

. (13)
The theoretical analysis of the limit properties of (13)
and the issue of optimal selection of the bandwidth
parameters h(N), e.g. by the cross-validation method,
is discussed in (Wand and Jones, 1995).
3.2 Orthogonal Expansion Method
Analogously, the numerator in (11) can be expanded
as follows
g(u) =
∞
∑
i=1
b
i
ϕ
i
(u), (14)
where the unknown coefficients b
i
’s can be estimated
as
b
b
i
=
1
N
N
∑
k=1
y
k
ϕ
i
(u
k
), (15)
and
b
a
i
’s are given by (7). Consequently,
b
R(u) =
∑
Q
i=1
b
b
i
ϕ
i
(u)
∑
Q
i=1
b
a
i
ϕ
i
(u)
. (16)
For details concerning properties of the estimate
(16), for various kinds of orthogonal basis, we refer
the reader to (
´
Sliwi
´
nski, 2013) and references cited
therein.
4 HAMMERSTEIN SYSTEM
IDENTIFICATION
The Hammerstein system (see Fig. 1) includes static
nonlinear element with the characteristic µ() followed
by the linear dynamic filter with the impulse response
n
γ
j
o
∞
j=0
. The interaction signal w
k
is hidden in the
sense that it cannot be measured. The system is de-
Nonparametric System Identification Matlab Toolbox
693

{
}
∞
=0j
j
γ
()
μ
k
u
k
w
k
z
k
y
Figure 1: Hammerstein system.
scribed by the following equation
y
k
=
∞
∑
j=0
γ
j
µ

u
k−j

+ z
k
. (17)
Assuming that the linear dynamics is asymptotically
stable, i.e.
∑
∞
j=0



γ
j



< ∞, the goal is to estimate both
characteristic µ () and the impulse response
n
γ
j
o
∞
j=0
from the input-output data
{
(u
k
, y
k
)
}
N
k=1
, collected in
the experiment. The crucial meaning has the fact that
for i.i.d. input sequence, it holds that
R(u) = γ
0
µ(u) + c
1
, (18)
where c
1
= Eµ (u
k
)
∑
∞
j=1
γ
j
= const, i.e. standard re-
gression R (u) is Hammerstein system is scaled and
shifted version of the nonlinear characteristic of its
static component. Assuming that µ (0) = 0, one can
avoid the offset c
1
, using the corrected nonparametric
regression estimate
b
µ(u) =
b
R(u) −
b
R(0). (19)
The observation (18) allows to generalize nonpara-
metric estimates (13) or (16) for dynamic system. It
can be proved that under standard conditions concern-
ing h(N) or Q(N) (see e.g. (Greblicki and Pawlak,
2008)), it holds that
b
µ(u) → γ
0
µ(u). The scale γ
0
is not identifiable independently of the identification
method, owing inaccessibility of w
k
. The Hammer-
stein systems µ (u) ×
n
γ
j
o
∞
j=0
and γ
0
µ(u) ×
n
γ
j
γ
0
o
∞
j=0
are equivalent from the input-output point of view.
As regards identification of linear block, for
i.i.d. input sequence one can apply standard cross-
correlation analysis. It can easily be shown that the
input-output cross-correlation coefficients
ς
j
= E

(u
k
−Eu
k
)y
k+ j

(20)
are proportional to the unknown impulse response el-
ements, i.e.
ς
j
= c
2
γ
j
, (21)
where c
2
= const for all j = 0, 1, 2.... It leads to the
following estimate
b
γ
j
=
1
N − j
N−j
∑
k=1
(u
k
−u)y
k+ j
, (22)
where u =
1
N
∑
N
k=1
u
k
. Asymptotically, for N → ∞, to
assure consistency of the cut model
n
b
γ
j
o
S(N)
j=0
of the
stable linear subsystem, the order S(N) should behave
such that S(N) → ∞, but
S(N)
N
→ 0.
Despite pure nonparametric estimates (19) and
(22) guarantee asymptotic convergence to the true
characteristic, the convergence rate is rather slow,
and the results can be not satisfying for moderate
number of measurements. Hence, the combined
parametric-nonparametric algorithms proposed firstly
in (Hasiewicz and Mzyk, 2004) are worth notifying.
They allow to decompose complex system identifica-
tion task into simpler local subproblems, and can be
applied under partial or uncertain knowledge of in-
dividual components. In step 1 (nonparametric) we
identify inaccessible interaction signal
b
w
k
=
b
R(u
k
) −
b
R(0) (23)
with the use of kernel orthogonal regression estima-
tors, and next, in step 2 (parametric) we incorporate
least squares or instrumental variables approach for
both static and dynamic subsystems using the pairs
{
(u
k
,
b
w
k
)
}
N
k=1
, and
{
(
b
w
k
, y
k
)
}
N
k=1
, respectively. For
example, under parametric knowledge that µ(u) =
µ(u, θ
∗
), the true vector of parameters, θ
∗
, is esti-
mated as follows
b
θ = arg min
θ
N
∑
k=1
(
b
w
k
−µ (u
k
, θ
∗
))
2
. (24)
Let us emphasize, that nonparametric estimate
b
w
k
is
plugged in to the definition of parameter estimate
b
θ.
The formal proofs of consistency of
b
θ and parametric-
nonparametric estimates for IIR linear dynamics can
be found in (Hasiewicz and Mzyk, 2009).
5 WIENER SYSTEM
IDENTIFICATION
The Wiener system (Fig. 2) includes the components
of Hammerstein system connected in reverse order. It
 

0j
j

k
u
k
x
k
z
k
y
() 
Figure 2: Wiener system.
is described by the equation
y
k
= µ
∞
∑
j=0
λ
j
u
k−j
!
+ z
k
. (25)
The Wiener structure has very wide scope of potential
applications (see (Giannakis and Serpedin, 2001)).
Unfortunately, since the hidden nonlinearity input,
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
694

x
k
, is correlated, the problem is much more diffi-
cult. In the contrary to Hammerstein system iden-
tification task, sufficient identifiability conditions for
Wiener system were formulated in the literature only
for some special cases. One of them is based on
application of Gaussian excitation. In this specific
situation, also the hidden process
{
x
k
}
is normally
distributed, and the Bussgang theorem holds. It al-
lows to identify impulse response elements λ
j
anal-
ogously to (22), i.e.,
b
λ
j
=
1
N−j
∑
N−j
k=1
(u
k
−u)y
k+ j
.
Using the FIR approximate model of the linear dy-
namic block, the interaction signal x
k
can be approx-
imated as follows
b
x
k
=
∑
S
j=0
b
λ
j
u
k−j
, and the charac-
teristic of the nonlinear component can be estimated
from the pairs
{
(
b
x
k
, y
k
)
}
N
k=1
, analogously to (24), i.e.
b
θ = argmin
θ
∑
N
k=1
(y
k
−µ (
b
x
k
, θ
∗
))
2
. The input density
restriction has been relaxed in (Mzyk, 2007), (Gre-
blicki, 2010), (Pawlak et al., 2007) and (Wachel and
Mzyk, 2016). For the survey of parametric and non-
parametric methods for identification of Wiener sys-
tem we refer the reader to (Mzyk, 2010).
6 WIENER-HAMMERSTEIN
SYSTEM IDENTIFICATION
Although Hammerstein and Wiener models general-
ize the class of linear systems, they are still not suf-
ficient in some practical applications. In this section
we consider cascade connection of Wiener and Ham-
merstein system, with the L-N-L (sandwich) structure
(see Fig. 3). The system is described by the equation
()

k
u
k
x
k
z
k
y
k
v


j

j0
p


j

j0
q
Figure 3: Wiener–Hammerstein system.
y
k
=
q
∑
j=0
γ
j
µ

x
k−j

+ z
k
, (26)
where x
k
=
∑
p
i=0
λ
i
u
k−i
.
First attempts to parametric-nonparametric identi-
fication of Wiener-Hammerstein system were made in
(Mzyk, 2012) and the proposed estimates were further
analyzed in (Mzyk and Wachel, 2017). The algorithm
consists of three steps.
Step 1. Nonparametric kernel identification on the
nonlinear characteristic
b
µ
N
(x) =
∑
N
k=1
y
k
·K

δ
k
(x)
h

∑
N
k=1
K

δ
k
(x)
h

, (27)
where
δ
k
(x) ,
p+q
∑
j=0


u
k−j
−x


. (28)
Step 2. Estimation of the convolution of impulse
response of linear dynamic objects
κ
j
= λ
j
∗γ
j
=
j
∑
i=0
γ
i
λ
j−i
, (29)
by the local cross-correlation censored by the kernel
technique
b
κ
τ
=
1
Nη
p+q+3
N−(p+q)
∑
k=p+q+1
u
k
y
k+τ
K

∆
k
η

, (30)
where η is a bandwidth (analogously to h) and
∆
k
= max
j=0,1,..., p+q


u
k−j


. (31)
Step 3. Splitting the polynomial
W (d) = κ
p+q
d
p+q
+ κ
p+q−1
d
p+q−1
+ ... + κ
1
d + κ
0
= κ
p+q
(d −d
1
)(d −d
2
)... (d −d
p+q
),
(32)
where Ω =

d
1
, d
2
, ..., d
p+q

denotes the set of roots
(generally complex), into two separate factors
W (d) = κ
p+q
Λ
Θ
(d) ·Γ
Θ
(d), (33)
where Λ
Θ
(d) =
∏
d
i
∈Θ
(d −d
i
), and Γ
Θ
(d) =
∏
d
i
∈Ω\Θ
(d −d
i
), such that
n
b
λ,
b
γ
o
= arg min
Θ∈Ω
b
Q(l
Θ
, g
Θ
), (34)
where
b
Q(l
Θ
, g
Θ
) =
1
N
∑
N
k=1
[y
k
−y
k
(l
Θ
, g
Θ
)]
2
and
y
k
(l
Θ
, g
Θ
) is the model output for impulse responses
l
Θ
, and g
Θ
, respectively.
Since the speed of convergence is sensitive on the
orders p and q, the algorithm is rather devoted to FIR
Wiener-Hammerstein systems with short memory.
7 HAMMERSTEIN-WIENER
SYSTEM IDENTIFICATION
Serial connection of Hammerstein system with
Wiener system leads to the N-L-N sandwich structure
(see Fig. 4). The system is describes as follows
y
k
= η
q
∑
j=0
γ
j
µ

u
k−j

!
+ z
k
. (35)
Nonparametric System Identification Matlab Toolbox
695

()

k
u
k
w
k
z
k
y
k
v
k
x
()


j

j0
q
Figure 4: Hammerstein–Wiener system.
Our algorithm (see (Biega
´
nski, 2018)) uses both
parametric and nonparametric system identification
tools to recover parameters of each individual block
and it estimates linear and nonlinear parts of the
Hammerstein–Wiener system separately. We assume
that nonlinear characteristics of the input and output
static blocks are described by the linear combinations
of a priori known base functions f and g
µ(u) = µ(u, a
∗
) = a
∗
T
f (u), (36)
a
∗
= (a
∗
1
, a
∗
2
, . . . , a
∗
m
)
T
, a
∗
∈ R
m
,
f (u) = ( f
1
(u), f
2
(u), . . . , f
m
(u))
T
,
η(x) = η(x, b
∗
) = b
∗
T
g(x), (37)
b
∗
= (b
∗
1
, b
∗
2
, . . . , b
∗
n
)
T
, b
∗
∈ R
n
,
g(x) = (g
1
(x), g
2
(x), . . . , g
n
(x))
T
.
Dimensions of the parameters vectors a
∗
and b
∗
are
fixed and known. Moreover it is assumed that static
nonlinear characteristics are both Lipschitz functions,
i.e. are uniformly continuous with bounded first
derivatives. Characteristics are twice differentiable
in arbitrarily small neighbourhoods of some points
u
0
and x
0
= µ(u
0
)
∑
q
j=0
γ
∗
j
and µ
0
(u
0
) 6= 0, η
0
(x
0
) 6=
0. Additionally, output characteristic is strictly
monotonous, and therefore invertible. Hence the
identification procedure is divided into four stages:
Stage 1. Direct identification of the finite impulse
response parameters γ
∗
of linear dynamic subsystem
in the presence of random input and random noise
with the use of kernel-censored least squares method
ˆ
γ =
N
∑
k=1
φ
k
φ
T
k
K

∆
k
h

!
−1
N
∑
k=1
φ
k
y
k
K

∆
k
h

!
,
(38)
where
φ
k
=

u
(1)
k
, u
(1)
k−1
, . . . , u
(1)
k−q

T
, (39)
and ∆
k
is the infinity norm of the regression vector
∆
k
=
k
φ
k
k
∞
= max
j=0,1,...,q



u
(1)
k−j



. (40)
Stage 2. Estimation of parameter vector b
∗
of
output nonlinear characteristic in active experiment
(binary sequence excitation) with the use of kernel
method
ˆ
η

x
[i]

=
∑
N
k=1
y
k
δ(φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)
, (41)
where
δ(φ
k
, ϕ
i
) =
(
1, if φ
k
= ϕ
i
0, otherwise
. (42)
The result of this step is given by the set of N
0
pairs

x
[i]
,
ˆ
η

x
[i]

N
0
i=1
. (43)
Using this set of pairs, we can find the most suitable
parameters with the least squares method
ˆ
b =

Ψ
T
Ψ

−1
Ψ
T
ζ, (44)
where Ψ and ζ are respectively
Ψ =

g(x
[1]
), g(x
[2]
), . . . , g(x
[N
0
]
)

,
ζ =

ˆ
η

x
[1]

,
ˆ
η

x
[2]

, . . . ,
ˆ
η

x
[N
0
]

.
Stage 3. Filtration of output signal y
k
in order to
generate additional process r
k
with the same condi-
tional expected value as non-measureable signal x
k
.
With
ς(y) = E
{
x
k
|y
k
= y
}
=
Z
∞
−∞
η
−1
(y −z) f (z)dz. (45)
we can generate additional signal
r
k
= ς(y
k
), (46)
with the same conditional expected value as x
k
, i.e.,
R(u) = E
{
r
k
|u
k
= u
}
= E
{
ς(y
k
)|u
k
= u
}
=
= E

Z
∞
−∞
η
−1
(y
k
−z) f (z)dz|u
k
= u

=
= E

Z
∞
−∞
η
−1
(η(x
k
)) f (z)dz|u
k
= u

=
= E

x
k
·
Z
∞
−∞
f (z)dz|u
k
= u

= E
{
x
k
|u
k
= u
}
.
Stage 4. Identification of input nonlinear charac-
teristic
b
R(u) =
∑
N
k=1
r
k
K

u
k
−u
h(N)

∑
N
k=1
K

u
k
−u
h(N)

. (47)
The idea was to develop a procedure that would adapt
itself to separate block-oriented structures, such as
Hammerstein and Wiener systems, even without any
additional a priori knowledge about the examined
system. The problem of identification of such com-
plicated structure is rather difficult, not only because
of existence of Wiener part in which linear dynam-
ics precedes static nonlinearity, but also because of
the correlation between non-measurable signals. In
the algorithm we benefit from multistage and two-
experiment approaches to achieve specific, advanta-
geous conditions in which linear and nonlinear parts
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
696

of the system were less complicated to identify. Addi-
tionally, further steps of the algorithm profit from the
former ones which significantly reduces the complex-
ity and dimensionality of the identification problem.
The uniqueness of the solution is strictly related to
the impulse response fulfilling the given assumptions
and for the output nonlinear characteristic satisfying
Haar condition. The main drawback of the algorithm
is that the effectiveness of the procedure is dependent
on the length of the finite impulse response, which
is characteristic for the whole class of Wiener-type
systems (”course of dimensionality”). Therefore the
proposed method is recommended for linear dynamic
blocks with short impulse response and more sophis-
ticated memoryless nonlinear characteristics.
Example 1. Let’s investigate the simple example of
compensator building under knowledge of η(x) and
f (z). Assume that nonlinear output block is described
by η(x) =
3
√
x and the system is disturbed by additive
random, uniformly distributed noise z
k
∼ U[−1, 1].
Compensator can be determined as follows
ξ(y) = E{x
k
|y
k
= y} =
Z
1
−1
(y −z)
3
·
1
2
dz = y
3
+ y,
i.e., r
k
= y
3
k
+ y
k
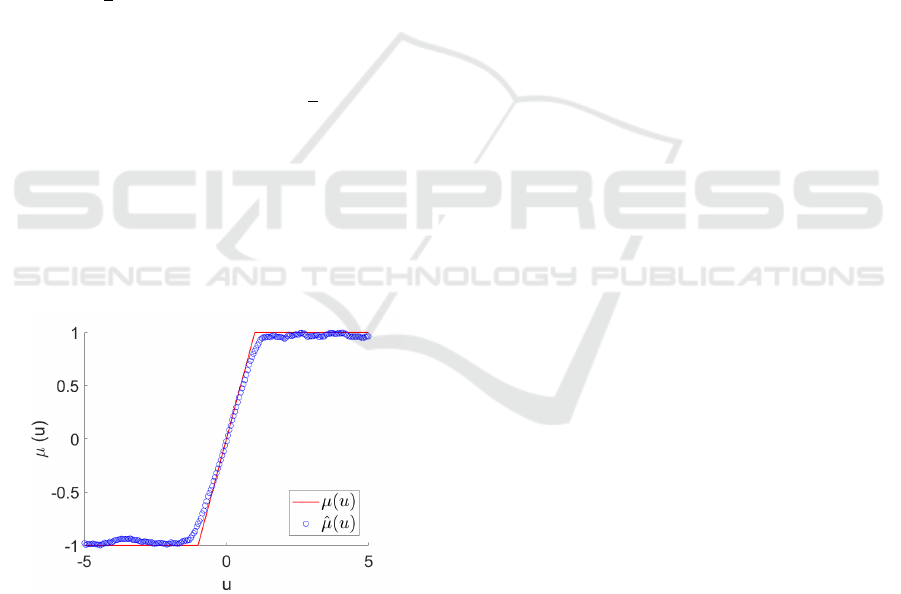
. Below, in Fig. 5, we present the
estimate (47) of Hammerstein system nonlinearity
µ(u) =

u , |u| ≤ 1
sgn(u) , |u| > 1
for γ = (γ
0
, γ
1
)
T
= (1, 1)
T
. The result illustrates ap-
plicability of the proposed method.
Figure 5: True characteristic µ(u) vs. the estimate ˆµ(u).
8 THE MATLAB TOOLBOX
The actual version of toolbox and its documentation
can be accessed at the WWW page
http://staff.iiar.pwr.wroc.pl/grzegorz.mzyk/KIT
Below we present the list of names of selected
functions:
cosineKernel() – returns value of the cosine kernel
function
epanechnikovKernel() – returns value of the
Epanechnikov kernel
gaussianKernel() – returns value of Gaussian ker-
nel
triangularKernel() – returns value of triangular
kernel
uniformKernel() – returns value of uniform
(Parzen) kernel
kernelDensityEstimation() – computes probability
density function estimate for a given point, by the ker-
nel method
orthogonalRegressionEstimation() – computes
model of the regression function using orthogonal ex-
pansion method
kernelRegressionEstimation() – computes model
of the regression function using kernel method
hammerstein() – identifies both components of
Hammerstein system using input-output data
wiener() – identifies both components of Wiener
system using input-output data
trigonometricOrthonormalBasis() – supporting
function generating trigonometric orthogonal basis
functions
estimateDynamicSubsystem() – identification of
linear dynamic block
crossValidation() – selection of optimal band-
width parameter in kernel methods, or the scale in or-
thogonal expansion methods
9 SUMMARY
The methods presented in the paper combine the non-
parametric and parametric tools. Such a strategy
allows to solve various kinds of specific obstacles,
which are difficult to be overcome in purely paramet-
ric or purely nonparametric approach. In particular,
the global identification problem can be decomposed
on simpler local problems, the measurement sequence
can be pre-filtered in the nonparametric stage, or the
rough parametric model can be refined by the non-
parametric correction when the number of measure-
ments is large enough. The schemes proposed in the
paper can be used elastically and have a lot of de-
grees of freedom. In most of them we can obtain
traditional parametric or nonparametric procedures by
simple avoiding of the selected steps of combined al-
gorithms. In this sense, the proposed ideas can be
treated as generalizations of classical approaches to
system identification.
Nonparametric System Identification Matlab Toolbox
697

ACKNOWLEDGEMENTS
The work was partially supported by the Grant No.
0401/0136/18, WUS&T, Poland.
REFERENCES
Bai, E. (2010). Non-parametric nonlinear system identifi-
cation: an asymptotic minimum mean squared error
estimator. IEEE Transactions on Automatic Control,
55(7):1615–1626.
Biega
´
nski, M. (2018). Multi-level identification of
Hammerstein-Wiener (N-L-N) system in active exper-
iment. In Proceedings of the 15th International Con-
ference on Informatics in Control, Automation and
Robotics, ICINCO, Porto, Portugal, pages 355–361.
Boyd, S., Chua, L. O., and Desoer, C. (1984). Analytical
foundations of Volterra series. IMA Journal of Math-
ematical Control and Information, 1(3):243–282.
Cristobal, J., Roca, P., and Manteiga, W. (1987). A class
of linear regression parameter estimators constructed
by nonparametric estimation. The Annals of Statistics,
15(2):603–609.
Efromovich, S. (1999). Nonparametric Curve Estimation.
Springer, New York.
Gauss, C. F. and Davis, C. H. (1857). Theory
of the motion of the heavenly bodies moving
about the sun in conic sections a translation of
Gauss’s. Boston,Little, Brown and company,. https://
www.biodiversitylibrary.org/bibliography/19023.
Giannakis, G. and Serpedin, E. (2001). A bibliography on
nonlinear system identification. Signal Processing,
81(3):533–580.
Giri, F. and Bai, E. W. (2010). Block-Oriented Nonlinear
System Identification. Lecture Notes in Control and
Information Sciences 404. Springer.
Greblicki, W. (2010). Nonparametric input density-free es-
timation of the nonlinearity in Wiener systems. IEEE
Transactions on Information Theory, 56(7):3575–
3580.
Greblicki, W. and Mzyk, G. (2009). Semiparametric ap-
proach to Hammerstein system identification. In Pro-
ceedings of the 15th IFAC Symposium on System Iden-
tification, Saint-Malo, France, pages 1680–1685.
Greblicki, W. and Pawlak, M. (1986). Identification of
discrete Hammerstein systems using kernel regression
estimates. IEEE Transactions on Automatic Control,
31:74–77.
Greblicki, W. and Pawlak, M. (2008). Nonparametric Sys-
tem Identification. Cambridge University Press.
Gyorfi, L., Kohler, M., Krzy
˙
zak, A., and Walk, H. (2002).
A Distribution-Free Theory of Nonparametric Regres-
sion. Springer Verlag, New York.
H
¨
ardle, W. (1990). Applied Nonparametric Regression.
Cambridge University Press, Cambridge.
Hasiewicz, Z. and Mzyk, G. (2004). Combined parametric-
nonparametric identification of Hammerstein sys-
tems. IEEE Transactions on Automatic Control,
48(8):1370–1376.
Hasiewicz, Z. and Mzyk, G. (2009). Hammerstein system
identification by non-parametric instrumental vari-
ables. International Journal of Control, 82(3):440–
455.
Hasiewicz, Z., Pawlak, M., and
´
Sliwi
´
nski, P. (2005). Non-
parametric identification of nonlinearities in block-
oriented systems by orthogonal wavelets with com-
pact support. IEEE Transactions on Circuits and Sys-
tems I: Regular Papers, 52(2):427–442.
Mzyk, G. (2007). A censored sample mean approach
to nonparametric identification of nonlinearities in
Wiener systems. IEEE Transactions on Circuits and
Systems – II: Express Briefs, 54(10):897–901.
Mzyk, G. (2010). Parametric versus nonparametric ap-
proach to Wiener systems identification. Lecture
Notes in Control and Information Sciences, 404:111–
125.
Mzyk, G. (2012). Nonparametric recovering of nonlinear-
ity in Wiener-Hammerstein systems. In Proceedings
of the 9th International Conference on Informatics in
Control, Automation and Robotics, ICINCO, Rome,
Italy, pages 439–445. IEEE.
Mzyk, G. (2014). Combined Parametric-Nonparametric
Identification of Block-Oriented Systems. Lecture
Notes in Control and Information Sciences 454.
Springer.
Mzyk, G. and Wachel, P. (2017). Kernel-based identifi-
cation of Wiener-Hammerstein system. Automatica,
83:275–281.
Nadaraya, E. (1964). On estimating regression. Teoriya
Veroyatnostei i ee Primeneniya, 9(1):157–159.
Narendra, K. and Gallman, P. G. (1966). An iterative
method for the identification of nonlinear systems us-
ing the Hammerstein model. IEEE Transactions on
Automatic Control, 11:546–550.
Pawlak, M., Hasiewicz, Z., and Wachel, P. (2007). On non-
parametric identification of Wiener systems. IEEE
Transactions on Signal Processing, 55(2):482–492.
Pintelon, R. and Schoukens, J. (2004). System Identifica-
tion: a Frequency Domain Approach. Wiley-IEEE
Press.
Rochdi, Y., Giri, F., Gning, J., and Chaoui, F. (2010). Iden-
tification of block-oriented systems in the presence
of nonparametric input nonlinearities of switch and
backlash types. Automatica, 46(5):864–877.
Ruppert, D., Wand, M., and Carroll, R. (2003). Semipara-
metric Regression, volume 12. Cambridge University
Press.
´
Sliwi
´
nski, P. (2013). Nonlinear System Identification by
Haar Wavelets. Lecture Notes in Statistics 210.
Springer.
Stone, C. (1982). Optimal global rates of convergence for
nonparametric regression. The Annals of Statistics,
10(4):1040–1053.
Wachel, P. and Mzyk, G. (2016). Direct identification of the
linear block in Wiener system. International Journal
of Adaptive Control and Signal Processing, 30(1):93–
105.
Wand, M. and Jones, H. (1995). Kernel Smoothing. Chap-
man and Hall, London.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
698