Security for Distributed Deep Neural Networks: Towards Data
Confidentiality & Intellectual Property Protection
Laurent Gomez
1
, Marcus Wilhelm
2
, Jos
´
e M
´
arquez
3
and Patrick Duverger
4
1
SAP Security Research, SAP Global Security, France
2
Hasso Plattner Institute, University of Potsdam, Germany
3
SAP Portfolio Strategy & Technology Adoption, SAP SE, Germany
4
Logistic & IT Services, City of Antibes Juan-les-Pins, France
Keywords:
Distributed Systems, Neural Networks, Intellectual Property, Data Protection & Privacy, Fully Homomorphic
Encryption.
Abstract:
Current developments in Enterprise Systems observe a paradigm shift, moving the needle from the backend to
the edge sectors of those; by distributing data, decentralizing applications and integrating novel components
seamlessly to the central systems. Distributively deployed AI capabilities will thrust this transition.
Several non-functional requirements arise along with these developments, security being at the center of the
discussions. Bearing those requirements in mind, hereby we propose an approach to holistically protect dis-
tributed Deep Neural Network (DNN) based/enhanced software assets, i.e. confidentiality of their input &
output data streams as well as safeguarding their Intellectual Property.
Making use of Fully Homomorphic Encryption (FHE), our approach enables the protection of Distributed
Neural Networks, while processing encrypted data. On that respect we evaluate the feasibility of this solution
on a Convolutional Neuronal Network (CNN) for image classification deployed on distributed infrastructures.
1 INTRODUCTION
1.1 Motivation
Until now, the backend (on-prem & cloud) deploy-
ments were considered as the single source of truth &
unique point of access in regards of Enterprise Sys-
tems (ES). Nevertheless, a paradigm shift has been
recently observed, by the deployment of ES assets to-
wards the Edge sectors of the landscapes; by distribut-
ing data, decentralizing applications, de-abstracting
technology and integrating edge components seam-
lessly to the central backend systems.
Capitalizing on recent advances on High Perfor-
mance Computing along with the rising amounts of
publicly available labeled data, Deep Neural Net-
works (DNN), as an implementation of AI, have and
will revolutionize virtually every current application
domain as well as enable novel ones like those on au-
tonomous, predictive, resilient, self-managed, adap-
tive, and evolving applications.
1.2 Problem Statement
Independant Software Vendors aim to protect both:
data and the Intellectual Property of their AI-based
software assets, deployed on potentially unsecure
edge hardware & platforms (Goodfellow, 2018).
The deployment of data processing capabilities
throughout Distributed Enterprise Systems rises sev-
eral security challenges related to the protection of in-
put & output data (Parliament and Council, 2016) as
well as of software assets.
In the specific context of distributed intelligence,
DNN based/enhanced software will represent key in-
vestments in infrastructure, skills and governance, as
well as in the acquisition of data and talents. The
software industry is therefore in the direct need to
safeguard these strategic investments by enforcing the
protection of this new form of Intellectual Property.
1.3 State-of-the-Art
Security of Deep Neural Networks is a current re-
search topic taking advantage of two major crypto-
graphic approaches: variants of Fully Homomorphic
Gomez, L., Wilhelm, M., Márquez, J. and Duverger, P.
Security for Distributed Deep Neural Networks: Towards Data Confidentiality Intellectual Property Protection.
DOI: 10.5220/0007922404390447
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 439-447
ISBN: 978-989-758-378-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
439

Encryption/FHE (Gentry, 2009) and Secure Multi-
Party Computation/SMC (Cramer et al., 2015). While
FHE techniques allow addition and multiplication on
encrypted data, SMC enables arithmetic operations
on data shared across multi-parties.
Several approaches can be found in the literature,
at different phases of the development and deploy-
ment of DNNs.
Secure Training. Secure DNN training has been
addressed using FHE (Graepel et al., 2012) and SMC
(Shokri and Shmatikov, 2015), disregarding protec-
tion once the trained model is to be productively de-
ployed. Other Machine Learning models such as lin-
ear and logistic regressions have also been trained in a
secure way in (Mohassel and Zhang, 2017). In those
approaches, confidentiality of training data is guaran-
teed, while runtime protection (i.e. input, model, out-
put) is out of scope.
Processing on Encrypted Data. At processing
phase, SMC has led to cooperative solutions where
several devices work together to obtain federated in-
ferences (Liu et al., 2017), not supporting deployment
of the trained DNN to trusted decentralized systems.
DNN processing on FHE encrypted data is covered
in CryptoNets (Gilad-Bachrach et al., 2016) More
recently, in (Boemer et al., 2018), the authors pro-
posed a privacy-preserving framework for deep learn-
ing, making use of the SEAL (SEAL, 2018) FHE li-
brary. While disclosure of data at runtime is prevented
in these solutions, protection of DNN models remains
out of the scope.
Intellectual Property Protection of DNN Model.
In (Uchida et al., 2017), the authors tackles IP pro-
tection of DNN models through model watermarking.
While infringement can be detected with this method,
it can not be prevented. Furthermore, runtime protec-
tion of input, model and output are out of scope.
To the best of our knowledge, no other publication
has holistically tackled the protection of both trained
DNN models and data, targeting distributed untrusted
systems.
1.4 Data & Intellectual Property
Protection for Deep Neural
Networks
In this paper we propose a novel approach
for the Intellectual Property Protection of DNN-
based/enhanced software while enabling data protec-
tion at processing time, making use of concepts such
as Fully Homomorphic Encryption (FHE).
Once trained, DNN model parameters (i.e.
weights, biases) are encrypted homomorphically. The
resulting (encrypted) DNN can be distributed across
untrusted landscapes, preserving its IP while mitigat-
ing the risk of reverse engineering. At runtime, FHE-
encrypted insights from encrypted input data are pro-
duced by the homomorphically encrypted DNN. Con-
fidentiality of both trained DNN, input and output
data will be therefore guaranteed.
In this paper, we evaluate the overall performance
(e.g. CPU, memory, disk usage) along with the accu-
racy of encrypted DNNs.
This paper is organized as follows: Section 2 de-
tails the fundamentals of our approach. Section 3 pro-
vides an overview of our solution. In Sections 3.3
and 4, we present the architecture and evaluation, con-
cluding with an outlook in Section 5.
2 FUNDAMENTALS
2.1 Deep Neural Network
DNNs are composed of L transformation layers:
1. An input layer, the tensor of input data X
2. L − 1 hidden layers, mathematical computations
transforming X sequentially.
3. An output layer, the tensor of output data Y.
We denote the output of layer i as a tensor A
[i]
,
with A
[0]
= X,and A
[L]
= Y . Tensors can have differ-
ent sizes and number of dimensions.
Each layer A
[i]
depends on the mathematical com-
putations performed at the previous layer A
[i−1]
. At
each layer A
[i]
, two types of function can be com-
puted:
• Linear: involving polynomial operations.
• Non-linear, involving non-linear operations, so
called activation function, such as max, exp,
division, ReLU, or Sigmoid.
2.1.1 Linear Computation Layer
For the sake of clarity, we exemplify the inner linear
computation with a Fully Connected (FC) layer, as
depicted in Figure 1.
A Fully Connected layer, noted A
[i]
, is composed
of n parallel neurons, performing a R
n
→ R
n
transfor-
mation (see Figure 1). We define:
a
[i]
=
h
a
[i]
0
. . . a
[i]
k
. . . a
[i]
N
i
T
as the output of layer A
[i]
;
SECRYPT 2019 - 16th International Conference on Security and Cryptography
440

Figure 1: Fully Connected layer with Activation Function.
z
[i]
=
h
z
[i]
0
. . . z
[i]
k
. . . z
[i]
N
i
T
as the linear output of layer
A
[i]
; (z
[i]
= a
[i]
if there is no activation function)
b
[i]
=
h
b
[i]
0
. . . b
[i]
k
. . . b
[i]
N
i
T
as the bias for layer A
[i]
;
W
[i]
=
h
w
[i]
0
. . . w
[i]
k
. . . w
[i]
N
i
T
as the weights for layer
A
[i]
.
Neuron k performs a linear combination of the
output of the previous layer a
[i−1]
multiplied by the
weight vector w
[i]
k
and shifted with a bias scalar b
[i]
k
,
obtaining the linear combination z
[i]
k
:
z
[i]
k
=
M
∑
l=0
w
[i]
k
[l] ∗ a
[i−1]
l
!
+ b
[i]
k
= w
[i]
k
∗ a
[i−1]
+ b
[i]
k
(1)
Vectorizing the operations for all the neurons in
layer A
[i]
we obtain the dense layer transformation:
z
[i]
= W
[i]
∗ a
[i−1]
+ b
[i]
(2)
where W and b are the parameters for layer A
[i]
.
2.1.2 Activation Functions
Activation functions are the major source of non-
linearity in DNNs. They are performed element-wise
(R
0
→ R
0
, thus easily vectorized), and are gener-
ally located after linear transformations such as Fully
Connected layers.
a
[i]
k
= f
act

z
[i]
k

(3)
Several activation functions have been proposed in
the literature but Rectified Linear Unit (ReLU) is cur-
rently considered as the most efficient activation func-
tion for DL. Several variants of ReLU exist, such as
Leaky ReLU(Maas et al., 2013), ELU(Clevert et al.,
2015) or its differentiable version Softplus.
ReLU(z) = z
+
= max(0, z)
So f t plus(z) = log(e
z
+ 1)
(4)
2.2 Homomorphic Encryption
While preserving data privacy, Homomorphic En-
cryption (HE) schemes allow certain computations on
ciphertext without revealing neither its inputs nor its
internal states. Gentry (Gentry, 2009) first proposed
a Fully Homomorphic Encryption (FHE) scheme,
which theoretically could compute any kind of arith-
metic circuit, but is computationally intractable in
practice. FHE evolved into more efficient schemes
preserving addition and multiplication over encrypted
data, such as BGV (Brakerski et al., 2011), FV (Fan
and Vercauteren, 2012) or CKKS (Cheon et al., 2018),
allowing approximations of multiplicative inverse,
exponential and logistic function, or discrete Fourier
transformation. Similar to asymmetric encryption, a
public-private key pair (pub, priv) is generated.
Definition 1. An encryption scheme is called homo-
morphic over an operation  if it supports the follow-
ing
Enc
pub
(m) =
h
m
i
pub
, ∀m ∈ M
h
m
1
 m
2
i
pub
=
h
m
1
i
pub

h
m
2
i
pub
, ∀m
1
, m
2
∈ M
where Enc
pub
is the encryption algorithm and M is
the set of all possible messages.
Definition 2. Decryption is performed as follows
Enc
pub
(m) =
h
m
i
pub
, ∀m ∈ M
Dec
priv
(
h
m
i
pub
) = m
where Dec
priv
is the decryption algorithm and M is
the set of all possible messages.
2.3 Challenges
Even though HE schemes seem theoretically promis-
ing, their usage comes with several drawbacks, par-
ticularly when applied to Deep Learning.
2.3.1 Noise Budget
In Gentry’s lattice-based HE schemes(Gentry, 2009)
and subsequent variants of it, ciphertexts contain a
small term of random noise drawn from some prob-
ability distribution. To estimate the current magni-
tude of noise, a noise budget can be calculated, that
starts as a positive integer, decreases with subsequent
operations and reaches 0 exactly when the ciphertext
becomes indecipherable. The noise budget is more
strongly affected by multiplications as by additions.
In order to cope with that challenge, encryption
parameters can be adjusted accordingly to the re-
quired computation depth of an arithmetic circuit.
Security for Distributed Deep Neural Networks: Towards Data Confidentiality Intellectual Property Protection
441

2.3.2 FHE Libraries and APIs
Multiple FHE libraries are available (Halevi and
Shoup, 2014), (PALISADE, 2018), (SEAL, 2018),
(Ducas and Micciancio, 2015). Depending on the
supported HE schemes, those libraries show notice-
able difference on performance (e.g. computational,
memory consumption), on supported operations type
(e.g. addition, multiplication, negative, square, di-
vision), datatype (e.g. floating point, integer), and
chipset infrastructure (e.g. CPU, GPU).
In addition, and regardless on their level of matu-
rity and performance, HE libraries can be configured
through several encryption parameters such as:
• Polynomial degree or modulus: which determines
the available noise budget and strongly affects the
performance.
• Plaintext modulus: which is mostly associated to
the size of input data.
• Security parameter: which sets the reached level
of security in bits of the cryptosystem (e.g. 128,
192, 256-bit security level).
Fine-tuning of those encryption parameters en-
ables developers to optimize the performance of en-
cryption and encrypted operations. The selection of
the right encryption parameters depends on the size
of the plaintext data, targeted accuracy loss or level of
security.
2.3.3 Linear Function Support Only
By construction, linear functions, composed of ad-
dition and multiplication operations, are seamlessly
protected by FHE. But, non-linear activation func-
tions such as ReLU or Sigmoid require approximation
to be computed with FHE schemes.
The challenge lies on the transformation of acti-
vation functions into polynomial approximations sup-
ported by HE schemes. We elaborate more on approx-
imation of activation functions in Section 3.2.
2.3.4 Supported Plaintext Type
The vast majority of HE schemes allow operations
on integers (Halevi and Shoup, 2014; SEAL, 2018)
, while others use booleans (Chillotti et al., 2018) or
floating point numbers (Cheon et al., 2018; SEAL,
2018). In the case of integer supporting HE schemes,
rational numbers can be approximated using fixed-
point arithmetic by scaling with a scaling factor and
rounding.
2.3.5 Performance
FHE schemes are computationally expensive and
memory consuming. In addition, ciphertexts are of-
ten significantly bigger than plaintexts and thus use
more memory and disk space.
Even if in the past years the performance of
FHE made it impractical, recent FHE schemes show
promising throughput. New FHE libraries take also
advantage of GPU acceleration.
In addition, modern implementations of HE
schemes such as HELib (Halevi and Shoup, 2014),
SEAL (SEAL, 2018), or PALISADE (PALISADE,
2018) benefit from Single Instruction Multiple Data
(SIMD), allowing multiple integers to be stored in
a single ciphertext and vectorizing operations, which
can accelerate certain applications significantly.
3 APPROACH
As introduced in Section 1.2, the delivery of DNN-
enriched insights come at a cost. ISVs aim to guar-
antee data security, together with the IP protection of
their DNN-based software assets, deployed on poten-
tially unsecure edge hardware & platforms. In order
to achieve those security objectives on DNN, we uti-
lize FHE schemes to operate on ciphertext at runtime.
Consequently, secure training of DNN is out of
scope of our approach as we focus on runtime exe-
cution. We assume that DNN training already pre-
serves both data privacy and confidentiality, and the
resulting trained model. Once a model is trained, as
discussed in Section 2.1.1, we obtain a set of param-
eters for each DNN layer; i.e weights W
[i]
and biases
b
[i]
. Those parameters constitute the IP to be pro-
tected when deploying a DNN to distributed systems.
3.1 Linear Computation Layer
Protection
Our approach is agnostic from the type of layer.
In (Gomez et al., 2018), we detail the encryp-
tion of layers such as Convolutional Layer or
Batch Normalization. For sake of simplicity,
we exemplify the encryption of DNN layers pa-
rameters on FC layers. Since FC are simply
a linear transformation on the previous layer’s
outputs, encryption is achieved straightforwardly as
SECRYPT 2019 - 16th International Conference on Security and Cryptography
442

follows
D
z
[i]
E
pub
=
D
W
[i]
∗ a
[i−1]
+ b
[i]
E
pub
=
D
W
[i]
E
pub
∗
D
a
[i−1]
E
pub
+
D
b
[i]
E
pub
(5)
3.2 Activation Function Protection
Due to their innate non-linearity, activation func-
tions need to be approximated with polynomials to be
encrypted with FHE. Several approaches have been
elaborated in the literature. In (Livni et al., 2014) and
(Gilad-Bachrach et al., 2016), the authors proposed to
use a square function as activation function. The last
layer, a sigmoid activation function, is only applied
during training. Chabanne et al. used Taylor polyno-
mials around x = 0, studying performance based on
the polynomial degree (Chabanne et al., 2017). In
(Hesamifard et al., 2017), Hesamifard et al. approx-
imate instead the derivative of the function and then
integrate to obtain their approximation.
Regardless on the approximation technique, we
denote activation function f
act
() approximation as
f
act
() ≈ f
approxact
() (6)
By construction, we have
D
a
[i]
k
E
pub
=
D
f
act

z
[i]
k
E
pub
≡
D
f
approxact

z
[i]
k
E
pub
(7)
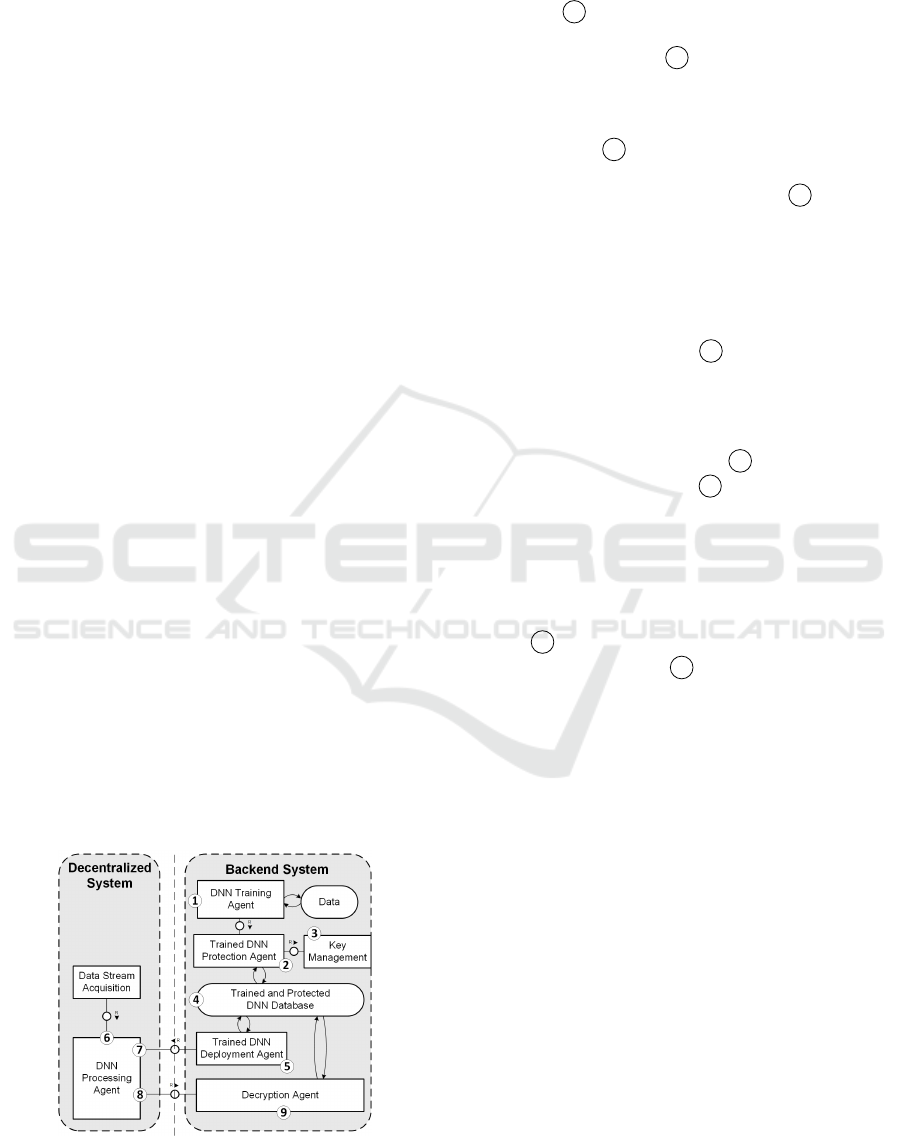
3.3 Architecture
In this section we outline the architecture of our IP
protection system, as depicted in Figure 2.
Figure 2: Overall Architecture.
3.3.1 Encryption of Trained DNN
In the backend, a DNN is trained within a DNN Train-
ing Agent, 1 . The outcome of the training (NN ar-
chitecture and parameters) is pushed to the Trained
DNN Protection Agent, 2 . Alternatively, an already
trained DNN can be imported directly into the Pro-
tection Agent. The DNN Protection Agent generates
a Fully Homomorphic key pair from the Key Genera-
tor component, 3 . The DNN is then encrypted and
stored together with its homomorphic key pair in the
Trained and Protected DNN Database, 4 .
3.3.2 Deployment of Trained and Protected
DNN
At the deployment phase, the Trained DNN Deploy-
ment Agent deploys the DNN on distributed systems,
together with its public key, 5 .
3.3.3 DNN Processing
On the distributed system, data is collected by a Data
Stream Acquisition component, 6 , and forwarded to
the DNN Processing Agent, 7 . The input layer does
not involve any computation, and therefore can be
seamlessly FHE encrypted as follows:
X
encryption
−−−−−−→ Enc
pub
(X) =
h
X
i
pub
(8)
Encrypted inferences are sent to the Decryption
Agent, 8 , for their decryption using the private key
associated to the DNN, 9 . FHE encryption propa-
gates across the DNN layers, from the input to the out-
put layer. By construction, the output layer is there-
fore encrypted homomorphically.
The decryption of the last layer’s output Y is done
with the private key priv:
D
A
[L]
E
pub
decryption
−−−−−−→ Dec
priv

D
A
[L]
E
pub

= Y (9)
The Intellectual Property of the DNN, together
with the input & output results, is protected from any
disclosure on the distributed system throughout the
entire process.
4 EVALUATION
As detailed in Section 2.3, FHE introduces addi-
tional computational costs at each step of the DNN
life-cycle. In this section, we evaluate performance
overhead from computation time, memory load and
Security for Distributed Deep Neural Networks: Towards Data Confidentiality Intellectual Property Protection
443

diskusage perspectives at DNN model and processing
encryption and output decryption.
4.1 Hardware Setup
As backend, we use a NVIDIA DGX-1
1
server, em-
powered with 8 Tesla V100 GPUs. This machine is
theoretically not resource-constrained (computation
& memory). We reasonably neglect the impact of the
performance overhead introduced by FHE on DNN
trained model encryption and output decryption.
We deploy and execute our encrypted DNN on a
NVIDIA Jetson-TX2
2
. Powered by NVIDIA Pascal
architecture, this platform embeds 256 CUDA cores,
CPU HMP Dual Denver 22 MB L2 + Quad ARM®
A572 MB L2, and 8 GB of memory. This platform
gets closer to the hardware configuration of a Dis-
tributed Enterprise System.
4.2 Software Setup
DNN Model. As demonstrated in Section 3, our ap-
proach is fully agnostic from NN topology, or imple-
mentation. For the sake of our evaluation, involving
several modifications to the NN model, we choose a
simple CNN classifier
3
, implemented with the Keras
library
4
. Two datasets have been used in our ex-
periment: CIFAR10
5
, for image classification, and
MNIST
6
for handwritten digits classification.
As depicted in Figure 3, we distinguish two main
parts in this CNN: a feature extractor and a classifier.
The feature extractor reduces the amount of informa-
tion from the input image, into a set of high level and
more manageable features. This step facilitates the
subsequent classification of the input data.
Composed of four layers, [FC → ReLU → FC →
Softmax], the classifier categorizes the input data ac-
cording to the extracted features, and outputs discrete
probability distribution over 10 classes of objects.
As reference point, we evaluate key performance
figures at model training and processing time without
encryption. Once trained, the size of the CNN plain-
text model is 9.6Mb. On Jetson TX2, single unen-
crypted image classification is computed on average
in 89.1ms.
1
https://www.nvidia.com/en-us/data-center/dgx-1/
2
https://www.nvidia.com/en-us/autonomous-
machines/embedded-systems-dev-kits-modules/
3
https://github.com/keras-
team/keras/blob/master/examples/cifar10 cnn.py
4
https://keras.io
5
https://www.cs.toronto.edu/ kriz/cifar.html
6
http://yann.lecun.com/exdb/mnist/
Figure 3: Keras Convolutional Neural Network.
FHE Library. As introduced in section 2.3, several
libraries are available for FHE. We use SEAL (SEAL,
2018) C library from Microsoft Research running on
CPU. This choice is motivated by the library’s per-
formance, support of multiple schemes such as BGV
(Brakerski et al., 2011), stability, and documentation.
The use of SEAL, implemented in C++, with the
Keras Python library requires some engineering ef-
forts. To enable both fast performance of the native
C++ library and rapid prototyping using Python, we
use Cython
7
.
We conduct our evaluation with the BGV scheme
(Brakerski et al., 2011), utilizing the integer encod-
ing with SIMD support. To handle the floating-point
DNN parameters, we use fixed-point arithmetic with
a fixed scaling factor, similarly to CryptoNets(Gilad-
Bachrach et al., 2016). This has no noticeable im-
pact on the classification accuracy, if a suitable scal-
ing factor is applied. The SIMD operations allow for
optimized performance through vectorization.
4.3 Linearization
We tackle the problem of linearization of the ReLU
functions following approaches: we approximate it
with a modified square function, and we skip activa-
tion function. The modified square function x
2
+ 2x
(see Figure 5) is derived from the ReLU approxima-
tion proposed in (Chabanne et al., 2017). In order to
optimize the computation of that function on cipher-
texts, we used simpler coefficients.
In order evaluate the impact of these approaches,
we trained the CNN on the CIFAR10 and MNIST
datasets, replacing the last ReLU activation. Depicted
in Figure 4, we report the accuracy loss. Both approx-
imations have merely a minor impact on the output
classification accuracy.
7
https://cython.org/
SECRYPT 2019 - 16th International Conference on Security and Cryptography
444

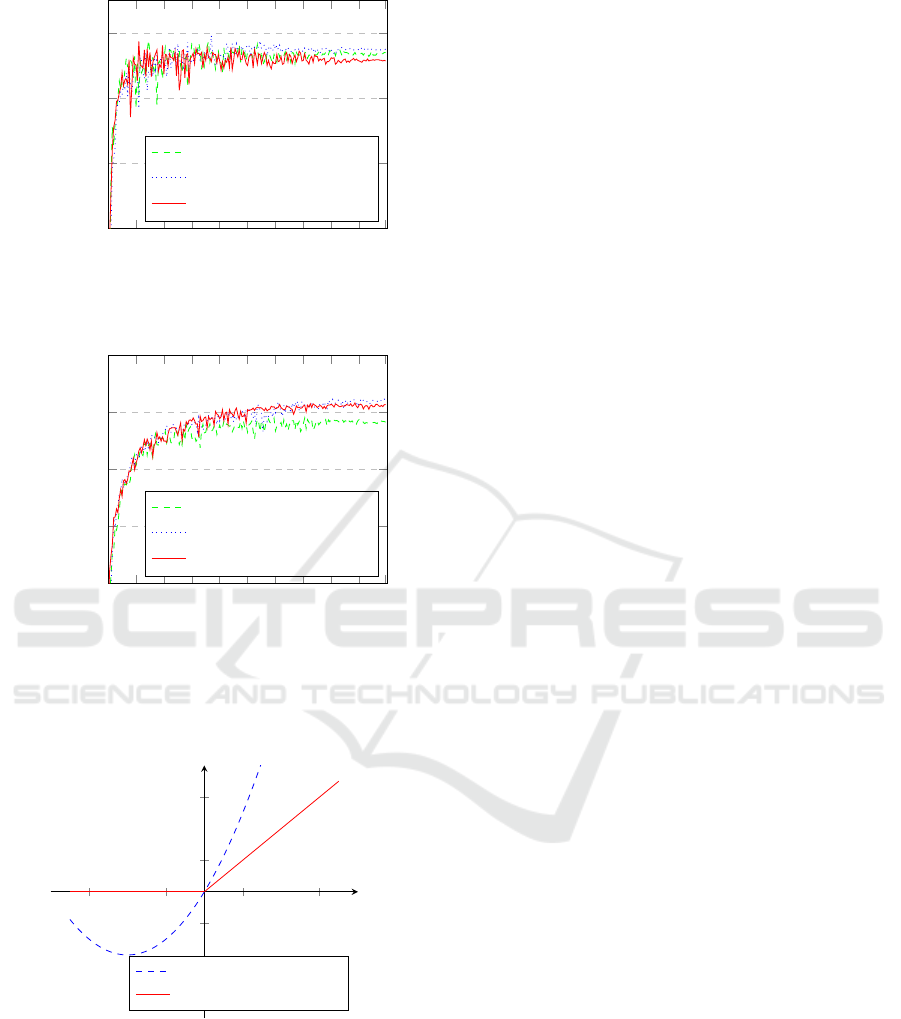
0 20 40
60
80 100120140
160
180199
0.96
0.97
0.98
0.99
Epoch
Validation accuracy
Original model
No activation function
x
2
+ 2x
(a) Experiment on MNIST dataset.
0 20 40
60
80 100120140
160
180199
0.5
0.6
0.7
0.8
0.9
Epoch
Validation accuracy
Original model
No activation function
x
2
+ 2x
(b) Experiment on CIFAR10 dataset.
Figure 4: Classification Accuracy with ReLU Approxima-
tion.
−1.5 −0.5 0.5 1.5
−1.5
−0.5
0.5
1.5
x
y
Square Approximation
ReLu
Figure 5: ReLU Approximation as Square Function.
Skipping the last activation function shows good
results on this simple CNN, but we do not want to
generalize to any other DNN or dataset.
4.4 Experimentation Results
4.4.1 Model & Data Protection
Intellectual Property-wise, we consider the feature ex-
tractor as of minor importance, as CNNs generally use
state of the art feature extractor. The IP of the model
rather lies in the parameters, weights and bias, of the
trained classifier. For that reason, we encrypt the clas-
sifier only, as a first step towards full model encryp-
tion, as depicted in Figure 3. To better understand
the impact of computation depth, we also complete
our evaluation with the encryption of the last FC layer
only.
Confidentiality-wise, we evaluate the impact of
extracted features encryption by comparing process-
ing performance on an encrypted model with plaintext
and encrypted feature extractor outputs.
As depicted in Figure 3, we evaluate our approach
on three modified versions of the model:
• Last FC Layer Encrypted
• Full Classifier Encrypted with no Activation
Function
• Full Classified Encrypted with our Modified
Square Activation Function
Confidentiality-wise, we evaluate the impact of
extracted features encryption by comparing process-
ing performance on an encrypted model with plaintext
and encrypted feature extractor outputs.
In order to optimize our approach, we omit the
Softmax layer within the classifier. This layer does
not have any influence on the classification results,
as Softmax layer is mostly required at training phase,
to normalize network outputs probability distribution,
for more consistent loss calculations.
The overall experiment as described in section 3.3
has been applied 5 times on each model. We report
average evaluation metrics for each step: model en-
cryption, processing encryption and decryption.
4.4.2 DNN Model Encryption
Each trained CNN model is encrypted on DGX-1’s
CPU. In Table 1, we depict the resource consumption
average on the following metrics:
• Time to Compute: Time to encrypt the model.
• Model Size: Size of resulting encrypted model.
• Memory Load: Overall memory usage for model
encryption.
We target three security levels: 128, 192, and 256-
bits. For each of those, we optimize SEAL parame-
ters as introduced in section 2.3, maximizing perfor-
mance, and minimizing leftover noise budget.
Security for Distributed Deep Neural Networks: Towards Data Confidentiality Intellectual Property Protection
445

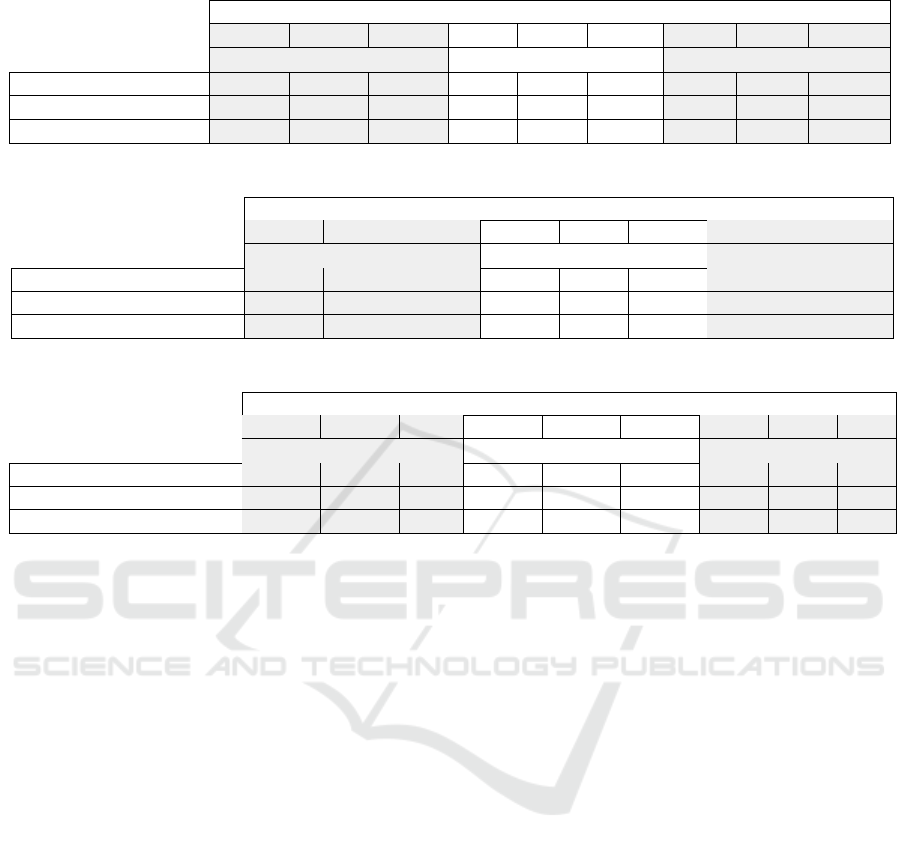
Table 1: Model Encryption.
Achieved Security Level (bits)
128 192 256 128 192 256 128 192 256
Full Classifier - x
2
+ 2x Full Classifier - No Act. Last Layer
Time to Compute (s) 256.7 191.5 212.6 86.9 78.0 96.0 3.4 3.4 7.3
Model Size 11G 6.4G 11G 2.5G 4.4G 2.5G 79Mb 79Mb 158Mb
Memory (Mb) 2257.9 1112.4 2389.5 557.9 459.2 566.1 300.6 301.4 324.2
Table 2: Runtime Encryption with Plaintext Input.
Achieved Security Level (bits)
128 192 256 128 192 256 128 192 256
Full Classifier - x
2
+ 2x Full Classifier - No Act. Last Layer
Time to Compute (s) 287.2 174.6 1221.3 43.7 32.9 90.2 2.1 2.1 4.5
Memory Load (Mb) 4683.1 2924.3 4899.2 1162.5 869.2 2342.3 53.9 54.0 117.7
Remaining Noise Budget 221.6 80.2 88.8 91.4 23.8 16.2 58.8 20.2 60.2
Table 3: Runtime Encryption with Encrypted Input.
Achieved Security Level (bits)
128 192 256 128 192 256 128 192 256
Full Classifier - x
2
+ 2x Full Classifier - No Act. Last Layer
Time to Compute (s) 2902.6 1048.6 5627 367.1 272.2 835.9 19.2 19.2 40.2
Memory Load (Mb) 5047.8 5809 4906 2314.8 1733.7 4644.5 119.5 118.5 253
Remaining Noise Budget 206.0 65.0 76.0 79.0 11.0 3.0 45.0 10.0 52.0
Compared to the plaintext model size (9.6Mb), en-
crypted model size increases by a factor of 8,22 in the
best case.
4.4.3 DNN Processing Encryption
The three encrypted CNN models deployed on Jetson-
TX2 for CPU based encrypted processing. At this
stage, we evaluate the following metrics
• Time to compute: Processing time for an en-
crypted classification.
• Memory: Memory usage for encrypted classifica-
tion.
• Remaining Noise Budget: At the end of process-
ing encryption, we evaluate the remaining noise
budget, which determines if additional encryption
operations could be performed on the output vec-
tor.
In Table 2 and Table 3, we depict the performance
of encrypted processing with plaintext and encrypted
previous layer outputs. We study the impact of confi-
dentality preservation of the preceding layer outputs.
SEAL library supports secure computation over plain-
text and ciphertext producing ciphertext. As a conse-
quence, output of the last MaxPooling2D layer can be
processed in FHE-encrypted Fully Connected layer.
Secure computation between plaintext and ciphertext
has a lower impact on performance.
We observe a slight performance improvement on
time to compute and memory between 128 and 192-
bit security level. This is due to the FHE parame-
ters optimization as described in Section 4.4.2, where
initial noise budget is oversized for 128-bit security
level, which has a direct impact to performance.
Experiment results show that, depending on the
level of achieved security, and targeted scenario, we
can achieve at best encrypted classification in 2.1s (for
128 level security and only one layer encrypted).
4.4.4 Decryption
Following our approach, encrypted output are de-
crypted by the backend, on DGX-1. We therefore
consider decryption as not computationally expen-
sive, compared to encryption. Results are available
in Table 4.
5 CONCLUSION
In this paper, we discuss and evaluate a holistic ap-
proach for the protection of distributed Deep Neural
Network (DNN) enhanced software assets, i.e. confi-
dentiality of their input & output data streams as well
as safeguarding their Intellectual Property. On that
matter, we take advantage of Fully Homomorphic En-
cryption (FHE). We evaluate the feasibility of this so-
SECRYPT 2019 - 16th International Conference on Security and Cryptography
446

Table 4: Decryption - Performance.
Achieved Security Level (bits)
128 192 256 128 192 256 128 192 256
Full Classifier - x
2
+ 2x Full Classifier - No Act. Last Layer
Time to Compute (s) 2.9 1.7 3.2 0.6 0.6 1.0 0.2 0.1 0.2
Memory Load (Mb) 963.8 397.4 2062.5 123.4 73.4 267.1 17.8 17.8 38.7
lution on a Convolutional Neural Network (CNN) for
image classification.
Our evaluation on NVIDIA DGX-1 and Jetson-
TX2 shows promising results on the CNN image clas-
sifier. Performances vary from 2.1s for an encrypted
classification, with only 53.9Mb consumed memory,
up to 1h33m with almost 5Gb of consumed memory.
REFERENCES
Boemer, F., Ratner, E., and Lendasse, A. (2018). Parameter-
free image segmentation with SLIC. Neurocomputing,
277:228–236.
Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2011).
Fully homomorphic encryption without bootstrap-
ping. Cryptology ePrint Archive, Report 2011/277.
Chabanne, H., de Wargny, A., Milgram, J., Morel, C., and
Prouff, E. (2017). Privacy-preserving classification
on deep neural network. IACR Cryptology ePrint
Archive, 2017:35.
Cheon, J. H., Han, K., Kim, A., Kim, M., and Song, Y.
(2018). Bootstrapping for approximate homomor-
phic encryption. IACR Cryptology ePrint Archive,
2018:153.
Chillotti, I., Gama, N., Georgieva, M., and Izabach
`
ene, M.
(2018). Tfhe: Fast fully homomorphic encryption
over the torus. Cryptology ePrint Archive, Report
2018/421. https://eprint.iacr.org/2018/421.
Clevert, D.-A., Unterthiner, T., and Hochreiter, S.
(2015). Fast and accurate deep network learning
by exponential linear units (elus). arXiv preprint
arXiv:1511.07289.
Cramer, R., Damg
˚
ard, I. B., et al. (2015). Secure multiparty
computation. Cambridge University Press.
Ducas, L. and Micciancio, D. (2015). Fhew: bootstrapping
homomorphic encryption in less than a second. In An-
nual International Conference on the Theory and Ap-
plications of Cryptographic Techniques, pages 617–
640. Springer.
Fan, J. and Vercauteren, F. (2012). Somewhat practical fully
homomorphic encryption. Cryptology ePrint Archive,
Report 2012/144.
Gentry, C. (2009). A Fully Homomorphic Encryption
Scheme. PhD thesis, Stanford University, Stanford,
CA, USA. AAI3382729.
Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K.,
Naehrig, M., and Wernsing, J. (2016). Cryptonets:
Applying neural networks to encrypted data with high
throughput and accuracy. In International Conference
on Machine Learning, pages 201–210.
Gomez, L., Ibarrondo, A., M
´
arquez, J., and Duverger,
P. (2018). Intellectual property protection for dis-
tributed neural networks - towards confidentiality of
data, model, and inference. In Samarati, P. and Obai-
dat, M. S., editors, Proceedings of the 15th Interna-
tional Joint Conference on e-Business and Telecom-
munications, ICETE 2018 - Volume 2: SECRYPT,
Porto, Portugal, July 26-28, 2018., pages 313–320.
SciTePress.
Goodfellow, I. (2018). Security and privacy of machine
learning. RSA Conference.
Graepel, T., Lauter, K., and Naehrig, M. (2012). Ml con-
fidential: Machine learning on encrypted data. In In-
ternational Conference on Information Security and
Cryptology, pages 1–21. Springer.
Halevi, S. and Shoup, V. (2014). Algorithms in helib. In
International cryptology conference, pages 554–571.
Springer.
Hesamifard, E., Takabi, H., and Ghasemi, M. (2017).
Cryptodl: Deep neural networks over encrypted data.
CoRR, abs/1711.05189.
Liu, J., Juuti, M., Lu, Y., and Asokan, N. (2017). Oblivi-
ous neural network predictions via minionn transfor-
mations. In Proceedings of the 2017 ACM SIGSAC
Conference on Computer and Communications Secu-
rity, pages 619–631. ACM.
Livni, R., Shalev-Shwartz, S., and Shamir, O. (2014). On
the computational efficiency of training neural net-
works. In Ghahramani, Z., Welling, M., Cortes, C.,
Lawrence, N. D., and Weinberger, K. Q., editors, Ad-
vances in Neural Information Processing Systems 27,
pages 855–863. Curran Associates, Inc.
Maas, A. L., Hannun, A. Y., and Ng, A. Y. (2013). Rec-
tifier nonlinearities improve neural network acoustic
models. In Proc. icml, volume 30, page 3.
Mohassel, P. and Zhang, Y. (2017). Secureml: A system
for scalable privacy-preserving machine learning. In
Security and Privacy (SP), 2017 IEEE Symposium on,
pages 19–38. IEEE.
PALISADE (2018). The palisade lattice cryptography li-
brary.
Parliament, E. and Council (2016). General data protection
regulation.
SEAL (2018). Simple Encrypted Arithmetic Library (re-
lease 3.1.0). https://github.com/Microsoft/SEAL. Mi-
crosoft Research, Redmond, WA.
Shokri, R. and Shmatikov, V. (2015). Privacy-preserving
deep learning. In Proceedings of the 22nd ACM
SIGSAC conference on computer and communications
security, pages 1310–1321. ACM.
Uchida, Y., Nagai, Y., Sakazawa, S., and Satoh, S. (2017).
Embedding watermarks into deep neural networks.
In Proceedings of the 2017 ACM on International
Conference on Multimedia Retrieval, pages 269–277.
ACM.
Security for Distributed Deep Neural Networks: Towards Data Confidentiality Intellectual Property Protection
447