Discrete-time Adaptive Regulation of Systems with Uncertain
Upper-bounded Input Delay: A State Substitution Approach
Khalid Abidi
1 a
and Hang Jian Soo
2,† b
1
Electrical Power Engineering Program, Newcastle University in Singapore, 567739, Singapore
2
National University of Singapore, 119260, Singapore
Keywords:
Adaptive Control, Discrete-time Systems, Time-delay Systems.
Abstract:
This paper proposes a discrete-time adaptive regulation approach for scalar linear time-invariant systems with
unknown, constant input time delay that has a known upper-bound, without explicitly estimating the time
delay. To cope with the unknown time delay, a state substitution is made that results in a delay free system that
simplifies the control law design. In addition, the proposed approach does not require that the system have
stable open-loop zeros. A stability analysis shows that the proposed regulator drives the system state to zero
asymptotically and simulation results are shown to verify the approach.
1 INTRODUCTION
Processes with time delays at the input (i.e. delayed
control action) are encountered in many situations re-
quiring the use of feedback control, and these delays
may have significant consequences if a controller is
not designed to compensate for them (Richard, 2003)
(Gu and Niculescu, 2003). For example, communi-
cations delays in bilateral teleoperation can cause the
force feedback loop to become unstable, possibly cre-
ating a hazard for the remote operator (Abidi et al.,
2016). In visual servoing, the computational com-
plexity of visual information processing may insert a
significant delay into the control loop that could af-
fect stability (Bjerkeng et al., 2014). Pneumatic ac-
tuators are commonly used in soft robots, where long
pneumatic lines and the compressibility of air can in-
troduce actuator delays (Skorina et al., 2017). In all
these applications it is clear that a practical controller
must be able to cope with uncertainty in the plant pa-
rameters, including the time delay.
There are two ways to approach the problem of
compensating for input time delay. The first ap-
proach explicitly recognises the need to predict the
future state of the system. To illustrate this, con-
sider a discrete-time time-invariant system x
k+1
=
f (x
k
,u
k−d
) where x
k
is the state and u
k−d
is the time-
a
https://orcid.org/0000-0002-4795-5360
b
https://orcid.org/0000-0003-4424-4755
†
MSc student with the National University of Singapore
delayed control input. Shifting this d steps ahead, i.e.
x
k+d+1
= f (x
k+d
,u
k
), it becomes obvious that in or-
der to affect the state at k+d +1 it would be desirable
to have knowledge of the future state at k + d. A rig-
orous argument for the case of linear time invariant
plants with a single input delay is found in (Mirkin
and Raskin, 2003). Examples of predictor-based con-
trol laws for linear and nonlinear plants are (Mani-
tius and Olbrot, 1979) (Abidi, 2014) and (Abidi and
Postlethwaite, 2019) respectively.
The second approach, commonly known as Art-
stein’s model reduction (Artstein, 1982), applies
specifically to linear, possibly time-varying systems
with input delay. A state substitution is used to trans-
form the original system into an equivalent delay-free
system, for which it is easier to derive a control law.
The control law for the former can then be found by
reversing the substitution. This in fact leads to the
same control laws as the first approach, but it simpli-
fies the derivation in the general case where there may
be multiple lumped and/or distributed input delays.
As this paper will show, it is also a useful starting
point for generalising to the case of uncertain plant
parameters and time delay.
To illustrate the method with a simple example
from (Richard, 2003), consider the linear system with
input delay ˙x(t) = Ax(t) + Bu(t − d). Introducing a
state substitution
z(t) = x(t) +
Z
t
t−d
e
A(t−d−τ)
Bu(τ)dτ (1)
Abidi, K. and Soo, H.
Discrete-time Adaptive Regulation of Systems with Uncertain Upper-bounded Input Delay: A State Substitution Approach.
DOI: 10.5220/0007922706990706
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 699-706
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
699

yields the equivalent delay-free system in z(t) given
by
˙z(t) = Az(t) + e
−Ad
Bu(t) (2)
The control law for the latter is simply a state-
feedback law u(t) = Kz(t) where K is chosen to sta-
bilise (A,e
−Ad
B). The control law for the original sys-
tem is then found by substituting the definition of z(t)
to get
u(t) = Kx(t) + K
Z
t
t−d
e
A(t−d−τ)
Bu(τ)dτ (3)
To cope with uncertainty in the plant parameters,
including the time delay, two paradigms are available.
The first paradigm is to make the controller robust to
the uncertainty. In delay-independent truncated pre-
dictor feedback (Wei and Lin, 2018), a state-feedback
controller is used with gains selected by a Lyapunov
equation based method which does not require knowl-
edge of the delay. However, this work assumes plant
parameters are known, and for unstable plants the
amount of delay that the method can handle is limited
(Wei and Lin, 2017). A more generally applicable but
mathematically involved alternative is to employ the
framework of robust control theory (Zhong, 2006).
The other paradigm to consider is adaptive con-
trol. Early work on adaptive controllers for time
delay systems only addressed uncertainty in the pa-
rameters but not the time delay (Ortega and Lozano,
1988)(Niculescu and Annaswamy, 2003). The reason
is that adaptive laws rely on the plant representation
being linear in the uncertain parameters, whereas the
time delay appears inside the argument of the con-
trol input. Krstic (Krstic, 2009) overcomes this by
expressing the plant dynamics in terms of the en-
tire input history over the delay interval (given by
the function u(x,t) where x parameterises a point on
the interval), and modelling the delay as a transport
PDE. Thus, the time delay can be estimated along
with other plant parameters, and used to compute a
predictor-based control law (Bresch-Pietri and Krstic,
2009). However, the resulting adaptive laws for both
time delay and parameter estimation are complicated.
Most time-delay controllers have been formulated
in a continuous-time setting, but they will almost cer-
tainly be implemented on a digital computer. Dis-
cretisation of continuous-time control laws, espe-
cially those for time-delay compensation, is fraught
with numerical pitfalls (Mirkin, 2004)(Zhong, 2004).
It may be more straightforward to design controllers
in discrete-time, for example the discrete-time APC
(Abidi et al., 2017) (Abidi and Xu, 2015). This is
a model-reference adaptive controller that achieves
reference trajectory tracking on a plant with an un-
known, constant, upper-bounded time delay. How-
ever, the model-tracking error does not vanish asymp-
totically, and its bound is dependent on the mismatch
between the delay upper-bound assumed by the con-
troller and the true delay. The adaptive law also con-
tains parameters that may be difficult to tune in prac-
tice.
This paper proposes a discrete-time adaptive regu-
lator for a scalar, linear time-invariant system with an
unknown, constant input time delay that has a known
upper-bound, without explicitly estimating the time
delay. Using an approach similar to Artstein’s model
reduction, a state substitution is devised that allows
the plant dynamics to be expressed in a delay-free
form, which facilitates derivation of a control law. In
order to apply the model reduction technique to the
case of unknown time delay, the plant dynamics and
the state substitutes are expressed in a manner that is
‘agnostic’ to the specific value of the time delay. This
also makes it possible to estimate the plant parameters
using recursive least squares, even without knowledge
of the time delay. A stability analysis shows that
the proposed regulator drives the plant state to zero
asymptotically.
2 PROBLEM DEFINITION
Consider the scalar system in continuous-time with
input delay given as
˙x(t) = ax(t) + bu(t − τ) (4)
where the state is x ∈ R, the input is u ∈ R, the system
parameters a,b ∈ R are uncertain parameters, and the
constant time delay τ ∈ R is uncertain but has a known
upper-bound, τ
p
, such that τ ≤ τ
p
.
Sampling this system at uniform time intervals T
(where in general the time delay τ may not be an in-
teger multiple of T ) gives a discrete-time system de-
scribed by
x
k+1
= φx
k
+ γ
1
u
k−d
+ γ
2
u
k−d−1
(5)
where φ, γ
1
,γ
2
∈ R are uncertain parameters, and d ∈
[0, p] ⊂ Z
+
is the uncertain constant delay known
to be at most p time-steps long. It is not neces-
sary to ensure that the sampled system has stable ze-
ros, i.e., if the system is written in the form u
k−d
=
1
γ
1
(−γ
2
u
k−d−1
+ x
k+1
− φx
k
) then the ratio
γ
2
γ
1
need
not be inside the unit-circle.
Assumption 1: The upper-bound on the delay in time-
steps, p, satisfies pT ≤ τ
p
≤ (p + 1)T .
Assumption 2: There exists a φ
min
> 0 such that φ ≥
φ
min
.
Assumption 3: There exists a γ
min
> 0 such that γ
1
+
γ
2
≥ γ
min
.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
700

The regulation problem is to find a bounded con-
trol input u
k
which will drive the system state to zero
asymptotically, i.e. lim
k→∞
x
k
= 0, while keeping all
system signals bounded.
Remark 1. Since the parameter φ is computed as φ =
e
aT
∀a ∈ R then it is reasonable to assume a positive
lower bound such that 0 < φ
min
≤ φ.
3 MAIN RESULT
In this section the design of the control law and adap-
tive law is presented which is then followed by a rig-
orous stability analysis of the system.
3.1 Adaptive Regulator
Consider the system (5) expressed in the form
x
k+1
= φx
k
+
p+1
∑
i=0
ψ
i
u
k−i
= θ
>
ζ
k
(6)
where θ
>
,

φ ψ
0
··· ψ
p+1

∈ R
p+3
is
the augmented parameter vector and ζ
>
k
,

x
k
u
k
··· u
k−p−1

∈ R
p+3
is the augmented
signal vector. The parameters ψ
i
∈ R are defined as
ψ
i
=





γ
1
i = d
γ
2
i = d + 1
0 otherwise
i ∈ [0, p + 1] (7)
Defining the variables η
k
and
ˆ
η
k
such that
η
k+1
= x
k+1
+
p+1
∑
i=1
ˆ
β
i,k
u
k−i+1
(8)
and
ˆ
η
k
= x
k
+
p+1
∑
i=1
ˆ
β
i,k
u
k−i
(9)
where
ˆ
β
i,k
∈ R. Consider now the system (6), adding
and subtracting the term
ˆ
φ
k
x
k
on the right-hand-side,
it is obtained that
x
k+1
=
˜
φ
k
x
k
+
ˆ
φ
k
x
k
+
p+1
∑
i=0
ψ
i
u
k−i
(10)
where
ˆ
φ
k
is the estimate of φ and
˜
φ
k
, φ −
ˆ
φ
k
is the es-
timation error. Substitution of (9) and (10) in (8) and
adding and subtracting the term
ˆ
β
0,k
u
k
on the right-
hand-side results in the delay free dynamics of the
form
η
k+1
=
˜
φ
k
x
k
+
ˆ
φ
k
ˆ
η
k
+
ˆ
β
0,k
u
k
−
ˆ
β
0,k
u
k
−
ˆ
φ
k
p+1
∑
i=0
ˆ
β
i,k
u
k−i
+
p+1
∑
i=0
ψ
i
u
k−i
+
p+1
∑
i=1
ˆ
β
i,k
u
k−i+1
=
˜
φ
k
x
k
+
p+1
∑
i=0
ψ
i
u
k−i
−

ˆ
β
0,k
−
ˆ
β
1,k

u
k
−
p
∑
i=1

ˆ
φ
k
ˆ
β
i,k
−
ˆ
β
i+1,k

u
k−i
−
ˆ
φ
k
ˆ
β
p+1,k
u
k−p−1
+
ˆ
φ
k
ˆ
η
k
+
ˆ
β
0,k
u
k
=
˜
φ
k
x
k
+
p+1
∑
i=0
ψ
i
u
k−i
−
p+1
∑
i=0
ˆ
ψ
i,k
u
k−i
+
ˆ
φ
k
ˆ
η
k
+
ˆ
β
0,k
u
k
(11)
where the adaptive parameters
ˆ
ψ
i,k
are the estimates
of ψ
i
and are defined as
ˆ
ψ
i,k
=





ˆ
β
0,k
−
ˆ
β
1,k
i = 0
ˆ
φ
k
ˆ
β
i,k
−
ˆ
β
i+1,k
i ∈ [1, p]
ˆ
φ
k
ˆ
β
i,k
i = p + 1
(12)
Note that the parameters
ˆ
β
i,k
∀i ∈ [0, p + 1] are com-
puted from the adaptative parameters as
ˆ
β
i,k
=











p+1
∑
j=0
ˆ
φ
− j
k
ˆ
ψ
j,k
i = 0
p+1
∑
j=i
ˆ
φ
− j+i−1
k
ˆ
ψ
j,k
i ∈ [1, p + 1]
(13)
which is obtained by rearranging (12). Finally, defin-
ing
˜
ψ
i,k
, ψ
i
−
ˆ
ψ
i,k
such that (11) is written as
η
k+1
=
˜
φ
k
x
k
+
p+1
∑
i=0
˜
ψ
i,k
u
k−i
+
ˆ
φ
k
ˆ
η
k
+
ˆ
β
0,k
u
k
=
˜
θ
>
k
ζ
k
+
ˆ
φ
k
ˆ
η
k
+
ˆ
β
0,k
u
k
(14)
where
˜
θ
k
, θ −
ˆ
θ
k
is the augmented parameter esti-
mation error vector and
ˆ
θ
>
k
,

ˆ
φ
k
ˆ
ψ
0,k
···
ˆ
ψ
p+1,k

∈
R
p+3
is the augmented adaptive parameter vector,
then from (14), the control law is selected as
u
k
= −
ˆ
β
−1
0,k
ˆ
φ
k
ˆ
η
k
(15)
With the formulation of the control law completed,
the adaptive law can be derived.
Remark 2. Note that the inverses of
ˆ
β
0,k
and
ˆ
φ
k
are
needed in (15) and (13), therefore, the adaptive law
must ensure that those terms are non-singular.
Proceeding with the adaptive law derivation, con-
sider the system (14) and the control law (15). Sub-
stitution of the control law results in the closed-loop
dynamics
η
k+1
=
˜
θ
>
k
ζ
k
(16)
Discrete-time Adaptive Regulation of Systems with Uncertain Upper-bounded Input Delay: A State Substitution Approach
701

From (16), the adaptive law is selected as
ˆ
θ
k
=



L

ˆ
θ
k−1
+ P
k
ζ
k−1
η
k

∀k ∈ (k
0
,∞)
ˆ
θ
k
0
∀k ∈ [0, k
0
]
(17)
P
k
=





P
k−1
−
P
k−1
ζ
k−1
ζ
>
k−1
P
k−1
1 + ζ
>
k−1
P
k−1
ζ
k−1
∀k ∈ (k
0
,∞)
P
k
0
∀k ∈ [0, k
0
]
(18)
where k
0
≥ 0 is the initial time-step, P
k
∈ R
p+3×p+3
is the symmetric positive-definite covariance matrix.
The purpose of the operator L[·] is to keep
ˆ
φ
k
and
ˆ
β
0,k
non-singular. The definition of the operator L [·] for
ˆ
φ
k
is given as
L [
ˆ
φ
k
] =
(
ˆ
φ
k
ˆ
φ
k
∈ (φ
min
,∞)
φ
min
ˆ
φ
k
∈ (−∞, φ
min
]
(19)
Before proceeding with the definition of the operator
L [·] for

˜
ψ
0,k
···
˜
ψ
p+1,k

, consider (13) and note that
for i = 0
ˆ
β
0,k
=
p+1
∑
j=0
ˆ
φ
− j
k
ˆ
ψ
j,k
. (20)
Since
ˆ
φ
k
> φ
min
and ideally
ˆ
ψ
j,k
≥ 0, then the only
possibility for a singular
ˆ
β
0,k
is if the adaptive param-
eters
ˆ
ψ
j,k
= 0, ∀ j ∈ [0, p + 1]. Therefore, the operator
L [·] will need to be defined under two scenarios. In
the first scenario, consider the case that one or more
but not all adaptive parameters
ˆ
ψ
j,k
are smaller than
or equal to zero, which leads to the L[·] being defined
as
L

ˆ
ψ
j,k

=
(
ˆ
ψ
j,k
ˆ
ψ
j,k
∈ (0, ∞)
0
ˆ
ψ
j,k
∈ (−∞, 0]
(21)
for all j ∈ [0, p + 1]. In the second scenario, con-
sider the case when all the adaptive parameters
ˆ
ψ
j,k
are smaller than or equal to zero, then the operator
L [·] is defined as
L

ˆ
ψ
j,k

=
γ
min
p + 2
(22)
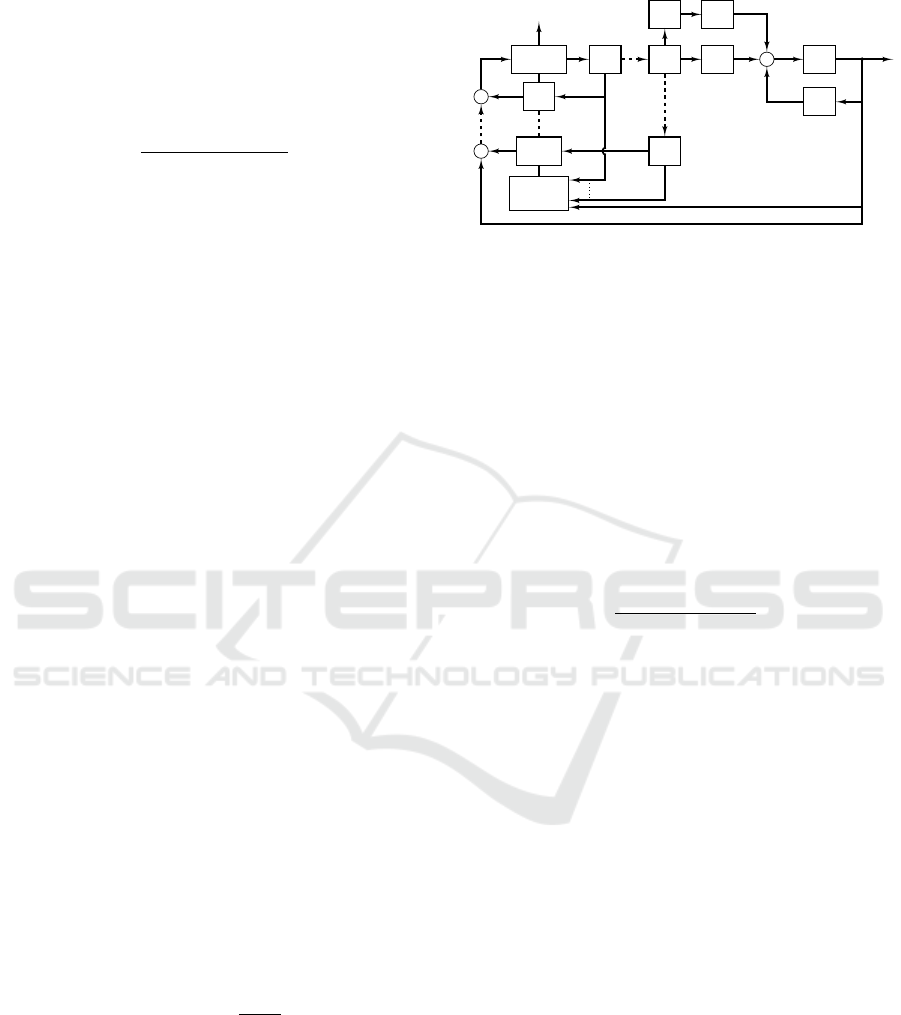
for all j ∈ [0, p + 1]. The block diagram of the result-
ing closed-loop system is shown in Fig. 1. Note that
in Fig. 1 the delay-operator is represented by q
−1
.
Remark 3. Note that since the delay d is uncertain,
it is not possible to assign the lower bound on γ
1
,γ
2
correctly in the case when all the values
ˆ
ψ
j,k
≤ 0.
Therefore, the average value of the lower bound γ
min
is assigned to every
ˆ
ψ
j,k
.
+
+
+
−β
−1
0,k
ˆ
φ
k
q
−1
q
−1
q
−1
γ
1
γ
2
q
−1
ˆ
β
1,k
ˆ
β
p+1,k
q
−1
φ
Adaptive
Law
d + 1
th
delay
p + 1
th
delay
ˆη
k
x
k+1
x
k
u
k
Figure 1: Block diagram depicting the proposed adaptive
regulator connected to the system.
3.2 Stability Analysis
In this section, it is shown that the parameter adapta-
tion produces bounded and convergent parameter es-
timates (Lemma 1), that the adaptive system model
converges in input-output behaviour to the true sys-
tem (Lemma 2), and that the proposed adaptive reg-
ulator drives the system state to zero with vanishing
control effort (Theorem 3).
Lemma 1. For the system (16) with the adaptive laws
(17) and (18) it is true that
lim
k→∞
η
2
k
1 + ζ
T
k−1
P
k−1
ζ
k−1
= 0 (23)
Furthermore, it is also true that the parameter estimate
ˆ
θ
k
is bounded, hence the parameter estimation error
˜
θ
k
is also bounded.
Proof. Consider the positive function
V
k
=
˜
θ
>
k
P
−1
k
˜
θ
k
(24)
The backward difference ∆V
k
is
∆V
k
= V
k
−V
k−1
=
h
˜
θ
>
k
P
−1
k
˜
θ
k
−
˜
θ
>
k−1
P
−1
k−1
˜
θ
k−1
i
(25)
Using the fact that, (Abidi and Xu, 2008),

θ − L

ˆ
θ
k

>

θ − L

ˆ
θ
k

≤

θ −
ˆ
θ
k

>

θ −
ˆ
θ
k

(26)
and that if P
−1
k
is positive-definite then it is obtained
that

θ − L

ˆ
θ
k

>
P
−1
k

θ − L

ˆ
θ
k

≤

θ −
ˆ
θ
k

>
P
−1
k

θ −
ˆ
θ
k

(27)
Substituting the (27) and the adaptative law (17) in
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
702

(25) leads to
∆V
k
= V
k
−V
k−1
=

˜
θ
k−1
− P
k
ζ
k−1
η
k

>
P
−1
k

˜
θ
k−1
− P
k
ζ
k−1
η
k

−
˜
θ
>
k−1
P
−1
k−1
˜
θ
k−1
=
˜
θ
>
k−1
P
−1
k
˜
θ
k−1
−
˜
θ
>
k−1
P
−1
k−1
˜
θ
k−1
−
˜
θ
>
k−1
P
−1
k
× (P
k
ζ
k−1
η
k
) − (P
k
ζ
k−1
η
k
)
>
P
−1
k
˜
θ
k−1
+ (P
k
ζ
k−1
η
k
)
>
P
−1
k
(P
k
ζ
k−1
η
k
)
=
˜
θ
>
k−1
(P
−1
k
− P
−1
k−1
)
˜
θ
k−1
− 2
˜
θ
>
k−1
ζ
k−1
η
k
+ ζ
>
k−1
P
k
ζ
k−1
η
2
k
(28)
and using the fact that P
−1
k
= P
−1
k−1
+ζ
k−1
ζ
>
k−1
, (Abidi
et al., 2017), it is obtained that (28) is simplified to
the form
∆V
k
=
˜
θ
>
k−1
ζ
k−1
ζ
>
k−1
˜
θ
k−1
− 2
˜
θ
>
k−1
ζ
k−1
η
k
+ ζ
>
k−1
P
k
ζ
k−1
η
2
k
(29)
Substituting in the model estimation error dynamics
(16) gives
∆V
k
= η
2
k
− 2η
2
k
+ ζ
T
k−1
P
k
ζ
k−1
η
2
k
= η
2
k
[−1 + ζ
T
k−1
P
k
ζ
k−1
] (30)
Furthermore, from (18) it is obtained that
ζ
T
k−1
P
k
ζ
k−1
=
ζ
T
k−1
P
k−1
ζ
k−1
1 + ζ
T
k−1
P
k−1
ζ
k−1
(31)
Substitution of (31) in (30) finally leads to
∆V
k
= η
2
k
"
−1 +
ζ
T
k−1
P
k−1
ζ
k−1
1 + ζ
T
k−1
P
k−1
ζ
k−1
#
= −
η
2
k
1 + ζ
T
k−1
P
k−1
ζ
k−1
(32)
From the result (32) it is evident that ∆V
k
is always
non-positive and, hence V
k
, is non-increasing. There-
fore, the parameter estimation error
˜
θ
k
and the param-
eter estimate
ˆ
θ
k
are bounded. Furthermore, the value
of V
k
is the accumulation of changes ∆V
k
to its initial
value V
k
0
V
k
= V
k
0
+
k−k
0
∑
i=1
∆V
i
(33)
Substituting (32) into (33) gives
V
k
= V
k
0
−
k−k
0
∑
i=1
η
2
i
1 + ζ
T
i−1
P
i−1
ζ
i−1
(34)
and using the result in (Abidi et al., 2017) it is con-
cluded that
lim
k→∞
∆V
k
= lim
k→∞
η
2
k
1 + ζ
T
k−1
P
k−1
ζ
k−1
= 0 (35)
Lemma 2. From Lemma 1, for the signals (8) and (9)
the following are true:
(a) |x
k
| ≤ c
0
max
i∈[0,p+1]
|
ˆ
η
k−i
|, for some positive
constant c
0
.
(b) |
ˆ
η
k
| ≤ d
0
+ d
1
max
i∈[0,p+1]
|η
k−i
|, for some posi-
tive constants d
0
and d
1
.
(c) lim
k→∞
ˆ
η
k
= η
k
.
(d) lim
k→∞
η
k
= 0 and lim
k→∞
ˆ
η
k
= 0.
Proof. Consider the signal (9) re-written as
x
k
=
ˆ
η
k
−
p+1
∑
i=1
ˆ
β
i,k
u
k−i
(36)
Substitution of the control law (15), it is obtained as
x
k
=
ˆ
η
k
+
p+1
∑
i=1
ˆ
β
i,k
ˆ
β
−1
0,k−i
ˆ
φ
k−i
ˆ
η
k−i
(37)
In Lemma 1 it is established that the adaptive param-
eters are bounded which implies that
ˆ
β
i,k
ˆ
β
−1
0,k−i
ˆ
φ
k−i
is bounded. Using the boundedness of the adaptive
paramters in (37), it is obtained that
|x
k
| ≤ |
ˆ
η
k
| +
p+1
∑
i=1
|
ˆ
β
i,k
ˆ
β
−1
0,k−i
ˆ
φ
k−i
||
ˆ
η
k−i
|
≤ c
0
max
i∈[0,p+1]
|
ˆ
η
k−i
| (38)
for some positive constant c
0
.
Consider now the difference of the two signals (9)
and (8) given as
ˆ
η
k
= −
p+1
∑
i=1

ˆ
β
i,k
−
ˆ
β
i,k−1

u
k−i
+ η
k
=
p+1
∑
i=1

ˆ
β
i,k
−
ˆ
β
i,k−1

ˆ
β
−1
0,k−i
ˆ
φ
k−i
ˆ
η
k−i
+ η
k
(39)
Expressing this in augmented form and defining
˜
β
i,k
,
ˆ
β
−1
0,k−i
ˆ
φ
k−i
(
ˆ
β
i,k
−
ˆ
β
i,k−1
) such that,
ˆ
¯
η
k
=






˜
β
1,k
˜
β
2,k
···
˜
β
p+1,k
1 0 ··· 0
0 1 ···
.
.
.
.
.
.
.
.
.
.
.
.
0






ˆ
¯
η
k−1
+




1
0
.
.
.
0




η
k
(40)
where
ˆ
¯
η
>
k−1
,

ˆ
η
k
ˆ
η
k−1
···
ˆ
η
k−p

. From Lemma
1 and using the results in (Abidi et al., 2017),
lim
k→∞
ˆ
β
−1
0,k−i
ˆ
φ
k−i
(
ˆ
β
i,k
−
ˆ
β
i,k−1
) = 0 and that implies
that the augmented system (40) is stable and a bound
on
ˆ
η
k
exists such that
|
ˆ
η
k
| ≤ d
0
+ d
1
max
i∈[0,p+1]
|η
k−i
| (41)
Discrete-time Adaptive Regulation of Systems with Uncertain Upper-bounded Input Delay: A State Substitution Approach
703

for some positive constants d
0
and d
1
.
Going back to the augmented system (40), at
steady state when k → ∞, the term
ˆ
β
−1
0,k−i
ˆ
φ
k−i
(
ˆ
β
i,k
−
ˆ
β
i,k−1
) will vanish resulting in an augmented system
of the form
ˆ
¯
η
k
=





0 0 ··· 0
1 0 ··· 0
0 1 ···
.
.
.
.
.
.
.
.
.
.
.
.
0





ˆ
¯
η
k−1
+




1
0
.
.
.
0




η
k
(42)
which has a solution
ˆ
η
k
= η
k
when k → ∞.
Finally, given the result in (35), the Key Tech-
nical Lemma states that η
k
vanishes if there exists
positive constants µ
0
,µ
1
∈ R such that |ζ
k−1
| ≤ µ
0
+
µ
1
max
κ∈[0,k]
|η
κ
|. To show that this is indeed true,
recall that ζ
>
k
,

x
k
u
k
··· u
k−p−1

. It has been es-
tablished that |x
k
| ≤ c
0
max
i∈[0,p+1]
|
ˆ
η
k−i
| and, since,
ˆ
β
−1
0,k−i
ˆ
φ
k−i
is bounded then |u
k
| ≤ c
1
|
ˆ
η
k
|. There-
fore, |ζ
k−1
| ≤ µ
0
+µ
1
max
κ∈[0,k]
|η
κ
| for some positive
constants µ
0
and µ
1
and, ultimately, lim
k→∞
η
k
= 0.
Furthermore, from (c) it has been established that
lim
k→∞
ˆ
η
k
= η
k
resulting in lim
k→∞
ˆ
η
k
= 0.
Theorem 1. The state of the closed-loop system, as
well as the control signal, approach zero asymptoti-
cally, i.e. lim
k→∞
x
k
= lim
k→∞
u
k
= 0.
Proof. Beginning with the closed-loop controller dy-
namics (15) and taking the limit of the norm of both
sides as k → ∞, it is obtained that
lim
k→∞
|u
k
|
= lim
k→∞



−
ˆ
β
−1
0,k
ˆ
φ
k
η
k



≤ lim
k→∞



ˆ
β
−1
0,k
ˆ
φ
k



|
η
k
|
= 0 (43)
Consider now the expression (8) as k → ∞ which is
given as
lim
k→∞
|x
k
| ≤ lim
k→∞
|
ˆ
η
k
| + lim
k→∞
p+1
∑
i=1
|
ˆ
β
i,k
u
k−i
|
= 0 (44)
which establishes the asymptotic stability of the state
x
k
.
4 SIMULATION EXAMPLE
Consider an unstable system with an unstable zero,
given by
x
k+1
= 1.05x
k
+ 1u
k−d
+ 1.1u
k−d−1
(45)
where the system delay is set as d = 0, 1, 2, 3, 4, 5
while the upper bound is set as p = 5. The initial
condition of the system is set at x
k
= 2.
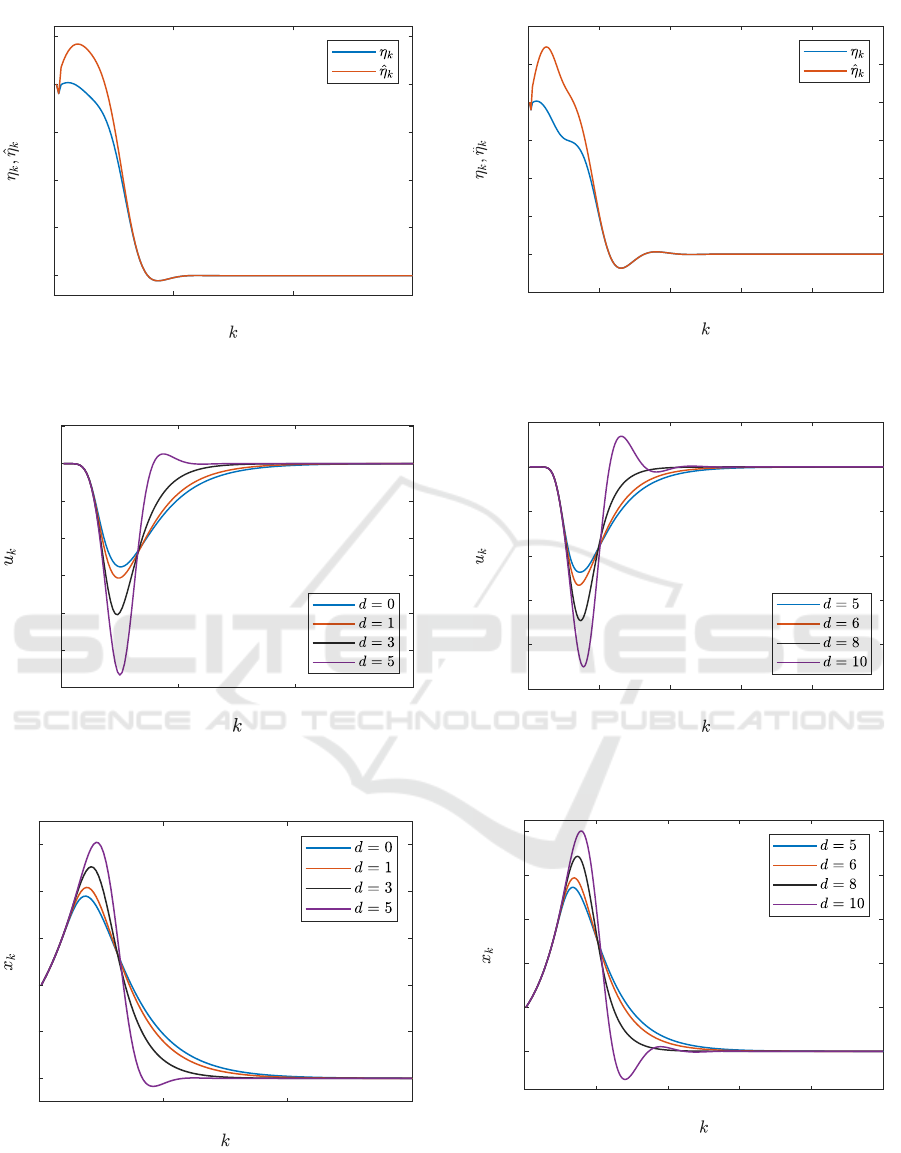
To investigate the adaptive performance of the
regulator with respect to mismatch between the de-
lay upper-bound p and the true delay d, the closed-
loop system is simulated using various values of d.
The adaptive regulator is initialised with P
0
= 5 ×
I
p+3×p+3
and
ˆ
θ
>
0
=

0.1 0.4 ··· 0.4

. In Fig. 2-4 the
results are shown for the convergence of the signals
η
k
,
ˆ
η
k
, the control input profile and state regulation
performance of the closed-loop system under various
values of the delay values. As expected, x
k
is regu-
lated to zero asymptotically. As it can be seen from
the results, the greater the mismatch between p and d,
the longer the settling-time. Note that with increasing
system delay, d, the initial divergence grows which
is to be expected as the controller cannot react fast
enough initially to force the system to converge.
Finally, the system is simulated with a longer sys-
tem delay, d, and an upper bound set at p = 10. The
adaptive regulator parameters are kept the same as
the previous case while the system delay is increased
from d = 5 until d = 10. The results are shown in
Fig. 5-7. The results for this case show a similar per-
formance to the shorter delay case. As it would be
expected, the convergence speed increases as the ac-
tual delay, d, and the upper bound, p, approach each
other.
5 CONCLUSIONS
In this paper, a discrete-time adaptive regulation ap-
proach was designed for a scalar system with an
unknown, constant time-delay with a known upper-
bound. The approach utilized a state substitution the
resulted in a delay-free system which simplified the
control law design. The approach is also capable of
handling systems with unstable zeros. A rigorous
stability proof was presented that shows the adaptive
control law drives the system state to zero asymptoti-
cally. Finally, numerical simulations were shown that
illustrate the ability of the adaptive control law to cope
with mismatches between the delay upper-bound and
the true delay in the system.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
704

0 50 100 150
0
0.5
1
1.5
2
2.5
Figure 2: Asymptotic convergence of η
k
and
ˆ
η
k
when d = 5
and p = 5.
0 50 100 150
-0.3
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
Figure 3: Control input profile on the system when p = 5,
with various values of the actual system delay d.
0 50 100 150
0
1
2
3
4
5
Figure 4: State regulation of the system when p = 5, with
various values of the actual system delay d.
0 50 100 150 200 250
-0.5
0
0.5
1
1.5
2
2.5
3
Figure 5: Asymptotic convergence of η
k
and
ˆ
η
k
when d =
10 and p = 10.
0 50 100 150 200 250
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
Figure 6: Control input profile on the system when p = 10,
with various values of the actual system delay d.
0 50 100 150 200 250
0
2
4
6
8
10
Figure 7: State regulation of the system when p = 10, with
various values of the actual system delay d.
Discrete-time Adaptive Regulation of Systems with Uncertain Upper-bounded Input Delay: A State Substitution Approach
705

REFERENCES
Abidi, K. (2014). A robust discrete-time adaptive con-
trol approach for systems with almost periodic time-
varying parameters. International Journal of Robust
and Nonlinear Control, 24(1):166–178.
Abidi, K. and Postlethwaite, I. (2019). Discrete-time adap-
tive control for systems with input time-delay and
non-sector bounded nonlinear functions. IEEE Ac-
cess, 7:4327–4337.
Abidi, K. and Xu, J. (2008). A discrete-time periodic
adaptive control approach for time-varying parame-
ters with known periodicity. IEEE Transactions on
Automatic Control, 53(2):575–581.
Abidi, K. and Xu, J. X. (2015). Advanced Discrete-Time
Control: Designs and Applications. Springer.
Abidi, K., Yildiz, Y., and Annaswamy, A. (2017). Con-
trol of uncertain sampled-data systems: An adaptive
posicast control approach. IEEE Transactions on Au-
tomatic Control, 62(5):2597–2602.
Abidi, K., Yildiz, Y., and Korpe, B. E. (2016). Explicit
time-delay compensation in teleoperation: An adap-
tive control approach. International Journal of Robust
and Nonlinear Control, 26(15):3388–3403.
Artstein, Z. (1982). Linear systems with delayed controls:
A reduction. IEEE Transactions on Automatic Con-
trol, 27(4):869–879.
Bjerkeng, M., Falco, P., Natale, C., and Pettersen, K. Y.
(2014). Stability analysis of a hierarchical architec-
ture for discrete-time sensor-based control of robotic
systems. IEEE Transactions on Robotics, 30(3):745–
753.
Bresch-Pietri, D. and Krstic, M. (2009). Adaptive trajec-
tory tracking despite unknown input delay and plant
parameters. Automatica, 45(9):2074–2081.
Gu, K. and Niculescu, S. (2003). Survey on recent results in
the stability and control of time-delay systems. Jour-
nal of Dynamic Systems, Measurement, and Control,
125(2):158–165.
Krstic, M. (2009). Delay Compensation for Nonlinear,
Adaptive, and PDE Systems. Birkh
¨
auser.
Manitius, A. and Olbrot, A. (1979). Finite spectrum assign-
ment problem for systems with delays. IEEE Trans-
actions on Automatic Control, 24(4):541–552.
Mirkin, L. (2004). On the approximation of distributed-
delay control laws. Systems & Control Letters,
51(5):331–342.
Mirkin, L. and Raskin, N. (2003). Every stabilizing dead-
time controller has an observer-predictor-based struc-
ture. Automatica, 39(10):1747–1754.
Niculescu, S. and Annaswamy, A. M. (2003). An adaptive
smith-controller for time-delay systems with relative
degree n
∗
≤ 2. Systems & Control Letters, 49(5):347–
358.
Ortega, R. and Lozano, R. (1988). Globally stable adap-
tive controller for systems with delay. International
Journal of Control, 47(1):17–23.
Richard, J. (2003). Time-delay systems: An overview of
some recent advances and open problems. Automat-
ica, 39(10):1667–1694.
Skorina, E. H., Luo, M., Tao, W., Chen, F., Fu, J., and Onal,
C. D. (2017). Adapting to flexibility: Model refer-
ence adaptive control of soft bending actuators. IEEE
Robotics and Automation Letters, 2(2):964–970.
Wei, Y. and Lin, Z. (2017). Maximum delay bounds of lin-
ear systems under delay independent truncated predic-
tor feedback. Automatica, 83:65–72.
Wei, Y. and Lin, Z. (2018). Stability criteria of linear sys-
tems with multiple input delays under truncated pre-
dictor feedback. Systems & Control Letters, 111:9–17.
Zhong, Q. (2004). On distributed delay in linear control
laws – part i: discrete-delay implementations. IEEE
Transactions on Automatic Control, 49(11):2074–
2080.
Zhong, Q. (2006). Robust Control of Time-Delay Systems.
Springer.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
706