
An Improved APFM for Autonomous Navigation and Obstacle
Avoidance of USVs
Xiaohui Zhu
1,2,3 a
, Yong Yue
1
, Hao Ding
3,4
, Shunda Wu
3
, MingSheng Li
3
and Yawei Hu
3
1
Department of Computer Science and Software Engineering, Xi’an Jiaotong-Liverpool University,
Suzhou, Jiangsu Province, 215123, P. R. China
2
Department of Computer Science, University of Liverpool, Liverpool, L69 3BX, U.K.
3
School of Information Science and Technology, Nantong University, Nantong, Jiangsu Province, 226019, P. R. China
4
Nantong Research Institute for Advanced Communication Technologies, Nantong, Jiangsu Province, 226019, P. R. China
Keywords:
Autonomous Navigation, Obstacle Avoidance, Improved APFM, USVs, Water Quality Monitoring.
Abstract:
Unmanned surface vehicles (USVs) are getting more and more attention in recent years. Autonomous navi-
gation and obstacle avoidance is one of the most important functions for USVs. In this paper, we proposed
an improved angle potential field method (APFM) for USVs. A reversed obstacle avoidance algorithm was
proposed to control the steering of USVs in tight spaces. In addition, a multi-position navigation route plan-
ning was also achieved. Simulation results in MATLAB show that the improved APFM can guide the USV
to autonomously navigate and avoid obstacles around the USV during navigation. We applied the algorithm
to a real USV, which is designed for water quality monitoring and tested in a real river system. Experimental
results show that the improved APFM can successfully guide the USV to navigate based on the predefined
navigation route while detecting both static and dynamic obstacles and avoiding collisions.
1 INTRODUCTION
With the development of sensor technology, mobile
network, autonomous navigation and artificial intel-
ligence (AI), unmanned surface vehicles (USVs) are
getting more and more attention in scientific research
(Liu et al., 2017), environmental missions (Polvara
et al., 2018a) , military operations and civilian ap-
plications (Liu et al., 2016). Many countries, espe-
cially those with vast water resources are vigorously
developing USVs (Zhou et al., 2015). US Naval Un-
dersea Warfare Center developed the Spartan Scout
USV, an advanced concept technology demonstration
in 2002 (Maguer et al., 2005). In Japan, Yamaha
developed two USVs, the Unmanned Marine Ve-
hicle High-Speed UMV-H and the Unmanned Ma-
rine Vehicle Ocean type UMV-O for monitoring bio-
geo-chemical parameters of oceans and atmosphere
(Enderle et al., 2004). The Portuguese Dynamical
Systems and Ocean Robotics Laboratory developed
several marine robotic vessels(Bertram, 2008). Ac-
cording to practical applications and requirements,
USVs have various appearances such as rigid inflat-
a
https://orcid.org/0000-0003-1024-5442
able hulls, kayaks, catamarans and trimarans (Naeem
et al., 2008; Peng et al., 2009). Due to catamaran’s
stability in heavy-weather situations and its ample
space for setting additional water quality monitoring
devices, it is widely used in environmental monitor-
ing.
Generally, USVs usually consist of three main
modules: data acquisition, path planning and naviga-
tion control. Many researchers have proposed vari-
ous algorithms for autonomous navigation and colli-
sion avoidance (Li et al., 2017; Wang et al., 2011;
Zhang et al., 2014a). Artificial potential field method
was a real-time obstacle avoidance approach (Khatib,
1986a). It use attractive force to allow robots to
reach the destination and use repulsion force to keep
robots away from obstacles. The resultant of these
two forces can guide the robot to avoid obstacles dur-
ing the navigation. The approach is widely used due
to its advantages of simplicity and small computing
requirement. However, it also has a disadvantage of
having local optimal solutions. Borenstein proposed
a vector field histogram(VFH) algorithm to achieve
obstacle avoidance for fast mobile robots in cluttered
environments (Borenstein and Koren, 1990). It uses a
two-dimensional Cartesian histogram grid as a world
Zhu, X., Yue, Y., Ding, H., Wu, S., Li, M. and Hu, Y.
An Improved APFM for Autonomous Navigation and Obstacle Avoidance of USVs.
DOI: 10.5220/0007922904010408
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 401-408
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
401

model. The VFH algorithm is efficient and robust.
However, the size of grid cells is highly related to the
computing performance. The smaller the grid cell,
the clearer the environmental information is drawn,
but the amount of computational time and storage
space will increase exponentially. With the develop-
ment of artificial intelligence (AI), AI algorithms such
as neural network and particle swarm optimization
were also used for autonomous navigation (Polvara
et al., 2018b; Zhang et al., 2014b). However, AI al-
gorithms usually need much more computational re-
sources. Due to the constrained electric energy and
computing resources on small USVs, it is not always
available for small USVs. The angle potential field
method (APFM) can guide mobile robots to reach the
destination by a combined force from obstacles and
the destination (Li and He, 2006).
In this paper, we review the fundamental concept
of APFM in Section II. Section III introduces the im-
proved APFM according to the particular requirement
of USVs. We simulate the improved APFM in MAT-
LAB to analysis the correctness and performance of
our algorithm in Section IV. We apply the algorithm
to a real USV and test in a lake in Section V. Finally,
we make a conclusion in Section VI.
2 ANGLE POTENTIAL FIELD
METHOD
The angle potential field method (APFM) was pro-
posed for outdoor mobile robots in 2006 (Li and He,
2006). The APFM is based on an artificial poten-
tial field concept (Khatib, 1986b). The main idea of
APFM is: each obstacle around the robot produces a
resistance to the robot, and the target point produces
an attraction to the robot. The accessibility of each
angle for the robot is determined by the ratio of at-
traction and resistance. The angle with maximal ac-
cessibility is the heading for the robot.
2.1 Resistance of Obstacles
The resistance to a robot is produced by surrounding
obstacles. When the linear distance D
l
between an
obstacle and the robot is decreased, the resistance is
increased. Otherwise, the resistance is decreased. We
assume D
ms
is the minimal safety lateral distance be-
tween the robot and an obstacle for the robot to safely
pass through the obstacle. The D
ms
is defined as fol-
lows.
D
ms
=
1
2
K
ms
W (1)
Figure 1: Risk collision area of an obstacle in the robot fixed
coordinate frame.
where W is the width of the robot, K
ms
is a coefficient
to extend the safety lateral distance between the robot
and an obstacle, and K
ms
≥ 1.
We let θ be the angle of an obstacle in the robot
fixed coordinate frame. Figure 1 shows the risk colli-
sion area of an obstacle to the robot in navigation. The
risk angle φ for the robot is defined by the following
equation.
φ = argsin(
D
ms
D
l
) (2)
Equation 2 means that if the heading of the robot is
within the angle φ, the robot will collide with the ob-
stacle. As we know that the robot may pass through
the obstacle from the right or left side, the collision
angle ϕ for the robot is shown as follows.
θ − φ ≤ ϕ ≤ θ + φ (3)
Let D
min
be the minimum safety linear distance
between an obstacle and the robot, D
max
be the max-
imum distance of obstacle detection, K
r
(θ,ϕ) be the
resistance of an obstacle at angle θ to the robot at an-
gle ϕ. We let K
r
(θ,ϕ) be a small constant when the
distance D
l
is larger than D
max
. if D
l
is smaller than
D
min
, it means that the robot will collide with the ob-
stacle and we let K
r
(θ,ϕ) be a infinite value. Oth-
erwise, K
r
(θ,ϕ) is inversely proportional to the dif-
ference between D
l
and D
min
. Equation 4 means that
when the heading of the robot is not within the colli-
sion angle, we do not need to calculate the resistance
of the obstacle. Otherwise, we should calculate the
resistance K
r
(θ,ϕ) and there are three situations we
should consider based on the distance D
l
between the
robot and the obstacle.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
402

K
r
(θ,ϕ) =
0, i f ϕ > θ + φ or ϕ < θ − φ
+∞, i f D
l
< D
min
and θ − φ ≤ ϕ ≤ θ + φ
1
D
l
−D
min
, i f D
min
≤ D
l
≤ D
max
and θ − φ ≤ ϕ ≤ θ + φ
1
D
max
−D
min
, i f D
l
> D
max
and θ − φ ≤ ϕ ≤ θ + φ
(4)
We let K
r
(ϕ) be the maximal resistance that all
obstacles in front of the robot at angle ϕ, which is
shown in Equation 5.
K
r
(ϕ) = max
ϕ∈[0 π]
(K
r
(θ,ϕ)) (5)
2.2 Abstraction of Target Point
To guide the robot to move towards the target point,
we define an attraction K
a
(ϕ) for the target point at
angle ϕ as follows.
K
a
(ϕ) = cos(ϕ − θ
destinaton
) (6)
where θ
destinaton
is the angle of the target point and
ϕ is the heading of the robot. From Equation 6 we
know that when the deviation between the heading
of the robot and the destination is increased, the at-
traction K
a
(ϕ) is decreased. otherwise, K
a
(ϕ) will be
increased.
2.3 Pass Function
Based on the maximum resistance of obstacles around
the robot and the attraction of the destination to the
robot, we define a pass function K
p
(ϕ) as follows.
K
p
(ϕ) = max
ϕ∈[0 π]
(
K
a
(ϕ)
K
r
(ϕ)
) (7)
We know from Equation 7 that the APFM tries to
find a angle ϕ in [0 π] which has maximal value of
K
p
(ϕ). Then we should let the robot turn to that angle
and move forward. The process continues until the
robot reaches the target point.
3 IMPROVEMENT OF APFM
3.1 Issues in APFM
As we know that mobile robots are quite different
from USVs as follows. They should be carefully con-
sidered and solved before we can apply the APFM to
USVs.
• Mobile robots can accurately control or rapidly
change their moving speed on land. However, af-
fected by the wind and water flows, it is difficult
for USVs to strictly and immediately control and
change sailing speed.
• The steering operation of mobile robots is easy to
achieve. Constrained by steering angle of the rud-
der and the servo, the steering operation of USVs
needs much more time than mobile robots.
• When the distance between obstacles and the
robot is too small for the robot to turn, the original
APFM simply stops the robot. It is not acceptable
when we apply this algorithm to a real USV.
• The original APFM only considers the straight
path planning of a single position. To a real USV,
multi-position path planning has to be achieved.
• Further research shows that there is a potential is-
sue when there is no obstacle around the robot,
which means the resistance K
r
(ϕ) is 0. Equation
7 indicates that when K
r
(ϕ) is 0, we get a maxi-
mal K
p
(ϕ) no matter what the value of K
a
(ϕ) is. It
is unreasonable when there is more than one angle
which has a resistance of 0. Because in this situa-
tion, we still should select an angle which has the
largest attraction to the destination and drive the
USV toward this angle.
3.2 Improved APFM
According to the issues proposed above, we improve
the APFM as follows.
• Firstly, to simplify the speed and heading control
of the USV, we assume the USV has a stable speed
during navigation. It is easy to achieve in a real
application by controlling the ESC to provide sta-
ble power to the motor in the USV.
• Secondly, we use a Proportional-Integral-
Derivative (PID) controller to control the heading
of USV. The PID controller can continuously
adjust the heading of USV until it reaches the
desired heading.
• Thirdly, we propose a reversed obstacle avoidance
algorithm. When the distance between obstacles
and the USV is too small to turn the heading of
the USV, we let a position which is symmetric
with the actual target point of the USV regarding
the current position of the USV be the virtual tar-
get point and let the stern direction of the USV
An Improved APFM for Autonomous Navigation and Obstacle Avoidance of USVs
403

Figure 2: Reversed obstacle avoidance.
as a virtual heading. We apply the APFM again
based on the virtual target point and the heading
to guide the USV to move far away from obsta-
cles. Finally, We continue the navigation process
again to let the USV reach the real target point.
Figure 2 shows the procedure of the reversed ob-
stacle avoidance algorithm.
From figure 2 we know that the USV is at the cor-
ner of a river. Due to the closeness to the right
bank and its current heading, the USV cannot find
a way to the original target point. In this situ-
ation, the reserved obstacle avoidance algorithm
will try to drive the USV back and head to the
virtual target point, which is symmetric with the
actual target point regarding the current position
of the USV. Finally, the heading of USV is turned
to the direction of the original target point, and the
navigation can be continued.
• Fourthly, we extend the single position path plan-
ning to multi-position path planning. Integrated
with the reversed obstacle avoidance algorithm,
At first, we let the first position as the current tar-
get point for the USV. When the USV reaches the
first target, we let the subsequent positions as the
current target of the USV one by one. Finally, the
USV can reach the final destination.
• Finally, to solve this potential issue when there is
no obstacle around the USV, we set the K
r
(ϕ) to a
very small constant when there is no resistance at
angle ϕ. we revise Equation 4 as follows. where
0 < ω < 1. It is easy to know that ω ∗
1
D
max
−D
min
is the smallest value in Equation 8, which means
there is no obstacle at the angle ϕ for the USV. So
the final heading of the USV will be determined
by the attraction K
a
(ϕ) in Equations 6 and 7.
4 SIMULATIONS AND ANALYSIS
We assume the length and width of USV are both one
meter and the turning radius of the USV is 2.5 meters.
We define a 50*50 m square as a river area for the test.
In addition, we let the minimum safety linear distance
(D
min
) between an obstacle and the USV be 2 meters,
the maximum distance (D
max
) for obstacle detection
be 8 meters and the minimal safety lateral distance
(D
ms
) between the USV and an obstacle be 1 meter.
We implemented the improved APFM in MATLAB
and considered several scenarios as follows.
4.1 Obstacle Detection and Avoidance
with Multiple Positions
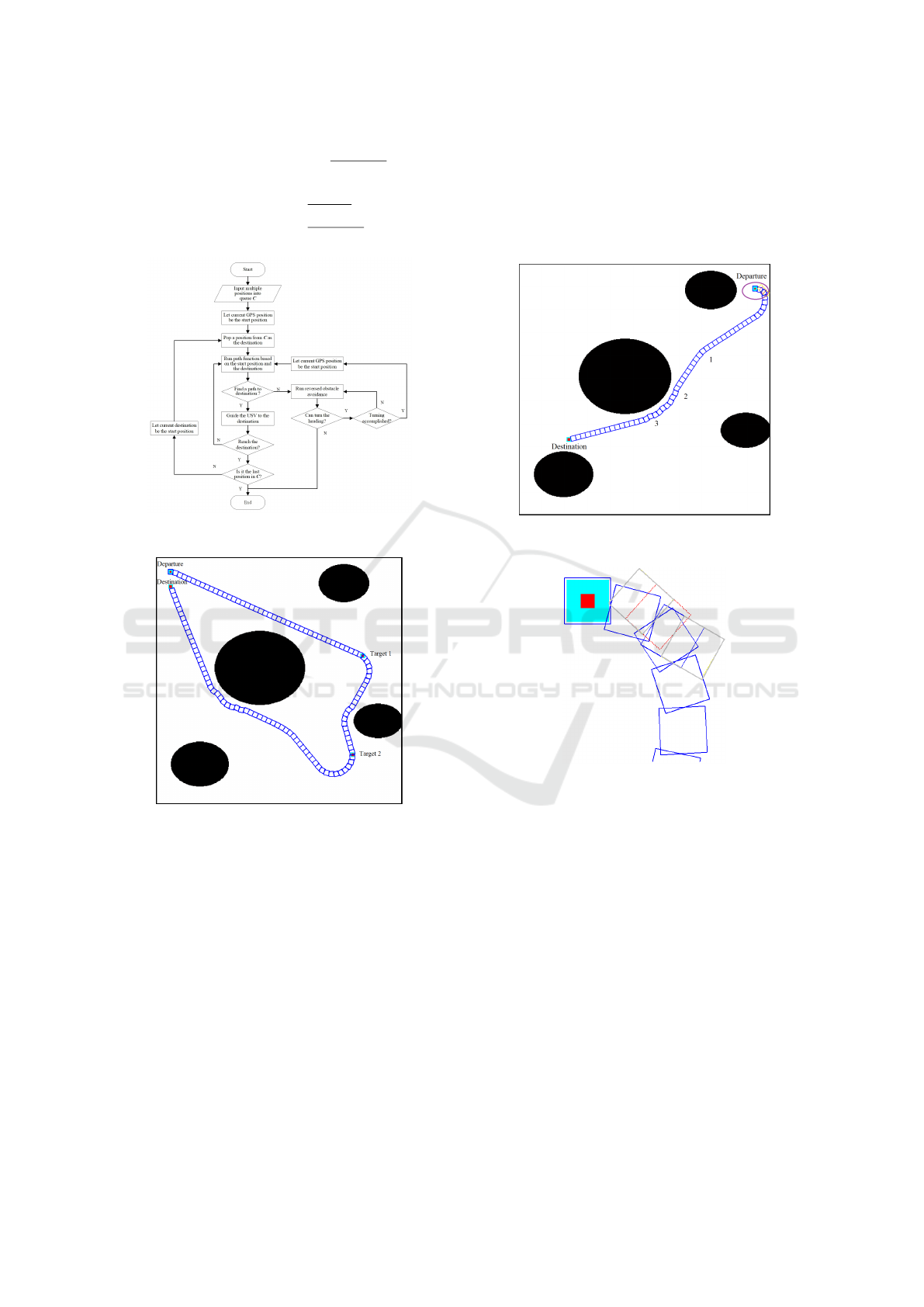
The multi-position path planning is shown in Figure
3. We set a scenario with four navigation positions.
We let the first position be the departure, and the
last position be the destination respectively. Figure 4
shows the navigation process. Because obstacles are
far away from the navigation route between the de-
parture position to the first target position, the cruise
track between these two positions is a straight line.
Attracted by the second target position, the USV turns
right and moves towards the second target position.
Influenced by the resistance of the right bottom obsta-
cle, the USV slightly turns right again to avoid the ob-
stacle on its left side and reaches the second target po-
sition. With the attraction of the destination position
at the right top, the USV turns right again and moves
ahead to the destination. Affected by the resistance of
the central obstacle, the USV starts to turn left when
it moves close to the central obstacle. However, at-
tracted by the destination, the USV turns slightly right
but still have enough safety distance from the obsta-
cle. Finally, it reaches the destination.
4.2 Reversed Obstacle Avoidance
between Two Positions
In this simulation, we set the departure position at the
right top, which is very close to the right bank of the
river and the destination position at the left bottom.
Similar to the previous simulation, there is an obsta-
cle between the departure and destination positions.
Figure 5 shows the simulation result.
The purple ellipse is the area where the reversed
obstacle avoidance algorithm works. Figure 6 shows
the detailed process of reversed obstacle avoidance.
The cruise track of the USV is the blue rectangles.
The grey rectangles represent the brake track of the
USV when it is close to the right border. The red rect-
angles are the cruise track when the reversed obstacle
avoidance algorithm works.
Constrained by the minimum turning radius of
the USV, during the turning process, the USV is too
close to the right border and cannot turn. The USV
is stopped when the distance between the USV and
the right border is smaller than the minimum safety
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
404
K
r
(θ,ϕ) =
ω ∗
1
D
max
−D
min
, i f ϕ > θ + φ or ϕ < θ − φ
+∞, i f D
l
< D
min
and θ − φ ≤ ϕ ≤ θ + φ
1
D
l
−D
min
, i f D
min
≤ D
l
≤ D
max
and θ − φ ≤ ϕ ≤ θ + φ
1
D
max
−D
min
, i f D
l
> D
max
and θ − φ ≤ ϕ ≤ θ + φ
(8)
Figure 3: Multi-position path planning.
Figure 4: Obstacle detection and avoidance with multiple
positions.
distance D
min
. Then, the reversed obstacle avoidance
algorithm guides the USV to go backwards and turn
right. As a result, the USV leaves far away from the
right border of the river and turns the heading to the
destination position. Finally, the USV has enough
turning radius and is guided by the improved APFM
to avoid obstacles and reaches the destination position
at the left bottom.
4.3 Obstacle Detection and Avoidance
with Moving Obstacles
We simulate a scenario with moving obstacles. We
add a referential USV with a speed of 1m/s as a mov-
Figure 5: Reversed obstacle avoidance between two posi-
tions.
Figure 6: Enlarged image for the process of reversed obsta-
cle avoidance.
ing obstacle and assume it can only detect static ob-
stacles. The referential USV moves from the left po-
sition towards the right bottom position. We use red
rectangles to identify the cruise track of the referen-
tial USV. Figure 7 demonstrates the process of mov-
ing obstacle detection and avoidance when two USVs
meet each other. We find that when two USVs are ap-
proaching, the referential USV cannot detect the ap-
proaching of another USV and does not change its
navigation route. However, the first USV can de-
tect the referential USV, and the resistance from the
referential USV to the first USV will be calculated.
Affected by another resistance from the obstacle and
the attraction from the immediate target position, the
USV slightly turns left to avoid the collision with the
referential USV and continues to go towards the des-
tination.
An Improved APFM for Autonomous Navigation and Obstacle Avoidance of USVs
405
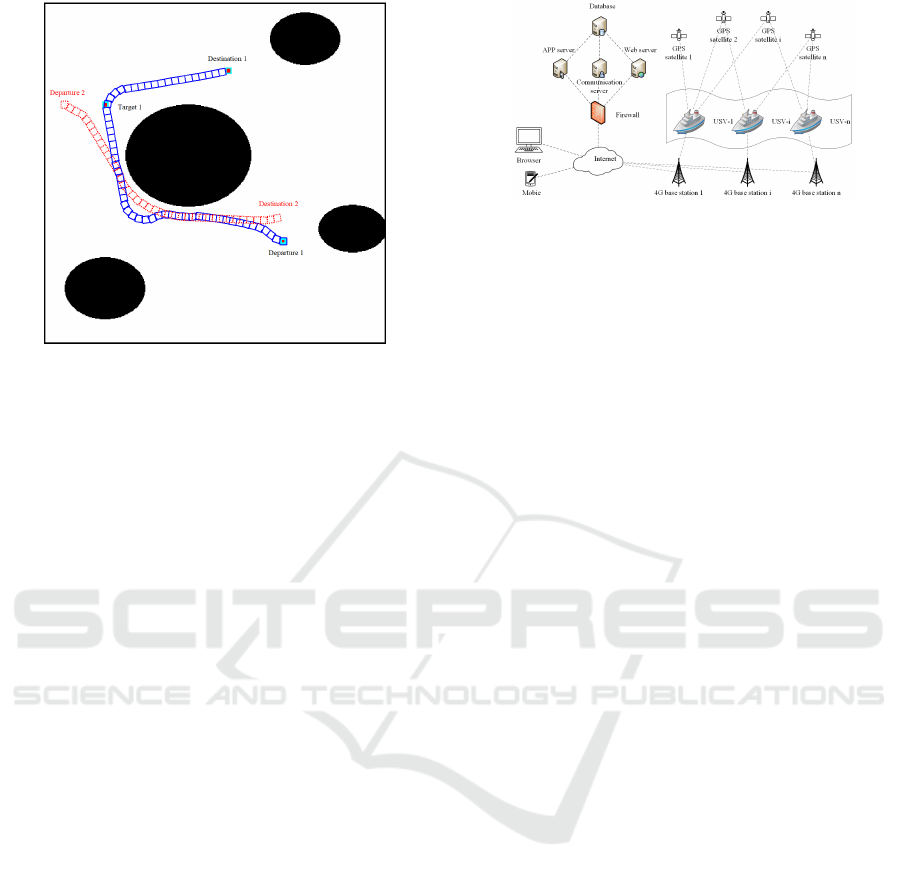
Figure 7: Obstacle detection and avoidance with moving
obstacles.
5 USVS AND EXPERIMENTAL
RESULTS
5.1 Architecture of USVs
We developed a USV for water quality monitoring.
The main architecture of the USV is shown in Figure
8. During navigation, the USV uses a simple commer-
cial GPS receiver to continuously obtain its positions
from GPS satellites. The positioning accuracy of the
GPS receiver is 1.5 meters. An inertial measurement
unit (IMU) is used to obtain the USV’s heading and
acceleration in real time. In addition, the USV can de-
tect surrounding obstacles protruding from the water
surface using a single-line LIDAR. The detection dis-
tance of the LIDAR is 10 meters. All these data will
be input to the algorithm of autonomous navigation
and obstacle avoidance to guide the navigation of the
USV based on a predefined navigation route. Water
quality sensors deployed under the USV body collect
water quality data at a regular interval. A 4G-based
data transfer unit (DTU) transfers water quality data
to the remote data center via the 4G mobile network
and the Internet. Finally, all the water quality data are
processed and saved in a database. Front end users
can use a web browser or an Android APP to query
and analyse water quality data respectively.
The USV is based on a catamaran. The stability,
payload capacity and ease of deck access make cata-
marans a compelling for USVs (Manley, 2008). Fig-
ure 9 shows the main components of the USV. All the
electronic devices such as the Raspberry Pi, battery,
DTU and GPS are all installed in the cabin. The wa-
ter quality monitoring sensors and a Doppler sensor
Figure 8: Architecture of USVs.
are deployed under the USV. Both live camera and
LIDAR are installed in the front of the USV.
5.2 Autonomous Navigation and
Obstacle Avoidance
5.2.1 Autonomous Navigation
The USV is tested in a small lake which is about 213
meters long and 196 meters wide. We select seven
positions using Google map to define a polygon and
zigzag navigation route respectively shown in Fig-
ures 10(a) and 10(b). The actual autonomous navi-
gation trajectory is shown in Figures 10(c) and 10(d).
Compared the actual navigation trajectory to the pre-
defined navigation route we find that the improved
APFM can guide the navigation of the USV based on
the predefined navigation route. However, affected by
the wind and the accuracy of the GPS receiver, there
is a little deviation between the actual trajectory and
the predefined route.
5.2.2 Obstacle Avoidance
We set another polygon route with five positions to
test the function of obstacle avoidance. We use two
balloons as static obstacles and one remote controlled
ship (RC ship) as a dynamic obstacle during the nav-
igation. The navigation route and the experimental
scenario are shown in Figure 11.
We use a RC ship to simulate a dynamic obstacle.
When the USV is navigating from the third position to
the fourth position, we remotely control the RC ship
move towards the USV to verify whether the USV can
detect the dynamic obstacle and avoid the collision
or not. From Figure 11(c) we find that controlled by
the algorithm of autonomous navigation and obstacle
avoidance, the USV can autonomously navigate based
on the predefined navigation route.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
406

(a) Components of the USV (b) Overall appearance of the USV
Figure 9: Main components of the USV.
(a) Polygon navigation route (b) Zigzag navigation route
(c) Actual track for polygon navigation route (d) Actual track for zigzag navigation route
Figure 10: Autonomous navigation without obstacles.
(a) Navigation route with obstacles (b) USV, balloons and RC ship (c) Actual track
Figure 11: Autonomous navigation with obstacles.
An Improved APFM for Autonomous Navigation and Obstacle Avoidance of USVs
407

6 CONCLUSIONS
We proposed an improved APFM for USVs. A re-
versed obstacle avoidance algorithm was developed
to improve the steering ability of the USV in tight
spaces. Integrated with multi-position path planning
approach and PID control, we simulated and tested
the improved APFM in MATLAB to validate the cor-
rectness and performance of our algorithm. Finally,
we applied our algorithm to a real USV and tested in
a real lake. Experimental results show that the USV
can autonomously navigate based on the predefined
navigation route and avoid static and dynamic obsta-
cles.
ACKNOWLEDGEMENTS
This work was partly supported by the AI University
Research Centre (AI-URC) through XJTLU Key Pro-
gramme Special Fund (KSF-P-02), Natural Science
Foundation of Suzhou City (SYG201837), Natural
Science Foundation of Nantong City(JC2018075)and
Nantong University-Nantong Joint Research
Center for Intelligent Information Technology
(KFKT2017A06).
REFERENCES
Bertram, V. (2008). Unmanned surface vehicles-a survey.
Skibsteknisk Selskab, Copenhagen, Denmark, 1:1–14.
Borenstein, J. and Koren, Y. (1990). Real-time obstacle
avoidance for fast mobile robots in cluttered environ-
ments. In Proceedings., IEEE International Confer-
ence on Robotics and Automation, pages 572–577.
IEEE.
Enderle, B., Yanagihara, T., Suemori, M., Imai, H., and
Sato, A. (2004). Recent developments in a total
unmanned integration system. In Proc. AUVSI Un-
manned Systems Conference, volume 9.
Khatib, O. (1986a). Real-time obstacle avoidance for ma-
nipulators and mobile robots. In Autonomous robot
vehicles, pages 396–404. Springer.
Khatib, O. (1986b). Real-time obstacle avoidance for ma-
nipulators and mobile robots. In Autonomous robot
vehicles, pages 396–404. Springer.
Li, Y. and He, K. (2006). A novel obstacle avoidance and
navigation method for outdoor mobile robot based on
laser radar. Robot, 28(3):275–278.
Li, Z., Bachmayer, R., and Vardy, A. (2017). Vector field
path following control for unmanned surface vehicles.
In OCEANS 2017-Aberdeen, pages 1–9. IEEE.
Liu, Y., Liu, W., Song, R., and Bucknall, R. (2017). Pre-
dictive navigation of unmanned surface vehicles in a
dynamic maritime environment when using the fast
marching method. International Journal of Adaptive
Control and Signal Processing, 31(4):464–488.
Liu, Z., Zhang, Y., Yu, X., and Yuan, C. (2016). Unmanned
surface vehicles: An overview of developments and
challenges. Annual Reviews in Control, 41:71–93.
Maguer, A., Gourmelon, D., Adatte, M., and Dabe, F.
(2005). Flash and/or flash-s dipping sonars on spar-
tan unmanned surface vehicle (usv): A new asset for
littoral waters. In Turkish International Conference on
Acoustics.
Manley, J. E. (2008). Unmanned surface vehicles, 15 years
of development. In OCEANS 2008, pages 1–4. Ieee.
Naeem, W., Xu, T., Sutton, R., and Tiano, A. (2008). The
design of a navigation, guidance, and control system
for an unmanned surface vehicle for environmental
monitoring. Proceedings of the Institution of Mechan-
ical Engineers, Part M: Journal of Engineering for the
Maritime Environment, 222(2):67–79.
Peng, Y., Han, J.-d., and Huang, Q.-j. (2009). Adaptive ukf
based tracking control for unmanned trimaran vehi-
cles. International Journal of Innovative Computing,
Information and Control, 5(10):3505–3516.
Polvara, R., Sharma, S., Wan, J., Manning, A., and Sutton,
R. (2018a). Obstacle avoidance approaches for au-
tonomous navigation of unmanned surface vehicles.
The Journal of Navigation, 71(1):241–256.
Polvara, R., Sharma, S., Wan, J., Manning, A., and Sutton,
R. (2018b). Obstacle avoidance approaches for au-
tonomous navigation of unmanned surface vehicles.
The Journal of Navigation, 71(1):241–256.
Wang, H., Wei, Z., Wang, S., Ow, C. S., Ho, K. T., and
Feng, B. (2011). A vision-based obstacle detection
system for unmanned surface vehicle. In 2011 IEEE
5th International Conference on Robotics, Automation
and Mechatronics (RAM), pages 364–369. IEEE.
Zhang, R., Tang, P., Su, Y., Li, X., Yang, G., and Shi, C.
(2014a). An adaptive obstacle avoidance algorithm for
unmanned surface vehicle in complicated marine en-
vironments. IEEE/CAA Journal of Automatica Sinica,
1(4):385–396.
Zhang, R., Tang, P., Su, Y., Li, X., Yang, G., and Shi,
C. (2014b). An adaptive obstacle avoidance algo-
rithm for unmanned surface vehicle in complicated
marine environments. IEEE/CAA Journal of Automat-
ica Sinica, 1(4):385–396.
Zhou, X., Ling, L., Ma, J., Tian, H., Yan, Q., Bai, G., Liu,
S., and Dong, L. (2015). The design and application
of an unmanned surface vehicle powered by solar and
wind energy. In Power Electronics Systems and Ap-
plications (PESA), 2015 6th International Conference
on, pages 1–10. IEEE.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
408
