
Autonomous Overtaking Maneuver Design based on Follow the Gap
Method
Munire Damla Demir
1
and Volkan Sezer
2
1
AVL Research and Engineering, Istanbul, Turkey
2
Control and Automation Engineering Department, Istanbul Technical University, Istanbul, Turkey
Keywords:
Collision Avoidance, Motion Planning, Safety, Overtaking, Merging, Autonomous Drive, Highway Driving,
Motion Control, Path Tracking, Stanley Controller, X-sin Function.
Abstract:
This paper proposes a solution for one of the most important components of autonomous driving: "overtaking
maneuver". Follow the Gap method (FGM) is oneof the most popular obstacle avoidance algorithms and
directly obtains steering angle from position of the obstacles around. This paper is the first study using FGM
to solve the overtaking problem. Different from previous studies where a trajectory is planned and then a
controller is designed to track it; we use FGM for motion planning and control together. This paper focuses
on overtaking maneuver in a challenging environment like highway traffic where the safety and fast response
are the key factors. After we adapt the FGM to overtaking problem, we compare it with an existing overtaking
method X-sin functions from literature. Since X-sin functions method requires a path tracker (controller),
Stanley method is combined with X-sin functions. At the end of this work, we show several advantages of
FGM comparing to the X-sin functions based overtaking approach.
1 INTRODUCTION
With the rapid development of technology in recent
years, the automotive industry is moving closer to full
autonomous vehicles. The most critical benefit of au-
tonomous driving is human safety. Every year ap-
proximately 1.35 million people die because of traf-
fic accidents according to "Global Status Report on
Road Safety" (Toroyan, 2018). In addition, 25-78%
of accidents happened as a result of driver inatten-
tion (Klauer et al., 2010) and 10% of all crashes hap-
pened during the lane change (G. M. Fitch and Din-
gus, 2009). In order to avoid crashes, one of the most
important thing to do is providing fast response.
Global path planning algorithms requires high
computational time for their operations. For exam-
ple A*, which is one of the most popular graph search
algorithm, finds a path from point A to B for static
maps (Likhachev and Ferguson, 2009). On the other
hand, it is not very convenient to find a new path
using A* if the map changes very often as in dy-
namic environments. D* is introduced as improved
A* which is more adaptable to moving obstacles but
still not as fast as obstacle avoidance methods (Stentz,
1994). Nonholonomic constrains of vehicle are con-
sidered in "Rapidly Exploring Random Tree (RRT)"
method which is a probabilistic approach and pro-
vides a smooth driving (Lavalle, 1998). The main
drawback of these kind of methods is the required
computational time. Moreover, afters suitable trajec-
tory is generated, the trajectory must be followed by
a path tracker algorithm.
The aim of a path tracker algorithm is to calculate
the required control inputs reach from one waypoint
to another. Stanley (Snider, 2009) method and Pure
Pursuit (Coulter, 1992) are two popular tracking al-
gorithms.The comparison of these two approaches is
shown (Cibooglu et al., 2017) which proposes a hy-
brid method at the end. According to the analysis,
Pure Pursuit does not provide a good performance
in cutting roads and Stanley method overshoots at
sharp corners. Another result from analysis is Stan-
ley method has more advantages than Pure Pursuit at
high speeds.
For the solution of overtaking problem, Mixed
Observable Markov Decision Process (MOMDP)
based solution is provided in (Sezer, 2018). However,
this solution is not suitable for real-time applications
due to its computational complexity. Moreover dis-
crete state space representation restricts the operation
of the method. Another overtaking approach X-sin is
proposed in (Zhang et al., 2014) which provides ap-
Demir, M. and Sezer, V.
Autonomous Overtaking Maneuver Design based on Follow the Gap Method.
DOI: 10.5220/0007923502950302
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 295-302
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
295

propriate path using special trigonometric functions.
It requires three main parameters for its operation and
calculation of the path is relatively easy. On the other
hand it still needs a controller algorithm in order to
track the desired path.
Obstacle avoidance algorithms are mostly used for
dynamic environments in order to avoid any obstacle
in a short time. For example bug algorithms (Zohaib
et al., 2013) are based on following the borders of
the obstacles but not useful to implement for high-
way driving and vehicle dynamics. Another obsta-
cle avoidance algorithm is Artificial Potential Field
Method (Zhu et al., 2006) and (Bounini et al., 2017)
which results smooth steering angles. However, the
tuning parameters can affect the steering angle a lot
and it should be adapted for every situation in high-
way driving while very different scenarios are possi-
ble. Local minimum problem is another critical dis-
advantage of this approach.
Follow the Gap method (Sezer and Gokasan,
2012) is a geometric obstacle avoidance algorithm
for autonomous driving. FGM selects the maximum
gap angle in the field of view, it combines the the
goal angle and gap angle considering minimum dis-
tance to obstacle. It also considers the nonholonomic
constraints of the vehicle, does not have local mini-
mum problem and is easy to tune with only one tun-
ing parameter. Improved Follow the Gap (FGM-I)
(Demir and Sezer, 2017) is an extended version of
FGM which solves two drawbacks of original FGM.
FGM-I eliminates chattering effect coming from un-
necessary gap change and chooses goal oriented gaps
in order to find a shorter path.
This paper examines the overtaking in highway
conditions where the speed values are relatively high.
Dynamic single track vehicle model is used in order to
obtain more realistic results comparing to pure kine-
matic models (Rajamani, 2011).
In this paper, FGM is implemented as motion
planning and controlling algorithm and compared
with X-sin functions planner and Stanley controller.
Vehicle model, FGM and X-sin planner with Stan-
ley controller (XwS) are explained in section 2, sim-
ulation environment and highway scenarios are ex-
plained in section 3 , and simulation results through
the implementation are shown in section 4. Conclu-
sion of the paper is examined in section 5. Future
Work is provided in section 6.
2 TECHNICAL APPROACH
The general approach in autonomous driving is de-
signing a motion planner and a controller as separated
components. As it is shown in Figure 1, X-sin func-
tion as a motion planner generates a collision free path
in accordance with environment (Zhang et al., 2014).
The path is controlled by the Stanley controller which
obtains the steering angle to be given to vehicle model
(Snider, 2009). From now on we call XwS for the
combination of X-sin functions motion planner and
Stanley controller. The principle of operation of X-sin
functions and Stanley method are explained in Sec-
tion 2.3.
The proposed approach is to combine motion
planner and controller using FGM for overtaking ma-
neuver as it is stated in Figure 2. Follow the Gap
method combines motion planner and controller by it-
self so that quick reaction in dynamic environment is
available while considering safety and comfort. The
principle of operation of FGM is explained in Section
2.2.
Figure 1: Concept of Motion Planing and Control using.
Figure 2: Concept of New Approach based on FGM.
2.1 Vehicle Model
In order to make realistic simulations, single track
dynamic vehicle model (Rajamani, 2011) is used in-
stead of a kinematic bicycle model which neglects
tire forces. Even though the kinematic model is ap-
plicable at lower speeds, dynamic model is required
for highway scenarios at high speeds. Since this
work concentrates on overtaking maneuver, longitu-
dinal speed is considered as constant. Dynamic bicy-
cle model is represented as it is shown in Figure 3. X,
Y represent the global coordinates, x, y represent the
local coordinate of vehicle where CG is the vehicle’s
center of gravity. L
f
is the distance from center of
gravity to front wheel and L
r
is the distance from CG
to rear wheel. δ and ψ are the steering angle and yaw
angle of the vehicle, respectively. Finally, F
y f
and F
yr
represent the lateral forces.
(1) and (2) are standard equations for lateral dy-
namics. x, y positions of ego vehicle and yaw angle
are obtained by the (2), (3) and (4).
m ˙v = F
y f
cos(δ) +F
yr
+ mv
x
˙
ψ (1)
I
z
¨
ψ = L
f
F
y f
cos(δ) −L
r
F
yr
(2)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
296
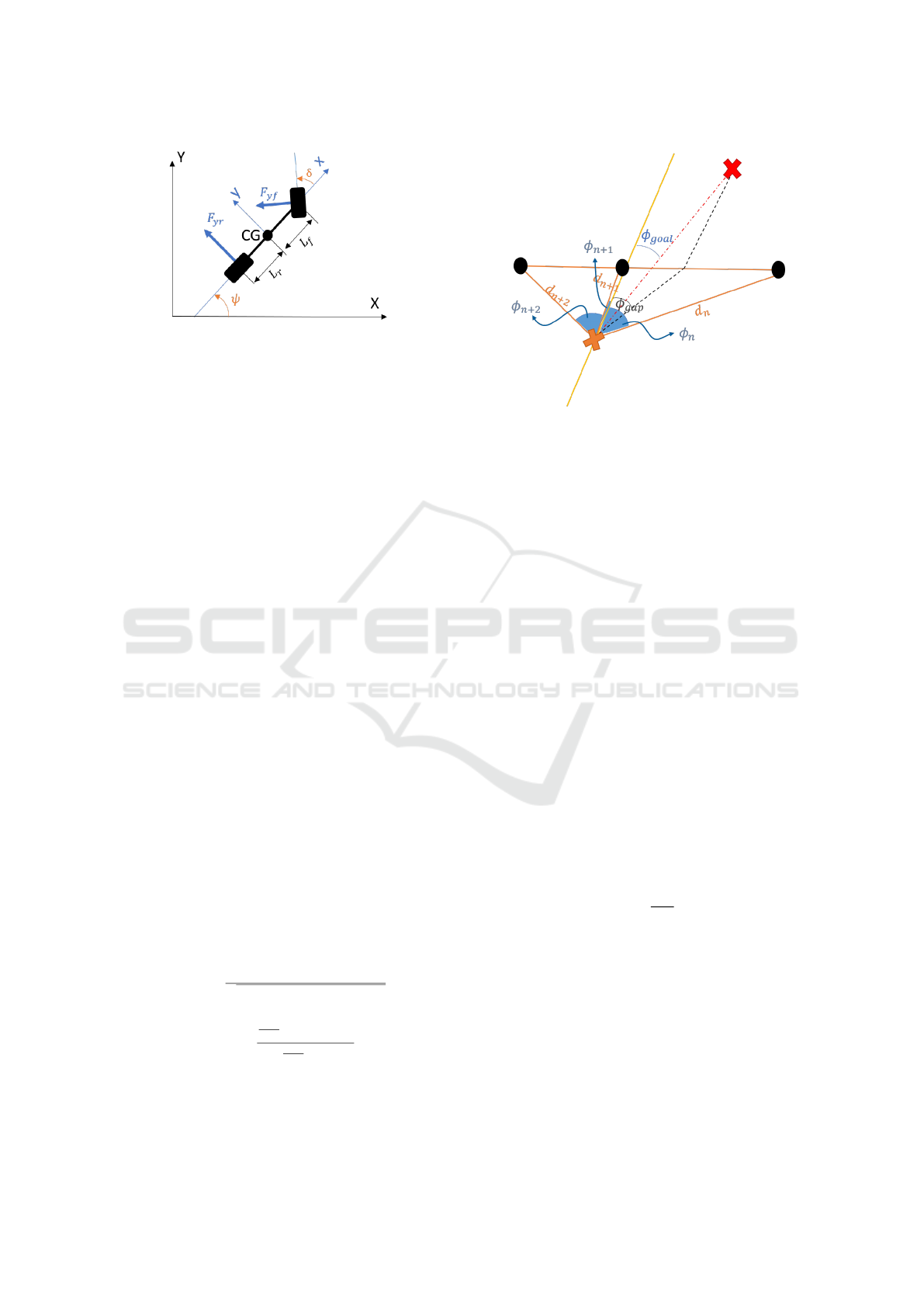
Figure 3: Single Track Lateral Dynamics.
˙x = v
x
cosψ −v
y
sinψ (3)
˙y = v
x
sinψ +v
y
cosψ (4)
2.2 Follow the Gap Method
FGM basically monitors the maximum gap between
the closest obstacles in field of view and generates
a steering angle which avoids the obstacles consider-
ing the goal point (Sezer and Gokasan, 2012). FGM
generates desired heading angle which can be used as
steering angle directly. Figure 4 shows the angles re-
garding to FGM; orange X is the starting point, red X
is the target point, black dots represent obstacles, red
dashed line represents the connection between start-
ing point and goal point, black dashed line represents
the connection between starting point and gap center
of selected obstacles in the field of view, d
n
is the dis-
tance from ego vehicle to the n
th
obstacle, φ
n
is the
angle of the n
th
gap, φ
gap
is the angle of the selected
gap which is developed by the FGM, φ
goal
is the angle
from ego the goal point. (5) calculates φ
gap
in terms
of measurable variables, and (6) provides φ
f inal
which
is the final angle for the vehicle. α is a tuning pa-
rameter and selected as 0.5 according to experimental
results. The higher α means the more importance on
φ
gap
so that φ
f inal
is closer to the φ
gap
. The lower α
means the more importance on φ
goal
therefore phi
f inal
is weighted more on φ
goal
. d
min
is the closest distance
from the nearest obstacle which weights φ
goal
and
φ
gap
automatically. According to (6), when the ego
vehicle approaches to an obstacle, φ
gap
is weighted
more than φ
goal
and vice versa.
φ
gap
n
= cos
−1
d
n
+d
n+1
cos(φ
n
+φ
n+1
)
q
d
2
n
+d
2
n+1
+2d
n
d
n+1
cos(φ
n
+φ
n+1
)
!
− φ
n
(5)
φ
f inal
=
α
d
min
φ
gap
+ φ
goal
α
d
min
+ 1
(6)
φ
f inal
is the desired heading angle but can be di-
rectly used as steering angle as it is implemented in
this paper. For different applications, an additional
Figure 4: Follow the Gap Angle Representation.
controller can be designed to calculate the steering an-
gle in order to get the desired heading angle.
2.2.1 Adaptation of FGM to Overtaking
Maneuver
In order to adapt FGM for overtaking maneuver, we
specify a single goal point that is located in front of
the actor vehicle. This goal point moves with the ac-
tor vehicle. Actor vehicle is also an obstacle for ego
vehicle. The borders of the road are also other obsta-
cles for ego vehicle. If FGM is used as an obstacle
avoidance algorithm to reach the goal point which is
defined in front of actor vehicle, the final trajectory
becomes an overtaking maneuver.
The flowchart of overtaking algorithm using FGM
is shown in Figure 5. First, time to collision T
tc
value
is calculated as shown in (7). The algorithm checks
whether that T
tc
value is lower than 2 seconds. This
experimental value is selected according to (Kristofer
D. Kusano, 2011). This first part of the approach is
preparation for lane change as shown in Figure 6. In
this figure, red X is defined as the goal point and blue
dots are obstacles. If T
tc
value is lower than 2 seconds,
the ego vehicle starts lane changing using FGM.
T
tc
=
d
eto
V
net
(7)
d
eto
: Distance between ego vehicle to obstacle [m],
T
tc
: Time to Collision [s], V
net
: Velocity difference
between ego and actor vehicles [m/s]
Secondly, FGM finds the gap goes forward to the
gap until it reaches the rear left corner of the front
actor vehicle which is shown in Figure 7. This is
the passing phase of overtaking maneuver. Look
ahead range (LAR) distance is added in order to avoid
the quick and dangerous merging so that ego vehicle
keeps its lane until it reaches the location that is de-
fined by LAR.
Autonomous Overtaking Maneuver Design based on Follow the Gap Method
297
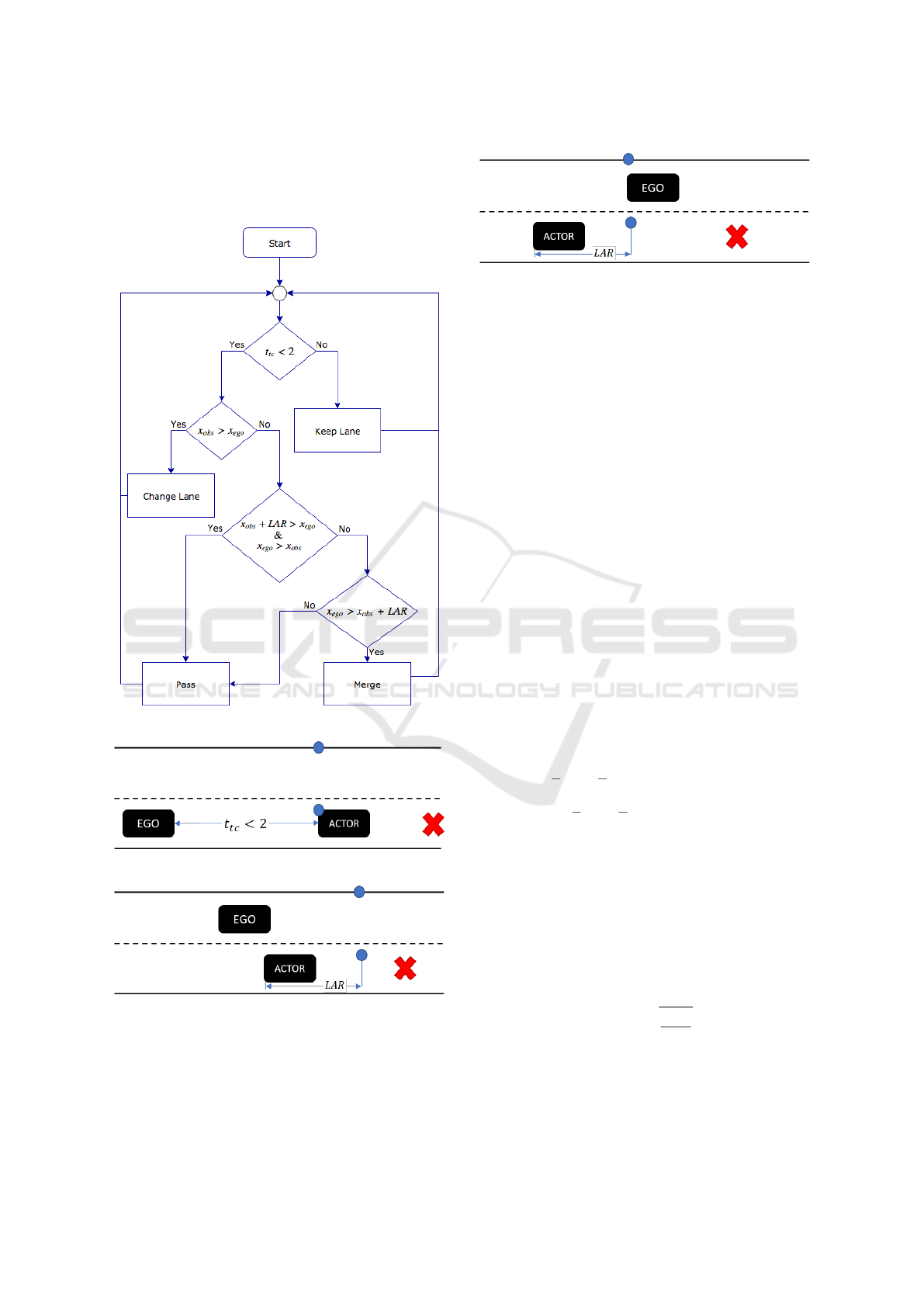
Finally, ego vehicle starts to steer to get back to
the initial lane where LAR away from actor vehicle.
This last phase of overtaking is called "merging" as
shown in Figure 8.
Figure 5: Algorithm of Overtaking.
Figure 6: Lane Change using FGM.
Figure 7: Passing the actor vehicle using FGM.
In section 4, three different speed scenarios are
presented and overtaking performances of FGM are
declared.
Figure 8: Merging using FGM.
2.3 X-sin Function as a Motion Planner
and Stanley Method as a Motion
Controller
2.3.1 X-sin Function as a Motion Planner
X-sin function was developed as a solution for over-
taking maneuver using standard mathematical func-
tions in (Zhang et al., 2014). X-sin is a partial func-
tion which calculates the lateral and longitudinal posi-
tion of the ego vehicle as illustrated in Figure 9. Over-
taking decision is made in the same way as in previous
FGM approach by using (7). Goal position is selected
in the end of the merging distance which dynamically
moves with actor vehicle.
Figure 9 shows the parameters and trajectory of
a typical X-sin function. L
d
is the distance of lane
changing, O
d
is defined as distance of passing which
is chosen as the length of the ego vehicle and M
d
is
the distance of merging which is selected as same as
L
d
.
Eq. (8) provides the mathematical function of X-
sin where x is the current position and y
d
is the lane
change distance in y axis.
y(x) =
y
d
h
2π
L
d
x −sin
2π
L
d
x
i
x ∈ [0,L
d
]
y
d
x ∈ [L
d
,L
d
+ O
d
]
y
d
− y
d
h
2π
L
d
x −sin
2π
L
d
x
i
x ∈ [L
d
+ O
d
,L
d
+ O
d
+ M
d
]
(8)
The L
d
parameter in X-sin is critical for a comfortable
overtaking maneuver. Original paper (Zhang et al.,
2014) proposes an equation which calculates a good
L
d
as shown in (9). The maximum allowed acceler-
ation limit a
max
is declared in (Zhang et al., 2014) as
between 1−4m/s
2
and v
x
is the longitudinal speed of
the ego vehicle. In this paper, a
max
is selected 3m/s
2
and L
d
is calculated according to the vehicle speed v
x
in section 4. M
d
is selected same as L
d
.
L
d
= v
x
r
2πy
d
a
max
(9)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
298

Figure 9: X-sin function representation.
2.3.2 Stanley Method as a Motion Controller
Stanley Method is commonly implemented as a
motion controller for autonomous vehicles (Snider,
2009). In this paper, Stanley method is developed
as a motion controller to track the trajectory which is
generated by X-sin function. Stanley controller cal-
culates the steering angle using yaw error and cross
track error which are represented in (10). Figure 10
illustrates the Stanley method and shows the steering
angle, heading angle, lateral error and longitudinal
speed variables in detail.
Figure 10: Stanley Controller Representation.
δ(t) = ψ(t) +tan
−1
ke(t)
v
x
(t)
(10)
Cross track error e(t) is the lateral error which means
the closest distance between the ego vehicle and the
path. Yaw error ψ is the difference between the head-
ing of closest path point and ego vehicle heading, v
x
is
longitudinal speed. k is the tuning parameter which is
selected as 10 using trial and error technique in order
to get the best performance.
3 SIMULATION ENVIRONMENT
Matlab/Simulink environment is used to generate ve-
hicle models, to implement algorithms, to create sim-
ulation scenarios, and to compare both of the meth-
ods. The scenarios are selected considering highway
traffic where the speed is between 10 - 35 m/s (KGM,
2018) with 3.5m lane width as it is defined in stan-
dards (EuroTest, 2007).
During simulations, initial positions, initial head-
ing, distance to goal point, environment and limita-
tions are in same manner for both of the methods for
a fair comparison. Goal point is selected as the end of
merging which is represented by M
d
away from the
actor vehicle. Goal point distance for FGM and XwS
are selected same in the simulations which is calcu-
lated in (9).
4 RESULTS
In this paper, FGM and XwS are compared accord-
ing to different speeds. This comparison is made us-
ing the safety metric, the comfort metric and the total
traveled distance. The related metrics are calculated
using the general norm equation which is shown in
(11). We select p as 2, which means second norm of
the signals are calculated. Similar metrics can be seen
in (Sezer and Gokasan, 2012) and (Demir and Sezer,
2017).
|| f ||
p
=
Z
| f (t)|
p
dt
1/p
(11)
The f (t) function for safety metric is defined as the
distance between the ego and the actor vehicle. It
means that if the distance between ego vehicle and
actor vehicle is generally high, the safety metric re-
sults with higher values in another words this is a
safer overtaking. The f (t) function for comfort met-
ric is defined as the yaw rate of the ego vehicle. The
increase in this metric means that the change ego ve-
hicle’s yaw angle is high which is an uncomfortable
situation for the passenger. Total path is additionally
calculated for comparison.
Figure 11 and Figure 12 illustrates the results of
overtaking for FGM and XwS. The time samples are
added to represent the locations of ego vehicle and
actor vehicle for each specific time sample.
Table 1 contains a detailed comparison of FGM
and XwS by comfort metric, safety metric and total
traveled path. For both FGM and XwS, the initial
positions are same, goal positions are calculated by
same method and both approaches are compared ac-
cording to the identical speeds. Table 1 shows that, at
the same speeds, both comfort metric and safety met-
ric values of FGM are higher than XwS. The result
of more comfortable and safer overtaking maneuver
is longer paths as shown in Table 1. For example
in Figure 11.a and Figure 12.a, it is clearly seen that,
the total path of FGM is greater than the total path of
Autonomous Overtaking Maneuver Design based on Follow the Gap Method
299

Figure 11: a. Overtaking by FGM at V
ego
= 20m/s, b. Overtaking by FGM at V
ego
= 25m/s, c. Overtaking by FGM at
V
ego
= 30m/s.
XwS when V
ego
= 20m/s. The longer path of FGM
occurs due to the passing part of overtaking maneu-
ver. During the passing phase, when the ego vehicle
is getting closer to the actor vehicle, d
min
value de-
creases and ego vehicle intends to avoid from actor
vehicle as calculated in (6).
Safer and more comfortable driving of FGM
makes the increase of the total path less important. In
Figure 12.c, the speed of ego vehicle is 30m/s and it
is clearly seen that, Stanley method causes overshoot
in control. This may cause more overshoots when the
speed of ego vehicle is higher.
Table 1: FGM and Comparison Table.
Speed / Metrics Comfort metric Safety metric Total Path [m]
20 m/s
FGM 216.45 21.21 146.84
XwS 333.24 19.37 135.54
25 m/s
FGM 282.34 30.65 161.30
XwS 484.05 25.50 153.77
30 m/s
FGM 371.90 40.16 184.27
XwS 648.70 31.60 174.88
1000 Monte Carlo simulations are implemented to
test FGM and in same environment to calculate the
average improvement rate of FGM. The speed of the
ego vehicle is assigned randomly between 10 - 20 m/s
and the speed of actor vehicle is assigned randomly
between 8 - 12 m/s. Each Monte Carlo simulation is
performed by giving the same random speeds to the
ego vehicle and the actor vehicle for FGM and XwS.
According to the speeds of ego and actor vehicles,
D
eto
, L
d
, M
d
and the goal position are calculated. Av-
erage results of 1000 simulations are shown in Table
2.
According to the results the average comfort met-
ric of FGM is 41% better and the average safety met-
ric of FGM is 13% better than XwS results. On
the other hand, the average total path of 1000 Monte
Carlo simulations of FGM is 2.41% longer which is
the result of safer paths. Overall, FGM is signifi-
cantly safer and more comfortable than XwS and re-
sults with a little bit longer paths.
Table 2: Results of 1000 Monte Carlo Simulations.
Method / Metrics Comfort metric Safety metric Total path [m]
FGM 290.15 31.21 164.02
XwS 493.96 27.01 160.15
Improvement Rate 41% 13% -2.41%
5 CONCLUSION
In this paper, FGM is adapted for overtaking maneu-
ver design and control. After this design, FGM is
compared with XwS in highway overtaking scenarios.
Dynamic single track vehicle model is used for sim-
ulations. One of the main differences between two
approaches is; in XwS we need two separated solu-
tions for planing and control while FGM is enough for
both operations. Monte Carlo results show that FGM
based overtaking solution is 13% safer and 41% more
comfortable than XwS while the total traveled path is
2.41% longer. These results show that FGM is very
suitable to solve the overtaking maneuver.
6 FUTURE WORK
Although FGM is an obstacle avoidance method, it is
observed that it gives better results than XwS at high-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
300
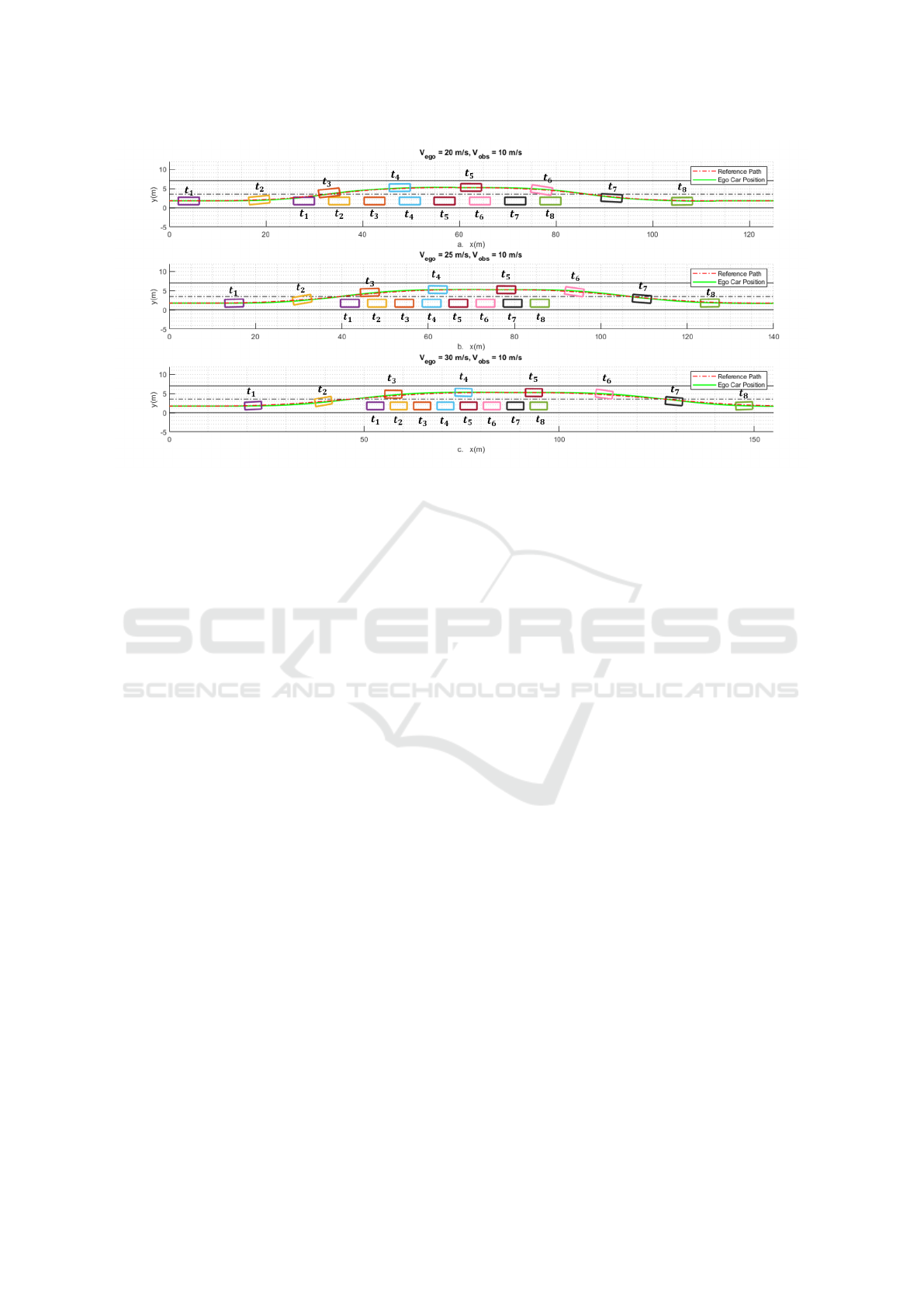
Figure 12: a. Overtaking by XwS at V
ego
= 20m/s, b. Overtaking by XwS at V
ego
= 25m/s, c. Overtaking by XwS at
V
ego
= 30m/s.
way conditions. The optimization of decision param-
eters for overtaking maneuver such as critical time to
collision value or LAR distance can be thought as a
future study. FGM would be very suitable for dy-
namic environments like urban because of its stability
against moving obstacles. FGM is also easily adapt-
able for intersections, roundabouts or different types
of junctions.
REFERENCES
Bounini, F., Gingras, D., Pollart, H., and Gruyer, D. (2017).
Modified artificial potential field method for online
path planning applications. pages 180–185.
Cibooglu, M., Karapinar, U., and Soylemez, M. T.
(2017). Hybrid controller approach for an autonomous
ground vehicle path tracking problem. In 2017 25th
Mediterranean Conference on Control and Automa-
tion (MED), pages 583–588.
Coulter, R. C. (1992). Implementation of the pure pur-
suit path tracking algorithm. Technical Report CMU-
RI-TR-92-01, Carnegie Mellon University, Pittsburgh,
PA.
Demir, M. and Sezer, V. (2017). Improved follow the gap
method for obstacle avoidance. In 2017 IEEE Inter-
national Conference on Advanced Intelligent Mecha-
tronics (AIM), pages 1435–1440.
EuroTest (2007). http://www.theaa.com/public_affairs/
reports/eurotest-motorway-roadworks-2007.pdf.
G. M. Fitch, S. E. Lee, S. K. J. H. J. S. and Dingus, T.
(2009). Analysis of Lane-Change Crashes and Near-
Crashes. National Highway Traffic Safety Adminis-
tration.
KGM (2018). Hizsinirlari. http://www.kgm.gov.tr/Sayfalar/
KGM/SiteTr/Trafik/HizSinirlari.aspx.
Klauer, S., Guo, F., Sudweeks, J., and Dingus, T. (2010). An
analysis of driver inattention using a case-crossover
approach on 100-car data.
Kristofer D. Kusano, H. G. (2011). Method for estimating
time to collision at braking in real-world, lead vehicle
stopped rear-end crashes for use in pre-crash system
design. SAE International.
Lavalle, S. M. (1998). Rapidly-exploring random trees: A
new tool for path planning. Technical report.
Likhachev, M. and Ferguson, D. (2009). Planning long dy-
namically feasible maneuvers for autonomous vehi-
cles. The International Journal of Robotics Research,
28(8):933–945.
Rajamani, R. (2011). Vehicle Dynamics and Control. Me-
chanical Engineering Series. Springer US.
Sezer, V. (2018). Intelligent decision making for overtaking
maneuver using mixed observable markov decision
process. J. Intellig. Transport. Systems, 22(3):201–
217.
Sezer, V. and Gokasan, M. (2012). A novel obstacle avoid-
ance algorithm: "follow the gap method". Robot. Au-
ton. Syst., 60(9):1123–1134.
Snider, J. M. (2009). Automatic steering methods for au-
tonomous automobile path tracking.
Stentz, A. (1994). Optimal and efficient path planning for
partially-known environments. In Proceedings of the
1994 IEEE International Conference on Robotics and
Automation, pages 3310–3317 vol.4.
Toroyan, T. (2018). Global status report on road safety.
page 2.
Zhang, S., Liu, W., Li, B., Niu, R., and Liang, H. (2014).
Trajectory planning of overtaking for intelligent vehi-
cle based on x-sin function. In 2014 IEEE Interna-
tional Conference on Mechatronics and Automation,
pages 618–622.
Zhu, Q., Yan, Y., and Xing, Z. (2006). Robot path planning
based on artificial potential field approach with sim-
Autonomous Overtaking Maneuver Design based on Follow the Gap Method
301

ulated annealing. Sixth International Conference on
Intelligent Systems Design and Applications, 2:622–
627.
Zohaib, M., Pasha, S. M., Javaid, N., and Iqbal, J. (2013).
Intelligent bug algorithm (iba): A novel strategy
to navigate mobile robots autonomously. CoRR,
abs/1312.4552.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
302
