
Exploring Robustness in a Combined Feature Selection Approach
Alexander Wurl
1
, Andreas Falkner
1
, Alois Haselb
¨
ock
1
, Alexandra Mazak
2
and Peter Filzmoser
3
1
Siemens AG
¨
Osterreich, Corporate Technology, Vienna, Austria
2
JKU, Department of Business Informatics Software Engineering (CDL-MINT), Austria
3
TU Wien, Institute of Statistics and Mathematical Methods in Economics, Austria
p.filzmoser@tuwien.ac.at
Keywords:
Feature Selection, Variable Redundancy, Hardware Obsolescence Management, Data Analytics.
Abstract:
A crucial task in the bidding phase of industrial systems is a precise prediction of the number of hardware
components of specific types for the proposal of a future project. Linear regression models, trained on data
of past projects, are efficient in supporting such decisions. The number of features used by these regression
models should be as small as possible, so that determining their quantities generates minimal effort. The
fact that training data are often ambiguous, incomplete, and contain outlier makes challenging demands on
the robustness of the feature selection methods used. We present a combined feature selection approach: (i)
iteratively learn a robust well-fitted statistical model and rule out irrelevant features, (ii) perform redundancy
analysis to rule out dispensable features. In a case study from the domain of hardware management in Rail
Automation we show that this approach assures robustness in the calculation of hardware components.
1 INTRODUCTION
Multiple linear regression is a standard approach to
predict the value of one or more output variables from
a set of input variables. An example is the predic-
tion of needed hardware components (i.e., output vari-
ables) from a defined set of features (i.e., input vari-
ables) in the bid phase of a Rail Automation project.
Features are properties of the future project that could
be determined by measuring or counting or even ex-
pert guessing. Examples from the Rail Automation
domain are the number of signals of various types,
the number of point branches, track lengths and dis-
tances between track elements. Output variables are
control modules, computers, interfaces, and various
other kinds of hardware components, that can be pre-
dicted from the feature values. On the one hand, a
precise estimation of the quantities of these hardware
modules is essential for a proposal. On the other hand,
time and resources in bid phases are usually critical
and it is very important that the set of features that are
to be determined/measured/estimated by the bid team
is as small as possible. Features that are not absolutely
necessary for the prediction of the hardware compo-
nents should not be requested to be measured, hence,
robust feature reduction methods should be used to
save feature measurement effort without compromis-
ing prediction quality.
Training data for the relationship of hardware
components and features are collected from the in-
stalled base, i.e., data and documents about systems
in the field. These data stem from heterogeneous
data sources. Apart from data integration techniques,
highlighted in (Wurl et al., 2017), selecting rele-
vant features that return a suitable quantity estima-
tion poses various challenges particularly in terms of
outliers in data. In previous work (Wurl et al., 2018)
we aim for finding proper regression models. In this
work, we continue with this topic and focus on the
selection of relevant and necessary features for the re-
gression models.
We recognized in our work on real data from Rail
Automation, that feature relevance analysis could be
combined with feature redundancy analysis to find
small feature sets with robust prediction capabilities.
For instance, let F
1
,. . . ,F
5
be a feature set of numer-
ical quantities for a particular hardware component.
Assume that the set of F
1
,...,F
4
is the result of ana-
lyzing relevant features by our method of choice. But
from expert experience we know that only F
1
and F
2
might be indispensable. The goal of combined feature
selection is to find out whether F
3
and F
4
are redun-
dant or not.
In the context of potential outliers, a robust ap-
84
Wurl, A., Falkner, A., Haselböck, A., Mazak, A. and Filzmoser, P.
Exploring Robustness in a Combined Feature Selection Approach.
DOI: 10.5220/0007924400840091
In Proceedings of the 8th International Conference on Data Science, Technology and Applications (DATA 2019), pages 84-91
ISBN: 978-989-758-377-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

proach is inevitable for such a scenario. In this paper,
we explore robustness as an advantageous property
in a combined feature selection approach: (1) rele-
vance analysis removes irrelevant features from the
entire set of features, and based on this reduced fea-
ture set, (2) redundancy analysis eliminates redundant
features. The result is a minimal feature set with a
suitable prediction accuracy for the estimation of the
hardware component quantities. In a case study, we
evaluate our approach w.r.t. robustness, i.e., we ana-
lyze the quantity of outliers detected in combination
with prediction accuracy. The detection of outliers
may prevent a severely distorted regression estima-
tion of hardware components and finally yields ro-
bustness in analyzing relevant features. Based on a
robust set of relevant features, redundant features are
eliminated.
The paper is structured as follows: In the next sec-
tion, we present the background of combining meth-
ods for feature selection. In Section 3, present a ro-
bust combined feature selection approach. In Sec-
tion 4, we present a case study in the domain of Rail
Automation. In Section 5, we present recent work re-
lated to our approach. We conclude this paper by an
outlook on future work in Section 6.
2 BACKGROUND
The input variables (i.e., features) of our regression
scenario are represented in the data matrix X ∈ R
n×p
with entries x
i j
. The output variables (e.g., hard-
ware component quantities) are represented in the ma-
trix Y ∈ R
n×d
with entries y
ik
. We assume that the
columns of X are mean-centered. In the following we
will focus on predicting a specific output variable y
k
,
for k ∈ {1,...,d}. In order to simplify the notation,
we will denote y := y
k
in the following, referring to a
model for a univariate outcome variable.
In the task of variable selection we assume a linear
relationship between the predictors X (features) and
the predictand y (hardware components),
y = Xβ + ε (1)
where β = (β
1
,...,β
p
)
T
is the vector of regression
coefficients, and ε = (ε
1
,...,ε
n
)
T
is the error term.
In order to find a set of indispensable features ex-
posing redundant features, generally, there are two
methods recommended: individual feature evalua-
tion, and subset evaluation (Guyon and Elisseeff,
2003). Individual evaluation methods are filter meth-
ods using a variable ranking method with a correlation
coefficient or mutual information. Subset evaluation
methods include two kind of methods: (1) Wrapper
methods use nested subset selection methods assess-
ing subsets of variables according to their usefulness
to a given predictor. (2) Embedded methods act in a
similar way but optimizes a two-fold objective func-
tion with a goodness-of-fit term and a penalty for a
large number of variables. The combination of both
methods seems to sharpen the evaluation of finding
an optimal feature set for a given regression task, as
described in Equation (1). An exemplary combinato-
rial framework of (Yu and Liu, 2004) shows the fun-
damental idea: firstly, evaluate relevant features, and
secondly, evaluate redundant features.
In the first step, a filter method is used assigning
correlation coefficient scores to each feature. The fea-
tures are ranked by the score. Typically there exists
a subset of coefficients that are small but not zero,
and that still contribute to the model and probably in-
crease prediction uncertainty. Conclusively, this natu-
rally triggers the question when and under which cir-
cumstances a feature is relevant to belong to a set of
indispensable features. Here, a given threshold by
a user minimizes the feature set accordingly. (Wurl
et al., 2019) show that cutting out uninformative coef-
ficients and their corresponding features by a thresh-
old remains vague as a high score feature value might
be caused by an outlier.
Having found a subset of relevant features the ap-
proach continuous with evaluating redundant features
by using a wrapper method. Basically, in wrapper
methods there are two flavors of strategies: forward
selection and backward elimination. In forward se-
lection variables are progressively added to larger and
larger subsets, whereas in backward elimination one
starts with all variables progressively eliminating the
least promising ones. Here, the backward elimination
is performed by correlation coefficient scores. This
means that the features previously selected as rele-
vant serve as input for the process of eliminating re-
dundant features. Consequently, the elimination pro-
cess is heavily biased by the limitations in the pre-
vious correlation analysis. In an industrial environ-
ment with potentially ambiguous data it is unlikely
that such a procedure operates efficiently determining
which combination of features would give best pre-
diction accuracy.
Since the present scenario in the bid phase of a
Rail Automation reveals a linear relationship between
X (features) and y (a hardware component), as de-
scribed in Equation (1), correlation analysis remains
inevitable. The approach to evaluate, firstly, rele-
vant features, and secondly, redundant features gener-
ally seems to have a certain justification. There exist
similar combinatorial regression approaches in liter-
ature considering correlation with a threshold as se-
Exploring Robustness in a Combined Feature Selection Approach
85

lection criteria to find an optimal feature set (Yu and
Liu, 2003; Radovic et al., 2017). Such a strategy of
both steps may produce reasonable results with cer-
tain space of interpretability but may also reveal draw-
backs in one common challenge, namely, robustness
towards outliers in ambiguous data. Considering this
aspect, finding a robust set of indispensable features
satisfactory to describe a hardware component y re-
mains worth to pursue.
3 ROBUST FEATURE
SELECTION
In this section we propose a combinatorial approach
which includes robustness as an advantageous prop-
erty in finding a minimal set of relevant features. We
focus on the univariate regression task and follow the
concept of (Yu and Liu, 2004) by firstly evaluating
relevant features, and secondly evaluating redundant
features.
Evaluating relevant features implies analyzing if a
feature is indispensable in a feature set and if its re-
moval results in deterioration of the prediction accu-
racy. Overcoming the search for an optimal threshold
as decision criteria for selecting which features are
relevant according to the coefficients measured, we
evaluate relevant features by employing Sparse Par-
tial Robust M-regression (SPRM), which can be de-
scribed as embedded method. SPRM provides esti-
mates with a partial least squares alike interpretabil-
ity that are sparse and robust with respect to both ver-
tical outliers (outliers in the response) and leverage
points (outliers in the space of the predictors) (Hoff-
mann et al., 2015). Instead of cutting out uninforma-
tive coefficients by a given threshold like in existing
combinatorial methods such as in (Yu and Liu, 2004),
a sparse estimator of β will have many coefficients
that are exactly equal to zero. The SPRM estimator is
built upon partial least squares, therefore, a so-called
latent variable model is assumed
y
i
= t
T
i
γ + ε
∗
i
, (2)
with q-dimensional score vectors t
i
and regression co-
efficients γ, and an error term ε
∗
i
. The latent compo-
nents (scores) T are defined as linear combinations of
the original variables T = XA, where a
k
the so-called
direction vectors (also known as weighting vectors or
loadings) are the columns of A. The scores t
i
are de-
fined intrinsically through the construction of latent
variables. This is done sequentially, for k = 1, 2, . . . , q,
by using the criterion
a
k
= argmax
a
Cov(y,Xa) (3)
under the constraints ka
k
k = 1 and Cov(Xa
k
,Xa
j
) = 0
for 1 ≤ j < k.
In order to obtain a robust version of T , SPRM
performs the following steps (for details we refer to
(Hoffmann et al., 2015)):
1. Case weights w
i
∈ [0, 1], for i = 1,...,n, are as-
signed to the rows of X and y. If an observation
has a large residual, or is an outlier in the covariate
in the latent regression model, this observations
will receive a small weight. The case weights are
initialized at the beginning of the algorithm.
2. The weights from the previous step are incorpo-
rated in the maximization of (3), by weighting the
observations, and thus maximizing a weighted co-
variance. In addition to that, an L
1
penalty is em-
ployed, which imposes sparsity in the resulting
vectors a
k
, for k = 1,...,q. The result is a sparse
matrix of robustly estimated direction vectors A
and scores T = X A.
3. The regression model (2) is considered, but the
regression parameters are estimated by robust M-
regression,
ˆ
γ = argmin
γ
n
∑
i=1
ρ(y
i
−t
T
i
γ). (4)
The function ρ is chosen to reduce the influence
of big (absolute) residuals y
i
− t
T
i
γ, see (Serneels
et al., 2005). Note that the least squares estimator
would result with a choice ρ(u) = u
2
, with an un-
bounded influence of big values u
2
. The updated
weights are based on w(u) = ρ
0
(u)/u, where ρ
0
is
the derivative of the function ρ.
Steps 2 and 3 are iterated until the estimated re-
gression coefficients stabilize. Note that there are now
two tuning parameters: the number q of components,
and the sparsity parameter, later on called η (“eta”);
η needs to be selected in [0,1], where η = 0 leads to
a non-sparse solution, and bigger values of η to more
and more sparsity.
After applying SPRM, the result is a feature set of
the original size but all irrelevant features found are
set to 0. Therefore, to receive relevant features only
we induce a reduced feature set.
Definition. A reduced feature set is a subset of the
initial feature set F
∗
>0
⊆ F.
The reduced feature set obtained consequently im-
plies the reduction of the underlying data set. Next,
the reduced feature set serves as input for the re-
dundancy evaluation. For this procedure, we employ
the wrapper method Recursive Feature Elimination
(RFE), which follows the concept of backward selec-
tion. Since RFEs are not sensitive towards outliers
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
86
(Johnson et al., 2002), outliers identified by SPRM
need to be filtered out before continuing with RFE.
This step assures that RFE starts with a reduced fea-
ture set robustly evaluated by SPRM.
The algorithm of RFE works with two loops
(Kuhn, 2012). In the the outer loop, a resampling
method such as 10-fold cross validation starts with
splitting the data set and trains the model to fit all pre-
dictors to the model. Next, each predictor is ranked
by the importance to the model, representing a se-
quence of ordered numbers which are candidate val-
ues for the number of predictors to retain. The inner
loop is responsible for selecting the most important
features, i.e., the top ranked predictors are retained,
and the model is refit and performance is assessed.
For the process of retaining the important features, the
method Random Forest (Breiman, 2001) seems to be
an efficient option, especially when (i) the predictors
are highly collinear, and (ii) the number of observa-
tions is relatively small compared to the number of
predictors (Strobl et al., 2008).
The final regression model of RFE is consid-
ered as minimal feature set including relevant fea-
tures without redundancies. The combined approach
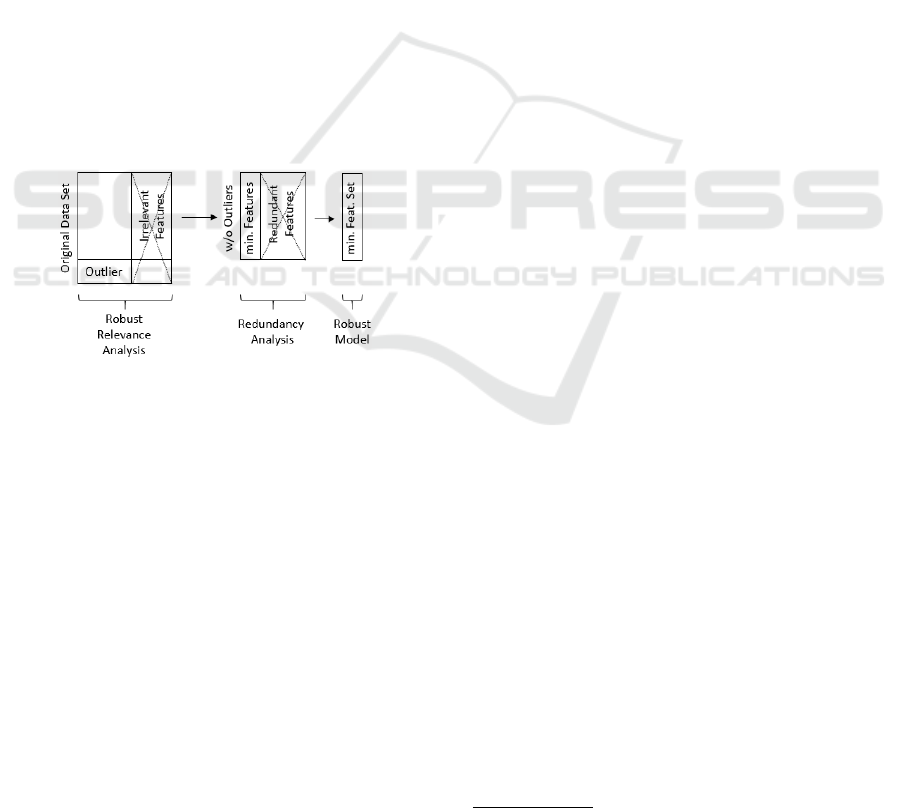
is summarized in Figure 1.
Figure 1: The combined approach for finding a minimal
feature set.
4 CASE STUDY
In this section, we perform an empirical case study
based on the guidelines introduced in (Runeson and
H
¨
ost, 2009). The main goal is to evaluate if the ap-
proach combining SPRM and RFE results in a suit-
able prediction accuracy, i.e., the amount of features
robustly and sparsely selected for a minimal feature
set are able to predict the quantity of hardware com-
ponents. In the planning phase of the domain of Rail
Automation it is crucial to identify most important
features of hardware components since the quantity
estimation of hardware components needed in the bid
phase may be accelerated and more precise. We con-
duct the case study for the business unit Rail Automa-
tion, in particular we identify most important features
regarding robustness and sparseness towards feature
selection.
4.1 Research Questions
Q1: Can a combined approach of SPRM and RFE
continuously reduce the set of features to a minimal
amount preserving a suitable prediction accuracy?
Q2: Can a combined approach of SPRM and RFE
reveal any advantages compared to RFE performed
individually?
Q3: How does the robustness behave applying RFE
to the result of SPRM? Is there a loss of robustness?
4.2 Case Study Design
Requirements. We perform our empirical evalua-
tion in a project planning scenario for Rail Automa-
tion. The data of hardware components is collected
from a set of rail automation projects and installed
railway stations. Before analysis starts, the collected
data are preprocessed to ensure a suitable data quality
(Wurl et al., 2017), i.e., ambiguities caused by data
integration are resolved. The data set retrieved is a
data frame structured as follows: each row represents
a project/station, and per project/station there exists
quantitative information of hardware components and
features represented by columns.
Setup. The architecture of the combined approach is
sketched in Figure 1. The software used for imple-
menting this approach is the programming environ-
ment of R
1
.
The input for the approach, and therefore for
the robust relevance analysis, is a data set contain-
ing quantitative information of features and hardware
components according to projects/stations. In the
course of the robust relevance analysis the precision
parameter must be defined which acts as targeted pre-
diction accuracy regarding the selection of relevant
features. This means, the higher the precision param-
eter is set the more explicitly relevant features can be
determined. The following parameters are automat-
ically adjusted via cross-validation: the number of
principal components, and the sparsity parameter. Af-
ter relevance analysis, the resulting reduced set of rel-
evant features is further used as input for redundancy
analysis. In the course of redundancy analysis, we
use the method Random Forest for eliminating redun-
dant features. Within this step, the maximal number
of features that should be retained has to be defined.
Since our approach reduces the underlying data
set in terms of feature reduction and outlier filtering,
1
www.r-project.org
Exploring Robustness in a Combined Feature Selection Approach
87

for the evaluation of robustness, we compare regres-
sion models built upon resulting data sets from the
following settings:
1. SPRM. Having received relevant features, we fil-
ter out all outliers identified.
2. SPRM+RFE. Outliers are filtered out and redun-
dant features are eliminated.
3. SPRM+RFE
ncl
. Based on the output of SPRM,
i.e., features are reduced but outliers in the data
set are not filtered out, therefore the data set is
not cleaned (ncl). Subsequently, RFE eliminates
redundant features.
4. RFE. Performing solely RFE by assuming no out-
liers exist, the output of the resulting underlying
data set reveals no redundant features.
In a first step we split the original data set in 80%
training data (Table 1) and 20% test data (Table 2).
The training data is used to learn a regression model.
The model is then applied to the test data. To assure
that the evaluation is not affected by potential ambigu-
ous data the regression models obtained are evaluated
by the function lmrob in the R package robustbase
2
,
which performs robust linear regression and enables
to analyze outliers.
4.3 Results
In this section, we present the results of our case study
from the perspective of achieved minimal feature sets.
Our main goal was to analyze robustness with respect
to performance and prediction accuracy.
Robust Feature Selection. We demonstrate our ap-
proach by describing the key steps of robust feature
selection on a concrete example in from Rail Automa-
tion. In the evaluation we split the data set in 80%
training data and 20% test data. The approach follows
the procedure to learn a model based on the training
data (Table 1), and subsequently test the performance
of the model based on the test data (Table 2).
In Figure 1, the steps are illustrated. In our ap-
proach we focus on one asset at the time, e.g., a
point operating module, which is component #3 in Ta-
ble 1. The input data reveals that several features may
influence the calculation of the quantity of a point
operating module. Applying our approach, in rele-
vance analysis we identify outliers and relevant fea-
tures with SPRM. Table 1 shows that 32 outliers and
43 features are found for a point operating module. A
typical example for an outliers is an observation, i.e.,
a project in which manual interactions reveal atypical
quantitative values of features related to the quantity
2
http://robustbase.r-forge.r-project.org/
of the point operating module. A typical example for
relevant features can be described by features which
have been identified to be related to the point oper-
ating module. On the other hand, from experts we
know that the amount of 43 features is not realistic.
Next, outliers and irrelevant features are filtered out
and in redundancy analysis we solely focus on redun-
dant features. After RFE is applied results show that
we receive two features with only 2 outliers.
Results in Robustness and Prediction Accuracy.
We performed the evaluation with a data set contain-
ing ca. 140 features (input variables), ca. 300 hard-
ware components, and ca. 70 observations (installed
systems/projects). For testing purposes we chose an
amount of 13 hardware components.
In the evaluation we measure the prediction accu-
racy with R
2
. The R
2
is a value in the interval [0,1],
and measures how much variance of the response is
explained by the predictor variables in the regression
model:
R
2
= 1 −
∑
(y
i
− ˆy
i
)
2
∑
(y
i
− y)
2
(5)
While R
2
stands for the prediction accuracy in
standard linear regression, rR
2
is calculated in the
same way but in the course of robust regression. The
latter measure is required since the standard linear re-
gression is not sensitive towards potential outliers in
the resulting data sets.
In the relevance analysis, we set a relatively high
precision value in SPRM, i.e., 0.9, to receive more
explicitly features. In redundancy analysis, when ap-
plying Random Forest in the course of RFE, we set
the number of features that should be retained in the
updated model by 10, since we know from domain
experts that this is a maximum of an experienced es-
timated value of features being related to a hardware
component.
In order to indicate the behavior and the perfor-
mance of models in the test data (cf. Table 2), in
addition to the quantity of outliers detected we use
the 10%-trimmed R
2
, writing R
2
t(0.1)
. R
2
t(0.1)
is applied
to 90% of the data set, ignoring 10% with the high-
est squared error of asset quantity estimations. These
10% of data would have the biggest error influence.
In case the data set is skewed then the trimmed mean
is closer to the bulk of the observations (Wilcox and
Keselman, 2003).
Table 1 and Table 2 show the results of the training
and test data. It was observed that
1. SPRM reduces the features and identifies several
outliers but with a high number of relevant fea-
tures. The majority of R
2
and rR
2
have a high
value of 1.00 which can be explained that SPRM
is not filtering out outliers, i.e., observations.
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
88

2. Our approach, i.e., SPRM+RFE, tremendously re-
duces the quantity of relevant features by filtering
out outliers and redundant features. R
2
and rR
2
are clearly lower than in SPRM. But the values
remain similar which means that the procedure of
detecting and filtering out outliers and redundant
features contributes to a robust feature selection.
3. SPRM+RFE
ncl
tremendously reduces the quan-
tity of features but without removing the outliers.
Since more observations are involved in measur-
ing the model fitting, this results in a relatively
high value of R
2
, rR
2
and R
2
t(0.1)
. On the other
hand, there are some peaks in the quantity of
outliers which indicates that some outliers exist.
Identifying and filtering out outliers is clearly ad-
vantageous since Random Forest is not sensitive
towards outliers.
4. In the test data, generally R
2
t(0.1)
reveals high
values. This means that mostly 10% of all re-
sulting data sets reveal outliers. The models
of SPRM+RFE reveals the least outliers, there-
fore our approach works efficiently in the training
phase.
4.4 Interpretation of Results
We analyze the results with regard to our research
questions.
Q1: Can a combined approach of SPRM and RFE
continuously reduce the set of features to a minimal
amount preserving a suitable prediction accuracy?
Generally speaking, according to the results shown in
Table (1) and (2), our method is capable to achieve
a minimal feature set compared to SPRM and RFE
performed individually. Test data show that the pre-
diction accuracy is preserved although a high amount
of features is eliminated.
Q2: Can a combined approach of SPRM and RFE re-
veal any advantages compared to RFE performed in-
dividually? Yes, considering robustness RFE, specifi-
cally Random Forest, is not sensitive towards outliers.
Since SPRM is able to identify outliers a combination
is preferable.
Q3: How does the robustness behave applying RFE to
the result of SPRM? Is there a loss of robustness? In
Table (1), we observe a little loss of rR
2
SPRM+RFE
compared to SPRM as a consequence of less obser-
vations. Table (2) shows a high R
2
t(0.1)
in both SPRM
and SPRM+RFE which indicates that the little loss of
robustness has rarely made a difference in prediction
accuracy.
4.5 Threats to Validity
The input data set is of high quality, but realistically
some ambiguities in data cannot be avoided. Al-
though the approach is able to identify outliers, the
procedure of relevant analysis may be accelerated by
controlling the data beforehand.
Our data set contains quantitative data from the
Rail Automation domain. Results may look different
for data sets of other types and other domains, like
sensor data from industry automation.
5 RELATED WORK
Feature selection is a commonly known technique in
many areas such as in statistics (Kuhn, 2012), and ma-
chine learning (Bischl et al., 2016). While classifica-
tion problems obviously attract more attention in re-
search, regression problems seem to be subordinated
(Guyon and Elisseeff, 2003).
The phase of relevance analysis in regression
problems mostly goes along with correlation anal-
ysis ranking and selecting a defined amount of the
top features for further operations (Yu and Liu, 2003;
Van Dijck and Van Hulle, 2006). (Wurl et al., 2018)
show that using such an approach may loose infor-
mation which might be relevant. On the other hand,
combined approaches of filter and embedded methods
leverage the evaluation of relevant features by mak-
ing a model sparse, i.e., reducing the feature set by
a penalty function (Ghaoui et al., 2010). Regarding
robustness towards outliers (Hoffmann et al., 2015)
propose Sparse Partial Robust M-regression (SPRM)
yielding a regression model that is sparse and robust
considering outliers in the response and in the predic-
tors.
Relevancy analysis aims to further reduce the fea-
ture set. (John et al., 1994) show that for some se-
lected features relevancy does not imply that a feature
must be in an optimal feature subset. In the course
of regression problems (Tuv et al., 2009; Saeys et al.,
2008) reduce a feature set in relevancy analysis fo-
cusing on predictors rather than considering the re-
sponse. Consequently, methods that are subsequently
continuing to eliminate redundant features lack in ro-
bustness, albeit embedded methods such as Random
Forest show significant results in selecting features
(Genuer et al., 2010).
Exploring Robustness in a Combined Feature Selection Approach
89

Table 1: Measured values in training data: R
2
, rR
2
, quantity of Outliers (Out.), quantity of selected features (Fs) for each
hardware component (Comp.) of the respective method.
SPRM SPRM+RFE SPRM+RFE
ncl
#Comp. R
2
rR
2
Σ Out. Σ Fs R
2
rR
2
Σ Out. Σ Fs R
2
rR
2
Σ Out. Σ Fs
1 1.00 1.00 27 43 1.00 1.00 28 43 1.00 1.00 40 43
2 1.00 1.00 31 43 0.76 0.69 2 3 0.87 0.87 5 1
3 1.00 1.00 32 43 0.76 0.73 2 2 0.87 0.87 5 1
4 1.00 1.00 33 46 0.80 0.77 1 8 1.00 1.00 36 46
5 0.75 0.67 1 10 0.75 0.67 1 2 0.75 0.69 1 4
6 1.00 1.00 29 41 0.81 0.71 1 7 0.79 0.77 1 6
7 1.00 1.00 0 38 1.00 1.00 0 9 0.92 0.92 0 6
8 1.00 1.00 29 44 1.00 1.00 3 6 0.96 0.96 0 8
9 1.00 1.00 31 74 1.00 1.00 1 2 0.80 0.73 27 8
10 1.00 1.00 0 39 0.93 0.93 1 1 0.96 0.96 1 1
11 1.00 1.00 25 36 0.95 0.89 3 4 0.99 0.95 3 8
12 1.00 1.00 31 74 0.94 0.36 3 7 0.93 0.61 2 7
Table 2: Measured values in test data: 10% trimmed R
2
t(0.1)
, quantity of Outliers (Out.) for each hardware component (Comp.)
of the respective method.
SPRM SPRM+RFE SPRM+RFE
ncl
RFE
#Comp. R
2
t(0.1)
Σ Out. R
2
t(0.1)
Σ Out. R
2
t(0.1)
Σ Out. R
2
t(0.1)
Σ Out.
1 1.00 23 1.00 20 1.00 24 1.00 37
2 1.00 22 0.82 3 0.48 2 0.99 2
3 1.00 21 0.68 3 0.48 2 0.98 5
4 1.00 25 0.89 7 1.00 24 1.00 41
5 0.94 3 0.94 3 0.94 3 0.73 2
6 1.00 16 0.97 0 0.98 2 0.96 1
7 1.00 22 1.00 4 0.97 1 1.00 40
8 1.00 26 1.00 3 0.97 3 0.97 0
9 1.00 25 1.00 0 0.98 24 0.89 25
10 1.00 23 0.99 1 0.99 1 0.99 1
11 1.00 25 0.99 1 1.00 1 0.98 5
12 1.00 23 0.96 0 0.96 0 0.96 2
6 CONCLUSION AND FUTURE
WORK
In this paper, we identified various issues in the pro-
cess of feature selection for the calculation of hard-
ware components. To address these issues, we pro-
posed a combined feature selection approach. We ex-
plored the robustness of our approach in the presence
of outliers caused by industrial data integration oper-
ations. In a case study, we validated the applicability
of our approach in the industrial environment of Rail
Automation. The results show that this approach as-
sures robustness in the calculation of hardware com-
ponents.
An extension of our approach is worth to follow
in future work: A multivariate robust setting, i.e., per-
forming feature selection for the calculation of sev-
eral hardware components at the time. This affects the
procedure of selecting features but it may accelerate
the selection process for features of multiple compo-
nents.
ACKNOWLEDGEMENTS
This work is funded by the Austrian Research Pro-
motion Agency (FFG) under grant 852658 (CODA).
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
90

This work has been supported by the Austrian Federal
Ministry for Digital and Economic Affairs, the Na-
tional Foundation for Research, Technology and De-
velopment. We thank Walter Obenaus (Siemens Rail
Automation) for supplying us with test data.
REFERENCES
Bischl, B., Lang, M., Kotthoff, L., Schiffner, J., Richter, J.,
Studerus, E., Casalicchio, G., and Jones, Z. M. (2016).
mlr: Machine learning in r. The Journal of Machine
Learning Research, 17(1):5938–5942.
Breiman, L. (2001). Random forests. Machine learning,
45(1):5–32.
Genuer, R., Poggi, J.-M., and Tuleau-Malot, C. (2010).
Variable selection using random forests. Pattern
Recognition Letters, 31(14):2225–2236.
Ghaoui, L. E., Viallon, V., and Rabbani, T. (2010). Safe
feature elimination for the lasso and sparse supervised
learning problems. arXiv preprint arXiv:1009.4219.
Guyon, I. and Elisseeff, A. (2003). An introduction to vari-
able and feature selection. Journal of machine learn-
ing research, 3(Mar):1157–1182.
Hoffmann, I., Serneels, S., Filzmoser, P., and Croux, C.
(2015). Sparse partial robust M regression. Chemo-
metrics and Intelligent Laboratory Systems, 149:50–
59.
John, G. H., Kohavi, R., and Pfleger, K. (1994). Irrelevant
features and the subset selection problem. In Machine
Learning Proceedings 1994, pages 121–129. Elsevier.
Johnson, R. A., Wichern, D. W., et al. (2002). Applied mul-
tivariate statistical analysis, volume 5. Prentice hall
Upper Saddle River, NJ.
Kuhn, M. (2012). Variable selection using the caret pack-
age. URL http://cran. cermin. lipi. go. id/web/pack-
ages/caret/vignettes/caretSelection. pdf.
Radovic, M., Ghalwash, M., Filipovic, N., and Obradovic,
Z. (2017). Minimum redundancy maximum relevance
feature selection approach for temporal gene expres-
sion data. BMC bioinformatics, 18(1):9.
Runeson, P. and H
¨
ost, M. (2009). Guidelines for conduct-
ing and reporting case study research in software engi-
neering. Empirical software engineering, 14(2):131.
Saeys, Y., Abeel, T., and Van de Peer, Y. (2008). Robust fea-
ture selection using ensemble feature selection tech-
niques. In Joint European Conference on Machine
Learning and Knowledge Discovery in Databases,
pages 313–325. Springer.
Serneels, S., Croux, C., Filzmoser, P., and Van Espen, P. J.
(2005). Partial robust m-regression. Chemometrics
and Intelligent Laboratory Systems, 79(1-2):55–64.
Strobl, C., Boulesteix, A.-L., Kneib, T., Augustin, T., and
Zeileis, A. (2008). Conditional variable importance
for random forests. BMC bioinformatics, 9(1):307.
Tuv, E., Borisov, A., Runger, G., and Torkkola, K. (2009).
Feature selection with ensembles, artificial variables,
and redundancy elimination. Journal of Machine
Learning Research, 10(Jul):1341–1366.
Van Dijck, G. and Van Hulle, M. M. (2006). Speeding up
the wrapper feature subset selection in regression by
mutual information relevance and redundancy analy-
sis. In International Conference on Artificial Neural
Networks, pages 31–40. Springer.
Wilcox, R. R. and Keselman, H. (2003). Modern robust
data analysis methods: measures of central tendency.
Psychological methods, 8(3):254.
Wurl, A., Falkner, A., Haselb
¨
ock, A., and Mazak, A.
(2017). Advanced data integration with signifiers:
Case studies for rail automation. In International Con-
ference on Data Management Technologies and Appli-
cations, pages 87–110. Springer.
Wurl, A., Falkner, A. A., Filzmoser, P., Haselb
¨
ock, A.,
Mazak, A., and Sperl, S. (to be published in 2019).
A comprehensive prediction approach for hardware
asset management. In International Conference on
Data Management Technologies and Applications.
Springer.
Wurl, A., Falkner, A. A., Haselb
¨
ock, A., Mazak, A., and
Sperl, S. (2018). Combining prediction methods for
hardware asset management. In Proceedings of DATA
2018., pages 13–23.
Yu, L. and Liu, H. (2003). Feature selection for high-
dimensional data: A fast correlation-based filter solu-
tion. In Proceedings of the 20th international confer-
ence on machine learning (ICML-03), pages 856–863.
Yu, L. and Liu, H. (2004). Efficient feature selection via
analysis of relevance and redundancy. Journal of ma-
chine learning research, 5(Oct):1205–1224.
Exploring Robustness in a Combined Feature Selection Approach
91
