Water-resource Optimization Problem of Inland Waterways based on

Network Flows with Flow Transition Time and Time Varying

Characteristics

Eric Duviella

1,2

, Baya Hadid

1,2

and D

ebora C. C. S. Alves

1,2

Institut Mines Telecom Lille Douai, F-59000 Lille, France

Univ. Lille, Lille, France

Keywords:

Model Graph, Large Scale Systems, Optimization, Modelling, Water System.

Abstract:

Water-resource allocation planning is a well studied problem that aims at sharing water-resource to answer to

multi-objective management. For inland waterways, water-resource has to be balanced among the networks

to guaranty navigation conditions as a priority. Hydraulic devices such as locks and gates are used to transfer

volumes of water between the interconnected navigation reaches that composed the network. By considering

a large spatial scale with a low control time scale, transport delays have to be considered. Hence, network

ﬂows with ﬂow transition time and time varying characteristics is proposed to deal with transport delays and

modiﬁcations of the operating conditions over time. Network ﬂows are then used for the optimization step.

The proposed model and optimization approach are illustrated by considering an inland waterway that is

composed of two navigation reaches.

1 INTRODUCTION

Hydrographical networks are large scale systems that

carry volumes of water. These systems have been de-

veloped over the time to meet human’ needs. They

have been equipped with dams to store the water, ex-

pansion areas to reduce ﬂood impacts, gates to con-

trol water dispatching, and locks to allow navigation.

Whatever the hydrographical networks, the water-

resource has to be shared between usages. Hence

multi-objective management has to be performed

(Tchangani, 2017; Amigoni et al., 2015; Xiong et al.,

2018; He et al., 2018). This management requires

the deﬁnition and the solving of water-resource opti-

mization problems. In (Duviella et al., 2018), water-

resource allocation planing based on quadratic opti-

mization technique is proposed to guaranty the nav-

igation conditions and to study the resilience of the

waterways against extreme events. The requirement

of good extreme event prediction based on accurate

rainfall/runoff model is discussed in (Hadid and Du-

viella, 2018). Rainfall/runoff models are based on

ofﬂine and recursive/online parameter estimation of

data-driven linear and nonlinear models (Hadid et al.,

2018). In addition, a predictive optimization ap-

proach is proposed in (Alves et al., 2018) to improve

again the water management. These approaches are

based on an integrated model of inland waterways

and on a weighted dynamic generative network ﬂow

that is introduced in (Fathabadi and Hosseini, 2010).

The management time corresponds to half of a day

implying that no transfer delays have been consid-

ered. Moreover, the arcs capacities and node sup-

plies/demands are functions of time. Based on these

assumptions, it is assumed that the transfer of water-

resource between two reaches is immediate between

two time steps. When the transfer delays have to be

considered in the optimization, the method requires

temporized ﬂow networks or ﬂow over time networks.

In (Ladeveze et al., 2010), a transportation network is

proposed to implement an algorithm leading to opti-

mal trajectories of a multi-objective short-term man-

agement of a dam-river system. A time expanded ﬂow

network formalism is used in (Ayoub et al., 2018)

to consider available hydraulic data. A similar ex-

tended ﬂow network is used in (Bencheikh et al.,

2017) to decrease the ﬂood impacts thanks to the use

of ﬂood expansion area with a real case-study located

in the south of France. The proposed transportation

networks are based on those described in (Kotnyek,

2003) that aim at considering the time for the ﬂow to

pass the arcs, the storage capability for each node, the

time varying characteristics of the nodes and arcs, and

the concept of throughput in the dynamics of the ﬂow

Duviella, E., Hadid, B. and Alves, D.

Water-resource Optimization Problem of Inland Waterways based on Network Flows with Flow Transition Time and Time Varying Characteristics.

DOI: 10.5220/0007924603030310

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 303-310

ISBN: 978-989-758-380-3

303

networks. The main objective is a well understanding

and representing of the dynamics of hydrographical

systems.

Flow network modeling is more dedicated to op-

timization applications. To this aim, a decomposition

of the hydrographical networks in conceptual mod-

els is required. In (Ladeveze et al., 2010; Ayoub

et al., 2018; Bencheikh et al., 2017; Duviella et al.,

2018), the nodes of the ﬂow networks correspond to

reaches or parts of reach between hydraulic devices

such as gates, locks, hydraulic inputs, etc. A system-

atically decomposition approach has been proposed

in (Wolfs et al., 2015). It allows considering concep-

tual models based on virtual reservoirs. In this pa-

per, the decomposition of inland navigation reaches

is based on the Integrator Delay (ID) model (Schuur-

mans et al., 1999) to take into account the backwater

effect that characterizes these systems. Indeed, nav-

igation reaches, depending of their size, can be con-

sidered as tanks due to the presence of locks. More-

over, most of them are characterized by a very small

slope or no slope that increases the backwater effect

and some resonance phenomena (Segovia et al., 2017;

Horv

ath et al., 2015; Horv

ath et al., 2014). These

three contributions are dedicated to predictive control

of water level and not on water resource dispatching.

By considering a large spatial scale and a low con-

trol time scale, the modelling of inland waterways

with ﬂow networks requires a priori ﬂow transition

time, storage capability, time varying characteristics

and throughput dynamics. Based on these concepts, a

network ﬂow with ﬂow transition time and time vary-

ing characteristics is proposed. It is well suited to in-

land waterways and optimal water-resource allocation

planning.

The paper is organized as follows: Section II de-

scribes the inland waterways and the modelling ap-

proach based on ID model. The network ﬂows with

ﬂow transition time and time varying characteristics

are detailed in Section III. Section IV deals with the

optimization approach. Finally, a case-study is given

in Section V to illustrate the modeling and optimal

water-resource allocation steps.

2 INLAND WATERWAYS

2.1 Description and Management

Objectives

Inland waterways are large scale and complex sys-

tems that are used principally for navigation. They

are usually composed with interconnected Navigation

Reaches, denoted NR, and equipped with locks that

allow guaranteeing the navigation condition whatever

is the landform. Artiﬁcial canals have been built to

connect natural rivers and to permit navigation trans-

port.

The main management objective consists in guar-

anteeing the navigation conditions at each time all

along the year. An objective that is denoted Normal

Navigation Level (NNL) and a navigation rectangle

are deﬁned for each NR. The navigation rectangle is

an interval around the NNL that is composed of a low

limit, the Low Navigation Level (LNL) and a high

limit, the High Navigation Level (HNL). The water-

resource management consists in allocating the avail-

able resource among the interconnected NR to keep

their water levels inside the deﬁned navigation rect-

angle and closest as possible to the NNL. The main

disturbances are from the navigation demand i.e. the

ships crossing the locks. At each lock operation, a

big water volume goes from the upstream NR to the

downstream one. Moreover, because inland water-

ways are strongly connected with other natural rivers,

and inside watersheds, they are also affected by cli-

matic events.

The water-resource allocation is performed thanks

to the controlled gates by taking into account the con-

ﬁguration of the waterways. Depending on the control

time scale, the transfer delay, i.e. the required time a

volume of water travels from an upstream to a down-

stream point, must be considered. Otherwise, an order

can be sent to a controlled gate before that the water

volume arrives this gate leading to deﬁcit of water.

2.2 Integrated Model

A ﬁrst model entitled integrated model is proposed

to well represent the waterways conﬁguration and the

possible interactions with naturals rivers or other hy-

draulic systems that are not considered by the water-

resource allocation planning (Duviella et al., 2018).

Fig. 1.a shows an example of a waterway composed

with ﬁve NR and the two elementary conﬁgurations;

a tributary and a distributary. The corresponding inte-

grated model is depicted in Fig.1.b, with:

• V

s,c

and respectively V

e,c

, the controlled volumes

from one or several upstream NR that supply and

(resp.) empty the NR

(s: supply, e: empty, c:

controlled),

• V

the controlled volumes from water intakes that

can supply or empty NR

. These volumes are

signed; positive if NR

is supplied, negative oth-

erwise,

• V

s,p

and (resp.) V

e,p

the controlled volumes from

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

304

pump that can supply and (resp.) empty the NR

denoted (p: pumped),

• V

the uncontrolled volumes from natural rivers,

rainfall-runoff, Human uses (u: uncontrolled).

These volumes are signed depending on their con-

tribution to the volume V

(k) in NR

• V

g,u

the uncontrolled volumes from exchanges

with groundwater (g: groundwater), that can be

associated to V

(a)

Lock

i-2

i-1

i+1

i+2

(b)

i-2

i-1

i+1

i+2

s,c

e,c

g,u

i-2

s,c

i-2

e,c

i-2

g,u

i-1

s,c

i-1

e,c

i-1

g,u

i+1

s,c

i+1

e,c

i+1

g,u

i+2

s,c

i+2

e,c

i+2

g,u

i-2

s,p

i-2

e,p

i-1

s,p

i-1

e,p

s,p

e,p

i+1

s,p

i+1

e,p

i+2

s,p

i+2

e,p

Figure 1: a. Inland waterways, b. corresponding integrated

model.

The dynamics of the reach NR

with a discrete

sample time T

is given by:

(k) = V

(k −1) +V

s,c

(k) −V

e,c

(k) +V

(k)

s,p

(k) −V

e,p

(k) +V

g,u

(k),

(1)

where k corresponds to the current period of time and

k −1 the last one.

This model is well suited for the representation

of waterways where no transfer delay has to be taken

into account. Otherwise, it is necessary to decompose

the NR in conceptual NR according to the transfer de-

lays and the control sample time.

2.3 Conceptual Navigation Reach

Model

The conceptual navigation reach model is designed

based on the Integrator Delay model (Schuurmans

et al., 1999). The ID model aims at linking the dis-

charges that supply/empty a reach to water levels of

the reach, at least on the two points that correspond to

the boundaries of the reach. It can be expressed as:







y(1,s)

...

y( j,s)

...

y(n,s)













(s) p

(s) ... p

(s)

... ... ... ...

(s) p

(s) ... p

(s)

... ... ... ...

(s) p

(s) ... p

(s)













q(1,s)

...

q(i,s)

...

q(m,s)







(2)

where y( j,s) is the j

water level, j ∈1 : n, q(i,s) the

discharge input/output, i ∈ 1 : m, with n the num-

ber of measurement points and m the number of dis-

charge points. p

(s) is a term of the ID model that is

expressed as:

(s) =

−τ

(3)

with A

the integrator gain that corresponds to the

area of the reach A = L ∗W , with L the length and

W the width of the reach. The transfer time delays

, (resp.) τ

i j

, between the points j and i that are L

meters apart, with j upstream to i, are expressed by:

(

−V

i j

(4)

with C

√

g.D and V

W.D

, where g is the gravity

and D the depth of the reach for the nominal discharge

Based on this model and considering a discrete

sample time T

, it is possible to represent the dynam-

ics of each part of the reach with a virtual tank of area

A that is supplied and emptied with the delayed dis-

charges. Thus:

(k) = y

(k −1) +

∑

i=1

(k −T

).T

(5)

with q

(k) a signed discharge and T

= bτ

where bc provides the ﬂoor integer number.

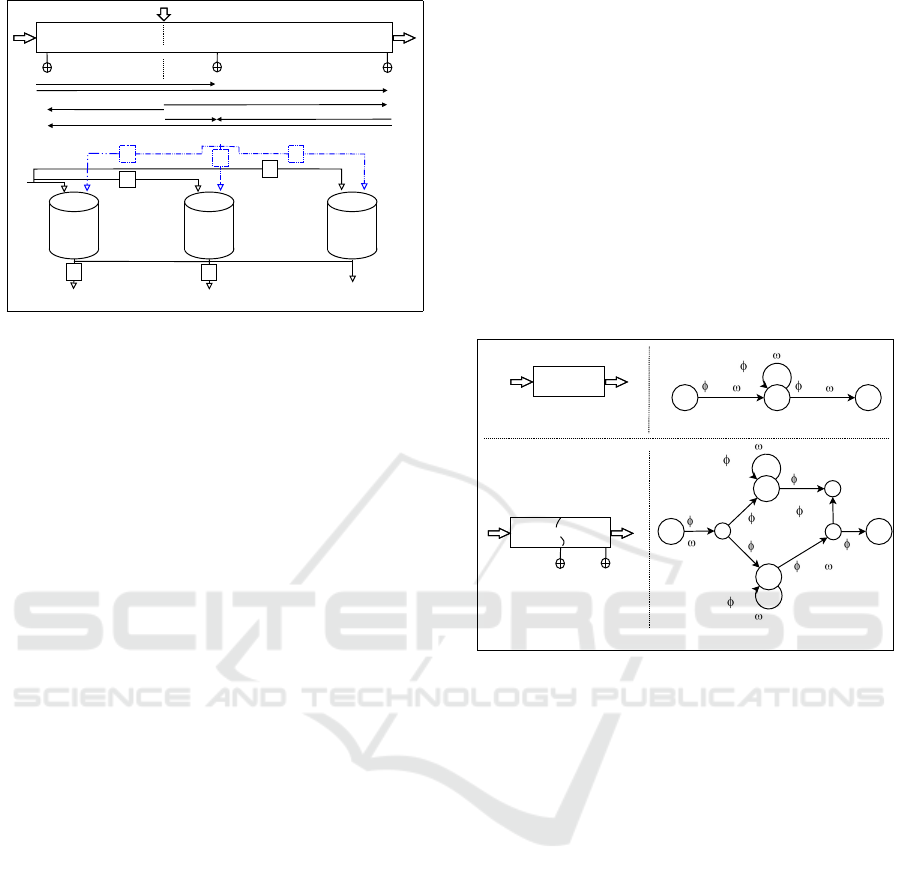
Fig.2.a depicts a schematic view of a NR with

multiple inputs/outputs (discharges Q

) and measure-

ment points (levels Y

), and the corresponding delays

between these points. Note that the delays T

when

i is located in the same place than j are not shown

because they are equal to 0. The corresponding con-

ceptual model is shown in Fig.2.b, where a tank is as-

sociated to each measurement point. The area of the

tanks is the same. These tanks are supplied/emptied

with delayed discharges according to the conﬁgura-

tion of the waterway. This conceptual model is then

used to design the network ﬂows.

3 NETWORK FLOWS

The deﬁnition and the description of static network

ﬂows are proposed in (Ahuja et al., 1993). In (Kot-

nyek, 2003), a state of the art of dynamic network

ﬂows is given. It aims at describing a formalism of

dynamic network ﬂows able to take into account ﬂow

time, storage capability, time varying characteristics,

and the concept of throughput. All these properties

are required to model inland waterways thanks to net-

work ﬂows. Hence, the proposed network ﬂow is de-

ﬁned on a direct graph G = (N, E,B,T,Ω,Φ), with:

Water-resource Optimization Problem of Inland Waterways based on Network Flows with Flow Transition Time and Time Varying

Characteristics

305

(a)

(b)

Figure 2: a. schematic view of a NR with transfer delays, b.

corresponding conceptual model.

• the nodes N = N

∪N

∪O∪S, with O the su-

persource, S the supersink that gather respectively

all the sources and all the sinks, N

the set of nodes

that corresponds to the NR or parts of NR, N

the

set of conceptual nodes, and N

the set of tempo-

rized nodes,

• the arcs E = E

∪E

, with E

the set of

arcs between NR, source O and sink S, E

the set

of conceptual arcs, E

the set of temporized arcs,

and E

the set of arcs starting from and entering

in the same NR allowing the modelling of the ca-

pacity of the nodes N

• the boundaries B = B

∪B

are composed of a

lower and a higher limits, l

i j

(k) and u

i j

(k) respec-

tively , with B

the set of boundaries associated to

arcs E

, and B

the set of boundaries associated to

arcs E

• the transfer delays T that are associated to the set

of arcs E

• the weights Ω = Ω

∪Ω

that are associated to the

set of arcs E

∪E

, respectively,

• the ﬂows Φ = Φ

∪Φ

that are trans-

ferred by the set of arcs E.

The limits and weights can change over the time.

They are expressed according to time k. Hence, the

network ﬂow has time varying characteristics.

For an inland waterway that is composed of one

NR where the maximum transfer delay is lower than

the sample time, i.e. maxbτ

c = 0, (see Fig.3.a),

the corresponding network ﬂow (see Fig.3.b) is de-

ﬁned as:

• N = N

∪O ∪S, with N

= {1}, N

= ∅ and N

∅,

• E = E

∪E

, with E

= {e

, e

}, E

= {e

}

where e

i j

is the arc between nodes i and j, E

= ∅

and E

= ∅,

• B = B

∪ B

, with B

{[l

(k), u

(k)], [l

(k), u

(k)]} and

= {[l

(k), u

(k)]}, where l

i j

(k) (resp.

i j

(k)) is the lower (higher) limit of the ﬂow that

passes trough the arc e

i j

• T = ∅,

• Ω = Ω

∪Ω

, with Ω

= {w

(k), w

(k)}, Ω

(k)},

• Φ = Φ

∪Φ

, with Φ = {φ

(k), φ

(k)}, Φ

{φ

(k)}, where φ

i j

(k) is the ﬂow that passes

through the arc e

i j

at time k, Φ

= ∅ and Φ

= ∅.

(a)

(b)

O S

[l (k), u (k)]

(k)

[l (k), u (k)]

(k)

(k-T )

(k)

[l (k), u (k)]

1O O

O 1 S

[l (k), u (k)]

(k)

[l (k), u (k)]

(k)

(k-T )

(k)

[l (k), u (k)]

(k)

1 C

(c)

(d)

Figure 3: a. NR without consideration of time delay, b.

corresponding network ﬂows, c) NR with consideration of

time delay, d) corresponding network ﬂows.

When the maximum transfer delays is higher than

the sample time (see Fig.3.c), i.e. maxbτ

c ≥ 1,

the corresponding network ﬂow (see Fig.3.d) is de-

ﬁned as:

• N = N

∪N

∪O∪S, with N

= {1a, 1b}, N

{C}, N

= {T

, T

• E = E

∪E

, with E

= {e

, e

= {e

, e

} and E

= {e

}, E

, e

• B = B

∪ B

, with B

{[l

(k), u

(k)], [l

(k), u

(k)]} and

= {[l

(k), u

(k)], [l

(k), u

(k)]},

where l

i j

(k) (resp. u

i j

(k)) is the lower (higher)

limit of the ﬂow that passes trough the arc e

i j

, at

time k,

• T = {T

, T

• Ω = Ω

∪ Ω

, with Ω

= {w

(k), w

(k)},

Ω

= {w

(k), w

(k)},

• Φ = Φ

∪ Φ

, with Φ

{φ

(k), φ

(k)} and Φ

= {φ

(k)},

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

306

= {φ

(k), φ

(k)} and Φ

{φ

(k), φ

(k −T

), φ

(k −T

)}.

The set of nodes N

veriﬁes the Kirchhoff’s law

such as:

∑

j∈E

(k) −

∑

j∈E

−

(k) = 0 (6)

with E

and E

−

(resp.), the set of arcs entering, out-

going (resp.) the node N

, and φ

the ﬂow associated

to the arc e

The set of temporized nodes N

do not verify the

conservation rule as it is speciﬁed in (Kotnyek, 2003).

It allows associating a transfer delay to each of the

ﬂow outgoing the temporized node:

(k) = φ

(k −T

) (7)

with j ∈ E

−

, the set of arcs outgoing the node N

the arc that enters the node N

, and T

the transfer

delay that is associated to the outgoing arc e

The set of conceptual node N

veriﬁes a conser-

vation law between the ﬂow on the arc outgoing the

nodes N

−

) and the ﬂow on the arc outgoing the

nodes N

−

), deﬁned as:

−

(k) = φ

−

(k −T

) (8)

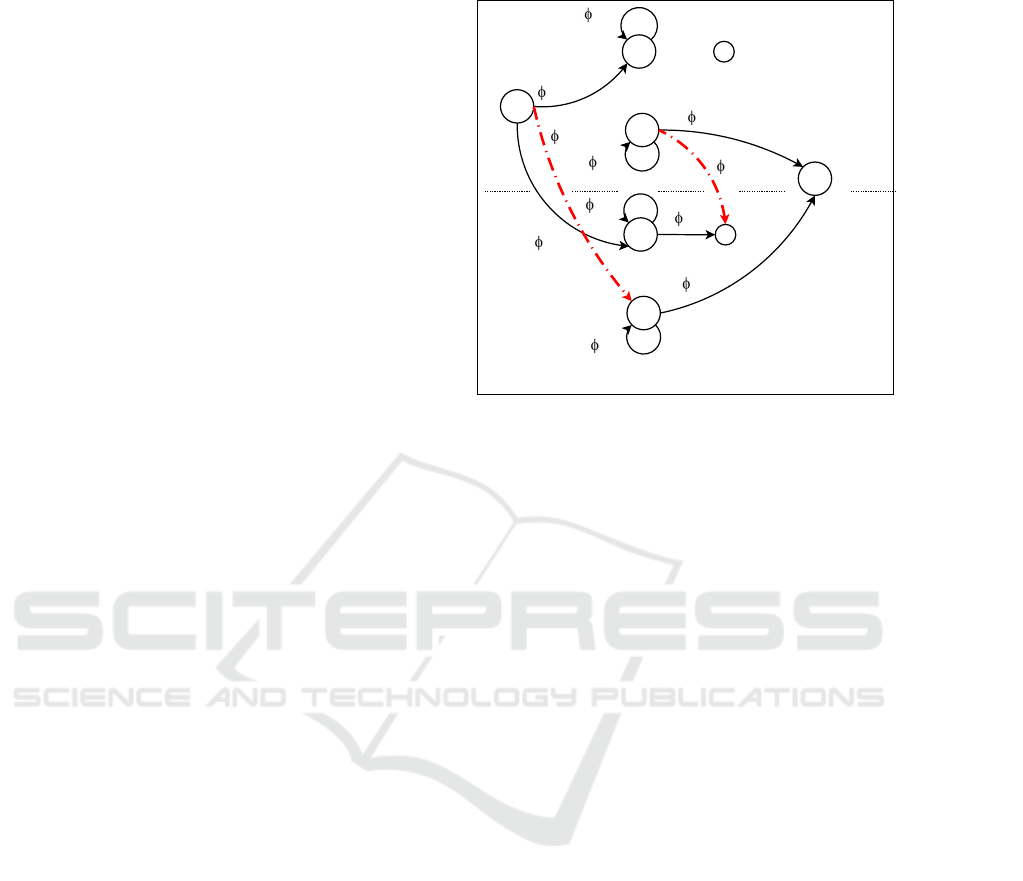
The optimization of dynamic network ﬂows leads

to NP-hard problem as it is stated in (Skutella, 2009).

To overcome this problem, a formalism of extended

network ﬂow has been proposed in (Fulkerson, 1966)

and used in (Ladeveze et al., 2010; Bencheikh et al.,

2017). The network ﬂows in Fig. 3.d is represented

in Fig.4 by considering T

= T

= 1 and two step

times from k = 1 to k = 2. The dashed red arcs rep-

resent the temporized ﬂows. Depending of the value

of maxbτ

c, a throughput is deﬁned and the opti-

mization can be done for each of it. In this example,

this throughput is equal to 2. Finally, some optimiza-

tion approaches can be applied.

4 WATER-RESOURCE

ALLOCATION PLANNING

The allocation planning consists in dispatching the

water-resource among the waterways by keeping the

volume inside each NR close to their objective (Du-

viella et al., 2018). These objectives are deﬁned in

relative value with the volumes that correspond to the

NNL. Thus, a capacity of a NR equal to 0 corresponds

to the NNL. The capacity boundaries are deﬁned with

the LNL and HNL, with negative and positive bound-

aries. They are associated with the boundaries B

(1)

(2)

(1)

(2)

1 C

(1)

k=1

k=2

Figure 4: Time representation of the network ﬂows depicted

in Fig.3.d.

The dynamics for inland waterways are deﬁned ac-

cording the relations (7-9) following the conﬁguration

of the network.

The water-resource allocation planning is per-

formed according to an optimization approach that

consists in minimizing the absolute value of the NR’s

capacity by exchanging water through the arcs be-

tween the source and the sink. In order to minimize

the water volume inside the NR, the weights Ω

that

are associated to the arcs E

have to be big. Other

weights Ω

that are associated to the arcs E

are tuned

according to the priority of the paths from a part of the

network to another one. Thus, the objective function

can be deﬁned as:

∑

∈E

∑

j∈E

(k)φ

(k)−

∑

j∈E

−

(k)φ

(k)| (9)

by considering the constraints given by relation (6),

the boundaries B, and the transfer delays T . That

means that the exchanges of water volumes between

each NR or part of NR have to be balanced between

the entering and outgoing ﬂows at each step time k.

For the waterway where the maximum transfer de-

lays is lower than the sample time (see Fig. 3.a), the

objective function to minimize is deﬁned as:

= |ω

(k)φ

(k) +ω

(k)φ

(k) −ω

(k)φ

(k)|

(10)

with:











(k) +φ

(k) −φ

(k) = 0,

(k) ∈ [l

(k), u

(k)],

(k) ∈ [l

(k), u

(k)],

(k) ∈ [l

(k), u

(k)],

(11)

where ω

(k)  ω

(k) and ω

(k)  ω

(k) .

Water-resource Optimization Problem of Inland Waterways based on Network Flows with Flow Transition Time and Time Varying

Characteristics

307

For the waterway where the maximum transfer de-

lays is higher than the sample time (see Fig. 3.c),

the objective function to minimize has to be deﬁned

by considering a throughput that is computed accord-

ing to the maximum transfer delay, i.e. from k to

k + maxbτ

c. In this case, by considering T

≥

, it is deﬁned as:

= |ω

(k)φ

(k) +ω

(k)φ

(k)−

(k −T

)φ

(k −T

)|+

|ω

(k −T

)φ

(k) +ω

(k)φ

(k)−

(k)φ

(k)|+

...

|ω

(k +T

)φ

(k +T

)φ

(k +T

)−

(k +T

−1)φ

(k +T

−1)|+

|ω

(k +T

−1)φ

(k +T

)φ

(k +T

)−

(k +T

)φ

(k +T

(12)

with, for k

∈ {k : k + T











) + φ

) −φ

−T

) = 0,

−T

) + φ

) −φ

) = 0,

) ∈ [l

), u

)],

) ∈ [l

), u

)],

) ∈ [l

), u

)],

(13)

where ω

)  ω

), ω

)  ω

), ω

)  ω

The optimization approach can be based on Con-

straints Satisfaction Problems (CSP) (Nouasse et al.,

2016b), on minimum cost problem (Kotnyek, 2003),

on linear programming (Nouasse et al., 2016a) or on

quadratic programming (Duviella et al., 2018). In this

paper, a linear programming approach based on the

Matlab function linprog

is used.

5 CASE-STUDY

The considered inland waterways is composed with

two NR as it is schematized in Fig. 5.a. The lengths of

the NR are L

= 5 km, L

= 20 km, with the same

width W = 20 m, nominal discharge Q

= 1 m

/s, and

depth D = 2.2 [m]. The parameters of the ID models

for both NR are identiﬁed (see Table 1). The sample

time is T

= 30 min. Thus, according to the transfer

delays, only NR

is decomposed in two parts. Fig.

5.b depicts the network ﬂows associated to the case-

study. Hydraulic devices like locks and gates supply

and empty the NR. Their characteristics are given in

https://www.mathworks.com/help/optim/ug/linprog

.html

Table 2. The locks are activated for navigation and a

lock operation corresponds to a transfer of water vol-

ume between two NR. The duration of a lock opera-

tion is equal to 15 min. The gates can be controlled

inside the proposed intervals. Two periods of man-

agement are considered for the gate downstream NR

during 6 hours it can be controlled on the operating

range [0;5], the next 6 hours between [0; 10] [m

/s].

(a)

(b)

[l (k), u (k)]

(k)

[l (k), u (k)]

(k)

(k-T )

O 1

[l (k), u (k)]

(k)

[l (k), u (k)]

(k)

(k-T )

(k)

[l (k), u (k)]

(k)

a a

Figure 5: a. Inland waterways composed with two NR, b.

network ﬂows model.

Table 1: ID model parameters - τ [min].

i j

0 −18 17 0

A 100,000

i j

0 −71 35 −36 70 0

A 400,000

Table 2: Characteristics of the inputs/outputs of the NR.

Lock during 15 min Gate [m

/s]

15,000 m

→ 16.66 m

/s -

6,000 m

→ 6.66 m

/s [0; 10]

7,000 m

→ 7.77 m

/s [0;(5 −10)

∗

]

The weights are tune such as ω

(k) = ω

(k) =

(k) = 1,000 and ω

(k) = ω

(k) =

1, with the objective to minimize the water that is

stored inside the NR. Finally, according to the ID pa-

rameters, T

= T

= 2 T

The lock operations over the future time horizon

are supposed to be known and depicted in Fig.

6. The discharge Q

is the equivalent discharge due

to the lock operation upstream NR

during 15 min.

The discharges Q

and Q

come from the lock op-

erations upstream and downstream NR

(L for lock).

This knowledge allows the optimization of the crite-

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

308

rion J

on horizon 2T

according to relation (9) and

the constraints given by relation (6).

A model of the considered inland waterway has

been implemented with Simulink/Matlab. The opti-

mization approach that is based on the linprog func-

tion is implemented with a matlab function. The sim-

ulation results are depicted in Fig. 7 with the con-

trolled discharges at the gates upstream and down-

stream NR

, i.e. Q

and Q

respectively (G for gate).

The resulting levels downstream NR

and NR

are de-

picted in Fig. 7.c and Fig. 7.d respectively. When no

optimization strategy is used, the simulation results

lead to the results depicted in dashed red line in Fig.

7.c and Fig. 7.d. These results are improved when the

proposed optimization approach is used as it is shown

in continuous blue line in Fig. 7.c and Fig. 7.d. The

maximum gap from the objective levels is lower when

the proposed approach is used.

Figure 6: a. The discharge due to the lock operations up-

stream NR

, b. the discharge due to the lock operations

upstream NR

, c. the discharge due to the lock operations

downstream NR

Figure 7: a. The controlled discharge upstream NR

, b. the

controlled discharge downstream NR

, c. the water level

downstream NR

, d. the water level downstream NR

6 CONCLUSIONS

In this paper a network ﬂows with ﬂow transition time

and time varying characteristics formalism is pro-

posed to deal with water-resource optimization of in-

land waterways. This formalism is based on the graph

theory. The design of the network ﬂows is achieved

thanks to the ID model allowing the determination

of transfer delays. Then, an optimization approach

based on a linear programming is used. The proposed

approach is illustrated by considering an academical

case-study that consists in a two navigation reaches.

The main objective is to deal with time delays and

time varying characteristics. Future works will aim

at adapting and applying this approach on real sys-

tems with outlets to the sea that require time varying

characteristics to deal with the tide effect. Another

perspective will be the comparison of this approach

with MPC.

REFERENCES

Ahuja, R.-K., Magnanti, T.-K., and Orlin, J.-B. (1993).

Network ﬂows - Theory, algorithms and applications.

New Jersey.

Alves, D. C. S., Duviella, E., and Doniec, A. (2018). Im-

provement of water resource allocation planning of in-

land waterways based on predictive optimization ap-

proach. In ICINCO, Porto, Portugal.

Amigoni, F., Castelletti, A., and Giuliani, M. (2015).

Modeling the management of water resources sys-

tems using multi-objective dcops. In Proceedings

of the 2015 International Conference on Autonomous

Agents and Multiagent Systems, AAMAS ’15, pages

821–829, Richland, SC. International Foundation for

Autonomous Agents and Multiagent Systems.

Ayoub, T., Ladeveze, D., Chiron, P., and Archim

ede,

B. (2018). Reconstruction of hydrometric data us-

ing a network optimization model. HIC conference,

Palermo, July 1st-6th.

Bencheikh, G., Tahiri, A., Chiron, P., Archimede, B.,

and Martignac, F. (2017). A ﬂood decrease strategy

based on ﬂow network coupled with a hydraulic sim-

ulation software 11this work was partially supported

by the urban community of le grand tarbes. IFAC-

PapersOnLine, 50(1):3171 – 3176. 20th IFAC World

Congress.

Duviella, E., Doniec, A., and Nouasse, H. (2018). Adap-

tive water-resource allocation planning of inland wa-

terways in the context of global change. Jour-

nal of Water Resources Planning and Management,

144(9):04018059.

Fathabadi, H. S. and Hosseini, S. A. (2010). Maximum ﬂow

problem on dynamic generative network ﬂows with

time-varying bounds. Applied Mathematical Mod-

elling, 34(8):2136 – 2147.

Water-resource Optimization Problem of Inland Waterways based on Network Flows with Flow Transition Time and Time Varying

Characteristics

309

Fulkerson, D. (1966). Flow networks and combinatorial op-

erations research. In American mathematical monthly,

volume 73.

Hadid, B. and Duviella, E. (2018). Water asset man-

agement strategy based on predictive rainfall/runoff

model to optimize the evacuation of water to the sea.

In ICINCO, Porto, Portugal.

Hadid, B., Duviella, E., and Lecoeuche, S. (2018). Im-

provement of a predictive data-driven model for

rainfall-runoff global characterization of aa river. cited

By 0.

He, Y., Chen, X., Sheng, Z., Lin, K., and Gui, F. (2018).

Water allocation under the constraint of total water-

use quota: a case from dongjiang river basin, south

china. Hydrological Sciences Journal, 63(1):154–167.

Horv

ath, K., Duviella, E., Petreczky, M., Rajaoarisoa, L.,

and Chuquet, K. (2014). Model predictive control of

water levels in a navigation canal affected by reso-

nance waves. In HIC 2014, 11th International Con-

ference on Hydroinformatics, New York.

Horv

ath, K., Rajaoarisoa, L., Duviella, E., Blesa, J., Pe-

treczky, M., and Chuquet, K. (2015). Enhancing in-

land navigation by model predictive control of water

level – the Cuinchy-Fontinettes case. Transport of Wa-

ter versus Transport over Water - Exploring the dy-

namic interplay between transport and water - Carlos

Ocampo-Martinez, Rudy Engenborn (eds).

Kotnyek, B. (2003). An annotated overview of dynamic

network ﬂows. INRIA Report n. 4936.

Ladeveze, D., Charbonnaud, P., and Archim

ede, B. (2010).

Multi-objective management of multi-resource hy-

drographical systems. IFAC Proceedings Volumes,

43(8):585 – 590. 12th IFAC Symposium on Large

Scale Systems: Theory and Applications.

Nouasse, H., Doniec, A., Duviella, E., and Chuquet, K.

(2016a). Efﬁcient management of inland navigation

reaches equipped with lift pumps in a climate change

context. 4

IAHR Europe Congress, Liege, Belgium

27-29 July.

Nouasse, H., Doniec, A., Lozenguez, G., Duviella, E., Chi-

ron, P., Archim

ede, B., and Chuquet, K. (2016b). Con-

straint satisfaction problem based on ﬂow transport

graph to study the resilience of inland navigation net-

works in a climate change context. IFAC Conference

MIM, Troyes, France, 28-30 June.

Schuurmans, J., Clemmens, A. J., Dijkstra, S., Hof, A.,

and Brouwer, R. (1999). Modeling of irrigation and

drainage canals for controller design. Journal of irri-

gation and drainage engineering, 125(6):338–344.

Segovia, P., Rajaoarisoa, L., Nejjari, F., Puig, V., and Du-

viella, E. (2017). Decentralized control of inland nav-

igation networks with distributaries: application to

navigation canals in the north of France. ACC’17,

Seattle, WA, USA, May 24–26.

Skutella, M. (2009). An introduction to network ﬂows over

time. In Research Trends in Combinatorial Optimiza-

tion, pages 451–482. Springer-Verlag.

Tchangani, A. P. (2017). Sustainable management of natu-

ral resource using bipolar analysis. application to wa-

ter resource sharing. IFAC-PapersOnLine, 50(1):3177

– 3182. 20th IFAC World Congress.

Wolfs, V., Meert, P., and Willems, P. (2015). Modular con-

ceptual modelling approach and software for river hy-

draulic simulations. Environmental Modelling & Soft-

ware, 71:60 – 77.

Xiong, W., Li, Y., Zhang, W., Ye, Q., Zhang, S., and

Hou, X. (2018). Integrated multi-objective optimiza-

tion framework for urban water supply systems un-

der alternative climates and future policy. Journal of

Cleaner Production, 195:640 – 650.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

310