
Design, Estimation of Model Parameters, and Dynamical Study of a
Hybrid Aerial-underwater Robot: Acutus
Ridhi Puppala, Nikhil Sivadasan, Abhijeet Vyas, Akshay Molawade,
Thiyagarajan Ranganathan and Asokan Thondiyath
Robotics Laboratory, Department of Engineering Design, Indian Institute of Technology Madras, India
Keywords: Multi Domain Vehicle, Hybrid Vehicle, Underwater Robot, Mathematical Modelling, Parameter Estimation,
Dynamics.
Abstract: Design of multi-domain vehicles has been a focus in robotics research in the recent past. The objective behind
developing such hybrid vehicle/robot is to combine the capabilities of systems operating in various domains.
They can be of great use in numerous applications, as it maximizes the reach in multiple operation
environments, especially in various challenging sectors to reduce risk to the human lives. This paper presents
the design of multi-domain vehicle: a hybrid aerial-underwater robot, Acutus. Dynamic modelling of Acutus
is one of the vital steps in the design process. The parameters involved in the model such as the hydrodynamic
drag and added mass are critical in determining the accuracy of the model. Mathematical modelling and
estimation of system parameters for Acutus are presented. The dynamics of the system, both in aerial and
underwater domains, are initially studied individually for different possible sets of inputs. Later, simulation
studies are carried out for transition between aerial and underwater domains. Preliminary mechatronic design
and the experimental setup details are also presented.
1 INTRODUCTION
The major inspiration for the development of multi-
domain vehicles has been from the nature.
Researchers have been working on the development
of bio-inspired amphibious robots capable of
swimming, walking and crawling similar to snake
(Crespi and Ijspeert, 2005), salamander (Crespi et al,
2013), etc. Such systems pose various challenges in
terms of design and control because of the drastic
variation in environment. These vehicles will be of
great use in multiple applications and one such
application is presented in (Michael et al., 2014)
wherein, a robot which can navigate on ground and
fly as well has been developed and demonstrated to
be used during natural calamities like earthquake.
Majority of research in design of multi-domain
vehicles is concentrated on either of these two
combinations: Ground-aerial or Ground-underwater.
Also, for multi-domain vehicles involving operations
in water, the design is majorly concentrated on
surface vehicles. Another important and challenging
combination is a hybrid aerial-underwater vehicle.
The combination of aerial and underwater vehicles is
interesting and challenging because of the very nature
of operation of these systems. Inherently different
properties like the density and viscosity of air and
water pose challenges in the design of such robots.
A concept of aerial-aquatic vehicle with ability to
traverse underwater and fly in air is discussed in
(Alzu’bi et al, 2018). It uses fixed wing aerial
configuration, capable of making self-propelled leaps
out of water and into the air. It builds up enough speed
under water to launch itself into air using a single
high-speed propeller. One of the aerial-aquatic
vehicles being developed uses quadrotor
configuration wherein the underwater motion is
achieved using an actively controlled ballast system
which allows the vehicle to suspend in a horizontal
position underwater at a required depth (Alzu’bi et al,
2018). A VTOL tail sitter is developed on the lines of
bio-inspired cross domain vehicles which can
conduct submerged operations as well as aerial flights
(Stewart et al., 2018). As discussed earlier, the very
nature of the domains in which the vehicles are to be
operated, demands intense design and simulation
analysis before it is fabricated.
Modelling of underwater systems involve a whole
lot of unknown variables, which needs to be
estimated. Some of the critical parameters to be
Puppala, R., Sivadasan, N., Vyas, A., Molawade, A., Ranganathan, T. and Thondiyath, A.
Design, Estimation of Model Parameters, and Dynamical Study of a Hybrid Aerial-underwater Robot: Acutus.
DOI: 10.5220/0007926104230430
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 423-430
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
423

estimated are the hydrodynamic derivatives, rigid
body and added mass coefficients. Modelling of
underwater systems have already been attempted
countless times in the past (Szymak, 2016), (Wang et
al., 2009), (Ai et al, 2018). Modelling of conventional
aerial multirotor systems are comparatively easier, as
most of the parameters can be directly obtained from
CAD models. Experimentally verified models of the
two popular UAV configurations, the fixed wing
(Khan and Nahon, 2016), (Bouabdallah and Siegwart,
2006) and VTOL (Fernando et al, 2013) can be
adopted to model similar configurations. (Zhang et
al., 2014) and (Kurak and Hodzic, 2018) discuss and
review all the existing popular quadrotor dynamics
modelling methods.
Estimation of parameters involved in the
mathematical model is the next vital step in modelling
a system. Some of estimation methods use a linear
approximation of the mathematical model of the
system, which then gives a least squares optimal
estimation of the parameters, using the Moore
Penrose Inverse method (Caccia et al, 2000). Sensory
instrumentation to measure the acceleration of
underwater systems is still not standardised and
calculation of acceleration by integrating velocity
may be erroneous. A low pass-filtering technique like
those discussed in (Wales, 1986), (Iisu et al., 1987)
and (Slotine and Li, 1989) may be required to
estimate the parameters numerically. (Smallwood and
Whitcomb, 2003) introduces a stable online adaptive
framework for the estimation of parameters.
(Ranganathan et al., 2018) introduces a different
method which makes use of concepts from both least
square method and free decay tests. The least square
sum (integral) of the error is minimised using a
gradient descent method.
In this paper, we propose the design of a hybrid
vehicle, Acutus, which is a fish-shaped aerial-
underwater vehicle that uses quadrotor for aerial
navigation and underwater thrusters for propulsion in
water. Underwater motion is achieved using a single
water thruster along with actuated control planes as
flaps and rudder. The presented model is capable of
independent manoeuvres in both aerial and
underwater environments. The quadrotor is enabled
over a switching mechanism wherein the quadrotor
arms can be retracted while diving underwater.
2 CONCEPTUAL DESIGN AND
WORKING PRINCIPLE
The conceptual CAD design of Acutus with right-
hand global frame co-ordinates O
G
: {X
G
, Y
G
, Z
G
} and
body frame co-ordinates O
B
: {X
B
, Y
B
, Z
B
} are shown
in Figure 1. Body frame origin (O
B
) is fixed to centre
of gravity (COG). The balance between weight and
buoyancy of Acutus is critical and the vehicle is
designed to be slightly positively buoyant (1N). The
flexibility in design is greatly narrowed down by the
intersection of constraints like the volume of
underwater capsule, weight during aerial flight and
structural integrity against underwater pressure. The
proposed design has an outer profile, best
approximated to the form of a fish. The streamlined
outer profile helps overcome the hydrodynamic drag.
Furthermore, design is conceptualized in such a way
that it minimizes the drag in aquatic medium by
minimal exposure of redundant extended surfaces
against the flow. Since the vehicle is designed to be
positively buoyant, the thrust required to dive-in
should be more than the residual buoyancy
(difference between weight and buoyancy). Hence,
there is also a need to regulate the weight and
buoyancy of the system while ensuring power
efficient use of thrusters.
Figure 1: Isometric view of Acutus.
The proposed model is a reconfigurable system
which switches from aerial configuration to
underwater configuration while entering water by
retracting the arms having aerial propellers. The
mechanism proposed for retraction of arms is a
double worm-drive arrangement, which actuates two
arms at the same time as shown in Figure 2. Worm-
drive mechanism ensures rigidity and non-back
drivability during underwater operation. The
mechanism is light and compact and allows
sequential retraction of both pair of arms while
avoiding collision.
Acutus is designed to have four controllable,
coupled degrees of freedom. The surge motion is
generated by a water thruster. Pitch is a coupled
degree of freedom achieved by vectoring the surge
velocity using the two flaps connected on either side
of the metallic body. Yaw can be achieved by
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
424

controlling the rudder connected right behind the
thruster. Roll is passively stabilized and heave is
achieved by coupling pitch along with surge.
Figure 2: Worm drive for retraction of quad rotor arms.
It is worthwhile to notice that most of the degrees
of freedom are coupled for underwater operation.
During navigation in air, the arms with aerial
propellers are extended. This allows Acutus to
manoeuvre in air with 4 degrees of freedom viz.
heave, yaw, pitch and roll. Once the air-water
interface is reached, the arms are retracted within the
body before diving inside water in order to minimize
the drag forces due to unnecessary extended parts of
the vehicle. The mass of the vehicle is distributed in
such a way that the vehicle rests with a slight pitch at
the transition stage (floating at the air-water
interface). This pitch helps the vehicle to dive in
completely when the thruster is turned on. Later by
controlling the right and left flaps, required pitching
motion is achieved. The aerial rotors are mounted
such that if the vehicle comes back at the air-water
interface, all the 4 air propellers lie outside water and
can be actuated to escape out of the water medium.
3 ESTIMATION OF MODEL
PARAMETERS AND
DYNAMICS
A mathematical model of the underwater and aerial
system has been developed to perform a detailed
analysis of the overall system at different operating
conditions. The 6 DOF underwater dynamics has
been subdivided into dynamics of fuselage and
dynamics of control planes and thruster.
3.1 Parameter Estimation for Fuselage
Dynamics
Fuselage of vehicle consists of the metallic body and
shroud. The Newton-Euler formulation is used in
modelling the dynamics of fuselage (Fossen, 2011).
The velocities, forces, and moments in body fixed and
earth fixed frame and the global pose are represented
based on SNAME convention (Fossen, 2011).
where,
(1)
The governing equation for overall dynamics of
underwater system is given in (1) has been
implemented in MATLAB Simulink.
ղ
is global pose
vector, ν is body frame velocity vector and τ is a
vector of forces and moments of dimensions 61.
Earth frame velocities can be computed from body
frame velocities using the kinematic transformation
where is the Jacobian matrix.
We employ computational methods to estimate
the model parameters. Mass matrix (M) is sum of
rigid body inertial matrix (M
RB
) and added mass
matrix (M
a
). Coriolis and Centripetal forces matrix
C(ν) can be expressed as a sum of rigid body and
added mass terms as shown in (1). The elements of
the matrices M
RB
and C
RB
(ν) are estimated from 3D
CAD model. M
a
and C
a
(ν) are estimated by
approximating the metallic body to standard
geometry. Current prototype is approximated to a
cylinder of same volume with the same length as real
prototype and diameter of 60mm. Damping matrix
D(ν) is square matrix consisting of linear and
quadratic hydrodynamic drag coefficients. Restoring
forces and moments vector g is a function of
ղ
capturing the effects of gravity, buoyancy, centre of
gravity (COG) and centre of buoyancy (COB) on the
body.
The linear and quadratic damping terms are
estimated from fluid flow analysis of the fuselage
using Computational Fluid Dynamics (CFD). CFD
simulations were performed for 10 equally spaced
linear velocities in the range of -0.5 to 0.5m/s along
X
G
, Y
G,
Z
G
axes, and similarly for rotational velocities
along roll, pitch and yaw directions. Velocity
contours and streamline plots for CFD simulations are
shown in Figure 3. Values of all six forces and
moments against every translational and rotational
velocities were tabulated and used for estimation of
damping coefficients.
Quadratic fit between damping forces during
translations is shown in Figure 4. For instance, the
coefficients along heave direction can be estimated
using the fit as Z
w
w + Z
w|w|
w|w|, where Z
w
and Z
w|w|
are linear and quadratic damping coefficients
respectively. A similar approach was adopted to
estimate other direct and cross coupled coefficients
with approximations. Due to asymmetric outer profile
of Acutus, forces are not same for equal positive and
negative velocities, which is evident from Figure 4.
Design, Estimation of Model Parameters, and Dynamical Study of a Hybrid Aerial-underwater Robot: Acutus
425
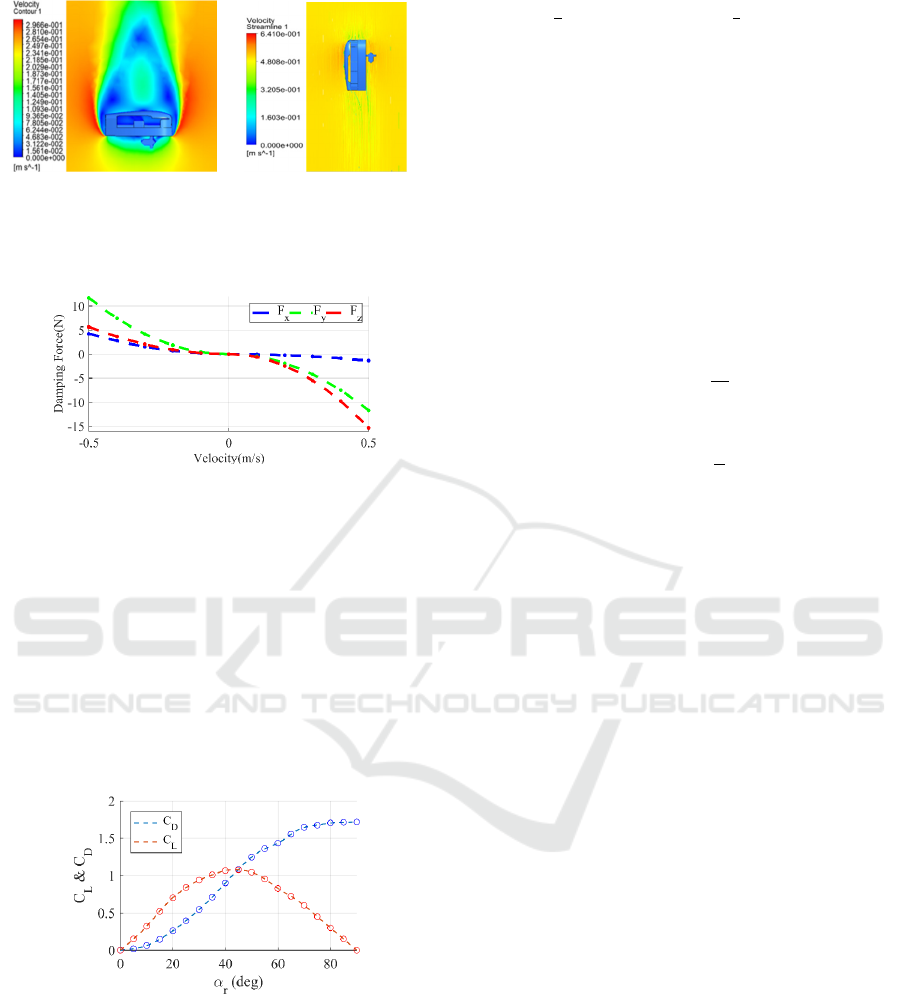
(a) (b)
Figure 3: (a) Velocity contours for 0.5m/s flow velocity
along negative Z
B
and (b) Streamlines for 0.5m/s flow
velocity along negative X
B.
Figure 4: Variation of damping forces along X
B
, Y
B
, Z
B.
3.2 Parameter Estimation for Control
Plane and Thruster Dynamics
Dynamics of control planes and water thruster are
modelled as the external forces and moments to the
fuselage system. External force and moment vector τ
in (1) are sum of forces and moments from two flaps,
rudder and thruster. Thruster produces a force along
surge direction and a reaction torque along the roll
axis. Thrust and torque versus input voltage data is
used to model the thruster.
Figure 5: Variation of C
L
and C
D
against α for rudder.
CFD simulations of rudder and flaps against
various flow angles are conducted to record the drag
force (F
d
) and lift force (F
l
) versus angle of attack (α).
Using equations as shown in (2), coefficients of drag
(C
D
) and coefficient of lift (C
L
) are estimated against
α ranging from 0
◦
to 90
◦
for flow velocity of up to
0.5m/s and gauge pressure of 1 bar.
ρ
is density of
water and A is area of the rudder plate. V is the relative
velocity w.r.to the flow.
|
|
and
||
(2)
Surge velocity (u) and sway velocity (v) are
resolved into u
0
and v
0
along rudder and its
perpendicular direction respectively as described in
the (3) and (4).
(3)
(4)
Rudder angle of attack (α
r
) and relative velocity
(V) can be calculated as shown in (5) and (6)
respectively. C
D
and C
L
for a rudder angle is
estimated from look up table modelled from data as
shown in Figure 5. Fuselage angle of attack (β
r
) is
given by the expression as shown in (7).
(5)
cos
sin
(6)
(7)
Forces generated by rudder can be calculated by
resolving the components of F
d
and F
l
along X
B
and
Y
B
. Drag (F
d
) is always anti-parallel to relative flow
velocity V and the lift (F
l
) can change directions for
different cases of sign of u
0
and v
0
. For the case with
positive u
0
and v
0
, the relationship between the above
said forces can be represented in matrix form as,
(8)
Rudder produces roll, pitch and yaw moments
about the COG due to the offset of point of
application of forces along all three axes. Centre of
gravity on the trapezium shaped flat surface can be
assumed as centre of pressure (CP) for rudder. F
x
and
F
y
act at CP which is at a distance r
z
along Z
B
from
COG. The distance between COG and axis of rotation
of rudder along X
B
is r
x
, and perpendicular distance
between CP and axis of rotation is a. Yaw moment
produced by rudder has a significant effect on rotation
of the fuselage in the yaw direction and coupled sway
motion. Moments about X
B
, Y
B,
Z
B
are calculated as
shown in (9).
(9)
(10)
Vector of forces and moments due to rudder is
represented as τ
rudder
= [F
x
F
y
F
z
M
roll
M
pitch
M
yaw
]
T
. A
similar method can be adopted to calculate forces and
moments vector for thruster, right and left flaps
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
426

represented by τ
thruster
, τ
rightflap
and τ
leftflap
respectively.
Net forces and moments vector can be expressed as a
sum of these vectors by neglecting external
disturbances in water as shown in (10).
3.3 Aerial Dynamics and Controller
As discussed earlier, Acutus reconfigures itself to a
quadrotor during its navigation in air. A mathematical
model has been developed for aerial operation of
Acutus based on dynamics of quadrotor derived in
(Bouabdallah et al, 2004). The convention for body
and global frame coordinate axes is the same as
discussed in section 3.1. Modelling of quadrotor
dynamics and controller design for multirotor
systems has been a topic of wide and active research.
The aerial dynamics of the robot can be expressed
using Newton-Euler formalism similar to (1) by
simply eliminating the added mass and hydrodynamic
drag terms for aerial dynamics. Buoyancy terms in
restoring forces and moments vector g are set to zero
for aerial model. The overall dynamics of aerial
system can be represented as shown in (11a).
,
,,
,
,
,Ω
,Ω
(11a)
ΩΩ
Ω
Ω
Ω
(11b)
The system inputs U
1
, U
2
, U
3
, U
4
are functions of
rotor speeds Ω
1
, Ω
2
, Ω
3
, Ω
4
. Disturbance Ω is function
of these speeds as defined in (11b). Torque applied on
the body of vehicle along an axis is difference
between the torque generated by each propeller on
other axis and can be expressed as functions of rotor
speeds (Bouabdallah et al, 2004).
A cascaded PI-PID controller as available on
commercial autopilots was implemented for
stabilization of the experimental quadrotor system in
aerial traversal as proposed in (Nandakumar et al,
2017).
The models of aerial and underwater systems can
be combined as shown in (12a). Here, ζ is the
switching variable using which these dynamics are
switched based on the rule shown in (12b).
ζ
,
,,
,
,
,Ω
1
ζ
,,,,
,,
ζ
,Ω
1‐ζ
(12a)
ζ
1;if 0
0;
(12b)
4 SIMULATIONS AND RESULTS
Numerical simulations have been carried out for
various input conditions in MATLAB Simulink for
aerial, underwater navigation and transition.
Simulation results are used to validate the design and
developed mathematical model, analyse the
performance of the system in different modes of
operation.
Zig-Zag manoeuvre is a standard test performed
to evaluate the zig-zag manoeuvrability, course-
keeping ability and underwater vehicle’s response to
rudder (Issac et al., 2008), (Yu et al, 2014). The
zigzag manoeuvre for robot is obtained by varying
rudder angle (θ
r
) between -θ
max
and θ
max
. Simulation
results for a zigzag manoeuvre of Acutus at 75% of
maximum thrust (~38N) are shown in Figure 6. Due
to offset between COG and COB along X
B
, a pitch of
-9° is observed in the robot.
(a)
(b)
Figure 6: Simulation results for 15° / 15° zigzag manoeuvre
(a) Rudder input (θ
r
) and yaw (ψ) (b) 3D trajectory of the
zigzag manoeuvre.
Pitch manoeuvrability of the robot can be
understood from simulation results for varying pitch
input under constant thrust as shown in Figure 7. The
robot was found to achieve high surge velocities up
to 2m/s at 75% of maximum thrust owing to the
streamlined profile.
Another test to evaluate the turning and course
changing ability of marine vehicles is turning circle
test and steady turning diameter acts as a quantitative
measure for steering manoeuvrability. Variation of
steady turning diameter against different rudder
angles under 75% maximum thrust is shown in Figure
8. Inherent pitch in the underwater system induces a
coupled heave motion despite zero flap angle.
Therefore, the system is observed to descend with a
Design, Estimation of Model Parameters, and Dynamical Study of a Hybrid Aerial-underwater Robot: Acutus
427

constant heave velocity tracing a helix with steady
turning diameter of ~87.3m for 35° rudder angle as
shown in Figure 8(c).
(a)
(b)
Figure 7: (a) Flap input (θ
f
) and pitch (θ) (b) Path traced by
robot over time.
(a)
(b)
Figure 8: (a) Steady turning diameter versus rudder input
(θ
r
) (b) Helical path traced by robot at constant thrust and
35° rudder angle.
Numerical simulations for complete sequence of
water to air and air to water traversal have been
conducted to understand the operation at transition
phase. Simulation results for water to air traversal are
shown in Figure 9. Underwater traversal is executed
for a duration of 32.5s. Transition is the intermediate
state occurring at z = 0m, where the mathematical
model switches from underwater dynamics to aerial
dynamics. Aerial traversal commences system after a
delay of 2.5s for retraction of the arms. Performance
of the tuned aerial controller was observed to be
satisfactory as demonstrated in Figure 9(b). Path
traced by robot in X
G
Z
G
plane starting from (0, 0, 5m)
is shown in Figure 9(c).
(a)
(b)
(c)
(d)
Figure 9: (a) Thruster voltage input and flap angle input for
underwater traversal (b) Desired and actual altitude for
aerial traversal starting at t = 35s (c) Trajectory of water to
air traversal for above inputs (d) Variation of position along
X
G
& Z
G
axis, and pitch (θ).
Simulation results for air to water traversal are
shown in Figure 10. Aerial traversal is executed for a
duration of 8s with a constant pitch reference of -1°.
Delay of 2s has been introduced at transition phase
for retraction of arms. Underwater traversal
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
428

commences after the delay with varying thruster
voltage and flap angle inputs as shown in Figure
10(a). Path traced by robot in X
G
Z
G
plane starting
from 4m above water is shown in Figure 10(c).
(a)
(b)
(c)
(d)
Figure 10: (a) Thruster voltage input and flap angle input
starting at t = 10s (b) Desired and actual altitude for aerial
traversal (c) Trajectory of air to water traversal for above
inputs (d) Variation of position along X
G
& Z
G
axis, and
pitch (θ).
5 EXPERIMENTAL SETUP
An experimental setup of the vehicle has been
developed after multiple design iterations and
simulation studies. The weight of the designed
prototype is 77N and the buoyancy is 78N. Hence, the
residual buoyancy is 1N underwater. For internal
stability of the quadrotor, COG of the system has
been adjusted to be below the centre of rectangle
formed by aerial rotors in their extended position.
Metallic body (capsule) is made of stainless steel and
houses electronics while providing a strong skeleton
to support all the on-board components. The capsule
is 0.62m long, 0.2m wide and can withstand a
pressure up to 10m underwater. A 3D printed shroud
has been used for streamlining the flow. Shroud is
fixed on top of the capsule and contains slots for
passage of aerial rotors and propellers during
retraction. Aluminium channels of suitable dimension
were chosen as structural members for retracting arms
based on FEA studies and cantilever bending load
calculations.
Three high torque metal gear servo motors are
used to drive the shafts of rudder and two flaps. Two
micro speed reduction metal gear box DC motors
drive the worm gear for retraction of the quadrotor
arms. A combination of 4 BLDC motors with a
maximum thrust of 45N each, 16x5.4-inch carbon
fibre propellers and 60A electronic speed controllers
(ESCs) have been chosen for aerial propulsion. The
water thruster can provide a maximum thrust of up to
50N. Underwater system is equipped with a pressure
sensor and a 9 DOF Inertial Measurement Unit
(IMU). Communications with the user console
happens over a neutrally buoyant long tether. Aerial
electronic architecture consists of a standard flight
controller and radio system embedded with
accelerometer and gyroscope. PI-PID controller is
being used for aerial operation. The prototype is being
tested for underwater traversal and aerial-aquatic
transition.
Figure 11: Experimental prototype (work in progress).
6 CONCLUSION
A hybrid aerial-underwater robot has been
conceptually designed and the same has been
mathematically modelled to analyse the behaviour.
Simulations were carried out to demonstrate the
capabilities. The results prove the concept and shows
that such robots can be used for multiple applications.
Design, Estimation of Model Parameters, and Dynamical Study of a Hybrid Aerial-underwater Robot: Acutus
429

A prototype has been developed after iterative
improvisations based on the simulation results and the
same is being tested. The work presented in this paper
is an analysis of design, parameter estimation and
dynamic model of the system. Further study on the
coupled underwater dynamics and closed loop
analysis of the coupled system are ongoing.
REFERENCES
Ai, X., Kang, S. and Chou, W. (2018) ‘System Design and
Experiment of the Hybrid Underwater Vehicle’, in
2018 International Conference on Control and Robots
(ICCR). Hong Kong, China: IEEE, pp. 68–72.
Alzu’bi, H., Mansour, I. and Rawashdeh, O. (2018) ‘Loon
Copter: Implementation of a hybrid unmanned aquatic–
aerial quadcopter with active buoyancy control’,
Journal of Field Robotics, 35(5), pp. 764–778. doi: 10.
1002/rob.21777.
Bouabdallah, S., Murrieri, P. and Siegwart, R. (2004)
‘Design and control of an indoor micro quadrotor’, in
IEEE International Conference on Robotics and
Automation, 2004. Proceedings. ICRA ’04. 2004. Los
Angels, USA, p. 4393–4398 Vol.5. doi: 10.1109/
ROBOT.2004.1302409.
Bouabdallah, S. and Siegwart, R. (2006) Dynamic
Modeling of Fixed-Wing UAVs, Swiss Federal institute
of technology,version 2.
Caccia, M., Indiveri, G. and Veruggio, G. (2000) ‘Modeling
and identification of open-frame variable configuration
unmanned underwater vehicles’, IEEE Journal of
Oceanic Engineering, 25(2), pp. 227–240.
Crespi, A. and Ijspeert, A. J. (2005) ‘Swimming and
Crawling with an Amphibious Snake Robot’, in
Proceedings of the 2005 IEEE International
Conference on Robotics and Automation. Barcelona,
Spain, pp. 24–28.
Crespi, A., Karakasiliotis, K. and Ijspeert, A. J. (2013)
‘Salamandra Robotica II : An Amphibious Walking
Gaits’, IEEE Transactions on Robotics, 29(2), pp. 308–
320.
Fernando, H. C. T. E., Silva, D. and Munasinghe, S. R.
(2013) ‘Modelling , Simulation and Implementation of
a Quadrotor UAV’, in IEEE International Conference
on Industrial and Information Systems. Peradeniya, Sri
Lanka. doi: 10.1109/ICIInfS.2013.6731982.
Fossen, T. I. (2011) Handbook of Marine Craft
Hydrodynamics and Motion Control. 1st edn,
Handbook of Marine Craft Hydrodynamics and Motion
Control. 1st edn. doi: 10.1002/9781119994138.
Iisu, P. et al. (1987) ‘Adaptive Identification and Control’,
in IEEE International Conference on Robotics and
Automation. Raleigh, USA, pp. 1210–1215.
Issac, M. T. et al. (2008) ‘Analysis of Horizontal Zigzag
Manoeuvring Trials from the MUN Explorer AUV’, in
Oceans 2008. Kobe, Japan.
Khan, W. and Nahon, M. (2016) ‘Modelling Dynamics of
Agile Fixed-Wing UAVs for Real-Time Applications’,
in International Conference on Unmanned Aircraft
Systems. Arlington, USA, pp. 1303–1312. doi: 10.1109/
ICUAS.2016.7502599.
Kurak, S. and Hodzic, M. (2018) ‘Control and Estimation
of a Quadcopter Dynamical Model’, Periodicals of
Engineering and Natural Sciences, 6(1), pp. 63–75. doi:
10.21533/pen.v6i1.164.
Michael, N. et al. (2014) ‘Collaborative Mapping of an
Earthquake Damaged Building via Ground and Aerial
Robots’, Journal of Field Robotics, pp. 33–47. doi:
10.1007/978-3-642-40686-7.
Nandakumar, G., Srinivasan, A. and Thondiyath, A. (2017)
‘Theoretical and Experimental Investigations on the
Effect of Overlap and Offset on the Design of a Novel
Quadrotor Configuration , VOOPS’, Journal of
Intelligent Robotic Systems. Journal of Intelligent &
Robotic Systems.
Ranganathan, T. et al. (2018) ‘Design and Analysis of a
Novel Underwater Glider – RoBuoy’, in International
Conference on Robotics and Automation (ICRA).
Brisbane, Australia.
Slotine, J.-J. E. and Li, W. (1989) ‘Composite adaptive
control of robot manipulators’, Automatica, 25(4), pp.
509–519. doi: 10.1016/0005-1098(89)90094-0.
Smallwood, D. A. and Whitcomb, L. L. (2003) ‘Adaptive
identification of dynamically positioned underwater
robotic vehicles’, IEEE Transactions on Control
Systems Technology, 11(4), pp. 505–515.
Stewart, W. et al. (2018) ‘Design and demonstration of a
seabird-inspired fixed-wing hybrid UAV-UUV system
Design and demonstration of a seabird-inspired fixed-
wing hybrid UAV-UUV system’, Bioinspiration &
Biomimetics. IOP Publishing.
Szymak, P. (2016) ‘Mathematical model of underwater
vehicle with undulating propulsion’, in 2016 Third
International Conference on Mathematics and
Computers in Sciences and in Industry (MCSI). IEEE,
pp. 269–274. doi: 10.1109/MCSI.2016.057.
Wales, N. S. (1986) ‘Adaptive computed torque control for
rigid link manipulators’, in Conference on Decision and
Control. Athens, Greece, pp. 68–73.
Wang, B. et al. (2009) ‘Modeling and motion control
system research of a mini underwater vehicle’, in 2009
International Conference on Mechatronics and
Automation. Changchun, China: IEEE, pp. 4463–4467.
doi: 10.1109/ICMA.2009.5244851.
Yu, C., Xiang, X. and Zhao, R. (2014) ‘Horizontal Zigzag
Maneuverability of UUV in Limited Space’, in Chinese
Control and Decision Conference. Changsha, China,
pp. 3306–3310.
Zhang, X. et al. (2014) ‘A Survey of Modelling and
Identification of Quadrotor Robot’, Abstract and
Applied Analysis, 2014.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
430
