An Unsupervised Drift Detector for Online Imbalanced Evolving

Streams

D. Himaja

, T. Maruthi Padmaja

and P. Radha Krishna

Department of Computer Science and Engineering, Vignan’s Foundation for Science, Technology and Research (Deemed

to be University), Guntur-Tenali Rd, Vadlamudi, Guntur, Andhra Pradesh, India

Department of Computer Science and Engineering, National Institute of Technology, Warangal, Telangana, India

Keywords: Class Imbalance, Evolving Stream, Concept Drift, Active Learning, Hypothesis Tests.

Abstract: Detecting concept drift from an imbalanced evolving stream is challenging task. At high degree of

imbalance ratios, the poor or nil performance estimates of the learner from minority class tends to drift

detection failures. To ameliorate this problem, we propose a new drift detection and adaption framework.

Proposed drift detection mechanism is carried out in two phases includes unsupervised and supervised drift

detection with queried labels. The adaption framework is based on the batch wise active learning.

Comparative results on four synthetic and one real world balanced and imbalanced evolving streams with

other prominent drift detection methods indicates that our approach is better in detecting the drift with low

false positive rates.

1 INTRODUCTION

Recently, learning from imbalanced data streams is

receiving much attention. This is a combined

problem of Online Class Imbalance and Concept

Drift according to (Ditzler et al, 2015 and Gama et

al, 2013) and can usually find in Fraud and Fault

detection domains. The class imbalance problem

occurs when one class of data severely outnumbers

the other classes of data. Due to this tendency the

learner performance bias towards the majority class.

In case of evolving streams this degree of imbalance

varies from time to time. Further due to lifelong

learning, the underlined concept generation function

prone to changes thus leads to concept drifts.

From (Gama et al, 2013) in terms of Bayesian

classifier, there are three types of concept drifts that

are due to the change in (i) the posterior probabilities

 (ii) the prior probabilities  without

effecting the  and (iii) the likelihood 











without effecting . In addition to this, a drift

coexist together. Generally, the concept drift is

countered by active or passive methods. The latter

methods first tracks and detect the drifts and then

adapt to the changes by instance forgetting and

weighing mechanisms. Whereas, in the formal

methods a single learner may continuously adapt to

the changes by resetting the parameters or a new

classifier may be added /removed/updated from an

ensemble, no explicit drift detection is carried out.

This paper focuses on the active method of drift

detection and adaption.

Further (Gama et al, 2013) discusses several drift

detection methods based on supervised learning.

These methods directly or indirectly detect the drift

based on the classifiers performance estimates such

as error, accuracy in both online and batch modes

and fail to detect the drift in case of imbalanced

streams due to poor or nil prediction from minority

class (Wang and Minku, 2017). There are solutions

based on tracking the changes in minority class True

Positive Rate (TPR) (Wang et al, 2013) and on

classifiers four rates such as TPR, False Positive

Rate (FPR), Positive Prediction value (PPV) and

Negative Prediction value (NPV) (Wang and

Abraham, 2015). Prequential AUC of online learners

is also proposed in (Brzezinski and Stefanowski,

2017) to detect drift in dynamic imbalanced streams

with concept drift. However all this methods are

based on supervised estimate of the minority class

and prone to false positives due to the dynamic

change in TPR.

To address this problem, we present a two-stage

drift detector with an unsupervised drift warning

indicator at Stage 1 and an unbiased supervised

estimator with queried labels for drift conformation

Himaja, D., Padmaja, T. and Krishna, P.

An Unsupervised Drift Detector for Online Imbalanced Evolving Streams.

DOI: 10.5220/0007926302250232

In Proceedings of the 8th International Conference on Data Science, Technology and Applications (DATA 2019), pages 225-232

ISBN: 978-989-758-377-3

225

at stage 2. Here the unsupervised drift warning

indicator is independent with target and only rely on

distribution changes. Then the supervised indicator

confirms the drift if there is a significant variation in

the performances. The learning and adaption of the

stream with proposed drift detector is through

querying the uncertainty samples by batch based

active learning.

The paper organization is as follows. Section 2

presents the work related to drift detection and

adaption, Section 3 describes the proposed batch

based drift detection and adaption. Data stream

description, experimental setup results and

discussion are presented in Section 4. Finally, this

paper concludes in section 5.

2 RELATED WORK

The drift detection methods are categorized into two:

(i) active (ii) passive. The active methods works

based on drift detection and adaption. The drift can

be detected using

 Hypothesis Tests: Validates the NULL

hypothesis, i.e., the two samples are derived

from same distribution (Patist, 2007 and

Nishida and Yamauchi, 2007).

 Change-point Method: Tracking the point of

change of the behaviour of distribution

function (Hawkins, Qiu and Wook kang,

2003).

 Sequential Hypothesis Test: Constantly

monitoring the stream until it attains enough

confidence to accept or reject the hypothesis

test (Wald, 1945).

 Change Detection Test: Identifies the drift

based on a threshold on a classification error or

on a feature value (Bifet and Gavalda, 2007).

The use of Hellinger distance and adaptive

Cumulative SUM test for change detection

between data chunks is also studied in (Ditzler

and Polikar, 2011 )

Once the drift is detected in an evolving stream,

the learning framework adapts it by learning a new

model on current knowledge and forgetting the old.

The forgetting mechanisms are of selecting random

samples to filter, or weighing the samples based on

their age so that the sample with largest age is

forgotten. Another method is of windowing, once

the change is detected, the samples which are

relevant to current learner only retained in the

window. But the size of the window is critical here,

the adaptive window size mechanisms based on

Intersection of Confidence Interval (ICI) are

proposed in (Alippi, Boracchi and Roveri, 2011).

Unlike the drift detection and adaption methods the

passive approaches, constantly update the model to

adapt the change with new evolving data. The model

updation is carried out by resetting the parameters

(single classifier adaption) or add/remove/update a

classifier in an ensemble.

So far the drift detection methods for supervised

learning are intended for balanced classes and used

supervised performance estimates such as error,

accuracy and four rates such as TPR, NPR, PPV and

NPV. However, recently, few drift detection

methods are proposed for imbalanced streaming

distributions. The Drift Detection Method Online

Class Imbalance (DDM_OCI) (Wang et al, 2013) is

a modification to DDM (Gama et al, 2004). Unlike

DDM, whose focus is on the change detection in

over all error rate, DDM_OCI tracks changes in TPR

assuming that the drift in the distribution leads to

significant changes when there is an imbalance in

the stream. But, DDM_OCI is quite sensitive to the

dynamic imbalance rate of change than the real

concept drift which results in many false positives.

Instead of tracking the changes only in TPR (Wang

and Abraham, 2015) proposed a Linear Four rates

tracking mechanism for drift detection. If significant

change is detected in any of the performance rates

such as TPR, FPR, PPV and NPV then the drift

signal is alarmed. In (Brzezinski and Stefanowski,

2017) proposed a Prequential AUC based drift

detection mechanism which identifies the drift in

Prequential AUC by Page-Hinkley test. In (Yu et al,

2019) proposed a two-layer drift detection method

where layer 1 adapts LFR and layer 2 is based on

permutation test and both layers are of supervised.

All these methods mainly based on tracking the

changes in supervised performance estimators and

can prone to false positives due to the sensitivity of

TPR towards dynamic imbalance rather than drift at

high degree of imbalance cases. We propose two-

stage drift detection based on unsupervised and

supervised change tracking.

3 PROPOSED METHOD

Figure 1 depicts the flow diagram for proposed drift

detection and adaption method. Here the Learning of

the stream as well as the adaption to the drift is

handled based on batch based active learning. The

drift detection is carried out in two stages, named it

as Kolmogorov-Smirnov_Area under Curve

(KS_AUC) method. This drift detector assumes

initial training set is labelled and the rest of the

stream evolved as unlabelled.

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

226

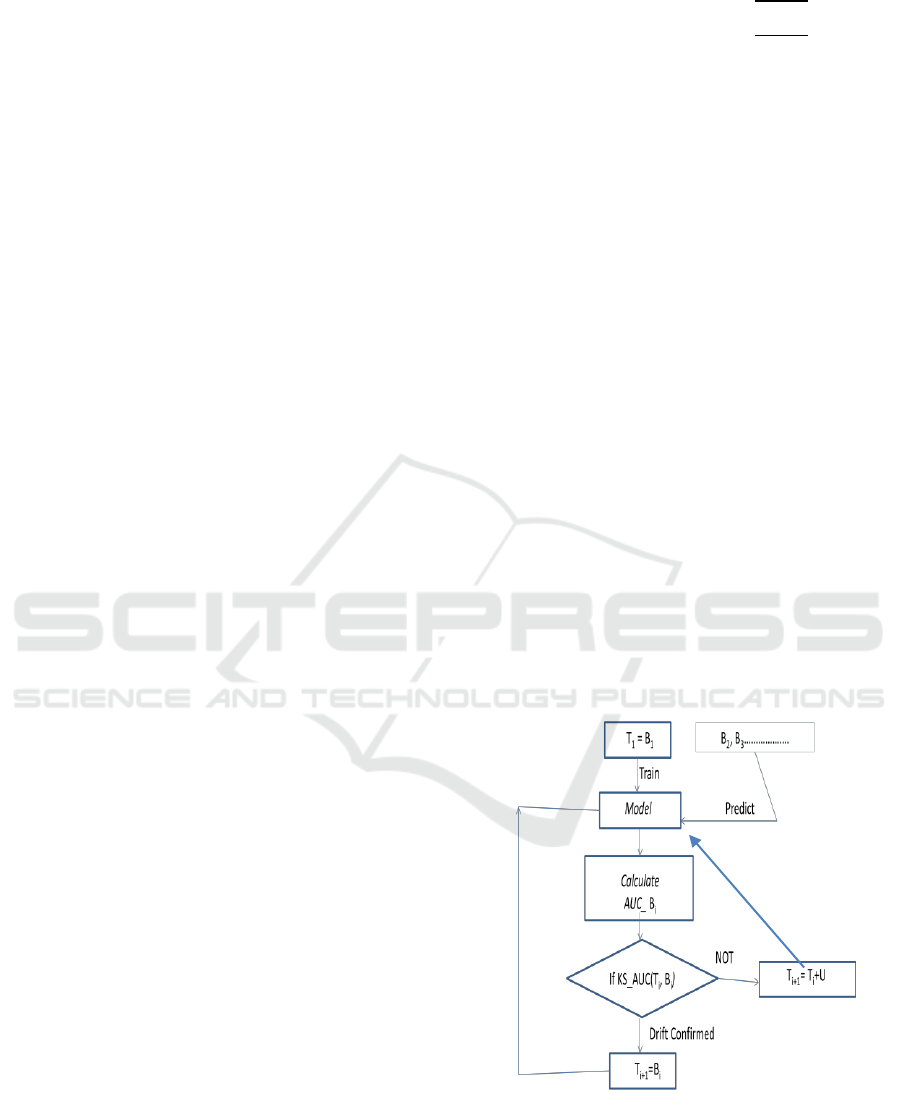
3.1 Learning and Adaption to the Drift

Here the stream is learned based on interleaved

training and testing of batches. The learning

mechanism is chosen as active learning of batches

(Pohl et al 2018) and presented in Algorithm 1. The

first batch is assumed as initial training set T

, a new

Model is learned, the corresponding class labels 

are predicted for each sample and the 



(Area

Under ROC Curve) is computed using (Fawcett,

2006). For each upcoming batch B

, at first the class

labels are predicted using already trained Model.

Later B

undergoes a two stage drift detection

KS_AUC ( ), considering current training T

reference window and B

as detection window

along with calculated AUC's, 



and 



The KS_AUC ( ) algorithm is presented in

Algorithm 2 in detail. If the concept drift is not

confirmed between the windows, the training set for

the next iteration T

i+1

is updated with the samples of

current training T

and with the uncertainty samples

which are less than a given threshold β . The labels

of these samples are queried by oracle. If the

concept drift between the two windows is

conformed then the old Model is replaced with a

new Model considering n+m samples from B

whose labels are obtained by querying the Oracle.

As the stream is with imbalanced class distributions

for the better probability to be the minority sample

getting labelled the n samples from B

are selected

whose uncertainty < α. In addition to this, m

random samples (i.e., 









)

are also selected from B

as new Training set T

i+1

for

the next iteration. Further, here. Then the

rest of the procedure iterates same like earlier.

3.2 Two Stage Drift Detection

KS_AUC

For unbalanced streaming distributions, the drift

detection methods based on supervised i.i.d's

(independent and identically distributed random

variables) prone to biased estimates (Wang et al.,

2018) thus, it is critical to detect the concept changes

in unsupervised manner. Therefore, the stage I of

KS_AUC is based on the hypothesis tests, without

label information the hypothesis tests are capable

enough to detect the changes across the

distributions. Here, a non parametric Kolmogorov-

Smirnov (KS) test is chosen to measure the distance

between the two distributions. KS test rejects the

NULL hypothesis i.e., the two samples drawn under

same distribution at significant level α provided for

the following inequality.













 





















(1)

Where m and n are the sizes of the two

distributions, 









and 









are empirical

distribution functions ( of the first and

second distributions,  is the supermom function,

 are considered from a known table with

significant level of α. The KS test is performed for

all attribute 









 for two

distributions by considering each 





and in 





common attribute X into reference W

and detection

window W

. If the NULL hypothesis is rejected for

any W1 and W

then the warning signal for the drift

is triggered. Instead of KS any other two-sample

hypothesis tests can also considered here. Usually

the hypothesis tests are of quite sensitive to all types

of distributional changes, they are much prone to

false positives. Therefore, the stage 1 used as

warning signal for the underlined drift and stage II

detection is incorporated for the confirmation of the

drift.

At Stage II an unbiased supervised performance

estimator AUC between the batches A and B are

used to confirm the drift. If the 







 >

λ then the drift conformation is signalled, here λ is a

threshold for AUC change between A and B. Here





is the Model performance on reference

window at T

where as 



is the Model

performance on the detection window.

Figure 1: Flow Diagram for KS_AUC Drift Detection.

An Unsupervised Drift Detector for Online Imbalanced Evolving Streams

227

4 EXPERIMENTAL RESULTS

This section presents the results of proposed drift

detectors when compared to existing drift detectors

such as DDM, EDDM, and HDDM_Atest. These

drift detectors are considered from MOA (Bifet et al,

2010). We used synthetic as well as real world data

sets for the experimental study. Number of drifts

confirmed is used as performance indicator in

evaluating the performance. Proposed drift detector

is validated on Naive Bayes, SVM, KNN classifiers.

These classifiers with proposed KS_AUC are

implemented.

4.1 Data Sets

The synthetic data streams i.e., SineV, Line, and

SineH are generated from (Minku, White and Yao,

2010) stream generating environment.

Corresponding data characteristics are shown Table

1. From these, two states of imbalances such as

STATIC and DYNAMIC, with single drift, multiple

drifts and without drift are generated. In STATIC

imbalance, the degree of imbalance remains static

for entire stream whereas in DYNAMIC imbalance

case the prior probabilities p(y) of the classes

changes dynamically as shown in Table 2.

The streams with specified settings are generated

for the length 1000. Here, the change in the data

stream is considered exactly from the middle of the

stream i.e., the Change Point (CP) is 501th time step.

For each of these imbalanced states, streams with

varied degrees of imbalance such as [1:9, 2:8 and

5:5] % are generated. In addition to the simulated

datasets, real world concept drift dataset electricity

is also used in the analysis.

4.2 Experimental Setup

This section analyses the results obtained towards

drift detection. Table 3 shows the results obtained

for static imbalance with or without the drift. Here

the drift is measured with number of drifts predicted

Vs known drifts in the data. The False positive

prediction of the drift here referred as False Alarm.

False negative prediction of the drift here referred as

possible unpredicted drift. Developed KS_AUC ( )

drift detector for semi supervised streams is

compared with supervised i.i.d based drift detectors

such as DDM, EDDM and HDDM_A test. The

viability of the KS_AUC ( ) drift detector is verified

on SVM, NB and KNN online batch learners.

In case of static degree of imbalance without

drifts there is no change in the entire stream even in

terms of probabilities or concept so the drift

detectors should not trigger any changes. From

Table 3 it is identified that EDDM triggered false

alarms where as DDM, HDDM_Atest and KS_AUC

( ) better performed by not triggering any false

Algorithm 2: KS_AUC the Batch wise KS and AUC

test.

Input: Reference Batch A, Detection Batch B, AUC of

batch A and B, AUC threshold λ, significant level α

and d number of dimensions.

Output: Drift detection status {1: Detected 0: Not

detected}

1. For i=1 to d do

1. W

= A

, W

= B

2. IF KS test on W

, W

with α rejects

the NULL hypothesis then break from

the loop

2. END for #Drift Warning

3. If (i>d) then return 0;

4. Else if |AUC (A)-AUC (B)|> λ, then

Return 1 #Drift Conformation

5. End If

5. END if

Algorithm 1: Active Learning Framework.

Input: Evolving Stream of Batches B1, B2, ∞,

uncertainty thresholds α, β  .

Output: Classification Model for every iteration

1. Initialize: Training set T

= B

2. For i=1 to ∞ do

Learn a Model using T

If (i==1)

Return the prediction outcome of each

sample in B

and AUC_B

Else

Predict B

using Model and

If (KS_AUC (T

AUC_T

AUC_B

, λ) ==1) then

Confirm Drift and request the

labels of the samples n from B

whose uncertainty < α and

random samples of size m.

Where 





. Learn New Model using

i+1

= (n+m) of B

and go to

step 2.

Else

Update Model using T

i+1

= T

(Uncertainty samples<β) in B

and

go to step 2.

3. End For

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

228

alarm. In this case EDDM has exhibited 12 false

alarms with respect to all synthetic streams of this

category. Hence with respect to above scenario

DDM, HDDM_Atest and KS_AUC yielded better

performance.

In case of static degree of imbalance with drift

(D) (i.e., p(y|x) change) proposed drift detector

predicted the drifts correctly on all datasets over

varied degree of imbalances such as [90:10, 80:20

and 50:50%]. However the other drift detectors

prone to either False Positives or False Negatives. In

particular at high degree of imbalance the drift

detectors are prone to False Negatives. In case of

balanced data streams DDM and HDDM_Atest has

exhibited False Negatives on SineH. In contrast

EDDM has exhibited false positives for SineH.

However DDM and EDDM are prone to false

positives for the streams like Line.

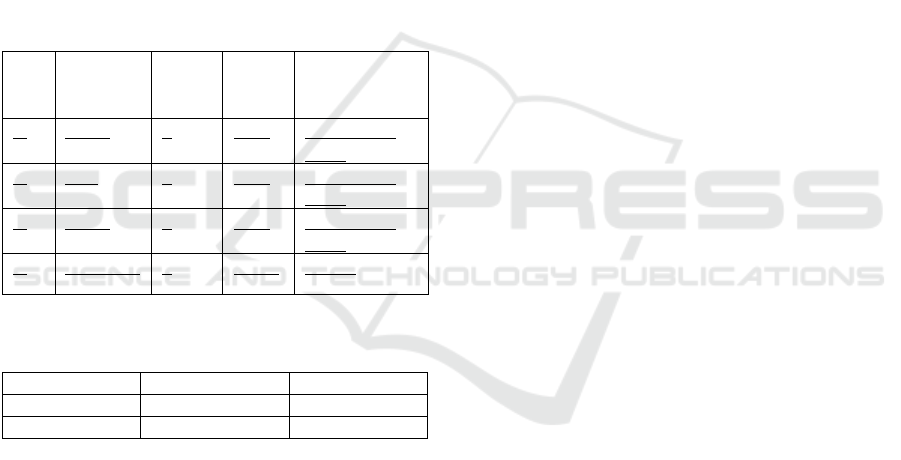
Table 1: Settings for Concept Drift Generator.

Table 2: Type of Imbalance Before and After the Drift for

1:9 case.

Imbalance

Before

After

LOW

1:9

HIGH

1:9

9:1

Even at high degree imbalanced cases such as 90:10

and 80:20, DDM and HDDM_A test has exhibited

false negatives in predicting the drifts for SineV and

Line datasets. However EDDM has exhibited false

negatives in 90:10 case of SineH dataset and false

positives for 80:20. So in this case we can say that

KS_AUC ( ) performed better than other drift

detectors in identifying the drift in case of high

degree of imbalance. Next to KS_AUC, EDDM

performed better. In case of multiple drifts DDM is

prone to false positives at balanced cases and at

highly imbalanced cases three drift detectors such as

DDM, EDDM and HDDM_Atest are prone to false

negatives. Hence in case of multiple drifts also our

algorithm KS_AUC performed well. Further, from

the number of labels queried by oracle is a

concerned, active learning batch based NB learner

queries more labels than SVM and KNN learners.

Table 4 shows Dynamic change in imbalance with

drift (i.e p(y) change). In Dynamic change of

imbalance with drift (i..e priors and concept also

changes) KS_AUC and HDDM_Atest performed

equally in predicting the drift except the multiple

drift stream Line. For this stream KS_AUC prone to

one false positive and HDDM_Atest prone two to

five false positives. This might be due to sudden

raise in performance due to p(y) change. Concerned

with balanced case the DDM has exhibited false

positives except SineH dataset whereas in case of

EDDM except sineH dataset the drifts are correctly

predicted for other data sets. In case of imbalanced

streams such as 80:20 and 90:10 in single drift case

DDM correctly identified the drift where as EDDM

prone to false positives in one drift scenario.

Whereas in multiple drift case (Line data set)

DDM has exhibited false positive at balanced case

where as at imbalanced cases every detector

exhibited false alarm where our algorithm exhibited

only one false positive hence in consideration with

overall performance our detector performed well.

Further, similar with Static imbalance case online

NB has queried more number of labels than the

SVM and KNN learners

Figure 2 and 3 depicts AUC plots for static and

dynamic cases with different imbalance ratios i.e.,

[50-50, 90-10, and 80-20] with respect to different

classifiers such as KNN, NB and SVM for Line

dataset with three drifts. Figure 4 shows AUC plot

for electricity data set. The X-axis represents

number of batches and Y-axis represents AUC. The

second level of KS_AUC, the AUC variation at the

batch with drift is indicated with a green vertical line

for all datasets except electricity dataset which is

indicated by red line. In case of static imbalance, for

KNN classifier a clear damping is observed, for NB

classifier in all the cases except 50-50 (at first drift

point) there is clear damping whereas for SVM there

is significant rise of AUC at drift points is observed.

In case of dynamic imbalance, KNN classifier shows

a clear damping at each and every drift point, NB

also shows a clear damping at every drift point

except third drift point (i.e. false drift) where as

SVM shows clear improvement in AUC at every

drift point except third drift point which is a false

drift.

Table 5 shows the results for real world data set

Electricity, in this case the number of drifts in this

case is not prior known. The obtained results are

concerned, DDM has shown 22 drifts, EDDM has

Data

Stream

No. Of

Attrib

utes

No. of

Sampl

% Degree of

Imbalance

SineV

1000

50:50,80:20,

90:10

Line

1000

50:50,80:20,

90:10

SineH

1000

50:50,80:20,

90:10

Electricity

45312

~60:40

An Unsupervised Drift Detector for Online Imbalanced Evolving Streams

229

Table 3: Static Imbalance with (D) and without (N) Drift, the Notation -(-) Indicates Drifts Predicted(Known Drift).

.Data

set

Imbalance

ratio

Drift Detection Status

Percentage of

labelling

DDM

EDDM

HDDM_Atest

KS_AUC

SVM

KNN

SineV

50-50

0(0)

1(1)

0(0)

1(1)

0(0)

1(1)

0(0)

1(1)

29.6

35.5

26.7

90-10

0(0)

0(1)

0(0)

1(1)

0(0)

0(1)

0(0)

1(1)

34.4

37.6

28.9

80-20

0(0)

0(1)

1(0)

2(1)

0(0)

0(1)

0(0)

1(1)

33.2

27.3

SineH

50-50

0(0)

0(1)

4(0)

3(1)

0(0)

0(1)

0(0)

1(1)

30.3

33.3

19.2

90-10

0(0)

0(1)

0(0)

0(1)

0(0)

0(1)

0(0)

1(1)

30.1

32.1

24.7

80-20

0(0)

1(1)

3(0)

7(1)

0(0)

0(1)

0(0)

1(1)

39.8

39.9

39.8

Line

50-50

0(0)

5(3)

0(0)

3(3)

0(0)

3(3)

0(0)

3(3)

24.5

30.2

15.8

90-10

0(0)

1(3)

0(0)

2(3)

0(0)

1(3)

0(0)

3(3)

20.8

36.7

25.5

80-20

0(0)

1(3)

4(0)

2(3)

0(0)

1(3)

0(0)

3(3)

25.5

30.2

Table 4: Drift Detection with Dyna/mic Imbalance Case (a Combined Problem of Change in Priors and Concept Drift).

Dataset

Imbalance

ratio

Drift detectors

Percentage of labelling

DDM

EDDM

HDDM_Atest

KS_AUC

SVM

KNN

SineV

50-50

2(1)

1(1)

30.5

38.8

19.2

90-10

1(1)

2(1)

1(1)

29.7

34.7

24.7

80-20

1(1)

5(1)

1(1)

31.3

35.5

36.8

SineH

50-50

1(1)

2(1)

1(1)

30.9

35.5

26.6

90-10

1(1)

5(1)

1(1)

34.1

39.5

29.9

80-20

1(1)

8(1)

1(1)

38.2

39.9

33.6

Line

50-50

5(3)

3(3)

31.2

90-10

5(3)

7(3)

5(3)

4(3)

26.5

23.5

80-20

6(3)

9(3)

7(3)

4(3)

24.9

36.5

21.5

Table 5: Real World Dataset (Electricity).

DRIFT DETECTORS

DDM

EDDM

HDDM_Atest

KS_AUC

Threshold=3%

Threshold=5%

Threshold=10%

SVM

KNN

SVM

KNN

SVM

KNN

307

319

shown 307 and HDDM_Atest has shown 319 drifts

respectively, whereas our KS_AUC exhibited 42

drifts at 3% uncertainty threshold  for all

classifiers. At 5% and 10% threshold SVM exhibited

41 drifts, KNN and NB exhibited 42 drifts

respectively. Since the considered methods for

comparison are all supervised i.i.d based drift

detectors, the experiments are also conducted for

KS_AUC in supervised manner with the target label

of each sample. From the results it is noticed that no

change in Drift Detection performance from

supervised to semi supervised versions of KS_AUC.

This is due to phase I of KS_AUC, which detects the

drift in unsupervised manner.

5 CONCLUSION

This paper proposes a new batch based drift

detection method for imbalanced evolving streams.

Proposed approach is based on two stages that

include unsupervised as well as supervised detection

with queried labels. Experimental results on

synthetic and real world streams reported that with

the proposed approach the drifts at both balanced

and unbalanced streams are correctly detected.

Further, in comparison with prominent drift

detectors such as DDM, EDDM, and HDDM_Atest

proposed method yielded better detection in case of

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

230

imbalanced streams. In case of imbalanced streams

the detection rate is on par with DDM, EDDM and

HDDM_Atest.

ACKNOWLEDGEMENTS

This work is supported by the Defense Research and

Development Organization (DRDO), India, under

the sanction code: ERIPR/GIA/17-18/038. Center

for Artificial Intelligence and Robotics (CAIR) is

acting as reviewing lab for the work is concerned.

Figure 2: AUC Plots for Static Imbalance Case.

Figure 3: AUC Plot for Dynamic Imbalance Case.

Figure 4: AUC Plot for Electricity Dataset Fir Svm

Classifier.

REFERENCES

Ditzler, G., Roveri, M., Alippi, C., Polikar, R., 2015.

Learning in Non Stationary Environments: A Survey.

In IEEE Computational Intelligence Magazine,

Volume 10, Issue 4, Pages 12-25.

Gama, J., Zliobaite, I., Bifet, A., Pechenizkiy, M.,

Bouchachia, A., 2013. A Survey on Concept Drift

Adaptation. In ACM Comput. Surv. 1, 1, Article 1

(January 2013), 35 pages.

Wang, S., Minku, LL., Yao, X., 2017. A Systematic Study

of Online Class Imbalance Learning With Concept

Drift. In IEEE Transactions on Neural Networks and

Learning Systems, Volume 29, Issue 10, DOI:

10.1109/TNNLS.2017.2771290, 2018.

Wang, S., Minku, LL., Ghezzi, D., Caltabiano, D., Tino,

P., Yao, X., 2013. Concepts drift detection for online

class imbalance learning. In The International Joint

Conference on Neural Networks(IJCNN).

Wang, H., Abraham, Z., 2015. Concept drift detection for

streaming data. In International Joint Conference of

Neural Networks 2015.

Brzezinski, D., Stefanowski, J., 2017. Properties of the

area under the ROC curve for data streams with

Concept drift. In Knowledge and Information Systems,

Volume 52, Issue 2, Pages 531-562.

Patist, JP., 2007. Optimal window change detection. In

Proceedings of 7th IEEE International Conference

of Data Mining Workshops, 2007, Pages 557-562.

Nishida, k., Yamauchi, K., 2007. Detecting concept drift

using statistical testing. In International Conference

on Discovery Science, Berlin, Germany, Pages 264–

269.

Hawkins, D. M., Peihua, Q, and Chang, W.K, 2003. The

change point model for statistical process control.

Journal of Quality Technology, Volume 35, Issue 4,

Pages 355–366.

Wald, A., 1945. Sequential tests of statistical hypotheses.

Ann. Math. Statist, Volume 16, Issue 2, Pages 117–

186.

Bifet, A., Gavalda, R., 2007. Learning from time-

changing data with adaptive windowing. In

Proceedings of the Seventh SIAM International

An Unsupervised Drift Detector for Online Imbalanced Evolving Streams

231

Conference on Data Mining, April 26-28, 2007,

Minneapolis, Minnesota, USA.

Ditzler, G., Polikar, R., 2011. Hellinger distance based

drift detection for nonstationary environments. In

Proceedings of IEEE symposium on computational

intelligence in dynamic and uncertain environments,

Pages 41- 48.

Alippi, C., Boracchi, G., Roveri, M., 2011. A just-in-time

adaptive classification system based on the

intersection of confidence intervals rule. In Neural

Networks, volume 24, Issue 8, Pages 791-800.

Gama, J., Medas, P., Castillo, G., Rodrigues, P., 2004.

Learning with drift detection. In Brazilian Symposium

on Artiﬁcial Intelligence, pp. 286-295.

Yu, S., Abraham, Z., Wang, H., Shah, M., Wei, Y,

Principe, JC., 2019. Concept Drift Detection and

adaptation with Hierarchical Hypothesis Testing.

Journal of the Franklin Institute. DOI:

10.1016/j.jfranklin.2019.01.043

Pohl, D., Bouchacia, A., Hellwagner, H., 2018. Batch-

based active learning: Application to social media data

for crisis management. In Expert system with

applications, Volume 93, Pages 232-244.

Fawcett, T., 2006. An Introduction to ROC Analysis.

Pattern recognition of letters, Volume 27, Issue 8,

Pages 861-874.

Bifet, A., Holmes, G., Kirkby, R., Pfahringer, B., 2010.

MOA: Massive online analysis. Journal of Machine

Learning Research, volume 11, Pages 1601–1604.

Minku, L.L., White, A.P., Yao, X., 2010. The Impact of

Diversity on On-line Ensemble Learning in the

Presence of Concept Drift. IEEE Transactions on

Knowledge and Data Engineering, volume 22, Issue 5,

Pages 730–742. DOI:10.1109/TKDE.2009.1

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

232