
Electromyography Signal Analysis to Obtain Knee Joint Angular
Position
Edinson Porras, Lina Peñuela and Alexandra Velasco
Universidad Militar Nueva Granada, Mechatronics Engineering Department, Bogota, Colombia
Keywords:
Electromyography, Knee Rehabilitation, Polynomial Adjustment, Locally Weighted Projection Regression.
Abstract:
Knee injuries are due to several causes and affect a large part of the population. In all of the cases, rehabilitation
is required to recover the joint mobility and strength. In this context, the use of technology, especially the
development of assistive devices may offer advantages to the patients, e.g. allow to perform correctly the
exercises, adapt to the users’ needs and help to comply with the prescribed physical therapy. These devices
may have specific requirements focused on not harming the patient. This is why control strategies are needed,
and therefore feedback sensing is highly important. In this paper we present an algorithm to determine the
knee joint angular position from surface Electromyography (EMG) measurements, using a curve fit from a
polynomial adjustment method and a Locally Weighted Projection Regression (LWPR) method. We validate
our approach, comparing the data obtained from the curve fitting with the measurements obtained with position
sensors. In this way, results show that indeed we can explain the joint angular position with the EMG data
taken in knee flexion-extension motion, applying a polynomial adjustment approach and the LWPR method.
1 INTRODUCTION
The amount of people suffering knee impairments
caused by accidents, cord injury, arthritis, and aging
is increasing (Koller-Hodac et al., 2010). To recover
partially or completely the normal functions, or to
avoid the joint degeneration, a rehabilitation process
is required in all cases. Part of the treatment includes
physiotherapy, which implies different procedures to
reduce pain and swelling, and to recover mobility and
strength (Huo et al., 2016), (Umivale, 2011). Tra-
ditionally, the subjects must attend limited therapy
sessions that most of the times are not enough to
recover the joints normal function (Jensen and Lor-
ish, 1994). Other times the subjects do not comply
with the prescribed treatment reducing its effective-
ness (Khan and Scott, 2009). Additionally, the treat-
ment evaluation is usually done in a visual or verbal
way, therefore it can be subjective (Umivale, 2011).
In some cases, as part of the treatment the physi-
cian prescribes the use of elements as orthoses, elastic
bands, and so on, to improve the subjects’ condi-
tion. However, the traditional orthoses are rigid struc-
tures which limit the user’s natural motion, and may
cause discomfort. This is why recently, there has
been an increasing interest in the development and
use of assistive robotic devices for physical rehabili-
tation (see e.g. (Fang et al., 2018) or (Koller-Hodac
et al., 2011)), which are oriented to improve the tradi-
tional rehabilitation methods, allowing the treatment
completion, as well as the adaptation to the users’ re-
habilitation process and requirements.
Several assistive devices are already available in
literature. For example, (Ren et al., 2017) address a
wearable ankle robotic device in passive and active
training in acute stroke. As part of the design, authors
report the need of controllers. This device senses and
tracks the patient’s motion (or intent of motion) of
the ankle without harm. It is worth to mention that
important considerations must be made for design-
ing systems oriented to stroke patients; however, this
topic is out of the scope of our paper.
Other assistive devices in literature do not have a
feedback control system, but use measurements (e.g.
electromyography (EMG)) to control the system in
open loop. This is the case of the upper limb exo-
skeleton in (Mghames et al., 2017), which is im-
plemented with a Variable Stiffness Actuator (VSA).
Authors obtain an analogy of the open loop control
parameters with those of the human muscle system,
tuning in that way the mechanical system paramet-
ers. The feed-forward control inputs are obtained by
directly mapping the estimation of the muscle activ-
ation, using EMG sensors. This approach shows in-
730
Porras, E., Peñuela, L. and Velasco, A.
Electromyography Signal Analysis to Obtain Knee Joint Angular Position.
DOI: 10.5220/0007927707300737
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 730-737
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

deed the importance of obtaining EMG signals, which
could further be used in closed loop (feedback) con-
trol strategies. Moreover, in (Yap et al., 2015) authors
present the design of a soft wearable hand exoskel-
eton with pneumatic actuation. The device is novel
and allows to perform different hand therapy exer-
cises. However, the authors discuss the need of a feed-
back system, which may include sensing elements
to make the device more robust and accurately con-
trolled. Other assistive devices are presented in (Li
and Cheng, 2017), or (Wang et al., 2009), just to name
a few. In all cases, the need of an accurate control
strategy is addressed, for which a sensing system and
signal processing algorithms are required.
On the other hand, control strategies for assistive
devices must track the desired reference accurately,
e.g. angular position, velocities and forces, so there
is no harm for the user (Ren et al., 2017). In order
to design and implement such strategies, information
from the system and from the patient must be ob-
tained. For instance, joint angular position is import-
ant to correct the system’s action. Moreover, EMG
data could help to evaluate parameters such as stiff-
ness and position (intended motion), to control assis-
tive systems like those based on the use of variable
stiffness actuators (VSA), or series elastic actuators
(SEA) (Ajoudani et al., 2012). As well, the EMG sig-
nal can be used to track the process progress (Alto-
belli et al., 2015; Fang et al., 2018; Akhtar, 2016;
Garabini et al., 2017; Ema et al., 2017; Earp et al.,
2013; Chen et al., 2018). A common approach to re-
cognize the intent of motion in walking is to sense the
ground forces of the foot and joint angles using in-
verse models (Ajoudani et al., 2012). Nevertheless,
the EMG signal is a promising interface between the
user and the system mainly for two reasons; first, the
easy way to obtain it in a non invasive way by means
of electrodes over the skin; second, the direct relation
between the EMG and the muscular activity, closely
related to the intent of motion (Ito et al., 2015). There-
fore, sensing systems and algorithms to obtain and
process EMG data are useful in assistive devices. Be-
sides, reducing computational cost and economic cost
are usually design parameters which can be satisfied
by limiting the number of sensors while obtaining the
required information. This can be achieved by us-
ing EMG sensors and an acqurate algorithm that al-
lows obtaining the angular position from these data.
After the data acquisition, the EMG signal needs pre-
processing (i.e. filtering, amplification and sampling)
(Freriks and Hermens, 2000).
We are interested in exploring the EMG-joint
angle relationships, which can be determined by us-
ing fitted EMG-joint angle curves. For this, two
different methods of Polynomial fitting to find the
joint angular positions from the EMG signals are
used and compared, namely a Polynomial Adjustment
method, and a Locally Weighted Projection Regres-
sion method (LWPR). Other algorithms have been
already developed in literature with this purpose. For
example, in (Chen et al., 2018) the authors evalu-
ate the root mean square value (RMS) from the elec-
tromyogram voltage signal, to determine the inten-
ded motion in flexion-extension action, employing a
fuzzy logic algorithm. Another approach is reported
in (Ito et al., 2015), where authors determine the wrist
angle using a bilinear model which takes into account
the muscle elasticity and viscosity, and the contract-
ing force of the flexor and extensor muscles. In gen-
eral, this kind of algorithms present advantages be-
cause they can be run online, while the one presented
in this paper can only be applied offline. However, in
our approach we certainly reduce the computational
cost, in terms of the running time of the algorithm.
Moreover, in general the EMG signal level depends
on some features as the muscular mass, muscle elasti-
city and viscosity, or the skin color, but some of the
algorithms that obtain information from EMG data do
not adapt to the specific features of the individuals.
Our approach, normalizes the EMG signal each time
so it can be adjusted to each individual. Efforts to ob-
tain musculo-tendon forces related to the joint angles
during the elbow flexion-extension movement have
also been addressed. For instance, in (Pang and Guo,
2013), authors use the Hill-based muscular model us-
ing the triceps and the biceps forces to calculate the
joint angle. This kind of approaches are interesting
in the study of intended motion but are different from
ours because they search the relationship of the EMG
signal with forces, while we are interested in obtain-
ing the angular position from EMG data.
In this paper we present an algorithm to determ-
ine the joint angular positions using a curve fitting in
two cases, i.e. a polynomial adjustment method and
alternatively a LWPR method. We compare the res-
ults and performance of both methods and we valid-
ate our approach by comparing the data obtained from
the curve fitting with the measurements taken in the
same conditions with position sensors NOTCH
1
. The
muscles from which we obtain the EMG signal are
the Vastus lateralis and the Vastus medialis, whose
contraction is mainly related to the knee extension.
For the validation we calculate the correlation coef-
ficient (CC) between the angular position measured
with the NOTCH and the angular position obtained by
applying the two approaches from the EMG signal. In
the case of the polynomial adjustment approach, the
1
https://wearnotch.com/
Electromyography Signal Analysis to Obtain Knee Joint Angular Position
731

CC is about 52%, while in the LWPR case the CC
is around 37%, considering the whole knee flexion-
extension motion. These results indicate that either
the polynomial adjustment and the LWPR methods
allow to explain the extension of the knee, being the
former method better than the latter. First, we give a
theoretical background on the curve fitting methods.
Then, we address the experiment performed with 20
participants. We use these data to develop and test
the algorithm in two cases, first using polynomial ad-
justment and then the LWPR method, and we validate
the results comparing them with angular positions ob-
tained from the NOTCH. Afterwards, we present and
discuss the results obtained.
2 THEORETICAL BACKGROUND
As introduced before, the EMG signal is related to the
intention of motion. This means that from the EMG
measurements we can also get the angular position
(Ajoudani et al., 2012), (Ito et al., 2015). This rela-
tionship can be obtained as a curve fitting of the EMG
data, using a proper method. However, this relation-
ship is complex and vastly individualized, i.e. it de-
pends on the physical characteristics of each person.
Several factors contribute to the EMG voltage level,
including the distance or orientation of the sensor on
the muscles or different physical features of people.
This is why a normalization is required and is pro-
posed in this paper.
Besides, to validate the results, the curves ob-
tained from the fitting need to be compared to the joint
angular position data. This is done by calculating the
correlation coefficient. In the process of fitting, large
amount of data and the algorithm have to be processed
and this may take some time depending on the inform-
ation available. In this way, the computational cost is
important and there is a trade off between this cost
and the obtained results.
In this section, we present the theoretical elements
required to develop an algorithm that allows to de-
termine the knee joint angular position from EMG
data in a flexion-extension motion, i.e. the two meth-
ods for the curve fitting that will be used.
2.1 Polynomial Adjustment
The polynomial adjustment method gives as a res-
ult the coefficients of a mathematical function that
describes the joint angle in terms of the EMG sig-
nal. This method uses a Vandermonde matrix V ∈
R
(n+1)×(n+1)
,
V p = Y , (1)
which can be written as
1 x
0
x
2
0
... x
n
−1
0
1 x
1
x
2
1
... x
n
−1
1
1 x
2
x
2
2
... x
n
−1
2
: : : : :
1 x
n
x
n
2
... x
n
−
1
n
p
0
p
1
p
2
:
p
n
=
y
0
y
1
y
3
:
y
n
. (2)
The columns of the matrix V relate the vector x of in-
dependent variables of the system. p ∈ R
n+1
is the
vector of the polynomial coefficients. Y ∈ R
n+1
is the
vector of dependent variables. The coefficients vector
of the polynomial fit p are calculated from (1) as a
Gaussian reduction.The polynomial order n depends
on the motion speed and on how precise the adjust-
ment is desired. In the experiment presented in this
paper, we use a polynomial fit of order n = 20, be-
cause the test is made either for slow and rapid con-
tractions, so the polynomial needs to reach every sig-
nal peak.
After the Gaussian reduction, the adjusted poly-
nomial p(x ) of order n can be defined as
p(x) = p
0
x
n
+ p
1
x
n−1
+ ..... + p
n
x + p
n−1
. (3)
Notice that x is the EMG signal voltage normalized.
2.2 Locally Weighted Projection
Regression LWPR
LWPR is a non-parametric technique in high di-
mensional space that provides a useful representa-
tion as well as training algorithms for learning about
complex phenomena based on incremental training.
It uses statistically cross validation to learn from
data acquired. For nonlinear function approxima-
tion, LWPR uses piece-wise linear models (Vijayak-
umar et al., 2006). This method allows to obtain a
model from the EMG signal x, which is then com-
pared with the validation signal from the NOTCH
sensor. The EMG signal is different on each person,
due to different features. The model obtained is ad-
aptable according to each subject. The prediction ˆy of
each point of the angular position, with K samples is
described by
ˆy =
∑
K
k=1
w
k
y
k
∑
K
k=1
w
k
, (4)
where w
k
is a weight for each data point (x
i
, y
i
), con-
sidering a Gaussian kernel, and it is defined as
w
k
(x) = e
−
1
2
(x)D
k
(x)
. (5)
Here, D
k
(x) is a metric distance. The algorithm finds
the best approximation of the joint angular position
for each subject. The details on the derivation of this
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
732

method are out of the scope of this paper. For fur-
ther details, the reader is encouraged to review for ex-
ample (Vijayakumar and Schaal, 2000; Vijayakumar
et al., 2006).
3 EXPERIMENT
To establish a relationship between the EMG sig-
nal and the knee angular position we evaluate the
maximum-effort contractions made by the vastus lat-
eralis and vastus medialis muscles in the flexion-
extension action. To evaluate the algorithms presen-
ted on section 2, we carried out an experiment which
is reported here. We present the experimental setup
and we describe how data was acquired, processed
and validated.
3.1 Measurement Setup
We invited 20 healthy participants, i.e. 10 women and
10 men of ages 20 to 45; height 150 cm to 175 cm, and
mass 50 to 85 Kg. The participants were informed
about the procedure and signed an informed consent.
The test consisted on performing maximal isokinetic
knee flexion and extension. EMG data and joint an-
gular position data were acquired from noninvasive
EMG sensors and Notch position sensors.
In general, each joint in the body is actuated by
at least a pair of muscles (agonist-antagonist). Then,
the knee flexion is mainly related to the contraction
of the Hamstrings (Biceps Femoris, the Semitendi-
nosus and the Semimembranosus) muscles, and the
extension is mainly related to the contraction of the
vastus medialis (VM), the vastus lateralis (VL) and
the rectus femoralis (RF) muscles. According to
(Stegeman and Hermens, 2007), to obtain informa-
tion of the knee joint motion, the EMG sensors must
be placed on these muscles. In this paper, we only
show the information from the VM and VL (related
to the extension), because we are interested in obtain-
ing position from EMG, therefore, we assume that if
the algorithms work for the knee extension they will
provide also accurate information in the case of flex-
ion and also for other muscles actuating other joints.
To use the EMG sensors properly, we have taken into
account the recommendations of the SENIAM pro-
ject
2
(Stegeman and Hermens, 2007). Then, EMG
2
Surface ElectroMyoGraphy for the Non-Invasive As-
sessment of Muscles (SENIAM) is a European concerted
action in the Biomedical Health and Research Program
(BIOMED II) of the European Union that provides recom-
mendations for sensors and sensor placement procedures
and signal processing methods for SEMG. More informa-
Figure 1: Flexion-extension movement. An angular pos-
ition of 150ºindicates that the leg is completely extended,
and at 0º, it is completely flexed.
electrodes and NOTCH sensors were placed as shown
in Figure 2. The trials were defined to be carried out
in sitting position with the legs stretched (i.e. flexed at
100º . Then each person was asked to perform a com-
plete flexion-extension movement (from 0º to 150º)
for seven times, continuously with a total duration of
15 seconds (see figure 1).
3.2 Data Acquisition and
Pre-processing
Data for the surface EMG signal was acquired
with a sampling frequency f
sE
= 1 KHz using the
MyoWare
TM
Muscle Sensor (AT-04-001). Two self-
adhesive surface electrodes of diameter 0.5 cm were
placed in a bipolar configuration over the VM and
VL muscles. The signal was digitally filtered using a
Butterworth band-pass filter of twentieth-order, with
a lower cutoff frequency of f
Lc
= 0.1 Hz and a higher
cutoff frequency of f
Lc
= 10 Hz. The main idea of this
filter is to eliminate non important frequencies and
noise. NOTCH data were sampled at f
sN
= 250 Hz.
This system saves the information on a smartphone.
Then, the data can be sent to a computer in order to
read and graph the joint angular position signal, which
is used in the experiment to validate the performance
and accuracy of the algorithms.
3.3 Processing and Post-processing
Once the signal is acquired and pre-processed, data is
normalized by dividing each value by the maximum
value of the signal. Afterwards, LWPR and polyno-
mial adjustment algorithms were applied separately.
Then, in order to validate the results of the algorithms,
tion can be found on: http://www.seniam.org/
Electromyography Signal Analysis to Obtain Knee Joint Angular Position
733

Figure 2: NOTCH and EMG sensors positions. Yellow
markings show the position of the electrodes in the bi-
polar configuration. Red markings indicate the position of
the EMG sensors’ ground. The white triangles show the
NOTCH sensors position.
we compared them to the NOTCH signal. For this,
the signal output from the algorithms is amplified and
shifted in time, because the EMG signal provides the
intention of motion. Additionally, we are working
with the normalized signal, and the NOTCH sensor
gives the angular position in the corresponding units.
Therefore, to determine the amplification gain, we re-
late the maximum and the minimum points of the nor-
malized EMG signal with the NOTCH signal.
3.4 Validation
The correlation coefficient (CC) allows to determine
the linear correlation or similarity between two vari-
ables, and −1 ≤ CC ≤ 1, where -1 means a complete
inverse linear relation between two signals, 0 indic-
ates no correlation between signals, and 1 denotes the
complete correlation between the signals. We com-
pare the joint angular position calculated from the
EMG signal in both muscles, the vastus medialis and
vastus lateralis, with the joint angular position meas-
ured by the NOTCH sensors. Given that the two
signals have a different number of samples, to com-
pare the signals, we generated another vector with the
samples of the NOTCH signal corresponding to the
same instant of time as the output of each algorithm.
The CC was evaluated using MATLAB
3
.
The computational complexity classifies the com-
putational problems due to their inherent difficulty, to
determine whether a certain problem could be solved
with a number of resources. The computational com-
plexity can be calculated as the number of operations
required to perform a task, or the total required pro-
3
https://la.mathworks.com/help/matlab/ref/corrcoef.html
cessing time. Other works, such as (Peng, 2008), ana-
lyze it by quantum theory. In this document, we will
calculate the processing time for the algorithms im-
plemented using the LWPR method and the polyno-
mial approximation, running on an ASUS G5551VW
PC with Intel Core i7-6700HQ processor, RAM of 16
GB and NVIDIA GeForce GTX 960M graphic card.
4 RESULTS AND DISCUSSION
The data in the experiment were obtained from
the twenty participants that performed the flexion-
extension exercises. These data were used for the ana-
lysis. In this section, to illustrate the results, we report
the mean correlation coefficient CC
mean
, considering
all the participants. In the same way, we show the
maximum computational cost applying the two dif-
ferent methods (adjusted polynomial and LWPR), as
well as the delay of the signals. The delay repres-
ents the time difference between the post-processed
signals and the validation signal from the NOTCH
sensor. Then, to exemplify the behavior of the EMG
signals of the VM and VL, as well as the results of
applying both methods (separately) to obtain the an-
gular position, we chose the results of one participant
to report it in the Figures in this section. Afterwards,
we compare these results with the NOTCH sensor
measurements to validate them.
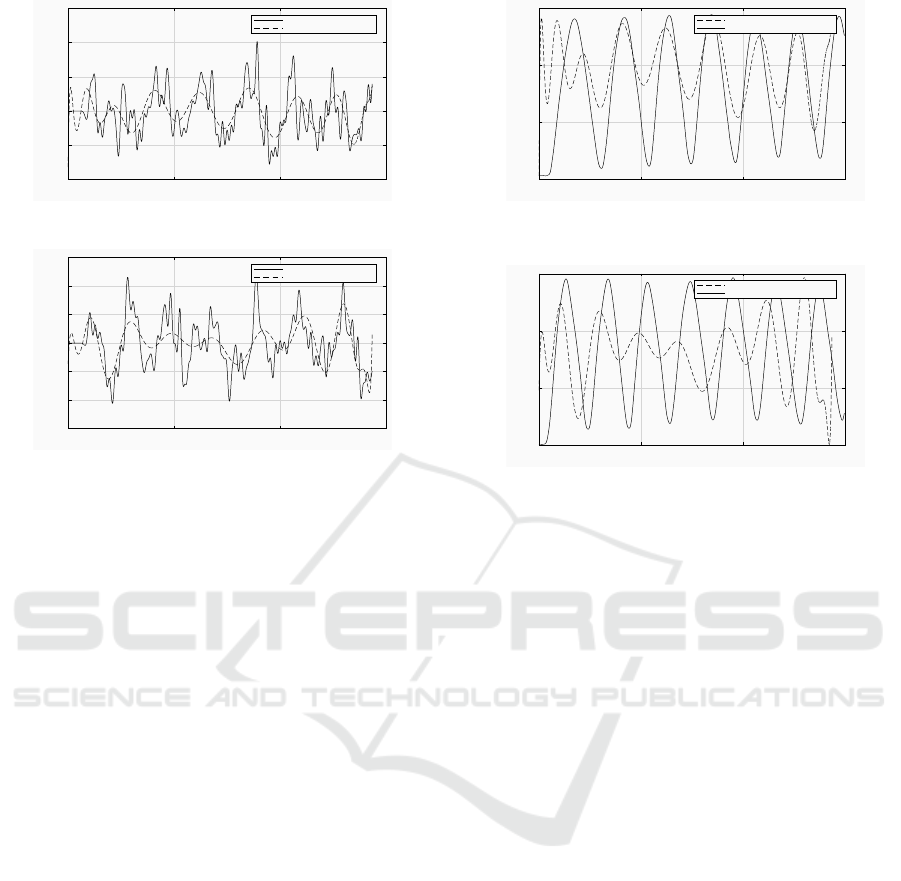
Figure 3 shows the results of applying the poly-
nomial adjustment method to both muscles, the VM
and the VL. Observe that the polynomial adjustment
curve follows the EMG signal trend even if it does
not reach the signal amplitude. As indicated before,
the polynomial obtained is of degree 20, which can
predict any signal peak. It is worth to remark that
a polynomial with a higher degree does not guaran-
tee better results but it implies a higher computational
cost. Other approaches may use lower degree polyno-
mials, e.g. (Earp et al., 2013) that obtains a 4th degree
polynomial, but the motion in that case is slow, while
here it can be either fast or slow.
To validate the polynomial adjustment method we
compare the post-processed signal with the NOTCH
signal obtained from the same experiment and at
the same time. Figure 4 shows the VM and the
VL muscles with the polynomial adjustment and
the validation signal, where we can see that the al-
gorithm takes approximately three seconds to follow
the NOTCH signal. It is worth to remark that the
highest peak on the Notch signal represents the sub-
ject’s muscle maximum-effort contraction. As a res-
ult, for the knee extension the angular position sig-
nal corresponds to the NOTCH output for the VM
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
734
0 5 10 15
Time(s)
-1
-0.5
0
0.5
1
1.5
Normalized EMG signal (v/v)
Polynomial adjustment vastus medialis
EMG
Polynomial adjustment
(a) Knee angular position from the Polynomial ad-
justment vs. EMG signal on the vastus medialis
0 5 10 15
Time(s)
-1.5
-1
-0.5
0
0.5
1
1.5
Normalized EMG signal (v/v)
Polynomial adjustment vastus lateralis
EMG
Polynomial adjustment
(b) Knee angular position from the Polynomial
adjustment vs. EMG signal on the vastus lateralis
Figure 3: Knee angular position obtained from the Poly-
nomial adjustment method and EMG signal from the vastus
lateralis and the vastus medialis muscles.
muscle in time and amplitude, while for the flexion
the polynomial adjustment follows the trend, but does
not reach the amplitude. The main reason for this is
that the VM and the VL are contracted mainly in the
knee extension. The mean correlation coefficient is
CC
mean
= 0.558, which indicates that half of the sig-
nal (the portion corresponding to the extension) is cor-
rectly predicted. Additionally, the VM muscle reveals
better results than the evaluation of the VL muscle.
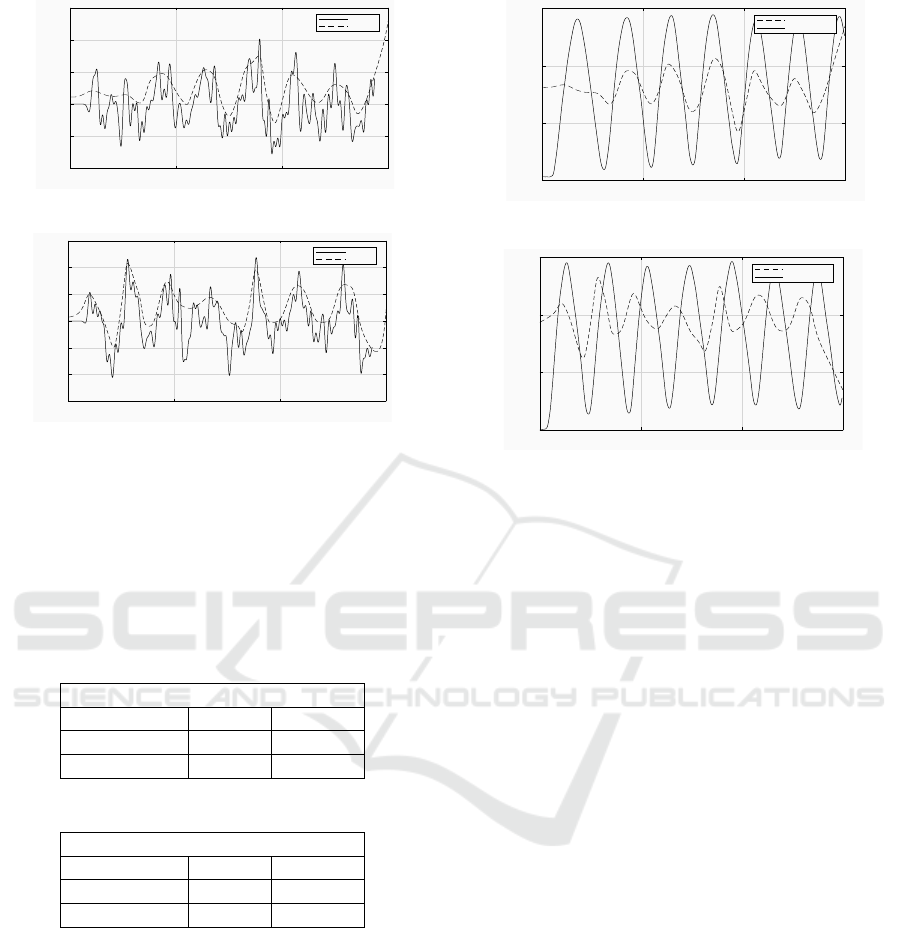
The results of the application of the LWPR
method are shown in Figure 5. As presented in sec-
tion 2.2, each point of the joint angular position is
estimated from the EMG signal for each user. Figures
5(a) and 5(b) show the angular joint position obtained
from the application of the LWPR approach for the
VM muscle, and for the VL muscle respectively. In
the former case, the algorithm works properly after
2.5 s of execution. This means that the first data, up
to 2.5 s are not valid and we do not consider them for
the validation. It can be seen that LWPR algorithm
tries to follow the maximum peaks of the signal for
both muscles, but it presents problems in following
the minimum values for the VL and the VM, differ-
ent from the polynomial approach that works better
in following both the minimum and maximum peaks.
Tables 1 and 2 show the correlation coefficient
(CC) obtained when comparing the NOTCH signal
with the outputs of the algorithms after the signal
0 5 10 15
Time(s)
0
50
100
150
Degrees
Adjusted polynomial vs validation signal vastus medialis
0
50
100
150
EMG polynomial adjustment
Notch signal
(a) Knee angular position from the Polynomial ad-
justment vs. Validation signal on the vastus me-
dialis
0 5 10 15
Time(s)
0
50
100
150
Degrees
Adjusted polynomial vs validation signal vastus lateralis
0
50
100
150
EMG polynomial adjustment
Notch signal
(b) Knee angular position from the Polynomial ad-
justment vs. Validation signal on the vastus lat-
eralis
Figure 4: Knee angular position from the Polynomial
adjustment compared to the validation signal of NOTCH
sensors on the vastus lateralis and the vastus medialis
muscles.
post-processing. As a result, for the VM muscle,
CC
mean
= 0.356 and CC
mean
= 0.558 for the LWPR
and the polynomial adjustment respectively. On the
other hand, for the VL muscle, CC
mean
= 0.3741 and
CC
mean
= 0.500 for the LWPR and the polynomial ad-
justment respectively. These results can also be ob-
served in Figures 4(a), and 6(a) previously analyzed,
where the polynomial adjustment reaches better res-
ults than the LWPR method. The CC shows that the
approaches of each algorithm explain the knee exten-
sion, because the VM and VL muscles are mainly
contracted when the knee is extended. However, in
order to evaluate the total range of motion during the
knee flexion-extension, it is necessary to use the sig-
nals obtained from other muscles such as the ham-
string. The VM EMG data allows to explain better the
joint angular position than the VL. This can be seen
comparing the CC, that in the first case is of about
50% while in the latter is about 37%.
Finally, to evaluate the computational cost in
terms of the time required to finish the processing, we
tested the algorithms on an ASUS G5551VW with In-
tel Core i7-6700HQ processor, RAM of 16 GB and an
NVIDIA GeForce GTX 960M graphic card. The time
required by the LWPR method was 310.55 s, while
the time required for the polynomial adjustment was
Electromyography Signal Analysis to Obtain Knee Joint Angular Position
735
0 5 10 15
Time(s)
-1
-0.5
0
0.5
1
1.5
Normalized EMG signal (v/v)
Locally Weighted Projection Regression vastus medialis
EMG
LWPR
(a) Polynomial set in the VM: knee angular posi-
tion obtained from the LWPR method
0 5 10 15
Time(s)
-1.5
-1
-0.5
0
0.5
1
1.5
Normalized EMG signal (v/v)
Locally Weighted Projection Regression vastus lateralis
EMG
LWPR
(b) Polynomial set in VL: knee angular position
obtained from the LWPR method
Figure 5: Knee angular position from the LWPR method
and EMG signal from the vastus lateralis and the vastus me-
dialis muscles.
0.222 s. The former method spends more time be-
cause of the learning processes and the prediction of
the required parameters.
Table 1: Validation data on vastus medialis.
Vastus medialis
Metod CC
mean
Delay(s)
LWPR 0.356 -0.325
P adjustment 0.558 -0.114
Table 2: Validation data on vastus lateralis.
Vastus lateralis
Metod CC
mean
Delay(s)
LWPR 0.3741 -0.775
P adjustment 0.500 -0.74
5 CONCLUSION
We have presented an algorithm to determine the joint
angular positions from surface Electromyography
(EMG) measurements with the aim of using these
data for control systems of assistive devices. Two ap-
proaches have been explored, i.e. a polynomial ad-
justment method and a LWPR method. These meth-
ods allow a curve fitting to obtain joint angular po-
sition from EMG. To validate the obtained curves,
we compared the data obtained from the curve fit
with the measurements obtained with position sensors
0 5 10 15
Time
-100
0
100
200
Degrees
LWPR vs validation signal vastus medialis
0
50
100
150
LWPR
Notch signal
(a) Knee angular position obtained from the
LWPR vs. Validation signal on vastus medialis
0 5 10 15
Time
-100
0
100
200
Degrees
LWPR vs validation signal vastus lateralis
0
50
100
150
LWPR
Notch signal
(b) Knee angular position obtained from the
LWPR vs. Validation signal on vastus lateralis
Figure 6: Knee angular position obtained from the LWPR
method compared with the validation signal of the vastus
lateralis and the vastus medialis.
NOTCH. In order to obtain EMG data from the
flexion-extension motion, an experiment was carried
out, in which 20 subjects participated. As a result, we
found that the polynomial adjustment method evalu-
ating the EMG signal over the vastus medialis muscle
reached a higher similarity compared to the NOTCH
sensor signal. This test allowed to obtain similar sig-
nals from the curve fitting of the EMG data, compared
with the NOTCH sensor in the extension of the knee.
This results are coherent because the muscles from
which we obtained the EMG data (i.e. the vastus lat-
eralis and the vastus medialis) are the main muscles
involved in the knee extension. Future work will
be oriented to use signals from other muscles to ex-
plain completely the flexion-extension range of mo-
tion. This analysis can be done using more EMG
sensors. We expect to use real time algorithms but
as a drawback the computational cost will be incre-
mented.
ACKNOWLEDGMENT
This work is funded by Universidad Militar Nueva
Granada- Vicerrectoría de Investigaciones, under re-
search grant for project PIC-ING-2679, entitled ’Cara-
cterización de señales de electromiografía dirigido al
control de sistemas de rehabilitación de rodilla’.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
736

REFERENCES
Ajoudani, A., Tsagarakis, N. G., and Bicchi, A. (2012).
Tele-impedance: Towards transferring human imped-
ance regulation skills to robots. In Robotics and Auto-
mation (ICRA), 2012 IEEE International Conference
on, pages 382–388. IEEE.
Akhtar, A. (2016). Estimation of distal arm joint angles
from EMG and shoulder orientation for transhumeral
prostheses. PhD thesis.
Altobelli, A., Bianchi, M., Catalano, M. G., Serio, A.,
Baud-Bovy, G., and Bicchi, A. (2015). An instru-
mented manipulandum for human grasping studies. In
Rehabilitation Robotics (ICORR), 2015 IEEE Interna-
tional Conference on, pages 169–174. IEEE.
Chen, J., Zhang, X., Cheng, Y., and Xi, N. (2018). Sur-
face emg based continuous estimation of human lower
limb joint angles by using deep belief networks. Bio-
medical Signal Processing and Control, 40:335–342.
Earp, J. E., Newton, R. U., Cormie, P., and Blazevich,
A. J. (2013). Knee angle-specific emg normaliza-
tion: The use of polynomial based emg-angle relation-
ships. Journal of Electromyography and Kinesiology,
23(1):238–244.
Ema, R., Wakahara, T., and Kawakami, Y. (2017). Effect of
hip joint angle on concentric knee extension torque.
Journal of Electromyography and Kinesiology.
Fang, C., Ajoudani, A., Bicchi, A., and Tsagarakis, N. G.
(2018). Online model based estimation of complete
joint stiffness of human arm. IEEE Robotics and Auto-
mation Letters, 3(1):84–91.
Freriks, B. and Hermens, H. (2000). European recommend-
ations for surface electromyography: results of the
SENIAM project. Roessingh Research and Develop-
ment.
Garabini, M., Della Santina, C., Bianchi, M., Catalano, M.,
Grioli, G., and Bicchi, A. (2017). Soft robots that
mimic the neuromusculoskeletal system. In Conver-
ging Clinical and Engineering Research on Neurore-
habilitation II, pages 259–263. Springer.
Huo, W., Mohammed, S., Moreno, J. C., and Amirat, Y.
(2016). Lower limb wearable robots for assistance
and rehabilitation: A state of the art. IEEE Systems
Journal, 10(3):1068–1081.
Ito, S., Inui, D., Tateoka, K., Matsushita, K., and Sa-
saki, M. (2015). Wrist angle estimation based on
bilinear model using electromyographic signals from
circularly-attached electrodes. In 2015 54th Annual
Conference of the Society of Instrument and Control
Engineers of Japan (SICE), pages 1167–1172.
Jensen, G. M. and Lorish, C. D. (1994). Promoting pa-
tient cooperation with exercise programs. linking re-
search, theory, and practice. Arthritis and Rheumat-
ism, 7:181–189.
Khan, K. M. and Scott, A. (2009). Mechanotherapy: how
physical therapists’ prescription of exercise promotes
tissue repair. British Journal of Sports Medicine,
43(4):247–252.
Koller-Hodac, A., Leonardo, D., Walpen, S., and Felder,
D. (2010). A novel robotic device for knee rehabili-
tation improved physical therapy through automated
process. In 2010 3rd IEEE RAS EMBS International
Conference on Biomedical Robotics and Biomechat-
ronics, pages 820–824.
Koller-Hodac, A., Leonardo, D., Walpen, S., and Felder, D.
(2011). Knee orthopaedic device how robotic tech-
nology can improve outcome in knee rehabilitation.
In 2011 IEEE International Conference on Rehabili-
tation Robotics, pages 1–6.
Li, H. and Cheng, L. (2017). Preliminary study on the
design and control of a pneumatically-actuated hand
rehabilitation device. In 2017 32nd Youth Academic
Annual Conference of Chinese Association of Auto-
mation (YAC), pages 860–865.
Mghames, S., Laghi, M., Santina, C. D., Garabini, M.,
Catalano, M., Grioli, G., and Bicchi, A. (2017).
Design, control and validation of the variable stiffness
exoskeleton flexo. In 2017 International Conference
on Rehabilitation Robotics (ICORR), pages 539–546.
Pang, M. and Guo, S. (2013). A novel method for elbow
joint continuous prediction using emg and musculo-
skeletal model. In 2013 IEEE International Confer-
ence on Robotics and Biomimetics (ROBIO), pages
1240–1245.
Peng, W. (2008). Energy analysis method of computa-
tional complexity. In 2008 International Symposium
on Computer Science and Computational Technology,
volume 2, pages 682–685.
Ren, Y., Wu, Y., Yang, C., Xu, T., Harvey, R. L., and Zhang,
L. (2017). Developing a wearable ankle rehabilitation
robotic device for in-bed acute stroke rehabilitation.
IEEE Transactions on Neural Systems and Rehabili-
tation Engineering, 25(6):589–596.
Stegeman, D. and Hermens, H. (2007). Standards for suface
electromyography: The european project surface emg
for non-invasive assessment of muscles (seniam). 1.
Umivale, P. S. (2011). Patología de la rodilla: Guía de
manejo clínico.
Vijayakumar, S., D’Souza, A., and Schaal, S. (2006). In-
cremental online learning in high dimensions. Neural
computation, 17:2602–34.
Vijayakumar, S. and Schaal, S. (2000). Locally weighted
projection regression: An o(n) algorithm for incre-
mental real time learning in high dimensional spaces.
In Proceedings of the Seventeenth International Con-
ference on Machine Learning (ICML 2000), volume 1,
pages 288–293, Stanford, CA. clmc.
Wang, P., McGregor, A. H., Tow, A., Lim, H. B., Khang,
L. S., and Low, K. H. (2009). Rehabilitation control
strategies for a gait robot via emg evaluation. In 2009
IEEE International Conference on Rehabilitation Ro-
botics, pages 86–91.
Yap, H. K., , Nasrallah, F., Goh, J. C. H., and Yeow, R. C. H.
(2015). A soft exoskeleton for hand assistive and reha-
bilitation application using pneumatic actuators with
variable stiffness. In 2015 IEEE International Con-
ference on Robotics and Automation (ICRA), pages
4967–4972.
Electromyography Signal Analysis to Obtain Knee Joint Angular Position
737
