Neural Networks Modelling of Aero-derivative Gas Turbine Engine:

A Comparison Study

Ibrahem M. A. Ibrahem

, Ouassima Akhrif

, Hany Moustapha

and Martin Staniszewski

Department of Mechanical Engineering, Ecole de Technologie Sup

erieure, 1100 Notre Dame St. W, Montreal, Canada

Department of Electrical Engineering, Ecole de Technologie Sup

erieure, 1100 Notre Dame St. W, Montreal, Canada

Digitalization Project Manager, Siemens Canada, 9545 Cote de Liesse Road, Montreal, Canada

martin.staniszewski@siemens.com

Keywords:

Neural Networks, NARX Model, Gas Turbine, Aero Derivative, Modelling, Simulation, Dynamic Neural

Networks.

Abstract:

In this paper, the modelling of aero derivative gas turbine engine with six inputs and ﬁve outputs using two

types of neural network is presented. Siemens three-spool dry low emission aero derivative gas turbine engine

used for power generation (SGT-A65) was used as a case study in this paper. Data sets for training and vali-

dation were collected from a high ﬁdelity transient simulation program. These data sets represent the engines

operation above its idle status. Different neural network conﬁgurations were developed by using of a compre-

hensive computer code, which changes the neural networks parameters, namely, the number of neurons, the

activation function and the training algorithm. Next, a comparative study was done among different neural

models to ﬁnd the most appropriate neural network structure in terms of computation time of neural network

training operation and accuracy. The results show that on one hand, the dynamic neural network has a higher

capability than the static neural network in representation of the engine dynamics. On the other hand however,

it requires a much longer training time.

1 INTRODUCTION

Aero-derivative gas turbine engines (ADGTE) are

widely used as a mechanical drive in oil and gas ap-

plication and power generation. These widespread

and increasing applications have sparked a great inter-

est among manufacturers to improve the performance

and increase the reliability of the engine, which in

turn requires an accurate and real time model to sim-

ulate the gas turbine engine dynamics. Siemens SGT-

A65 is a three spool ADGTE. The thermodynamic

physics based model for this engine conﬁguration is

very complicated because of the high number of sub-

systems and the high number of non linear equations

that require to be solved iteratively at the expense of

computation time (Hanachi et al., 2015). This makes

it challenging if not impossible to use physics based

modelling approach in real time model based control

applications.

An alternative approach to physics based mod-

elling is data driven based modelling. Neural net-

works (NNs) is one of the data driven based (black

box) modelling approaches which can be used when

no or little information is available about the physics

of the system. It has the advantage of high computa-

tional speed allowing real time applications. The NN

model can be used in the development and operational

stages of an engine’s life to predict the engine’s per-

formance, test the performance of the engine control

systems and for engine health monitoring.

The main idea behind neural network modelling

is to create a simple model of human brain in order

to solve complex scientiﬁc and industrial problems in

many ﬁelds. Neural networks can be classiﬁed into

two main categories, static and dynamic neural net-

works. Static neural networks are the simplest neu-

ral networks, and are characterized by memoryless

non linear equations, which means that there are no

feedback elements and no delays in the network in-

put. Therefore, the output parameters from the static

NN depend only on the current values of the input pa-

rameters as shown in Fig. 1a. The multi layer feed

forward neural networks (MFFNN) are considered as

static neural networks because they have only feed

forward transformation of the information from the

input layer to the output layer.

738

Ibrahem, I., Akhrif, O., Moustapha, H. and Staniszewski, M.

Neural Networks Modelling of Aero-derivative Gas Turbine Engine: A Comparison Study.

DOI: 10.5220/0007928907380745

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 738-745

ISBN: 978-989-758-380-3

On the other hand, in the case of dynamic neu-

ral networks, output parameters from the network de-

pend not only on the current input parameters of the

network, but also on the previous input and output pa-

rameters of the network. Furthermore, dynamic neu-

ral networks can be divided into two categories: those

that have only feedforward connections (input/output

delays), and those that have feedback as shown in

Fig. 1b, or recurrent connections as shown in Fig. 1c.

(a) Static NN.

(b) Dynamic feed forward NN with input delay.

Figure 1: Neural network types(Beale et al., 2015).

There are many works in the literature regarding

the usage of static neural networks in modelling and

simulation of industrial gas turbine engines. (Laz-

zaretto and Toffolo, 2001), (Fast et al., 2009), (Asgari

et al., 2013) and (Rahmoune et al., 2015) are con-

sidered to be major research activities in this area.

These works are based on feed-forward NNs, with

a single hidden layer and different numbers of neu-

rons, trained by using a back propagation learning

algorithm. More recently, dynamic neural networks

have been employed for modelling gas turbine en-

gines. Non linear autoregressive network with exoge-

nous inputs (NARX) is a recurrent dynamic network,

with feedback connections enclosing several layers of

the network. (Salehi and Montazeri-Gh, 2018), (As-

gari et al., 2016) and (Bahlawan et al., 2017) used

NARX neural network to model ADGTE.

In this paper, a comparison study between MIMO

static feed forward neural network and MIMO NARX

dynamic neural networks was performed to model a

three spool ADGTE (SGT-A65) above its idle sta-

tus. A comprehensive computer program was used

for both types of NN to change the neural network

parameters, namely, the neuron number(from 1 to 20),

the activation function (tansig or logisg) as well as dif-

ferent training algorithms (trainlm, trainbr and train-

scg). After that, a comparative study was done among

different neural models to ﬁnd the most appropriate

neural network structure in terms of training time and

accuracy by calculating the overall root mean square

error value.

2 AERO-DERIVATIVE GAS

TURBINE ENGINE

ADGTE are a popular choice for energy generation as

a result of their high reliability, efﬁciency and ﬂexibil-

ity. ADGTE have also been widely used in pumping

applications for gas and oil transmission pipelines,

offshore platforms and naval propulsion. This kind

of gas turbines are derived from high bypass turbofan

engines. In this paper, a three spool dry low emis-

sion aero derivative gas turbine engine (SGT-A65)

was modelled as shown in Fig. 2. This engine con-

sists of two stages low axial low pressure compressor

(LPC), eight stages axial intermediate pressure com-

pressor (IPC), six stages axial high pressure compres-

sor (HPC), single stages high and intermediate tur-

bines and ﬁve stages low pressure turbine. The low

pressure shaft was connected with the power gener-

ator. Therefore, it should rotate at ﬁxed revolution

(3600 rpm for electricity generation with 60 Hz).

The engine speciﬁcations are illustrated in Ta-

ble 1.

Figure 2: Siemens SGT-A65 aero derivative gas turbine en-

gine.

Table 1: Gas turbine technical data.

Parameter Value

Exhaust mass ﬂow rate 171kg/s

Output power 65MW

Power turbine speed 3600rpm

Total compression ratio 38 : 1

Exhaust temperature 437

Neural Networks Modelling of Aero-derivative Gas Turbine Engine: A Comparison Study

739

3 NEURAL NETWORK

MODELLING METHOD

3.1 Available Field Data

In this paper, simulated data sets, which were used for

training and validation of the neural networks, were

provided to us by Siemens high ﬁdelity transient sim-

ulation program for the SGT-A65 engine at ISO con-

ditions with a sampling rate of 0.1 sec. Note that,

the data was generated from a closed loop set-up with

Siemens own controller as the SGT-A65 engine can

not be run in open loop. Two sets of six inputs and

ﬁve outputs data were generated by changing the en-

gine load to cover the entire operating range of the

engine:

• Random load change (used for training) consist-

ing of 24170 samples;

• Square load change (used for validation) consist-

ing of 12890 samples;

As can be seen, a large number of training patterns

(samples) were used to train the NN. The number of

training patterns has an effect on the NN accuracy:

a low number of training patterns may increase the

NN error due to network over ﬁtting. This means that

NN loses its ability to generalize. On the other hand,

this large number of training patterns may increase

the training computation time.

The SGT-A65 ADGTE input and output parame-

ters that are used, are illustrated in Table 2 and Table 3

respectively.

Table 2: The ADGTE input parameters.

Fuel ﬂow G

LPC bleed off valve LPBOV

Variable inlet guide vans VIGV

IPC bleed off valve NBIP8

IPC variable stator vans IPVSV

HPC bleed off valve NBHP3

Table 3: The ADGTE output parameters.

Low-pressure shaft speed N

Intermediate shaft speed e N

High-pressure shaft speed N

Engine shaft power POWER

Intermediate turbine exit temperature TGT

Fig. 3 and Fig. 4 show the change of the normal-

ized input and output parameters for the SGT-A65

ADGTE used for training operation. Since the input

data to the NN represent the output from the engine

controller, the saturations in Fig. 3 are imposed by the

controller.

3.2 MIMO Static Neural Model

For this MIMO model, a feed forward multilayer

neural network was used to simulate the SGT-A65

ADGTE. This type of NN consists of an input layer

with a number of nodes equal to the number of in-

puts, one or more hidden layers with a certain num-

ber of neurons, and an output layer with a number of

neurons equal to the number of NN outputs. The ﬁrst

parameter to be ﬁxed is the number of hidden lay-

ers the static NN needs to have. Cybenco (Cybenko,

1989) proved that NN with one hidden layer of hyper-

bolic tangent or sigmoid activation function and one

output layer of linear activation function could simu-

late any non linear system. Therefore, in this study,

one hidden layer feed forward neural network was

used. To get an optimized neural network structure

which can represent the ADGTE dynamics, a com-

prehensive computer program was generated and run

in Matlab environment. This program generates dif-

ferent neural models by changing the following pa-

rameters:

• Change of the number of neurons from 1 to 20.

• Usage of two activation functions logsig and tan-

sig.

• Usage of three training algorithms: Levenberg-

Marquardt training algorithm (trainlm), Scaled

conjugate gradient training algorithm (trainscg)

and Bayesian regularization training algorithm

(trainbr).

At each computation cycle, training of the NN was

performed by using random load change data sets.

The stop network training parameters used are: (i)

the mean square error performance function which is

minimized until it reaches its minimum value (0.01),

(ii) the maximum number of training epochs (1000)

which represents the number of times that all the the

training patterns are presented to the NN and (iii) the

maximum number of validation increase (100) which

represents the number of successive epochs in which

the performance function fails to decrease. Training

operation was repeated three times for the same neu-

ral network with the same input data set to increase

the accuracy of the network. A preliminary analysis

which was carried out to evaluate the inﬂuence of

the number of training repetition showed that the

use of training repetition higher than three requires

a great computational effort, while it only allows a

small improvement of NN performance. Note that

the training operation was done in a computer with

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

740

Figure 3: Normalized input parameters for model training.

Figure 4: Normalized output parameters for model training.

64 GB RAM and processor intel(R)Xeon(R) CPU

E3-1225 v6 @ 303GHz.

After that, validation of the trained network was

performed with another data set (Square load change

data set). The results of each computation cycle were

recorded in a matrix form which includes the network

structure, the root mean square error (RMSE) for

training process, RMSE for validation process and

training time. RMSE was used for the comparison of

the NNs. It was calculated for the whole set of data

of each output parameter from the NN, and deﬁned

according to Eqn. (1),

RMSE =

∑

i=1

(

− y

)

(1)

where, n is the number of data samples, y

is the ac-

tual output and y is the predicted output. An over-

all RMSE of NN was also calculated as the sum of

RMSE of each output parameter.

To select the most appropriate static neural model

structure, the output data from the developed com-

puter program was divided into two groups as follows:

First Group. Static NNs with tansig activation func-

tion, different numbers of neurons and different train-

ing algorithms.

Neural Networks Modelling of Aero-derivative Gas Turbine Engine: A Comparison Study

741

Second Group. Static NNs with logsig activation

function, different numbers of neurons and different

training algorithms.

Next, the best NN from each group was selected

based on the minimum value of overall RMSE during

validation operation and minimum value of training

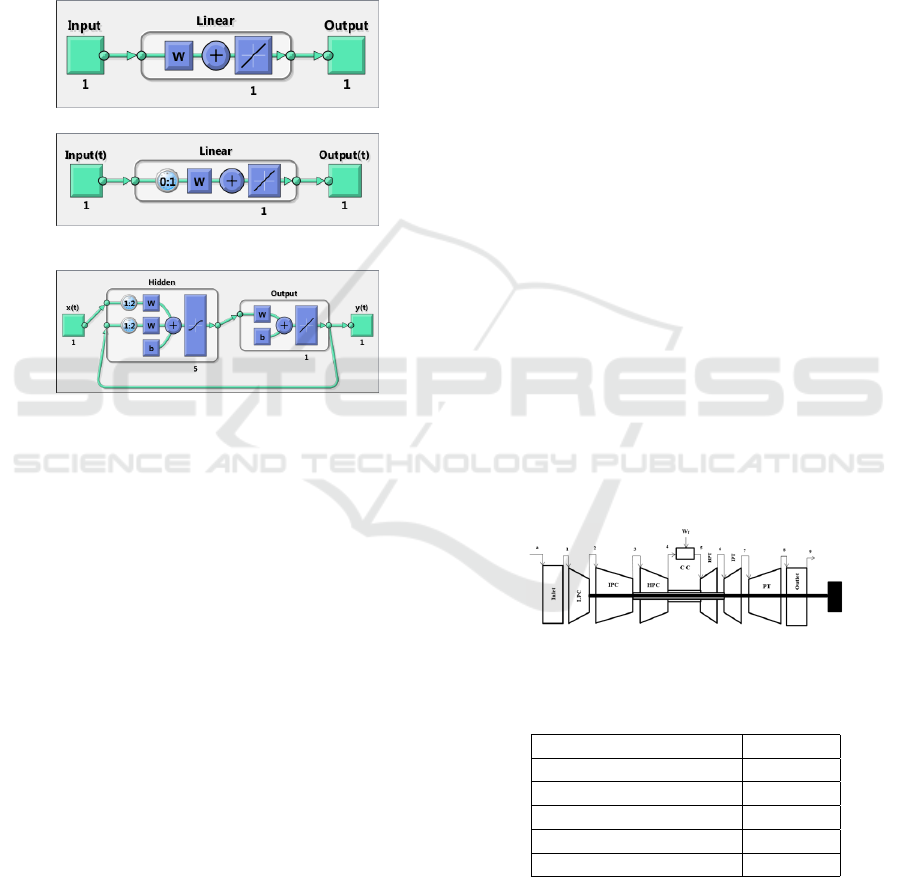
time. Fig. 5 shows the results analysis for ﬁrst group

with respect to the overall value of the RMSE. Fig. 6

shows the results analysis for ﬁrst group with respect

to the time consumed in the training phase.The results

of the second group are not shown for space reasons.

It can be noticed that the overall RMSE decreases

and the training time increases as number of neurons

in hidden layer increases. In particular, when NN

was trained by usage of trainlm or trainbr algorithms,

overall RMSE is smaller than overall RMSE of NN

trained by trainscg algorithm. On the other hand,

NNs trained by trainscg algorithm had the smallest

training time. However, the fast reduction in training

time by using (trainscg) was due to the fact that the

maximum number of validation increase was reached.

Table 4 summarizes the best result from each group.

As can be seen from Table 4 the best static MIMO

neural model conﬁguration which can represent SGT-

A65 ADGTE should have eighteen neurons in the hid-

den layer, using tansig as activation function and us-

ing Levenberg-Marquardt (trainlm) as training algo-

rithm. In addition, the difference in the training time

between the best NN model in the ﬁrst and second

group is small, which can be neglected in comparison

to network accuracy.

Figure 5: Inﬂuence of number of neurons with tansig acti-

vation function and different training algorithms.

Figure 6: Inﬂuence of number of neurons with tansig activa-

tion function and different training algorithms on the train-

ing time.

3.3 MIMO Dynamic Neural Model

There are many types of dynamic neural networks in

the literature (Norgaard et al., 2000). In this paper,

MIMO NARX recurrent dynamic neural network is

employed to simulate the SGT-A65 ADGTE, which

has feedback connections enclosing several layers of

the network. The following equation relates NARX

model output parameters to its input parameters,

(t) = f (y

(t − 1), y

(t − 2), · · · ,y

(t − n

)

(t − 1), u

(t − 2), · · · ,u

(t − n

))

(2)

where, n

and n

are the number of regressed outputs

and regressed inputs respectively. These two param-

eters represent the most important parameters in the

NARX network conﬁguration, and can be evaluated

by using system order estimation. In this study , we

used n

= 2 and n

= 2 based on the literature (Asgari

et al., 2016; Bahlawan et al., 2017).

Another important parameter in the NARX con-

ﬁguration is the training architecture. The NARX net-

work training can be implemented via two architec-

tures:

Series-parallel Architecture (S&Pr) the network is

trained in open loop mode then transformed to

closed loop mode for validation operation.

Parallel Architecture (Pr) the network is trained

and validated in closed loop mode.

To get the optimal NARX model structure which

can represent the ADGTE dynamics, a comprehen-

sive computer program was generated and run in Mat-

lab environment. This program generates different

NARX models by changing the neural network pa-

rameters as shown in the static neural network for fair

comparison purposes. These parameters are as fol-

lows:

• Change of the number of neurons from 1 to 20.

• Usage of two activation functions logsig and tan-

sig.

• Usage of three training algorithms trainlm, train-

scg and trainbr.

• Train the network as series-parallel architecture

and parallel architecture.

The stop network training parameters are the same as

the ones for the MIMO static neural network, also the

training operation was performed on the same com-

puter as for MIMO static network. At each compu-

tation cycle, training of the NARX network was per-

formed by using random load change data set. After

that, validation for the trained network was performed

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

742

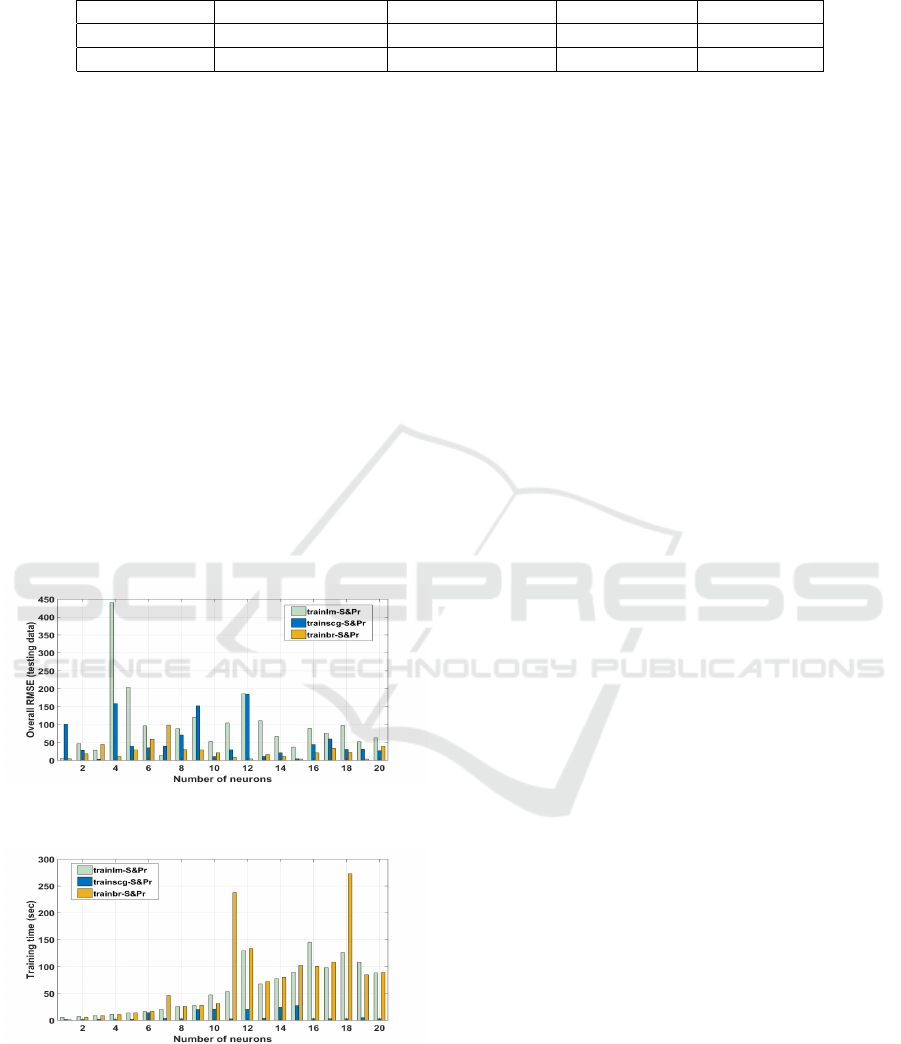
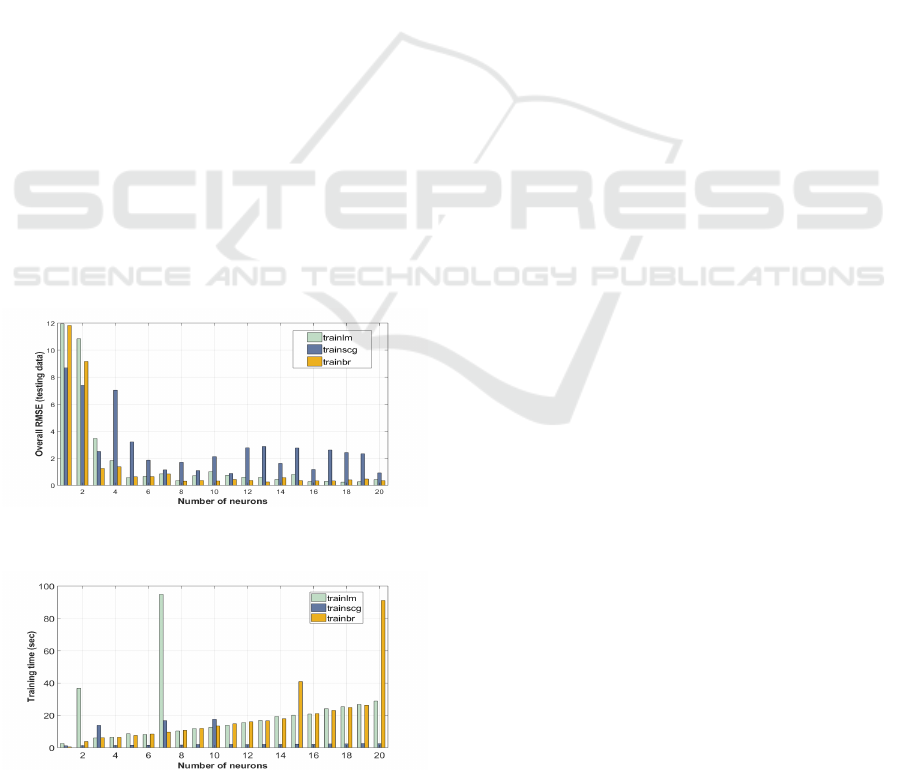
Table 4: The best result from each group of MIMO static neural model.

No of neurons activation function training algorithm Testing RMSE training time

18 tansig trainlm 0.2388 25.404 sec

14 logsig trainlm 0.2475 17.844 sec

with another data set (Square load change data set).

The results of each computation cycle were recorded

in a matrix form which includes the network struc-

ture, RMSE for each output parameters in training

and validation phases, the overall root mean square

error RMSE for validation phase and training time.

The output data from the developed computer pro-

gram was divided into four groups as follows:

First Group: series-parallel NARX with tansig acti-

vation function, different numbers of neurons and dif-

ferent training algorithms [Fig. 7 and Fig. 8].

Second Group: series-parallel NARX with logsig ac-

tivation function, different numbers of neurons and

different training algorithms.

Third Group: parallel NARX with tansig activation

function, different numbers of neurons and different

training algorithms.

Fourth Group: parallel NARX with logsig activation

function, different numbers of neurons and different

training algorithms.

Figure 7: Inﬂuence of number of neurons with tansig acti-

vation function and different training algorithms.

Figure 8: Inﬂuence of number of neurons with tansig acti-

vation function and different training algorithms.

Note that, only ﬁgures from the ﬁrst group will

be shown for space reasons. As can be seen, NARX

network with logsig activation function trained in par-

allel architecture with trainscg or trainbr algorithms

gave the best results with respect to the overall RMSE

values. However, this improvement in network accu-

racy came at the expense of increasing the training

time. On the other hand, the fast training time was

due to the stop of network training as the value of

maximum number of validation increase was reached.

Note also that the training time increases as the num-

ber of neurons in the hidden layer increases. More-

over, in a comparison of different structures of the

NARX NN, the results showed that the logsig acti-

vation function was superior to the tansig activation

function.

Table 5 summarizes the best result from each

group. As can be seen, the best MIMO NARX

model conﬁguration which can represent SGT-A65

ADGTE should be a fourteen neurons in the hid-

den layer, using logsig as activation function and us-

ing Bayesian regularization (trainbr) as training algo-

rithm in the parallel architecture. This selected net-

work took much more time for training but made a

good prediction for all of the engine parameters, es-

pecially the low pressure spool speed (RMSE for low

pressure spool speed was 0.0009). On the other hand,

NARX network with eighteen neurons, tansig activa-

tion function, and trained in parallel architecture with

trainbr algorithm gave a lower training time than the

selected network. However, the RMSE for the low

pressure spool speed (0.0059) is higher than the one

in the selected network.

4 COMPARISON RESULTS

In this section, a comparison between the best MIMO

static neural model and the best MIMO NARX dy-

namic neural model was performed. Both MIMO

static neural model and MIMO NARX dynamic neu-

ral model were tested against the square data set. The

results are presented in Fig. 9 to Fig. 12 and summary

of these results was shown in Table 6. In a compari-

son of MIMO static NN with MIMO NARX dynamic

NN, the following results are obtained:

• The MIMO static NN and MIMO NARX dynamic

NN could represent the ADGTE with acceptable

accuracy.

• Eventhough the MIMO static NN has slightly

better performance (in term of overall RMSE)

than the MIMO NARX dynamic NN, the MIMO

NARX dynamic NN captures better the fast

Neural Networks Modelling of Aero-derivative Gas Turbine Engine: A Comparison Study

743

Table 5: The best result from each group of MIMO NARX model.

No of neurons activation function training algorithm S & PR / Pr Testing RMSE Training time

3 tansig trainscg S & PR 2.8760 1.7020 sec

18 logsig trainscg S & PR 1.1524 12.5930 sec

18 tansig trainbr Pr 0.3268 299.9670 sec

14 logsig trainbr Pr 0.3225 1333.9 sec

change in low pressure spool speed parameter,

high pressure spool speed, intermediate pressure

spool speed and intermediate turbine exit temper-

ature.

• The training time in the MIMO NARX dynamic

NN is higher than that in the MIMO static NN.

The increase in training time of the NARX net-

work may be due to the feedback connections and

the higher number of parameters which should be

evaluated during training phase.

• The generalization capability of the MIMO

NARX dynamic NN is higher than that in the

MIMO static NN.

• The MIMO static NN gave satisfactory results,

because a sufﬁcient and adequate training data set

was used.

Figure 9: Variation of NH for the testing data.

Figure 10: Variation of NI for the testing data.

Dynamic networks are generally more powerful

than static networks. Therefore, the dynamic neural

networks can be used in multi step ahead prediction

applications. However, it takes much more training

time.

Figure 11: Variation of NL for the testing data.

Figure 12: Variation of TGT for the testing data.

Figure 13: Variation of power for the testing data.

5 CONCLUSIONS

In this paper, data driven modelling and identiﬁca-

tion of Siemens SGT-A65 ADGTE is done using two

types of neural networks; static feed forward NN and

NARX dynamic NN. First, two sets of simulated data

from a high ﬁdelity transient simulation program were

collected for training and validation process of the

networks. Second, selection of the best appropriate

neural model structure in both the static and dynamic

networks was performed by using a comprehensive

computer program, which changes the NN parameters

and performs training and validation of the produced

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

744

Table 6: Static and dynamic neural model comparison results.

Output parameter Static NN RMSE NARX model RMSE

0.01120 0.00098

0.00190 0.00039

0.00150 0.00047

POWER 0.21890 0.31890

TGT 0.00530 0.00170

Overall RMSE 0.23880 0.32250

Training time 25.404 sec 1333.9 sec

networks. The output data from this program were

recorded in a matrix form. After that, analysis of these

recorded data was performed by dividing the data into

different groups and selection of the best model struc-

ture from each group based on the minimum value

of RMSE. Finally, comparison results between static

NN and dynamic NN showed a good capability of the

dynamic neural networks over the static neural net-

works in representation of the dynamic response of

ADGTE. However, the training time of the dynamic

NN was higher than that in the static NN.

Since, there is no general methodology or rule to

deﬁne the neural network parameters, the way to se-

lect the best network conﬁguration is traditionally ob-

tained by trial-and-error. This paper may work as

a guideline for researchers in selection of the best

feed forward and NARX neural network conﬁgura-

tion which can represent ADGTE during its full range

above its idle status.

In general, the developed NN models for the

ADGTE can be an effective tool for real time simu-

lation of gas turbines and model based control appli-

cations.

REFERENCES

Asgari, H., Chen, X., Menhaj, M. B., and Sainudiin, R.

(2013). Artiﬁcial neural network–based system identi-

ﬁcation for a single-shaft gas turbine. Journal of Engi-

neering for Gas Turbines and Power, 135(9):092601.

Asgari, H., Chen, X., Morini, M., Pinelli, M., Sainudiin,

R., Spina, P. R., and Venturini, M. (2016). Narx

models for simulation of the start-up operation of a

single-shaft gas turbine. Applied Thermal Engineer-

ing, 93:368–376.

Bahlawan, H., Morini, M., Pinelli, M., Spina, P. R., and

Venturini, M. (2017). Development of reliable narx

models of gas turbine cold, warm and hot start-up. In

ASME Turbo Expo 2017: Turbomachinery Technical

Conference and Exposition.

Beale, M. H., Hagan, M. T., and Demuth, H. B. (2015).

Neural network toolbox

user’s guide. In R2015b,

The MathWorks, Inc., 3 Apple Hill Drive Natick, MA

01760-2098, , www.mathworks.com.

Cybenko, G. (1989). Approximation by superpositions of

a sigmoidal function. Mathematics of control, signals

and systems, 2(4):303–314.

Fast, M., Assadi, M., and De, S. (2009). Development and

multi-utility of an ann model for an industrial gas tur-

bine. Applied Energy, 86(1):9–17.

Hanachi, H., Liu, J., Banerjee, A., Chen, Y., and Koul, A.

(2015). A physics-based modeling approach for per-

formance monitoring in gas turbine engines. IEEE

Transactions on Reliability, 64(1):197–205.

Lazzaretto, A. and Toffolo, A. (2001). Analytical and neural

network models for gas turbine design and off-design

simulation. International Journal of Thermodynam-

ics, 4(4):173–182.

Norgaard, M., Ravn, O., Poulsen, N., and Hansen, L.

(2000). Neural networks for modelling and control

of dynamic systems: a practitioner’s handbook. Ad-

vanced textbooks in control and signal processing.

Springer, Berlin.

Rahmoune, M. B., Hafaifa, A., and Guemana, M. (2015).

Neural network monitoring system used for the fre-

quency vibration prediction in gas turbine. In Control,

Engineering & Information Technology (CEIT), 2015

3rd International Conference on, pages 1–5. IEEE.

Salehi, A. and Montazeri-Gh, M. (2018). Black box model-

ing of a turboshaft gas turbine engine fuel control unit

based on neural narx. Proceedings of the Institution of

Mechanical Engineers, Part M: Journal of Engineer-

ing for the Maritime Environment.

Neural Networks Modelling of Aero-derivative Gas Turbine Engine: A Comparison Study

745