
A Method for Static and Dynamic Interval Detection within the IMU
Calibration Procedure
Andrejs Zujevs, Valters Vecins and Aleksandrs Korsunovs
Riga Technical University, Kalku iela 1, Riga, Latvia
Keywords:
IMU, MEMS, Calibration, Static Detector.
Abstract:
An Inertial Measuring Unit (IMU) is used for measuring linear accelerations and angular velocities in 3D/2D
space. IMU devices are usually designed as micro-electro-mechanical systems (MEMS), which are produced
in small form factor and are widely used in robotics, mobile phones and drones. Depending on the quality
of the device, they can be divided into low-cost and high-cost IMUs. The main difference between them is
the accuracy of measurements and IMUs mechanical alignment on the printed circuit board. The high-cost
IMUs are well calibrated and have a relatively small error and noise level for different kinds of parameters.
In contrast, the low-cost IMUs have a larger error component, where body frame axes are non-orthogonal
for both the accelerometer and gyroscope due to weak factory calibration, high noise and high sensitivity de-
pendence from the temperature, misalignment of body frame due to packaging and assembly processes. This
paper provides a new method for the IMU static and dynamic interval detection within the IMU calibration
procedure, which is designed by other authors for the case of IMU calibration without any external equipment.
This procedure uses a sequence of alternating static and dynamic intervals for accelerometer calibration and
then gyroscope calibration. The accuracy of the IMU calibration procedure depends strongly on how precisely
static and dynamic intervals have been detected. Otherwise, the calibration results are unsuitable. The new
method for static and dynamic interval detection provides more robust and less noisy results, requires a sig-
nificantly smaller number of operations and is easy to implement. The paper provides comparative results for
both methods and refers to the source code for the new method.
1 INTRODUCTION
An Inertial Measurement Unit (IMU) is a sensor used
for measuring linear accelerations and angular veloc-
ities in 3D/2D space. With the help of these measure-
ments, it is possible to track changes in sensor rotation
and translation. One of the main applications of the
IMU is providing information about an objects body
frame orientation in global coordinates with no addi-
tional information about the world. Since the current
state evaluation using only an IMU depends on the ac-
curacy of the previous state evaluation, it is thus prone
to error accumulation. Usually, for additional local-
isation information, IMU data are fused with other
sensors onboard a mobile robot, a drone, or another
mobile platform (Le Gentil et al., 2018). The most
recent applications of IMU have been in the field of
visual odometry and visual-inertial SLAM (Qin et al.,
2018; Mur-Artal and Tardos, 2016; Vidal et al., 2017).
As part of the multi-sensor system, an IMU provides
high-frequency measurements, necessary for a robot’s
or drone’s systems to compensate translation or ro-
tation movement, while slower sensors evaluate the
global position. By integrating measured values of an
accelerometer, gyroscope and often a magnetometer,
over time it becomes possible to estimate the move-
ment trajectory (Qin et al., 2018).
IMUs that are used in robotics and mobile
phones are usually based on MEMS (micro-electro-
mechanical systems) technology because of their
small form factor. Most of them are a combination of
several triaxial units: an accelerometer, a gyroscope
and often a magnetometer. The MEMS may be di-
vided in low-cost (up to 5$) and high-cost (starting
from 100$) devices. The main difference between
them is the accuracy of the measurements provided
by the units and the accuracy of the IMUs mechani-
cal alignment on a PCB. The high-cost IMUs are well
calibrated and have a relatively small error component
for the different types of IMU parameters. Also, they
have low error values for misalignment. In contrast,
low-cost IMUs have a larger error component.
Body frame axes are non-orthogonal for both the
accelerometer and the gyroscope) due to weak factory
746
Zujevs, A., Vecins, V. and Korsunovs, A.
A Method for Static and Dynamic Interval Detection within the IMU Calibration Procedure.
DOI: 10.5220/0007929007460751
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 746-751
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

calibration, high noise, sensitivity dependence from
the temperature and misalignment of the body frame
due to packaging and assembly processes. Axis mis-
alignment in a triaxial device (Figure 1) is a major
source of measurement error, which is caused due to
weak factory calibration or/and IMU soldering accu-
racy and alignment on a PCB (Looney, 2015).
IMU device
z
y
x
gx
gz
gy
z’
x’
y’
Ѱy
Ѱz
Ѱx
Figure 1: Misalignment of IMU device gyroscope’s axes
(dotted blue lines) in right-hand coordinate system. The
figure adopted from (Looney, 2015), where misaligned axes
are x
0
, y
0
, z
0
and global frame axes are x, y, z and angle Ψ is
the misalignment angle for each axis relative to the global
frame axis. Circular bullets around each global frame axis
show both gyroscope rotation direction and speed for an
axis.
In order to improve IMU performance, it is nec-
essary to perform a calibration procedure in addition
to the factory calibration. Some of the sensors from
the high-price segment come with calibration matri-
ces calculated individually for each sensor in the fac-
tory. Cheaper sensors have less precise calibration,
which should be compensated to achieve the desired
performance. In addition to the IMU parameter cali-
bration, it is necessary to determine the relative posi-
tion of the sensor and the body frame.
The best calibration results can be achieved
by utilising dedicated calibration tools. Chambers
with temperature control and very precise multi-axis
turntables allow to calibrate and compensate most
of IMU parameters such as non-orthogonality (Deng
et al., 2017). However, since the operation of such
equipment is expensive, it is not accessible for every
researcher. Also, it is unfounded for cheaper IMUs
because of the difference in the precision grade of the
equipment and the sensor that needs to be calibrated.
Systems that use multiple sensors can be cal-
ibrated by performing an inter-sensor calibration.
When multiple sensors perform measurements of the
same quantity using different phenomena, those mea-
surements can be cross-validated in order to achieve
better precision and use the more suited sensor as a
reference to calibrate the parameters of the other sen-
sor (Lv, J., Ravankar, A.A., Kobayashi, Y., Emaru,
2016). Similarly, by performing body frame position
evaluation with multiple sensors, it is possible to com-
pensate for inter-sensor spatial and temporal offsets
(Furgale et al., 2013).
IMU self-calibration is the simplest method of
calibration in terms of resource utilisation - in most
cases, the only things needed are a flat surface and
an operator. Most of the work in this type of calibra-
tion relies on specific manoeuvres performed on the
sensor to collect a set of calibration data (Shin and
El-Sheimy, 2002; Ren et al., 2015).
This paper focuses on the low-cost IMU MEMS
calibration method without the use of external equip-
ment, as presented in (Tedaldi et al., 2014). In that
work proposed IMU calibration method solves the
body-frame non-orthogonality cause of errors, also
known as sensor misalignment. This paper provides
an improvement of the static detector described as a
part of the IMU calibration procedure or framework
(Tedaldi et al., 2014). All the experiments and evalua-
tions of the new method were conducted with a device
equipped with mouse-based ADNS-9500 microchip
(optical flow sensor) (Briod et al., 2012; Beyeler and
Floreano, 2009) and LSM6DSL (STMicroelectronics,
2017) IMU device onboard.
2 THE IMU CALIBRATION
PROCEDURE
The IMU calibration procedure proposed in (Tedaldi
et al., 2014) is intended for IMU MEMS calibra-
tion without external equipment. The procedure uses
raw accelerometer and gyroscope data as input data,
which are prepared in a specific way. An IMU device
is placed in N different static attitudes, where each
lasts for 1-2 seconds. The procedure starts with the
initial static position lasting T seconds, which for a
particular IMU device may vary between 15 - 30 sec-
onds. Then, a sequence of alternating dynamic and
static positions of the IMU device has to be done.
The initial static interval called the initialization pe-
riod is used to find an appropriate threshold value of
the accelerometer’s Allan Variance (Barnes and Al-
lan, 1990) magnitude. This threshold value is used
for static intervals detection in the raw accelerome-
ter data. The overall calibration procedure is shown
in Figure 2. The static detector processing the raw
accelerometer data detects a sequence of static inter-
vals (when IMU lies in a static position, without any
movement). The data from the static intervals are then
used as input data in the step of the accelerometer cal-
ibration. The accelerometer rotation, scaling, and bias
matrices are estimated and used in the next step for the
gyroscope calibration. The data within the dynamic
A Method for Static and Dynamic Interval Detection within the IMU Calibration Procedure
747

Leave the IMU static for T sec.
Rotate the IMU and then lay it in
a different attitude
Wait for at least M seconds
Have you
rotated the IMU
N times?
No
Yes
Calibrate Accelerometer
and then Gyroscope
Apply the static interval detector
Figure 2: The overall IMU calibration procedure. Figure
adopted from (Tedaldi et al., 2014).
intervals and data from the calibrated accelerometer
are used as the input data in the gyroscope calibra-
tion. As a result, rotation and scaling matrices are es-
timated (Tedaldi et al., 2014). Figure 3 shows an ex-
ample of raw data gathering when a device equipped
with IMU is sequentially placed in different static at-
titudes for a period of 1-2 seconds.
Figure 3: A device equipped with LSM IMU which was
placed in different static attitude positions.
3 STATIC DETECTOR
The task of the static detector is to determine from
IMU’s raw data such intervals of data when a device
is in a static state (without any movement), and re-
ferred to as a static interval further in this paper. Ac-
cordingly to the calibration procedure, such intervals
of data which are located between neighbour static in-
tervals belong to the IMU movement from one static
position to another and are named as dynamic inter-
vals. Figure 4 shows an example of the detected static
and dynamic intervals, where the accelerometer sig-
nal (within ax, ay and az axes) in a static interval fluc-
tuates around the same value level, and, in contrast, in
a dynamic interval, the signal changes significantly.
The accuracy of the calibration depends strongly on
Figure 4: Static intervals determined by the static detector
and the dynamic intervals between them.
the correctness of the determined static and dynamic
intervals. This statement is based on the fact that
(Tedaldi et al., 2014) the accelerometer is calibrated
by using the averages for each axis from static inter-
vals, and the gyroscope is calibrated by using the cal-
ibrated accelerometer data and the gyroscope’s data
integrated within the dynamic intervals. This paper
provides an improvement of the variance based static
detector introduced in (Pretto and Grisetti, 2014).
3.1 The Original Version
The static detector introduced in (Pretto and Grisetti,
2014) is variance based and uses an operator of vari-
ance in magnitude estimation for each accelerometer
sample (a
t
x
, a
t
y
, a
t
z
) at time t:
ς(t) =
q
[var
t
w
(a
t
x
)]
2
+ [var
t
w
(a
t
y
)]
2
+
[var
t
w
(a
t
z
)]
2
(1)
where var
t
w
(a
t
) is a variance operator which com-
putes variance of signal a
t
within a time window
centered at t, t
w
- length of the time window. The
static and dynamic intervals are classified based on
the threshold value, simply checking if it is lower or
greater than ς(t) squared. The threshold is an integer
multiplier of the ς
init
squared. The multiplier is esti-
mated within the initialization period T
init
. The length
of the period is determined by estimating the Allan
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
748
variance for each gyroscope axis, where σ
2
a
is defined
as:
σ
2
a
=
1
2K
K
∑
k=1
(x(
˜
t, k) − x(
˜
t, k − 1))
2
(2)
where x(
˜
t, k) is k − th interval average which spans
˜
t
seconds, and K is the number of intervals that the total
considered time is segmented in. The time interval
in which the Allan variances of the three gyroscope
axes converge to a small value may be an appropriate
initialization period T
init
(Tedaldi et al., 2014).
3.2 A New Version
The new version of the static detector
1
is expressed
in the pseudocode (Algorithm 1). The detector uses
three input parameters t
w
- a time window for which
magnitude is estimated by 1 eq.; t
st
- the minimal
length of a static interval in seconds; t
dyn
- the min-
imal length of a dynamic interval in seconds, and
raw accelerometer data with the timestamps of the
records. Estimated magnitude values estimated by 1
eq. are in a relatively large value range. Therefore, it
is better to use a logarithmic function, which reduces
relative differences between values and makes inter-
val detection more robust. In this work, the logarithm
to the base 10 is used. When the magnitude of ac-
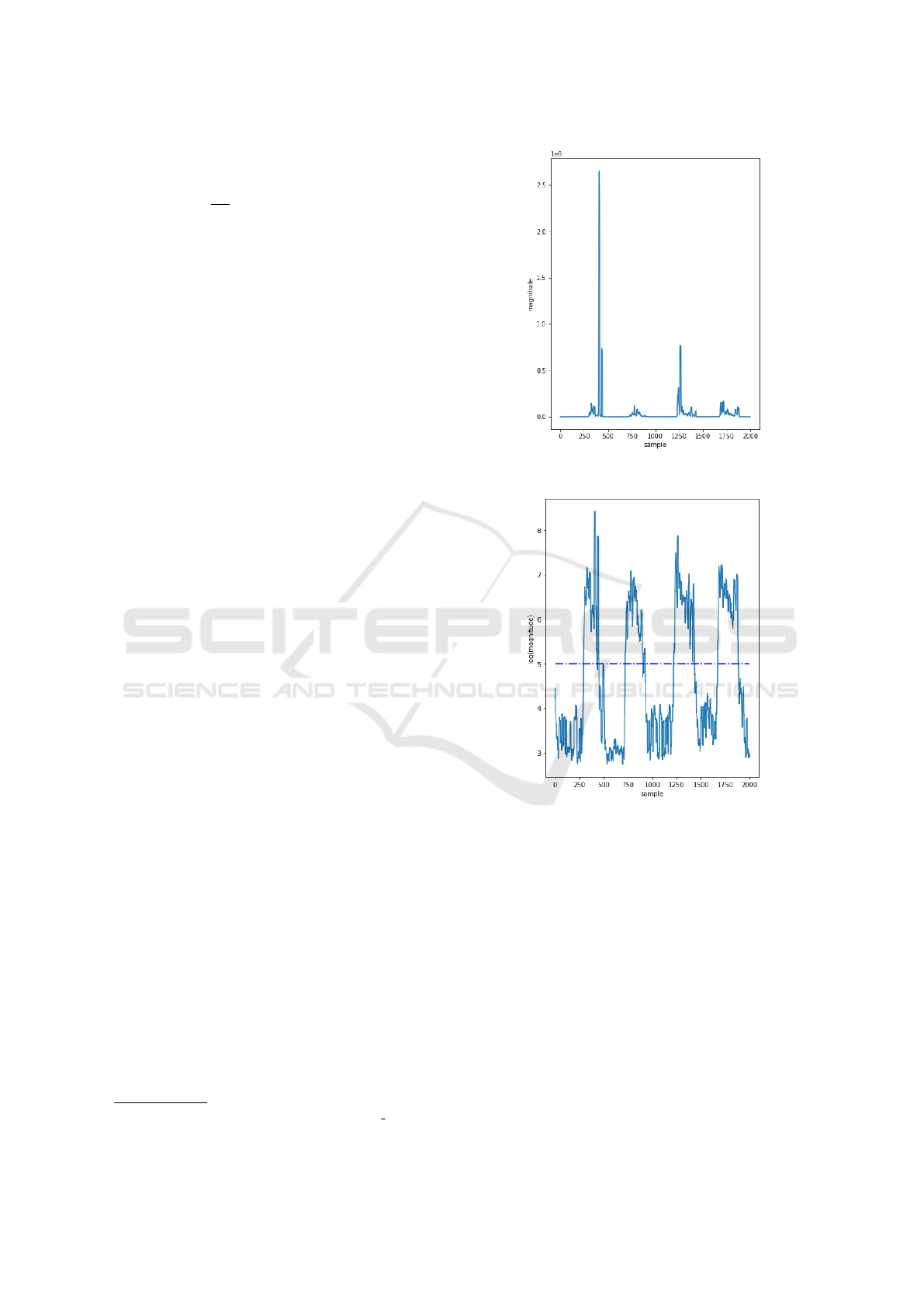
celerometer data variance has been evaluated (Figure
5), the value of the magnitude threshold will be es-
timated as magnitude average for values greater than
log(1.0) (small bias). This threshold is used to split
raw data into static and dynamic intervals (Figure 6).
Because of the fact that raw accelerometer data are
usually formed by values in a range of positive and
negative numbers, it’s important to note that we need
to add some bias and make all values positive before
performing the logarithmic magnitude estimation.
3.3 Comparative Analysis
We compared the previous version of the static detec-
tor proposed by (Tedaldi et al., 2014) and our version.
Unfortunately, within this work scope, it is difficult to
provide some quantitative metrics on how well both
detectors performed. To solve this issue, we should
use a manually marked dataset or apply the IMU cal-
ibration procedure on the same dataset using deter-
mined intervals from both detectors. On the other
hand, we may do some comparison based on Fig-
ures and computation time. All experiments were per-
formed on the dataset from our device and with total
of 16343 samples on the host computer equipped with
Intel Core i7 CPU 965 @ 3.20GHz 8 and with 16GB
1
https://github.com/IKSAResearchLab/IMU Calibration.git
Figure 5: Estimated magnitude by Eq.1 without using loga-
rithm function.
Figure 6: Estimated logarithmic magnitude and the deter-
mined threshold value (the blue horizontal line) used for
splitting data in static and dynamic intervals.
of RAM with the original detector’s MATLAB2018b
program was performed in 64.22 seconds, where the
used value of t
w
was 9 samples. However, our de-
tector on the same host and a program implemented
in C processes the same dataset in 0.01 seconds. In
our detector, we used t
w
= 0.05 seconds or a 9-sample
long time period, t
st
= 1.0 seconds and t
dyn
= 0.4 sec-
onds. The original detector generated too much noise
if t
w
value was too small as the one mentioned above
(Figure 7), but generated good results if t
w
was set
to 120 samples long time window, no noise was ob-
served (Figure 8). The new detector is more config-
urable and it is possible to set the minimal value of
the static and dynamic interval, which reduces noise
A Method for Static and Dynamic Interval Detection within the IMU Calibration Procedure
749

Figure 7: The results of interval detection with both de-
tectors. The sub-window of the overall dataset is shown,
where t
w
= 0.05 seconds or is 9 samples long. The origi-
nal detector produced noise within the static intervals. The
accelerometer values have been normalized for better rep-
resentation.
Figure 8: The results of intervals detection with both de-
tectors. The sub-window of the overall dataset is shown,
where t
w
= 0.5 seconds or is 120 samples long. The orig-
inal detector provided good results. The new detector gen-
erated more narrowed intervals than the original one. The
accelerometr’s values were normalized for better represen-
tation.
in detected intervals and, therefore, will improve the
calibration accuracy and increase the quality of the
validation process. Results of the new detector are de-
pended to selected values of t
w
. If the value is small
as the one used above, then the borders of the static
intervals are more close to the dynamic signals of the
accelerometer. In the case of the high values, on the
contrary, the borders of the static intervals are far from
the dynamic signals of the accelerometer as shown in
Figure 8. After many experiments with both detec-
tors, it has been concluded that the new detector pro-
vides smoother results (is less noisy) than the origi-
nal one. The new detector provides the quality metric
for the detected static intervals. The metric is imple-
mented as a variance operator, which is applied to the
logarithmic magnitude values of a static interval. The
lower this metric value is, the more useful is the static
interval.
Algorithm 1: The new version of static detector.
Require: ACC
(n,3)
,t
w
,t
st
,t
dyn
∈ R
1: function GET-MAGNITUDE(ACC,t
w
)
2: Returns logarithmic magnitude of ACC
3: M ← hi;m
avg
← 0
4: for all µ ∈ ACC do
5: M
i
← log
10
(ς(µ) + 1.0) see eq. 1
6: end for
7: m
avg
← avg(M) for all M
i
> b
8: return (M, m
avg
)
9: end function
10: function GET-INTERVALS(M ∈ R
m
, m
avg
,t
st
,t
dyn
)
11: The function detects stat. and dyn. interv.
12: j, k ← 0;
13: S, D ← hi Stat. and dyn. interv. sequences
14: for all M
i
∈ M, (0 6 i < m) do
15: if M
i
≤ m
avg
and len(S
curr
) ≤ t
st
then
16: Stat
j
← (start
idx
, stop
idx
)
17: j = j +1
18: end if
19: if M
i
> m
avg
and len(Dyn
curr
) ≤ t
dyn
then
20: Dyn
k
← (start
idx
, stop
idx
)
21: k = k + 1
22: end if
23: end for
24: return (S, D)
25: end function
26: (M, m
avg
) ← GET-MAGNITUDE(ACC,t
w
)
27: (S, D) ← GET-INTERVALS(M, m
avg
,t
st
,t
dyn
)
28: narrow(S, D, count) Narrow all static intervals
in S
29: var(S) Estimate variance of magnitude for all
static intervals (quality metric)
4 CONCLUSIONS
The accuracy of the IMU calibration procedure de-
pends strongly on how precisely static and dynamic
intervals have been determined. The original detector
performs sufficiently well if the time window value
interval used in the variance magnitude estimation is
not too small. At the same time, the original detec-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
750

tor is more computationally expensive, especially if it
is necessary to find an appropriate value of the time
window parameter.
The new detector was implemented in C and is
much quicker and easily implementable than the orig-
inal one. It also provides more options for parame-
ter settings. Finally, it provides a quality metric for
the determined static intervals. This metric is useful
in the accelerometer calibration step and in the gy-
roscope calibration step when the triads of static and
dynamic intervals have been selected.
In further research activities, we should make a
numerical analysis of the static detector within the
IMU calibration procedure and compare obtained cal-
ibration accuracy for the proposed and other static de-
tectors.
ACKNOWLEDGEMENTS
This work has been supported by the European Re-
gional Development Fund within the Activity 1.1.1.2
Post-doctoral Research Aid of the Specific Aid Ob-
jective 1.1.1 To increase the research and inno-
vative capacity of scientific institutions of Latvia
and the ability to attract external financing, invest-
ing in human resources and infrastructure of the
Operational Programme Growth and Employment
(No.1.1.1.2/VIAA/2/18/334).
REFERENCES
Barnes, J. A. and Allan, D. W. (1990). Variances based on
data with dead time between the measurement. NIST
Tech. Note, 1318:296–335.
Beyeler, A. and Floreano, D. (2009). optiPilot : control of
take-off and landing using optic flow. Eur. Micro Air
Veh. Conf. Compet. 2009 (EMAV 2009).
Briod, A., Zufferey, J. C., and Floreano, D. (2012). Au-
tomatically calibrating the viewing direction of optic-
flow sensors. Proc. - IEEE Int. Conf. Robot. Autom.,
pages 3956–3961.
Deng, Z., Sun, M., Wang, B., and Fu, M. (2017). Anal-
ysis and Calibration of the Nonorthogonal Angle in
Dual-Axis Rotational INS. IEEE Trans. Ind. Elec-
tron., 64(6):4762–4771.
Furgale, P., Rehder, J., and Siegwart, R. (2013). Unified
temporal and spatial calibration for multi-sensor sys-
tems. In 2013 IEEE/RSJ International Conference on
Intelligent Robots and Systems, pages 1280–1286.
Le Gentil, C., Vidal-Calleja, T., and Huang, S. (2018). 3D
Lidar-IMU Calibration Based on Upsampled Prein-
tegrated Measurements for Motion Distortion Cor-
rection. 2018 IEEE International Conference on
Robotics and Automation (ICRA), pages 2149–2155.
Looney, M. (2015). The Basics of MEMS IMU/Gyroscope
Alignment. Analog Dialogue, 49(June):1–6.
Lv, J., Ravankar, A.A., Kobayashi, Y., Emaru, T. (2016).
A method of low-cost IMU calibration and alignment.
SII 2016 - 2016 IEEE/SICE International Symposium
on System Integration, pages pp. 373—-378.
Mur-Artal, R. and Tardos, J. (2016). Visual-inertial monoc-
ular slam with map reuse. IEEE Robotics and Automa-
tion Letters, PP.
Pretto, A. and Grisetti, G. (2014). Calibration and perfor-
mance evaluation of low-cost IMUs. 18th Internation-
alWorkshop on ADC Modelling and Testing.
Qin, T., Li, P., and Shen, S. (2018). VINS-Mono: A Ro-
bust and Versatile Monocular Visual-Inertial State Es-
timator. IEEE Transactions on Robotics, 34(4):1004–
1020.
Ren, C., Liu, Q., and Fu, T. (2015). A Novel Self-
Calibration Method for MIMU. IEEE Sensors Jour-
nal, 15(10):5416–5422.
Shin, E. and El-Sheimy, N. (2002). A new calibration
method for strapdown inertial navigation systems. Z.
Vermess, 127:1–10.
STMicroelectronics (2017). Lsm6dsl datasheet.
Tedaldi, D., Pretto, A., and Menegatti, E. (2014). A ro-
bust and easy to implement method forIMU calibra-
tion without external equipments. Proceedings - IEEE
International Conference on Robotics and Automa-
tion, pages 3042–3049.
Vidal, A. R., Rebecq, H., Horstschaefer, T., and Scara-
muzza, D. (2017). Ultimate SLAM? Combining
Events, Images, and IMU for Robust Visual SLAM
in HDR and High Speed Scenarios. IEEE Robotics
and Automation Letters, 3(2):994–1001.
A Method for Static and Dynamic Interval Detection within the IMU Calibration Procedure
751
