Event-B Decomposition Analysis for Systems Behavior Modeling

Kenza Kraibi

, Rahma Ben Ayed

, Joris Rehm

, Simon Collart-Dutilleul

1,3

, Philippe Bon

1,3

and Dorian Petit

1,4

Institut de Recherche Technologique Railenium, F-59300, Famars, France

CLEARSY, Strasbourg, France

Univ. Lille Nord de France, IFSTTAR, COSYS, ESTAS, F-59650 Villeneuve d’Ascq, France

Universit

e Polytechnique Hauts-de-France, LAMIH UMR CNRS 8201, F-59313 Valenciennes, France

dorian.petit@uphf.fr

Keywords:

Formal Methods, Event-B, Reﬁnement, Decomposition, Systems Behavior, Railway Systems.

Abstract:

Applications of formal methods to critical systems such as railway systems have been studied by several

research works. Their ultimate goal is to increase conﬁdence and to ensure the behavior correctness of these

systems. In this paper, we propose to use the Event-B formal method. As a central concept in Event-B,

reﬁnement is used to progressively introduce the details of systems requirements, but in most cases, it leads to

voluminous and complex models. For this purpose, this paper focuses on decomposition techniques in order

to manage the complexity issue in Event-B modeling. It presents a state of the art and an analysis of existing

decomposition techniques. Then, an approach will be proposed following this analysis.

1 INTRODUCTION

The analysis and modeling activities of railway dy-

namic behaviors are major tasks requiring rigorous

mechanisms. Based on mathematical foundations,

formal methods can help to rigorously carry out these

activities and reduce the ambiguity of the speciﬁcities

of critical systems such as railway signaling systems.

The use of formal methods is recommended by the

CENELEC 50128 standard (CENELEC, 2011) ded-

icated to the railway sector. In this paper, we pro-

pose to use the Event-B formal method (Abrial et al.,

2010; Abrial, 2010) providing appropriate techniques

for system modeling based on the B method (Abrial,

1996). B/Event-B methods have been widely used

in the railway ﬁeld in research such as the PER-

FECT

and NExTRegio projects (Ben Ayed et al.,

2016; Ben Ayed et al., 2014) and in industry sectors

as in the METEOR project (Behm et al., 1999). In

the same context, CLEARSY

has also driven railway

projects using formal proofs (Sabatier, 2016).

Modeling of critical systems such as railway sig-

naling systems can lead to complex and voluminous

PERFECT: http://www.agence-nationale-

recherche.fr/Projet-ANR-12-VPTT-0010

CLEARSY: https://www.clearsy.com/

models. One of the Event-B techniques for this is-

sue is reﬁnement. Reﬁnement consists in detailing

the design to reach a concrete level by progressive

steps. However, the ﬁnal level of modeling is still

difﬁcult to manage. In order to reduce this complex-

ity, reﬁnement can be completed by another technique

called decomposition of atomicity (Butler, 2009a).

Model decomposition is another technique that can

reduce the complexity of large models and increase

their modularity. This technique consists in divid-

ing a model into sub-models that can be reﬁned sepa-

rately and more easily than the original one. Several

model’s decomposition approaches have been pro-

posed. Some of them are supported by Rodin

(Butler

and Hallerstede, 2007) plugins

(Silva et al., 2011).

In this paper, we present in sections 2 and 3, a sur-

vey of the existing decomposition techniques. Sec-

tion 4 describes a railway case study for the existing

approaches analysis presented in section 5. Then, this

last one illustrates the semantics need of modularity

and gives a presentation of the proposed approach and

its application to the case study.

Rodin: http://www.event-b.org/

Modularization:

http://wiki.event-b.org/index.php/Modularisation Plug-in

278

Kraibi, K., Ben Ayed, R., Rehm, J., Collart-Dutilleul, S., Bon, P. and Petit, D.

Event-B Decomposition Analysis for Systems Behavior Modeling.

DOI: 10.5220/0007929602780286

In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 278-286

ISBN: 978-989-758-379-7

2 REFINEMENT AND EVENT

ATOMICITY DECOMPOSITION

Nowadays, reﬁnement is used to solve complex mod-

eling problems (Badeau and Amelot, 2005). In Event-

B, we ﬁnd two principal types of reﬁnement: data re-

ﬁnement (Back, 1989) and events reﬁnement. Data

reﬁnement consists in reﬁning the system state by

introducing new variables. It allows the deﬁnition

of gluing invariants and the invariance properties of

the new variables. These invariants allow the correc-

tion proof of the reﬁnement (Abrial, 2010). Events

reﬁnement consists in introducing new events reﬁn-

ing the skip in order to observe the concrete behavior

that does not appear in the abstraction (Abrial, 2010).

Events reﬁnement allows reﬁning existing events by

strengthening their guards and reﬁning their actions.

A proposition in (Butler, 2009a) is called de-

composition of event atomicity. This approach is

a structuring mechanism for reﬁnement in Event-B.

This mechanism is based on decomposing an ab-

stract atomic event to many sub-events, where one

event reﬁnes this abstract event. Decomposing atomic

events is inspired from Jackson System Develop-

ment (JSD) approach (Butler, 2009b) and it is repre-

sented by the ERS approach (Event Reﬁnement Struc-

tures) (Dghaym et al., 2016; Dghaym et al., 2017).

The idea of the ERS approach is to enrich the Event-

B reﬁnement with a graphical tree notation able to

represent explicitly the events decomposition in the

reﬁnement and the behavior sequencing (Fathabadi

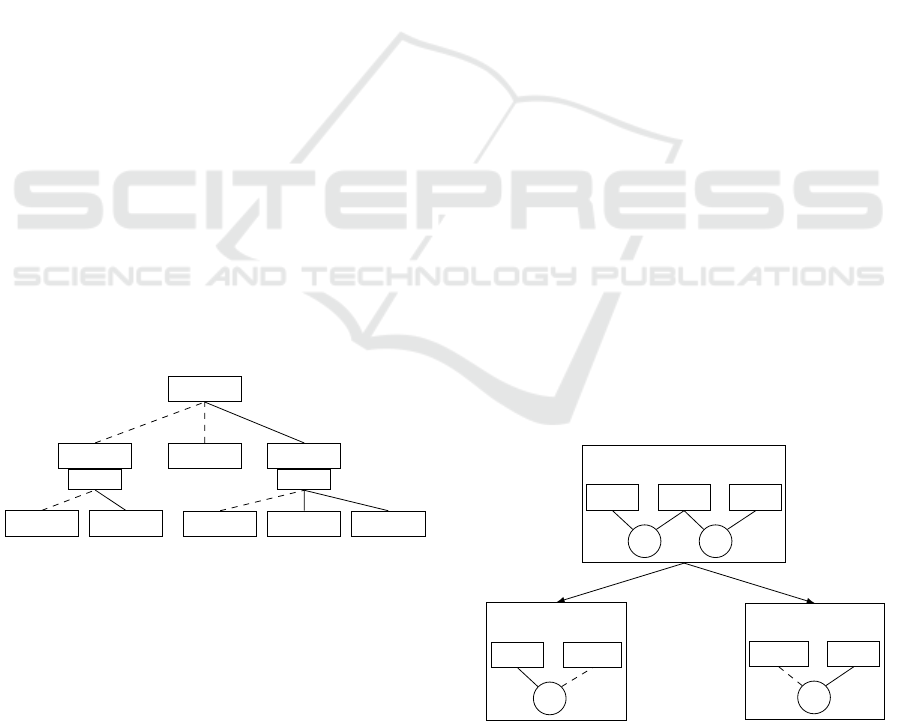
et al., 2011). Figure 1 presents a sub-tree. The child

nodes of each node are transformed into events in the

reﬁnement.

event

AND

event

XOR

event

skip

reﬁnes

Figure 1: Example of Event Reﬁnement Structures (ERS)

diagram.

The nodes order describes the order of events ob-

servation (from left to right). XOR speciﬁes the ob-

servation of one and only one event. In case of XOR,

an event can be reﬁned by many events or any event.

AND allows the interlaced execution of events. De-

spite these reﬁnement virtues, they do not tackle vo-

luminous models issues.

3 MODEL DECOMPOSITION

An Event-B machine can have so many events and

state variables that an additional reﬁnement can be-

come difﬁcult to manage. Model decomposition tack-

les this difﬁculty by providing a mechanism to divide

a large model into several sub-models. For different

decomposition techniques (Hoang et al., 2011), de-

scending steps are deﬁned by: modeling the system in

an abstract machine, reﬁning the abstract model to ﬁt

the structure expected by a given decomposition tech-

nique, applying the decomposition, then reﬁning the

resulting sub-models independently. Following this

guideline, global properties are captured early in the

model and guaranteed in the ﬁnal models by combin-

ing reﬁnement and decomposition.

3.1 Shared Event Decomposition

The shared event decomposition is an evolution of de-

composition of event atomicity. The author in (Butler,

2009a) proposes this method which makes it possi-

ble to separate the variables of a system in two dif-

ferent sub-machines by decomposing a shared event.

To decompose a machine using this method, vari-

ables to partition in each sub-component are cho-

sen then the decomposition is applied. Generated

machines contain the selected variables, and shared

events are deﬁned in two different signatures for each

sub-machine. These events describe the variables

changes.

As illustration, let M

be the machine as in ﬁg-

ure 2. Variables v1 and v2 of this machine are parti-

tioned respectively in two sub-machines M

and M

event2 is decomposed in the two sub-components as

two events event2’ and event2”, each event describes

the change of state applied to v1 and v2 respectively.

event1

event2

event3

event1

event2’

M1b

event2”

event3

Figure 2: Decomposition by shared event.

Event-B Decomposition Analysis for Systems Behavior Modeling

279

3.2 Shared Variable Decomposition

Abrial proposes in (Abrial and Hallerstede, 2007) the

shared variable decomposition which consists in dis-

tributing events of a machine between several sub-

machines. This approach proposes to manage shared

variables between several events. It is used also for

decomposing parallel programs (Hoang and Abrial,

2010). During the machine decomposition, events

to be separated are selected in each sub-machine and

considered as internal events. A variable that occurs

only in the internal events is a private variable. If a

variable is involved in internal events of different sub-

machines, it is deﬁned in each of them as a shared

variable that cannot be reﬁned. External events of a

sub-machine are events that simulate the change of

state of the external variables in the abstract machine.

Figure 3 illustrates the decomposition by shared

variable. The machine M

is deﬁned by four events

and it is decomposed into two sub-machines M

and

by partitioning its events. Events event1 and

event2 (resp. event3 and event4) are internal events

to the sub-machine M

(resp. M

). The variable v1

(resp. v2) is private to M

(resp. M

). As for v2, it

is a shared variable. Consequently, the machine M

(resp. M

) contains the external event event3’ (resp.

event2’) which simulates the state changes made by

event3 (resp. event2) on v2 in M

event1 event2 event3 event4

v1 v2 v3

M1a

event1 event2 event3’

v1 v2

M1b

event2’ event3 event4

v2 v3

event1, event2 event3, event4

Figure 3: Decomposition by shared variable.

3.3 Other Decomposition Methods and

Summary

In addition to reﬁnement and decomposition by

shared variable, generic instantiation is another

proposition of Abrial in (Abrial and Hallerstede,

2007). It is based on the reuse of the abstract model

with slight modiﬁcations by instantiating sets and

constants of this model. In (Hoang et al., 2011), the

modularization is another proposition based on deﬁn-

ing interfaces in B method. This approach promotes

the use of USES clause in order to call operations.

Fragmentation and distribution approach in (Siala

et al., 2016) deﬁnes a speciﬁcation using DSL (Do-

main Speciﬁc Language) (Van Deursen et al., 2000)

to decompose a model. In the same context, (Hoang

et al., 2017) propose also a technique based on the

use of a classical-B clause. This approach proposes

the use of a composition mechanism based on the use

of INCLUDES clause. So, the including machine can

use variables and invariants of the included machine.

Our target is to use speciﬁc systems behavior tech-

niques for modeling. In opposition, the previous cited

approaches rely on the implication of some classical-

B method semantics or the use of another language as

DSL.

Currently, the railway industry models its systems

on the basis of a linear modeling. However, the ob-

tained models are voluminous and difﬁcult to man-

age. The aim of our work is, on the one hand, mod-

eling the behavior of railway signaling systems and

the management of the resulting models complexity

on the other hand. For this point, we choose to pro-

ceed with model decomposition through shared vari-

able decomposition and shared event decomposition.

4 RAILWAY CASE STUDY

In order to analyze the existing approaches and illus-

trate our contribution, we have modeled and formally

proved a case study of railway signaling systems on

Atelier B

and Rodin tools. The aim is to model a sys-

tem which allows the trains control, in other words

ensure a safe train circulation in a certain railway net-

work containing signals, points, crossings... The main

goal of this case study is to avoid trains rear-end col-

lisions as in ﬁgure 4.

This case study is a simple example that focuses

on a particular requirement of a railway network and it

contains relevant elements to the decomposition anal-

ysis. This example is representative of what is done in

the industrial railway ﬁeld and in sub-systems trafﬁc

management such as the European Rail Trafﬁc Man-

agement System

(ERTMS).

Figure 4: Example of a train rear-end collision.

In a one-way trafﬁc split into blocks B

as shown

in ﬁgure 5, let consider two trains Train A and Train

Atelier B tool: https://www.atelierb.eu/

European Rail Trafﬁc Management System:

http://www.ertms.net

ICSOFT 2019 - 14th International Conference on Software Technologies

280

B. Train A follows Train B. The trains are moving

by a certain number of steps. The trains movements

are based on the position of the front train and of the

end train of each train. Each block has a front block

and an end block. Two block states are possible: oc-

cupied (red block) or free (green block).

Figure 5: Case study description.

Abstract Machine. In an abstract machine M

(cf.

Figure 6), we deﬁne trains movements. M

de-

ﬁnes the variables describing the trains front and the

trains end positions (line 2 in ﬁgure 6): front trainA,

front trainB, end trainA and end trainB, and the

events that describe the trains movements:

• move front trainA: as shown in ﬁgure 6, change

the position of the Train A front (line 9) without

catching up the next train.

• move end trainA: change the Train A end position

taking into consideration the position of its front.

• move front trainB: change the Train B front posi-

tion.

• move end trainB: change the position of the Train

B end taking into consideration its front position.

1. MACHINE M

2. VARIABLES front trainA, front trainB, end trainA,

end trainB

3. INVARIANTS front trainA < end trainB & ...

4. EVENTS

5. move

front trainA =

6. ANY step

7. WHERE step : NATURAL1

8. & front trainA + step < end trainB

9. THEN front trainA := front train1 + step

10. END;

11. ....

12. END

Figure 6: Abstract machine excerpt of the case study.

To avoid a rear-end collision, the position of the

Train B end must always be in front of the position of

the Train A front. This is speciﬁed by the invariant:

f ront trainA < end trainB

Reﬁnement. In a second phase, we deﬁne a more

concrete machine introducing the blocks notation and

the trains movements on blocks. M

reﬁning M

and

seeing a context C (cf. ﬁgure 7).

The context C, as in ﬁgure 8, speciﬁes the blocks,

their beginnings and ends positions and some track

MACHINE M

REFINEMENT M

REFINES M

CONTEXT C

REFINES

SEES

Figure 7: Structure of the case study model.

properties (axioms) such as the blocks do not inter-

sect, etc. A block can be Free or Occupied.

1. CONTEXT C

2. DEFINITIONS Block == NATURAL

3. SETS BlockState = {Free,Occupied};

4. SUBSYS = {TRAIN, TRACK}

5. CONSTANTS front block, end block, next block

6. AXIOMS front block : Block → NATURAL

7. & end block : Block → NATURAL

8. & next block = %bk.(bk : Block | bk+1)

9. & ...

10. END

Figure 8: The context deﬁning blocks.

In machine M

(cf. Figure 9), the variables that

describe the change of the blocks states by block state

and the intermediate variables are deﬁned.

1. REFINEMENT M

REFINES M

2. VARIABLES front trainA, front trainB, end trainA,

3. end trainB, block state,next turn,

4. f st tAblock, lst tAblock, f st tBblock,lst tBblock

5. INVARIANTS f st tAblock < lst tBblock

6. & end train(lst tBblock) ≤ end trainB

7. & ∀bk.(bk : Block & next turn = T RAIN&

8. block state(bk) = Free ⇒ bk 6= lst tBblock)

9. & ...

10. EVENTS

11. enter tAblock ref move front trainA =

12. ANY step

13. WHERE step : NATURAL1

14. & block state(next block(fst tAblock)) = Free

15. & front block(fst tAblock)≤ front trainA+step

16. & front trainA + step <

22. front block(next block(fst tAblock))

17. & next turn = TRAIN

18. THEN

19. next turn := TRACK

20. || front trainA := front trainA + step

21. || fst tAblock := next block(fst tAblock)

22. END;

23. ...

24. END

Figure 9: The case study reﬁnement machine.

These intermediate variables allow the communi-

cation between the train and the track such as the oc-

cupied block by a train (lines 4 in ﬁgure 9). Train

A can occupy more than one block, so variables

fst tAblock and lst tAblock respectively describe the

occupied block by the Train A front and the block oc-

cupied by the Train A end. In the same way are de-

Event-B Decomposition Analysis for Systems Behavior Modeling

281

ﬁned fst tBblock an lst tBblock for Train B. The vari-

able next turn allows the transition from a Track be-

havior to a Train behavior and vice versa.

The events of this machine are those deﬁned in M

reﬁning themselves and other new reﬁning events:

• enter tAblock (resp. enter tBblock): occupies

a block by Train A (resp. Train B) reﬁning

move front trainA (resp. move front trainB).

• free tAblock (resp. free tBblock): frees a

block by Train A (resp. Train B) reﬁning

move end trainA (resp. move end trainB);

• TRACKevent: a new event changing the block

state.

A block can be occupied at most by one train,

in other words the occupied block by the end of

Train B named lst tBblock should always be in

front of the occupied block by the front of Train

A named fst tAblock as deﬁned in the invariant:

f st tAblock < lst tBblock. Another useful invari-

ant is also deﬁned in order to ensure the distance

between Train A and Train B: ∀ bk.( bk:Block &

next turn = TRAIN & block state(bk) = Free ⇒ bk

6= lst tBblock)

Figure 10 shows an example of a possible sce-

nario of trains movements. Using ProB

(Leuschel

and Butler, 2003), an animation is elaborated on the

model.

Figure 10: An example of trains movement scenario.

In a ﬁrst step, each of Train A and Train B occupy

distinct blocks. Then, in step 2 Train B moves to the

next block and occupies it. The blue train shadow

presents the previous train position. As a third step,

while Train A is moving inside the associated block,

Train B releases the previous block. Hence, in step 4

Train A enters the next free block. Note that not all

the model elements are presented in the paper

ProB: www3.hhu.de/stups/prob/index.php/Main Page

The case study model and proof in Atelier B and Rodin,

animation in ProB and different Rodin plugins application

can be provided on demand.

5 PROPOSED APPROACH

5.1 Analysis

As mentioned in subsection 3.3, this paper focuses

on the shared variable decomposition and the shared

event decomposition. Both approaches are start-

ing from a machine and decomposing it into two

other new machines, then reﬁning the resulting sub-

machines separately. Let apply the decomposition by

the shared event and by the shared variable plugins.

The machine to decompose is M

and the resulting

sub-machines are M

and M

During the shared event decomposition, not all

actions are accepted to be decomposed and variables

partitioning is not always possible. Table 1 shows

different types of actions that make variables states

evolve. v1 and v2 are an example of the case study

variables.

Table 1: Application of the shared event decomposition.

Actions types of M

(v1) M

(v2)

act1 v1 :| (v1=1) k

v2 :| (v2=2)

v1 :| (v1=1) v2 :| (v2=2)

act2 v1,v2 :| (v1=2

∧ v2=v1+2)

– –

act3 v1,v2 := 1,2 v1 := 1 v2 := 2

act4 v1 := v2+1 – –

act5 v1 :: {v2,1,2} – –

An error message is displayed asking to sim-

plify the actions: the assignment is too complex be-

cause it refers to elements belonging to different sub-

components. The obtained errors are shown by this

symbol ’–’. For the shared event decomposition,

predicates (invariants and guards) and actions should

not refer to variables that must be partitioned into dif-

ferent sub-components. As an example, the substitu-

tion becomes such that in act2 cannot be decomposed:

v1,v2 :| (v1 = 2 ∧ v2 = v1 + 2)

For the shared variable decomposition, the event

partition is always possible and can generate sub-

components. However, this decomposition may be

less relevant because the model to be decomposed

contains a large number of shared variables, espe-

cially in case of decomposing complex reﬁnements

rich with shared variables (Silva et al., 2011) which

is the case in the case study. Furthermore, there ex-

ists a restriction of this method: shared variables and

external events must be present in the resulting sub-

components and cannot be reﬁned when reﬁning these

sub-components (Abrial, 2009).

For these reasons, it may be necessary to proceed

with an intermediate preparation step to resolve com-

plex predicates such as invariants, guards and axioms,

ICSOFT 2019 - 14th International Conference on Software Technologies

282

as well as substitutions (actions) by separating the

variables assigned to different sub-components. This

separation is done by applying an additional man-

ual reﬁnement step before the decomposition (Abrial,

2009). The user must explicitly separate the variables

in this reﬁnement by introducing an auxiliary parame-

ter p. For example, the predicate v1 = v2 becomes p =

v2 & v1 = p. If this manual reﬁnement step is not per-

formed, the complex predicates and substitutions are

automatically marked by the tool via a message frame

and then the user’s intervention is required to perform

the separation explicitly. After this plugins experi-

mentation, we had identiﬁed some limitation and is-

sues in the generated machine:

• States changes of several variables in the same ac-

tion, such as becomes such that substitution, can-

not be decomposed and should be dealt with the

user’s intervention by an intermediate step of re-

ﬁnement and replacing the variables in the predi-

cate with parameters;

• Loss of information when decomposing guards;

• Loss of shared invariant involving shared vari-

ables. As long as the resulting sub-machines are

not reﬁning the initial machine, the shared invari-

ant is not preserved;

• Generation of empty events in the sub-

component;

• Need of an intermediate step of a manual reﬁne-

ment before applying the decomposition.

5.2 Discussion

The choice of a decomposition method depends on

the work ﬁnality:

• Shared variable decomposition can decompose

models by functionality, for instance in the rail-

way ﬁeld, an initial railway signaling model can

be decomposed into three sub-components: train

integrity, block release and train communication;

• Shared event decomposition is based on partition-

ing the behavior of a system, e.g. partitioning ac-

cording to different types of trains movement such

as movement under the national Automatic Train

Protection (ATP) system or under ERTMS levels.

Nonetheless, the industrial need is to reason on

sub-systems, in other words, to take into account both

the behavior and the functionality. The use of shared

variable decomposition or the shared event decompo-

sition does not address this need. Hence, after this

analysis of the existing approaches and according to

our industrial needs, some limitations to these tech-

niques are identiﬁed, among others, the loss of shared

invariants preserving a major safety property. Also,

after the generation of the sub-machines by the plu-

gin, the link between the original machine and the

sub-machine is not explicit.

5.3 Proposed Approach

The analysis above leads us to build a new decom-

position approach that corresponds to the industrial

need. This technique is based on the decomposi-

tion by reﬁnement. By reﬁning the abstract machine

while the decomposition, the resulting sub-machines

keep the preservation of shared invariants, especially,

safety invariants. In addition, this approach deﬁnes a

new semantic link between sub-machines: REFSSES.

This link allows variables, invariants, constants, sets

and properties visibility of a sub-machine by the other

sub-machines.

The REFSSES is a similar notion to the SEES of

the classical-B with a particular characteristics, The

name of the REFSEES clause is a combination of RE-

FINEMENT and SEES which means it allows a re-

ﬁnement machine to see another reﬁnement machine.

So we add a clause REFSEES to the machine M

(resp. M

), which would make reference to the vari-

ables of the machine seen M

(resp. M

). So there,

we have a circular dependency with this notion of

REFSEES. In classical-B there is normally no circu-

lar dependency and machines cannot see a reﬁnement

machine. Contrary to SEES clause, REFSEES can

have a reﬁnement machine as identiﬁer and can be

used in a cyclic way.

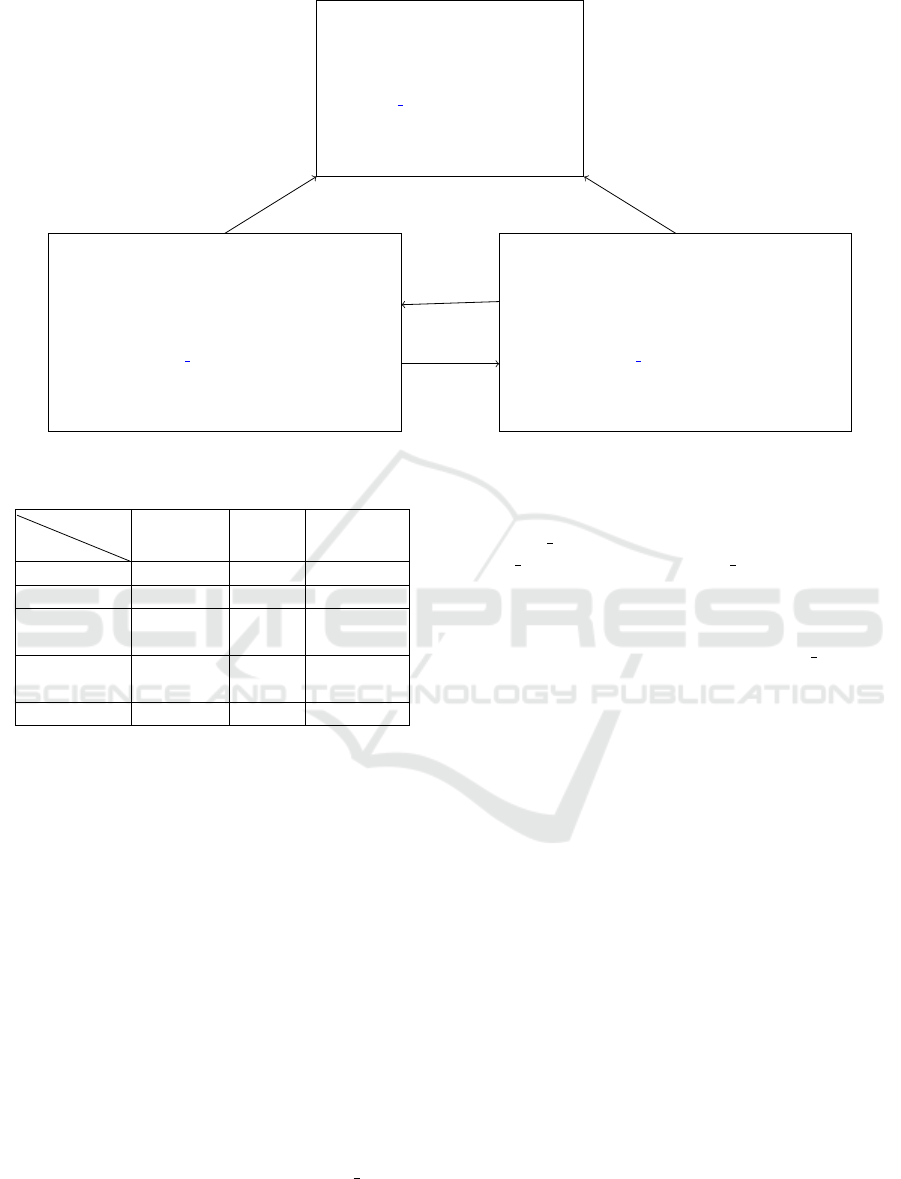
Figure 11 illustrates the decomposition by reﬁne-

ment of a machine M

into two sub-machines M

and

• M

deﬁnes variables x, y and z, invari-

ants to be preserved I(x,y,z) and abstract event.

An abstract event contains guards G(x,y,z) and

before/after predicates R(x,y,z,x’,y’,z’).

• The resulting sub-machine M

(resp. M

) de-

ﬁnes the private variable x

(resp. y

) reﬁning

x (resp. y). z is considered as a shared variable

which can be reﬁned by z

(resp. z

) in M

(resp. M

). Each machine deﬁnes gluing invari-

ants J

and J

. abstract event is reﬁned by re

in M

and by re

in M

. The variable x

(resp.

) is visible by re

(resp. re

) in M

(resp.

Table 2 is a visibility table of REFSEES. Sets

and constants of M

are visible by axioms, invariants

and events of M

. Private variables of M

are only

visible by M

events. As for shared variables, they

are visible and able to be modiﬁed by both the sub-

machines.

Event-B Decomposition Analysis for Systems Behavior Modeling

283

MACHINE M

VARIABLES x, y, z

INVARIANTS I(x,y,z)

EVENTS

abstract event

when G(x,y,z)

then x, y,z : |R(x,y, z,x

)

end

REFINEMENT M

REFINES M

REFSEES M

VARIABLES x

INVARIANTS J

(x,z,x

)

EVENTS

ref abstract

event

WHEN G

)

THEN x

: |R

)

END

REFINEMENT M

REFINES M

REFSEES M

VARIABLES y

INVARIANTS J

(y,z,y

)

EVENTS

ref abstract

event

WHEN G

)

THEN y

: |R

)

END

REFINES REFINES

REFSEES

Figure 11: Decomposition by reﬁnement on two sub-machines.

Table 2: REFSEES visibility of M

by M

AXIOMS INV

INIT /

EVENTS

Sets visible visible visible

Constants visible visible visible

Private

variables

visible

Shared

variables

visible

Events

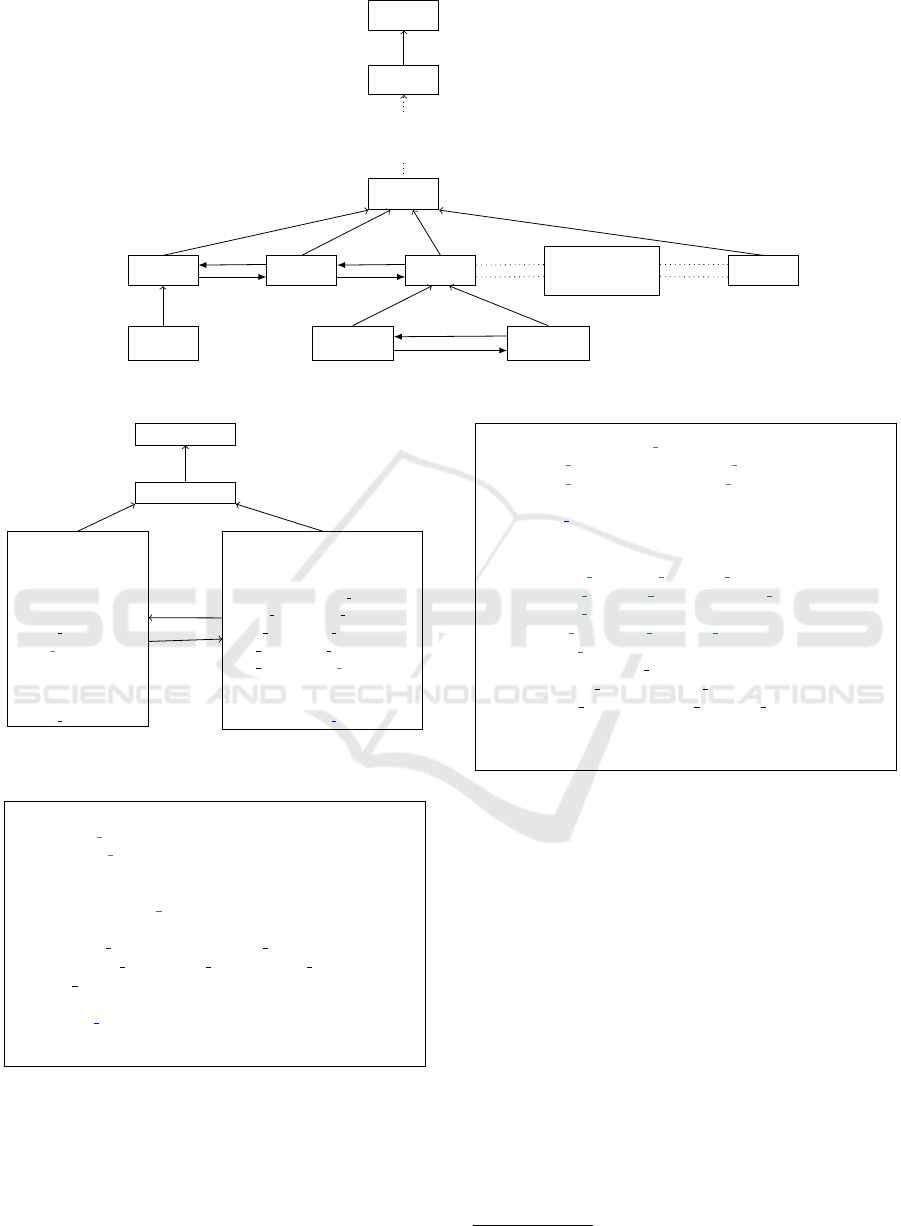
Figure 12 shows the general structure of the pro-

posed approach. The decomposition can be applied

on a certain level of reﬁnement and done by multi-

ple horizontal reﬁnements. As shown in the ﬁgure a

machine M

n−1

can be reﬁned by m machines. These

resulting sub-machines keep the reﬁnement link with

the root.

5.4 Application of the Approach to the

Case Study

The goal is to decompose the machine M

by separat-

ing track and train behaviors and functionalities using

the decomposition by reﬁnement as presented in ﬁg-

ure 13.

The Track machine, in ﬁgure 14, reﬁnes M

and

refsees the Train machine through the REFSEES

link. Track contains the variables associated to the

track like the blocks states variable: block

state. It

contains also events that make these variables evolve

such as TRACKevent.

As for the Train machine, in ﬁgure 15, it re-

ﬁnes M

and refsees the Track machine through

the REFSEES link. It describes the train variables

like front trainA and the trains movement events e.g.

enter tAblock. The variable next turn is a shared vari-

able of Track and Train. Partitioned events keep

their guards in the sub-machines. Events that are not

needed in a sub-machine are reﬁned such that they

cannot be observed anymore such as enter tAblock in

the Track machine. In Rodin, this is done automati-

cally since the event is not displayed in the reﬁning

machine.

6 CONCLUSION

Modeling railway signaling systems in Event-B pro-

duces complex models rich with variables and events.

Various techniques have been proposed to cope with

this voluminosity issue such as the decomposition

technique. Although decomposition approaches pro-

mote the modularization of critical systems, some of

them do not totally cope with this issue. The analysis

of these approaches, on the base of the deﬁned case

study, leads to the identiﬁcation of certain restrictions.

As a consequence, we propose in this paper a new ap-

proach based on the decomposition by reﬁnement us-

ing a new link between sub-machines that addresses

the deﬁnition of a new semantic. This approach will

guarantee the preservation of invariants through the

reﬁnement and the visibility of private variables of

other sub-machines through the REFSEES link. Our

aim is that this approach will be used by both Rodin

and Atelier B tools. In a future work, we will deﬁne

ICSOFT 2019 - 14th International Conference on Software Technologies

284

Multiple levels

of reﬁnement

n−1

(n+1)a

(n+1)c1

(n+1)c2

Multiple

sub-machines

REFINES

REFINES REFINES

REFINES

REFSEES

Figure 12: Structure of the proposed approach.

MACHINE M

REFINEMENT

Track

REFINES M

REFSEES Train

VARIABLES

block state,

next turn

INVARIANTS J

EVENTS

ref

abstract event

REFINEMENT Train

REFINES M

REFSEES Track

VARIABLES front trainA,

front trainB, end trainA,

end trainB , fst tAblock,

lst tAblock, fst tBblock,

lst tBblock, next turn

INVARIANTS J

EVENTS

ref abstract event

REFINES

REFINES REFINES

REFSEES

Figure 13: Application of the decomposition by reﬁnement

on the case study.

10. INVARIANTS

11. block state : Block → BlockState

12. & next turn : SUBSYS & ...

13. EVENTS

14. TRACKevent =

15. SELECT next turn = TRACK

16. THEN

17. next turn:=TRAIN || block state:=(Block*Free)

< + ((lst tAblock..fst tAblock U lst tAblock ..

fst tAblock) *Occupied)

18. END;

19. enter tAblock=SELECT 0=1 THEN skip END;

20. ...

21. END

Figure 14: Resulting sub-machine Track.

proof obligations formulas for these new notations.

As consequence, for each sub-machine proof obliga-

tions are generated taking into account the link to the

other sub-machines.

10. INVARIANTS next turn : SUBSYS

11. & fst tAblock : Block & lst tAblock : Block

12. & fst tBblock : Block & lst tBblock : Block

13. EVENTS

14. enter tAblock

15. ANY step

16. WHERE step : NATURAL1

17. & block state(next block(fst tAblock)) = Free

18. & front block(fst tAblock)≤ front trainA+step

19. & front trainA+step<

front block(next block(fst tAblock))

20. & next turn = TRAIN

21. THEN next turn := TRACK

22. || front trainA := front trainA + step

23. || fst tAblock := next block(fst tAblock)

24. END; ...

25. TRACKevent = SELECT 0=1 THEN skip END

26. END

Figure 15: Resulting sub-machine Train.

ACKNOWLEDGMENT

This work is supported by PRESCOM (Global

Safety Proofs for Modular Design/PREuves de

ecurit

e globale pour la COnception Modulaire) as a

part of IRT Railenium

projects in collaboration with

CLEARSY.

REFERENCES

Abrial, J.-R. (1996). The B-Book: Assigning Programs to

Meanings. Cambridge University Press, New York,

NY, USA.

Railenium: https://railenium.eu/

Event-B Decomposition Analysis for Systems Behavior Modeling

285

Abrial, J.-R. (2009). Event Model Decomposition. Tech-

nical report/[ETH, Department of Computer Science,

626.

Abrial, J.-R. (2010). Modeling in Event-B: System and Soft-

ware Engineering. Cambridge University Press, New

York, NY, USA.

Abrial, J.-R., Butler, M., Hallerstede, S., Hoang, T. S.,

Mehta, F., and Voisin, L. (2010). Rodin: an open

toolset for modelling and reasoning in Event-B. In-

ternational journal on software tools for technology

transfer, 12(6):447–466.

Abrial, J.-R. and Hallerstede, S. (2007). Reﬁnement, De-

composition, and Instantiation of Discrete Models:

Application to Event-B. Fundamenta Informaticae,

77(1-2):1–28.

Back, R.-J. (1989). Reﬁnement Calculus, Part II: Parallel

and Reactive Programs. In Workshop/School/Sympo-

sium of the REX Project (Research and Education in

Concurrent Systems), pages 67–93. Springer.

Badeau, F. and Amelot, A. (2005). Using B as a high

level programming language in an industrial project:

Roissy VAL. In International Conference of B and Z

Users, pages 334–354. Springer.

Behm, P., Benoit, P., Faivre, A., and Meynadier, J. M.

(1999). M

eor: A Successful Application of B in a

Large Project. In Wing, J., Woodcock, J., and Davies,

J., editors, FM’99 - Formal Methods, volume 1708 of

Lecture Notes in Computer Science, pages 369–387.

Springer Berlin Heidelberg.

Ben Ayed, R., Collart-Dutilleul, S., Bon, P., Idani, A., and

Ledru, Y. (2014). B Formal Validation of ERTM-

S/ETCS Railway Operating Rules. In International

Conference on Abstract State Machines, Alloy, B,

TLA, VDM, and Z, pages 124–129. Springer.

Ben Ayed, R., Collart-Dutilleul, S., and Prun, E. (2016).

“Formal Methods To Tailored Solution For Single

Track Low Trafﬁc French Lines”. In International

Railway Safety Council (IRSC), Paris, France.

Butler, M. (2009a). Decomposition Structures for Event-

B. In International Conference on Integrated Formal

Methods, pages 20–38. Springer.

Butler, M. (2009b). Incremental Design of Distributed Sys-

tems with Event-B. Engineering Methods and Tools

for Software Safety and Security, 22(131).

Butler, M. and Hallerstede, S. (2007). The Rodin for-

mal modelling tool. In BCS-FACS Christmas 2007

Meeting-Formal Methods In Industry, London.

CENELEC, E. (2011). 50128. Railway applications-

Communication, Signaling and Processing Systems-

Software for Railway Control and Protection Systems.

Dghaym, D., Butler, M., and Fathabadi, A. S. (2017). Ex-

tending ERS for Modelling Dynamic Workﬂows in

Event-B. In Engineering of Complex Computer Sys-

tems (ICECCS), 2017 22nd International Conference

on, pages 20–29. IEEE.

Dghaym, D., Trindade, M. G., Butler, M., and Fathabadi,

A. S. (2016). A Graphical Tool for Event Reﬁnement

Structures in Event-B. In International Conference on

Abstract State Machines, Alloy, B, TLA, VDM, and Z,

pages 269–274. Springer.

Fathabadi, A. S., Rezazadeh, A., and Butler, M. (2011).

Applying Atomicity and Model Decomposition to a

Space Craft System in Event-B. In NASA Formal

Methods Symposium, pages 328–342. Springer.

Hoang, T. S. and Abrial, J.-R. (2010). Event-b decompo-

sition for parallel programs. In International Con-

ference on Abstract State Machines, Alloy, B and Z,

pages 319–333. Springer.

Hoang, T. S., Dghaym, D., Snook, C., and Butler, M.

(2017). A composition mechanism for reﬁnement-

based methods. In 2017 22nd International Confer-

ence on Engineering of Complex Computer Systems

(ICECCS), pages 100–109. IEEE.

Hoang, T. S., Iliasov, A., Silva, R. A., and Wei, W. (2011).

A Survey on Event-B Decomposition. Electronic

Communications of the EASST, 46.

Leuschel, M. and Butler, M. (2003). ProB: A Model

Checker for B. In FME, volume 2805, pages 855–

874. Springer.

Sabatier, D. (2016). Using formal proof and B method at

system level for industrial projects. In International

Conference on Reliability, Safety and Security of Rail-

way Systems, pages 20–31. Springer.

Siala, B., Tahar Bhiri, M., Bodeveix, J.-P., and Filali,

M. (2016). Un processus de D

eveloppement Event-

B pour des Applications Distribu

ees. Universit

e de

Franche-Comt

Silva, R., Pascal, C., Hoang, T. S., and Butler, M. (2011).

Decomposition tool for Event-B. Software: Practice

and Experience, 41(2):199–208.

Van Deursen, A., Klint, P., and Visser, J. (2000). Domain-

speciﬁc languages: An annotated bibliography. ACM

Sigplan Notices, 35(6):26–36.

ICSOFT 2019 - 14th International Conference on Software Technologies

286