
Evolutionary Split Range Controller for a Refrigeration System
Gerardo José Amador Soto and Jesús-Antonio Hernandez-Riveros
Universidad Nacional de Colombia, Facultad de Minas, Cra. 80 #65-223, Medellín, Colombia
Keywords: Refrigeration, Adaptive and Learning Systems, Controller Design, Evolutionary Algorithms, Split Range
Control, Multiobjective Control.
Abstract: Every year more than 80 million units of domestic refrigerators are produced worldwide. Hundreds of millions
are used continuously so the impact on electricity is significant. Typical initiatives in energy efficiency for
refrigeration systems are aimed at: a) redesigns b) new materials and c) good use practices. A different
approach in energy efficiency for Vapour Compression Refrigeration Systems (VCRS) is the implementation
of control strategies that directly reduce energy consumption while guaranteeing operating conditions. The
difficulty lies in the multiple energy domains of the system (electric/mechanical/hydraulic/thermal), high
coupling, multiplicity of variables, strong non-linearity and non-stationary regime. This paper focuses on
increasing the energy efficiency of a VCRS with the implementation of an optimal split range and multi-
objective evolutionary control. The evolutionary control is expanded to variable speed compressors and
electronic expansion valves. The effectiveness of the evolutionary method was demonstrated through the
Benchmarking of the IFAC. Now, in the multi-domain model of the VCRS, the MAGO algorithm is applied
to optimally tune a split range controller to achieve a more precise behaviour and multi-objective to save
energy. The cases studied go from traditional control to multivariable and multivariable-multi-objective
control, the results in energy saving are outstanding.
1 INTRODUCTION
Heating, ventilation and air conditioning (HVAC) has
become a technological option that provides many
ways to contribute to humanity, the conservation of
meals through the control of indoor air quality, etc.
Approximately 30% of the total energy in the world
is consumed in HVAC processes, as well as in
refrigerators and water heaters (Jahangeer, Tay and
Raisul Islam, 2011). It is expected that the world's
energy consumption rates will increase by 33% from
2010 to 2030 (Khan, Ryan and Abebe, 2017). In
industry, refrigeration systems consume large
amounts of electricity, where refrigeration can be
responsible for up to 85% of total energy
consumption (depending on the industry sector). To
address this problem, the aim is to improve the
efficiency of the systems (HVAC).
The IIR (Industrial Info Resources) estimates the
number of refrigeration systems in operation
worldwide (Coulomb, Dupon and Pichard, 2015), as
summarized in Figure 1. The total number of HVAC
in operation worldwide is approximately 3 billion,
including 1.5 billion domestic refrigerators.
Annually, more than 80 million units of domestic
refrigerators are produced worldwide (Corte et al.,
2014). Today hundreds of millions are used, therefore
the global impact of the electric power consumption
of these systems is significant. In some countries, the
use of refrigeration systems has become an increasing
need allowing the development of technologies and
equipment with high efficiencies to fulfil this type of
tasks, in addition to the concern to reduce the
environmental impact.
Figure 1: Refrigeration systems in operation worldwide
(Coulomb, Dupon and Pichard, 2015).
Soto, G. and Hernandez-Riveros, J.
Evolutionary Split Range Controller for a Refrigeration System.
DOI: 10.5220/0007930803410351
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 341-351
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
341
This paper presents a proposal to improve the energy
performance of a vapour compression refrigeration
system (VCRS) by means of implementing an
evolutionary control structure. To do this, two case
studies are presented. The first case seeks to improve
the energy performance of the system by controlling
the superheat temperature therefore improving the
thermal cycle of the system. For the second case, the
aim is to directly reduce the energy consumption on
the external power source by implementing different
evolutionary control strategies. In both cases the
temperature behaviour inside the cold chamber is the
direct control goal to satisfy. In the second case,
saving energy from the external power source is
added as a new objective.
This paper is organized as follows. In section 2 the
basics on VCRS is presented. In section 3 the
evolutionary control method is described together
with the optimizing process. In Section 4, the
effectiveness of the evolutionary control method is
verified with two case studies. Conclusions are
presented in section 5
2 VAPOUR COMPRESSION
REFRIGERATION SYSTEMS
The VCRS are the most used among all refrigeration
systems. These systems belong to the general class of
vapour cycles, where the working fluid (refrigerant)
presents phase changes at least during one
compression process. In a VCRS, cooling is obtained
by extracting thermal energy from an insulated space
to reduce its temperature. The input to the system is
in the form of mechanical energy required to run the
compressor. Hence, these systems are also called as
mechanical refrigeration systems. VCRS are
available to suit almost all applications with
refrigeration capacities ranging from few watts to few
megawatts. A wide variety of refrigerants can be used
to suit different applications, capacities etc. The
actual vapour compression cycle is based on Evans-
Perkins cycle, which is also called as reverse Rankine
cycle. In principle, all vapour compression
refrigeration systems are used to remove heat from
one location and transfer it to another by means of
mechanical power (compression).
A VCRS has four main components: a
compressor, a condenser, an expansion device and an
evaporator. In a cycling process, a circulating
refrigerant enters the compressor as saturated vapour
and it is compressed to a higher pressure, resulting in
a higher temperature as a superheated vapour. This
hot compressed vapour is condensed to liquid by
cooling air flowing across a coil carrying away heat
from the system. This high-pressure, high
temperature liquid leaving the condenser when
passing through an expansion valve is cooled and
reduced in pressure. In the evaporator, this low
pressure, low temperature liquid is converted to
vapour, absorbing heat from the refrigerated space
and keeping it cool, to then return to the compressor
and repeat the process. (see Figure 2).
Figure 2: A vapour compression refrigeration cycle scheme
(Bejarano, 2017).
3 EVOLUTIONARY CONTROL
STRATEGIES FOR A VCRS
VCRS refrigeration systems are closed cycles whose
components are connected through several pipes and
valves. This implies a difficulty in controlling these
processes due to some of the characteristics of the
system, such as multiple energy domains (electric /
mechanical / hydraulic / thermal), high coupling and
multiplicity of variables; operating under conditions
of strong non-linearity and in a non-stationary
regime. The inherent complexity of these systems
combined with the implementation of new control
strategies is not a trivial task. To overcome these
complexities, an optimization problem arises, since
the main objective is to find a combination of
controller parameters whose objective function
through maximization or minimization guarantees the
search for solutions that allow to improve the indexes
of efficient performance of the process. Given its
nature as a global optimizer of problems in different
areas of science, engineering and other branches of
knowledge (Fleming and Purshouse, 2002) one way
to address the problem of energy efficiency in VCRS
is through evolutionary algorithms (EA). The EA will
calculate the optimum points of operation of the
process based not only on the achievement of the
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
342

desired production objectives, but also on the
reduction of energy consumption; both objectives are
to be met in this work.
The traditional control system for VCRS is an
on/off strategy applied on the expansion valve. The
highest efficiency of the evaporator is achieved if the
refrigerant at the outlet of the evaporator is saturated
vapour. Through the development of new
technologies such as variable speed compressors or
electronic expansion valves, it is possible to operate
the cycle with a certain degree of superheating of the
refrigerant at the outlet of the evaporator. This
approach requires a multivariable control, which is
very demanding technique in the system modelling
and in the tuning of the controllers. This paper
describes the strategy to tune a PID controller applied
to two actuating elements on the system (compressor
speed and expansion valve) to satisfy the expected
cooling demand and maximizing the energy
efficiency of the VCRS. The applied strategy is based
on the split range control (Smith, 2010). This control
technique is used when a single controller is applied
to manage two final control elements. The PID
controller strives to keep a temperature behaviour in
the cooling chamber manipulating simultaneously the
compressor speed and the expansion valve aperture.
In strong coupled systems, as VCRS, the split range
control could oscillate. The common practice is
configuring the sequencing of the final control
elements, in complementary, exclusive or progressive
modes, defining their range of operation, and
establishing a dead band between the two ranges. But,
here, the split range controller is complete free.
Besides this, the split range controller is tuned for a
multiobjective system, saving energy in the power
source and simultaneously fulfilling the desired
behaviour.
3.1 Multidynamics Algorithm for
Global Optimization (MAGO)
The MAGO (Hernández-Riveros and Ospina, 2010)
is an auto-organized EA that has only two parameters:
number of generations and population size. MAGO
uses statistical operators instead of genetic operators
and through the covariance matrix of the population
in each generation considers the relationships among
variables from the problem. MAGO is a real-value
EA that has shown its capacity solving engineering
problems (Hernández-Riveros Jesús-Antonio and
Cindy, 2018), (Balarezo-Gallardo and Hernández-
Riveros, 2017), (Bejarano et al., 2018). MAGO has
three different autonomous dynamics for evolving the
population, this way getting a larger exploration-
exploitation balance and less likelihood to
convergence to a local optimum are guaranteed.
In each generation, MAGO partitions the
population in three subgroups, each one with its own
evolutionary dynamics. To determine the number of
individuals for each dynamic, the actual population is
observed as in a normal distribution. The average of
the current generation, really a virtual individual, is
calculated on purpose. The number of elements
within one standard deviation of the actual population
conforms the cardinality of the Emergent Dynamics.
The cardinality of the Crowd Dynamics corresponds
to the difference between the first and second
deviation. The number of remaining elements is the
cardinality of the Accidental Dynamics. These
cardinalities change in each generation. Once the
number of individuals within each dynamic is
determined, MAGO proceeds to create individuals
who will make up the new population and so
continuing with the evaluation of new solutions.
From the fitness function evaluation of each
individual, the actual population is reorganized from
the best to the worst individual. The first N1
individuals within one standard deviation of the
actual population compose the Emergent Dynamics.
This N1 individuals obtaining the best values in their
objective function mutate applying the Nelder-Mead
method of numerical derivation, Equation 1.
()
=
()
+
()
×(
(
)
−
(
)
)
(1)
Where
(
)
is the best individual of generation j
and
()
is a randomly selected individual, usually the
same test individual.
()
is a matrix that includes
information about the covariance of the problem
variables, Equation 2.
()
=
()
‖
()
‖
(2)
With
()
is the sample covariance matrix of the
individual population in generation j.
Emergent Dynamics is improved elite making
faster convergence of the algorithm but keeping an
equilibrium between exploitation-exploration among
the best individuals.
The Crowd Dynamics keeps the memory of the
evolution process and is a sampling from a uniform
distribution determined by the upper and lower limits
of the second dispersion and the mean of the current
population, on the hyper-rectangle [LB
(j)
, UB
(j)
].
Equations3 and 4 are vectors with the diagonal of the
population dispersion matrix of the generation j,
described by Equation 5.
Evolutionary Split Range Controller for a Refrigeration System
343
()
=
()
−
(
()
)
(3)
()
=
()
+
(
()
)
(4)
(
)
(
)
=
(
)
(
)
…
(
)
(5)
The Accidental Dynamics are samples from a
uniform distribution throughout the searching space,
similarly as in the initial population. It is smaller in
magnitude but has two basic functions: maintaining
the diversity of the population, and ensuring
numerical stability of the algorithm. Following is the
MAGO pseudo code:
1: j:= 0; Random initial population with a uniform
distribution.
2: Repeat
3: Evaluate each individual with the fitness function.
4: Calculate the population covariance matrix and the
first, second and third dispersion of the population.
5: Calculate cardinalities N1, N2 and N3 of the 3
dynamics.
6: Select the N1 best individuals, move toward the
best of all according to equation 1, make compete
with their parents, and choose the best of them to the
next generation j + 1.
7: Sample N2 individuals from a uniform distribution
in the hyper rectangle [LB(j), UB(j)], and pass to the
next generation j + 1.
8: Sample N3 individuals with a uniform distribution
over the entire search space. Pass to the next
generation j + 1.
9: j = j + 1
10: Until to satisfy a stopping criterion.
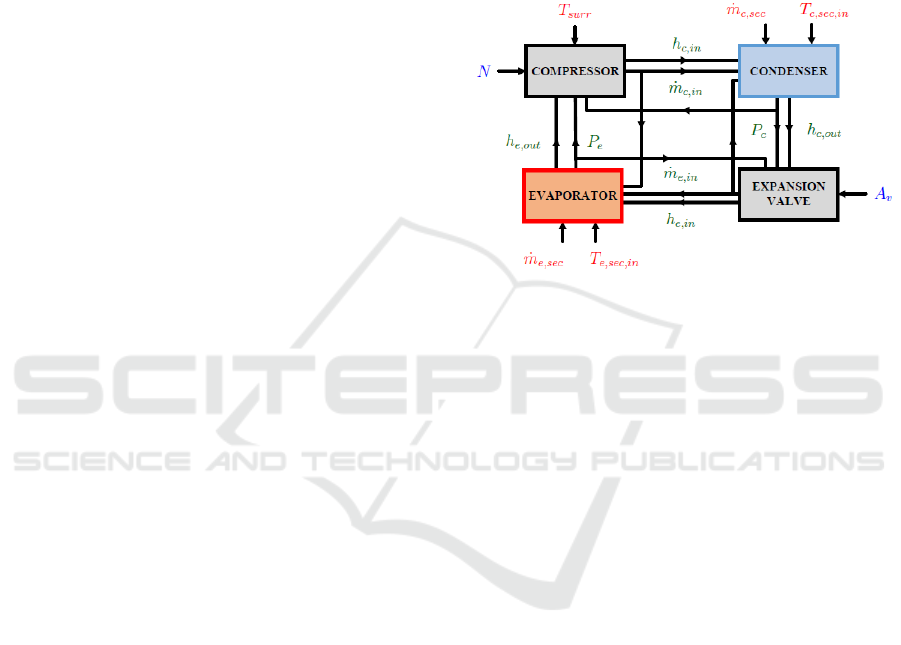
4 SPLIT RANGE CONTROL
STUDY CASES
Next, two cases of application of the MAGO
algorithm in different control structures for a VCRS
to improve its efficiency and control the temperature
inside the cold chamber are presented. The first study
case corresponds to the IFAC benchmark which only
represents the thermodynamic behaviour of the
VCRC. This case is presented to demonstrate the
effectiveness of the evolutionary control strategy
using the MAGO. The second case study corresponds
to a complete VCRS, whose entire model includes
multiple energy domains (electric, mechanical,
hydraulic and thermal). Three multivariable and
multi-objective control strategies are proposed.
Besides to the temperature control inside the cooling
chamber, an additional objective is added, that is, the
energy saving on the power source of the VCRS.
4.1 Case 1: Benchmark IFAC (Only
Thermal Model)
The model for the Benchmark (Bejarano et al., 2018)
is a refrigeration cycle of one compression stage and
one load. This model cannot be modified. The main
features of the model are:
1) Relatively low complexity, while
faithfully capturing the dynamics of the essential
plant and its non-linearities in a wide range of
operation.
2) Oriented to control because the
manipulated variables, the controlled variables and
the significant disturbances are shown.
3) The model is realistic since restrictions are
considered in the manipulated variables.
Figure 3: Discrete decentralized controllers included by
default in the refrigeration control benchmarking (Bejarano
et al., 2018).
Table 1: Benchmark control strategy.
Control Objectives
1. Reach a desire value of outlet temperature of
the evaporator secondary flux by manipulating
the opening of the expansion device.
2. Reach a desire value of superheat temperature
by manipulating the compressors speed.
Control Variables
Output variables
y1: outlet temperature of the evaporator
secondary flux (
,,
)
y2: superheat temperature (
)
Controlled variables
u1: Expansion device opening (
)
u2: Compressors speed ()
Elements
System: VCRC
Actuator 1: Expansion Valve.
Actuator 2: Compressor.
Mono Objective Optimization Problem
Minimization of the controlled variables error
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
344
The multivariable control structure included by
default in the PID Benchmark 2018 consist of a
discrete decentralized control scheme (Figure 3) in
which the variables to control are the outlet
temperature of the evaporator secondary flux and the
degree of superheating (Table 1). The control system
is designed to obtain these two variables, tracking
their references as efficiently as possible, in the
presence of disturbances. The coefficient of
performance is used as an indicator of steady-
state quality.
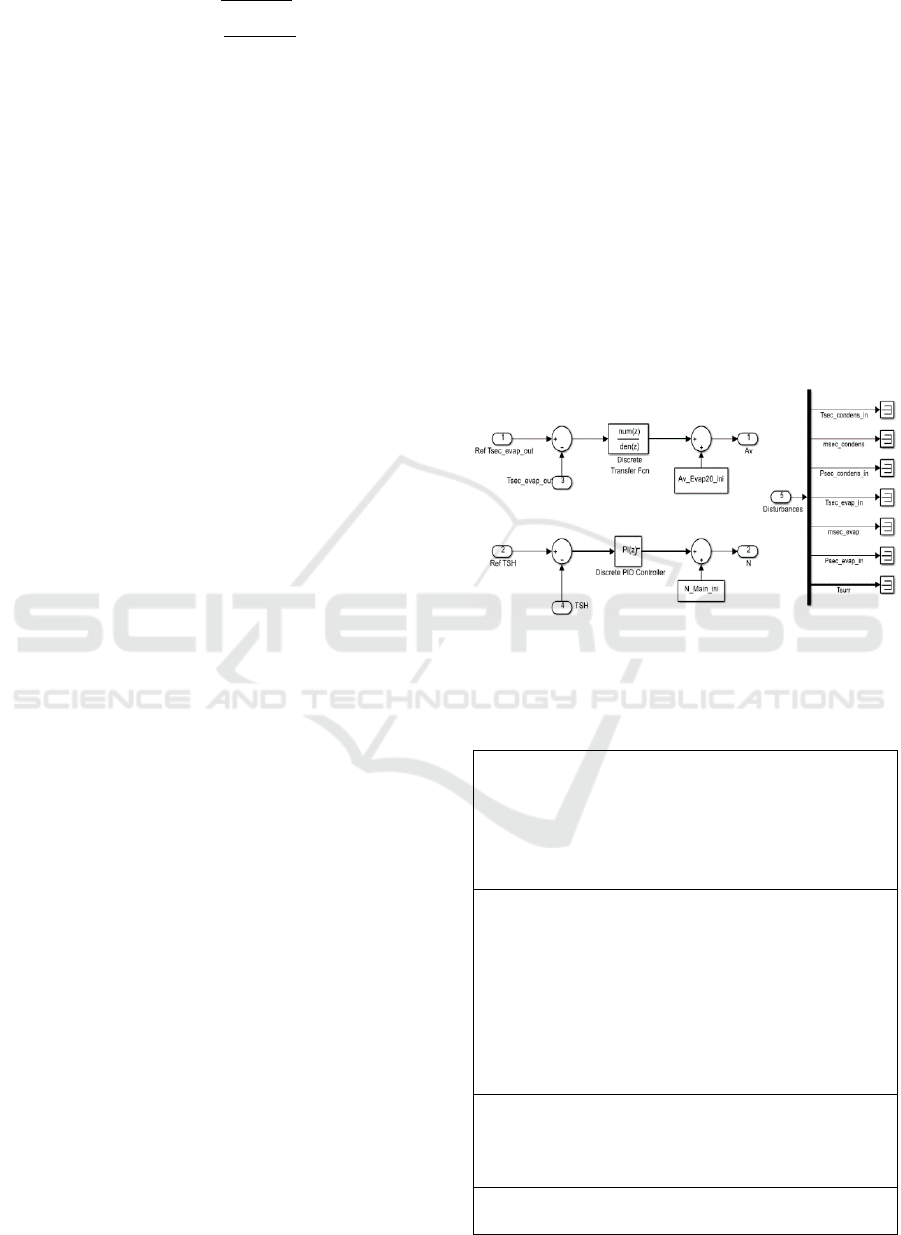
Tuning Procedure of the Discrete Controllers and
Optimization of the IFAC Benchmark’s VCRS.
As can be seen in Figure 4 the VCRS is composed of
two controllers; the first one is a discrete transfer
function that acts on the aperture of the expansion
valve. The second is a discrete PI controller that
corresponds to the compressor’s speed.
Figure 4: Coupled evolutionary tuning procedure for the
Benchmark IFAC 2018.
Table 2 shows the input data for the MAGO algorithm.
This mono-objective optimization approach seeks to
minimize the error between the reference and output signals
of the control variables.
Table 2: Input data for MAGO.
Data Values
Individuals 20
Generations 10
Upper bound [-1 0 1 -1.9 1 2.7 2.7]
Lower bound [-1.3 -0.6 0.7 -2 0.9 0.4 0.5]
Table 3 presents the obtained parameters for each
controller for the benchmarking applying MAGO.
Table 3: Parameters of each controller applying MAGO.
Expansion Valve
(Controller1)
Compressor
(Controller 2)
Benchmark
C1
−1,0136 − 0,0626 0,9988
1 − 1,9853 0,9853
P: 0,4200
I: 0.9524
MAGO
C2
1,1039 − 0,2901 0,8961
1 − 1,9185 0,9184
P: 1,2829
I: 1,6916
The results obtained for the temperature of the
secondary flux in the evaporator, Te sec out, and the
temperature of superheating, Tsh, are presented in
Figure 5 and Figure 6. The C1 controller corresponds
to the Benchmark and C2 to the results with MAGO.
The MAGO was implemented with a decentralized
MIMO control structure consisting of two discrete
controllers (a transfer function and a PI). The MAGO,
independent of the structure and domain of the
controller, finds the parameters in the function of
achieving both control objectives. As can be seen in
Figure 5 the optimal tuning method of controllers
applying the MAGO evolutionary strategy manages
to reach the reference values, achieving a behaviour
like the Benchmark's default strategy but improving
in the handling of temperature variation. The facility
to implement evolutionary tuning through the MAGO
algorithm in a complex system is highlighted, whose
model was not available to adapt it to the control
strategy that was to be applied.
Figure 5: Controlled variables.
Figure 6: Manipulated variables.
4.2 Case 2: Complete VCRS
(Multi-domain Energy based
Model)
The multi-domain energy-based model for a complete
VCRS is presented in Figure 9. The bond-graph (BG)
method is a graphical modelling approach in which
energy ports are connected by bonds that specify the
transfer of energy between system components.
Power, the rate of energy transport between
Evolutionary Split Range Controller for a Refrigeration System
345
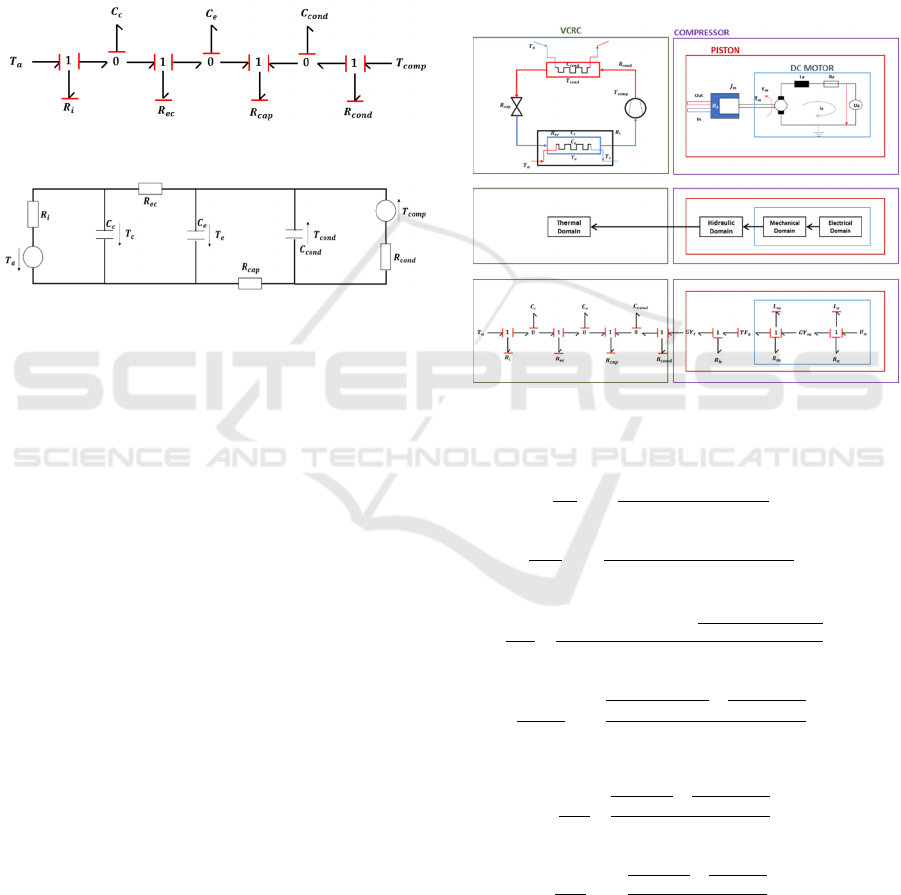
components, is the universal currency of physical
systems (Gawthrop and Bevan, 2007). The main
advantage of the BG technique lies in its ability to
determine the energy consumption of a system, in
general, as well as its components, which is of vital
relevance for this second case study. Another
advantage is that the mono-domain models generated
from the BG have a modular coupling facility (unified
base) which can result in a coupled multi-domain
model.
Figure 7: BG base model of a VCRC (thermal behaviour).
Figure 8: Base model of a VCRS. Adapted from (Schné,
Jaskó and Simon, 2015).
The final model arises from the modular union of
the BG base model Figure 7 that corresponds only to
the thermal dynamics of the VCRC whose approach
was developed by (Schné, Jaskó and Simon, 2015)
Figure 8. The construction of the step-by-step model
is detailed in (Amador Soto, 2019).
From the base model described above
representing the dynamics of a VCRS, there is a need
to detail with greater precision the action of the
compressor (simplified in the base model by its
output temperature Tcomp). The reason for this is that
the impact of the compression action on the cooling
system is usually known, but it is not its direct energy
consumption seen from the power source. That is why
once having the BG representation of the thermal
cycle it is necessary to have also the representation
for the compressor and finally joint both models,
which does not imply a problem in the use of the BG
technique due to its modular nature (see Figure 9).
The system of coupled differential equations (6-11)
emerges from of the BG model. The state variables
are
: Armature current,
: Motor rotational
speed,
: Hydraulic flow,
: Temperature in
the condenser,
: Temperature in the evaporator,
: Temperature inside the cold chamber.
4.2.1 On-off Control Baseline
To control the temperature inside the refrigerator
there is thermostat, whose sensor is connected to the
evaporator, Figure 10. The round knob inside a
refrigerator compartment can do the thermostat
setting. When the set temperature is reached inside
the refrigerator, the thermostat stops the electric
supply to the compressor and the compressor stops.
When the temperature falls below certain level it
restarts the supply to the compressor.
Figure 9: BG representation for the complete energy-based
model of the VCRS.
=−
∗
−
+
∗
(6)
=−
∗
−
∗
+
∗
(7)
=
∗
−
∗
+
−
∗
(8)
=−
−
∗
+
+
(9)
=
−
−
+
(10)
=−
−
+
−
(11)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
346

Figure 10: Conventional ON-OFF VCRS basic scheme.
While conventional on-off control commonly has
a fluctuating behaviour (Figure 11), other control
options have arisen due to the growth of the
electronics field. Variable speed compressors and
electronic expansion valves have gradually replaced
older single speed compressors and thermostatic
expansion valves, respectively. Such new
components allow the development of smarter control
strategies, not only to save energy but also to reduce
fluctuations in the controlled variables and therefore
achieve a more accurate control (Bejarano et al.,
2018). In this sense, in this document continuous
controllers are implemented for temperature control
and simultaneously reduce energy consumption.
Figure 11: Typical thermal behaviour for a conventional
VCRS by ON-OFF control.
4.2.2 Continuous Control Strategies
A multivariable SISO and MISO control structures
are presented, both consisting on a continuous
centralized control scheme in which the variable to
control is the outlet temperature of the cold chamber
while at the same time reducing the energy
consumption from the power source.
Tuning Procedure of the Energy-based Complete
VCRS Model.
Three different control strategies are applied.
• First Control Strategy:
Centralized control SISO (manipulated Variable:
aperture of the expansion valve). See Table 5, Table
6, Figure 12, Figure 13, and Figure 14.
• Second Control Strategy:
Centralized control SISO (manipulated Variable:
compressor speed). See Table 7, Table 8, Figure 15,
Figure 16, and Figure 17.
• Third Control Strategy:
Centralized control MISO (manipulated Variables:
compressor speed + aperture of the expansion valve).
See Table 9, Table 10, Figure 18, Figure 19, Figure
20.
In all cases the MAGO runs with the same set of
parameters of the algorithm, Table 4. The operation
of the actuator opening the expansion valve goes from
0% to 100%, and the compressor speed goes from 0
to 1200 RPM. For the evolutionary tuning of the split
range controller, there is not sequencing, restrictions
on the range nor dead band among the two actuators.
Table 4: Input data for MAGO.
Data Values
Individuals 50
Generations 25
Upper bound [10 10 10]
Lower bound [-10 -10 -10]
Table 5: First, control strategy (by expansion valve
aperture).
Control objective
A set of stable temperature inside the cold chamber
(2, 1, 0 -1 ℃)
Energy objetive
Reduce the energy consumption of the power
source of the system.
Control variables (SISO) Elements
Output variable (y):
Temperature inside the cold
chamber (
)
Controlled variable (u):
Expansion device opening
(
)
System:
CompleteVCRC
Actuator:
Expansion Valve.
Multi objective optimization problem
1. Minimization of the controlled variable error
2. Minimization power source energy
Evolutionary Split Range Controller for a Refrigeration System
347

Table 6: Obtained controller parameters applying MAGO.
Expansion Valve (PID
Controller)
Kp: 0.0959
Ti: 1.8297
Td: 4.3237
Figure 12: VCRC intervention applying the first control
strategy for temperature control and power source’s energy
reduction.
Figure 13: Controlled variable for the first control strategy.
Figure 14: Manipulated variable for the first control
strategy.
Table 7: Second control strategy (by compressor speed).
Control Objective
A set of stable temperature inside the cold chamber
(2, 1, 0 -1 ℃).
Energy Objective
Reduce the energy consumption on the power
source of the system.
Control Variables (SISO) Elements
Output variable (y):
Temperature inside the cold
chamber (
)
Controlled variable (u):
Compressors speed (
)
System:
CompleteVCRC
Actuador:
Compressor.
Multi Objective Optimization Problem
1. Minimization of the controlled variable error
2. Minimization power source energy
Table 8: Obtained controller parameters applying MAGO.
Compressor
(PID Controller)
Kp: 0.0965
Ti: 2.993
Td: 1.5037
Figure 15: VCRC intervention with the second control
strategy for temperature control and power source’s energy
reduction.
Figure 16: Controlled variable for the second control
strategy.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
348

Figure 17: Manipulated variable for the second control
strategy.
Finally, the energy consumption corresponding to
each control strategy applied to the system is
presented in Table 11.
Table 9: Third control strategy (by expansion device
aperture + compressor speed).
Control Objective
A set of stable temperature inside the cold chamber
(2, 1, 0 -1 ℃).
Energy Objective
Reduce the energy consumption of the power
source of the system.
Control Variables (MISO) Elements
Output variable (y):
Temperature inside the cold
chamber (
)
Controlled variable (u1):
Expansion device opening
(
)
Controlled variable (u2):
Compressors speed (
)
System:
CompleteVCRC
Actuador1:
Expansion device
Actuador2:
Compressor.
Multi Objective Optimization Problem
1. Minimization of the controlled variable error
2. Minimization Power Source energy
Table 10: Obtained controller parameters applying MAGO.
Expansion Valve
(PID Controller 1)
+
Compressor
(PID Controller 2)
Kp: 0.7096
Ti: 4.295
Td: -1.7924
Figure 18: VCRC intervention with the third control
strategy for temperature control and power source’s energy
reduction.
Table 11: Summary energy consumption of control
strategies applying MAGO.
Figure 19: Controlled variable for the third control strategy.
Figure 20: Manipulated variables for the third control
strategy.
Comparing results between the three proposed
control strategies, it was found that, by controlling the
speed of the compressor, applying a voltage profile, it
is possible to obtain better results in reducing energy
consumption. On the other hand, manipulating the
expansion device improves the behaviour of the
controlled variable (temperature), reaching the
reference values in less time. However, changing the
Evolutionary Split Range Controller for a Refrigeration System
349

opening value of the expansion device alters the
demands on the compressor, increasing the motor
current while applying a fixed voltage. This is
reflected in an increase in energy consumption. For
its part, the third strategy combines the benefits of
both previous strategies, so it is possible to achieve
good results in reducing energy consumption and
good behaviour of the controlled variable, quickly
reaching the reference values without increasing the
demand of the compressor.
4 CONCLUSIONS
The proposed evolutionary control approach was
applied for two different developments in VCRS
(case study 1 - only the thermal part, and case study 2
- including the electrical, rotational, hydraulic and
thermal parts) under conditions of multivariability,
high coupling, non-linearity and restrictions, among
others. The results obtained for both study cases show
that intervention inside the refrigeration system by
means of applying control structures can achieved
energy savings for the thermal circuit and for the
whole system. The MAGO algorithm achieves
remarkable results for the different control strategies,
independently of both the structure and the domain of
the controller to be tuned.
For the first study case, we use a predefined model
formulated for control purpose (by transfer function)
that tries to reach the temperature behaviour
improving indirectly the energy performance of the
system. On the other hand, case study 2 illustrates the
use of a single unified energy based model (by
differential equations of the whole system) to reduce
directly the source's energy consumption and at the
same time achieving the desired temperature
behaviour for the system using three different control
strategies. Evolutionary tuning was applied to the two
different systems without additional procedures. The
split range controller was expanded to multivariable
and after to multiobjective purposes. This
evolutionary control method can be implemented
without any inconvenience in developments for
control of cooling systems of multiple loads and
stages.
Savings and control opportunities were identified
according to the strategy (MISO or MIMO). The
more variables in the process are controlled, the
greater energy savings are obtained.
Future work is to combine the advantages of the
manipulation of the compressor speed and the
opening of the expansion valve with two independent
but coupled controllers. A greater range of solutions
is foreseen to improve the savings in energy
consumption while satisfying the expected cooling
demand.
REFERENCES
Amador Soto, G. J. (2019) Control de Procesos
Industriales con Minimización de Consumo Energetico.
Universidad Nacional de Colombia. Available at:
http://bdigital.unal.edu.co/71599/.
Balarezo-Gallardo, S.-F. and Hernández-Riveros, J. A.
(2017) “Evolutionary Parameter Estimation of Coupled
Non-linear Oscillators,” in: Solano, A. and Ordoñez, H.
(eds.) Advances in Computing. Cham: Springer
International Publishing, pp. 457–471.
Bejarano, G. (2017) Optimization and multivariable control
of refrigeration systems. Universidad de Sevilla.
Available at: https://idus.us.es/xmlui/handle/11441/
63847 (Accessed: February 12, 2019).
Bejarano, G. et al. (2018) “BENCHMARK PID 2018
Benchmark for PID control of refrigeration systems
based on vapour compression,” pp. 1–20. Available at:
http://servidor.dia.uned.es/~fmorilla/benchmarkPID20
18/.
Corte, E. et al. (2014) “Sistemas de refrigeración doméstica
- estado del arte de las mejoras en la eficiencia
energética,” Revista de la Facultad de Ciencias
Químicas de la Universidad de Cuenca Ecuador, 9, pp.
19–40. Available at: https://publicaciones.ucuenca.
edu.ec/ojs/ index.php/quimica/article/view/253.
Coulomb, D., Dupon, J. L. and Pichard, A. (2015) “The
Role of Refrigeration in the Global Economy,” The
29th Informatory Note on Refrigeration Technologies,
29(November, 2015), p. 16.
Fleming, P. and Purshouse, R. (2002) “Evolutionary
algorithms in control systems engineering: a survey,”
Control Engineering Practice, 10(11), pp. 1223–1241.
doi: 10.1016/S0967-0661(02)00081-3.
Gawthrop, P. J. and Bevan, G. P. (2007) “Bond-Graph
Modeling: A tutorial introduction for control
engineers,” IEEE Control Systems, 27(2), pp. 24–45.
doi: 10.1109/MCS.2007.338279.
Hernández-Riveros, J. and Ospina, J. D. (2010) “A multi
dynamics algorithm for global optimization,”
Mathematical and Computer Modelling, 52(7–8), pp.
1271–1278. doi: 10.1016/j.mcm.2010.03.024.
Hernández-Riveros Jesús-Antonio, Carmona Cindy, Urrea
Q. Jorge. (2018) “Evolutionary Control Systems,” (in:
Incorporating Nature-Inspired Paradigms). doi:
10.4018/978-1-5225-5020-4.
Jahangeer, K. A., Tay, A. A. O. and Raisul Islam, M. (2011)
“Numerical investigation of transfer coefficients of an
evaporatively-cooled condenser,” Applied Thermal
Engineering. Elsevier Ltd, 31(10), pp. 1655–1663. doi:
10.1016/j.applthermaleng.2011.02.007.
Khan, K. H., Ryan, C. and Abebe, E. (2017) “Optimizing
HVAC Energy Usage in Industrial Processes by
Scheduling Based on Weather Data,” IEEE Access, 5,
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
350

pp. 11228–11235. doi: 10.1109/ACCESS.2017.2715
239.
Schné, T., Jaskó, S. and Simon, G. (2015) “Dynamic
models of a home refrigerator,” MACRo 2015- 5th
International Conference on Recent Achievements in
Mechatronics, Automation, Computer Science and
Robotics, pp. 105–114. doi: 10.1515/macro-2015-0010.
Smith, C. (2010) Advanced Process Control: Beyond Single
Loop Control. Wiley.
Evolutionary Split Range Controller for a Refrigeration System
351
