
Computation of Trajectory Sensitivities with Respect to Control and
Implementation in PSAT
Ramij Raja Hossain
a
and Ratnesh Kumar
b
Department of Electrical and Computer Engineering, Iowa State University, Ames, Iowa 50011, U.S.A.
Keywords:
Power System, PSAT, Static VAR Compensator, Trajectory Sensitivity wrt Control, Under Load Tap Changer.
Abstract:
Trajectory sensitivity based analysis is widely regarded as an important tool for real time protection scheme
of power systems. Model Predictive Control (MPC) for voltage instability is one such protection scheme
which computes a sequence of control actions depending upon the trajectory behaviour of the dynamics of the
power systems. Thus, computation of trajectory sensitivities with respect to control input can be an integral
part for designing a real-time protection scheme. In this context, it is important to note that for the state-
of-the-art Power System Analysis Tool (PSAT)(Milano, 2005), (Milano et al., 2008), while it is relatively
easy to compute the trajectory sensitivities with respect to any system variables, the computation of trajectory
sensitivities with respect to control inputs is not explicitly supported. This paper presents a method to extend
the functionality of PSAT to also compute the trajectory sensitivities with respect to control inputs, which
ultimately forms the basis for real-time protection schemes such as MPC. The proposed method is validated
using direct time-domain simulation results.
1 INTRODUCTION
In today’s deregulated market scenario, power utili-
ties are compelled to do trade-off between cost and
design, which results in most power systems operat-
ing close to their capacity, making them susceptible to
disturbances. To cope with this as well as the ever in-
creasing load demand and meet customer satisfaction
index, it is imperative to adopt measures to avert any
large scale shutdown following the occurrence of se-
vere fault and disturbances. Thus a basic requirement
is to set up certain real time protection schemes which
can take necessary control actions upon detecting any
potential instability in the system.
Model Predictive Control (MPC) is a promising
control strategy for tackling voltage instability fol-
lowing contingencies in a power system. Briefly,
MPC works on the principle of receding horizon con-
trol and computes optimal control strategies depend-
ing upon the dynamics of the system that can be repre-
sented by the trajectories of its states. Trajectory sen-
sitivity provides a valuable insight into the behavior
of a dynamic system: It estimates how the system tra-
jectory would change when there is a slight change in
a
https://orcid.org/0000-0003-0224-7245
b
https://orcid.org/0000-0003-3974-5790
input, state, or output, which would not be otherwise
obvious only from its nominal trajectory (Hiskens and
Pai, 2000).
In (Zima and Andersson, 2003), MPC based con-
trol using trajectory sensitivity is discussed but only
a preliminary idea of calculating trajectory sensitivity
is given. Trajectory sensitivity based Model Predic-
tive Control protection scheme for power systems is
presented in (Jin et al., 2010) and (Jin et al., 2007).
These papers utilize shunt capacitors, i.e., reactive
power compensation technique for control purposes
and determine capacitor switching sequence by min-
imizing an objective function which includes the tra-
jectory deviation of voltage and cost of control. Tra-
jectory sensitivities are used to estimate the effect of
controls on the voltage behavior in a linearized man-
ner. An MPC based voltage control strategy is also
proposed in (Hiskens and Gong, 2005), where the ob-
jective is to find optimized control of load depending
upon the trajectory behavior of bus voltages.
Trajectory sensitivity based analysis for nonlinear
and hybrid systems, such as power systems, is well
studied in control domain. According to (Hiskens and
Pai, 2000), the approach is based upon linearizing the
system around a nominal trajectory rather than around
an equilibrium point. It is therefore possible to deter-
mine directly the change in a trajectory due to (small)
752
Hossain, R. and Kumar, R.
Computation of Trajectory Sensitivities with Respect to Control and Implementation in PSAT.
DOI: 10.5220/0007931307520759
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 752-759
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

changes in initial conditions, parameters, and/or con-
trols. Trajectory sensitivities have a potential for en-
abling both preventive and emergency control. A sur-
vey on application of trajectory sensitivity in power
system is provided in (Tang and McCalley, 2013), and
importance is given to the accuracy refinement of the
calculation. In (Ferreira et al., 2004) some basics of
trajectory sensitivity based analysis for transient sta-
bility, dynamic voltage stability and influence of load
shedding are mentioned, and different case studies are
shown. These papers relied on the software package
EUROSTAG for their study. In (Ghosh et al., 2004),
trajectory sensitivity analysis is used in determining
stable operating range of TCSC and in (Chatterjee
and Ghosh, 2007), trajectory sensitivity analysis is
used to study the effect of the FACTs controller on
the transient stability; in both of these papers, sensi-
tivity with respect to system parameters is calculated
numerically using a much simpler method than ana-
lytical computation. (Nasri et al., 2014), (Nasri et al.,
2013b), and (Nasri et al., 2013a) has presented trajec-
tory sensitivity based analysis for optimal location of
series, shunt capacitors, and FACTs devices respec-
tively; these papers calculated trajectory sensitivities
of rotor angles with respect to line reactance and reac-
tive power injected at different nodes, and for simula-
tion the commercial software SIMPOWER is used. In
(Abdelsalam et al., 2017), trajectory sensitivity with
respect to a system parameter is used to design the
LQR based voltage control of wind generation but
detailed architecture of trajectory sensitivity compu-
tation is not discussed. The theory of calculating tra-
jectory sensitivities is comprehensively described in
the papers (Hiskens and Pai, 2000), (Laufenberg and
Pai, 1997) and (Hiskens and Pai, 2002), and there are
other works where this derivation of sensitivities are
used for designing of different control strategies.
The main contribution of our paper is to calculate
trajectory sensitivities with respect to control input in
PSAT/MATLAB platform. The computed trajectory
sensitivity values are validated with simulation results
for an example run of a power system.
The rest of the paper is organized in 5 sections.
First, the background on basics of trajectory sensitiv-
ity calculation is presented, and the issues in comput-
ing trajectory sensitivity in PSAT framework with re-
spect to control inputs are discussed. Next, the pro-
posed solution of the problem is presented. This is
followed by the implementation details and the ex-
tension to PSAT, together with the validation results.
Finally, the paper is concluded.
2 BACKGROUND
2.1 Trajectory Sensitivity Overview
A power system can be modeled using Differential
Algebraic Equations (DAEs) of the form:
˙x = f (x,y,u), (1)
0 = g(x,y,u), (2)
where x is a vector containing dynamic state variables,
y is a vector of algebraic variables, and u is a vec-
tor of control input variables. The solution of these
two equations provide the trajectories of state and al-
gebraic variables for a given initial state vector, and
control trajectory. To device the impact of changing
control actions on system behavior, a main interest is
to determine the effect of change of control input u on
state variables x and algebraic variables y. From this
point of view the derivation of trajectory sensitivities
of state and algebraic variable with respect to control
becomes important.
Trajectory Sensitivity of x and y with respect to
u is defined as the rate of change of x and y around
the nominal trajectory with respect to an infinitesimal
change in control input u. Then, using Taylor series
approximation, the trajectory sensitivity of x and y
with respect to u is given by their 1st-order approx-
imations, x
u
(t) =
∂x(t)
∂u
and y
u
(t) =
∂y(t)
∂u
respectively.
The dynamics of x
u
and y
u
can be obtained by dif-
ferentiating equations (1) & (2) with respect to control
input u, resulting in,
˙x
u
(t) = f
x
x
u
(t) + f
y
y
u
(t) + f
u
, (3)
0 = g
x
x
u
(t) + g
y
y
u
(t) + g
u
, (4)
Note the Jacobian matrices f
x
, f
y
, g
x
, g
y
, f
u
, g
u
are
all time varying. Thus, the calculation of trajectory
sensitivities x
u
and y
u
requires the knowledge of all
the above 6 Jacobians at each sampling instant, along
with a time domain simulation of equations (3) & (4).
More details on trajectory sensitivity can be found in
(Hiskens and Pai, 2000) and (Hiskens and Pai, 2002).
2.2 MPC for Voltage Stability
In general, Model Predictive Control (MPC) refers
to a class of algorithms that compute a sequence of
control variable adjustments in order to optimize the
future behavior of a plant. The principle of MPC is
graphically depicted in Figure 1 (Jin et al., 2010),
which shows that the control is recomputed at each
sample instant for the remaining control horizon by
using a model prediction over a prediction horizon.
The latest measurements are used to better estimate
Computation of Trajectory Sensitivities with Respect to Control and Implementation in PSAT
753

the current state and thereby improving the predic-
tion, and the trajectory sensitivities with respect to the
control are used for quickly estimating the trajectories
in the prediction horizon. Only the computed control
of the first instant is applied, and then the process is
repeated at the next sample instant.
In context of power systems, MPC can be used
to exercise optimal control action upon any severe
disturbance, following which different complications
may arise; one most common occurrences is the drop
in bus voltages. To mitigate this risk of voltage in-
stability, the two major techniques are: a) Reactive
Power Compensation by switching on shunt capaci-
tors and b) Under Load Tap-changer (ULTC) Control.
Apart from these, in some severe contingencies, ex-
ercising load-shedding becomes essential to maintain
the overall stability of the network.
Figure 1: Principle of MPC.
3 PROPOSED EXTENSIONS TO
PSAT TO ENABLE
TRAJECTORY SENSITIVITY
COMPUTATION
3.1 Enhancing PSAT to Store the
Jacobians that It Already Computes
Equations (3) & (4) explicitly imply that for calcula-
tion of trajectory sensitivities x
u
and y
u
, the knowl-
edge of f
x
, f
y
, g
x
, g
y
, f
u
, g
u
is required at each time
instants. Out of these 6, the first 4 Jacobians, f
x
, f
y
,
g
x
, g
y
are the components of an unreduced Jacobian
J =
f
x
f
y
g
x
g
y
, which are calculated by PSAT at
each time instant in course of the time domain simu-
lation of any system. However, due to a limited ca-
pacity of storage, PSAT stores f
x
, f
y
, g
x
, g
y
only for
the final time instant. We implemented a slight addi-
tional coding within PSAT in its time domain integra-
tion subroutine to alleviate this problem.
3.2 Our Approach to Computing
Trajectory Sensitivities wrt Controls
One significant limitation of PSAT is that during time
domain simulation, the values of the Jacobians f
u
, g
u
are not computed. In particular, if shunt capacitors are
to be used as a control input, computing the values of
f
u
and g
u
during the time domain simulation would
require major changes in the original PSAT code. On
the other hand, in case of Under Load Tap-changer,
its model in PSAT has its own state variable, and that
can be used to compute f
u
and g
u
by treating con-
trols as additional state variables with zero-dynamics,
as explained Section 3.3. Once all 6 Jacobians are
obtained, the trajectory sensitivities x
u
and y
u
can be
obtained by solving equations (3) & (4) numerically,
as also explained below.
We first propose to compute the Jacobians f
u
and
g
u
by treating u as a state variable, having zero-
dynamics ( ˙u = 0), so it remains held constant at its
current value, and the trajectory sensitivity with re-
spect to control around that nominal u gets computed.
A similar idea was proposed in (Hiskens and Pai,
2002) for computing trajectory sensitivity with re-
spect to a parameter (rather control).
With the control variables augmented as part of
the state variables, the equations (1) & (2) also get
augmented:
˙x = f (x,y,u) (5)
˙u = 0 (6)
0 = g(x,y,u) (7)
We denote the control-augmented state variables
as, x =
x
u
, algebraic variables as y, and note the
dimensions of the various variables as: x ∈ R
n
,y ∈
R
m
,u ∈ R
p
.
Combining equations (5), (6) & (7) we have,
˙
x =
˙x
˙u
=
f (x,y,u)
0
= f (x,y) (8)
0 = g(¯x,y) (9)
Differentiating equations (8) & (9) with respect to
control input u, results in,
˙
x
u
(t) = f
x
x
u
(t) + f
y
y
u
(t) (10)
0 = g
x
x
u
(t) + g
y
y
u
(t) (11)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
754

Note f
x
=
f
x
f
u
0 0
, f
y
=
f
y
0
, and g
x
=
g
x
g
u
. As discussed earlier, with the above
control-augmented states, in PSAT at each time in-
stant the Jacobians f
x
, f
y
, g
x
and g
y
are calculated
in course of the time domain simulation from which
we can extract the desired f
u
and g
u
from
¯
f
¯x
and g
¯x
respectively.
Once the Jacobians
¯
f
¯x
,
¯
f
y
,g
¯x
,g
y
are obtained from
PSAT, equations (10) and (11) can be numerically
solved to obtain the required trajectory sensitivities x
u
and y
u
. At an initial time t
0
, ¯x
u
(t
0
)=
x
u
(t
0
)
u
u
(t
0
)
is a
(n + p) × p matrix where x
u
(t
0
) = 0
n×p
and u
u
(t
0
) =
I
p×p
, so that ¯x
u
(t
0
)=
0
n×p
I
p×p
. This is because a
change in any control only changes that control with
rate 1, whereas none of the initial states or the other
controls are affected by it. Then the initial value of
y
u
(t
0
) can be obtained using equation (11), resulting
in:
y
u
(t
0
) = −g
y
(t
0
)
−1
g
x
(t
0
)x
u
(t
0
) (12)
Now, using trapezoidal integration, x
u
and y
u
in
equations (10) and (11) can be approximated as,
h
2
f
k+1
x
− I
h
2
f
k+1
y
g
k+1
x
g
k+1
y
!
x
k+1
u
y
k+1
u
=
h
2
(− f
k
x
x
k
u
− f
k
y
y
k
u
)
0
(13)
In equation (13), the superscript k is used for the vari-
able values at that kth sampling instant. Thus starting
from t
0
, by solving the linear equation (13) at each
time instant, trajectory sensitivities for all state and
algebraic variables with respect to control input, x
k
u
and y
k
u
, can be calculated at each sample instant k.
3.3 Case of SVC Control
The modeling of control input as a new state vari-
able is not straightforward in PSAT. Here, we first
discuss the modeling for shunt capacitors, which we
have been able to do by utilizing the TYPE-1 Static
VAR Compensator (SVC) model in PSAT (Milano,
2005). The SVC model itself is shown in Figure 2.
Equations (14) & (15) provide the DAEs repre-
senting this model,
˙
b
SVC
=
K
r
(V
re f
−V ) − b
SVC
T
r
(14)
Q = b
SVC
V
2
(15)
From equations (14) & (15), it is clear that this TYPE-
1 SVC itself has a dynamic and can generate output
Figure 2: SVC TYPE-1 block.
controls b
SVC
to mitigate the risk of voltage collapse.
Here, it is important to mention one specific feature of
this model, that the regulator has an anti-windup lim-
iter, so the output susceptance b
SVC
saturates if one
of the maximum or minimum limits is reached. Ba-
sically, if the output b
SVC
is lower than b
min
(resp.,
higher than b
max
), then the output will take the value
b
min
(resp., b
max
).
In order to make this device behave like an ordi-
nary shunt capacitor, we make an appropriate selec-
tion of the parameters of TYPE-1 SVC model. In
doing this, we choose the time-constant T
r
very high
whereas make the gain K
r
very low, so
˙
b
SVC
is always
near 0 and consequently b
SVC
always takes the con-
stant value b
min
. Thus treating u as a state variable
in TYPE-1 SVC model, and setting large T
r
, small
K
r
, and b
min
, we are able to ensure u has zero rate
of change, and remains initialized at b
min
, maintain-
ing that constant value. The desired f
u
& g
u
are then
extracted from the Jacobian J of controls-augmented
states as explained in the previous section and hence,
trajectory sensitivities x
u
and y
u
can be calculated.
Figure 3: WECC 3-generator 9-bus test system.
To validate that our above scheme works, a 9-bus
3-generator WECC system of Figure 3 was simulated
in PSAT. We considered a three-phase fault at bus 5 at
t = 1.0 second, which gets cleared at t = 1.15 seconds
by the tripping of the line between buses 4 and 5. The
system is comprised of shunt capacitors at buses 5,
7, and 8, each having 0.01 initial value. To compute
the trajectory sensitivities with respect to these shunt
capacitors around the said nominal values, those are
replaced by SVC blocks with large T
r
and small K
r
.
Computation of Trajectory Sensitivities with Respect to Control and Implementation in PSAT
755

The parameters of the SVC block are chosen as, V
re f
=
1 p.u.; b
max
= 0.8 p.u.; b
min
= 0.01 p.u.; K
r
= 10
−7
; T
r
= 10
5
sec. Figure 4 & 5 confirm that the thus mod-
eled SVC blocks replicate the behaviors of the shunt
capacitors. Also, the value of state variables b
SVC
ob-
tained from PSAT database is constant equaling 0.01,
demonstrating that the output of SVC block remains
fixed at b
min
.
Figure 4: Plot of Voltages with Shunt block.
Figure 5: Plot of Voltages with SVC block modeled like
Shunt block.
3.4 Case of ULTC Control
Next, for the case of ULTC, its continuous model (Mi-
lano, 2011) for voltage control, shown in Figure 6, is
quite similar to the model representing the SVC. For
continuous control action, the dynamics of the model
is represented by the equation (16),
˙m = −K
d
m + K
i
(V
m
−V
re f
) (16)
Figure 6: ULTC Block for Voltage Control.
Thus, for the ULTC based control scheme as well,
an appropriate assignment of the model parameters
K
d
and K
i
can be done for making its inherent dy-
namics zero as desired, to obtain the desired Jacobians
with respect to the controls and use those to compute
the desired trajectory sensitivities.
3.5 Case of Load Control
Loads of any power network can be of different
types, e.g. static loads, voltage dependent loads, fre-
quency dependent loads, exponential recovery loads,
ZIP loads etc. To study voltage instability related is-
sues, it is reasonable to consider exponential recovery
loads. The dynamics of exponential recovery load of
any bus is represented by the following DAEs.
For active power,
˙x
P
= −x
P
/T
P
+ P
0
(V /V
0
)
α
s
− P
0
(V /V
0
)
α
t
(17)
P = x
P
/T
P
+ P
0
(V /V
0
)
α
t
(18)
P
0
= K
1
P
B
(19)
For reactive power,
˙x
Q
= −x
Q
/T
Q
+ Q
0
(V /V
0
)
β
s
− Q
0
(V /V
0
)
β
t
(20)
Q = x
Q
/T
Q
+ Q
0
(V /V
0
)
β
t
(21)
Q
0
= K
2
Q
B
(22)
where, P and Q are the active and reactive power con-
sumption at the respective bus, x
p
and x
q
are state
variables related to active and reactive power dynam-
ics, T
P
and T
Q
are time constants of the exponential
recovery response, α
s
and β
s
are exponents related
to the steady-state load response, α
t
and β
t
are ex-
ponents related to the transient load response, V and
V
0
are current and initial bus voltages, respectively.
Now, P
0
= K
1
× P
B
and Q
0
= K
2
× Q
B
depend on
the base active power (P
B
) and reactive power (Q
B
)
of the respective buses. These P
B
and Q
B
serve as
the control parameters, for to exercise load-shedding,
a reduction in the base load (P
B
+ jQ
B
) of a particu-
lar bus is required. Thus, to measure the impact on
bus voltages for infinitesimal change of base load, we
have to compute the trajectory sensitivity of bus volt-
ages with respect of P
B
and Q
B
.
In doing so, we have introduce two new state vari-
ables x
PB
= P
B
and x
QB
= Q
B
with zero dynamics and
modified the load dynamics equations accordingly as
follows. For active power,
˙x
P
= −x
P
/T
P
+ K
1
x
PB
(V /V
0
)
α
s
− K
1
x
PB
(V /V
0
)
α
t
(23)
P = x
P
/T
P
+ K
1
x
PB
(V /V
0
)
α
t
(24)
˙x
PB
= 0 (25)
For reactive power,
˙x
Q
= −x
Q
/T
Q
+ K
2
x
QB
(V /V
0
)
β
s
− K
2
x
QB
(V /V
0
)
β
t
(26)
Q = x
Q
/T
Q
+ K
2
x
QB
(V /V
0
)
β
t
(27)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
756
˙x
QB
= 0 (28)
Next using the technique detailed in Section 3.2,
the desired Jacobians with respect to controls are
computed and stored for calculating trajectory sensi-
tivities. Note, to introduce new state variables, the
corresponding sub-routine of PSAT for exponential
load requires certain modifications that we have also
performed.
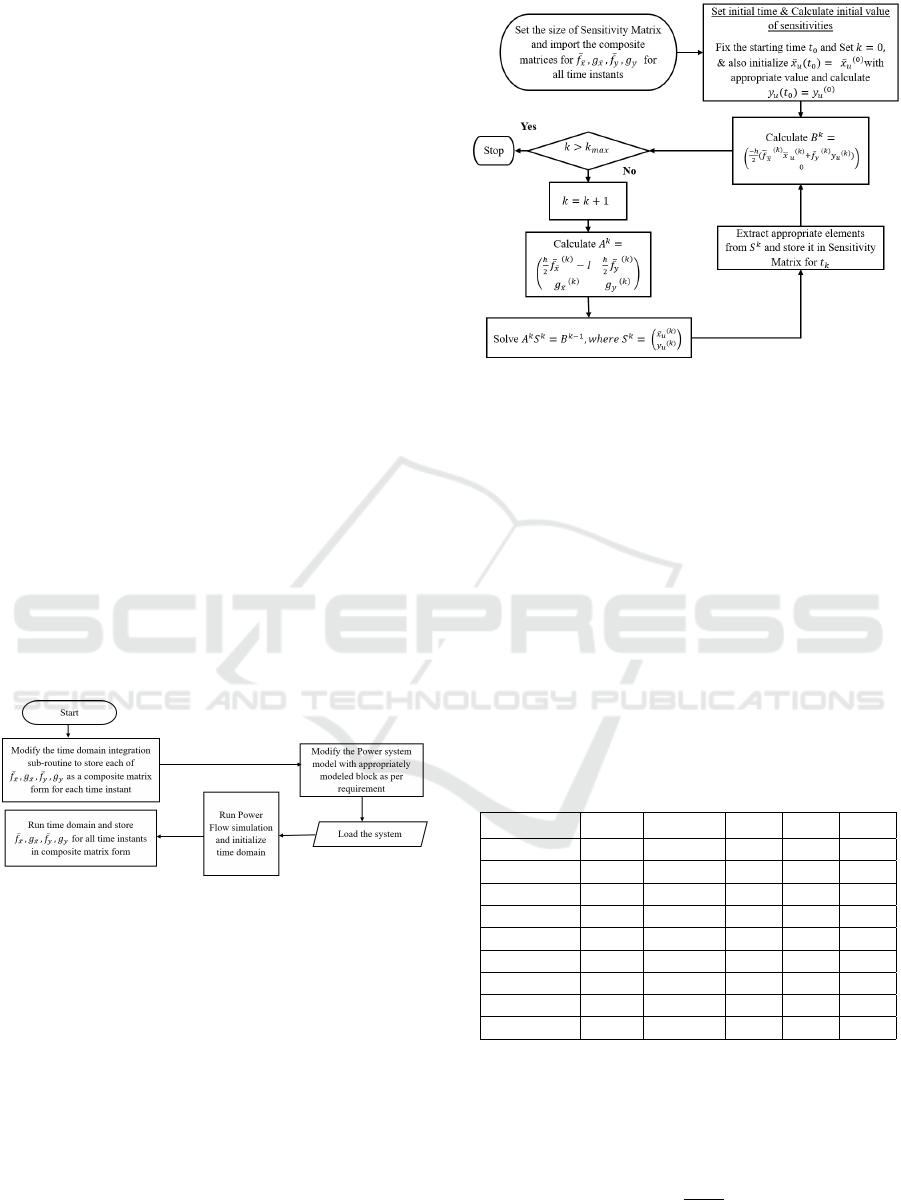
4 ARCHITECTURE OF
EXTENDED PSAT FOR
TRAJECTORY SENSITIVITIES
A proposed architecture for computing tarjectory sen-
sitivities with respect to control input is shown in
Figure 7 & 8; it consists of two blocks: the basic
PSAT algorithm (Block-1), and the Trajectory Sen-
sitivity Calculation block (Block-2). The PSAT al-
gorithm of Block-1 includes the power flow solution
and the modified time domain integration subroutines
for controls-augmented states to yield
¯
f
¯x
,
¯
f
y
,g
¯x
,g
y
at
all sampling instants from which all the 6 Jacobians
are extracted. The Trajectory Sensitivity Calculation
block (Block-2) then imports all the required elements
from Block-1 and computes and stores the trajec-
tory sensitivity values ¯x
u
, y
u
for each sampling instant
from which x
u
and y
u
can further be extracted.
Figure 7: Block-1.
4.1 PSAT Implementation & Validation
For validation, the same 9-bus 3-generator WECC test
system shown in Figure 3, with 3 appropriately mod-
eled SVC blocks at bus 5, bus 7, and bus 8 is selected.
These are designated as control-1 (u
1
), control-2 (u
2
),
control-3 (u
3
). The entire system is simulated in
PSAT and for each sampling instant, the trajectory
sensitivities of bus voltages with respect to u
1
, u
2
, and
u
3
are computed, using the algorithm mentioned in
the previous section.
Letting S
n j
denote the trajectory sensitivity of nth
bus voltage at its nominal value, V
n
, with respect the
jth control input as, u
j
, when the jth control input is
Figure 8: Block-2.
changed by ∆u
j
amount, the resulting voltage
b
V
n
of
the nth bus can be approximated by,
b
V
n
= V
n
+
∑
j
S
n j
∆u
j
(29)
In the simulation of the nominal system, the con-
trol inputs are chosen as, u
1
= 0 p.u., u
2
= 0 p.u., and
u
3
= 0 p.u. This system is simulated in PSAT and for
analysis purposes, the voltages of buses 4, 5, and 8, at
3 different sampling instants are tabulated in Table 1,
along with the corresponding trajectory sensitivities.
Using equation (29), the predicted voltages
b
V
n
are cal-
culated for the change in control inputs ∆u
1
= 0.01
p.u., ∆u
2
= 0.01 p.u., and ∆u
3
= 0.01 p.u. The values
of
b
V
n
are listed in Table 2.
Table 1: Simulation Results under Base Load.
Time-instant Bus no. V
n
(in p.u.) S
n1
S
n2
S
n3
t = 1.15s Bus 4 0.9652 0.0248 0.0298 0.0334
t = 1.15s Bus 5 0.7098 0.1511 0.1150 0.0977
t = 1.15s Bus 8 0.8204 0.0755 0.0907 0.1014
t = 22.75s Bus 4 1.0172 0.0781 0.0718 0.0868
t = 22.75s Bus 5 0.8403 0.2233 0.1427 0.1355
t = 22.75s Bus 8 0.9426 0.1283 0.1208 0.1472
t = 40.05s Bus 4 0.9852 0.2437 0.2019 0.2210
t = 40.05s Bus 5 0.7781 0.5483 0.3987 0.3941
t = 40.05s Bus 8 0.8956 0.3861 0.3238 0.3533
To validate the estimated results, the system is
now simulated with u
1
= 0.01 p.u., u
2
= 0.01 p.u. &
u
3
= 0.01 p.u., while the simulated bus voltages V
0
n
are also depicted in Table 2. The percentage error of
simulated versus estimated values of bus voltages are
determined by %error =
b
V
n
−V
0
n
V
0
n
× 100. The last col-
umn of Table 2 shows the values of percentage errors
which are all well below 0.5%.
Computation of Trajectory Sensitivities with Respect to Control and Implementation in PSAT
757

Table 2: Percentage Error of Estimated results and Simu-
lated results for ∆u
1
= 0.01 p.u.,∆u
2
= 0.01 p.u. & ∆u
3
=
0.01 p.u.
Time instant Bus no.
b
V
n
(in p.u.)
V
0
n
(in p.u.) % error
t = 1.15s Bus 4 0.9661 0.9662 -0.0073
t = 1.15s Bus 5 0.7134 0.7131 0.0503
t = 1.15s Bus 8 0.8231 0.8229 0.0261
t = 22.75s Bus 4 1.0196 1.0197 -0.0007
t = 22.75s Bus 5 0.8454 0.8453 0.0017
t = 22.75s Bus 8 0.9466 0.9465 0.0012
t = 40.05s Bus 4 0.9918 0.9915 0.0341
t = 40.05s Bus 5 0.7916 0.7907 0.1025
t = 40.05s Bus 8 0.9063 0.9056 0.0691
In order to validate our approach of computing the
trajectory sensitivity with respect to loads as the con-
trol inputs, we designate the load at bus 6 as control-
4 (u
4
), where u
4
= P
4
B
+ jQ
4
B
. Now, keeping other
control inputs u
1
, u
2
and u
3
unchanged, for ∆u
4
=
∆P
4
B
+ j∆Q
4
B
= 0.01 + j0.01, the trajectory-sensitivity
based predicted versus the simulated voltages are ob-
tained using the process as described earlier in Ta-
ble 3, followed by the calculation of percentage er-
rors, which was found to less than 0.5% (see Table 4).
Note in Table 3, in accordance to the previous nota-
tion, S
P
B
n j
& S
Q
B
n j
, represents trajectory sensitivity of nth
bus with respect to base active power (P
B
) and base
reactive power (Q
B
) of the jth load.
Table 3: Simulation Results under Base Load.
Time-instant Bus no. V
n
(in p.u.) S
P
B
n4
S
Q
B
n4
t = 8.50s Bus 4 1.0222 -0.0729 -0.0625
t = 8.50s Bus 5 0.89336 -0.0514 -0.0405
t = 8.50s Bus 8 0.96806 -0.0576 -0.0480
t = 28.00s Bus 4 1.0089 -0.1348 -0.0888
t = 28.00s Bus 5 0.86050 -0.1051 -0.0665
t = 28.00s Bus 8 0.94473 -0.1084 -0.07099
t = 38.60s Bus 4 0.99538 -0.1877 -0.1144
t = 38.60s Bus 5 0.83686 -0.1782 -0.1068
t = 38.60s Bus 8 0.92645 -0.1718 -0.1051
These results validate the proposed method of
computation of trajectory sensitivities with respect
to the control inputs as proposed by our control-
augmented state-space method, numerical integra-
tion, and their PSAT implementation.
4.2 A Specific Application of the
Implementation
The proposed implementation extends the functional-
ity of the software PSAT for computation trajectory
Table 4: Percentage Error of Estimated versus Simulated
results for ∆u
4
= 0.01 + j0.01 with ∆u
1
= ∆u
2
= ∆u
3
= 0.
Time instant Bus no.
b
V
n
(in p.u.) V
0
n
(in p.u.) % error
t = 8.50s Bus 4 1.0235 1.02276 0.0797
t = 8.50s Bus 5 0.89428 0.89364 0.07134
t = 8.50s Bus 8 0.96912 0.96839 0.0755
t = 28.00s Bus 4 1.0112 1.0096 0.1545
t = 28.00s Bus 5 0.86222 0.8608 0.1602
t = 28.00s Bus 8 0.94652 0.94511 0.1498
t = 38.60s Bus 4 0.99841 0.99619 0.2219
t = 38.60s Bus 5 0.83971 0.83735 0.2810
t = 38.60s Bus 8 0.92922 0.92697 0.2427
sensitivities with respect to any control inputs and pa-
rameters other than the system variables, enhancing
the PSAT’s capabilities beyond simulation, to control
synthesis.
As an example, in Model Predictive based con-
troller based voltage stability scheme, the common
control actions are switching of shunt capacitors, rais-
ing/lowering of Under load tap-changers, and exer-
cising load-shedding in a coordinated manner. The
corresponding optimization problem is complex in
case of large power system comprising of highly non-
linear component dynamics. In this context, the com-
putation of voltage trajectory sensitivities with respect
to control inputs provides an efficient way to estimate
the effect of control inputs on voltage trajectories, and
selecting an optimal control strategy.
As discussed earlier, in the available version of
PSAT, there is no specific sub-routine to calculate
trajectory sensitivity with respect to control inputs.
Further such computation also requires the computa-
tion of the Jacobian matrices with respect to controls,
which are also not made available in PSAT. Our im-
plementation extends PSAT to facilitate the computa-
tion of such Jacobians with respect to control inputs
as well as parameterized loads by augmenting the re-
spective control inputs and load parameters into the
state variables, with zero dynamics. This not only
helps to compute trajectory sensitivities with respect
to controls, but also enables the computation of load
margin sensitivity, and study of neighbouring trajec-
tories under different control actions or variation of
parameters.
5 CONCLUSION
This paper presented a way of computing trajectory
sensitivity with respect to control in PSAT based
on augmentation of state-space with zero-dynamics
controls. Three types of control were considered:
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
758

SVC, ULTC, and Loads. With proper modification
of certain parameters of available control models in
PSAT, it became possible to achieve the desired zero-
dynamics of control, and then to calculate the desired
trajectory sensitivities. Our approach thus enables a
convenient way for designing of real-time protection
schemes, such as MPC, that use trajectory sensitives
to quickly estimate future behaviors due to changes in
inputs and initial state/algebraic variables. The paper
also described the structure of the algorithm for com-
puting trajectory sensitivities, and presented the vali-
dation of the trajectory sensitivity computation results
by computing the same values through direct simula-
tions of trajectories under various control inputs. The
percentage error was found to be no more than 0.5%.
The extended PSAT implementation is further be-
ing developed for model-predictive control applica-
tion.
ACKNOWLEDGEMENTS
The work was supported in part by the Na-
tional Science Foundation under the grants, NSF-
CCF-1331390, NSF-ECCS-1509420, and NSF-IIP-
1602089.
REFERENCES
Abdelsalam, H. A., Suriyamongkol, D., and Makram, E. B.
(2017). A tsa-based consideration to design lqr auxil-
iary voltage control of dfig. In 2017 North American
Power Symposium (NAPS), pages 1–6. IEEE.
Chatterjee, D. and Ghosh, A. (2007). Transient stability
assessment of power systems containing series and
shunt compensators. IEEE Transactions on Power
Systems, 22(3):1210–1220.
Ferreira, C. M., Pinto, J. D., and Barbosa, F. M. (2004).
Transient stability assessment of an electric power
system using trajectory sensitivity analysis. In 39th
International Universities Power Engineering Con-
ference, 2004. UPEC 2004., volume 3, pages 1091–
1095. IEEE.
Ghosh, A., Chatterjee, D., Bhandiwad, P., and Pai, M.
(2004). Trajectory sensitivity analysis of tcsc com-
pensated power systems. In IEEE Power Engineering
Society General Meeting, 2004., pages 1515–1520.
IEEE.
Hiskens, I. and Gong, B. (2005). Mpc-based load shedding
for voltage stability enhancement. In Proceedings of
the 44th IEEE Conference on Decision and Control,
pages 4463–4468. IEEE.
Hiskens, I. A. and Pai, M. (2000). Trajectory sensitivity
analysis of hybrid systems. IEEE Transactions on Cir-
cuits and Systems I: Fundamental Theory and Appli-
cations, 47(2):204–220.
Hiskens, I. A. and Pai, M. (2002). Power system ap-
plications of trajectory sensitivities. In 2002 IEEE
Power Engineering Society Winter Meeting. Confer-
ence Proceedings (Cat. No. 02CH37309), volume 2,
pages 1200–1205. IEEE.
Jin, L., Kumar, R., and Elia, N. (2007). Application
of model predictive control in voltage stabilization.
In 2007 American Control Conference, pages 5916–
5921. IEEE.
Jin, L., Kumar, R., and Elia, N. (2010). Model pre-
dictive control-based real-time power system protec-
tion schemes. IEEE Transactions on Power Systems,
25(2):988–998.
Laufenberg, M. J. and Pai, M. (1997). A new approach to
dynamic security assessment using trajectory sensitiv-
ities. In Proceedings of the 20th International Confer-
ence on Power Industry Computer Applications, pages
272–277. IEEE.
Milano, F. (2005). An open source power system analy-
sis toolbox. IEEE Transactions on Power systems,
20(3):1199–1206.
Milano, F. (2011). Hybrid control model of under load
tap changers. IEEE Transactions on Power Delivery,
26(4):2837–2844.
Milano, F., Vanfretti, L., and Morataya, J. C. (2008). An
open source power system virtual laboratory: The psat
case and experience. IEEE Transactions on Educa-
tion, 51(1):17–23.
Nasri, A., Eriksson, R., and Ghandhari, M. (2013a). Suit-
able placements of multiple facts devices to improve
the transient stability using trajectory sensitivity anal-
ysis. In 2013 North American Power Symposium
(NAPS), pages 1–6. IEEE.
Nasri, A., Eriksson, R., and Ghandhari, M. (2014). Using
trajectory sensitivity analysis to find suitable locations
of series compensators for improving rotor angle sta-
bility. Electric Power Systems Research, 111:1–8.
Nasri, A., Ghandhari, M., and Eriksson, R. (2013b). Tran-
sient stability assessment of power systems in the
presence of shunt compensators using trajectory sensi-
tivity analysis. In 2013 IEEE Power & Energy Society
General Meeting, pages 1–5. IEEE.
Tang, L. and McCalley, J. (2013). Trajectory sensitivities:
Applications in power systems and estimation accu-
racy refinement. In 2013 IEEE Power & Energy Soci-
ety General Meeting, pages 1–5. IEEE.
Zima, M. and Andersson, G. (2003). Stability assessment
and emergency control method using trajectory sensi-
tivities. In 2003 IEEE Bologna Power Tech Confer-
ence Proceedings,, volume 2, pages 7–pp. IEEE.
Computation of Trajectory Sensitivities with Respect to Control and Implementation in PSAT
759
