Optimal Waypoint Navigation for Underactuated Cruising AUVs

Kangsoo Kim

National Maritime Research Institute, National Institute of Maritime, Port, and Aviation Technology, 6-38-1 Shinkawa,

Mitaka, Tokyo 181-0004, Japan

Keywords: Navigation, Waypoint, Optimization, Depth, Altitude, Cruising AUV, Bottom Collision.

Abstract: An advanced approach to the waypoint-based navigation for near-bottom survey of a cruising AUV is

presented. Pursuing vehicle safety as well as high-definition bottom survey data, we apply GDS-based

optimization technique for achieving waypoint-based minimum-altitude flight of an underactuated cruising

AUV. While the objective of our optimization is minimizing average altitude of a vehicle throughout its flight

interval, depth or altitude references on waypoints are used as control inputs. In our optimization, bottom

bathymetry is incorporated as a constraint used for bottom collision avoidance. As another constraint, dynamic

model of an AUV is included. By solving the dynamic model in time domain, motion responses of the vehicle

following reference waypoints are derived. Our approach of the optimal waypoint navigation is validated by

not only simulation but also at-sea deployment of an AUV.

1 INTRODUCTION

Providing far higher resolution bottom survey data

than can be obtained from surface vessels, AUVs are

increasingly being used in a diverse range of

applications in the scientific, military, commercial,

and policy sectors (Wynn et al., 2014). However, as

its altitude from the bottom decreases, an AUV is

faced with higher risk of bottom collision. The risk of

bottom collision is especially serious when an

underactuated vehicle exercises low-altitude flight

over a steep and rugged terrain. It is common to

classify AUVs into two categories according to their

behavioral character: hovering and cruising (McPhail

et al., 2010). It can be said that cruising AUVs are

typically the choice for higher-speed, longer-range

missions. In general, a hovering AUV can hover and

maneuver around an operating point, while most

cruising AUVs cannot. This is because most cruising

AUVs are underactuated, and thus have restricted

path-following capability (Lea et al., 1999). Due to

this restriction, a cruising AUV has difficulty in

avoiding impending collision with the obstacles in

close proximity, which discourages it from flying

over a steep and rugged terrain. Another concern of

the flight of a cruising AUV over a steep and rugged

terrain is that its onboard sonar altimeter is

susceptible to so called "loss of bottom lock". Once

occurs, the loss of bottom lock disables the use of

correct vehicle altitude, leading to the increased

hazard of bottom collision (Keranen et al., 2012). In

this paper, we demonstrate that the loss of bottom

lock is especially favored by a bottom-following

flight over a steep and rugged terrain. Unlike altitude,

the depth of an underwater vehicle is highly accurate

and reliable, being obtainable merely by measuring

ambient water pressure. In this paper, we present

depth-based optimal waypoint navigation as an

alternative for the altitude-based acoustic navigation.

By following the waypoints derived by GDS

(gradient descent search)-based optimization, an

AUV achieves minimum-altitude flight over a steep

and rugged terrain avoiding bottom collision.

2 WAYPOINT NAVIGATION

In underwater vehicle navigation, waypoints are the

set of 3D coordinates identifying the navigational

points defined as the latitude, longitude, and depth or

altitude pairs. Within the framework of waypoint

navigation, a vehicle moves toward a destination

passing through the reference waypoints. Figure 1

shows a sample of waypoints generated for AUV-

based near-bottom survey of a submarine volcano. As

shown, the reference path is spontaneously defined by

the waypoints. In Fig. 1, it is noted that the numbers

attached to each waypoint represent reference depths.

124

Kim, K.

Optimal Waypoint Navigation for Underactuated Cruising AUVS.

DOI: 10.5220/0007931901240134

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 124-134

ISBN: 978-989-758-380-3

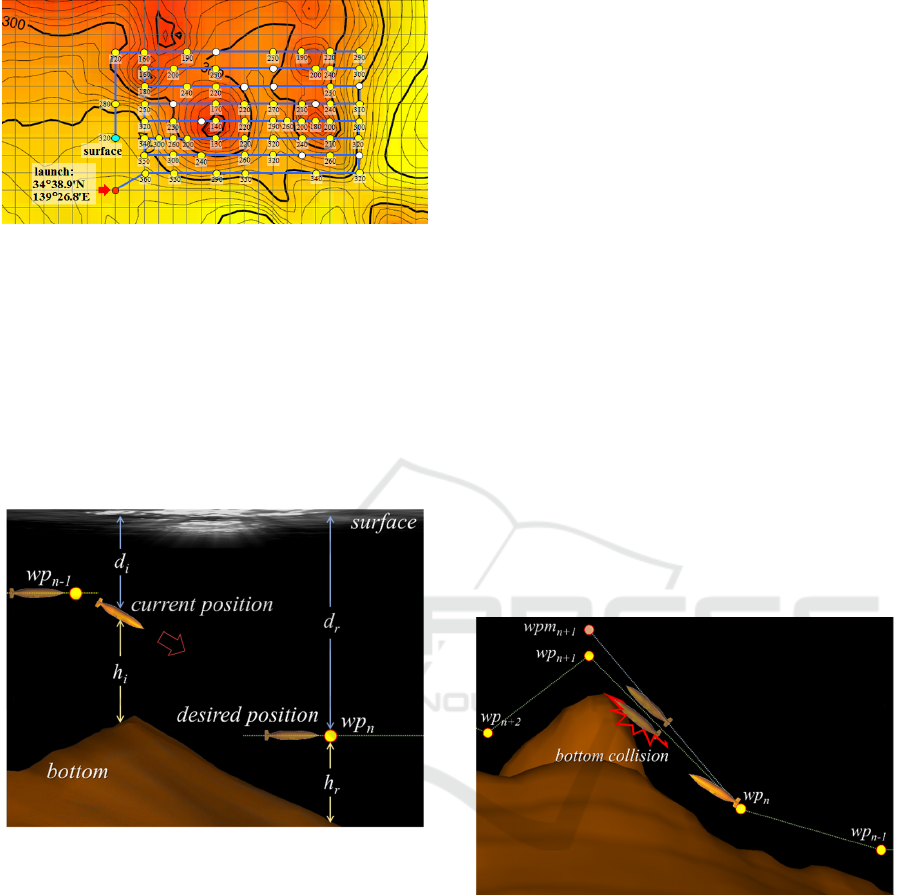
Figure 1: Waypoints and reference path generated for a

near-bottom survey by an AUV.

In our waypoint-based navigation, the reference depth

of n-th waypoint, (i.e. wp

) shown in Fig. 1 is the

desired depth to be reached by a vehicle during its

transit between wp

n-1

and wp

. Therefore, no sooner

has the vehicle arrived at wp

n-1

, its target vertical

position is updated to the reference depth of wp

(Fig.

2). In Fig. 2, d

and d

are the current and the desired

(reference) vehicle depths, while h

and h

are their

altitude counterparts, respectively.

Figure 2: Waypoint-based depth control of an AUV.

It is to be noted here that instead of depth, altitude

from the bottom also can be used for controlling the

vertical position of an underwater vehicle. In our

work, altitude means the absolute altitude in air

navigation, i.e., the height of a vehicle above the

terrain over which it is traversing (U.S. Air Force,

2005). The altitude control works on the basis of the

altitude error e

defined as the difference between the

reference and the current altitude of a vehicle. It is

noted that, however, by substituting the altitude error

with its depth error counterpart, a depth controller is

also able to exercise the altitude control equivalently.

Hence, it is very common that a depth controller of an

AUV is also in charge of the altitude control (McPhail

et al., 2010; Kim and Ura, 2015). In such cases, we

can recognize that for the altitude control

= -e

(1)

where e

is the depth error counterpart of the current

vehicle altitude error e

= h

- h

3 NEAR-BOTTOM SURVEY

FLIGHT

Near-bottom survey of a seafloor is one of the most

important AUV missions in its diverse applications.

Being able to fly close to the bottom, AUVs are

capable of collecting seafloor mapping, profiling and

imaging data of far higher resolution and navigational

accuracy than surface vessels (Wynn et al., 2014).

However, moving close to the bottom inevitably

raises the risk of bottom collision. This is especially

serious when a cruising AUV is flying over a rugged

and steep terrain keeping low altitude above the

bottom.

3.1 Bottom Collision

Figure 3 illustrates the possible bottom collision of a

cruising AUV during its waypoint-based near-bottom

mission over a steep and rugged terrain.

Figure 3: Bottom collision of an underactuated cruising

AUV over steep and rugged terrain.

Suppose that the reference depth of any waypoint is

merely assigned as the depth determined by an

arbitrary constant altitude above the bottom. Then,

although the reference path generated by interlinking

adjacent waypoints runs over the seafloor without any

interference with the terrain, an underactuated vehicle

following the waypoints can cause a bottom collision

(Fig. 3). This is because the reference path has been

generated without considering the constraint of

vehicle dynamics which can let the vehicle faced with

too low altitude to avoid imminent bottom collision.

In Fig. 3, bottom collision occurs within the path

Optimal Waypoint Navigation for Underactuated Cruising AUVS

125

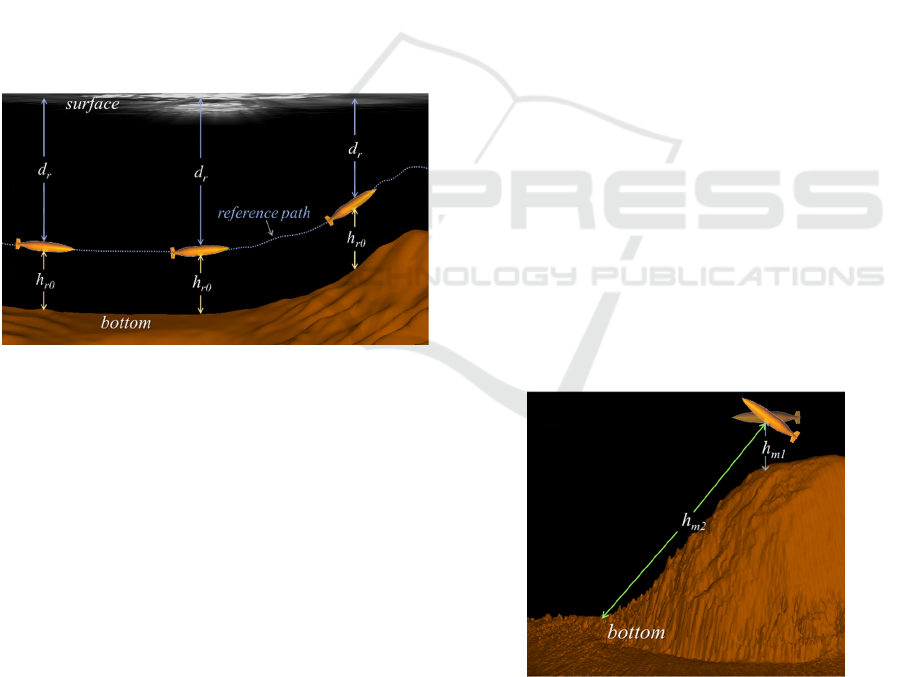
interval between [wp

~ wp

n+1

]. However, by

modifying the reference depths of the waypoints

within the interval, i.e., by substituting wpm

n+1

for

n+1

, for example, we can make the vehicle avoid

bottom collision, as shown in the figure. As can be

noticed from Fig. 3, in order to avoid bottom collision,

the constraint of vehicle dynamics as well as the

bottom topography should be considered.

3.2 Bottom-following Flight

As mentioned previously, altitude can be used in

determining the vertical reference position of a

vehicle. A typical example of such approach is the

navigation so called bottom following (Caccia et al.,

2003). In the bottom-following flight, a vehicle is

controlled to follow the bottom maintaining a fixed

altitude above it (Fig. 4). Thus, a device for

measuring current vehicle altitude is essential for

practicing a bottom-following flight. Most modern

AUVs are equipped with a bottom-lock sonar such as

DVL (Doppler Velocity Log) for this purpose.

Figure 4: Bottom-following flight of a cruising AUV.

In Fig. 4, h

is the constant reference altitude

assigned for a bottom-following flight. It is noted that

while h

is constant, d

changes according to current

vehicle position. When the bottom-following flight

works without fail, a vehicle exactly follows the

reference path defined as the along-track bottom

section parallelly shifted upward by h

(Fig. 4). In

practice, however, the bottom following is not so

reliable as the waypoint-based depth control because

it relies entirely on real-time vehicle altitudes

provided by a bottom-lock sonar.

4 ACOUSTIC NAVIGATION

In general, depth sensor installed in most modern

AUVs is a quartz crystal pressure sensor calculating

current vehicle depth from the direct measurement of

ambient seawater pressure. It is known that such

pressure sensor provides very high precision whose

accuracy of 0.01% of full scale (Kinsey et al., 2006).

Therefore, it is noted that waypoint-based depth

control is a highly reliable means for achieving stable

and robust underwater vehicle navigation in vertical

plane. As regards vehicle altitude, a bottom-lock

sonar working on the basis of the single range

acoustic time-of-flight navigation is used in

estimating its current value above the bottom.

Varying with the frequency of carrier signal,

precision of echo sounding is said to be 0.01 ~ 1.0 m

(Kinsey et al., 2006). The precision seems to be

acceptable for near-bottom flight of a cruising AUV.

However, there still is a serious concern in acoustic

time-of-flight navigation. Altitude measurement by

using a bottom-lock sonar system is highly vulnerable

to the surrounding environment.

4.1 Altitude Overestimation

The first vulnerability of the altitude-based bottom-

following flight of a cruising AUV is possible

overestimation of the vehicle altitude over a steep

terrain. As shown in Fig. 5, over a steep terrain, even

a small change in vehicle's attitude may result in a

large variation of indicated altitude. Suppose that a

vehicle following the bottom is instantaneously

taking large nose-up attitude when it has reached a

steep downhill. Then, indicated altitude h

is used

for ongoing bottom-following flight instead of h

the true altitude. Since h

is largely overestimated

compared to its true counterpart, the vehicle may try

to approach the bottom further lowering its altitude

even when h

is smaller than h

Figure 5: Indicated and true altitudes over a steep terrain.

4.2 Loss of Bottom Lock

In order for a bottom-lock sonar system to work

properly, its receiver signal-to-noise ratio (SNR)

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

126

should be higher than the detectable limit called

threshold SNR (Urick, 1982). Since the acoustic

energy projected by a transmitter dissipates due to the

transmission losses, echoes show markedly reduced

acoustic intensity from the source level (SL).

Moreover, when a travelling acoustic wave

encounters sea bottom leading to an echo event, some

fraction of its energy is transmitted into the bottom.

Dissipation in seawater and transmission into the sea

bottom of acoustic energy are the major sources of

reduced echo level (EL) lowering SNR (Urick, 1982).

When the EL of sonar echo is so small as for its SNR

to be lower than the threshold value, a bottom-lock

sonar is no longer able to lock on to the seafloor. This

state is called "loss of bottom lock" in which any

bottom-reference sonar observation is unavailable.

Losing the information of current altitude, an

underwater vehicle following a seafloor for near-

bottom flight is faced with the serious risk of bottom

collision when loss of bottom lock occurs.

5 MOTION INSTABILITIES

We experienced serious motion instabilities of a

cruising AUV during its mission of surveying a

submarine volcano called NW Rota-1. Figure 6

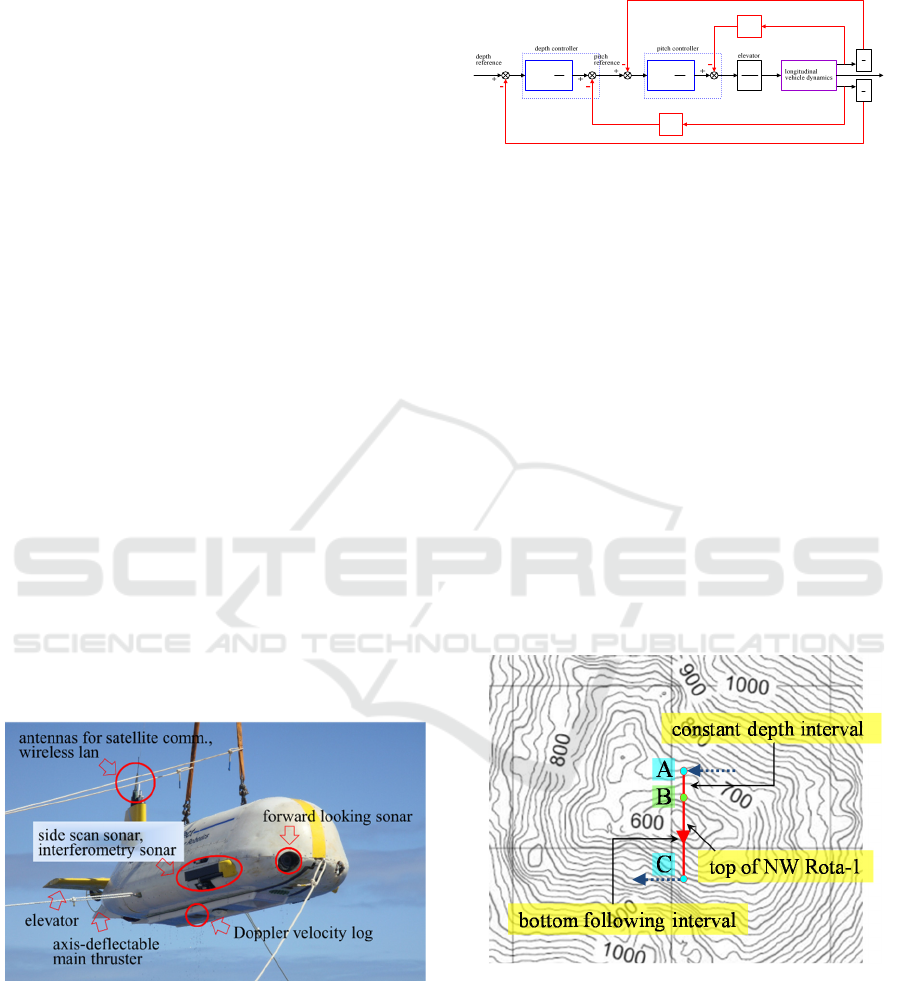
shows the AUV r2D4 having been deployed in NW

Rota-1 site. The r2D4 is a cruising AUV developed

by Institute of Industrial Science, the University of

Tokyo (Kim and Ura, 2009). NW Rota-1 is an active

submarine volcano, located in 64 km NW of the

island of Rota in the western Pacific Ocean.

Figure 6: Overall layout of r2D4.

5.1 Control and Navigation

Figure 7 shows the schematic block diagram of depth

control implemented in r2D4 (Kim and Ura, 2009). It

is noted here that the duality mentioned above is

applied to the depth and altitude control or r2D4. That

is, it is the depth controller shown in Fig. 8 that

actually works corresponding to the altitude control

exercised by bottom following.

Figure 7: Block diagram of the depth control of r2D4.

In Fig. 7, e

and e



are depth and pith errors;



and



are reference and output pitch; d is vehicle depth; q is

pitch rate; u and w are surge and heave velocities; and



and



Cel

are elevator deflection and its command,

respectively. K denotes controller gain while T

derivative or integral time.

Figure 8 shows the navigation applied to r2D4 during

its NW Rota-1 survey mission. In Fig. 8, AC is a part

of the reference path generated for r2D4 flight #16.

AC is called the "near-the-top" interval, generated for

covering the area in the vicinity of the top of NW

Rota-1. In flight #16, both constant depth flight and

bottom following were used as the navigation for

bottom survey. To the anterior section AB of the near-

the-top interval, constant depth flight with the

reference depth of 510 m was applied. Along the

posterior section BC, on the other hand, vehicle was

made to follow the bottom keeping its altitude 150 m

off the bottom.

Figure 8: Navigation applied to near-the-top path interval.

5.2 Motion Instabilities over a Steep

Terrain

Figure 9 shows the bottom cross section of NW Rota-

1 taken along the near-the-top interval. Bottom

bathymetry along a vehicle trajectory is obtained

merely by summing the vehicle depth and the altitude

)















1K-

dzpz

TK-

(s)



















(s)e







(s)

Cel



(s)



q(s)

w(s)

(s)



w(s)

d(s)

(s)



q(s)



d(s)

u(s)

Optimal Waypoint Navigation for Underactuated Cruising AUVS

127

sequences. In the bottom cross section obtained, we

find saw-teeth like, large and unnatural subsidence

continuing along the descending terrain (Fig. 9).

Figure 9: Vertical cross section of submarine volcano NW

Rota-1 along near-the-top path interval.

Motivated by this too unrealistic shape of the bottom

cross section, we checked the time sequences of

vehicle's depth, altitude, and pitch taken from the log

of r2D4 flight #16. Figure 10 shows depth and

altitude sequences taken along the near-the-top path

interval shown in Figs. 8 and 9.

Figure 10: Vehicle depth and altitude.

In Fig. 10, we notice that while fluctuating slightly,

the depth sequence seems normal, since its rate of

change is reasonable within the normal range of the

heave rate of r2D4. On the other hand, however, the

altitude is definitely erroneous since the maximum

value of its time derivative reaches 13.8 m/s which is

more than 9 times the cruising speed of r2D4. Figure

11 shows pitch sequence of the vehicle together with

its altitude counterpart. As can be expected from

intrinsic heave-pitch coupling of a longitudinally

asymmetrical slender body, vehicle's pitch also

fluctuates synchronizing with the altitude fluctuation.

It is noted here that pitch fluctuates bounded within

the range of -25 to 25 which are the predefined

lower and upper limits of the pitch reference. Judging

from its magnitude as well as rate of change, pitch

does not show any notable abnormality.

Acknowledging that the measured vehicle depth is

normal, we can conclude that it is erroneous vehicle

altitude that is responsible for the unrealistic bottom

cross section obtained.

Figure 11: Pitch and altitude.

5.3 Acoustic Bottom Backscatter

If we apply the sonar equation (Urick, 1983; Morgan,

1978; Miline, 1983) to our DVL altimeter, the echo

level (EL) of returned signal is

EL = SL - 2TL +TS (2)

where SL, TL, TS are the source level, the

transmission loss, and the target strength, respectively.

If NL denotes the noise level, we obtain the receiver

SNR as follows.

SNR = EL - NL = SL - 2TL +TS – NL (3)

In (3), energy loss arising from bottom scattering is

expressed by means of the target strength (Morgan,

1978; Urick, 1983). In an active sonar, the target

strength is a measure of the reflecting power of a

sonar target defined as

(4)

where I

and I

are the incident and the scattered

acoustic intensities, respectively.

As the bottom is an effective reflector and scatterer of

sound, it acts to redistribute a portion of the sound in

10logTS 

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

128

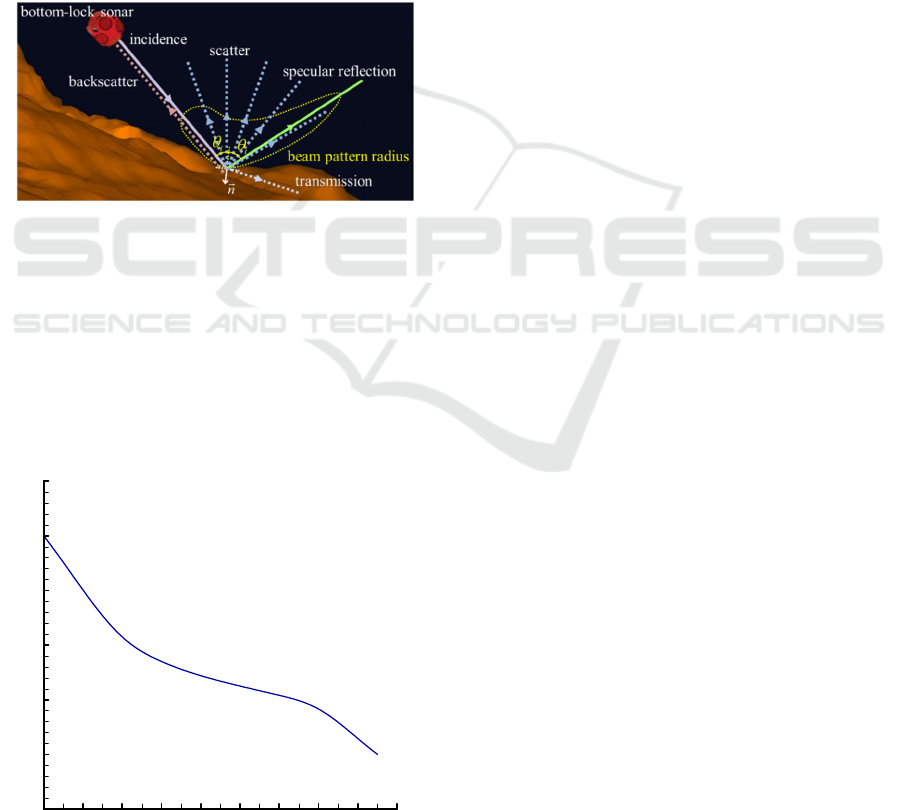
the ocean (Urick, 1983). Not all of the sound is

reflected or scattered, however, but some fraction of

acoustic energy is transmitted into the bottom. The

acoustic bottom backscatter is the reflection of sound

on a sea bottom back to the direction from which it

came (Fig. 12). Therefore, it is the backscattered

sound that primarily activates a bottom-lock sonar. In

case of acoustic bottom scatter, TS, the sonar target

strength is frequently referred to as bottom strength.

Also, it is well known that the bottom strength

directly depends on the incidence angle of impinging

acoustic ray. More precisely, providing the maximum

strength at normal incidence, i.e., zero incidence

angle, the bottom strength decreases notably as the

incidence angle increases (Urick, 1983; Moustier and

Alexandrou, 1991).

Figure 12: Sound redistribution on the bottom by the

impinging acoustic ray of incidence angle



It is well known that bottom strength is also

dependent on the sound frequency of impinging

acoustic ray (Mackenzie, 1961; Urick, 1983). In r2D4,

a 300 kHz, 4-beam DVL is used as altimeter. Li et al.

(2012) presents a smooth curve of 300 kHz bottom

acoustic backscatter as a function of incidence angle

(Fig. 13). By using the curve, we can easily evaluate

corresponding to any incidence angle on the bottom.

Figure 13: Bottom backscatter strength of 300 kHz sound.

It is officially announced that the source level and the

maximum range of our DVL are 216.3 dB and 200 m,

respectively (Teledyne RD Instruments, 2013). This

enables us to estimate the threshold SNR of our DVL

altimeter to be 35.7 dB (Kim and Ura, 2015).

Transmission loss in (2) and (3) can be calculated by

TL = TL

+ TL

= 20log

R +



(5)

where TL

and TL

are the spherical spreading and

the attenuation, respectively which are two major

components of the transmission loss experienced by

an acoustic signal travelling in a fluid medium

(Morgan, 1978; Urick, 1983; Miline, 1983). In (5), R

is the distance from the source and



is the

logarithmic absorption coefficient relating the signal

intensity to range (Urick, 1983).

For the noise level, we consider external background

noise only ignoring cross-sensor acoustic interference.

This is because in general, an AUV employs multiple

sonars of totally different operating frequencies

(Edward et al., 2007), and so does r2D4. It is noted

that at the frequencies over 50 kHz, thermal noise

begins to dominate the underwater background noise

(Urick, 1984). In evaluating the thermal noise level

denoted as NL

, we use the following relation

(Mellen, 1952)

= -15 + 20 log

f (6)

where f is the frequency of interest in kHz.

5.4 Simulated Bottom-following Flight

By using the mathematical model of underwater

acoustics given as (2) ~ (6) and the vehicle dynamics

of r2D4 (Kim and Ura, 2009), the near-bottom flight

of r2D4 following the path interval AC (Fig. 9) has

been simulated. All conditions of the simulation, e.g.,

the sea bottom topography, the flight path, and the

navigation were taken from the r2D4 flight #16

mentioned above. Figure 14 shows the time history of

simulated vehicle altitude. In Fig. 14, altitude log of

the actual flight is superposed on the simulated result.

As seen, like the actual flight, the simulation also

demonstrates severely fluctuating vehicle motion.

Moreover, as in the case with the actual flight, the

largest altitude peak comes first followed by the

gradually decaying smaller peaks. Figure 15 shows

the simulated vertical cross section of NW Rota-1

along the interval AC. The flight simulation generates

the same pattern of the bottom cross section as was

obtained from the actual flight. Simulated vehicle

pitch and the pitch log of the actual flight are shown

in Fig. 16. Over the whole, it is noted that the vehicle

incidence angle (deg)

om bac

sca

eng

0 102030405060708090

-60

-50

-40

-30

-20

-10

Optimal Waypoint Navigation for Underactuated Cruising AUVS

129

behaviors and the along-track bottom bathymetry

obtained by the simulation show intrinsic similarities

to those taken from the actual flight.

Figure 14: Simulated and actual vehicle altitudes.

Figure 15: Simulated and actual bottom cross sections.

Figure 16: Simulated and actual vehicle pitch.

6 ALTERNATE NAVIGATION

6.1 Vulnerability of Acoustic

Navigation

In the previous section, bottom-following flight

simulation has reproduced the longitudinal motion

instabilities of a cruising AUV r2D4 having been

experienced during its actual near-bottom mission. In

the previous literature by the author, a probable

scenario explaining the generating mechanism of the

motion instabilities are presented (Kim and Ura,

2015). In this scenario, the loss of bottom lock of

DVL altimeter and the altitude overestimation are

identified as two major sources inducing instabilities

in longitudinal vehicle motion. Figure 18 shows the

receiver SNR of our 300 kHz DVL altimeter derived

from the flight simulation shown above. As already

mentioned, a bottom-lock sonar gets trapped into the

loss of bottom lock when the receiver SNR is lower

than its threshold. By comparing Fig. 15 to 17, we can

find that a sharp reduction in receiver SNR happens

when the vehicle is about to pass through the top of

NW Rota-1. And from Figs. 16 and 17, we notice that

the interval in which the receiver SNR drops below

its threshold nearly coincides with that of the first

peak of altitude fluctuation. Thus, it is natural to infer

that the large reduction in SNR is the direct source of

the first peak in altitude fluctuation.

Figure 17: Simulated receiver SNR of DVL altimeter.

The reason of the sharp reduction in receiver SNR can

be explained by the abrupt increase in acoustic

incidence angle on the bottom near the top of the

mountain. In order to follow an ascending terrain, a

cruising AUV has to get nose-up. For a bottom-lock

travel distance (m)

e(m)

0 100 200 300 400 500 600

120

160

200

240

: simulation

:ac

ual

ligh

avel distance

(

)

bottom

epth (m)

0 100 200 300 400 500 600

500

600

700

800

: simulation

: actual flight

travel distance (m)

ch (deg)

0 100 200 300 400 500 600

-30

-20

-10

:simulation

: actual flight

travel distance (m)

eceive

SNR (

0 100 200 300 400 500 600

threshold SNR (35.7 dB)

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

130

sonar, nose-up over an ascending terrain forms a

favorable operating condition, making incidence

angle small. Approaching the top of the mountain

with nose-up, however, makes the insonification

switched to descending terrain which leads to abrupt

increase in acoustic incidence angle (Fig. 18). Since

backscattered bottom strength weakens remarkably

as the bottom incidence angle increases (Fig. 13),

switched insonified area is thought to be the cause of

the sharp drop in receiver SNR, and eventually the

loss of bottom lock.

Figure 18: Switched insonified area.

Although the generation of the first altitude peak can

be well explained by the sudden drop of receiver SNR,

others cannot. In Fig. 17, we see whereas the altitude

continues to fluctuate, there is only one significant

SNR drop after 300 m of travel distance. As the

reason that r2D4 continued nodding motion even after

the extinction of significant SNR drop, we take notice

of the large variation in measured altitude over a steep

terrain. After recovering from the loss of bottom lock,

r2D4 pitches nose up over steep descent, resulting in

altitude overestimation. Once a cruising AUV gets a

largely overestimated altitude, it unduly pitches nose

down, in turn, in order to reduce the exaggerated

altitude immediately. In our scenario, the repeated

nose ups and nose downs, i.e., the nodding motion, of

excessive magnitude triggered by the loss of bottom

lock is the substance of motion instabilities appearing

irrespective of the SNR drop (Fig. 19).

Figure 19: Repetitive nodding motion of a cruising AUV

due to altitude overestimation.

6.2 Depth-based Navigation

As noticed from the simulation results shown above,

altitude-based acoustic navigation for a cruising AUV

has serious vulnerability to uneven bottom of steep

slope. When the motion instabilities explained so far

are detected during a near-bottom flight, it indicates

that the vehicle is currently exposed to a significant

hazard, since the occurrence of motion instabilities

implies that the vehicle is blind to its true altitude.

Furthermore, if the reference altitude is particularly

low, e.g., below tens of meters, the motion

instabilities put the vehicle at higher risk of bottom

collision. Therefore, in order to circumvent the risk of

bottom collision, more sophisticated navigation

strategy for near-bottom flight is required.

As already mentioned, the measured depth of an

underwater vehicle is far more reliable and accurate

compared to the measured altitude. Therefore, being

fundamentally free from the vulnerability to uneven

and steep terrain, depth-based navigation ensures

stable vehicle motion. Most depth-based navigation is

put into practice by means of waypoints. Controlling

actual vehicle trajectory, in practice, determining

reference depths on waypoints is highly important for

waypoint-based navigation. It is not easy, however,

for us to derive the reference waypoint depth which

produces the best performance in carrying out an

assigned mission.

6.3 Waypoints for Minimum Altitude

The definition of optimal waypoints differs according

to individual AUV flight missions. At present, it is

widely accepted that high-resolution bottom survey is

one of the most important and anticipative

expectations for AUV flight missions (Wynn et al.,

2013). In fact, the author's institute, National

Maritime Research Institute (NMRI) of Japan also

developed four cruising AUVs for high-resolution

survey of submarine hydrothermal sites (Kim and

Tamura, 2016). Considering these, we regard high-

resolution bottom survey as the major mission of our

AUV applications. Pursuing high-resolution bottom

survey, an AUV has to travel in as close proximity to

terrain as possible. Therefore, our optimal waypoints

are defined as those accomplishes the minimum-

altitude flight of an AUV. Figure 20 describes the

basic concept of our approach. By following the

optimal waypoints, an AUV conducts a near-bottom

flight minimizing the average altitude along its flight

path. In Fig. 20, h

is the minimum allowable altitude

within the flight path interval. It is noted here that h

Optimal Waypoint Navigation for Underactuated Cruising AUVS

131

should be identical to the lowest (i.e., minimum)

altitude actually marked within the interval.

Figure 20: Minimum-altitude flight accomplished by

following optimal waypoints.

6.4 Problem Formulation

To treat the problem of optimal waypoint navigation,

two sets of coordinate system are employed: the

inertial (earth-fixed) coordinate system o-xz and the

body-fixed coordinate system o-x'z' (Fig. 21). While

waypoint optimization is carried out with respect to

the inertial frame, the motion response of a vehicle is

calculated using the equation of motion defined with

respect to the body-fixed frame.

Figure 21: Coordinate systems and schematic description of

the optimal waypoint derivation.

As already mentioned, the objective of our optimal

waypoint navigation problem is to derive the

waypoint set that minimizes average vehicle altitude

along a given flight path. Therefore, the performance

index of the problem is

(7a)

subject to

h(x)  h

for x



, x

]

(7b)

where h(x) is the vehicle altitude at a specified along-

track position x. In (7b), x

and x

are the along-track

coordinates of the lower and the upper limits of the

flight path interval of interest, and h

is the minimum

allowable altitude. It is obvious that once the

minimum allowable altitude h

is given, the ideal

behavior of a vehicle is to follow the bottom

throughout with its altitude of h

. Hence, the target

trajectory for optimizing the waypoints are given as

the envelope line of the bottom section shifted

upward (i.e., in -z direction) by h

, as shown in Fig.

21. In consequence, our problem results in the

optimization making the deviation between the target

and the result trajectories as small as possible. Let us

introduce so called "control grid" represented by the

cross symbol in Fig. 21. The control grid is a set of

arbitrarily spaced discrete points on x-axis at which

the deviation between the target and the result

trajectories is evaluated. Accordingly, by using the

control grid the performance index (7a) can be

redefined as

(8)

where z

and z

are the downrange position vectors of

the target trajectory and the vehicle defined at control

grids. Note that in this paper, variables in boldface

type denote vector or matrix. As already mentioned,

we use a GDS-based solution algorithm in

minimizing the performance index J in (8). In

deriving the solution, our algorithm works in an

iterative manner (Kim et al., 2011). By applying the

algorithm, the downrange position vector of the

waypoints is updated as

(9)

where z

is the downrange position vector of the

waypoints at i-th iteration step, estimated by adding

z

to z

i-1

. In (9), z

is the correction amount of z

computed by

(10a)

where

(10b)

In (10a),



is the gain and



is the non-physical

variable for the fictitious dimension of iteration. It is

noted that G is the Jacobian matrix of z

with respect

to the input vector z





(x)dxh

J zz

1-i

zzz 





G--











ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

132

7 RESULTS

The efficacy of waypoint-based minimum-altitude

navigation was validated through an actual near-

bottom survey mission using an AUV. In 2018, we

deployed an AUV called C-AUV#04 (Fig. 22) in a

potential hydrothermal vent site located in western

Pacific Ocean near Japan. C-AUV#04 is a high

maneuverability cruising AUV developed by NMRI

of Japan, having controllable pitch range of 80

(Kim et al., 2019). C-AUV#04 controls its flight

attitude by deflecting four movable fins mounted on

the stern (Fig. 22). It is noted that two horizontal fins

function as elevator and ailerons, while two vertical

fins as rudder. As for the depth or altitude control, C-

AUV#04 shares the same scheme of r2D4 explained

in section 5.1.

Figure 22: Overall layout of C-AUV#04.

When planning the path for C-AUV#04 flight #02

conducted for the near-bottom survey of the site, we

derived optimal reference depths for the waypoints

constituting the path interval covering western slope

of a sea mound. Figure 23 shows the waypoints with

their path interval superimposed on the bathymetric

map of the site. As seen, fourteen waypoints are to be

optimized in order to accomplish a depth-based,

minimum-altitude flight along the path.

Figure 23: Waypoints and path interval.

The results of near-bottom survey flight following

optimal waypoints are shown in Fig. 24. In

optimizing the waypoints, we assigned the initial

values of their reference depths with the water depths

at the points 120 m above the bottom (Fig. 24). And

it is also noted that the minimum allowable altitude is

set to 80 m.

Figure 24: Results of minimum-altitude flight.

By modifying the waypoints, the GDS-based solution

algorithm shifts the result trajectory away from the

initial waypoints lowering vehicle altitudes within the

flight path interval. Once a vehicle altitude derived by

the flight simulation reduces to around the minimum

allowable altitude, our algorithm terminates waypoint

modification and outputs current waypoint set as the

optimal solution. In this example, we can see small

overshoots in descending intervals, but the vehicle

successfully approaches the target trajectory, as a

whole (Fig. 24). Since they are quite close to the

minimum allowable altitude, the minimum altitudes

let the solution algorithm terminate waypoint

modification and take current waypoints as the

optimal waypoints for the minimum-altitude flight.

Uploaded to onboard storage device, derived optimal

waypoints are used for the near-bottom survey

mission. As can be seen in Fig. 24, by following the

optimal waypoint set derived by our simulation-based

approach, C-AUV#04 is able to complete near-

bottom survey mission successfully.

8 CONCLUSIONS

A systematic procedure for deriving optimal

waypoints used for AUV navigation has been

presented. Using GDS-based optimization, the

procedure derives optimal waypoints by following

which an underactuated cruising AUV accomplishes

minimum-altitude flight avoiding bottom collision.

Being a depth-based approach, the optimal waypoint

navigation is highly robust and fundamentally free

from the vulnerability of acoustic navigation. It is a

pregenerative approach, however, that requires the

real time revision of optimal waypoints in case the

vehicle is largely deviated from the planned path.

Optimal Waypoint Navigation for Underactuated Cruising AUVS

133

ACKNOWLEDGEMENTS

This work is partly supported by Council for Science,

Technology and Innovation (CSTI), cross-ministerial

Strategic Innovation Promotion Program (SIP), next-

generation technology for ocean resources

exploration (lead agency: JAMSTEC). Also, the

author would like to express special thanks to Japan

Marine Surveys Association (JAMSA) and Mr.

Takumi Sato of National Maritime Research Institute

(NMRI) of Japan, for their supports in AUV

operation.

REFERENCES

Wynn, B., Russel et al. (2014). Autonomous Underwater

Vehicles (AUVs): Their past, present and future

contributions to the advancement of marine geoscience.

Marine Geology, 352 (2014), 451–468.

McPhail, S., Furlong, M., and Pebody, M. (2010). Low-

altitude terrain following and collision avoidance in a

flight-class autonomous underwater vehicle.

Journal of

Engineering for the Maritime Environment

, 224 (4),

279–292

Lea, R. K., Allen R., and Merry S. L. (1999). A comparative

study of control techniques for an underwater flight

vehicle.

International Journal of System Science, 30 (9),

947–964.

Keranen, J. et al., (2012). Remotely-operated vehicle

applications in port and harbor site characterization:

Payloads, platforms, sensors, and operations.

Proc. of

IEEE Oceans 2012 Hampton Roads

U.S. Air Force (2005).

Air navigation. University Press of

the Pacific, Honolulu, ISBN 978-1410222466.

Kim, K. and Ura, T. (2015). Longitudinal motion instability

of a cruising AUV flying over a steep terrain,

IFAC-

PapersOnline

, vol.48, issue 2, 56–63.

Caccia, M., Bruzzone, G., Veruggio, G. (2003). Bottom-

following for remotely operated vehicles: Algorithms

and experiments.

Autonomous Robots, 14, 17–32.

Kinsey, J.C., Eustice, R.M., Whitcomb, L.L. (2006). A

survey of underwater vehicle navigation: Recent

advances and new challenges.

Proc. of 7th IFAC

Conference on Manoeuvring and Control of Marine

Craft

Urick, R.J. (1983).

Principles of underwater sound (3rd

edition)

. McGraw-Hill, New-York, ISBN 0-07-

066087-5.

Kim, K., and Ura, T. (2009). Optimal guidance for

autonomous underwater vehicle navigation within

undersea areas of current disturbance.

Advanced

Robotics

, 23 (5), 601–628.

Morgan, M.J. (1978).

Dynamic Positioning of Offshore

Vessels

, PPC Books Division, ISBN 0-87814-044-1.

Miline, P.H. (1983).

Underwater Acoustic Positioning

Systems

, E. & F. N. Spon Ltd, ISBN 0-419-12100-5.

Moustier, C.D., and Alexandrou, D. (1991). Angular

dependence of 12-kHz seafloor acoustic backscatter.

Acoust. Soc. Am.

, 90(1), 522–531.

Mackenzie, K.V. (1961). Bottom reverberation for 530 and

1030 cps sound in deep water.

J. Acoust. Soc. Am., 33,

1498–1504.

Li, M.Z., Sherwood, C.R., and Hill, P.R. (ed.) (2012).

Sediments, Morphology and Sedimentary Processes on

Continental Shelves: Advances in technologies,

research and applications, Wiley-Backwell.

Edward, T., James, R., and Daniel, T. (2007). Integrated

control of multiple acoustic sensors for optimal seabed

surveying.

IFAC Proceedings Volumes, vol.40, issue 17,

367–372.

Urick, R.J. (1984).

Ambient noise in the sea. University of

Michigan Library, ASIN: B003U4V052.

Mellen, R.H. (1952). Thermal-noise limit in the detection

of underwater acoustic signals.

J. Acoust. Soc. Am.,

24(5), 478–480.

Teledyne RD Instruments, Inc. (2013).

Navigator Doppler

velocity log technical manual

. Teledyne RD

Instruments, Inc.

Kim, K. and Tamura, K. (2016). The Zipangu of the Sea

project overview: focusing on the R&D for

simultaneous deployment and operation of multiple

AUVs.

Proc. of OTC-Asia 2016, OTC-26702-MS.

Kim, K. and Ura, T, Kashino, M., and Gomi, H. (2011). A

perioral dynamic model for investigating human speech

articulation.

Multibody System Dynamics, 26(2),

pp.107-134, DOI: 10.1007/s11044-011-9253-z.

Kim, K., Sato, T., and Matsuda, T. (2019). Advanced AUV

navigation and operation towards safer and efficient

near-bottom survey.

Proc. of MTS/IEEE OCEANS 2019

Marseille

(to appear).

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

134