
Method for Vector Map Protection based on using of a Watermark
Image as a Secondary Carrier
Yuliya Vybornova
1
and Vladislav Sergeev
1,2
1
Department of Geoinformatics and Information Security, Samara National Research University, Moskovskoye Shosse,
Samara, Russia
2
Image Processing Systems Institute оf RAS – Branch of the FSRC “Crystallography and Photonics” RAS, Samara, Russia
Keywords: Digital Watermarking, Geographic Information Systems, GIS, Vector Map, Raster Image, Discrete Fourier
Transform, Pseudorandom Sequences, Data Protection.
Abstract: In this paper, we present a study of the watermarking method for vector cartographic data based on a cyclic
shift of a polygon vertex list. We propose a method modification to provide an accurate authentication
procedure, as well as to increase the method robustness against map contents modification. The main idea of
the improved method is to use a noise-like image as a secondary carrier for a watermark, represented in the
form of a bit vector. An algorithm for construction of a noise-like image carrying a watermark sequence, as
well as an algorithm for extraction of such a sequence, are given. An experimental study explores the
information capacity of the carrier image and its robustness against quantization and noise adding, i.e.
distortions simulating the embedding into map objects. The efficiency of the method is also demonstrated
on real cartographic data. Conclusions comprise optimal parameters for reliable extraction depending on the
number of polygons on the vector map.
1 INTRODUCTION
The existing methods of active protection (i.e. the
protection by using digital watermarking
technology) of vector map data are mostly
performed by introducing slight (in terms of map
accuracy) distortions into the coordinate information
of vector objects (Abubahia and Cocea, 2017).
Depending on the level of watermark resistance to
distortions, these methods are aimed at solving
various problems of vector map security.
Methods (Abubahia and Cocea, 2015; Lee and
Kwon, 2013; Peng et al., 2015; Wang, Yang and
Zhu, 2017; Yan, Zhang and Yang, 2017; Zope-
Chaudhari, Venkatachalam and Buddhiraj, 2017) are
designed for solving the problem of copyright
protection (protection against unauthorized
distribution) using the technology of robust
watermarks. Methods of protection against
modifications are implemented on the basis of semi-
fragile (Ren, Wang and Zhu, 2014; Da et al., 2018)
and fragile (Wang, Bian and Zhang, 2015)
watermarks, which are used to ensure the
authenticity and integrity of vector data respectively.
Also, one of the common approaches to protect
vector data against changes is the so called "zero-
watermarking" technology (Peng and Yue, 2015)
which implies constructing a watermark on the basis
of the carrier features. Here, the embedding
procedure as such is missing: the watermark is
necessary only for the verification process. The
combined use of different watermarking
technologies, which is called "multiple
watermarking" (Peng et al., 2017), allows to provide
comprehensive protection of vector data from
unauthorized distribution and modification.
There are situations where even minor changes
introduced into the data are unacceptable. For this
reason, another class of vector data protection
methods, "reversible watermarking" (Cao, Men and
Ji, 2015; Peng, Yan and Long, 2017; Wang, Zhao
and Xie, 2016), has emerged, providing the
opportunity to restore the coordinate values after the
watermark extraction. However, these methods do
not demonstrate the required robustness, therefore,
map distortions can negatively affect the correct
restoration of the original coordinate values.
It should be noted that all the above mentioned
methods have the following disadvantages:
284
Vybornova, Y. and Sergeev, V.
Method for Vector Map Protection based on using of a Watermark Image as a Secondary Carrier.
DOI: 10.5220/0007932402840293
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 284-293
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

- Despite the fact that all conversions are performed
with a given accuracy and almost invisible to the
legitimate user, any distortion of the map gives an
attacker the opportunity to detect the presence of the
embedded watermark even without knowing the
watermarking scheme, i.e. by using blind
steganalysis.
- When embedding and extracting the watermark, a
set of map objects must be strictly ordered. Since the
location of objects on the map is quite random, there
is a need to store extra identifiers for objects or
watermark positions.
The embedding approach, we proposed earlier in
(Vybornova and Sergeev, 2019), allows to avoid the
above disadvantages. First, the method does not
imply a change in vertex coordinates: the protective
information is embedded into cartographic data by
cyclically shifting the list of vertices of each
polygon. Secondly, instead of a bit sequence we
consider a raster image superimposed on a vector
map as a digital watermark, so there is no need to fix
the object indexation order when embedding and
extraction procedures. Consequently, this approach
to vector map protection can form the basis for a
whole group of methods, focused on specific tasks,
such as copyright, authenticity and integrity
protection of map data, as well as localization of
unauthorized changes introduced into a vector map.
In this paper, we propose a specific way of using
a noise-like image as a secondary carrier for the
watermark presented in the conventional form of a
bit sequence, and also we explore the issue of the
information capacity of such a carrier.
The rest of the paper is organized as follows. In
Section 2, the basic approach, which we developed
earlier, is presented. Also, this section describes in
detail a new enhanced approach. Section 3
comprises experimental research of the proposed
method for model and real data. Section 4 provides
general conclusions and the main issues of the future
work.
2 METHODS
2.1 Original Watermarking Method
for Vector Maps
The basic watermarking method for vector
cartographic data, that we proposed in (Vybornova
and Sergeev, 2019), is based on the following
features of polygonal map objects:
a) all polygons are closed shapes;
b) the polygon vertices are numbered
consecutively.
These properties provide the ability to cyclically
shift the indices of all vertices in the polygon vertex
list, without changing the coordinate values, that is,
avoiding the introduction of distortions into the
vector map contents.
The first idea of the method (Vybornova and
Sergeev, 2019) is that the digital watermark is
embedded into data by cyclically shifting the list of
vertices of each polygon. For example, to embed one
watermark bit into each polygon, a polygon vertex
list can be shifted in such a way as to change the
first element in the list to either the uppermost
(north) or the lowermost (south) vertex, depending
on the value of the watermark bit. To embed two
watermark bits into the polygon, the leftmost (west)
and rightmost (east) vertices should be also taken
into consideration. In general, an n-bit binary
number can be embedded into each polygon. It
should be noted that for a fixed first vertex of the
list, there is an opportunity to embed an additional
watermark bit into each polygon by altering the
direction of vertex traversal: clockwise or
counterclockwise, depending on the bit value.
The second idea of the method is to use a raster
image superimposed on a selected fragment of the
vector map as a watermark. Certainly, the vector
map does not provide an opportunity to place raster
data, but its objects (in our case, polygons) can be
mapped to the image in such a way as to
geometrically coincide with some pixels. The set of
pixels, corresponding to polygons, forms an
irregular grid, and thus the entire image can be
approximately restored by using one of the existing
interpolation methods (Vybornova, 2018).
2.2 Proposed Enhancement of Original
Method
In method (Vybornova and Sergeev, 2019), the
raster image itself is used as a robust watermark
providing copyright protection for a digital map.
Accordingly, the map authentication is performed by
visually matching the original watermark with the
image restored (usually with large errors) after
extracting from the vector map. So, this can be
regarded as an obvious limitation on the method
applicability.
Developing the basic method, we propose to use a
noise-like image as a secondary carrier for the
watermark, represented in the form of a bit sequence
(Glumov and Mitekin, 2010). This allows to
automate the map authentication procedure, since
Method for Vector Map Protection based on using of a Watermark Image as a Secondary Carrier
285

the watermark sequence can itself carry all the
necessary identifying information and its analysis
does not require the comparison with the original
watermark.
In order to ensure robustness of the embedded bit
sequence against image interpolation errors, addition
or removal of map objects, geometrical
transformations and cropping of the map, and etc.,
each bit embedded in the carrier image should not
correspond to a separate point (pixel) or a local area
on the image plane. We propose to embed a bit
sequence in the spatial-frequency domain of the
carrier image so that each bit is extended on the
entire image plane "holographically", i.e. in the form
of a two-dimensional sinusoid of the corresponding
spatial frequency.
2.3 Watermark Image Construction
For simplicity, we assume the carrier image is
continuous – f
c
(t
1
, t
2
). We also assume it carries a
watermark in the form of an arbitrary binary
sequence S of length L.
We propose to form a two-dimensional spatial
spectrum - F
c
(ω
1
, ω
2
) - of an image represented as
2(L+2) two-dimensional unit impulses located in the
spectral domain on two rings of different radii: r и
r+Δr, as illustrated in Fig. 1 for one half-plane of the
two-dimensional spectrum (because the image is real
the second half-plane displays the spectrum
symmetrically about the center). In figure 1, unit
impulses are indicated with black circles. All but
two impulses are located with equal step (angle)
starting from the spectrum origin on a ring of
smaller or larger radius, depending on the value of
the corresponding bit of the watermark sequence.
Two impulses located on both rings at the same (e.g.
zero) angle indicate the beginning of the sequence.
Figure 1: Embedding of a binary sequence into image
spectrum.
The resulting spectrum of an image can be
described by the formula:
12
12
1
1 2 1 2
12
1
1 2 1 2
( , )
( cos , sin )
( , ) ( , )
( cos , sin )
( , ) ( , ).
c
L
l l l l
l
L
l l l l
l
F
r r r
r r r
(1)
where
ll
r s r
,
1
l
l
L
, and
12
( , )
is a
two-dimensional unit impulse.
To get the two-dimensional image function, we
apply the two-dimensional inverse Fourier transform
to the spectrum (1):
1 1 2 2
12
()
1 2 1 2
2
( , )
1
( , ) d d .
4
c
i t t
c
f t t
Fe
(2)
By substituting (1) into (2), and taking into
account the Euler's formula, we obtain:
1 2 1
2
1
2 1 2
1
( , ) cos[( cos )
2
( sin ) ] cos( ) cos[( ) ]
L
c l l
l
ll
f t t t
t rt r r t
(3)
The above relations describe only the idea of
how to embed a binary sequence into a carrier
image. In practice, when working with a digital
image instead of a continuous spectrum, it is
necessary to use a discrete Fourier transform (DFT),
taking into account the well-known features of such
a conversion: integer arguments in the spatial and
spectral domain, periodicity of functions in two
dimensions, possible overlap effects, etc. In this
case, there are two ways to form a noise-like image,
carrying a watermark of size
12
NN
pixels:
1) By directly using the "discretized" analogue of the
formula (3):
1 2 1 2
12
1
12
12
cos sin
( , ) cos[2 ( )]
2 2 ( )
cos( ) cos[ ],
L
l l l l
l
f n n n n
NN
r r r
nn
NN
SECRYPT 2019 - 16th International Conference on Security and Cryptography
286

where
12
,nn
are the integer arguments of the digital
image,
1 1 2 2
0 1, 0 1n N n N
.
2) By directly using the "discretized" analogue of
unit impulse delta function, called unit sample
function. Unit samples are arranged on two rings in
two-dimensional discrete spectral domain as
described above, and then the resulting image can be
obtained by using the inverse DFT.
For small lengths of sequences, the first method
may be computationally more efficient.
Contrariwise, when lengths are large enough, the
second method may perform in a better way.
It should be noted that due to the spectrum
discreteness, the coordinates of unit samples, i.e.
magnitudes
cos
ll
,
sin
ll
,
r
,
()rr
should be
rounded to integer values and, therefore, may
overlap when arranging on the rings. Thus, the DFT
dimensions and the radii
r
,
()rr
must be
sufficiently large, so that rounding errors could not
affect the watermark extraction.
As the last step of constructing the carrier image,
the values of its pixels can be normalized to a
standard range, for example, [0, 255]:
12
12
12
1 2 1 2
,
255 1 2
1 2 1 2
,
,
( , ) min ( , )
( , ) 255
max ( , ) min ( , )
nn
nn
nn
f n n f n n
f n n
f n n f n n
An example of the resulting noise-like image
with embedded watermark sequence corresponding
to spectrum in Figure 1 is shown in Figure 2.
Figure 2: Example of noise-like image carrying the
watermark sequence (N
1
= N
2
= 512, r = 8, ∆r = 4, L = 15,
S = {101101001011101).
2.4 Watermark Extraction
The extraction of a sequence from an image
approximately (with interpolation) reconstructed
from a vector map consists of the following obvious
steps:
calculation of a two-dimensional discrete
spectrum of the image (using DFT);
detection of spectral components with a large
amplitude (impulses) and determination of
their coordinates;
detection of the fact of watermark presence, i.e.
the fact that the impulses are located on two
concentric rings in the spectral plane;
estimation of the radii of these rings;
search of the sequence beginning key, i.e. a
pair of impulses located at the same angle to
the spectrum origin;
reading of the watermark sequence bits
clockwise or counterclockwise starting from
the sequence beginning key.
The proposed method of watermark construction
(in the form of impulses on circles in the spectral
plane), together with the extraction procedure
described above, ensures the watermark robustness
against the main geometric deformations of the
image and, accordingly, of the vector map into
which this image is embedded: scaling, rotation,
translation and cropping .
3 EXPERIMENTAL RESULTS
AND DISCUSSION
To investigate the potential use of a noise-like image
embedded into the vector map as a secondary
container for the watermark presented in the form of
a bit sequence, we have conducted two
computational experiments.
In all experiments, digital images of size
12
512 512NN
pixels are generated. Bit
sequences are embedded into rings of radii
r
and
()rr
in the discrete spectrum domain of the
image (for certainty, it is assumed that
4,r
since
due to the discreteness of the bitmap it is the
minimum acceptable value). The "low-frequency"
( 10,50)r
and "mid-frequency"
( 60,100)r
noise-like images are considered.
The lengths of the bit sequences are ranged from
10 100.L
For each combination of parameters,
100 watermark sequence implementations are
generated. The values of sequence bits are obtained
using a random number generator as equiprobable
and independent in total.
Interpolation of an image extracted from a vector
map is performed using the nearest neighbor method
Method for Vector Map Protection based on using of a Watermark Image as a Secondary Carrier
287
based on a triangulated irregular network
(Vybornova, 2018).
Spectral impulses are determined using a simple
rule:
12
12
1 2 1 2
,
( , ) (0,0)
1
( , ) max ( , )
2
kk
kk
F k k F k k
where
12
( , )F k k
is the image DFT,
12
,kk
are the
integer arguments of the discrete spectrum
1 1 2 2
(0 1,0 1).k N k N
3.1 Experiment 1
Obviously, the main sources of errors during the
reconstruction of a carrier image from a vector map
and, consequently, errors during the bit sequence
extraction, are:
- the image is extracted from the map as a set of
spaced pixels corresponding to the polygonal map
objects;
- extracted pixels are quantized due to the fact that
only few binary digits can be embedded into each
polygon.
To evaluate the effect of these distortions on the
watermark sequence, we conducted the following
computational experiment. K pixels of the generated
noise-like image are selected randomly
(independently and equally likely for each
coordinate). Each pixel is quantized to a b-bit
binary number (i.e. into 2
b
levels). Next, the image is
interpolated and attempt to extract the watermark
sequence is performed.
As an indicator of the watermark sequence
integrity, the experimentally estimated probability of
its correct extraction, P, depending on the number
of reference pixels K, is considered. Estimation of
the extraction probability is calculated for the
sample of 100 images.
The variable values are: radius r, bit depth (i.e.
number of bits per pixel b), and sequence length L.
The minimum values of r are established
experimentally and can approximately be described
by the formula:
0,36rL
.
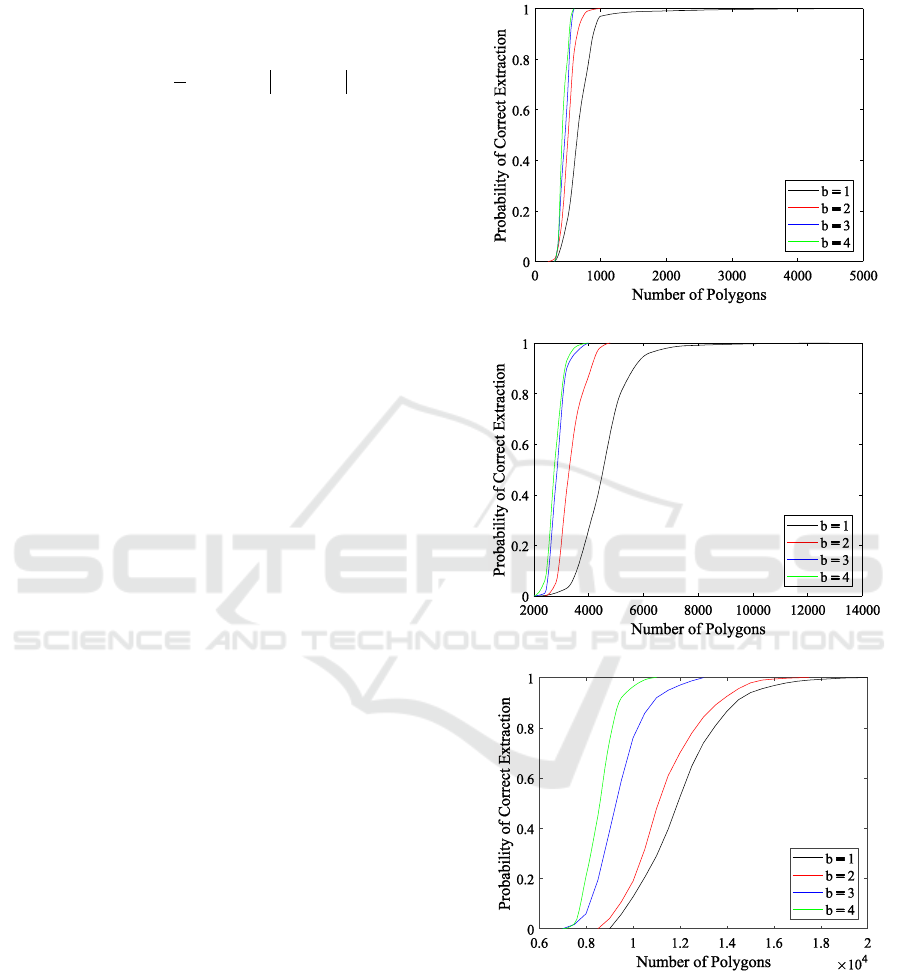
Figure 3 shows the dependence of the extraction
probability on the number of polygons with varying
values of bit depth for the following cases: a) L = 10,
b) L = 50, c) L = 100 (in each case, the radii are
selected in such a way as to provide the most
accurate extraction, i.e. they are assigned the lowest
accebtable values).
(a)
(b)
(c)
Figure 3: Dependence of the extraction probability on the
number of polygons with variable values of bit depth b for
а) L = 10, r = 10; b) L = 50, r = 20; c) L = 100, r = 40.
Figure 4 shows the dependence of the extraction
probability on the number of polygons with varying
values of the radii for the following cases: а) L = 10,
SECRYPT 2019 - 16th International Conference on Security and Cryptography
288
b) L = 50, c) L = 100 (the bit value in this case is
fixed as b = 3)
(a)
(b)
(c)
Figure 4: The dependence of the extraction probability on
the number of polygons with varying values of the radii
for a) L = 10, b = 3; b) L = 50, b = 3; c) L = 100, b = 3.
Some obvious conclusions follow from the
presented results.
The more objects on the map (pixels
corresponding to polygons), the higher the
probability of correct extraction. At the same time,
the longer the watermark sequence, the higher the
requirements for the number of objects needed for
extraction.
The quality of the extraction increases with an
increase in the bit depth of the pixels corresponding
to the map objects. It also looks natural, since an
increase in the bit depth reduces the pixel
quantization noise and, consequently, the error of the
carrier image reconstruction decreases. However,
when setting the bit depth value higher than b = 3,
we see almost no effect of improving the quality.
Moreover, in practical applications it is difficult to
implement persistent high bit depth due to the fact
that on the real map simple polygons (mostly,
quadrangles) dominate: therefore, no more than
three-digit binary numbers can be embedded: two
digits by setting the first vertex in the polygon vertex
list, and one of digit - by altering the direction of
vertex traversal.
For a fixed length of the bit sequence, the
extraction quality is higher, the smaller the r, i.e. the
lower the frequency of the carrier image. On the
other hand, the minimum possible value of this
parameter is limited by the discreteness of the two-
dimensional image spectrum, namely, its ring into
which a sequence of length L is embedded.
Figure 5 shows the dependence of the watermark
image capacity
bL
on the number of polygons for
a fixed values of the achievable probability.
Figure 5: Dependence of carrier image capacity on the
number of polygons for various probabilities.
3.2 Experiment 2
In the previous experiment, the map watermarking
procedure is simulated, but the embedding into real
data is not performed. To confirm the performance
Method for Vector Map Protection based on using of a Watermark Image as a Secondary Carrier
289

of the proposed method for real vector cartographic
data, we have conducted a second experiment using
a fragment of the urban development map containing
9327 polygons (Figure 6). The quantized values of
the corresponding pixels were embedded into each
polygon of the map and then extracted.
Figure 6: Carrier map.
As already mentioned, the proposed map
watermarking method has features that in one way
or another influence the extraction of the binary
vector watermark hidden in the noise-like image:
1) the noise-like image extracted from the map
forms an irregular grid over which interpolation is
performed.
2) despite the fact that when embedding we set pixel
values quantized by a given level, when extraction
these values can be rounded, because to embed a b-
bit number into a polygon without errors, this
polygon should have
1
2
b
vertices (obviously, this
condition may not be met).
Consequently, in addition to confirmation of the
method applicability on real data, this experiment is
aimed at the qualitative assessment of the effect
arising from errors introduced by such data
regarding the model case presented in the previous
experiment.
When modeling data from experiment 1,
interpolation is performed on uniformly scattered
points, and quantization is carried out strictly at a
given level. Thus, in experiment 2 we investigate the
probabilities of the correct extraction from noise-like
images of three types at once:
1) The ideal case (model data from experiment 1).
Interpolation is performed using a mask with evenly
scattered 9327 points superimposed on noise-like
images quantized at a given level.
2) Interpolation is performed on an irregular grid of
9327 pixels extracted from a map (Figure 7)
superimposed on noise-like images quantized at a
given level. This data allow us to trace how the
unevenness of the grid affects the result of
interpolation and the result of extraction in general.
3) Data extracted from the map. This data allow us
to trace how the unevenness of the number of
polygon vertices affects the result of extraction.
To calculate the probabilities of correct
extraction, the experiment is conducted on samples
of size 100 for
10,100L
(in each case, radii are
assigned minimum acceptable values).
Figure 7: Non-uniform interpolation grid.
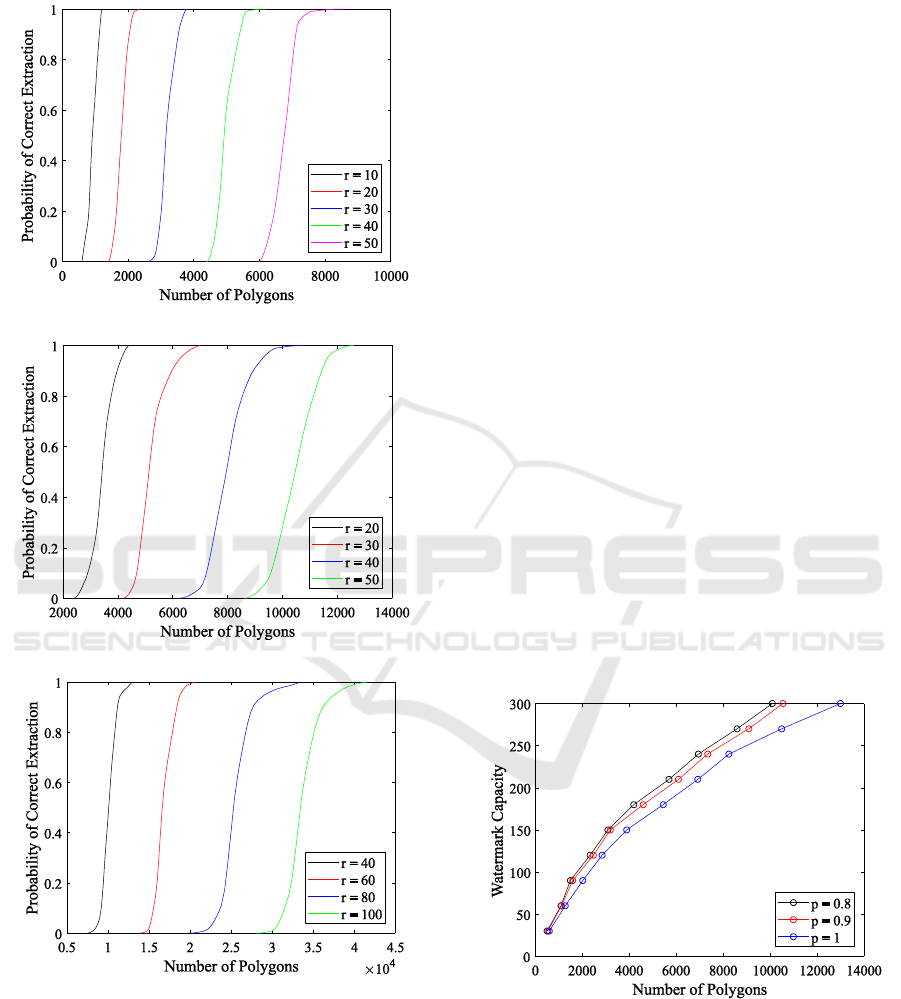
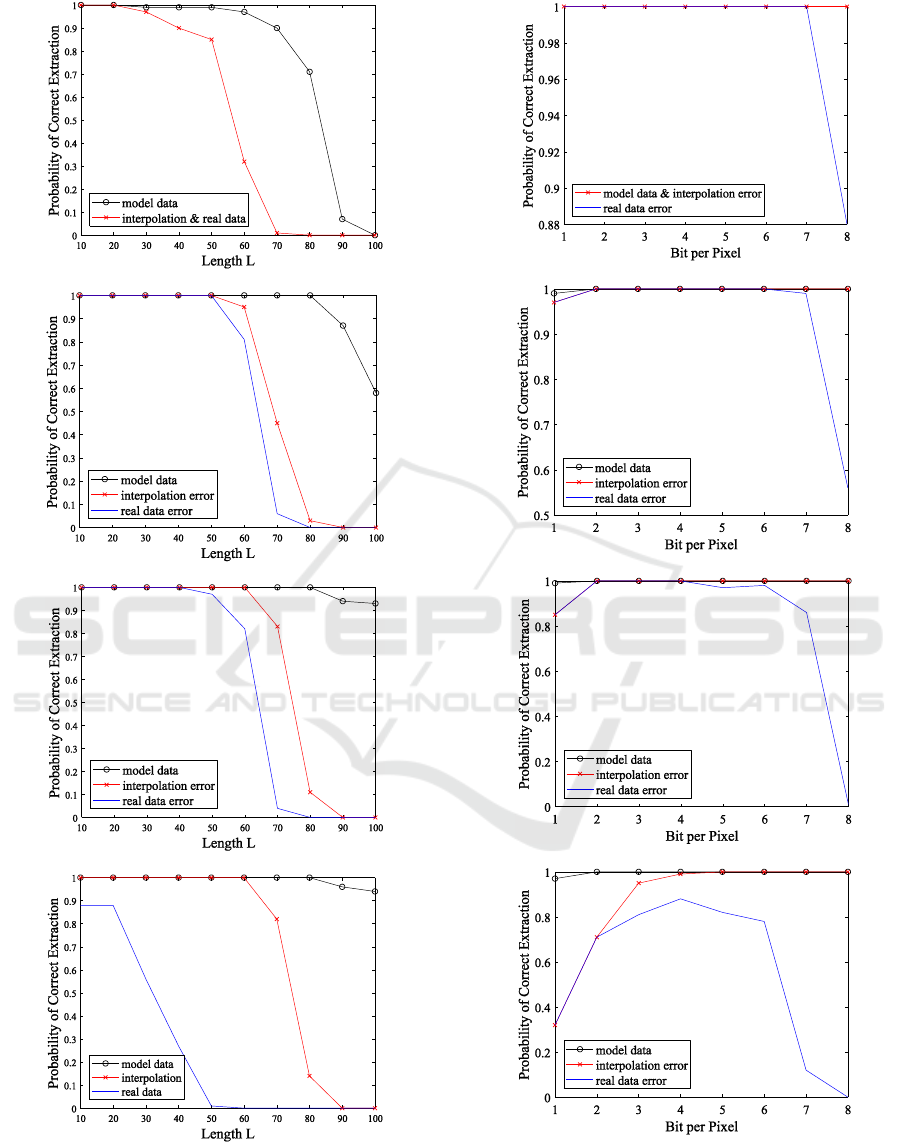
The dependence of the extraction probability on
the length of the bit sequence with varying values of
b are shown in Figure 8.
For b = 1, 2, the result of the real data extraction
error coincides with errors introduced by
interpolation on irregular grid. For b ≥ 3, when
extraction from real data, rounding errors occur, as
discussed above.
The dependence of the extraction probability on
the number of image quantization levels with
varying values of the sequence length are shown in
Figure 9.
The findings of experiment 1 tell us that the
quality of extraction is higher, the greater the b. On
real data, the statement remains true only for
b = 1,2,3,4. The larger L, the greater the drop in
quality when b > 4. When b = 8, extraction is not
possible for any L.
The results obtained for real map data are mostly
influenced from uneven distribution of the number
of vertices in each polygon. Figure 10 shows the
statistics on the number of vertices for the map from
Figure 6.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
290
(a)
(b)
(c)
(d)
Figure 8: The dependence of the extraction probability on
the sequence length for a) b = 1; b) b = 3; c) b = 5; d) b =
8.
(a)
(b)
(c)
(d)
Figure 9: The dependence of extraction probability on the
number of image quantization levels for a) L = 10; b) L
= 30; c) L = 50; d) L = 60; e) L = 70; f) L = 80.
Method for Vector Map Protection based on using of a Watermark Image as a Secondary Carrier
291

(e)
(f)
Figure 9: The dependence of extraction probability on the
number of image quantization levels for a) L = 10; b) L
= 30; c) L = 50; d) L = 60; e) L = 70; f) L = 80 (cont.).
Figure 10: The distribution of the number of vertices for a
fragment of urban development map.
Embedding of a b-bit number into a polygon can
be performed with no errors, if the polygon consists
of at least 2
b-1
vertices. For example, to embed a 3-
bit number, we should take a polygon of 4 vertices.
Such polygons are most likely for maps representing
buildings. Embedding of 5 bits requires 16 vertices,
which is unlikely for the type of vector maps
considered in this paper.
4 CONCLUSIONS
In this paper, we present a study of the
watermarking method for vector cartographic data
based on a cyclic shift of a polygon vertex list. We
propose a method modification to provide an
accurate authentication procedure, as well as to
increase the method robustness against map contents
modification. The main idea of the improved method
is to use a noise-like image as a secondary carrier for
a watermark, represented in the form of a bit vector.
An algorithm for construction of a noise-like image
carrying a watermark sequence, as well as an
algorithm for extraction of such a sequence, are
given. An experimental study explores the
information capacity of the carrier image and its
robustness against quantization and noise adding, i.e.
distortions simulating the embedding into map
objects. The efficiency of the method is also
demonstrated on real cartographic data. Conclusions
comprise optimal parameters for reliable extraction
depending on the number of polygons on the vector
map.
Future work is supposed to be directed towards the
following issues:
1) a development of computationally efficient and
accurate interpolation methods for restoring the
undefined pixels on irregular grid;
2) a study on the watermark robustness against
geometrical transformations and operations
changing the map contents, such as
simplification (vertex removal), interpolation
(vertex addition), object addition / removal,
and layer removal;
3) a development of methods for increasing the
watermark robustness against various types of
attacks on vector map data.
ACKNOWLEDGEMENTS
This work is supported by Russian Foundation for
Basic Research (grant № 19-07-00474 A).
REFERENCES
Abubahia, A. and Cocea, M. (2017). Advancements in
GIS map copyright protection schemes - a critical
review. Multimedia Tools and Applications, 76(10) . –
pp. 12205-12231.
Abubahia, A. and Cocea, M. (2015).A clustering approach
for protecting GIS vector data. In: Advanced
SECRYPT 2019 - 16th International Conference on Security and Cryptography
292

Information Systems Engineering: 27th International
Conference. pp. 133-147.
Cao, L., Men, C. and Ji, R. (2015).High-capacity
reversible watermarking scheme of 2D-vector data.
Signal, Image and Video Processing, 9. –pp. 1387–
1394.
Da, Q., Sun, J., Zhang, L., Kou, L. Wang, W. Han, Q.
and Zhou, R. (2018). A Novel Hybrid Information
Security Scheme for 2D Vector Map. In: Mobile
Networks and Applications. pp. 1-9.
Glumov, N.I. and Mitekin, V.A. (2010). The new
blockwise algorithm for large-scale images robust
watermarking. In: Proceedings of International
Conference on Pattern Recognition. pp. 1453-1456.
Lee, S.H. and Kwon, K.R. (2013). Vector watermarking
scheme for GIS vector map management. Multimedia
Tools and Applications, 63(3). – pp. 757-790.
Peng, F., Yan, Z.J. and Long, M. (2017). A Reversible
Watermarking for 2D Vector Map Based on Triple
Differences Expansion and Reversible Contrast
Mapping. In: International Conference on Security,
Privacy and Anonymity in Computation,
Communication and Storage. pp. 147-158.
Peng, Y. and Yue, M. (2015). A Zero-Watermarking
Scheme for Vector Map Based on Feature Vertex
Distance Ratio. Journal of Electrical and Computer
Engineering, 2015. pp. 1-6.
Peng, Y., Lan, H., Yue, M. and Xue, Y. (2017).
Multipurpose watermarking for vector map protection
and authentication. Multimedia Tools and
Applications, 77(1). – pp. 1-21.
Peng, Z., Yue, M., Wu, X. and Peng, Y. (2015). Blind
watermarking scheme for polylines in vector geo-
spatial data. Multimedia Tools And Applications, 74. –
pp. 11721-11739.
Ren, N., Wang, Q. and Zhu, C. (2014). Selective
authentication algorithm based on semi-fragile
watermarking for vector geographical data In: 22nd
International Conference on Geoinformatics. pp. 1-6.
Vybornova, Y.D. (2018). Application of spatial
interpolation methods for restoration of partially
defined images. CEUR Workshop Proceedings, 2210.
– pp. 89-95.
Vybornova, Y.D. and Sergeev V.V. (2019). A New
Watermarking Method for Vector Map Data. In:
Proceedings of SPIE 11041, Eleventh International
Conference on Machine Vision (ICMV 2018). pp.
1104111 (1-8).
Wang, N., Bian, J. and Zhang, H. (2015). RST Invariant
Fragile Watermarking for 2D Vector Map
Authentication. International Journal of Multimedia
and Ubiquitous Engineering, 10(4). – pp. 155-172.
Wang, N., Zhao, X. and Xie, C. (2016). RST Invariant
Reversible Watermarking for 2D Vector Map.
International Journal of Multimedia and Ubiquitous
Engineering, 11(2). – pp. 265-276.
Wang, Y., Yang, C. and Zhu, C. (2017). A multiple
watermarking algorithm for vector geographic data
based on coordinate mapping and domain subdivision.
In: Multimedia Tools And Applications. pp. 1–19.
Yan, H., Zhang, L. and Yang, W. (2017). A
normalization-based watermarking scheme for 2D
vector map data. Earth Science Informatics, 10(4). –
pp. 471–481.
Zope-Chaudhari, S., Venkatachalam, P. and Buddhiraj, K.
(2017). Copyright protection of vector data using
vector watermark. In: Geoscience and Remote Sensing
Symposium. pp. 6110-6113.
Method for Vector Map Protection based on using of a Watermark Image as a Secondary Carrier
293
