Ensemble Learning based on Regressor Chains: A Case on Quality

Prediction

Kenan Cem Demirel

, Ahmet S¸ahin

and Erinc Albey

Department of Industrial Engineering,

Ozye˘gin University, Istanbul, 34794, Turkey

Keywords:

Industry 4.0, Ensemble Methods, Multi-Target Regression, Regression Chains, Quality Prediction, Textile

Manufacturing.

Abstract:

In this study we construct a prediction model, which utilizes the production process parameters acquired from

a textile machine and predicts the quality characteristics of the ﬁnal yarn. Several machine learning algorithms

(decision tree, multivariate adaptive regression splines and random forest) are used for prediction. An ensem-

ble method, using the idea of regressor chains, is developed to further improve the prediction performance.

Collected data is ﬁrst segmented into two parts (labeled as “normal” and “unusual”) using local outlier factor

method, and performance of the algorithms are tested for each segment separately. It is seen that ensemble

idea proves its competence especially for the cases where the collected data is categorized as unusual. In such

cases ensemble algorithm improves the prediction accuracy signiﬁcantly.

1 INTRODUCTION

With the advances in communication technologies,

data gathering from machines and processes at in-

dustrial plants becomes easier. Industrial internet-

of-things (IIoT) revolution along with the fog com-

puting idea, change the way data is being treated in

manufacturing plants. Live data from manufacturing

processes, machines and products are being collected

with high resolution and executing advance analytic

tasks at the industrial plant premises becomes possi-

ble. Considering the analytics efforts in the manufac-

turing plants, it is seen that quality prediction and pre-

dictive maintenance stand out as the most frequently

addressed analytics application examples.

In this paper we focus on a quality prediction ap-

plication at a textile plant, Deteks Fashion Co.Ltd. We

ﬁrst implement a set of well-known machine learn-

ing algorithms (decision tree, multivariate adaptive

regression splines and random forest) with proven

performance in quality prediction. For each model,

the performance is tested by using three different

quality metrics. Considering the performance of im-

plemented machine learning algorithms, we propose

an ensemble algorithm, which is based on regressor

https://orcid.org/0000-0002-5398-378X

https://orcid.org/0000-0002-9223-3420

https://orcid.org/0000-0001-5004-0578

chain idea. The most important ﬁnding of the paper

is that once production is taking place different than

the usual settings, prediction accuracy of the classical

machine learning algorithms signiﬁcantly drops for

some quality metrics. For such cases, the ensemble

algorithm turns out to be useful, yielding lower pre-

diction error in two thirds of the dataset.

The rest of the paper is organized as follows.

Section 2 provides brief background information on

the textile manufacturing process and outlines the

methodology used in the study. Section 3 presents

the data and results of the numerical analysis. Final

section lists the concluding remarks.

2 BACKGROUND AND

METHODOLOGY

2.1 Textile Manufacturing Processes

Textile manufacturing process we chose to analyze

mainly consists of three main processes: 1) warp-

ing, 2) weaving, 3) ﬁnishing. In the ﬁrst stage, yarns

are made suitable for weaving by passing through the

winding, unraveling, sizing, weaving draft and knot-

ting steps. In these steps, the yarns are wrapped in

desired tension and order, and subjected to various op-

erations to gain strength. In the weaving process, the

Demirel, K., ¸Sahin, A. and Albey, E.

Ensemble Learning based on Regressor Chains: A Case on Quality Prediction.

DOI: 10.5220/0007932802670274

In Proceedings of the 8th International Conference on Data Science, Technology and Applications (DATA 2019), pages 267-274

ISBN: 978-989-758-377-3

267

fabrics are subjected to mouth opening, weft insertion

and tufting to ensure that the warp and weft yarns in-

tersect. In the ﬁnishing stage, which is the last stage

of production, the desired color, touch and special ef-

fects are provided to the fabric. After these manufac-

turing stages, some samples are taken randomly from

the ﬁnal product to conduct various quality control

tests in laboratory.

In this work, we concentrate on the ﬁnishing pro-

cess and integrate our algorithm into the production

process of the ﬁnishing machine such that production

parameters and information from the incoming fabric

constitute the input for the algorithm; and the qual-

ity data (output) of the process is obtained from con-

ducted laboratory tests. Collected input and outputs

are matched with each other by using time mapping

scenarios, in which time tags in the database is taken

into account. The input data is collected through data

collection devices (i.e. gateways) and programmable

logic controller (PLC) of the ﬁnishing machine. The

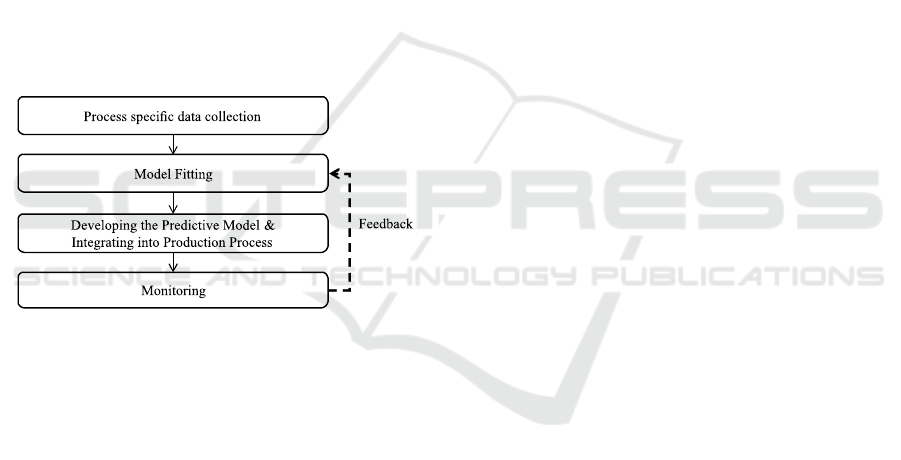
general ﬂowchart of proposed methodology is pre-

sented in Figure 1.

Figure 1: Framework of the proposed method.

As can be seen in Figure 1, after process speciﬁc

data is collected, a model ﬁtting phase is executed.

Details of the selected models are presented in the

next subsections. We ﬁrst present the multi-target re-

gression and regression chain idea, then list the pre-

dictive models used in the study. After model ﬁtting,

the selected model (or models) are integrated into

PLC and production is tarted to be monitored with live

quality predictions. A natural next step is integrating

an auto-learning mode (through feedback from pro-

cess data), which enables re-learning of the model

parameters in the course of the production, without

manual intervention.

2.2 Multi-Target Regression

Multi-Target Regression (MTR) or Multi-Output Re-

gression indicates regression models which uses a

common training set (input variables) to predict mul-

tiple targets (output variables). In a literature sur-

vey about MTR methods by (Borchani et al., 2015),

there are mainly two ideas behind the MTR meth-

ods in literature: transforming multi-target problems

into single-target (ST) problems, then applying tra-

ditional regression models and concatenating the re-

sults such as Multi-Target Regressor Stacking (MTS)

(Spyromitros-Xiouﬁs et al., 2012), Regressor Chains

(RC) (Spyromitros-Xiouﬁs et al., 2012) and Multi-

Output SVR (MO-SVR) (Zhang et al., 2012); or using

algorithm adaptation methods which have the abil-

ity to capture internal relationships between the target

variables, such as Churds and Whey method (Simil¨a

and Tikka, 2007), Simultaneous Variable Selection

(Struyf and Dˇzeroski, 2005), Multi-Target Regres-

sion Trees (De’Ath, 2002) and extended MO-SVR

(Vazquez and Walter, 2003).

According to the benchmark comparison con-

ducted on twelve different datasets with different

shapes, statistical methods fail to improve ST regres-

sion results in cases where a true and linear relation-

ship between outputs is not veriﬁed; rather they could

produce a detriment of the predictive performance

(Borchani et al., 2015). On the other hand, some other

algorithm adaptation methods (e.g. MO-SVR) bene-

ﬁt only in terms of calculation time and complexity

reduction, while the regression trees method achieves

improvement in predictive performance as well, com-

pared to the ST approach. In addition to these ﬁnd-

ings, a clear inference could not be made about the

beneﬁt of problem transformation methods (MTS and

RC). This is because the predictive performance of

MTS and RC approaches is so sensitive in the ran-

domization process of these approaches (e.g. due to

the order of the chain) (Borchani et al., 2015).

MTS and RC methods are ﬁrstly introduced as

extensions of problem transformation approaches of

multi-label classiﬁcation in the multi-target regres-

sion context. These two methods are basically based

on the approach of training independent single-target

regression models for each target variables and train-

ing a comprising model by augmenting the input

space dimensions with gathered prediction results. In

this paper, we are going to focus on a real-life appli-

cation of RC approach and its extension Ensemble of

Regressor Chains (ERC) proposed in (Spyromitros-

Xiouﬁs et al., 2012).

2.2.1 Regressor Chains and Ensemble of

Regressor Chains

RC is inspired by the Classiﬁer Chains method and

the main idea behind it is chaining single-target mod-

els. RC is based on building of regression models for

each target variable by sequentially training the tar-

gets in order of a randomly determined chain. For the

ﬁrst target variable selected within the speciﬁed se-

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

268

quence of the chain, the regression model is trained

independently of the other target variables, and the

predicted target values are added to the training set

as a new input vector for prediction of the next target

variable. The regression model of the new target vari-

able within the chain sequence is trained with the re-

sulting augmented input matrix and the same process

is repeated for all subsequent targets in the chain.

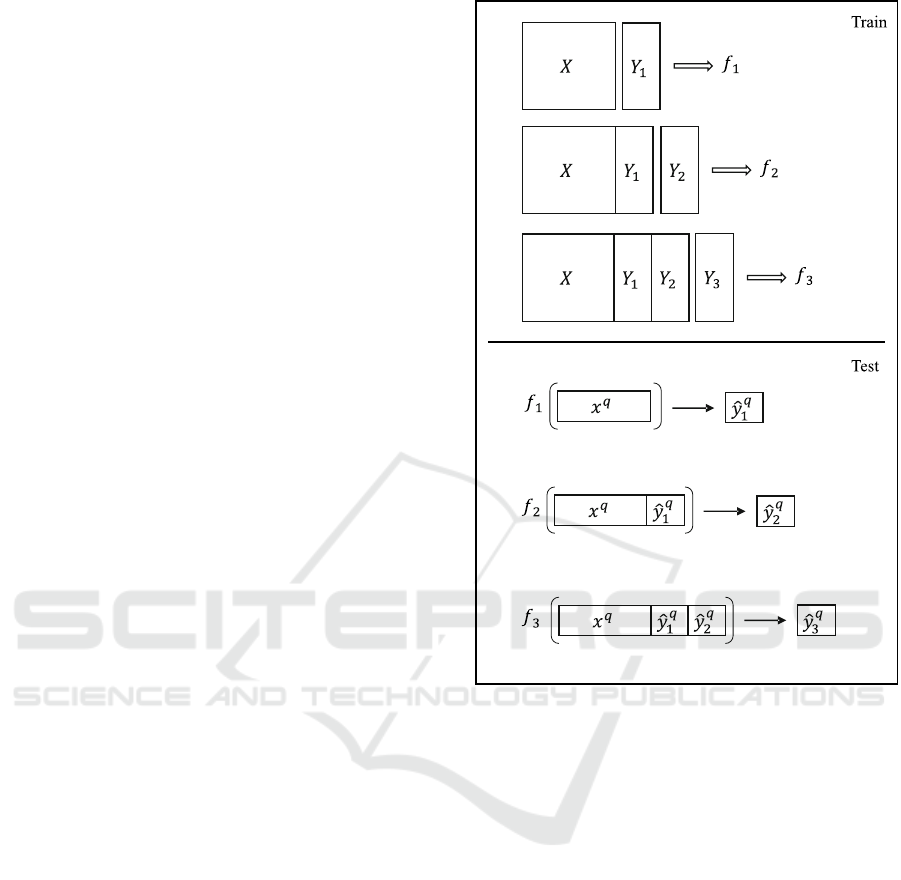
Graphical illustration of RC is shown in Figure 2.

In the illustration, there are three output (target) vari-

ables (y

, y

, and y

) and training input data (X). In

the ﬁrst stage of training process starts with ﬁtting a

model (f

) for the ﬁrst output variable (y

) by using

base inputs (X). Then, in the second stage, a new

model (f

) is ﬁtted for the second output variable (y

)

by using modiﬁed input that is created with concate-

nating base inputs (X) and the actual values of the ﬁrst

output (y

). Finally, f

is created by using the third

output variable (y

) and concatenated data (X,y

, and

) in the third stage.

In testing process, predictions for the ﬁrst output

(ˆy

) are made by using (f

). Then, the ﬁrst predic-

tions are added to the test input data (x

), and it is

used for predicting the second output (ˆy

) by model

). In the last step, ﬁrst two predictions (ˆy

, and ˆy

)

concatenated with the test input data (x

), and ˆy

predicted by model 3 (f

The main problem of this method is that the ran-

domness in determining chain sequence causes signif-

icant differences in predictive performance. In order

to avoid this problem, ERC method is proposed by

(Spyromitros-Xiouﬁs et al., 2012). The ERC method

suggests using a set of regression chains consisting of

all possible chains or a group of chains which is ran-

domly selected if the output dimension is too high,

in an ensembled structure. After determining the set

of chain sequences, the ERC approach predicts the

target variable for each stage of the chain and ﬁnally

presents their averages as predicted values for each

target variable.

The difference between RC and ERC is that RC

takes the single prediction for each output in a certain

sequence. However, ERC makes predictions for all

permutations of sequence and gives the ﬁnal predic-

tion as the average of all predictions for each output.

2.3 Predictive Models

MTR is a meta-learner which can use different es-

timators and set of learning sequences in a pre-

determined conﬁguration. In this part, we introduce

three common regression techniques to conduct a

benchmark test and determine the most appropriate

one to apply our dataset. These estimators are: 1) De-

Figure 2: Graphical illustration of RC.

cision Tree Regressor, 2) Random Forest Regressor,

and 3) Multivariate Adaptive Regression Splines.

2.3.1 Decision Tree Regressor

Decision Tree induction is one of the most important

supervised learning methods which is used for clas-

siﬁcation and regression. Decision Tree Regressor

constructs a ﬂowchart-like structure where each in-

ternal (non-leaf) node denotes a test on an attribute,

each branch corresponds to an outcome of the test,

and each external (leaf) node denotes a class predic-

tion. At each node, the algorithm chooses the “best”

attribute to partition the data into individual classes

(Han et al., 2011). The main idea here is to create

a decision tree model that minimizes error on each

leaf. Different algorithms may be applied to build

decision threes such as Classiﬁcation and Regression

Trees (CART) which uses Gini Index as metric and

Iterative Dichotomiser 3 (ID3) which uses Entropy

function and Information gain as metrics (Quinlan,

1986). We used Gini method in CART algorithm.

Ensemble Learning based on Regressor Chains: A Case on Quality Prediction

269

2.3.2 Random Forest Regressor

Random Forest is an ensemble learning method that

aims to improve predictiveaccuracy and preventover-

ﬁtting by ﬁtting multiple decision trees on various

sub-samples of the dataset and combining them un-

der a single meta-estimator (Breiman, 2001). Ran-

dom Forest Regressor (RF) uses the average predic-

tion for regression of trees which are constructed by

training on different data sample. These samples are

created by Bootstrap Aggregation (or bagging).

2.3.3 Multivariate Adaptive Regression Splines

Multivariate Adaptive Regression Splines (MARS)

is a non-parametric extension of the standard linear

model without any assumption about the underlying

functional relationship between the dependent and in-

dependent variables. MARS model is obtained by

using combination of piece-wise basis functions, for-

ward and backward passing procedures in the regres-

sion models. Each term in a MARS model is a prod-

uct of so called “hinge functions”. A hinge function

is a function that’s equal to its argument where that

argument is greater than zero and is zero everywhere

else (Friedman et al., 1991).

MARS builds a model which is formed follow-

ingly:

f(x) =

∑

i=0

), (1)

where x is a vector of sample features, B

is a piece-

wise function that consists of a set of basis functions

and c

the coefﬁcient. Basis function may behave in

three different ways based on the input range: First, it

can be constant 1, to reduce bias. Second, it can be a

hinge function h(x) = max(0, x −t) or max(0,t −x),

where t is a constant, so the model represents non-

linearities. Third, it can be a product of multiple hinge

functions to combine interactions between features.

3 EXPERIMENTAL SETUP

3.1 Dataset

In this study, we apply the algorithms to dataset ob-

tained from paired process data (signals) of textile

manufacturing. There are total of 1,511 rows, one row

for each lab sample in dataset, and each lab sample

has 19 signal values, such that weaving speed, tem-

perature, and yarn tension, as input for algorithms;

and 3 quality metrics, water permeability (Metric 1),

tear strength (Metric 2), and abrasion resistance (Met-

ric 3), that are obtained after lab sample assessed in

the laboratory as output of algorithms.

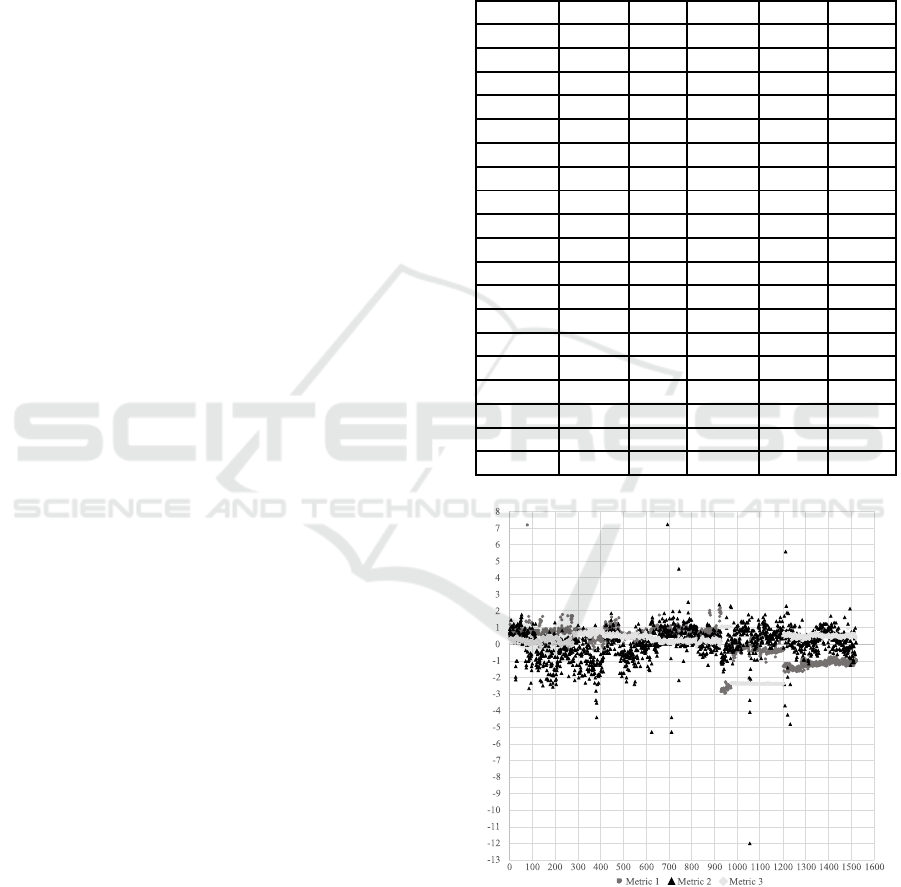
The statistical summary of the 19 features is

shown in Table 1. Also, the Z-normalization of tar-

get metrics 1, 2 and 3 is given in Figure 3.

Table 1: Feature Summary Statistics.

Feature Mean Std CoV* Min Max

0 70.0 1.0 0.0 65.7 74.5

1 -10.8 1.2 -0.1 -14.5 -7.7

2 -4.2 1.2 -0.3 -8.5 -2.2

3 -0.2 0.1 -0.3 -0.4 0.0

4 -0.3 0.2 -0.5 -0.3 0.0

5 7.4 2.1 0.3 0.0 14.8

6 31.9 2.6 0.1 28.5 53.7

7 302.9 77.1 0.3 198.9 401.4

8 27.2 0.0 0.0 27.2 27.2

9 37.9 0.0 0.0 37.9 37.9

10 25.2 2.8 0.1 20.3 31.8

11 49.9 4.1 0.1 42.3 57.3

12 63.0 6.9 0.1 44.4 70.4

13 28.3 1.6 0.1 23.2 32.3

14 25.3 2.2 0.1 18.8 31.8

15 152.6 4.9 0.0 143.4 163.7

16 146.5 8.8 0.1 119.1 154.6

17 225.8 0.6 0.0 225.1 226.3

18 20.7 1.5 0.1 17.7 25.2

*CoV: Coefﬁcient of Variation

Figure 3: Distribution of Target Data.

After examining the target data, it is observed that

the variance of Z-values of Metric 2 is much higher

than that of other metrics. Feature importance anal-

ysis is performed for each metric to see whether the

characteristics of Metric 3 shows similarities in terms

of ability to be expressed by features. Analysis results

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

270

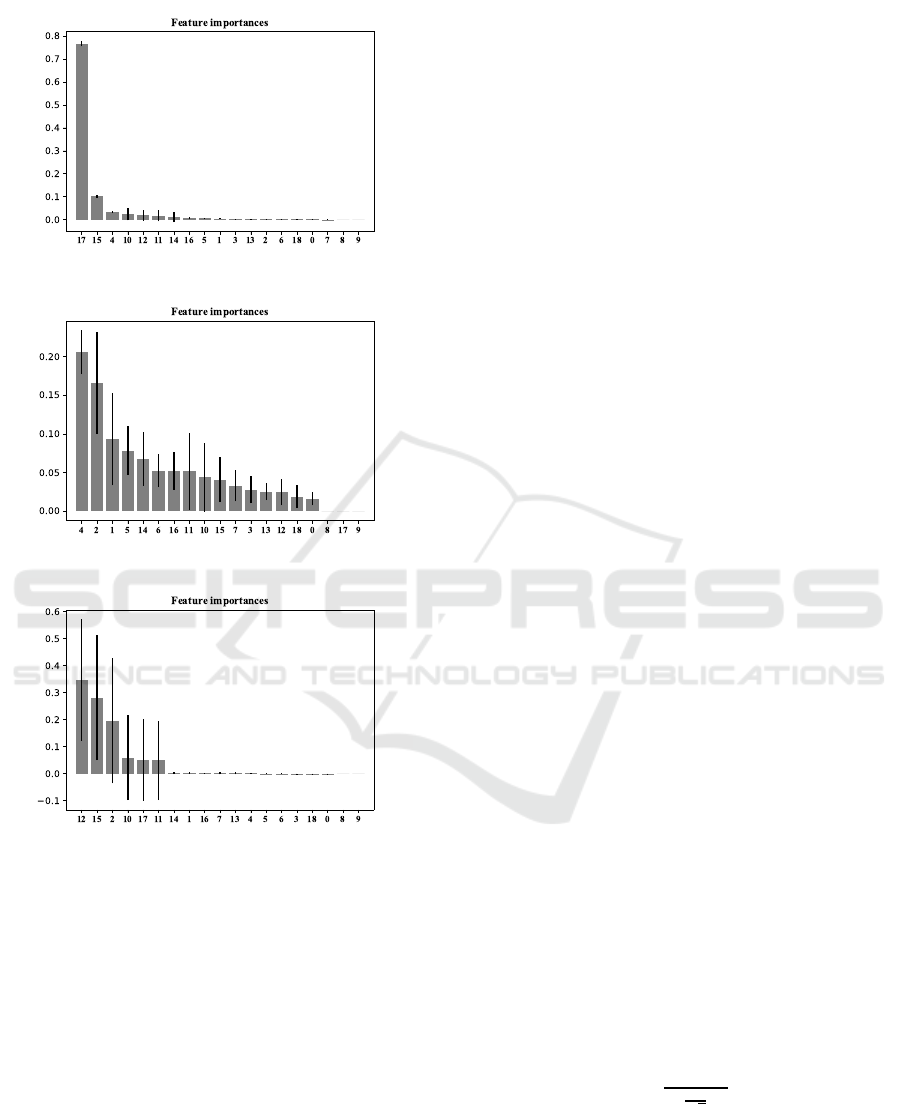
can be seen in Figure 4, 5 and 6.

Figure 4: Feature Importance of Metric 1.

Figure 5: Feature Importance of Metric 2.

Figure 6: Feature Importance of Metric 3.

According to the feature importance analysis,

while there are at least one features have minimum

of 20% importance on Metric 1 and 3, the importance

rate of all features are less than 20% for Metric 2. In

this sense, it can be concluded that Metric 2 is dis-

advantageous compared to other metrics in terms of

both the distribution character and the power to be ex-

pressed by existing feature set.

3.2 Outlier Detection

In order to obtain the most suitable models for the

natural characteristics of production process, the data

is divided into clusters according to the Local Outlier

Factor (LOF) method (Breunig et al., 2000). For any

given data instance, the LOF score is equal to ratio of

average local density of the k-nearest neighbors of the

instance and the local density of the data instance it-

self (Chandola et al., 2009). The local density of each

sample is compared with the local densities of the

neighbors and the samples with signiﬁcantly lower

density than their neighbors are speciﬁed as outliers.

In this study, the number of neighbors, k, is assumed

as 10, and the cluster which has greatest dissimilar-

ity is extracted and labeled as “unusual”. Segmen-

tation yields two segments of size 1,431 (“normal”

segment) and 80 (“unusual” segment). We divide the

“normal” dataset further into training and testing sets,

which have 1,144 and 287 data points respectively.

In the next section, we use several machine learn-

ing algorithms and compare their prediction perfor-

mance using a series of statistical analysis. The anal-

ysis conducted in two major steps. First, analysis

regarding the “normal” data is presented. Then, the

analysis for the “unusual” data is presented, where it

is seen that the ensemble of regressor chains signiﬁ-

cantly outperforms the single target model.

3.3 Implementation and Analysis

In the ﬁrst step of the numerical analysis, single-target

regression models are created for each metric in the

“normal” dataset. Then, the best performing single-

target regression model is selected to be compared

with the ERC model. During the comparisons, we use

MAPE as the key performance metric and conduct a

set of statistical tests/analysis, which are vector com-

parison, paired t-test and one-way ANOVA test. In

the second step, similar comparison between single-

target regression model and ERC is conducted using

the “unusual” dataset.

For the sake of completeness, we present the de-

tails of the metrics, statistical tests and analysis we

use during the comparison.

In paired t-test, the mean of the observed values

for a variable from two dependent samples are paired

and compared. As we use different algorithms to pre-

dict the same set of data points, pairing is direct pos-

sible as a natural consequence of the process. The test

is used to decide whether the sample means compared

are identical or not. The differences between all pairs

are calculated by the following equation:

t =

−µ

√

., (2)

where

and s

are the mean and standard devia-

tion of those differences, respectively. The constant

equals to zero if the underlying hypothesis assumes

the two samples are coming from populations with

identical means, and n represents the number of pairs.

Ensemble Learning based on Regressor Chains: A Case on Quality Prediction

271

The one-way ANOVA test compares whether

mean of two or more samples are the same. The main

assumptions of ANOVA test is that the distribution of

each sample is normal and the samples are indepen-

dent.

In vector comparison analysis, algorithms are

scored for their prediction performance for each and

every data point separately. The algorithm yielding

the minimum absolute percentage error for the given

data point receives 1 (winner), others receive 0. Test

results for MAPE comparison, vector comparison and

t-test comparison are given in Table 2, Table 3, Table

4 and Table 5 respectively. In Table 2, test and (train)

errors are given respectively.

Table 2: MAPE Comparison for ST Models.

RF DTR MARS

Metric 1 0.020 0.023 0.027

(0.011) (0.017) (0.024)

Metric 2 0.045 0.046 0.047

(0.030) (0.044) (0.046)

Metric 3 0.003 0.030 0.007

(0.002) (0.030) (0.007)

Table 3: Vector Comparison.

RF DTR MARS

Metric 1 126 78 83

Metric 2 95 104 88

Metric 3 132 107 48

Table 4: Paired t-test Comparison.

y− ˆy

DTR

y− ˆy

MARS

Metric 1 0.818 0.694 0.914

Metric 2 0.621 0.459 0.536

Metric 3 0.982 0.398 0.275

Table 5: One-way ANOVA Comparison.

p-value

Metric 1 0.935

Metric 2 0.983

Metric 3 0.308

When the MAPE values are examined, it is ob-

served that the values are very close to each other

but the best test results are obtained by RF for three

metrics. The best results for Metric 1 and Metric 3

are taken by RF in the vector comparison, whereas

MARS model predicted nine lab samples better than

RF for Metric 2.

Paired t-test results presented in Table 4 reveal

that all predictions yielded residuals with zero mean.

For the constant variation assumption, RF model’s

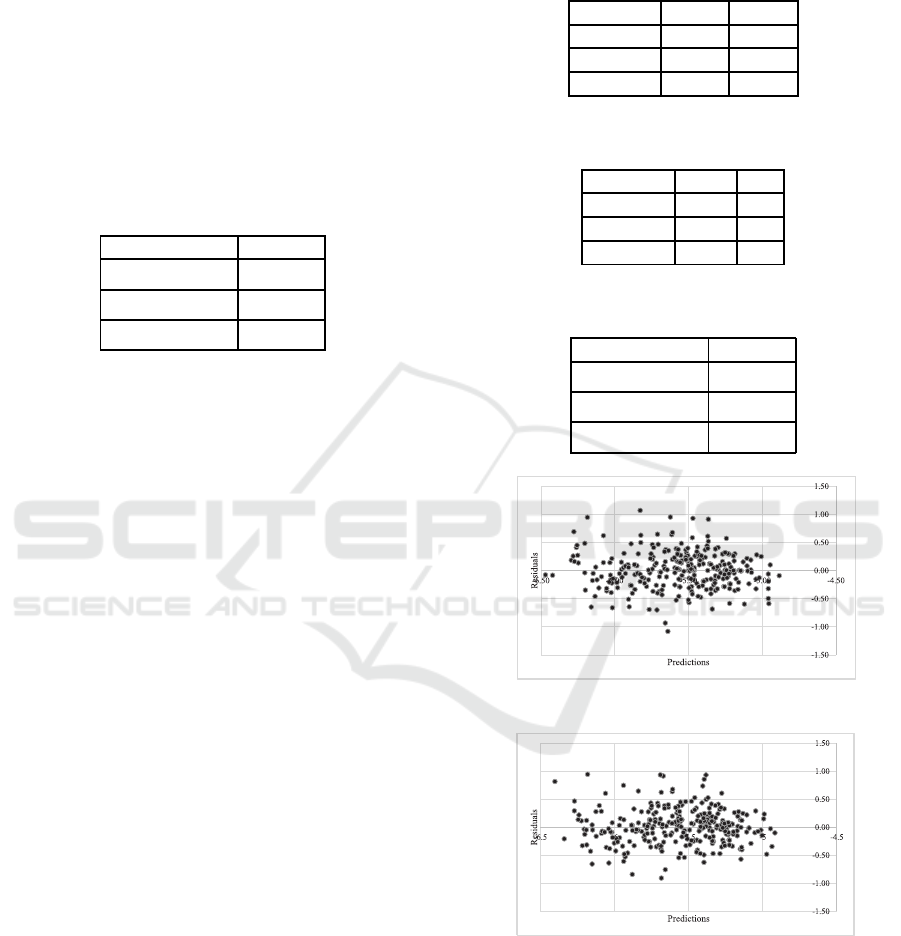
residual vs. ﬁtted plot for Metric 2 is presented in

Figure 7. Figure 7 reveals that there is no indication

for the violation of constant variation assumption.

Following these, analyzes it is determined that

working with RF would be more appropriate for this

dataset and it is chosen as the baseline model.

The noteworthy point here is that the MAPE value

of Metric 2 is higher than MAPE values of other two

variables. In order to better understand the relation-

ship between outputs, correlation between the output

values are measured and it is seen that there is no lin-

ear relationship between the output of Metrics 1-2 and

2-3 as shown in Table 6.

Table 6: Correlation Matrix of Output Variables.

Metric 1 Metric 2 Metric 3

Metric 1 1 -0.019 0.018

Metric 2 -0.019 1 -0.200

Metric 3 0.018 -0.200 1

At this point, multi-output regression approach

can be seen as an opportunity to improve the rela-

tively bad performance we observe for Metric 2. With

the regressor chains method, all input and output vari-

ables can be evaluated together, thus the dependencies

and internal relationships between them that have a

positive impact on the predictive performance may be

unveiled (Borchani et al., 2015). Since we have small

number of outputs, regression models are trained for

all possible chain sequences by applying the ERC

framework, and the mean of the predicted values from

each model are recorded as ﬁnal predictions. MAPE

comparison, vector comparison and paired t-test re-

sults are shown in Table 7, Table 8 and Table 9.

Table 7: ERC vs ST Mape Comparison for testing.

ERC ST

Metric 1 0.019 0.020

Metric 2 0.042 0.045

Metric 3 0.003 0.003

Table 8: ERC vs ST Vector Comparison for testing.

ERC ST

Metric 1 159 129

Metric 2 150 138

Metric 3 133 155

According to Table 7, ERC approach provides %5

and %4.5 improvement over the performance of ST

in predicting Metric 1 and Metric 2 respectively. The

beneﬁt of the ERC approach for Metric 1 and 2 is also

obvious in the vector comparison test. For Metric 3,

on the other hand, the number of predictions with im-

proved error value is small. This can be explained by

the fact that the given MAPE value is already very

low for that metric. In other words, we can conclude

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

272

that Metric 3 is easy to predict compared to predicting

Metric 1, and especially Metric 2. It is seen in Table 9

that there is no evidence to conclude that ERC method

is superior to ST method in predicting Metric 1 and

3, since the p-values for the test statistic for compar-

ing residual vectors for ERC and ST are larger than

the conventional signiﬁcance level threshold 0.05. On

the other hand, result for Metric 2 conveys a different

message. It is seen that prediction performance ERC

is signﬁcantly better that of ST at 0.05 signiﬁcance

level.

Table 9: ERC vs ST residuals t-test Comparison for testing.

represents residual vector of algorithm i for metric j.

Residuals p-Value

ERC

−

0.115

ERC

−

0.025

ERC

−

0.382

In the second phase of the analysis, the effect of

the ERC approach on predictive performance is mea-

sured for “unusual” dataset. Since this piece of the

dataset is outside of the general production character-

istics, it is obvious that the regression models which

are trained by the data that has usual production pa-

rameters will give worse results for this set.

The results of Metric 2, which are already rela-

tively poor, will be worsened for the “unusual” data

segment. However, with ERC approach, the unveiled

internal relations between target and input variables

provide some improvement in the prediction accu-

racy. Comparison results are presented in Table 10,

Table 11 and Table 12.

It is seen in MAPE comparison table that ERC ap-

proach provides %6.9, %8 improvement for Metric 1

and 2, respectively. The apparent superiority of the

ERC approach compared to the ST is clearly seen in

vector comparisons as well. For Metric 2, ST beats

ERC in prediction of only 29 samples, whereas the

ERC beats ST in 51 samples. It is seen in Table 12

if the signiﬁcance level is chosen tobe 0.1, then ERC

dominates ST in all three metrics. On the other hand,

when the signiﬁcance level is set to 0.05, then we may

say there is not enough evidence to conclude that ERC

method is superior to ST method in predicting Metric

3. However, for Metric 1 and 2, ERC signiﬁcantly

outperfoms in ST approach even at 0.05 threshold.

As the ﬁnal analysis, we present residual vs. ﬁtted

plots for i) ST and ERC models (for Metric 2 under

“normal” test dataset) in Figure 7 and Figure 8; and

ii) ST and ERC models (for Metric 2 under “unusual”

test dataset) in Figure 9 and Figure 10 . Residual anal-

yses of ST and ERC for other metrics (for both normal

and unusual test datasets) are behaving similar char-

acteristics.

Table 10: ERC vs ST Mape Comparison for unusual seg-

ment.

ERC ST

Metric 1 0.027 0.029

Metric 2 0.127 0.138

Metric 3 0.004 0.004

Table 11: ERC vs ST Vector Comparison for unusual seg-

ment.

ERC ST

Metric 1 43 37

Metric 2 51 29

Metric 3 44 36

Table 12: ERC vs ST residuals t-test Comparison for un-

usual segment.

Residuals p-Value

ERC

−

0.006

ERC

−

ERC

−

0.078

Figure 7: ST-Prediction vs Residuals for Metric 2 in testing.

Figure 8: ERC-Prediction vs Residuals for Metric 2 in test-

ing.

It is seen in Figure 7 and Figure 10 that resid-

uals are scattered randomly around mean zero with

constant variance. This indicates that both predictive

models are adequate in modeling the variation in the

response variables in “normal” test data.

Similar to the above discussion, it is seen Figure 7

and Figure 10 that residuals can be assumed to have

Ensemble Learning based on Regressor Chains: A Case on Quality Prediction

273

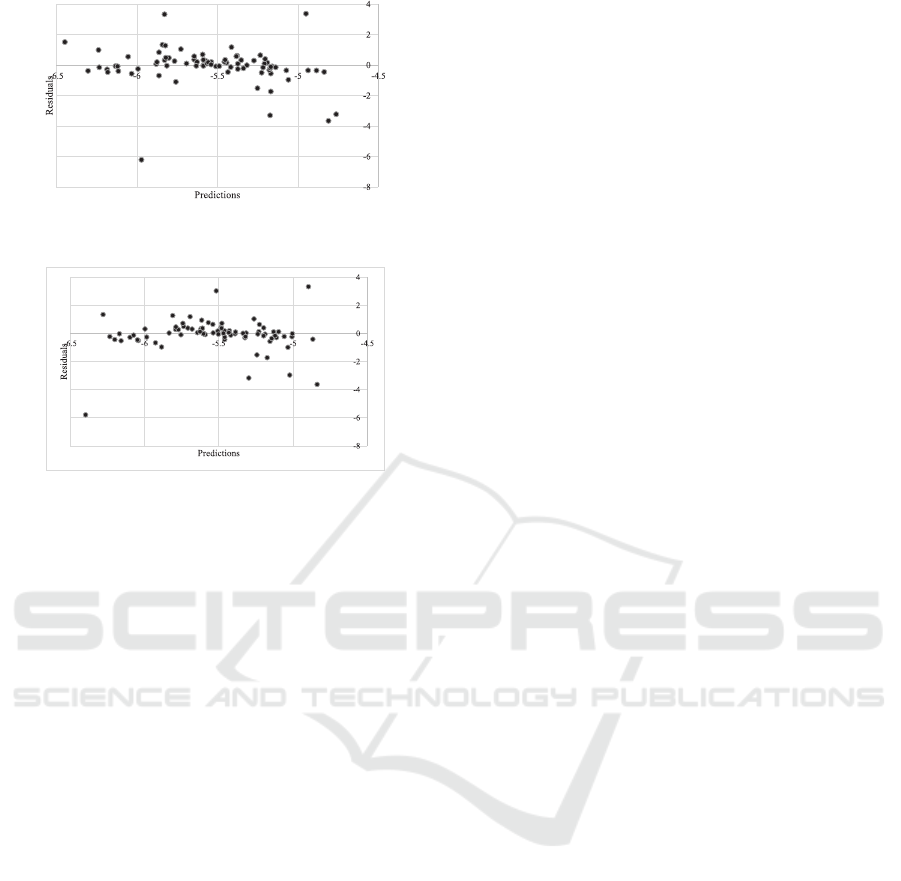
Figure 9: ST-Predictionvs Residuals for Metric 2 in unusual

segment.

Figure 10: ERC-Prediction vs Residuals for Metric 2 in un-

usual segment.

zero mean value and show a constant variation be-

haviour, which is again can be seen as an indication

that both predictive models are adequate in modeling

the variation in the response variables in ”unusual”

test data. Although we observe some outliers in the

residuals. we could say that this is normal consider-

ing that the ”unusual” dataset is statistically different

than the dataset we train our machine learning algo-

rithms.

4 CONCLUSION

In this paper we proposedan ensemble machine learn-

ing algorithm in order to predict the ﬁnished yarn

quality. The data is ﬁrst segmented into ten clusters

nine of which is denoted as ”normal” and the one

with the highest distance from the general mean as

”unusual” via local outlier factor method. The former

cluster refers to production data one may expect due

to the nature of the process and latter is the dataset

showing an usual pattern compared to expected pro-

cess data. Then a set of classical machine learning

algorithms are applied and performances of the algo-

rithms is compared. It is seen that for the unusual

segment, performance of the classical algorithms gets

worse especially for one of the quality metrics. As

a remedy, an ensemble algorithm based on regressor

chains is recommended and yielding higher predic-

tion performance in two thirds of the dataset.

As the next step, implemented algorithm will be

fully tested at the facility. If the prediction perfor-

mance remains satisfactory, we’re going to move on

the next phase and start using the predictive tool as a

recommendation engine for the machine operator. At

this stage, operator will be informed about the sug-

gested production settings for the machine and the

recommendation system will perform as a decision

support tool, meaning that the recommendations of

the tool are push forward to the machine only if the

operator gives consent. Once the second phase is suc-

cessful, the recommendation engine will be plugged

into PLC and start changing set parameters of the ma-

chine as a part of the automation system. After the

third phase, the manufacturing plant will have its ﬁrst

full-scale industry 4.0 application.

REFERENCES

Borchani, H., Varando, G., Bielza, C., and Larra˜naga, P.

(2015). A survey on multi-output regression. Wiley

Interdisciplinary Reviews: Data Mining and Knowl-

edge Discovery, 5(5):216–233.

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

Breunig, M. M., Kriegel, H.-P., Ng, R. T., and Sander, J.

(2000). Lof: identifying density-based local outliers.

In ACM sigmod record, volume 29, pages 93–104.

ACM.

Chandola, V., Banerjee, A., and Kumar, V. (2009).

Anomaly detection: A survey. ACM computing sur-

veys (CSUR), 41(3):15.

De’Ath, G. (2002). Multivariate regression trees: a new

technique for modeling species–environment relation-

ships. Ecology, 83(4):1105–1117.

Friedman, J. H. et al. (1991). Multivariate adaptive regres-

sion splines. The annals of statistics, 19(1):1–67.

Han, J., Pei, J., and Kamber, M. (2011). Data mining: con-

cepts and techniques. Elsevier.

Quinlan, J. R. (1986). Induction of decision trees. Machine

learning, 1(1):81–106.

Simil¨a, T. and Tikka, J. (2007). Input selection and shrink-

age in multiresponse linear regression. Computational

Statistics & Data Analysis, 52(1):406–422.

Spyromitros-Xiouﬁs, E., Tsoumakas, G., Groves, W.,

and Vlahavas, I. (2012). Multi-label classiﬁcation

methods for multi-target regression. arXiv preprint

arXiv:1211.6581, pages 1159–1168.

Struyf, J. and Dˇzeroski, S. (2005). Constraint based induc-

tion of multi-objective regression trees. In Interna-

tional Workshop on Knowledge Discovery in Inductive

Databases, pages 222–233. Springer.

Vazquez, E. and Walter, E. (2003). Multi-output supp-

port vector regression. IFAC Proceedings Volumes,

36(16):1783–1788.

Zhang, W., Liu, X., Ding, Y., and Shi, D. (2012). Multi-

output ls-svr machine in extended feature space.

In 2012 IEEE International Conference on Compu-

tational Intelligence for Measurement Systems and

Applications (CIMSA) Proceedings, pages 130–134.

IEEE.

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

274