
Modeling Dynamic Processes with Deep Neural Networks: A Case Study
with a Gas-fired Absorption Heat Pump
Jens Lippel, Martin Becker and Thomas Zielke
University of Applied Sciences D
¨
usseldorf, M
¨
unsterstr. 156, 40476, D
¨
usseldorf, Germany
Keywords:
Deep Neural Networks, Machine Learning, Dynamic Processes, Gas-fired Absorption Heat Pump, Simulation,
Modeling.
Abstract:
Deriving mathematical models for the simulation of dynamic processes is costly and time-consuming. This
paper examines the possibilities of deep neural networks (DNNs) as a means to facilitate and accelerate this
step in development. DNNs are machine learning models that have become a state-of-the-art solution to a
wide range of data analysis and pattern recognition tasks. Unlike mathematical modeling approaches, DNN
approaches require little to no domain-specific knowledge. Given a sufficient amount of data, a model of the
complex nonlinear input-to-output relations of a dynamic system can be learned autonomously. To validate
this DNN based modeling approach, we use the example of a gas-fired absorption heat pump. The DNN is
learned based on several measurement series recorded during a hardware-in-the-loop (HiL) simulation of the
heat pump. A mathematical reference model of the heat pump that was tested in the same HiL environment is
used for a comparison of a mathematical and a DNN based modeling approach. Our results show that DNNs
can yield models that are comparable to the reference model. The presented methodology covers the data
preprocessing, the learning of the models and their validation. It can be easily transferred to more complex
dynamic processes.
1 INTRODUCTION
Heat pumps are complex nonlinear dynamic systems
with several input and output variables. It has long
been known that artificial neural networks (ANNs)
are suited for the empirical modeling of such systems
(Carriere and Hamam, 1992). The modeling is based
on measurements of the input and output variables of
a real system in its relevant operation conditions and
can often be realized without any prior knowledge
about the system behavior. An ANN uses the mea-
surements to approximate the system behavior with
the help of a learning algorithm. While (Carriere and
Hamam, 1992) used the learned model to design a
controller, the more general modeling goal is often
the continuous analysis of the system behavior with
respect to a specified scope per input variable – this
includes the modeling of system states not explicitly
reflected by the given set of measurements (Bechtler
et al., 2001) (Wang et al., 2013).
The ANN based modeling approach is often only
carried out without considering the system’s dynamic
behavior (cf. (Bechtler et al., 2001), (Shen et al.,
2015), (Ledesma and Belman-Flores, 2016), (Reich
et al., 2017)). In this case, the measurement of the
input and output variables at a given point in time is
treated as temporally isolated, i.e. it is not viewed in
relation with its temporally adjacent measurements.
One way to realize a time series based learning is to
use so-called recurrent neural networks (Frey et al.,
2011) (Kose and Petlenkov, 2016). Another way is to
extract temporal features from the time series and use
them as additional input variables for the learning of
an ANN (Le Guennec et al., 2016).
In this paper, we describe two approaches to the
extraction of temporal features. These features serve
as additional input variables for the learning of large
multilayer ANNs, so-called deep neural networks
(DNNs) (Stuhlsatz et al., 2010). We consider a gas-
fired absorption heat pump as an exemplary dynamic
system. However, the described temporal feature ex-
traction, the subsequent learning of DNNs and the fi-
nal validation of the resulting models are applicable to
any dynamic system with continuous input and output
variables.
1.1 Database and Objective
The measured data that form the basis of the DNN
based modeling approach have been recorded dur-
Lippel, J., Becker, M. and Zielke, T.
Modeling Dynamic Processes with Deep Neural Networks: A Case Study with a Gas-fired Absorption Heat Pump.
DOI: 10.5220/0007932903170326
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 317-326
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
317
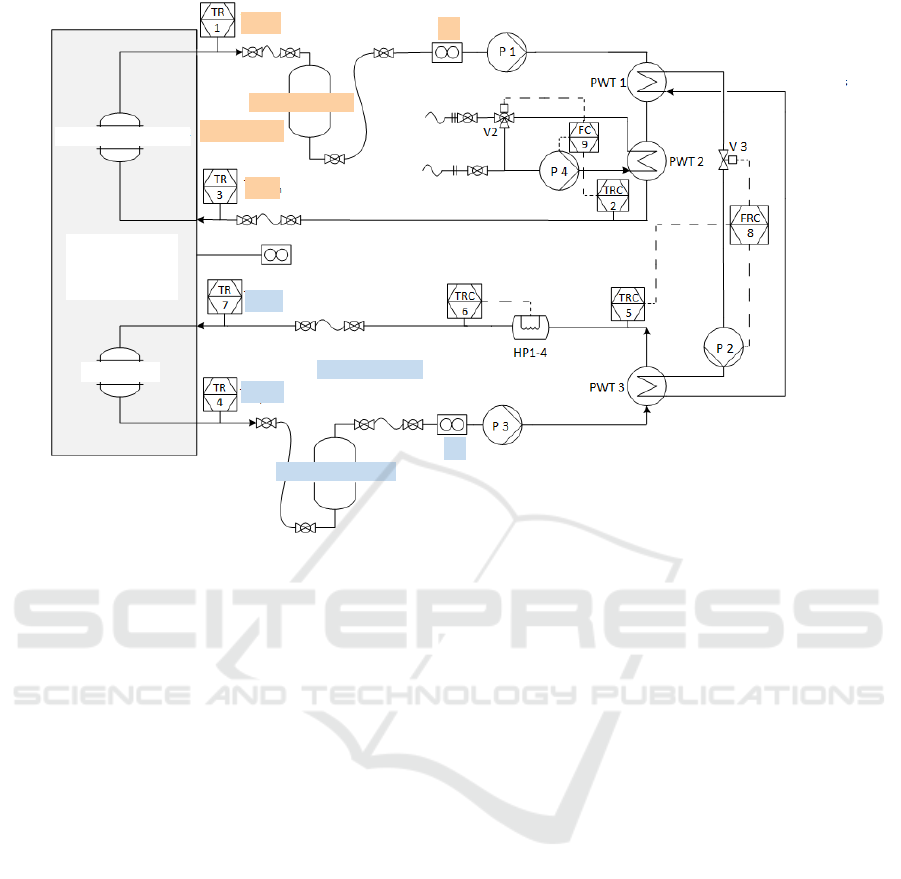
T
h,out
condenser / absorber
evaporator
heat accumulator
heating circuit
˙
V
gas
T
h,in
T
c,in
T
c,out
cold water circuit
cold water reservoir
˙
V
h
external cooling
internal circuit
˙
V
c
gas-fired
absorption
heat pump
Figure 1: Hydraulic circuit diagram of the hardware-in-the-loop (HiL) test bench. It was used to run all simulations. During
the simulations the input variables
˙
V
gas
, T
h,in
, T
c,in
,
˙
V
h
and
˙
V
c
as well as the output variables T
h,out
and T
c,out
were recorded
with a sample frequency of 1 Hz over a period of 25 days.
ing a hardware-in-the-loop (HiL) simulation of the
considered heat pump; a Buderus GWPW41 with
an ammonia-water absorption cycle. The heat pump
is operated as a system component in a realistically
modeled environment. It interacts with other system
components and reacts to simulated weather condi-
tions as well as a simulated user behavior. The HiL
test bench functions as a coupling point between the
simulation (interface connection) and the hardware
(hydraulically connected). The system’s outlet flow
temperature is passed to the simulation via its inter-
face connection. Then, the return flow temperature is
simulated and passed back to the test bench, where
it serves as a set point for the regulation of the fluid
flows that enter the heat pump.
A hydraulic circuit diagram of the HiL test bench
is depicted in Figure 1. The annotations show where
the input variables
•
˙
V
gas
[m
3
/h]: volume flow rate of used gas
• T
h,in
[
◦
C]: inlet temperature (heating circuit)
• T
c,in
[
◦
C]: inlet temperature (cold water circuit)
•
˙
V
h
[m
3
/h]: volume flow rate (heating circuit)
•
˙
V
c
[m
3
/h]: volume flow rate (cold water circuit)
and the output variables
• T
h,out
[
◦
C]: outlet temperature (heating circuit)
• T
c,out
[
◦
C]: outlet temperature (cold water circuit)
of the heat pump are measured.
The goal of our research is to learn a DNN that is
capable of predicting the output variables of the heat
pump when given its input variables. To this end, we
have access to several measurement series. Each was
recorded at a sample frequency of 1 Hz. The overall
data set includes about 25 days of measurements and
covers all relevant operation conditions. More details
on the data set are given in Section 2.4.
To assess the prediction accuracy of the learned
model, we compare it with the mathematical model
presented by (Goebel et al., 2015). Their modeling
is not based on the chemical and physical processes
of the heat pump as this leads to an overly complex
model and a long simulation time. Instead, they used
characteristic diagrams that represent sufficiently ac-
curate look-up tables for the modeling of the input-
to-output relations of the heat pump. This model was
validated with the above measurement series and it
is therefore well suited as a reference model for the
DNN based model.
To further show that too simple machine learning
methods are less suited than DNNs, we also applied a
multivariable linear regression (Duda et al., 2001) to
obtain prediction models (cf. Section 3).
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
318
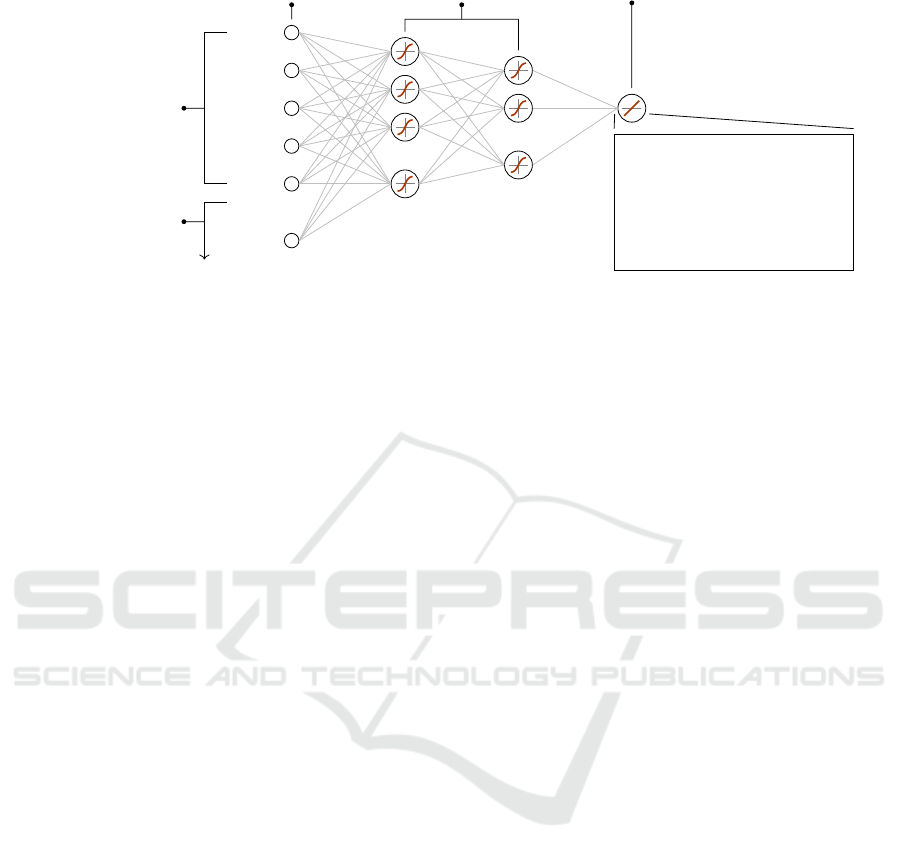
.
.
.
.
.
.
.
.
.
e
T
h,out
(t)
˙
V
gas
(t)
T
h,in
(t)
T
c,in
(t)
˙
V
h
(t)
˙
V
c
(t)
input neurons hidden neurons
output neuron
raw features
temporal features
∑
t∈Φ
|
e
T
h,out
(t) − T
h,out
(t)|
2
Φ := random set of observation times
e
T
h,out
:= predicted output
T
h,out
:= measured output
Figure 2: General structure of a DNN. A DNN consists of several layers of artificial neurons. The original, non-preprocessed
measurements of the input variables (raw features) are fed into the DNN via input neurons. The same applies to the extracted
temporal features (i.e. the results of the data preprocessing with Method A or B). Each of the features is fed into a separate
input neuron. The final prediction is generated through at least two layers of hidden neurons and one output neuron. The
DNN’s optimization is carried out with respect to the loss stated in the lower right box.
Regarding the comparison of the learned models
and the reference model, it is important to note that
all simulations were carried out in a cyclic operation
mode where the cold water circuit was switched off
during the deactivation phase of a cycle. During this
phase, the used simulation does not provide accurate
temperatures. However, they quickly become accu-
rate once the cold water circuit has been switched on
again. In (Goebel et al., 2015), the validation of the
model is therefore not based on measurements where
˙
V
c
(t) 6= 0. In our research, these measurement peri-
ods are not considered for the same reason: They are
neither used for the learning of models nor for their
validation. As a result, the effective data set size had
to be reduced to approximately 12 days (of originally
25 days) of measurements.
1.2 Deep Neural Networks
ANNs, and especially DNNs, have been shown to be
powerful parametric machine learning models. One
main advantage of DNNs is that there exists a wide
range of learning algorithms that carry out an efficient
and automatic parameter optimization. An adaption
of these learning algorithms to the concrete learning
task at hand is often not necessary and it is therefore
generally not required to fully understand the princi-
ples that they are based on.
In this work, we use a slightly modified version
of a DNN called ReNDA, a Regularized Nonlinear
Discriminant Analysis (Becker et al., 2017). So far,
this DNN and its predecessor GerDA (Generalized
Discriminant Analysis) have primarily been used to
solve classification tasks (cf. (Gaida et al., 2012),
(Stuhlsatz et al., 2012)). In the course of this work,
we extended ReNDA so that it can be applied to mul-
tivariable nonlinear regression tasks. This allowed
us to learn the desired prediction model. Our exten-
sion preserves the preoptimization strategy described
in (Stuhlsatz et al., 2012). It is a measure that has
been shown to decrease the risk of converging towards
poor local optima in the DNN’s parameter space (Er-
han et al., 2010).
2 METHODOLOGY
As mentioned in the introduction, one way to realize
the time series based learning of a DNN is to extract
temporal features from the time series and use them
as additional input variables. Suitable approaches to
the extraction of temporal features are usually based
on prior knowledge about the application at hand. In
most scenarios, acquiring this knowledge goes hand
in hand with planning the recording of the data. At
a later time, the initial approaches can be gradually
improved based on own results, or results from other
researchers.
In the following, we describe two quite differ-
ent approaches to extracting temporal features. Here
and subsequently, we refer to them as Method A and
Method B. They can both be understood as a form
of data preprocessing that has to be carried out be-
fore the actual learning of a DNN. The features result-
ing from this data preprocessing are fed into a DNN’s
input neurons along with the non-preprocessed mea-
surements (also called raw features). As can be seen
in Figure 2, each feature is fed into a separate input
neuron.
Figure 2 also shows the structure of a DNN and
states the loss function that is used to optimize it. In
Modeling Dynamic Processes with Deep Neural Networks: A Case Study with a Gas-fired Absorption Heat Pump
319

Figure 3: Graphical explanation of the averaged past values (APVs) as defined by (2). The displayed example for N = 1200
and M = 5 is also used as a setup in our experiments (cf. Section 3.1).
Section 2.3, we give a brief explanation of these two
aspects (cf. (Becker et al., 2017) for further details).
Moreover, we introduce two different metrics for the
validation of the learned prediction models.
2.1 Method A: Time Series
Representation
Because heat pumps are dynamic systems, predicting
T
h,out
(t) and T
c,out
(t) based on the already measured
time series of its input variables; namely
˙
V
gas
(t − n),
T
h,in
(t − n), T
c,in
(t − n),
˙
V
h
(t − n) and
˙
V
c
(t − n) for
n ∈ {0,1,.. .,N} with N ≥ 0; is reasonable. In this
way, we consider the measurements at observation
time (n = 0) and N past measurements (1 ≤ n ≤ N).
In the case of ReNDA and most other DNNs, N has to
be constant during the entire learning process, i.e. the
time series must be of equal length. Assuming that
the first sample of a time series has the index 1, the
first possible time series of length N corresponds to
the observation time t = N + 1.
A second reasonable assumption is that measure-
ments of the input variables in the closer past (n ≈ t)
have a more direct effect on T
h,out
(t) and T
c,out
(t) than
those of the distant past (n t). Because this is true
for a wide range of dynamic systems, we developed
the following general method for the extraction of
temporal features from a time series of length N: Let
m ∈ {1,2,.. ., M} with M ≤ N and let
a
m
:= b(m − 1)
γ
c + 1
b
m
:= bm
γ
c
(1)
with γ := log
M
(N). We call each
˙
V
m
gas
(t) :=
1
b
m
− a
m
+ 1
b
m
∑
n=a
m
˙
V
gas
(t − n) (2)
an averaged past value (APV) of
˙
V
gas
. See Figure 3
for a graphical explanation. The following holds for
the resulting M APVs:
•
˙
V
1
gas
(t) =
˙
V
gas
(t − 1) since a
1
= 1 = b
1
.
•
˙
V
M
gas
(t) includes
˙
V
gas
(t − N) since b
M
= N.
• All M intervals [b
m
|a
m
] are non-overlapping since
a
m
6= b
m−1
for all m ∈ {2,3,.. ., M}.
•
˙
V
m
gas
(t) =
˙
V
gas
(t − m) for all m ∈ {1, 2,. .. ,M} if
M = N, i.e.
˙
V
m
gas
(t) is the original time series.
• The index m can be seen as a replacement of the
original time index n.
The APVs T
m
h,in
, T
m
c,in
,
˙
V
m
h
and
˙
V
m
c
of the other input
variables are computed analogously and thus share
the above properties. Since we consider a total of 5
input variables, feeding both the raw features and the
APVs into a DNN requires 5 · (1 + M) input neurons
(cf. Figure 2).
Clearly, the above APV definition can be easily
applied to any time series of length N, i.e. it is not
limited to the considered heat pump scenario. In the
next section, we describe an alternative method that
relies on expert knowledge about the examined heat
pump.
2.2 Method B: Definition of a Status of
the Heat Pump
Generally applicable methods like the one described
in the previous section are especially helpful if there
exists no knowledge about a given application. In the
following, we define a temporal feature representing
the status of the heat pump. By means of this status,
we demonstrate the use of expert knowledge based
temporal features.
Let S
hp
denote the status of the heat pump. It is
defined as follows:
• If the gas burner is switched on at an observation
time t, the sign of S
hp
(t) is positive. Otherwise,
the sign is chosen to be negative.
• The absolute value of S
hp
(t) indicates the period
of time for which the gas burner has already been
in its current state; either switched on or off.
• S
hp
is measured in seconds.
For instance, if the gas burner has been switched off
for 5 seconds at observation time t, the status of the
heat pump is S
hp
(t) = −5s.
Note that using S
hp
requires a fixed number of 6
input neurons as opposed to a minimum number of
5 · (1 + M) = 10 for M = 1 in Method A. Note also
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
320

that choosing M = 1 yields a rather unsophisticated
representation of a time series: the average of all N
past values. Therefore, it is recommended to choose
M > 1, which implies the use of a DNN with 15 or
more input neurons. Consequently, Method B leads
to a significantly lower computational effort during
the learning of a DNN.
2.3 Model Optimization and Feature
Processing
Once Method A or B has been applied to extract tem-
poral features, each raw and each temporal feature is
fed into its respective input neuron. Then, a layered
structure of hidden neurons followed by one output
neuron generates a prediction (cf. Figure 2). Although
it is generally possible to use multiple output neurons,
we choose to learn one DNN per output variable (i.e.
separate prediction models for T
h,out
and T
c,out
). The
intuition behind this is that it is easier for a DNN to
adapt itself to only one output variable. Studying a
DNNs capability to simultaneously adapt to two or
more output variables is subject to future work.
Subsequently, we give a brief explanation on how
a DNN is optimized and how it processes features. To
improve clarity, we focus on the DNN for T
h,out
; the
explanation is also valid for T
c,out
.
As stated in Figure 2, the optimization of a DNN
is based on a loss given by
∑
t∈Φ
e
T
h,out
(t) − T
h,out
(t)
2
(3)
where Φ is a random set of observation times. First,
the DNN generates the predictions
e
T
h,out
(t), which is
done by processing the respective raw and temporal
features. The above loss and its derivative are then
used to realize a gradient descent based update of all
parameters of the DNN. These two steps are carried
out for several random sets Φ until the loss becomes
sufficiently small.
The parameters updated during this optimization
are the adjustable weights and biases of the hidden
neurons and the output neuron. Each individual neu-
ron processes its input signals x
i
via
f
b +
∑
w
i
· x
i
(4)
where f is called an activation function, b is called a
bias and each w
i
is called a weight. In our case, f is
defined by f (ξ) := sigm(ξ) := 1/(1 + exp(−ξ)) for
each hidden and by f (ξ) := ξ for the output neuron.
While the search of suitable activation functions is a
hot topic (Basirat and Roth, 2018), practitioners can
often already achieve good learning results by choos-
ing an appropriate DNN topology (the number of lay-
ers of hidden neurons and the number of neurons per
layer). The DNN topology ultimately determines the
overall number of adjustable weights and biases of a
DNN; it therefore represents the number of degrees
of freedom that can be used to learn a good prediction
model.
2.4 Model Validation
In addition to the loss (3), we consider two different
metrics to measure the goodness of the learned pre-
diction models. One is the relative error
err
rel
:=
1
|Φ|
∑
t∈Φ
e
T
h,out
(t)
T
h,out
(t)
− 1
!
· 100% (5)
where |Φ| denotes the number of randomly selected
observation times. The other is the absolute error
err
abs
:=
1
|Φ|
∑
t∈Φ
|
e
T
h,out
(t) − T
h,out
(t)|. (6)
In the case of both metrics, we used
e
T
h,out
and T
h,out
in
◦
C. For lowest values of ≈ 3
◦
C, we experienced
no numerical issues when calculating (5); here, a di-
vision through 0
◦
C would have been problematic. In
the case of err
abs
, all results are stated in Kelvin (K)
as it is common with temperature differences.
The ultimate goal of any machine learning based
modeling approach is to learn a model that performs
well on unseen data (e.g. future measurements). It is
therefore necessary to split the data into training and
validation data. Learning a model, i.e. updating its
parameters, is solely based on the training data. The
validation data, on the other hand, simulates unseen
data that does not serve as a learning basis. It is only
used to monitor the learning process and, especially,
to prevent the learning of an overfitted model (Tetko
et al., 1995).
In our experiments, we consider the 3 data pack-
ages (DP1 to DP3) specified in Table 1. To simulate
unseen data in the most realistic way, the validation
data of each data package comes from exactly 1 of 6
mutually independent measurement series. To speed
up the DNN learning process, we use 400,000 ran-
domly selected measurements from the remaining 5
measurement series as training data. This amount of
training data proved to be sufficient for the learning of
a prediction model (i.e. the learning led to a gradual
improvement of the model). Using 3 data packages
enables us to compare the learning performance un-
der different training conditions.
Modeling Dynamic Processes with Deep Neural Networks: A Case Study with a Gas-fired Absorption Heat Pump
321

Table 1: Definition of different data packages. Each consists of different training and validation samples. For the partitioning
of the data into sets of training and validation samples, we simply used the IDs of the measurement series. In the case of all
data packages, the validation is based on 1 of 6 mutually independent measurement series that was not used for the learning
of the DNN. This realistically simulates unseen data for a proper model validation (cf. Section 2.4).
Data package Training data Validation data
Measurement series ID No. of measurements meas. series ID No. of meas.
DP1 321; 324; 350; 351; 353 548,771
∗
319 485,339
DP2 319; 324; 350; 351; 353 562,113
∗
321 471,997
DP3 321; 321; 350; 351; 353 969,207
∗
324 64,903
∗
) To speed up the learning process, we only
use 400,000 randomly sampled measurements.
Table 2: Average relative and absolute errors and the corresponding standard deviation of the predictions obtained from
different DNN based models. The last column shows the comparative results obtained from the reference model (Goebel
et al., 2015). The results highlighted in bold are the best result within this table. The results highlighted in green are the best
results within this table and Table 3.
Experimental setup
Model DNN Reference
Data preprocessing Method A Method B N/A
M in Eq. (2) 3 5 10 20 N/A N/A
Input neurons 20 30 55 105 6 N/A
Hidden neurons 3 layers with 50, 25 and 100 neurons, respectively N/A
Output neurons 1 neuron since we chose to learn one DNN per output variable N/A
Results
T
h,out
DP1
% 0.87 ± 1.61 0.80 ± 1.38 0.97 ± 1.26 1.26 ± 1.79 0.75 ± 1.17 0.88 ± 2.48
K 0.37 ± 0.63 0.35 ± 0.46 0.42 ± 0.43 0.56 ± 0.53 0.31 ± 0.37 0.35 ± 0.91
DP2
% 0.48 ± 0.98 0.37 ± 0.65 0.48 ± 0.84 0.93 ± 1.31 0.66 ± 1.18 1.08 ± 2.71
K 0.20 ± 0.33 0.16 ± 0.21 0.21 ± 0.23 0.43 ± 0.43 0.28 ± 0.42 0.45 ± 1.08
DP3
% 0.64 ± 1.57 0.54 ± 1.25 0.50 ± 0.92 0.59 ± 1.23 0.69 ± 1.71 1.44 ± 2.98
K 0.23 ± 0.44 0.19 ± 0.34 0.18 ± 0.22 0.21 ± 0.31 0.25 ± 0.61 0.48 ± 0.79
T
c,out
DP1
% 2.05 ± 3.60 1.84 ± 3.02 2.55 ± 4.51 5.60 ± 7.01 1.33 ± 2.12 2.10 ± 5.23
K 0.18 ± 0.34 0.16 ± 0.25 0.22 ± 0.44 0.46 ± 0.46 0.12 ± 0.19 0.17 ± 0.31
DP2
% 1.06 ± 2.29 1.18 ± 1.72 1.65 ± 2.18 4.00 ± 6.10 1.05 ± 1.78 2.09 ± 6.47
K 0.09 ± 0.14 0.10 ± 0.13 0.14 ± 0.19 0.31 ± 0.37 0.10 ± 0.16 0.16 ± 0.37
DP3
% 0.92 ± 2.00 0.87 ± 1.83 1.04 ± 2.77 1.65 ± 3.88 0.93 ± 2.54 1.08 ± 2.27
K 0.13 ± 0.34 0.12 ± 0.36 0.15 ± 0.57 0.23 ± 0.73 0.12 ± 0.27 0.16 ± 0.39
Table 3: Average relative and absolute errors and the corresponding standard deviation of the predictions obtained from
different multivariable linear regression models. The table is organized and designed as Table 2.
Experimental setup
Model Multivariable linear regression Reference
Data reprocessing Method A Method B N/A
M in Eq. (2) 3 5 10 20 N/A N/A
Results
T
h,out
DP1
% 1.35 ± 1.84 0.52 ± 0.89 0.45 ± 0.87 0.45 ± 0.85 1.39 ± 2.70 0.88 ± 2.48
K 0.59 ± 0.72 0.22 ± 0.35 0.19 ± 0.34 0.20 ± 0.33 0.57 ± 0.97 0.35 ± 0.91
DP2
% 1.25 ± 1.95 0.55 ± 0.83 0.52 ± 0.76 0.51 ± 0.74 1.96 ± 2.90 1.08 ± 2.71
K 0.53 ± 0.76 0.25 ± 0.30 0.24 ± 0.27 0.23 ± 0.26 0.84 ± 1.02 0.45 ± 1.08
DP3
% 2.42 ± 3.38 0.95 ± 1.74 0.86 ± 1.64 0.85 ± 1.62 3.50 ± 5.31 1.44 ± 2.98
K 0.90 ± 1.17 0.34 ± 0.53 0.31 ± 0.49 0.31 ± 0.49 1.27 ± 1.67 0.48 ± 0.79
T
c,out
DP1
% 4.15 ± 3.58 2.54 ± 2.05 2.36 ± 1.96 2.47 ± 1.97 3.30 ± 4.33 2.10 ± 5.23
K 0.34 ± 0.32 0.21 ± 0.19 0.19 ± 0.18 0.20 ± 0.18 0.29 ± 0.41 0.17 ± 0.31
DP2
% 2.70 ± 3.59 1.63 ± 1.99 1.60 ± 1.91 1.58 ± 1.90 4.30 ± 4.60 2.09 ± 6.47
K 0.23 ± 0.33 0.13 ± 0.17 0.12 ± 0.16 0.12 ± 0.16 0.35 ± 0.43 0.16 ± 0.37
DP3
% 3.16 ± 3.93 1.30 ± 1.96 1.21 ± 1.85 1.20 ± 1.84 4.18 ± 5.42 1.08 ± 2.27
K 0.39 ± 0.53 0.17 ± 0.35 0.16 ± 0.34 0.16 ± 0.33 0.52 ± 0.70 0.16 ± 0.39
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
322

3 EXPERIMENTS
In this section, we present the setup and results of a
series of experiments that we carried out in order to
find answers to the following questions:
• Are the proposed data preprocessings (Method A
and B) suitable for the DNN based modeling of
dynamic systems?
• Does the DNN based approach yield models that
are comparable with the reference model (Goebel
et al., 2015)?
• How does the number M of APVs (Method A,
cf. Section 2.1, Eq. (2)) effect the accuracy of the
learned prediction model?
• How do the learned models compare with simple
multivariable linear regression models?
3.1 Experimental Setup and Average
Results
In general, the successful DNN based modeling of
a dynamic system depends on various DNN-specific
hyperparameters. The most relevant are stated in the
experimental setup subtable of Table 2. We consider
Method A (for N = 1200 and 4 different numbers of
APVs) and Method B with a common layered struc-
ture of hidden and output neurons. Since we defined
3 data packages (Table 1) and chose to learn separate
models for T
h,out
and T
c,out
, we see the results of 30
experiments. The results obtained with the reference
model are stated in the last column of Table 2. In all
cases, the average relative and absolute error and the
associated standard deviations are based on the vali-
dation data of the respective data package. The best
result – the minimum average error – of each row is
highlighted in bold.
Concerning our first question, we see that there is
always at least one concrete data prepocessing strat-
egy for which the DNN outperforms the reference
model. This already answers the second question. In
the case of the third question, we can only observe a
slight tendency: In almost all rows, the relative and
absolute error become larger as M increases.
Table 3 helps us to answer the fourth question. It
shows comparative results of 30 multivariable linear
regression models that are based on the exact same
data processing setups as the DNN based models. It is
organized as Table 2 – the last column of Table 2 and
Table 3 are identical. To facilitate a comparison of
Table 2 and Table 3, the green highlightings mark the
best overall results. The multivariable linear regres-
sion models for the prediction of T
h,out
whose model
parameters are based on DP1 (Method A with either
M = 10 or M = 20) are the only models that outper-
form the corresponding DNN based models.
Going beyond the four questions posed, there are
further interesting aspects to discover in Table 3. As
can be seen, the reference model appears to perform
better in three cases. Observe however, that the cor-
responding standard deviations are quite large. It is
therefore likely that the multivariable linear regres-
sion models learned a better time series approxima-
tion of their respective output variable.
3.2 Time Series Approximation Results
While average results provide a good overview over
the suitability of a large number of models, they fail
to reflect a model’s power to accurately approximate
output variables that represent time series.
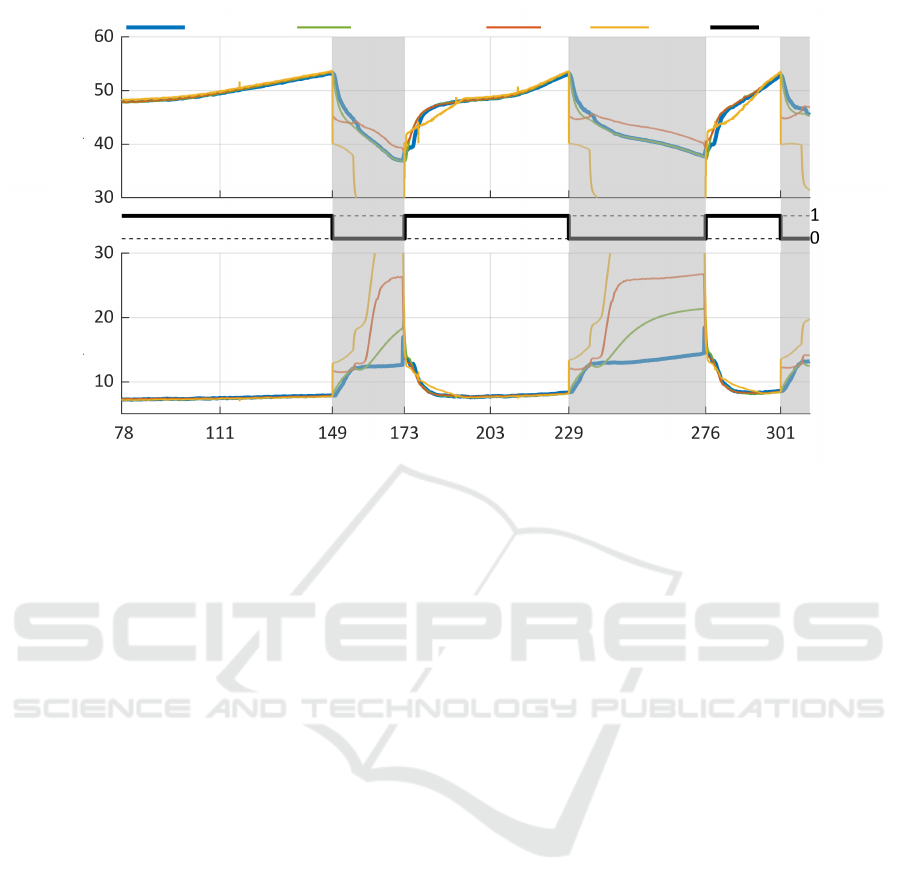
Figure 4 shows a short time series snippet of both
T
h,out
and T
c,out
. The snippet covers about 4 hours of
measurements and predictions; the latter come from
the DNN model and the multivariable linear regres-
sion model whose parameters are based on features
extracted with Method B (cf. Section 2.2). Both the
reference model and the DNN based model yield an
accurate approximation of T
h,out
and T
c,out
during the
activation phases (
˙
V
c
(t) 6= 0). Because the learning of
the DNN is only based on activation phase measure-
ments (cf. Section 1.1), the approximation is signifi-
cantly less accurate during the displayed deactivation
phases (gray highlighted areas). This behavior is es-
pecially pronounced in the case of the multivariable
linear regression model. However, all three models
improve towards the end of an activation phase. The
small outliers of the graph of the multivariable linear
regression model predictions appear to occur at ran-
dom and most likely come from rounding errors. An
analysis of this effect is part of our future research.
A natural question that arises when studying Fig-
ure 4 is the following:
• Which of the three models performs best shortly
after the reactivation of the heat pump (i.e. at the
beginning of each activation phase)?
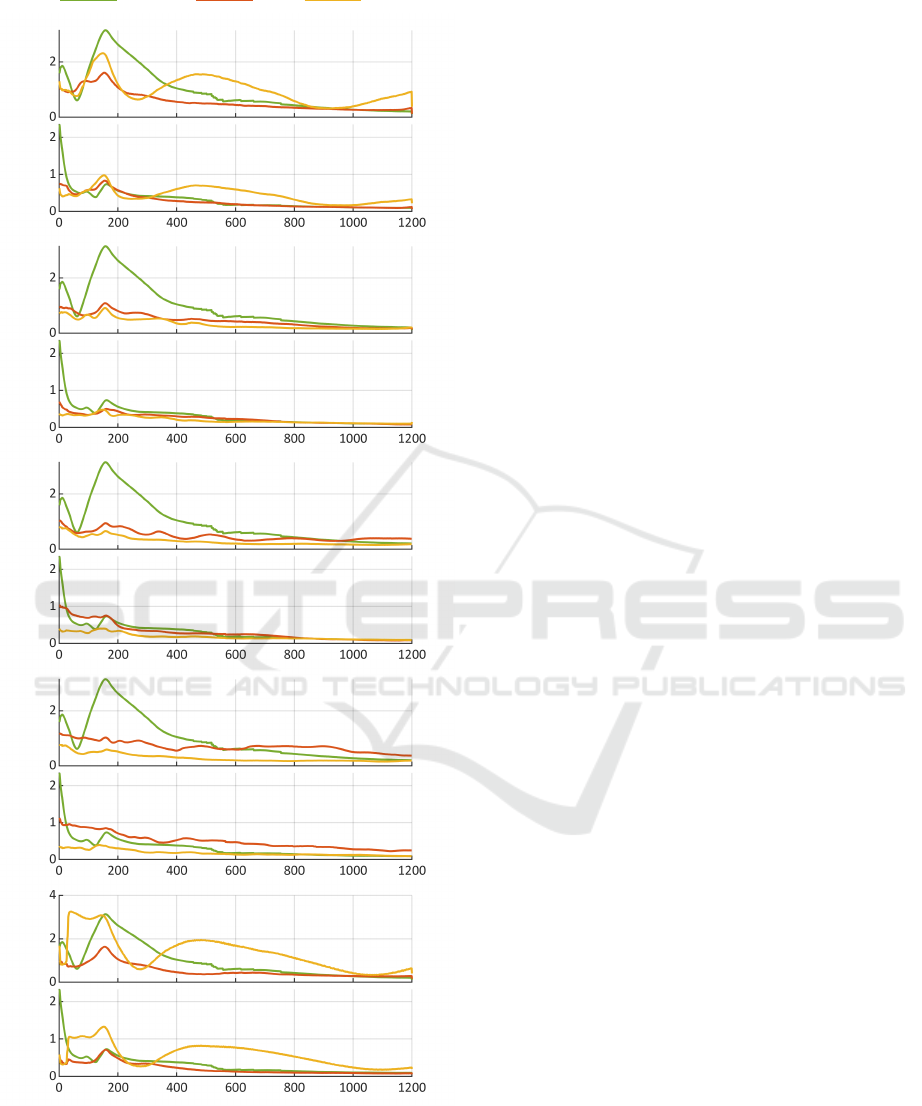
Figure 5 shows our first idea on how to approach the
above question. To get a statistically significant esti-
mate of the average post-activation-behavior of each
model, we consider the validation data of all 3 data
packages DP1 to DP3. Together, they contain a total
number of 549 activation events. Based on these 549
events, we extracted 549 time frames covering up to
1200 seconds after an activation event. In the case of
an activation duration shorter than 1200 seconds, the
corresponding time frame is limited to the respective
activation duration. Each graph depicted in Figure 5
Modeling Dynamic Processes with Deep Neural Networks: A Case Study with a Gas-fired Absorption Heat Pump
323
temperature in
◦
Ctemperature in
◦
C
measurement
reference model
DNN
lin.reg.
˙
V
c
6= 0
time after last activation in minutes
Figure 4: Short time series snippet of measurements and predictions – T
h,out
and
e
T
h,out
(top); T
c,out
and
e
T
c,out
(bottom). The
predictions come from the reference model (green), the DNN based model (red) and the multivariable linear regression model
(yellow). The latter two models are based on a data preprocessing with Method B of the validation data from the data package
DP2 (cf. Section 2.4 and Table 1, respectively).
represents the average absolute approximation error
of all 549 time series that come from one model. In
the case of
e
T
h,out
, this means that each curve point is
the average of
|
e
T
k
h,out
(t) − T
k
h,out
(t)| (t ∈ [0|1200]) (7)
along k, where k (for 1 ≤ k ≤ 549) denotes the time
frame associated with the kth activation event. Since
the time frames are of different length, the average
per time step requires the division by the number of
available values; this non-constant normalization is
the reason for the small occasional jumps that can be
seen in some of the graphs.
Each double plot in Figure 5 shows the average
absolute approximation errors of
e
T
h,out
(top plot) and
e
T
c,out
(bottom plot) for the stated data preprocessing
method. As already indicated by our average results
(cf. Section 3.1) the DNN based model often yields
comparable and sometimes even better results than
the reference model. Only for Method A with 10 or
20 APVs the reference model shows a slightly better
long-term behavior. An aspect not yet addressed is
that the multivariable linear regression benefits from
a larger number M of APVs (see Table 3). In Figure
5, we see that this might be due to lower errors right
after an activation event. For M = 10 and M = 20, a
multivariable linear regression is even more suitable
than a DNN, or more precisely, a DNN that tends to
learn models that are too non-linear.
3.3 Discussion
Especially the last aspect hints at a number of ques-
tions that can help to better understand and improve
the proposed DNN based approach to modeling dy-
namic systems. It raises the question
• why multivariable linear regression models bene-
fit from a larger number of APVs and why DNN
based models show a better overall performance
with a smaller number of APVs.
While answering this question in general (i.e. for
all or special types of dynamic systems) is chal-
lenging, the observation itself suggests to encourage
DNN based models that are more linear. Possible
approaches to achieve this are to determine a less
complex DNN topology and/or to further regularize
the considered DNN. If there exist more linear DNN
based models that also benefit from a larger number
of APVs, a next observation/question could be:
• So far, we only consider the APVs of the input
variables. At the time we wish to predict either
T
h,out
(t) or T
c,out
(t), we may also have access to
N past values T
h,out
(t − n) or T
c,out
(t − n) of the
output variables (n ∈ {1, 2,. .. ,N}). This would
allow us to calculate APVs of the output variable
that we wish to predict and use them as further
inputs for the learning of a DNN. Whether using
such output variable based APVs leads to further
improvements would be interesting to study.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
324
DNN
reference
lin.reg.
time after activation in seconds
Method B,
e
T
h,out
Method A, M = 3,
e
T
h,out
Method A, M = 5,
e
T
h,out
Method A, M = 10,
e
T
h,out
Method A, M = 20,
e
T
h,out
e
T
c,out
e
T
c,out
e
T
c,out
e
T
c,out
e
T
c,out
Figure 5: Average absolute approximation errors depicted
in the form of a time series covering 1200 seconds after an
activation event (cf. Section 3.2).
This latter idea can also be naturally extended in the
following way:
• An inclusion of APVs of already generated pre-
dictions, which directly leads to concept behind
recurrent neural networks (NARX (Tsungnan Lin
et al., 1996) or LSTM (Sak et al., 2014)), would
enable a fair comparison between our approach
and other recurrent neural network approaches.
Of course, further practical experiments that need to
be conducted consider other dynamic systems:
• Our recent experiment results support our claim
that our DNN based modeling approach is gener-
ally applicable. This (yet to be published) work
includes measurements from an evaporator (Zhu
et al., 1994), an industrial dryer (Maciejowski,
1996) and a (chemical) gas sensor array (Burgu
´
es
and Marco, 2018).
4 CONCLUSION
In this paper, we described two approaches to the ex-
traction of temporal features. These features served
as additional input variables for the learning of DNNs.
Method A uses a time series representation with aver-
aged past values (APVs). The APV definition can be
easily applied to any time series, i.e. it is not limited
to the considered heat pump scenario of this paper. In
contrast to that, we presented Method B which uses
a status representation of the heat pump as an addi-
tional knowledge based feature. We considered two
different metrics to measure the goodness of the pre-
diction models. We compared the learned DNN mod-
els with a reference model. Furthermore we compared
the learned models with simple multivariable linear
regression models. Our results show that the proposed
data preprocessings are suitable for the DNN based
modeling of dynamic systems. It can also be seen
that the DNN based approach yields models that out-
performs the reference model. Surprisingly, the mul-
tivariable linear regression models partially outper-
forms the DNN models, especially with an increasing
number of APVs.
ACKNOWLEDGEMENTS
An earlier version of this article was presented at the
German conference DKV (Lippel et al., 2017). We
would like to thank Max Huth for carrying out new
experiments for the present paper, as well as Lena
Frank and Johannes Goebel (Center for Innovative
Modeling Dynamic Processes with Deep Neural Networks: A Case Study with a Gas-fired Absorption Heat Pump
325

Energy Systems; ZIES) for their contributions to the
work presented in the DKV article.
REFERENCES
Basirat, M. and Roth, P. M. (2018). The quest for the golden
activation function. CoRR, abs/1808.00783.
Bechtler, H., Browne, M., Bansal, P., and Kecman, V.
(2001). Neural networks—a new approach to model
vapour-compression heat pumps. International Jour-
nal of Energy Research, 25(7):591–599.
Becker, M., Lippel, J., and Stuhlsatz, A. (2017). Regular-
ized nonlinear discriminant analysis. an approach to
robust dimensionality reduction for data visualization.
In International Conference on Information Visualiza-
tion Theory and Applications.
Burgu
´
es, J. and Marco, S. (2018). Multivariate estimation
of the limit of detection by orthogonal partial least
squares in temperature-modulated mox sensors. An-
alytica chimica acta, 1019:49–64.
Carriere, A. and Hamam, Y. (1992). Heat pump emula-
tion using neural networks. In [Proceedings 1992]
IEEE International Conference on Systems Engineer-
ing. IEEE.
Duda, Stork, and Hart (2001). Pattern Classification, 2nd
Edition. John Wiley & Sons, Inc.
Erhan, D., Bengio, Y., Courville, A., Manzagol, P.-A.,
and Vincent, P. (2010). Why does unsupervised pre-
training help deep learning? Journal of Machine
Learning Research, 11:625–660.
Frey, P., Ehrismann, B., and Dr
¨
uck, H. (2011). Devel-
opment of artificial neural network models for sorp-
tion chillers. In Proceedings of the ISES Solar World
Congress 2011. International Solar Energy Society.
Gaida, D., Wolf, C., Meyer, C., Stuhlsatz, A., Lippel, J.,
B
¨
ack, T., Bongards, M., and McLoone, S. (2012).
State estimation for anaerobic digesters using the
ADM1. 66(5):1088.
Goebel, J., Kowalski, M., Frank, L., and Adam, M. (2015).
Rechnersimulationen zum winter- und sommerbetrieb
einer abwasser-gasw
¨
armepumpe/-k
¨
altemaschine. In
Deutsche K
¨
alte- und Klimatagung.
Kose, A. and Petlenkov, E. (2016). System identification
models and using neural networks for ground source
heat pump with ground temperature modeling. In
Neural Networks (IJCNN), 2016 International Joint
Conference on, pages 2850–2855. IEEE.
Le Guennec, A., Malinowski, S., and Tavenard, R. (2016).
Data augmentation for time series classification us-
ing convolutional neural networks. In ECML/PKDD
Workshop on Advanced Analytics and Learning on
Temporal Data.
Ledesma, S. and Belman-Flores, J. M. (2016). Analysis
of cop stability in a refrigeration system using artifi-
cial neural networks. In Neural Networks (IJCNN),
2016 International Joint Conference on, pages 558–
565. IEEE.
Lippel, J., Becker, M., Frank, L., Goebel, J., and Zielke,
T. (2017). Modellierung dynamischer prozesse
mit deep neural networks am beispiel einer gas-
absorptionsw
¨
armepumpe. In Deutsche K
¨
alte- und Kli-
matagung 2017.
Maciejowski, J. (1996). Parameter estimation of multivari-
able systems using balanced realizations. NATO ASI
SERIES F COMPUTER AND SYSTEMS SCIENCES,
153:70–119.
Reich, M., Adam, M., and Lambach, S. (2017). Comparison
of different methods for approximating models of en-
ergy supply systems and polyoptimising the systems-
structure and components-dimension. In ECOS 2017
(30th International Conference on Efficiency, Cost,
Optimisation, Simulation and Environmental Impact
of Energy Systems).
Sak, H., Senior, A., and Beaufays, F. (2014). Long short-
term memory recurrent neural network architectures
for large scale acoustic modeling. Proceedings of the
Annual Conference of the International Speech Com-
munication Association, INTERSPEECH, pages 338–
342.
Shen, C., Yang, L., Wang, X., Jiang, Y., and Yao, Y.
(2015). Predictive performance of a wastewater
source heat pump using artificial neural networks.
Building Services Engineering Research and Technol-
ogy, 36(3):331–342.
Stuhlsatz, A., Lippel, J., and Zielke, T. (2010). Discrim-
inative feature extraction with deep neural networks.
In The 2010 International Joint Conference on Neu-
ral Networks (IJCNN). Institute of Electrical and Elec-
tronics Engineers (IEEE).
Stuhlsatz, A., Lippel, J., and Zielke, T. (2012). Feature ex-
traction with deep neural networks by a generalized
discriminant analysis. 23(4):596–608.
Tetko, I. V., Livingstone, D. J., and Luik, A. I. (1995). Neu-
ral network studies. 1. comparison of overfitting and
overtraining. Journal of chemical information and
computer sciences, 35(5):826–833.
Tsungnan Lin, Horne, B. G., Tino, P., and Giles, C. L.
(1996). Learning long-term dependencies in narx re-
current neural networks. IEEE Transactions on Neu-
ral Networks, 7(6):1329–1338.
Wang, G., Zhang, Y., Wang, R., and Han, G. (2013). Perfor-
mance prediction of ground-coupled heat pump sys-
tem using nnca-rbf neural networks. In Control and
Decision Conference (CCDC), 2013 25th Chinese,
pages 2164–2169. IEEE.
Zhu, Y., van Overschee, P., de Moor, B., and Ljung, L.
(1994). Comparison of three classes of identification
methods. IFAC Proceedings Volumes, 27(8):169–174.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
326
