
Hybrid 6D Object Pose Estimation from the RGB Image
Rafal Staszak
a
and Dominik Belter
b
Institute of Control, Robotics and Information Engineering, Poznan University of Technology, Poznan, Poland
Keywords:
Object Pose Estimation, Convolutional Neural Networks, Deep Learning in Robotics.
Abstract:
In this research, we focus on the 6D pose estimation of known objects from the RGB image. In contrast to
state of the art methods, which are based on the end-to-end neural network training, we proposed a hybrid
approach. We use separate deep neural networks to: detect the object on the image, estimate the center of the
object, and estimate the translation and ”in-place” rotation of the object. Then, we use geometrical relations on
the image and the camera model to recover the full 6D object pose. As a result, we avoid the direct estimation
of the object orientation defined in SO3 using a neural network. We propose the 4D-NET neural network to
estimate translation and ”in-place” rotation of the object. Finally, we show results on the images generated
from the Pascal VOC and ShapeNet datasets.
1 INTRODUCTION
Collaborative robotic arms are designed to share
workspace with humans or even physically interact
with operators. This is possible mainly due to con-
trol algorithms which make the robot compliant when
robot unexpectedly touches an obstacle. Also, simple
safety sensors stop or slow down the robot when the
human operator get too close to the dangerous area.
These types of robot become very popular in man-
ufacturing to perform repetitive tasks. In our research,
we are interested in the autonomy of such robots. A
collaborative arm, which is mounted on the mobile
platform, can move freely in the factory and perform
production tasks or help humans in daily activity. To
this end, the mobile robot should be equipped with
the perception system which allows detecting and es-
timating the pose of the objects and then perform ma-
nipulation tasks (Fig. 1).
In this paper, we consider the problem of visual
objects detection and pose estimation. Most of the
state of the art methods are based on the visual or
depth features (Hinterstoisser et al., 2012; Hodan
et al., 2015), which are used to detect and find the
6D pose (position and orientation) of the object. Re-
cently, great progress was made in this field. Kehl et
al. (Kehl et al., 2017) showed that the Deep Convolu-
tional Neural Network can be applied to detect objects
on the RGB images and simultaneously estimate the
a
https://orcid.org/0000-0002-5235-4201
b
https://orcid.org/0000-0003-3002-9747
Figure 1: Mobile-manipulating robot used in this research
equipped with RGB-D cameras mounted in robot’s head
and wrists.
pose of the object. On the other hand, the traditional
methods based on online optimization have proven
to be very efficient. (Bibby and Reid, 2016; Tjaden
et al., 2016; Prisacariu and Reid, 2012). Bibby et al.
propose the object tracking method which minimizes
the error defined directly on the RGB image. The
silhouette generated from the object model is com-
pared with the intensity of pixels on the current im-
age. The pose of the object model is modified using
the gradient-based method. The algorithm is designed
for object tracking. It means that the algorithm re-
quires a very accurate initial guess and can’t be used
for object detection.
In this research, we propose a new hybrid method
for 6D object pose estimation (3D translation and ro-
tation). In contrast to end-to-end solutions, we pro-
pose a method which utilizes deep neural network
Staszak, R. and Belter, D.
Hybrid 6D Object Pose Estimation from the RGB Image.
DOI: 10.5220/0007933105410549
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 541-549
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
541

pose estimator and a geometrical model of the cam-
era.
1.1 Related Work
Many traditional approaches to 6D objects pose es-
timation are based on visual RGB or depth features.
Then, the features are compared with the reference
models to produce an object category and pose esti-
mation. In (Hinterstoisser et al., 2012), which is an
extension of the LINEMOD method (Hinterstoisser
et al., 2011), the color gradient features located on
the object silhouette and surface normal features in-
side the object silhouette are selected to describe dis-
cretized object pose. The detector is trained using
texture-less 3D CAD models of the objects. In (Ulrich
et al., 2012) RGB edges are used for objects detection
and pose estimation. The pose estimation is boosted
by the hierarchical view model of the object (Ulrich
et al., 2012). Hodan et al. propose a sliding window
detector based on surface normals, image gradients,
depth, and color (Hodan et al., 2015). The pose of
the object is estimated using a black-box optimization
technique (Particle Swarm Optimization) which mini-
mizes the objective function defined using the current
depth image and the synthetic image generated from
the CAD model of the object.
To detect an object in the image a Random For-
est classifier can be used (Brachmann et al., 2016).
The obtained distribution of object classes is used to
obtain preliminary pose estimates for the object in-
stances. Then, the initial poses are refined using ob-
ject coordinate distributions projected on the RGB
image. Similar Latent-Class Hough Forests allow
learning the pose estimator using RGB-D LINEMOD
features (Tejani et al., 2016).
Another method for pose estimation is Iterative
Closest Point algorithm (Segal et al., 2009). In con-
trast to previously mentioned methods, the ICP relies
on depth data (point clouds). In practice the point
cloud obtained from popular Kinect-like sensors are
noisy. We avoid using depth data and rely mainly on
the RGB images for pose estimation because the er-
ror of the single depth measurement can be larger than
5 cm on our depth sensor (Kinect v2) (Khoshelham,
2011). We also avoid methods similar to ICP because
they are very sensitive to initial guess about the object
pose. The initial pose of the object should be close to
the real pose of the object because the ICP is prone to
local minima.
Another group of object detection methods is
based on Deep Convolutional Neural Networks. Kehl
et al. (Kehl et al., 2017) proposed the extension to
the Single Shot Detector (SSD) (Liu et al., 2016), to
detect the position of the objects on the image and
produces 6D pose hypotheses of the objects. The net-
work is trained using synthetic images generated from
the MS COCO dataset images as a background and
3D CAD models of the objects. The 6D pose hy-
potheses of each object are later refined using RGB-D
images.
Also, Xiang et al. use a Convolutional Neural Net-
work to estimate the 6D pose of the objects from the
RGB image (Xiang et al., 2018). In this case, the es-
timation of translation and rotation of the object is
decoupled. To estimate the translation of the object
the neural network estimates the center of the object.
Then, the translation of the object is computed from
the camera model. The orientation of the object is es-
timated by the neural network working on the Region
of Interests (bounding boxes) detected on the input
image. In the method proposed by Thanh-Toan Do et
al., the neural network estimates the distance to the
camera only (Do et al., 2018). The remaining compo-
nents of the translation vector are estimated from the
bounding box. The rotation of the object is estimated
using Lie algebra representation.
Estimation of the orientation of the object is the
most challenging part of the 6D pose estimation.
In (Sundermeyer et al., 2018) the orientation of the
object is defined implicitly by samples in latent space.
Utilizing the depth data improves the results (Wang
et al., 2019) but also template matching-based method
has been proven to be efficient in this case (Konishi
et al., 2018).
To deal with the 6D pose estimation we decouple
the solution into two sub-problems. First, we use the
neural network to find the pose of the object with re-
spect to the camera frame assuming that the camera
axis goes through the center of the object. Then, we
analytically correct the estimated pose of the object
using camera model. Moreover, we have used degen-
erated representations for describing 6D pose in order
to simplify specific tasks.
2 4D-2D POSE ESTIMATION
Given an RGB input image, the task of pose estima-
tion pipeline is to estimate the rigid transform be-
tween coordinate systems O and C belonging to the
object and the camera, respectively. We state that
the full representation of the rigid transform can be
retrieved through an ensemble of specific tasks with
reduced dimensionality. The first constraint reduc-
ing the dimensionality to four parameters is the re-
lation between the z-axis of C coordinate system and
the origin position of O coordinate system. If we as-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
542

sume that the z-axis belonging to C intersects the ori-
gin of O coordinate system then it is possible to cre-
ate a rigid transform using only four parameters: XYZ
translation and in-place rotation angle θ. The XYZ
translation determines the location of camera as well
as the direction of its z-axis. The x and y axes of the
camera rigid transform depend on the in-place rota-
tion angle. It can be perceived as a tilt movement of
camera. in-place rotation angle determines the mea-
sure of camera rotation around its z-axis.
The neural network estimates transformation be-
tween the camera C
0
and the object frame O. Because
we assume that the z axis of the C
0
frame goes through
the center of the object frame O the neural network
has to estimate only four parameters. The natural
choice is the representation with three Euler angles
and distance to the object z. In this case, x and y is al-
ways zero. However, the Euler angles are not the best
choice to represent the orientation of the object be-
cause of singularities and nonlinearity. Another possi-
bility is to represent the pose of the object by the axis-
angle representation and distance to the object. How-
ever, we chose the representation which contains three
parameters defined in the Euclidean space (translation
from the object frame O to the camera frame C
0
) and
the in-place rotation angle θ. As it was stated before
the translation represents the position of the camera
on a spherical surface around the object and the θ an-
gle represents the rotation around z axis of the camera.
The rotation angles around x and y axis of the camera
frame C
0
are always set to zero because the camera
axis z goes through the center of the object. Finally,
our neural network estimates three parameters defined
in the Euclidean space avoiding the ambiguities of the
Euler angles representation.
The imposed constraint assumes that the object is
always located in the image center. Therefore we can
obtain the two lost degrees of freedom by determining
the object center expressed in image coordinates and
refine the pose. Thus, the resultant coordinate system
C’ defined by XYZR vector can be refined by rotating
it to make its z-axis intersect the image center.
2.1 Methodology
Let C denote a rigid transform between the object
and the camera coordinate system given by O and C,
which are shown in Fig. 2 Apart from that let C
0
de-
note a rigid transform whose z-axis intersects the ori-
gin of the O coordinate system. The homogeneous
matrix representation of C
0
is derived from transla-
tion vector C
0
T
and in-place rotation angle θ. In order
to determine the matrix representation of C
0
we as-
sume that the x-axis of camera coordinate system is
parallel to the O
XY
plane if θ equals zero. Given these
assumptions we determine C
0
as follows:
z =
C
0
T
||C
0
T
||
, (1)
x =
[−z
2
,z
1
,0]
T
q
z
2
1
+ z
2
2
, (2)
y = z × x, (3)
C
0
=
x y z C
0
T
0 0 0 1
·
.cos(θ) −sin(θ) 0 0
sin(θ) cos(θ) 0 0
0 0 1 0
0 0 0 1
.
(4)
The method of calculating the x vector leads to a sin-
gularity when the first two components of z vector
equal zero. In practical implementation it is very un-
likely for a neural network to output such values of its
rarity in single-precision floating-point number for-
mat. However, we assign a constant value to x in order
to ensure that the computation will not fail.
Further calculation of the goal representation of C
rigid transform can be carried out when the relevant
camera parameters are known. Let w,h be the width
and height of images produced by the camera. Addi-
tionally the camera parameters are defined by f
x
and
f
y
which denote camera field of view for width and
height, respectively. If we know the actual position
I
xy
of the object’s centre on the image I, then the cor-
rection T that should be applied is represented by:
φ
x
=
I
x
w
−
1
2
· f
x
,
φ
y
=
I
y
h
−
1
2
· f
y
,
T =
cos(φ
y
) 0 sin(φ
y
) 0
0 1 0 0
−sin(φ
y
) 0 cos(φ
y
) 0
0 0 0 1
·
·
1 0 0 0
0 cos(φ
x
) −sin(φ
x
) 0
0 sin(φ
x
) cos(φ
x
) 0
0 0 0 1
.
(5)
2.2 Architecture
The whole pipeline for 6D pose estimation presented
in Fig. 3 consists of three modules: object extrac-
tor (Mask R-CNN (He et al., 2017)), camera coarse
Hybrid 6D Object Pose Estimation from the RGB Image
543
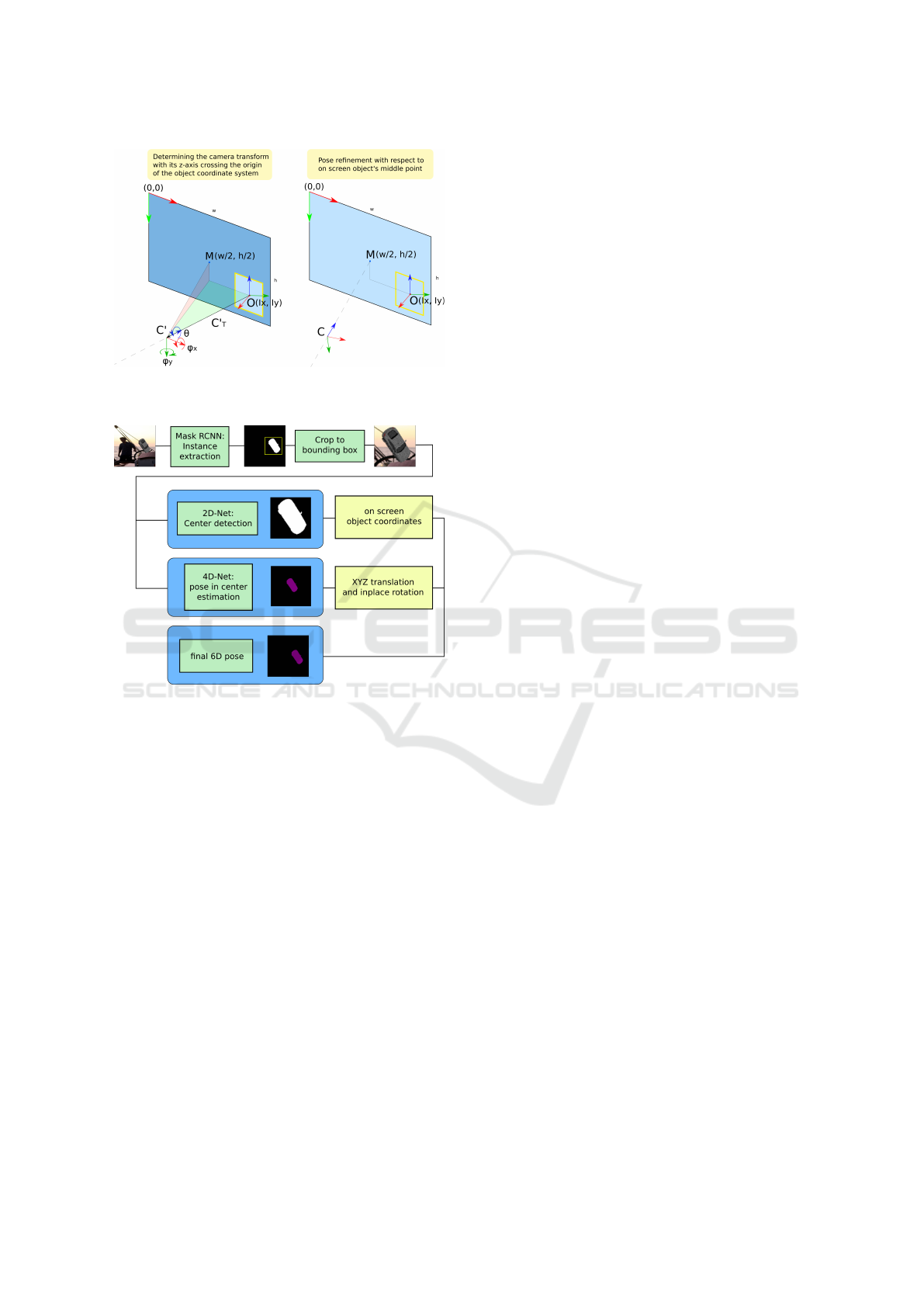
Figure 2: Visualization of the consecutive steps of our pose
estimation approach.
Figure 3: The pipeline of the 6D pose estimation frame-
work.
position estimator (4D-NET) and object’s centre es-
timator (2D-NET). In practice, the object can be lo-
cated in any random position on an image plane. With
no prior knowledge as to where the object is located
and what area it covers it is complicated to predict
the pose precisely. Object extraction is therefore of
paramount importance, since the ratio of relevant and
irrelevant information might be very low given the
full, uncropped image. Furthermore, the image may
contain several objects and every one of them should
be addressed separately.
The image extractor’s main task is to provide de-
tailed image and class information about objects in
the scene. The modules responsible for parameter es-
timation are trained separately for every single object.
The class information derived from the image extrac-
tor serves as a selector for the modules that should be
run to analyze the image excerpt.
2.3 Object Extractor
The first network in the pipeline is the object extrac-
tor. The object extractor is fed by RGB data and out-
puts the mask and bounding box information about all
the detected objects. We use the Mask R-CNN archi-
tecture which provides the 2D mask, class informa-
tion and bounding boxes of objects (He et al., 2017).
After successful detection all the objects are cut out
from the image according to their bounding boxes.
The input shape of 4D-NET and 2D-NET is constant
and square which involves reshaping bounding boxes
in order to match the dimensions.
2.4 4D-NET Architecture
The architecture of the 4D-NET is presented in Fig.
4. The base of the network is built in a fully convolu-
tional manner. The input of the network has a shape of
64 × 64 × 3. We use strides of 1 and kernel of shape
3 × 3 across the whole network. We apply weights
regularization according to the L2 rule with a scale
coefficient set to 0.01. At the beginning of the train-
ing weights are initialized with the usage of Xavier
initializer. The reasons behind a convolutional-based
architecture are its proven capabilities of separating
relevant image data and overall generalization prop-
erties. The output of the last convolutional layer is
flattened and fed then to another two fully connected
layers with 512 and 4 units. The latter layer provides
a prediction of relative translation from the camera to
the object as
ˆ
T coordinates and in-place rotation an-
gle θ. In order to avoid overfitting the convolutional
layers are trained with batch normalization technique
and the fully connected layers apply dropout omitting
half of the connections. The ReLU activation function
is used across the entire network.
2.5 4D-NET Loss Function
Since the goal of estimating XYZ translation and in-
place rotation angle is to determine the C
0
rigid trans-
form we have decided not to treat each parameter sep-
arately but rather couple them all together. Impre-
cise XYZ prediction results in an increasing angle
error between target and predicted rigid transforms
when we compare them in angle-axis representation.
With that in mind, we have introduced a loss func-
tion which penalizes the network for any trial to com-
pensate the distance error at the expense of rotation.
Moreover, the order of magnitude of translation error
may vary significantly within the dataset. This kind
of data instability is alleviated by varying normalizing
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
544

Figure 4: The architecture of 4D-NET. The network takes as input a three-channel color image and converts it into four-
element vector through consecutive convolutional and two dense layers. The resultant vector consist of relative camera to
object XYZ translation and in-place rotation angle.
Figure 5: The architecture of 2D-NET. The input of 2D-NET is a three-channel color image, same as in 4D-NET, and it
outputs a two-element vector, which describes the center of the object projected on the image plane. The image coordinates
are normalized during training and the network outputs values within a range of 0 to 1.
term which is directly dependent on the translation la-
bel.
Let T,
ˆ
T,R,
ˆ
R denote the target and predicted
translation vectors and the rigid transforms’ rotation
matrices. The function G(R,
ˆ
R) defines the angle dif-
ference between target and predicted rotation matrices
in angle-axis representation:
G
R,
ˆ
R
= arccos
Tr
R ·
ˆ
R
− 1
2
. (6)
The overall loss function is a sum of resultant dis-
tance and rotation errors. The λ coefficient has been
added in order to weigh the practically incomparable
distance and rotation measures:
`(T,
ˆ
T , R,
ˆ
R) =
||T −
ˆ
T ||
2
||T ||
2
+ λ · G
R,
ˆ
R
. (7)
2.6 2D-NET Architecture
The architecture of the 4D-NET is presented in Fig. 5.
The architecture of the network consists of 6 con-
volutional, 3 pooling and 2 fully connected layers.
The network uses strides of 1 and kernels of shape
3x3 for convolutional layers. The convolutional lay-
ers increase the overall filters count after every max-
pooling layer. As in the 4D-NET the batch normaliza-
tion, dropout and L2 regularization have been applied.
The network outputs two parameters which stand for
the I
xy
location (the center of the object on the image
plane). Fairly minimalist setup suits well the problem
and the network extracts relevant features and does
not need much computational power for training.
2.7 2D-NET Loss Function
For training 2D-NET the Euclidean distance loss has
been employed. We did not notice any major im-
provement when changing the loss function to Man-
hattan distance as both approaches tend to be easily
minimized during learning process.
2.8 Dataset
We have prepared a synthetic dataset for validation
of our method. The dataset consist of objects of six
classes (car, faucet, chair, phone, screen, pistol) and
the models were derived from the ShapeNet dataset
(Chang et al., 2015). The selected objects from the
dataset are presented in Fig. 6. The objects are charac-
terized by different shape, size and visual features. In
a real-world setting it would be an extremely arduous
effort to create an annotated dataset, which fully cov-
ers all objects’ representation in the space of all pos-
sible Euler rotations with varying distance. The cur-
rently available non-synthetic datasets such as YCB
Video (Xiang et al., 2018) and LineMOD (Hinter-
stoisser et al., 2011) provide very detailed images and
Hybrid 6D Object Pose Estimation from the RGB Image
545

annotations of object of different classes but the ob-
jects are not sampled uniformly and some camera an-
gles are omitted due to the manual camera operation.
Figure 6: Representations of objects from our dataset (from
the top row: car, chair, faucet, phone, pistol, screen).
The easiness of creating synthetic sceneries with
predefined conditions suits best the scenario of train-
ing neural networks for big data consumption. We
have therefore rendered multitude of samples for ev-
ery aforementioned object.
The dataset consists of 256 × 256 px RGB images
and binary masks. The camera points from which the
objects have been rendered were laid out uniformly
on a surface of unit sphere. These points have been
also multiplied by random distance factor in order to
achieve representations of varying magnitude and per-
spective. The in-place rotation angle ranged from -60
up to 60 degrees with a step of 3 degrees.
Each object has been rendered with random back-
ground images which have been derived from the Pas-
cal VOC dataset.
2.9 Training the Networks
We trained every module of pose estimation pipeline
independently. The Mask R-CNN network was al-
ready pretrained on the COCO dataset, containing 80
classes. As a next step we fine-tuned the pretrained
network on a smaller dataset of objects.
Training both 4D-NET and 2D-NET was common
when it comes to data preparation stage. It is worth to
mention that the visual centre of bounding box does
not necessarily match the geometrical center of ob-
ject. Moreover, the input data has to be cropped to the
dimensions of 64 × 64px The rectangular bounding
box must be properly transformed to a square shape
with respect to the center position. The Mask R-CNN
does not extract instances perfectly in all cases. For
that reason we shift and scale the bounding boxes, so
that the final crops are not matched perfectly. Bound-
ing boxes randomization increases robustness to im-
precisely detected mask through Mask R-CNN.
The 4D-NET was trained with the batch size of
2 and learning rate=0.001. The network was being
trained 12 hours on Nvidia Titan XP before reaching
satisfactory results. The 2D-NET was trained with
the batch size of 5 and with the same learning rate
as the previous network. It turned out that the centre
detection is not challenging and the network provides
close to zero error after one hour of training.
3 RESULTS
3.1 Center Estimation
We have tested the performance of the network for
middle point detection on the test data from our
dataset. The samples provided by the dataset contain
images with binary masks and middle point coordi-
nates of the objects. Therefore we used this informa-
tion to create excerpts using bounding boxes of ran-
domized origin positions and dimensions. The idea
bounding box randomization resembles the case of
inexact instance segmentation of the object extractor.
This approach allowed us to test the robustness of the
network while having only limited data.
The used error metrics for center point estimation
was the Euclidean distance between for both normal-
ized and absolute 2D image coordinates. We use im-
age excerpt coordinates in order to compare the accu-
racy of middle point detection. At the very end the
excerpts are resized to match the dimensions of the
input layer of neural network.
The testing procedure using randomized bounding
boxes always ensures that the object is present in an
image. However, some part the object may be invisi-
ble. We have observed that the network performs very
well given a valid object excerpt. Images presented in
Fig. 7 reflect sample predictions produced be the net-
work.
The pixel distance error is represented by follow-
ing equation:
e
distance
=
q
( ˆx − x)
2
+ ( ˆy − y)
2
. (8)
The results of the center estimation for each object
from the dataset are presented in Tab. 1. The average
inference error was within 1.72 px for all of the ob-
jects in our dataset. We did not noticed any significant
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
546

outliers during the testing phase. The resultant error
exerts only a slight influence on the ultimately esti-
mated pose. The final error derived from the network
for center detection depends linearly on the initial res-
olution of an image except due to the scale factor.
Table 1: Results of the object’s center estimation.
car chair faucet screen phone pistol average
e
distance
[px] 1.89 1.77 1.07 1.75 1.64 2.17 1.72
e
distance std
[px] 1.53 1.45 1.06 1.60 1.55 2.10 1.55
Figure 7: Example results of the object center estimation.
3.2 Pose Estimation
In the case of pose estimation we have tested the
whole pipeline consisting of three neural networks to
evaluate the inference error. The resultant inference
error is influenced only to a small degree by the cen-
ter detection network. Therefore the final pose pre-
diction may be impaired estimated when the 4D-NET
network does not perform well. The input data for
testing procedure were the object representations de-
tected by Mask-RCNN network. We only evaluated
the error metrics for valid detections.
We considered the Euclidean distance error, the
distance between rotation in angle-axis representation
and IoU as the metrics applied for testing the valid-
ity of the method. In order to disregard the distance
disparity among the rendered objects of different size
we normalize the absolute distance error separately
for each label. The results on the pose estimation are
summarized in Tab. 2.
We have established that is possible to retrieve
6D pose based within a tolerable margin using only
color data. The average distance error adds up to 9
cm which is an acceptable result since we use only
cropped and resized color data. The relative distance
can therefore be determined according to the minor
changes of object representation caused by camera
projection. The rotation error lies within a range from
9 to 12 degrees. We noticed that the in-place angle
step used for dataset creation has a major impact on
the rotation error. The more in-place angles are used
for every single camera position, the better rotation
estimation becomes. During the inference stage we
have observed outliers to occur rarely for both dis-
tance and rotation parts. The effectiveness of cen-
ter point estimation allowed to achieve representation
with a high IoU factor as the binary masks overlap
each other to a very large extent in most of the cases.
The normalized distance and rotation errors are
defined by equation (9). We express the rotation dif-
ference between two rotation matrices in degrees:
e
distance
=
||T −
ˆ
T ||
2
||T ||
2
· 100%,
e
rotation
= arccos
Tr
R ·
ˆ
R
− 1
2
·
180
π
.
(9)
Table 2: Pose estimation results.
car chair faucet screen phone pistol average
e
distance
[%] 5.43 6.19 5.87 6.59 7.12 5.57 6.12
e
distance std
[%] 5.12 5.79 6.27 7.04 7.53 5.23 6.16
e
rotation
[degrees] 2.83 3.19 3.03 3.76 4.22 3.58 3.43
e
rotation std
[degrees] 3.21 3.68 3.46 4.15 4.59 4.01 3.85
acc
IoU
[%] 97.2 95.6 96.4 96.1 95.8 96.1 96.4
Figure 8: Example estimated 6D poses compared to the
ground truth data.
Figure 9: Invalid pose predictions. The overlaying projec-
tions does not match silhouettes of the presented objects.
We also visualize the pose error on the image
plane by projecting the estimated object pose on the
RGB image. The example results are presented in
Fig. 8.
Hybrid 6D Object Pose Estimation from the RGB Image
547

In some cases the output of the 4D-NET did not
match the ground truth accurately, as it is shown in
the Fig. 9. We have noticed that the biggest error was
caused by rotation disparity. In most of the cases this
was affected by improper in-place angle prediction,
while the translation influenced the rotational differ-
ence to a relatively small extent. We have established
that such situations make up 8% of all cases during
testing phase.
3.3 Runtime
The biggest overhead in the computation pipeline is
imposed by the Mask R-CNN network. The infer-
ence time for both 4D-NET and 2D-NET are negli-
gible and they jointly provide a result in 7 millisec-
onds on Nvidia Titan XP. Therefore we can report the
runability at approximately 13-15 frames per second.
The complexity of computation is not influenced sig-
nificantly for multi-object pose estimation since the
proposed network architectures are quite lightweight.
4 CONCLUSIONS AND FUTURE
WORK
In this paper, we show that the 6D pose estimation
can be split into two smaller sub-problems. First, the
neural network (4D-NET) estimates the camera trans-
lation and in-place rotation with respect to the ob-
ject. At this stage, we assume that the camera axis
goes through the center of the object. Second, the full
3D pose of the camera with respect to the object is
computed using the mathematical model of the cam-
era. The two-stage solution to the object pose esti-
mation allows simplifying the problem in comparison
to end-to-end solutions (Kehl et al., 2017). As a re-
sult, the neural network used for the pose estimation
(4D-NET) can be more compact and computationally
efficient.
To detect the object on the RGB image we use
the Mask R-CNN method (He et al., 2017). The cen-
ter of the detected bounding box does not correspond
with the projection of the object’s center on the image
plane. Thus, we designed the neural network which
estimates the center of the object on the image plane
(2D-NET). Finally, we show results on the publicly
available dataset. The obtained average translation
error is smaller than 7% and the obtained rotation er-
ror is smaller than 5 degrees. It means that we can
precisely and efficiently (up to 15 frames per second)
estimate the pose of known objects in the 3D space
using RGB image only.
In the future, we are going to verify the method
in real-world robotics applications. We are going to
use the proposed method to detect and grasp the ob-
jects by the mobile manipulating robot. We also plan
to investigate the accuracy of the proposed method in
real-world scenarios and work on the precision of the
pose estimation.
ACKNOWLEDGEMENTS
This work was supported by the National Centre for
Research and Development (NCBR) through project
LIDER/33/0176/L-8/16/NCBR/2017. We gratefully
acknowledge the support of NVIDIA Corporation
with the donation of the Titan Xp GPU used for this
research.
REFERENCES
Bibby, C. and Reid, I. (2016). Robust Real-Time Visual
Tracking Using Pixel-Wise Posteriors. In Forsyth D.,
Torr P., Z. A., editor, Computer Vision – ECCV 2008.
Lecture Notes in Computer Science, vol. 5303, pages
831–844. Springer, Berlin, Heidelberg.
Brachmann, E., Michel, F., Krull, A., Yang, M. Y.,
Gumhold, S., and Rother, C. (2016). Uncertainty-
Driven 6D Pose Estimation of Objects and Scenes
from a Single RGB Image. In IEEE Conference
on Computer Vision and Pattern Recognition, pages
3364–3372. IEEE.
Chang, A., Funkhouser, T., Guibas, L., Hanrahan, P.,
Huang, Q., Li, Z., Savarese, S., Savva, M., Song, S.,
Su, H., Xiao, J., Yi, L., and Yu, F. (2015). Shapenet:
An information-rich 3D model repository. In arXiv
preprint arXiv:1512.03012.
Do, T.-T., Cai, M., Pham, T., and Reid, I. (2018). Deep-
6DPose: Recovering 6D Object Pose from a Single
RGB Image. In arXiv.
He, K., Gkioxari, G., Doll
´
ar, P., and Ross, G. (2017). Mask
R-CNN. In IEEE International Conference on Com-
puter Vision, pages 2980–2988. IEEE.
Hinterstoisser, S., Holzer, S., Cagniart, C., Ilic, S., Kono-
lige, K., Navab, N., and Lepetit, V. (2011). Multi-
modal templates for real-time detection of texture-less
objects in heavily cluttered scenes. In IEEE Inter-
national Conference on Computer Vision, pages 858–
865. IEEE.
Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradsky,
G., Konolige, K., and Navab, N. (2012). Model Based
Training, Detection and Pose Estimation of Texture-
Less 3D Objects in Heavily Cluttered Scenes. In et al.,
L. K., editor, Computer Vision – ACCV 2012, Lecture
Notes in Computer Science, vol. 7724, pages 548–562.
Springer, Berlin, Heidelberg.
Hodan, T., Zabulis, X., Lourakis, M., Obdrzalek, S., and
Matas, J. (2015). Detection and Fine 3D Pose Es-
timation of Textureless Objects in RGB-D Images.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
548

In IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 4421–4428. IEEE.
Kehl, W., Manhardt, F., Ilic, F. T. S., and Navab, N. (2017).
SSD-6D: Making RGB-Based 3D Detection and 6D
Pose Estimation Great Again. In IEEE International
Conference on Computer Vision (ICCV), pages 1530–
1538. IEEE.
Khoshelham, K. (2011). Accuracy Analysis of Kinect
Depth Data, International Archives of the Photogram-
metry. In Remote Sensing and Spatial Information
Sciences, pages 133–138. IEEE.
Konishi, Y., Hattori, K., and Hashimoto, M. (2018). Real-
Time 6D Object Pose Estimation on CPU. In arXiv.
Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S., Fu,
C.-Y., and Berg, A. (2016). SSD: Single shot multibox
detector, European Conference on Computer Vision.
In et al., L. B., editor, LNCS vol. 9905, pages 21–37.
Springer.
Prisacariu, V. and Reid, I. (2012). PWP3D: Real-time seg-
mentation and tracking of 3D objects. Int. Journal on
Computer Vision, 98(3):335–354.
Segal, A., Haehnel, D., and Thrun, S. (2009). Generalized-
ICP. In In Robotics: Science and Systems.
Sundermeyer, M., Z.-C, Marton, Durner, M., Brucker, M.,
and Triebel, R. (2018). SSD: Single shot multibox
detector, European Conference on Computer Vision.
In European Conference on Computer Vision, pages
699–715.
Tejani, A., Tang, D., Kouskouridas, R., and Kim, T. (2016).
Latent-Class Hough Forests for 3D Object Detection
and Pose Estimation. In et al., F. D., editor, Computer
Vision – ECCV 2014, Lecture Notes in Computer Sci-
ence, vol. 8694, pages 462–477. Springer, Cham.
Tjaden, H., Schwanecke, H., and Schomer, E. (2016). Real-
Time Monocular Segmentation and Pose Tracking of
Multiple Objects. In Leibe, B., Matas, J., Sebe, N.,
and Welling, M., editors, Computer Vision – ECCV
2016. Lecture Notes in Computer Science, vol. 9908,
pages 423–438. Springer, Cham.
Ulrich, M., Wiedemann, C., and Steger, C. (2012). Combin-
ing Scale-Space and Similarity-Based Aspect Graphs
for Fast 3D Object Recognition. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
34(10):1902–1914.
Wang, C., Xu, D., Zhu, Y., Martin-Martin, R., Lu, C., Fei-
Fei, L., and Savarese, S. (2019). DenseFusion: 6D
Object Pose Estimation by Iterative Dense Fusion. In
Computer Vision and Pattern Recognition.
Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2018).
PoseCNN: A Convolutional Neural Network for 6D
Object Pose Estimation in Cluttered Scenes. In
Robotics: Science and Systems.
Hybrid 6D Object Pose Estimation from the RGB Image
549
