Analysis, Simulation and Control of a New Measles Epidemic Model

Paolo Di Giamberardino and Daniela Iacoviello

Dept. Computer, Control and Management Engineering Antonio Ruberti, Sapienza University of Rome,

via Ariosto 25, 00185 Rome, Italy

Keywords:

Epidemic Modeling, System Analysis, Optimal Control.

Abstract:

In this paper the problem of modeling and controlling the measles epidemic spread is faced. A new model

is proposed and analysed; besides the categories usually considered in measles modeling, the susceptible,

the exposed, the infected, the removed and, less frequently, the quarantine individuals, two new categories

are herein introduced: the immunosuppressed subjects, that can not be vaccinated, and the patients with an

additional complication, not risky by itself but dangerous if caught togeter with the measles. These two

novelties are taken into account in designing and scheduling suitably control actions such as vaccination,

whenever possible, prevention, quarantine and treatment, when limited resources are available. An analysis of

the model is developed and the optimal control strategies are compared with other not optimized actions. By

using the Pontryagin principle, it is shown the prevailing role of the vaccination in guaranteeing the protection

to immunosuppressed individuals, as well as the importance of a prompt response of the society when an

epidemic spread occurs, such as the quarantine intervention.

1 INTRODUCTION

Despite a vaccination of the measles exists since

1963, it is still an important cause of death, espe-

cially among young children. The measles is caused

by a virus that infects the respiratory tract and then

spreads all over the body; it is highly contagious: it

is transmitted by infected patients through droplets

from nose, mouth and throat. After about 10 days

from the infection the main symptoms are high fever,

bloodshot eyes and tiny white spots inside the mouth;

then, a rash spread all over the body, starting from the

face. Generally, for good healthy people, the measles

does not represents a serious illness; it becomes risky

if the infected subjects is a poorly nourished chil-

dren (age less than 5 years old) with insufﬁcient vi-

tamin A or subjects with the immune system weak-

ened by chemotherapy, or HIV/AIDS or other dis-

eases. In these cases complications may lead to death;

the most commons are: diarrhoea (about 70% of the

hospitalized persons with measles in the US), pneu-

monia (more than 9% among children with less than 5

years old) and other respiratory infections (more than

50% among hospitalized children with measles), en-

cephalitis (mainly occurring in patients with HIV in-

fection or leukaemia, ocular complications (R.T.Perry

and N.A.Halset, 2004).

Mathematical modeling of epidemic diseases al-

lows to describe and analyse epidemic diseases,

(Nowzari et al., 2016), (Nowak and May, 2000),

(Pinto and Rocha, 2012), (Naresh et al., 2009),

(Di Giamberardino et al., 2018),(Kuniya and Nakata,

2012), (TW et al., 2003). The availability of suitable

model allows to determine the most effective control

strategy and resources allocation, (Di Giamberardino

and Iacoviello, 2018a), (X.Yan and Y.Zou, 2008),

(Di Giamberardino and Iacoviello, 2017), (Ledzewicz

and Schattler, 2011), (Iacoviello and Stasio, 2013).

The most common models for the measles uses the

SEIR representation, where S stands for the Suscep-

tible individuals, that are the healthy people; E rep-

resents the compartment of the Exposed, that are the

subjects infected but not yet infectious; I is the com-

partment of infected and infectious patients; R con-

tains the subjects Recovered, including the individu-

als that have got the immunity by vaccination or hav-

ing got the measles previously, (A.A.Momoh et al.,

2013), (L.Pang et al., 2015), (O.O.Onyejekwe and

E.Z.Kebede, 2015). Sometimes also the class of

isolated subjects is introduced, (S.O.Adewale et al.,

2016), that is the class Q of subjects induced to iso-

lation to avoid new infections; in this framework it is

shown the existence of a unique endemic equilibrium

point as well as the most efﬁciency of the vaccina-

550

Di Giamberardino, P. and Iacoviello, D.

Analysis, Simulation and Control of a New Measles Epidemic Model.

DOI: 10.5220/0007934405500559

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 550-559

ISBN: 978-989-758-380-3

tion control strategy with respect to the treatment and

the campaign aiming at educating the society to man-

age the measles infection. Another interesting im-

provement of the classical SEIR model is proposed

in (S.Verguet et al., 2015) where the Exposed individ-

uals are not considered, stressing the subjects vacci-

nated susceptible, vaccinated infected and vaccinated

recovered, taking into account the risks of measles

infection also for vaccinated subjects. An interest-

ing study that takes into account the life histories of

interacting individuals is proposed in (E.A.J.Fischer

et al., 2008), where a general approach that could

be applied also to the measles disease is discussed;

it is based on microsimulation models, considering

birth, death and general demographic events. The

possibility of taking into account the complications

is considered in (Di Giamberardino and Iacoviello,

2018b), where a general infectious disease (not nec-

essarily the measles) is considered, and suitable con-

trol strategies for an efﬁcient resources allocation are

proposed. In this paper, it is stressed that some sub-

jects in the population could not be vaccinated, for

example the immunosuppressed people; moreover it

is considered that the patients infected by the measles

are particularly exposed to complications, dangerous

for weak people and/or young children. The model in-

troduced takes into account the different peculiarities

in a susceptible population: two categories of suscep-

tible subjects are introduced, distinguishing among

healthy individuals that can or cannot be vaccinated.

Then, it is included the classical categories of Ex-

posed; as in (S.O.Adewale et al., 2016), it is consid-

ered the category of isolated subjects Q. The category

of Infected patients is split in order to consider the

subjects infected by the infectious disease and those

that have caught also the complication. Finally there

is the class of Removed people. The possible control

strategies introduced to face in particular the presence

of subjects that can not be vaccinated as well as the

possibility of complications include the following ac-

tions:

• prevention actions, such as vaccination (when

possible) and informative campaign;

• treatment control to those patients that have got

the infection;

• treatment control to those subjects that have got

also the second not infectious disease.

The paper is organized as follows; Section 2 is divided

into three subsections: in the ﬁrst two, the considered

model is deeply described and analysed discussing the

existence of the equilibrium points. In the third Sub-

section optimal control strategies are introduced. In

Section 3 numerical results and discussion are pro-

posed; conclusions and future developments are sum-

marized in Section 4.

2 MATERIALS AND METHODS

In this Section a new model of the measles spread is

described, Subsection 2.1, and analysed, Subsection

2.2. In Subsection 2.3 the optimal control strategy is

proposed.

2.1 The Mathematical Model

The mathematical model here analysed takes into ac-

count the most important issues of the measles:

• the possibility that some subjects in the population

could not be vaccinated and therefore it is advis-

able to get the herd immunity;

• the risky condition of having also a complication

along with the infectious disease.

To this aim seven classes of people are introduced:

the Susceptible subjects S1, healthy people not in-

fected; the Susceptible subjects S

, healthy people not

infected that cannot be vaccinated; the Exposed in-

dividuals E, infected people, not yet infectious; the

Quarantine patients Q, patients that from the Exposed

class are isolated; the Infected patients I

, that may

transmit the virus; the Infected patients I

, that may

transmit the virus and with also the non infectious

complication; the Recovered people R, that have been

immunized by vaccine or have been recovered from

the I

or the I

stage. Note that the Q patients get

the measles, they become infected and infectious, but

they cannot infect any other susceptible subject

In Fig.1 it is shown the block diagram of the pro-

posed model. The control actions introduced include

Figure 1: Block diagram of the proposed model.

preventions and treatments; among the former the

predominant one is the vaccination that could be ap-

plied only on the S

individuals. The treatments in-

clude both the actions to face the infectious disease

and the complication; also the patients in the quar-

antine compartment could be considered the effect of

a treatment, meaning that they could not infect any

Analysis, Simulation and Control of a New Measles Epidemic Model

551

susceptible individual. Therefore the proposed model

could be described by the following differential equa-

tions:

= b

− d

− β

+δ

− δ

(1)

= b

− d

− β

+δ

(2)

E = b

− d

E + β

+ β

+β

+ β

− δ

E (3)

Q = −d

Q − γ

Q + δ

T 1

E − δ

T 2

Q (4)

= b

− d

+ δ

(1 − u

T 1

)E − γ

− σ

+σ

− δ

T 3

(5)

= b

− d

− γ

+ σ

− σ

−δ

T 4

(6)

R = b

− d

R + γ

+ γ

Q + δ

+δ

T 2

Q + δ

T 3

+ δ

T 4

(7)

where, using for notation’ reasons the subscripts

1,...,6 referring to quantities in the S

, S

, E, I

, I

and R respectively, b

, i = 1, ...,6 is the rate of new

people entering the compartments; d

, j = 1,...,7 is

the removed rate from every compartments S

, S

, E,

Q, I

, I

and R respectively, including also deaths; β

i j

i = 1,2 j = 1,2 is the contact rate between the subjects

in the compartment S

and the ones in I

; σ

, i = 1,2

is the infection rate with respect to the complication

disease involving the subjects in the I

and the I

com-

partments; γ

, i = 1,2 is the recovery rate from the I

and the I

compartment respectively; δ

, i = 1, 2,..,7

is related with the control success for the actions u

, i = 1,2 and u

T j

, j = 1, ..,4, respectively. Let us

deﬁne the state vector:

X =



S1 S

E Q I



(8)

and the control vector:

U =



T 1

T 2

T 3

T 4



(9)

We introduce the vector F

F =





(10)

where the f

are the r.h.s. functions of equations (1)-

(7).

The proposed complete model with complications

may be written in a compact form as follows:

X = F(X, U, t) (11)

starting from the initial conditions:

X(0) = X

(12)

The control actions are assumed bounded:

0 ≤ U

(t) ≤ U

(13)

being U

the i- th component of the control U given

by (9) and U

its corresponding possible maximum

value. In particular, note that for the u

T 1

control the

maximum value allowed could be no more than 1.

A subject in the S

compartment could be healthy

all life long, or, if vaccinated, he could reach the

recovered class R or he could become exposed and

therefore get the infectious disease and, eventually,

the complication. For a subject in the S

class the

best condition is to remain in that class, since the only

other possibility is to get the infection and maybe also

the risky complication. For the patients infected, but

not yet infectious, two possibilities are allowed: to go

in the quarantine compartment Q, thus avoiding to in-

fect other S

and S

subjects, or to proceed in the I

and, maybe, in the I

classes. Note that the patients in

the Q class could get also the complication; they dif-

fer from the I

and I

patients since they can not infect

any other susceptible individuals.

These considerations suggest the importance of a

suitable control strategy and in particular to reach the

herd immunity; it is important not only for the im-

munosuppressed subject, already weakened by other

therapies, but for all the population since the com-

plications in conjunction with the infectious disease

could be fatal, especially for very young children and

for old people. The analysis of the model with its

equilibrium points is proposed in the next Subsection

2.2.

2.2 The Model Analysis

In this Subsection the model (11) is analysed; the de-

termination of the equilibrium points is not an easy

task, due to the high number of parameters of the

model. Nevertheless, some general considerations

may be proposed and veriﬁed in the numerical results

section.

To determine the equilibrium points in the model

(11) the control inputs U

are assumed null, as well as

the entries b

, j = 3,...,6. Therefore, the equation:

F(X) = 0 (14)

must be solved; as obvious, it is always Q

= 0. As it

can be easily veriﬁed, the point:



0 0 0 0 0



(15)

is always an equilibrium one.

To check the possible existence of other equilib-

rium points, the equation (6) is considered by impos-

ing its equality to zero; it can be deduced that the

numbers of infected subjects I

and I

patients in the

equilibrium point (if it exists) are proportional:

= m

(16)

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

552

having deﬁned

(σ

+ γ

+ d

)

> 0 (17)

From equation (7) it is deduced:

= m

(18)

with

+ γ

> 0 (19)

Analogously, equation (5) allows to write

= m

(20)

with

+ γ

+ σ

− σ

> 0 (21)

It is important to stress that from equation (1) it can be

deduced that if an acceptable value for the equilibrium

exists, then also S

is deﬁned; in fact

+ (β

+ β

]

(22)

Analogously, also S

is well deﬁned once I

is, as it is

deduced from (2)

+ (β

+ β

]

(23)

Note that if I

is equal to zero the equilibrium point

is determined. By summing (1), (2), (3) and sub-

stituting the expression (22) and (23), the following

equation is determined:

+ b

−

+ (β

+ m

+ β

−

+ (β

+ m

+ β

((d

+ γ

+ σ

− σ

(24)

By rearranging (24), if I

6= 0, a second order

equation is obtained:

+ BI

+C = 0 (25)

where

A = d

(β

+ β

)(β

+ β

)[(d

+ γ

+σ

− σ

] (26)

B = [(d

+ γ

+ σ

− σ

][d

(β

+β

) + d

(β

+ β

)]

−(β

+ β

)(β

+ β

)(b

+ b

)δ

(27)

C = d

[(d

+ γ

+ σ

− σ

]

−b

(β

+ β

) − b

(β

+ β

)

(28)

The coefﬁcient A is always positive; to establish the

sign of the equation (25) it necessary to check if both

B and C can be positive (thus no real root is possible),

or if there is one change of sign in the coefﬁcients A,

B and C (thus one positive root exists), or if there are

two changes of sign (thus two positive roots exist).

The latter case corresponds to the condition: B < 0

and C > 0, being A always positive. In that case, from

the deﬁnitions of (27) and (28) one has:

(β

+ β

)(β

+ β

)(b

+ b

)δ

> [d

(β

+ β

) + d

(β

+ β

)]

[(d

)

−1

(β

+ β

) +

)

−1

(β

+ β

) (29)

which is absurd, resulting

0 > b

(β

+ β

)

+ b

(β

+ β

)

Therefore, it can be concluded that it is not possible

to have two solutions from equation (25).

The condition for which no root of (25) exists is

veriﬁed once B > 0 and C > 0. From the deﬁnitions

(27) and (28) it can be deduced that this occurs when:

[(d

+ γ

+ σ

− σ

] > max[B

] (30)

where

(β

+ β

)(β

+ β

)(b

+ b

)δ

(β

+ β

) + d

(β

+ β

)]

(31)

and

(β

+ β

) + b

(β

+ β

)

(32)

In the two situations discussed up to now no equilib-

rium point is determined from equation (25) and the

unique equilibrium point is P

. Now we deduce the

conditions under which one real positive solution ex-

ists of equation (25); it occurs when B > 0 and C < 0

and when B < 0 and C < 0. The former inequalities

imply:

(β

+ β

) + b

(β

+ β

)

> d

[(d

+ γ

+ σ

− σ

]

> d

(β

+ β

)(β

+ β

)(b

+ b

)δ

(β

+ β

) + d

(β

+ β

)

Therefore the conditions B > 0 and C < 0 are veriﬁed

(β

+ β

)

+ b

(β

+ β

)

> b

(1 − d

)(β

+ β

)(β

+ β

) (33)

Analysis, Simulation and Control of a New Measles Epidemic Model

553

Finally, with similar arguments as in the case B,C > 0,

it can be stated the condition for which the last situa-

tion occurs, that is B < 0 and C < 0:

[(d

+ γ

+ σ

− σ

] < min[B

] (34)

From all this analysis it can be deduced that the pro-

posed measles epidemic spread model allows at most

two equilibrium points, P

and the solution, if it ex-

ists and is admissible, of equation (25).

Finally, to establish the stability of the deter-

mined equilibrium point(s) the jacobian matrix is cor-

respondingly evaluated to determine the eigenvalues;

in the numerical Section this calculus is provided for

the proposed choice of parameters.

2.3 The Optimal Control Problem

The natural framework in which epidemic control is

faced is the optimal control theory that allows to allo-

cate the limited resources in an efﬁcient way.

The control strategies proposed in this paper are

the preventions and the treatments; the former include

the most important one, the vaccination, whereas the

latter range from the sensibilization to enter in the

quarantine condition to the treatment speciﬁc for the

infectious disease, and for the complication.

The idea is to choose the control (9) in such a way

that the number of infected patients, both with and

without complications, is minimized. The proposed

cost index is:

J =

L(X,U,t)dt



+ A

+ B

T 1

+ B

T 2

+ B

T 3

+ B

T 4



dt (35)

In view of the use of the Pontryagin principle, the

Hamiltonian function is deﬁned as:

H =

L(X,U,t)+ λ

(t)F(X,U,t)

∑

i=1

∑

j=1

+ λ

(t)F(X,U,t)

(36)

where λ

, i = 1,2, ...,7 are the costate functions. The

necessary conditions of optimality are given by:

= −

∂H

∂X

, i = 1, 2,..., 7 (37)

0 =

∂H

∂u

, j = 1,..,7 (38)

with ﬁnal conditions:

) = 0, i = 1,2,...,7 (39)

By solving conditions (38) and taking into account

the constraints (13), along with the (37), the optimal

control U

, i = 1, ..,7 are determined:

= max{min{

(λ

− λ

)δ

},0}(40)

= max{min{

−λ

},0} (41)

= max{min{

−λ

},0} (42)

T 1

= max{min{

(λ

− λ

)δ

},0} (43)

T 2

= max{min{

(λ

− λ

)δ

},0} (44)

T 3

= max{min{

(λ

− λ

)δ

},0} (45)

T 4

= max{min{

(λ

− λ

)δ

},0} (46)

Note that the optimal controls require the solution

of the costate equations (37) with the ﬁnal condition

(39) in addition to the state equation (11) with the ini-

tial conditions (12).

3 NUMERICAL RESULTS AND

DISCUSSION

In this Section, a numerical analysis is performed to

study the proposed measles epidemic model and to

evaluate the effects of different control strategies in a

ﬁxed time period [0, 30] years. As far as the choice of

the model parameters, they are strictly dependent on

the speciﬁc population on which the model is referred

to: different healthy, economic and social conditions

could vary signiﬁcantly its numerical values. In all

the cases analysed the initial conditions are set equal

to X



900 10 5 1 1 0 0



, whereas for

the model parameters the values

= 10, b

= 1, j = 2,. ..,5, b

= 0,

= d

= 0.015, d

= 0.02,

= d

= 0.05, d

= 0.08, d

= 0.09

i j

= 0.01, i = 1,2, j = 1,2,

= 0.4, σ

= 0.2,

= γ

= 0.1, γ

= 0.07

= 0.9, δ

= δ

= 0.2, δ

= 0.4, j = 4,.., 7

are assumed. Note the higher values of death param-

eters for the subjects in the I

and I

classes corre-

sponding to the risky condition of being infected and,

most of all, of being infected with a complication.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

554

The parameter σ

is assumed larger than σ

to stress

the larger rate of getting the complication rather than

recovering from it. By using the analsyis of Subsec-

tion 2.2, the obtained equilibrium points for the pro-

posed choice of parameters are:



667 50 0 0 0 0 0)



(47)

always present, and:



2 0 219 0 245 272 2906



(48)

These results are consistent with what stated previ-

ously; in fact by evaluating the parameters A, B, and

C given by (26), (27) and (28) respectively, it is found:

A = 10

−6

, B = −0.0016, C = −0.0016 (49)

Therefore a second equilibrium point, besides P

, ex-

ists. The evaluation of the Jacobian matrix in each of

these points and the determination of the correspond-

ing eigenvalues allow to state that P

is not stable,

whereas the P

is locally asymptotically stable, hav-

ing all the eigenvalues real and negative.

The optimal control actions proposed are intro-

duced in the model and compared with three situa-

tions: free evolutions (Case 1), only constant vacci-

nation (Case 2), only constant prevention campaign

(without vaccination) with constant treatments (Case

3). The comparison is proposed both from graphical,

Figs. 2–8, and numerical, Table 1 and Table 2, point

of view. The indicators introduced aim at evaluating

the effectiveness of the actions with respect to the pe-

culiarities of the epidemic disease considered, that is

to avoid susceptible subjects S

to get the infections

and to avoid infected subjects I

to get the complica-

tion, thus entering in the I

class. The optimal con-

trol strategy is referred as Case 4. The indicators pro-

posed in Table 1 are:

• the percentage of dead patients infected, i.e. the

total number of dead patients in the E, Q, I

and

compartments with respect to the total number

of dead people in the population;

• the number S

t f

of susceptible subjects in S

at the

end of the control period;

• the percentage

of susceptible subjects S

in the

entire control period;

• the percentage

of infected patients I

in the en-

tire control period;

• the percentage

of infected patients I

in the en-

tire control period;

• the percentage

R of removed individuals R in the

entire control period.

Moreover, also the cost of each strategy is evaluated

by considering the total control effort

of each U

see Table 2.

As far as the control actions, they are assumed

bounded between 0 and 0.8. In the cost index the

control actions are weighted, aiming at an efﬁcient

resources allocation; the solution of the optimal con-

trol problem depends on the choice of the parameters

in the cost index, as usual; the proposed setting cor-

responds to the need of allowing a deeper prevention

campaign trying to avoid as much as possible the risky

condition of the infection. Therefore, the following

choices are proposed:

= 10

−4

, i = 1, 2,3 B

= 0.01, i = 4, ..,7

Hence, the treatments are considered more expensive

than the prevention controls. As far as the parame-

ters of the optimal control problem formulations, they

have been chosen as A

= 0.1 and A

= 10; this means

that the aim is to minimize mainly the number of in-

fected subjects I

, being the ones that are risking more

with the infection and the complication. Of course

other choices are possible; in this case it is stressed

the dangerousness of being in the I

class. In Figs.

2–8 the evolutions of the state variables in the four

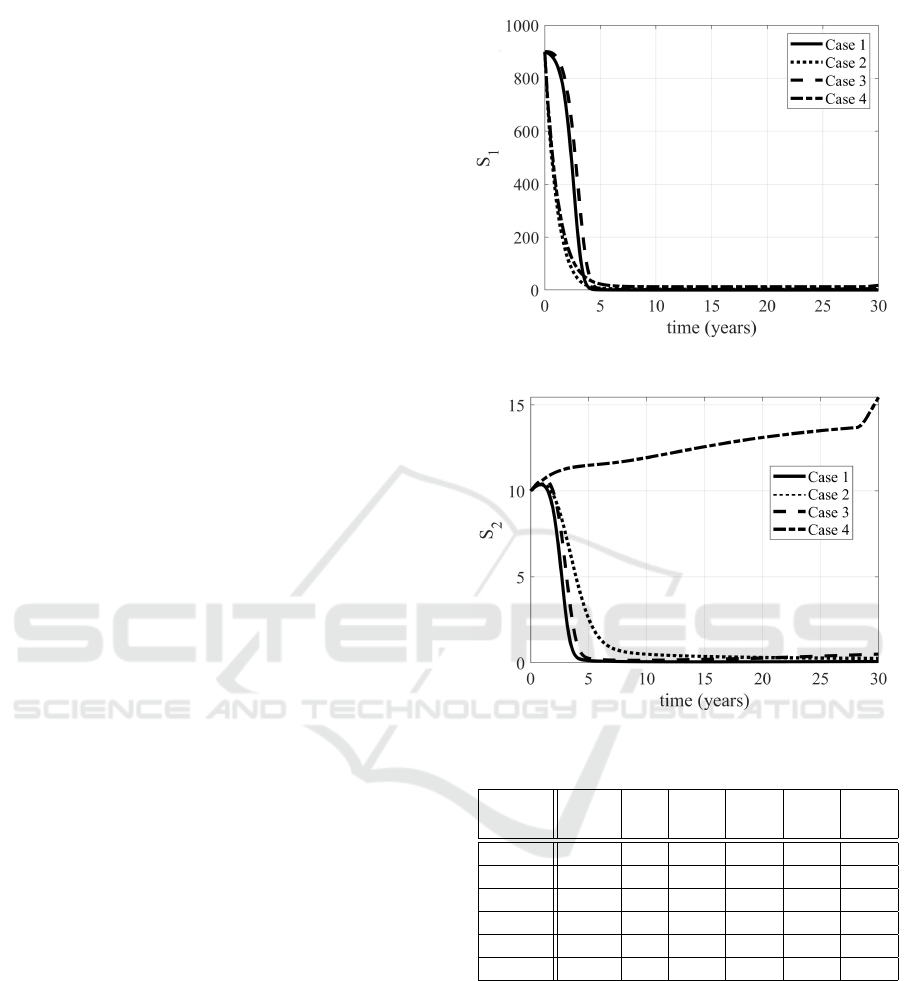
cases considered are proposed. The increased num-

ber of S

subjects is evident, as well as the decrease

of the infected subjects (patients in E, Q, I

and I

The Case 3, devoted to the treatments, allows a

large number of people to enter in the quarantine con-

dition, sensibly more than in Case 4; this is reason-

able, since in the latter, being possible all the control

actions together, it has been chosen to weight more

the treatments, assuming more costly (also from a so-

cial point of view) to act after the infection, rather

than preventing it. It it worth to be noted the evolu-

tion of the removed subjects: in the non controlled

case (Case 1) the population will enter in the R class,

sooner or later; with the optimal control the idea is to

avoid people to enter in the epidemic path (E, Q or I

and maybe I

) and getting the immunity or remaining

in the susceptible condition S

, reducing the number

of dead patients (see Table 1). Therefore the evolution

of the R subjects is rather constant in Case 4.

As far as the optimal control actions it is worth to

be noted that the vaccination is required at its upper

bound for most of the control period, as well as the

control u

T 1

, that induces patients to quarantine, thus

avoiding to infect susceptible people. This is reason-

able, having chosen to minimize the number of in-

fected patients.

From Table 1 it is evident the advantage of allo-

cating efﬁcently the resources; in fact the number of

dead people is one order lower in Case 4 with respect

Analysis, Simulation and Control of a New Measles Epidemic Model

555

to the absence of control (Case 1); the decrease is ev-

ident also with respect to constant controls applied,

Case 2 (control only by the vaccination) and Case 3

(control only by the prevention, without vaccination,

and treatments).

The advantages in Case 4 are evident when con-

sidering the number of susceptible people S

at the

end of the control period; moreover also the num-

ber of recovered people, that is immunized subjects

(where the immunization is obtained by vaccination

or after having caught the disease), strongly increases

in Case 4. Obviously, the efﬁcient use of all the avail-

able controls is more expensive, rather than do not do

nothing (Case 1) or use only some of the control ac-

tions, as evidenced in Table 2.

It is interesting to note what happen if in the cost

index the weights of the control are increased of two

orders of magnitude, meaning that it becomes more

expensive (for all the controls) to minimize the in-

fected patients I

and I

. The numerical values are

shown in Table 1 and Table 2, indicated as Case 5;

it is important to note that from a numerical point of

view the results appear rather equivalent, slightly less

expensive than in the Case 4, see Table 2. What is

interesting is the behaviour of the controls u

, u

and u

, as shown in Figs. (12), (13), (14). In fact,

while the evolutions of the treatments control do not

vary signiﬁcantly, in Case 5 the vaccination is at its

maximum value for less than ﬁve years, with a re-

quired increase of the other two prevention controls

and u

. Therefore, the optimal control formula-

tion allows to allocate optimally the more expensive

resources obtaining almost comparable numerical re-

sults for the indicators, as noted.

As noted, the results of the optimal control strat-

egy depend on the weights A

, i = 1,2 and B

, j =

1,...,7. The choice proposed in Case 4 and Case 5

aims at reducing mainly the number of patients I

, be-

ing the ones more at risk. Since in the model it is as-

sumed that a subjects becomes a member of the risky

class I

only after entering in the I

class, a strategy

could be to avoid strongly the infection, and thus as-

signing an higher weight to A

, than to A

. Therefore,

in the following Case 6 it assumed A

= 10, A

= 0.1,

with the same values of the weight B

, j = 1,...,7 as in

Case 4. It can be noted the slight increase of the per-

centage of dead patients with respect to Case 4 but the

almost equivalent results for the other indicators of

Table 1. The cost of the vaccination increases, while

there is a sensible decrease in the prevention actions

and u

, see Table 2; this result could be justiﬁed,

considering that, besides any complication, the best

strategy to avoid people to get the measles the most

effective strategy is the vaccination.

Figure 2: Evolutions of the S

subjects in Cases 1,2,3,4.

Figure 3: Evolutions of the S

subjects in Cases 1,2,3,4.

Table 1: Evaluation of the cases proposed.

Dead S

t f

(%) (%) (%) (%) (%)

Case 1 87.7 0 0.03 19.6 19.9 37.9

Case 2 60.5 0 0.28 7.8 7.6 59.6

Case 3 78.8 1 0.12 11.6 9.18 44.6

Case 4 7.98 15 1.38 0.25 0.3 90.7

Case 5 8.17 21 1.51 0.26 0.3 90.4

Case 6 8.00 15 1.38 0.25 0.3 90.8

4 CONCLUSIONS

The measles infectious disease represents a risk for

subjects that can not be vaccinated, mainly for the

possible complications. In this paper this problem is

faced by proposing a new model that extends the clas-

sical SEIR scheme usually adopted introducing the

speciﬁc class of immunosuppressed subjects and the

one of subjects infected with complication. The aim

is to determine the best global control strategy includ-

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

556

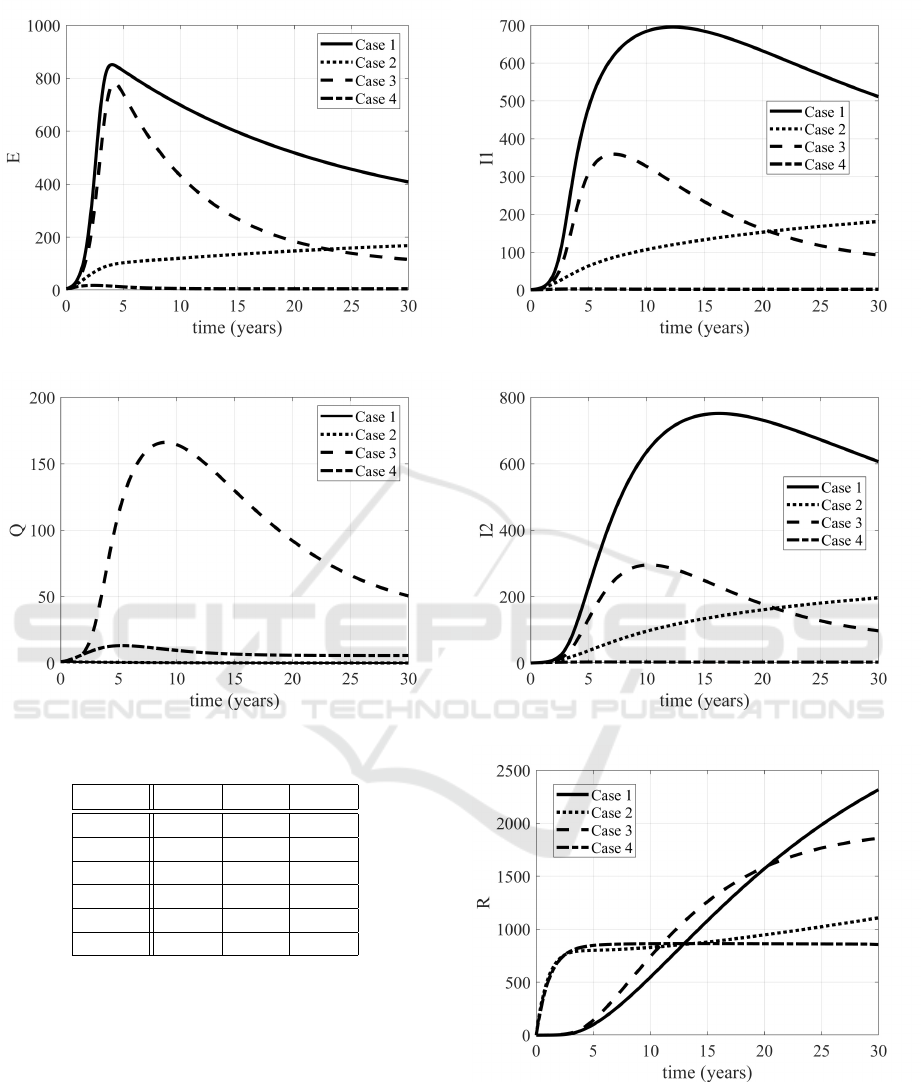
Figure 4: Evolutions of the E subjects in Cases 1,2,3,4.

Figure 5: Evolutions of the Q subjects in Cases 1,2,3,4.

Table 2: Evaluation of the control strategies.

∑

Case 1

Case 2 24

Case 3 6 24

Case 4 23.58 1.1 82.42

Case 5 21.6 9.1 81.28

Case 6 23.75 0.61 82.32

ing vaccination, other prevention actions (such as in-

formative campaign) and treatments. In the frame-

work of optimal control theory and under the hy-

pothesis of limited resources, an optimal solution to

the problem of decreasing the number of infected pa-

tients is proposed. The central role of vaccination is

conﬁrmed, along with a synergy among all the intro-

duced actions; the improvements due to the optimal

control determined are evident when compared with

the absence of control or with strategies that consider

treatments and preventions (but not vaccination) or

those that introduce only the vaccination. Future work

should identify the model parameters referring to spe-

Figure 6: Evolutions of the I

subjects in Cases 1,2,3,4.

Figure 7: Evolutions of the I

subjects in Cases 1,2,3,4.

Figure 8: Evolutions of the R subjects in Cases 1,2,3,4.

ciﬁc scenarios, taking into account socio-economics

and cultural conditions. Consequently, also the pa-

rameters referring to the control actions should be re-

considered taking into account the economic cost of

prevention and of treatments. In the proposed formu-

lation the ﬁnal time is ﬁxed at 30 years; nevertheless

Analysis, Simulation and Control of a New Measles Epidemic Model

557

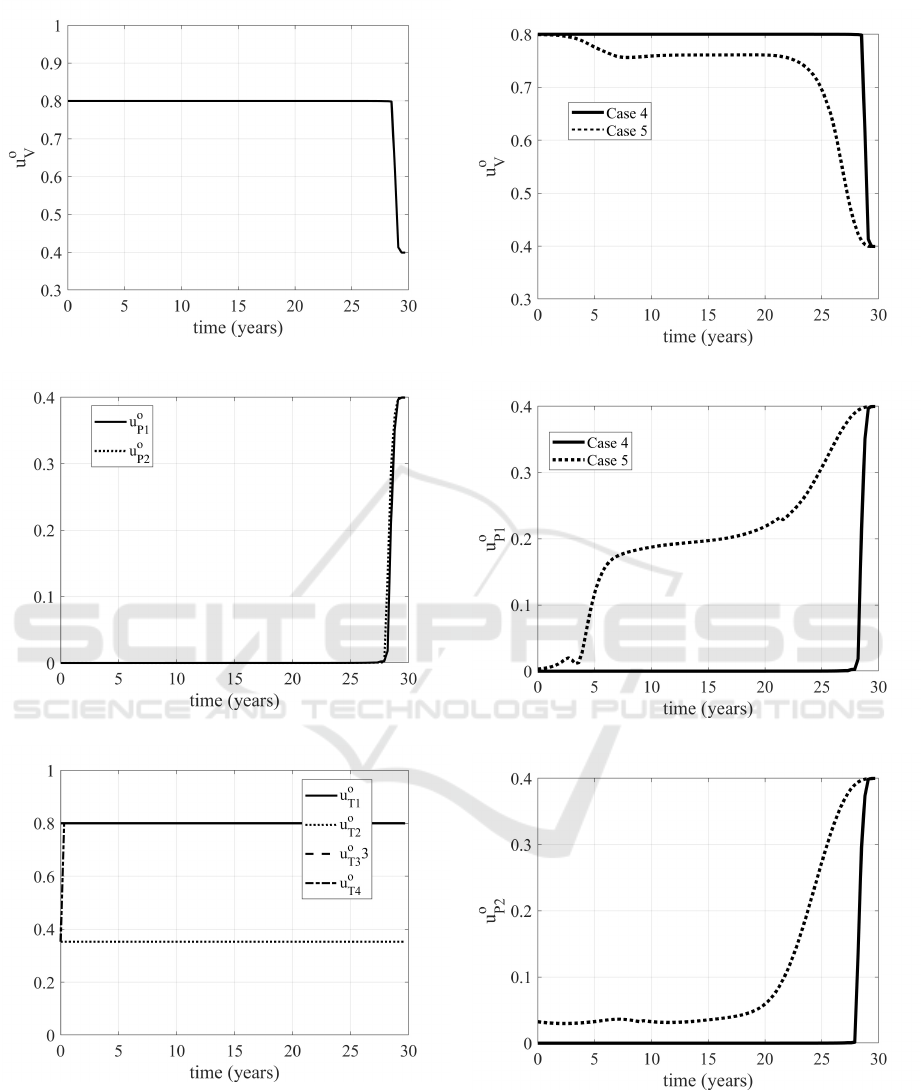
Figure 9: Evolution of optimal vaccination u

Figure 10: Evolutions of the u

and u

controls.

Figure 11: Evolutions of the u

T j

, j = 1,..,4 controls.

it could be interesting, referring to particular cases, to

determine the best strategy to reduce the number of

infected patients in the minimum time.

Figure 12: Evolution of the u

control in Cases 4 and 5.

Figure 13: Evolution of the u

control in Cases 4 and 5.

Figure 14: Evolution of the u

control in Cases 4 and 5.

REFERENCES

A.A.Momoh, Ibrahim, M., i.J.Uwanta, and S.B.Manga

(2013). Mathematical model for control of measles

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

558

epidemiology. International Journal of Pure and Ap-

plied Mathematics, 87(5):707–718.

Di Giamberardino, P., Compagnucci, L., Giorgi, C. D., and

Iacoviello, D. (2018). Modeling the effects of pre-

vention and early diagnosis on hiv/aids infection dif-

fusion. IEEE Transactions on Systems, Man and Cy-

bernetics: Systems.

Di Giamberardino, P. and Iacoviello, D. (2017). Optimal

control of SIR epidemic model with state dependent

switching cost index. Biomedical Signal Processing

and Control, 31.

Di Giamberardino, P. and Iacoviello, D. (2018a). Lq control

design for the containment of the hiv/aids diffusion.

Control Engineering Practice, 77.

Di Giamberardino, P. and Iacoviello, D. (2018b). Model-

ing and control of an epidemic disease under possible

complication. Proceedings of the 22nd International

Conference on System Theory, Control and Comput-

ing, pages 67–72.

E.A.J.Fischer, Vlas, S., J.H.Richardus, and Habbema, J.

(2008). Musidh, multiple use of simulated demo-

graphic histories, a novel method to reduce com-

putation time in microsimulation models of infec-

tious diseases. Computer Methods and Programs in

Biomedicine, 91:185–190.

Iacoviello, D. and Stasio, N. (2013). Optimal control for

sirc epidemic outbreak. Computer Methods and Pro-

grams in Biomedicine.

Kuniya, T. and Nakata, Y. (2012). Permanence and extinc-

tion for a nonautonomous seirs epidemic model. Ap-

plied Mathematics and Computation, 218.

Ledzewicz, U. and Schattler, E. (2011). On optimal sin-

gular controls for a general SIR-model with vaccina-

tion and treatment. Discrete and continuous dynami-

cal systems.

L.Pang, S.Ruan, S.Liu, Z.Zhao, and X.Zhang (2015).

Transmission dynamics and optimal control of

measles epidemics. Applied mathematics and com-

putations, 256:131–147.

Naresh, R., Tripathi, A., and Sharma, D. (2009). Modeling

and analysis of the spread of aids epidemic with immi-

gration of hiv infectives. Mathematical and Computer

Modelling, 49.

Nowak, M. and May, R. (2000). Virus Dynamics.

Nowzari, C., Preciado, V. M., and Pappas, G. J. (2016).

Analysis and control of epidemics. a survey of spread-

ing processes on complex networks. IEEE Control

Systems Magazine.

O.O.Onyejekwe and E.Z.Kebede (2015). Epidemiological

modeling of measles infection with optimal control

of vaccination and supportive treatment. Applied and

computational mathematics, 4(4):264–274.

Pinto, C. and Rocha, D. (2012). A new mathematical model

for co-infection of malaria and hiv. 4th IEEE Interna-

tional Conference on Nolinear Science and Complex-

ity.

R.T.Perry and N.A.Halset (2004). The clinical signiﬁcance

of measles: a review. The Journal of Infectious Dis-

eases, 189(1):4–16.

S.O.Adewale, I.A.Olopade, S.O.Ajao, and G.A.Adeniran

(2016). Optimal control analysis of the dynamical

spread of measles. International Journal of research,

4(5):169–188.

S.Verguet, M.Johri, S.K.Morris, C.L.Gauvreau, P.Jha, and

M.Jit (2015). Controlling measles using supplemen-

tary immunization activities: a mathematical model to

inform optimal policy. Vaccine, 33(10):1291–1296.

TW, N., Turinici, G., and A.Danchin (2003). A double epi-

demic model for the sars propagation. BMC Infect

Dis., 10.

X.Yan and Y.Zou (2008). Optimal and sub-optimal quaran-

tine and isolation control in sars epidemics. Mathe-

matical and computer modelling, 47.

Analysis, Simulation and Control of a New Measles Epidemic Model

559