
Improved Model for Small-scale Turbofan Engine Weight Estimation
Evgeny Filinov and Yaroslav Ostapyuk
Department of Aircraft Engine Theory, Samara National Research University, Samara, Russian Federation
Keywords: Mathematical Model, Regression Model, Small-scale Turbofan Engine, Weight.
Abstract: Weight estimation plays a crucial role at the initial stages of gas turbine development. A number of weight
estimation models are described in the open sources, but design data available at these stages is scarce, so
these models tend to have low accuracy. This study examines the features of available models and proposes
improved weight estimation model. The database of the existing 50 turbofans with thrust lower than 50kN
was developed to compare models with the statistical information, and to update the regression coefficients
of the proposed model. Standard deviations and correlation factors of models were determined. Refining of
model coefficients was obtained as a result of minimization of a standard deviation value.
1 INTRODUCTION
Gas turbine weight estimation is necessary for
assessment of technical and economic efficiency of
aircraft and engine cycle optimization at the stage of
concept designing. Using this model more adequate
solution accounted main restrictions can be obtained.
Analysis of turbofan engine weight models of
authors such as Torenbeek E., Raymer D. P.,
Jenkinson L. R., Svoboda C., Clavier J., Guha A.,
Byerley A. R. and Kuzmichev V. S., showed that with
respect to small-scale engines, they give poor
accuracy (Kuz’michev, 2018).
At the present day small-scale turbofan engines
are widely adopted. These engines are used for light
aeroplanes, UAVs, cruising missiles, and as the
auxiliary power plants. They may also be converted
for use with distributed propulsion.
The regression models of turbofan engine weight
based on statistical data of existing advanced gas
turbine engines are used at the conceptual design
stage. The accuracy of these models depends on the
amount and adequacy of available information on
existing engines.
Current regression weight models should be
constantly refined considering modern design and
technological solutions in gas turbine industry. This
fact defines the relevance of this study. Targeting the
small-scale gas turbine engines is the particularity of
the presented study. The objective of this work is to
increase the accuracy of the weight model of small-
size scale turbofan engines by refining the empirical
coefficients.
2 WEIGHT MODEL
In the article, Kuz’michev gas turbine weight model
(Kuz'michev, 1991) developed at Aircraft Engine
Theory Department of Samara University is
considered. Model refining is proposed to increase
model accuracy of weight assessment at initial stage
of aircraft engine designing. The weight model
depends on 5 engine workflow parameters:
eng 22corr 4
, , , , .W f BPR OPR G T FPR
(1)
In General, the weight is calculated by expression:
eng PF SF mixer ab e lf
W W W W W k k
(2)
where:
2
1
4
0,286
PF 22corr
1
k
k
T
OPR
W B G k
FPR
–
weight of the engine core;
0,286
22corr 21corr
F
11
11
η
G G FPR
FPR
–
corrected mass flow rate at the primary flow fan
exit;
21corr
G
– corrected mass flow rate at station 21;º
0,903 0,104 1,193
SF Σ t-o
2,865W G BPR FPR
– weight of
the fan, fan turbine and bypass duct;
0,753
mixer Σ t-o
2,316WG
– weight of the mixer duct
(if presented);
338
Filinov, E. and Ostapyuk, Y.
Improved Model for Small-scale Turbofan Engine Weight Estimation.
DOI: 10.5220/0007948103380343
In Proceedings of the 9th Inter national Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 338-343
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: Values of coefficients for engine weight estimation.
Type of gas turbine engine
22corr
0,5 5G
kg/s
22corr
5 50G
kg/s
22corr
50G
kg/s
B
k
1
k
2
B
k
1
k
2
B
k
1
k
2
Turbojet, turbofan
5OPR
20,9
0,8
0,5
15,2
1
0,5
6,96
1,2
0,5
Turbojet, turbofan
5OPR
16,0
0,8
0
11,6
1
0
5,32
1,2
0
ab Σ t-o
2,9WG
– weight of the afterburner (if
presented);
e
k
– coefficient of engine sophistication impact
(changes over the years) (Figure 1);
lf
k
– coefficient of engine life impact:
lf
1,0 1,07 – for subsonic aircraft;
1,0 – for military long-range aircraft;
0,9 – for fighters.
k
(3)
4
4
4 max
1 2 10 1200
T
kT
– coefficient of
turbine cooling system impact.
Values of
B
,
1
k
,
2
k
were obtained statistically and
are shown in Table 1. Further, these coefficients are
proposed to be refined for small-scale turbofan
engines taking into account enhanced statistical data.
Figure 1: Coefficient of engine sophistication impact
against the year of engine production startup.
3 REFINING OF EMPIRICAL
COEFFICIENTS
3.1 Search and Preparation of Input
Data
Dimensions of a gas turbine engine significantly
influence the accuracy of weight estimation.
Increasing of standard deviation is observed in case
of small-scale engines due to the fact that
conventional weight models were created and
suitable for middle- and large-scale engines. This was
primarily caused by the lack of information about the
parameters of small-scale turbofan engines in public
access.
In this regard, the database consisting of 151
turbofan engines with a thrust less than 50 kN was
collected to provide statistical data for model
refinement. It includes different types (turboprop,
turbojet, turbofan) and configurations of engines for
civil and military aviation. Production start date of
accounted engines relate to the range from 1964 to
2018.
The search of input data was based on the analysis
of works (Torenbeek, 1976; Raymer, 1992;
Jenkinson, 1999; Svoboda, 2000; Lolis, 2014; Guha,
2012; Byerley, 2013; Roux, 2007; Sorkin, 2010;
Skibin, 2010; Shustov, 2000). Commonly, there is no
information about the cycle parameters in open
access. Only 42 engines among 151 had all required
cycle parameters. Basically, just basic engine features
and a brief design description are presented. Quite
often there is no information about the inlet turbine
temperature, and if it is presented, the corresponding
cross-section and mode of operation are usually not
specified. Not always the information on the air mass
flow rate and the overall pressure ratio is available.
Therefore, for some engines the missing
information was obtained using the CAE-system
ASTRA, developed at the Department of Aircraft
Engine Theory of Samara University (Kuz'michev,
2017; Krupenich, 2017).
Reconstruction of the dataset by minimizing the
deviation between published and calculated data
provided necessary information on the
thermodynamic parameters of additional 8 engines.
Thus, final database of the parameters required for
weight estimation includes 50 engines.
For these engines (Table 2), the empirical
coefficients have been corrected. Table 3 shows that
the range of cycle parameters for this dataset is quite
wide.
Improved Model for Small-scale Turbofan Engine Weight Estimation
339

Table 2: Main technical data of turbofan engines.
Parameter
Year
t-o
G
t-o
P
OPR
4
T
BPR
eng
W
F
D
FPR
Quantity dimension
−
kg/s
kN
−
K
−
kg
m
−
Adour RT.172 Mk.811
1977
43,1
24,5
11,3
1413
0,75
738
0,559
2,7
AdourMk151 RT.172-06
1973
41,2
23,2
11
1427
1
594
0,567
2,6
AI-22
2000
125,3
36,82
15,87
1455
4,77
765
1,02
1,65
AI-222-25
2008
50,2
24,5
15,9
1480
1,19
440
0,63
1,7
AI-222-28
2014
50,6
27,47
16,9
1590
1,13
520
0,63
1,7
AI-25TL
1973
46,8
16,86
9,5
1230
1,98
400
0,985
1,7
AL-55
2007
28,5
17,26
17,5
1445
0,515
315
0,59
2,5
ALF502L
1982
116
33,4
13,7
1423
5,7
606
1,02
1,6
ALF-502R-3
1981
111
29,81
11,6
1428
5,71
576
1,27
1,6
AS907-1-1-A
2002
86,8
30,8
21
1550
4,2
619
0,87
1,8
Astafan IVG
1981
36,7
7,75
8,5
1273
9
220
0,56
1,6
ATF3-6
1981
73,5
22,9
24
1448
3
460
0,853
1,6
ATF3-6-1C
1981
73,5
22,45
21
1448
2,8
529
0,79
1,6
CF34-3A
1996
147
41,013
21
1477
6,2
737
1,118
1,44
CFE738-1
1992
108,9
26,3
23
1643
5,3
551
0,902
1,7
CFE738-1-1B
1993
109
26,35
30
1650
5,9
601
0,801
1,7
DB-730F
1966
34,5
9,37
5,5
1148
5,5
240
0,9
1,29
DV-2
1987
49,4
21,58
13,5
1463
1,46
450
0,645
2,2
F104
1978
73,5
24,2
21
1448
3
510
0,583
1,6
F106
1970
5,71
2,73
13,9
1280
1
56,7
0,32
2,1
F107-WR-100
1979
6,1
2,67
13,75
1282
1,03
58
0,305
2,08
F107-WR-101
1975
6,15
2,88
13,8
1280
1,03
64
0,305
2,1
F109-GA-100
1985
20,3
5,92
20,7
1423
5
190
0,756
1,6
F3-IHI-30
1987
34
16,37
11
1213
0,9
340
0,56
2,6
FJ44-1
1992
28,7
8,45
12,8
1291
3,28
202
0,483
1,6
FJ44-1A
1992
28,6
8,46
12,8
1350
3,28
209
0,531
1,5
JT15D
1971
33,1
9,79
10
1283
3,2
231
0,691
1,5
JT15D-5
1983
42,2
13,55
12,6
1288
3,3
287
0,521
1,6
JT15D-5D
1993
34,1
13,55
13,1
1288
3,3
284
0,686
1,8
Larzac 04-C20
1983
28,6
14,22
11,13
1433
1,038
302
0,451
2,3
Larzac 04-C6
1977
26,6
13,19
10,6
1413
1,13
280
0,451
2,3
LF507
1991
116,1
31,138
13,8
1365
5,6
628
1,272
1,45
M45-H-01
1974
108
33,73
16
1355
3
708
0,87
1,6
M88-2
1996
65
50
24,5
1850
0,3
897
0,696
3,9
Model 471-11DX
1975
5,9
2,9
13
1280
1
56,6
0,317
2,2
PW305A
1992
77,2
20,83
23
1350
4,3
450
0,87
1,8
PW305B
1990
81,6
23,39
15,5
1350
4,3
450
0,779
1,8
PW306B
1999
81,7
26,91
20,58
1460
4,24
522,1
1,138
1,57
PW308A
2001
92,6
30,74
21
1600
3,88
618
0,93
1,88
RB.199-34R-04 Mk.103
1972
73,1
40,7
23,5
1598
1,06
1061
0,734
3,4
RD-1700
2005
30
16,7
14,3
1460
0,78
297,5
0,624
2,5
RD-33
1977
77
49,5
21,7
1680
0,55
1217
0,746
3,15
TF30-PW-3
1964
105,7
47,82
17,1
1144
1,1
1769
1,346
1,87
TF34-GE-2
1972
153
42
21
1500
6,2
813
1,27
1,5
TFE731-1
1969
51,3
15,55
19
1285
2,7
272
0,716
1,5
TFE731-2
1972
51
15,9
19
1283
2,66
340
1
1,65
TFE731-3
1974
53,7
16,47
14,6
1353
2,8
343
0,716
1,54
TFE731-5
1983
65
19,16
19,4
1378
3,4
375
0,886
1,67
TFE731-60
1995
84,8
22,26
17,8
1450
3,9
448
0,78
1,7
WR19-A2
1974
5,3
2,12
7,62
1180
1,15
41
0,305
1,45
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
340
Table 3: Ranges of cycle parameters.
Parameter
t-o
G
, kg/s
t-o
P
, kN
OPR
4
T
, K
BPR
eng
W
, kg
F
D
, m
FPR
Year
min
20
8,45
9,8
1291
0,16
180
0,452
1,44
1992
max
1436
406
50
2273
11
7893
3,124
7
2016
3.2 Evaluation of the Weight Model
Accuracy for Small-scale Turbofan
Engines
The accuracy of the model may be defined as the
standard deviation of the calculated and the actual
values. Statistical models are considered to have a
satisfactory accuracy if the standard deviation is less
than 10-15%. The accuracy of weight model is
evaluated by four main indicators: the standard
deviation, the average relative error of the
approximation, the correlation index and the Fisher
criterion. These indicators allow choosing the most
accurate model in their comparative analysis. They
can be used to select the appropriate model. For the
collected database, the standard deviation of the
original model is 16%, the average approximation
error was 13%, and the correlation index was 0.905.
The value of the Fisher criterion is 106. The table
value of the Fisher criterion at the level of
significance 0.05 is 3.2. As F
calc
> F
tab
(106 > 3,2), so
the model is deemed to be statistically significant and
reliable.
Analysis of the model accuracy shows that its
coefficients need to be updated as the relative
standard deviation of the model does not meet the
required value.
3.3 Adjusting the Statistical
Coefficients of the Weight Model
of Small-scale Turbofan Engines
The selected engines are divided into 2 groups. The
first group includes engines with the corrected air
flow rate through the fan less than 10 kg/s, the second
group of engines with the corrected air flow rate
through the fan from 10 kg/s to 20 kg/s. This is done
in order to update empirical coefficients taking into
account their differences, that positively influences
on the accuracy of the model. The first group included
27 engines, and the second – 23.
Using collected data empirical coefficients of the
weight model for two engine groups have been
refined. Adjustment was made by standard deviation
minimization. New values of coefficients are
presented in Table 4. According to the obtained
results, graphs of actual and calculated weight
deviation are presented on Figures 2-3.
Table 4: The refined values of coefficients for small-scale
engine weight estimation.
Type of gas
turbine
engine
22corr
0,5 10G
kg/s
22corr
10 20G
kg/s
B
k
1
k
2
B
k
1
k
2
Turbojet,
turbofan
*
CΣ t-o
π5
15,49
0,87
0,15
6,81
1,19
0,16
Standard deviation is 14.1 percent for the first
group of engines and the adjusted empirical
coefficients. Standard deviation is 11.8 percent for the
second group. The relative standard deviation of the
model improved from 16 to 13.5 percent (the average
approximation error is 10.4 percent), which satisfies
the adequacy requirements. The correlation index for
the updated empirical coefficients is 0.959, and the
value of the Fisher criterion is 270. The critical value
of the Fisher criterion at the significance level of 0.05
is 3.2, so the statistical model may be considered as
statistically reliable.
4 CONCLUSIONS
This research provided the reconstructed dataset of
the 50 turbofans, which was used to update the weight
models, described in the open sources.
The results of this study show that Kuzmichev
weight estimation has the highest accuracy, showing
standard deviation of 11.8 percent for turbofan flow
rates of 10 to 20 kg/s and standard deviation of 13.5
percent for the flow rates below 10 kg/s.
For the next step, authors plan to create a software
based on artificial neural network to collect new data
on the existing engines and update the weight model.
This will allow continuous updating of empirical
coefficients of the model using new statistical data.
Improved Model for Small-scale Turbofan Engine Weight Estimation
341
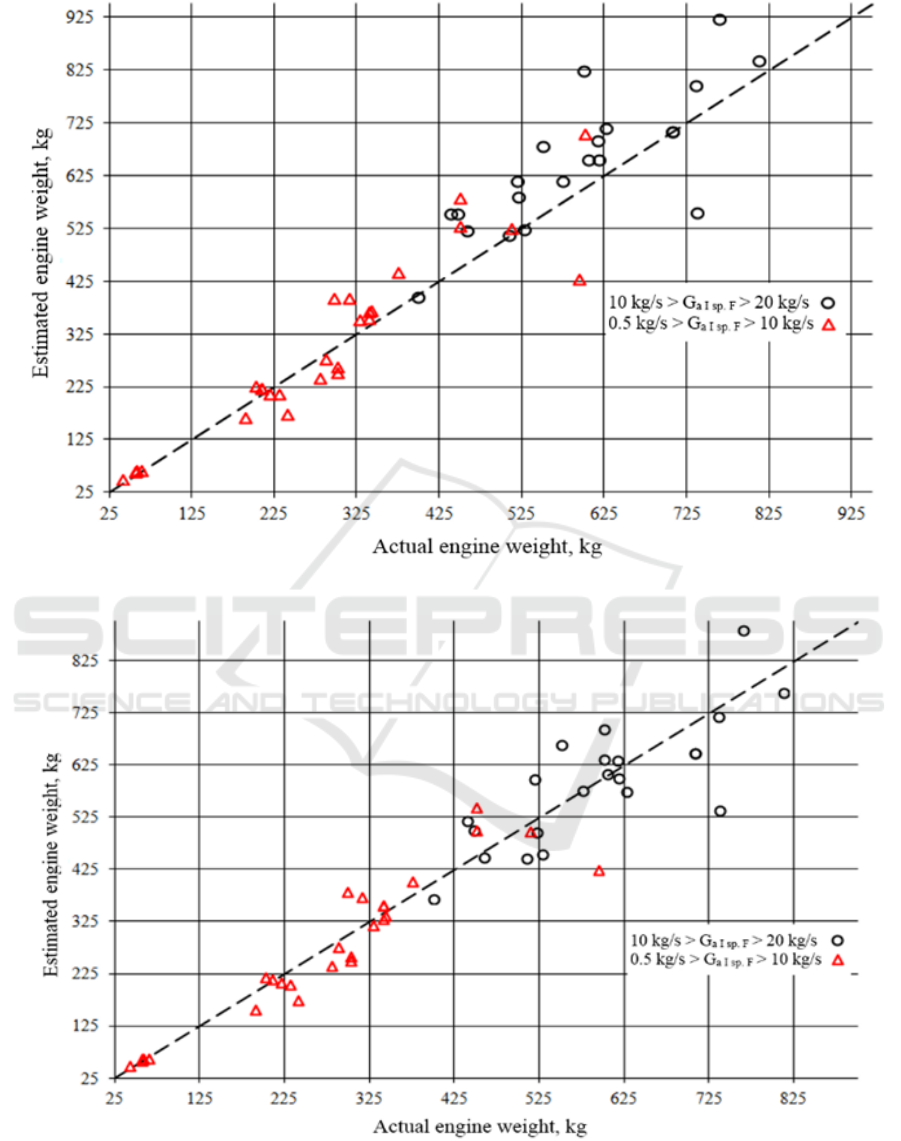
Figure 2: Deviation of actual and calculated values of engine weight for the original model.
Figure 3: Deviation of actual and calculated values of engine weight for the improved model.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
342

NOMENCLATURE
BPR = bypass ratio
D = diameter
FPR = fan pressure ratio
G = mass flow rate
OPR = overall pressure ratio
P = thrust
T = total temperature
W = weight
Subscripts
a = air
C = compressor
eng = engine
F = fan
t-o = take-off
Σ = overall
4 = section after combustion chamber
ACKNOWLEDGEMENTS
This work was supported by the Ministry of education
and science of the Russian Federation in the
framework of the implementation of the Program of
increasing the competitiveness of Samara University
among the world's leading scientific and educational
centers for 2013-2020 years.
REFERENCES
Kuz'michev, V.S., Krupenich, I.N., Filinov, E.P.,
Ostapyuk, Y.A., 2018. Comparative Analysis of
Mathematical Models for Turbofan Engine Weight
Estimation. In MATEC Web of Conferences.
Kuz'michev, V.S., Morozov, M. A., 1991. Conception of
method of pattern recognition of working process of gas
turbine engines in conditions of information deficit. In
Izvestiya VUZ: Aviatsionnaya Tekhnika.
Torenbeek, E., 1992. Synthesis of Subsonic Airplane
Design, Delft University Press. Rotterdam.
Raymer, D.P., 1992. Aircraft Design: A Conceptual
Approach, AIAA. Washington.
Jenkinson, L.R., Simpkin, P., Rhodes, D., 1999. Civil Jet
Aircraft Design, AIAA. Reston.
Svoboda, C., 2000. Turbofan Engine Database as a
Preliminary Design Tool. In Aircraft Design.
Lolis, P., 2014. Development of a Preliminary Weight
Estimation Method for Advanced Turbofan Engines.
Ph.D. Thesis, Cranfield University.
Guha, A., Boylan, D., Gallagher, P., 2012. Determination
of Optimum Specific Thrust for Civil Aero Gas Turbine
Engines: a Multidisciplinary Design Synthesis and
Optimization. In Proc. IMechE Part G: J Aerospace
Engineering.
Byerley, A.R., Rolling, A.J., Van Treuren, K.W., 2013.
Estimating Gas Turbine Engine Weight, Costs, and
Development Time During the Preliminary Aircraft
Engine Design Process. In Proceedings of ASME Turbo
Expo.
Roux, E., 2007. Turbofan and Turbojet Engines: Database
Handbook, Elodie Roux. Blagnac.
Sorkin, L.I., Vedeshkin, G.K., Knyazev, A.N., 2010.
Foreign aviation engines and power plants: reference
book, CIAM. Moscow.
Skibin, V.A., Solonin, V.I., 2010. Efforts of the leading
companies developing the aviation engines in creating
the future engines: analytical survey, CIAM. Moscow.
Shustov, I.G., 2000. Engines of 1944-2000: aviation,
rocket, naval engines and power plants. Encyclopedia,
AKS-Konversalt. Moscow.
Kuz'michev, V.S., Ostapyuk, Y.A., Tkachenko, A.Y.,
Krupenich, I.N., Filinov, E.P., 2017. Comparative
analysis of the computer-aided systems of gas turbine
engine designing. In International Journal of
Mechanical Engineering and Robotics Research.
Krupenich, I.N., Filinov, E.P., Ostapyuk, Y.A.,
Tkachenko, A.Y., 2017. Investigation of the efficiency
limits of the traditional gas turbine engines. In
International Journal of Mechanical Engineering and
Robotics Research.
Improved Model for Small-scale Turbofan Engine Weight Estimation
343
