Moving-object Tracking with Lidar Mounted on

Two-wheeled Vehicle

Shotaro Muro

, Yohei Matsui

, Masafumi Hashimoto

and Kazuhiko Takahashi

Graduate School of Doshisha University, Kyotanabe, Kyoto 6100321, Japan

Faculty of Science and Engineering, Doshisha University, Kyotanabe, Kyoto 6100321, Japan

Keywords: Moving-object Tracking, Lidar, Two-wheeled Vehicle, Distortion Correction, Map Subtraction.

Abstract: This paper presents a tracking (estimating position, velocity and size) of moving objects, such as cars, two-

wheeled vehicles, and pedestrians, using a multilayer lidar mounted on a two-wheeled vehicle. The vehicle

obtains its own pose (position and attitude angle) by on-board global navigation satellite system/inertial

navigation system (GNSS/INS) unit and corrects the distortion in the lidar-scan data by interpolating the pose

information. The corrected lidar-scan data is mapped onto 3D voxel map represented in the world coordinate

frame. Subsequently, the vehicle extracts the interested lidar-scan data from the current lidar-scan data using

the normal distributions transform (NDT) scan matching based map-subtraction method. The extracted scan

data are mapped onto an elevation map, and moving objects are detected based on an occupancy grid method.

Finally, detected moving objects are tracked based on the Bayesian Filter. Experimental results show the

performance of the proposed method.

1 INTRODUCTION

In mobile robotics and vehicle automation domains,

tracking (estimation of position, velocity, and size) of

moving objects, such as cars, two-wheeled vehicles,

and pedestrians, is an important technology to

achieve the advanced driver assistant system (ADAS)

and autonomous driving. A lot of studies of moving-

object tracking using cameras, lidars, and radars have

been actively conducted (Mukhtar et al., 2015, Mertz

et al., 2013).

When compared with vision-based tracking, lidar-

based tracking is robust to lighting conditions and

require less computational time. Furthermore, lidar-

based tracking provides tracking accuracy better than

radar-based tracking due to higher spatial resolution

of lidar. From these reasons, we have presented a

lidar-based tracking of moving objects (Hashimoto et

al., 2006, Tamura et al., 2017).

Most methods of moving-object tracking have

been applied to ADAS and autonomous driving for

four-wheeled vehicles traveling on flat road surfaces.

Although moving-object tracking is required for

advanced rider assist systems (ARAS) for two-

wheeled vehicle, there are few studies on moving-

https://orcid.org/0000-0003-2274-2366

object tracking with sensors mounted on two-wheeled

vehicles (Amodio et al., 2017, Barmpounakis et al.,

2016, Jeon and Rajamani, 2018).

In this paper, we present a method of moving-

object tracking using a lidar mounted on a two-

wheeled vehicle. Moving-object tracking by a two-

wheeled vehicle is more difficult than that by a four-

wheeled vehicle, because the attitude of a two-

wheeled vehicle changes more drastically than that of

a four-wheeled vehicle, and the sensing accuracy then

deteriorates.

The occupancy grid method (Thrun et al., 2005),

in which the grid map is represented in the world

coordinate frame, is usually applied to moving-object

detection and tracking. In order to perform accurate

moving-object detection, it is necessary to accurately

map a lidar-scan data obtained in the sensor

coordinate frame onto a grid map using a vehicle's

pose (position and attitude angle). Since the lidar

obtains data by the laser scanning, all scan data within

one scan cannot be obtained at the same time when

the vehicle is moving or changing its own attitude.

Therefore, if all scan data within one scan are mapped

onto the world coordinate frame using the vehicle's

Muro, S., Matsui, Y., Hashimoto, M. and Takahashi, K.

Moving-object Tracking with Lidar Mounted on Two-wheeled Vehicle.

DOI: 10.5220/0007948304530459

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 453-459

ISBN: 978-989-758-380-3

453

pose at the same time, distortion in the lidar-scan data

occurs (Inui et al., 2017).

In addition, when the lidar is mounted on a two-

wheeled vehicle, the mapping accuracy deteriorates

due to the large swing motion of the lidar. As a result,

undetection and false detection of moving objects

increase. In order to address this problem, in this

paper, we estimate the vehicle’s pose every shorter

period than lidar-scan period, and then using the pose

estimates, we correct the distortion in lidar-scan data.

Furthermore, the differences (subtracted scan

data) are extracted between the 3D-point cloud

environment map acquired in advance and the current

lidar-scan data, and only the subtracted scan data is

mapped onto the grid map. Thereafter, moving-object

detection and tracking are performed by the

occupancy grid method and Baysian filter.

The rest of this paper is organized as follows. In

Section 2, an overview of the experimental system is

given. In Section 3, the methods of distortion

correction and map subtraction are described. In

Section 4, method of detecting and tracking moving

objects is described. In Section 5, experimental

results are presented, followed by conclusions in

Section 6.

2 EXPERIMENTAL SYSTEM

Figure 1 shows the overview of two-wheeled vehicle.

As a first step of the study, we use a bicycle (Yamaha

PAS-GEAR-U) as a two-wheeled vehicle. On the

upper part of the bicycle, a 32-layer lidar (Velodyne

HDL-32E) is mounted, and a global navigation

satellite system/inertial navigation system (GNSS/

INS) unit (Novatel PwrPak7-E1) is mounted on the

rear part.

The maximum range of the lidar is 70 m, the

horizontal viewing angle is 360° with a resolution of

0.16°, and the vertical viewing angle is 41.34° with a

resolution of 1.33°. The lidar acquires 384

measurements including the object’s position every

0.55 ms (at 2° horizontal angle increments). The

period for the lidar beam to complete one rotation

(360°) in the horizontal direction is 100 ms, and about

70,000 measurements are acquired in one rotation. In

this paper, one rotation in the horizontal direction of

the lidar beam is referred to as one scan, and the data

including measurements acquired by the one scan is

referred to as the lidar-scan data.

The GNSS/INS unit outputs the 3D position and

attitude angle (roll, pitch and yaw angles) every 100

ms. The horizontal and vertical position errors (RMS)

are 0.02 m and 0.03 m, respectively. The roll and

pitch angle errors (RMS) are 0.02°, and the yaw angle

error (RMS) is 0.06°.

Figure 1: Experimental bicycle.

3 SUBTRACTION OF SCAN

DATA

3.1 Distortion Correction

The lidar-scan data are obtained in the sensor

coordinate frame Σ

fixed on the lidar, and they are

mapped on the world coordinate frame Σ

using the

bicycle’s pose. The output of the GNSS/INS unit can

be used as the bicycle’s pose in GNSS environments.

The observation period of the GNSS/INS unit is

100 ms at which the lidar makes one rotation, and

scan data every 0.55 ms are captured 180 times within

one rotation of the lidar. Therefore, the bicycle's pose

is estimated every 0.55 ms by interpolating the

bicycle's pose from the GNSS/INS unit every 100 ms.

For the i-th (i = 1, 2, ...) measurement in the scan

data, we define the position vector in Σ

as p

= (x

, z

)

and that in Σ

as p

= (x

)

. p

can be

converted to p



























)(



(1)

where

zyx ),,,,,(



X

is the bicycle’s pose.

(x, y, z)

and

),,(



are the position and attitude

angle (roll, pitch, and yaw angles) of the bicycle,

respectively, in

. T(X) is the following

homogeneous transformation matrix:

cos cos sin sin cos cos sin cos sin cos sin sin

cos sin sin sin sin cos cos cos sin sin sin cos

()

sin sin cos cos cos

00 01

    

 





















ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

454

3.2 Extraction of Scan Data Related to

Object

After correcting the distortion in the lidar-scan data,

scan data related to road planes are removed and those

related to objects are extracted to detect moving

objects.

As shown in Fig. 2, we consider 32 measurements

captured every horizontal resolution (about 0.16°) of

the lidar. We assume that the measurement

, which

is the closest measurement to the bicycle, is the

measurement related to road planes. We obtain the

angle of a line connecting the adjacent measurements

and r

relative to the XY plane in

. If it is less

than 15°, the measurement

is determined to belong

to the road planes. If the angle is larger than 15°, the

measurement

is determined to belong to the object.

By repeating this process for all the lidar-scan data,

we can find the scan data related to objects and apply

them to detect moving objects.

3.3 Scan-data Subtraction

We assume that the bicycle has an environment map

(3D point-cloud map related to static objects) in

advance. As shown in Fig. 3, current scan data are

compared with the environment map, and the scan

data that subtract background from current scan data

are extracted.

Since the environmental map and the current scan

data contain a lot of scan data, it takes much

computational cost for the scan-data subtraction.

Therefore, as shown in Fig. 4, to reduce the

computational cost, we apply a voxel grid filter

(Munaro et al., 2012); scan data related to the

environment map and current scan data are

downsized by the voxel grid filter. Thereafter, scan

data are mapped onto the 3D grid map (voxel map).

Here, the voxel used for the voxel grid filter is a cube

with a side-length of 0.2 m, whereas the voxel for the

voxel map is a cube with a side-length of 0.5 m.

Next, the current scan data are matched with the

environment map using the normal distributions

transform (NDT) scan matching (Biber and Strasser,

2003). The NDT scan matching conducts a normal

distribution transformation for the scan data in each

voxel of the environmental map; it calculates the

mean

and covariance Ω

of 3D positions of the scan

data. Then, the likelihood function



of the current

scan data

P’(t) ={p

(t), p

(t), ..., p

(t)}

is calculated by





















iii

))('())('(

exp qpΩqp



(2)

Figure 2: Extraction of lidar-scan data related to objects.

Red and blue points indicate the scan data related to the road

planes and objects, respectively.

Figure 3: Map-subtraction method.

Figure 4: Mapping sequence of lidar-scan data.

Then, the bicycle’s pose X that maximizes Λ is

calculated, and the coordinates of the current scan

data in

is calculated by Eq. (1). The scan-data

subtraction is performed by comparing the

environmental map with the current scan data. In this

study, we use the point cloud library (PCL) (Rusu and

Cousins, 2011) for the NDT scan matching.

Moving-object Tracking with Lidar Mounted on Two-wheeled Vehicle

455

4 MOVING-OBJECT

DETECTION AND TRACKING

We apply an elevation map to detect moving objects

at small computational cost; the subtracted scan data

are mapped onto the elevation map. In this study, the

cell of the elevation map is a square with a side-length

of 0.3 m.

A cell in which scan data exist is referred to as an

occupied cell. For scan data related to moving

objects, the time to occupy the same cell is short,

whereas for scan data related to static objects, the

time is long. Therefore, by using the occupancy grid

method based on the cell occupancy time (Hashimoto

et al., 2006), we classify two kinds of cells: moving

and static cells. The moving cell is occupied by the

scan data related to moving objects, and the static cell

by the scan data related to static objects.

Since scan data related to an object usually

occupies more than one cell, adjacent occupied cells

are clustered. Then, clustered moving cells (moving-

cell group) and clustered static cells (static-cell

group) are obtained.

When moving-object detection is completed,

moving-object tracking (estimating position,

velocity, and size) is performed. In this paper, the

shape of the tracking object is represented by a cuboid

with a width W, a length L, and a height H as shown

in Fig. 5. As shown in Fig. 6, we define an X

coordinate frame, on which the Y

-axis aligns with the

heading of a tracked object. From moving-cell group,

we extract the width W

meas

and length L

meas

When a moving object is perfectly visible, its size

can be estimated from these moving-cell groups. In

contrast, when it is partially occluded by other objects,

its size cannot be accurately estimated. Therefore, the

size of a partially visible object is estimated using the

following equation (Tamura et al., 2017):

() (1) ( (1))

meas

Wt Wt GW Wt

Lt Lt GL Lt

 





 



(3)

where t and t-1 are time steps. G is the filter gain.

The height of the moving-cell group uses as the

height estimate H.

We then define the centroid position of the

rectangle estimated from Eq. (3) by

),( yx in Σ

From the centroid position, the pose of the tracked

object in Σ

is estimated using the Kalman filter

under the assumption that the object is moving at an

almost constant velocity (Tamura et al., 2017).

To track objects in crowded environments, we

need data association (i.e., one-to-one or one-to-many

Figure 5: Cuboid around the tracked object (car).

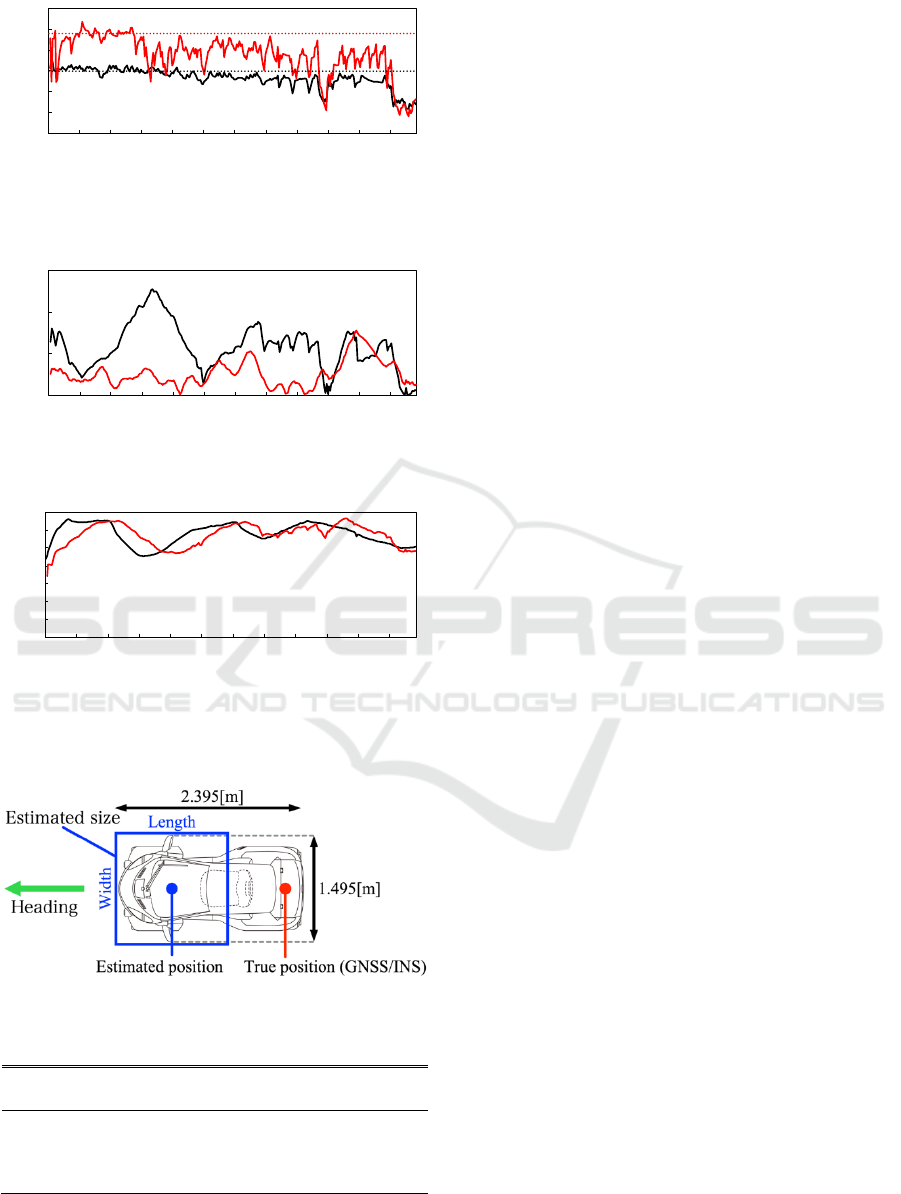
Figure 6: Observed vehicle size. Red squares and green

arrow indicate moving cells and vehicle heading direction,

respectively. Blue rectangle and circle indicate observed

size and centroid, respectively.

matching of tracked objects and moving-cell groups).

We exploit the global-nearest-neighbour (GNN)

based and rule-based data association to accurately

perform data association (Tamura et al., 2017).

The number of moving objects in the sensing

areas of the lidar changes over time. Moving objects

enter and exit the sensing area of the lidar. They also

interact with and become occluded by other objects in

environments. To handle such conditions, we

implement a rule-based data handling method

including track initiation and termination (Hashimoto

et al., 2006).

5 EXPERIMENTAL RESULTS

We conducted experiments in our university campus

as shown in Fig. 7. The maximum speed of the bicycle

is 15 km/h. Figure 8 shows the roll and pitch angles

of the bicycle. To change the attitude of the lidar

largely, we rode the bicycle in zigzag.

Figure 7: Photo of experimental environment (bird-eye

view). Red line indicates moved path of the bicycle.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

456

Figure 8: Attitude angles of bicycle. Black and red lines

indicate the roll and pitch angles, respectively.

To confirm the performance of moving-object

tracking by the bicycle, a four-wheeled vehicle (a car)

followed the bicycle. The car is equipped with a

GNSS/INS unit, which performance is the same as

that mounted on the bicycle.

Figure 9 (a) shows the tracks of four pedestrians

and a car estimated by the bicycle’s lidar. Figure 9 (b)

shows the result of tracking the car in area #1, and

Figure 9 (c) shows the result of tracking three

pedestrians in area #2. In Figs. 9 (b) and (c), all scan

data (black dots) are plotted in order for readers to

easily understand these figures. In addition, the

estimated size (blue cuboid) is plotted every 1 s (10

scans), and the estimated position (blue dot) every 0.1

s (1 scan).

In Fig. 9 (c), pedestrians #2 and #3 are tracked as

a large rectangle, because they walk side by side, and

their neighbouring moving cells are then clustered as

the same group.

Figure 10 shows the performance of the car

tracking shown in Fig. 9 (b). Figure 10 (a) shows the

result of an estimated size of the car. Figure 10 (b)

shows the error of an estimated position of the car. A

true position of the car is obtained by the GNSS/INS

unit mounted on the car. Figure 10 (c) shows the

result of an estimated velocity of the car. A true

velocity of the car is obtained by the GNSS/INS unit

mounted on the car.

As shown in Fig. 10 (a), the estimated error of

length becomes large after 150 scans, because a

distance between the bicycle and the car is large; in

75–150 scans, the distance is about 6 m, and scan data

of the whole car can thus be captured. However, after

150 scans, the distance becomes about 11 m, and scan

data of only the front part of the car can then be

captured. This is why the estimated length of the car

is smaller than the true length.

As shown in Fig. 10 (b), the position error is large

in the

X direction. In the world coordinate frame Σ

the east-west aligns with the

X axis, and the north-

south does with the

Y axis. The bicycle and car ran

from east to west. In the proposed method, the

centroid of the estimated rectangle is used as position

(measurement) of the tracked object. Because the car

follows the bicycle, the position on the front part of

the car is always estimated as shown in Fig. 11. On

the other hand, the GNSS/INS unit outputs the

position information of the rear part of the car. This is

why the position error in the

X direction is large.

We conducted another experiment, in which 34

pedestrians and a car existed. We compare the

tracking performance in the following four cases.

Case 1: Tracking using distortion correction and

map subtraction (proposed method),

Case 2: Tracking using map subtraction and no

distortion correction,

Case 3: Tracking using distortion correction and no

map subtraction, and

Case 4: Tracking using neither distortion correction

nor map subtraction.

Table 1 shows the tracking result, where

untracking means that tracking of moving objects

fails, and false tracking means that static objects are

tracked. It is clear from the table that the proposed

method (case 1) provides the tracking performance

better than the other cases.

(a) Estimated track of a car and pedestrians.

(b) Estimated track and size of a car in area #1.

Figure 9: Tracking result of a car and pedestrians (top

view).

-15

-10

-5

0 25 50 75 100 125 150 175 200 225 250 275 300 325 350

ude [deg]

Time [scan]

-50

-40

-30

-20

-70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 5

Y [m]

X [m]

Pedestrian #1

Pedestrians #2 and #3

Pedestrian #4

Car

Bicycle

Area #1

Area #2

Moving-object Tracking with Lidar Mounted on Two-wheeled Vehicle

457

(a) Size. Black and red lines indicate the estimated width

and length, respectively. Their true values are indicated by

dashed lines.

(b) Position error. Black and red lines indicate the error of

the estimated positions in X and Y directions, respectively.

estimated velocities, respectively.

Figure 10: Tracking result of a car.

Figure 11: Estimated size and position of a car (top view).

Table 1: The number of correct and incorrect tracking.

Correct

tracking

Untracking

False

tracking

Case 1 35 0 1

Case 2 26 9 (pedestrians) 1

Case 3 35 0 6

Case 4 26 9 (pedestrians) 10

6 CONCLUSIONS

This paper presented a moving-object tracking

method with the lidar mounted on a two-wheeled

vehicle. The self-pose of the vehicle at the time when

the lidar-scan data is captured was estimated by

interpolating the self-pose outputted from the

onboard GNSS/INS unit, and based on the estimated

self-pose, the distortion in the scan data was

corrected.

By comparing the corrected lidar-scan data with

the environment map, the subtracted scan data was

mapped onto the elevation map to detect and track

moving objects. The NDT scan matching method was

applied to the scan-data subtraction. The

experimental results of tracking pedestrians and a car

by a 32-layer lidar mounted on a bicycle validated the

efficacy of the proposed method.

As future works, we will extend the proposed

method to moving-object tracking in GNSS-denied

environments, in which the GNSS/INS unit cannot

work well. In addition, we will build moving-object

tracking system with a lidar mounted on a

motorcycle.

ACKNOWLEDGEMENTS

This research was partially supported by the JSPS-

Japan Society for the Promotion of Science

(Scientific Grants, Foundation Research (C) No.

18K04062).

REFERENCES

Amodio, A., Panzani, G., and Savaresi, S, M., 2017, Design

of a Lane Change Driver Assistance System with

Implementation and Testing on Motorbike, In

Proceeding of IEEE Intelligent Vehicles Symposium

(IV), pp. 947–952.

Barmpounakis, E, N., Vlahogianni, E, I., and Golias, J, C.,

2016, Intelligent Transportation Systems and Powered

Two Wheelers Traffic, In IEEE Transactions on

Intelligent Transportation Systems, Vol. 17, No. 4, pp.

908–916.

Biber, P. and Strasser, W., 2003, The Normal Distributions

Transform: A New Approach to Laser Scan Matching,

In Proceedings of IEEE/RSJ International Conference

on Intelligent Robots and Systems (IROS 2003), pp.

2743–2748.

Hashimoto, M., Ogata, S., Oba, F., and Murayama, T.,

2006, A Laser Based Multi-Target Tracking for Mobile

Robot, In Intelligent Autonomous Systems 9, pp. 135–

144.

0.5

1.5

2.5

75 100 125 150 175 200 225 250 275 300 325 350

Size [m]

[

scan

]

0.5

1.5

75 100 125 150 175 200 225 250 275 300 325 350

Position e

[m]

Time [scan]

75 100 125 150 175 200 225 250 275 300 325 350

Velocity [km/h]

Time [scan]

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

458

Inui, K., Morikawa, M., Hashimoto, M., Tokorodani, K.

and Takahashi, K., 2017, Distortion Correction of Laser

Scan Data from In-vehicle Laser Scanner based on

NDT scan-matching, In Proceedings of the 14th

International Conference on Informatics in Control,

Automation and Robotics (ICINCO 2017), pp. 329–

334.

Jeon, W., and Rajamani, R., 2018, Rear Vehicle Tracking

on a Bicycle Using Active Sensor Orientation Control,

In IEEE Transactions on Intelligent Transportation

Systems. Vol. 19, No. 8, pp. 2638–2649.

Mertz, C., Navarro-Serment, L, E., MacLachlan, R.,

Rybski, P., Steinfeld, A., Suppe, A., Urmson, C.,

Vandapel, N., Hebert, M., Thorpe, C., Duggins, D., and

Gowdy, J., 2013, Moving Object Detection with Laser

Scanners, In Journal of Field Robotics, Vol. 30, pp. 17–

43.

Mukhtar, A., Xia, L., and Tang, T, B., 2015, Vehicle

Detection Techniques for Collision Avoidance

Systems: A Review, In IEEE Transactions on

Intelligent Transportation Systems, Vol.16 No. 5, pp.

2318–2338.

Munaro, M., Basso, F., and Menegatti, E., 2012, Tracking

People within Groups with RGB-D Data, In

Proceedings of IEEE/RSJ International Conference on

Intelligent Robots and Systems (IROS 2012), pp. 2101–

2107.

Rusu, R, B. and Cousins, S., 2011, 3D is Here: Point Cloud

Library (PCL), In Proceedings of 2011 IEEE

International Conference on Robotics and Automation

(ICRA).

Tamura, Y., Murabayashi, R., Hashimoto, M., and

Takahashi, K., 2017, Hierarchical Cooperative

Tracking of Vehicles and People Using Laser Scanners

Mounted on multiple mobile robots, In International

Journal on Advances in Intelligent Systems, Vol. 10,

No. 1& 2, pp. 90–101.

Thrun, S., Burgard, W., and Fox, D., 2005, Probabilistic

Robotics, In MIT press.

Moving-object Tracking with Lidar Mounted on Two-wheeled Vehicle

459