
Real-time Nonlinear Signal Processing Super Resolution of 8K
Endoscope Cameras
Seiichi Gohshi
1
, Chinatsu Mori
1
, Kenkichi Tanioka
2
and Hiromasa Yamashita
3
1
Kogakuin University, 1-24-2 Nishi-Shinjuku, Shinjuku-ku, Tokyo, 163-8677, Japan
2
Medical Consortium Network Group, Japan
3
Kairos Co., Ltd., 4-13-2 Shiba, Minato City, T
¯
oky
¯
o-to 105-0014, Japan
Keywords: Video, Image, Non-linear Signal Processing, Super Resolution, Focus, 8K, Endoscope.
Abstract:
Presently, 8K is the highest resolution of video systems. Originally, 8K research started only for broadcasting
services. However, aside from broadcasting, 8K resolution video systems have also an important application in
medical field, and endoscopic surgery is in its practical stage. In endoscopic surgery, a 0.02 mm thread is used.
This 0.02 mm thread is not visible when using a 4K endoscope. However, when an 8K endoscope is employed,
the thread is visible; however, fine focus is still necessary. Moreover, adjusting the focus of 8K by using the
common tools only, such as view finders or small monitors, is very difficult. Hence, commercial HD/4K
cameras are equipped with auto-focus functions; however, the central areas are not always the focus points.
The focus is very deep and the focus points change during endoscopic surgeries. Owing to these reasons, a
surgeon should manually control the endoscope focus. It is always very difficult to adjust the focus accurately.
Super resolution (SR) has been proposed to sharpen out-of-focus images. However, a real-time SR technology
is necessary for the 8K endoscope. In this study, a nonlinear signal processing super resolution (NLSP) is
introduced to improve the resolution of 8K endoscope cameras. NLSP can enhance the 8K endoscope images
and improve the camera’s focus depth.
1 INTRODUCTION
The progress in video technologies has been remark-
able. High-definition televisions (HDTVs) are the
standard TV since a long time ago. HDTVs (2K),
which are already unavailable in the market, have
been replaced with 4K televisions. Broadcasting in
8K, which has four times the resolution of 4K, be-
gan in 2018 and 8K commercial TVs were also re-
leased. Aside from broadcasting services, 4K/8K is
also applied in the medical field. Endoscope cam-
eras are one of the important applications of 4K/8K.
An endoscopic surgical operation targeted for the 8K
endoscope system is the laparoscopic surgery. Dur-
ing a laparoscopic surgery, small holes are made in
the abdominal or chest wall of a patient. The sur-
geon inserts the endoscope into the body cavity of
the patient and all the operations are performed using
a monitor. The medical doctor cannot directly view
the target areas. Laparoscopic surgery is a popular
operation because patients’ physical load is minimal,
with shorter recovery time than that of laparotomy.
Given that the 1992 laparoscopic surgery became the
subject of health insurances in Japan, the number of
operations is increasing annually. The proposal of
the Ministry of Health, Labor and Welfare aims to
shift 70% of the total number of operations into la-
paroscopic surgery. However, the actual percentage
of laparoscopic surgeries remains at 30%–40%. Al-
though current laparoscopic surgery requires a high
degree of skill and experience owing to the insuffi-
cient resolution of an endoscope, the lack of trained
surgeons is the reason that the needs of patients are
not fully catered for. An 8K endoscope provides a
sufficient video resolution for laparoscopic surgery; in
other words, it has a good visibility and the difficulty
level of endoscopic surgery is low. Aside from im-
proving the safety of patients, the number of capable
surgeons is expected to increase. By using 8K endo-
scopes, surgeons can already view the thread used in
laparoscopic surgery with a diameter of 0.02–0.029
mm, wherein this thread is not visible when 4K en-
doscopes are utilized. In other words, the 4K en-
doscope cannot meet the resolution required for the
laparoscopic surgery. However, accurately adjusting
the focus of the 8K endoscope is necessary to locate
Gohshi, S., Mori, C., Tanioka, K. and Yamashita, H.
Real-time Nonlinear Signal Processing Super Resolution of 8K Endoscope Cameras.
DOI: 10.5220/0007950603430349
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 343-349
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
343

the 0.02–0.029 mm thread on a monitor.
According to clinical experiments, the surgeon
cannot precisely adjust the focus of the 8K endo-
scope because the focus point on the screen constantly
shifted during operation. Thus, the high-resolution
(HR) advantage of the 8K endoscope cannot be fully
utilized. During surgical operation, the region of in-
terest (ROI) always changes. Although the ROI might
be at the center of the screen at the beginning of
the operation, the image must often be refocused at
the top-left or bottom-right regions. Generally, auto-
focus functions automatically adjust the focus at the
center of the screen. Moving the endoscope to set the
ROI at the center position of the screen is possible.
However, freely moving the endoscope during opera-
tion is not advisable because organs might be affected,
causing the patient to feel pain. Hence, the endoscope
should be placed in a fix position during operation and
the focus is manually controlled. Aside from the op-
erating surgeon, another surgeon is required to super-
vise the 8K endoscope focus. Because freely adjust-
ing the focus with a small monitor is impractical, an
LCD monitor with the size of more than 50 in. must
be used for the surgery. However, accurately control-
ling the focus is still very challenging even if a 50
in. monitor is used. The 8K cameras’ focus control
is also an issue in broadcasting and content-making
industries. Commercial HD/4K/8K cameras are not
equipped with auto-focus function because focus con-
trol is one of the special areas of content production.
The focus point in a frame is one of the techniques of
content direction, and the focus position is not always
at the center of a frame. Hence, focus adjustment de-
pends on the camera man’s technique, and the camera
man manually controls the focus depending on the di-
rectors’ request. Until the HDTV development, the
camera man can manually adjust the focus by using
the view finder, which was usually built in the cam-
era. However, adjusting the focus of 4K cameras with
the view finder becomes challenging even for a pro-
fessional camera man because this view finder is too
small to accurately control the focus. Even if the fo-
cus seems fine on the view finder, the result is often
out of focus when the footage will be viewed on a
larger screen. Thus, focus control becomes more dif-
ficult for 8K cameras. In 8K content production, a 55
in. 8K monitor and a focus person are necessary.
Professional 4K cameras are equipped with fo-
cus assist function (Funatsu et al., 2013)(Ikegami,
2015)(Hitachi, 2015). The principle of the focus as-
sist function is very simple; in other words, the edges
are detected from the image and are superimposed.
The focus is controlled by maximizing the superim-
posed edges in the ROI. This method is similar to the
enhancer technique (unsharp mask). The edges are
detected using a high pass filter (HPF), the absolute
value is calculated, and the absolute value edges are
superimposed on the image. Then, the camera man
adjusts the focus by maximizing the edges. Given
that the edges are detected using an HPF, the edges
caused by noise appear on the entire frame when noise
is mixed into the image. When the lighting condition
is good, the noise is suppressed. However, a good
lighting condition is very rare and generally noise is
mixed into the images. Owing to the noise issue, the
focus assist is not applicable to general videos. The
noise results in the difficulty of adjusting the appro-
priate focus position. Although the focus is not fine,
clear images can be captured if the depth of the focus
is high. However, the depth of an organ captured by
the endoscope has a wide range. Thus, a signal pro-
cessing method is required to widen the focus depth.
2 SUPER RESOLUTION (SR)
SR is a technology used in enhancing the resolution
of an image/video. Although many SR proposals ex-
ist (Ledig et al., 2017)(Houa and Liu, 2011)(van Eek-
eren et al., 2010)(Shahar et al., 2011)(Bannore, 2010),
they are only applicable to still images and cannot
work real-time because they need iterations. A real-
time signal processing is necessary for laparoscopic
surgery. One issue of existing SR technologies is
first capturing an HR image and then developing low-
resolution (LR) images from the HR ones. However,
no HR is available and we only have one LR. Thus,
we must create an HR from only one LR. If we apply
SR for the endoscope video, then we should create
HR from every frame, and their several parts are out
of focus. In previous SR papers, reconstructed HR
is compared with the original HR based on the peak
signal-to-noise ratio (PSNR). However, determining
the PSNR in practical applications is impossible be-
cause we do not have the original HR and we only
have one LR. Because we cannot measure the PSNR,
we must define SR. In this study, we define SR first
as a technology that can produce high-frequency ele-
ments that do not possess the original LR, and, then,
it can also enhance image quality. The former defi-
nition can be easily proven by using two-dimensional
fast Fourier transform (2D-FFT). However, most of
the SR studies did not report the FFT results of the LR
and HR images. The latter definition indicates that
invisible things can become visible by the SR pro-
cessing in this study. In the laparoscopic surgery, a
0.02 mm diameter thread is used and is only visible
when an 8K endoscope with fine focus is used. How-
SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications
344
ever, even in fine focus condition, viewing the 0.02
mm thread by using the 4K endoscope is still impos-
sible. Meanwhile, even if the focus is not fine, the
0.02 mm thread is still visible when an 8K endoscope
is utilized. If the 0.02 mm thread on out-of-focus ar-
eas can be seen with the SR signal processing, then,
SR is proven to improve the image quality.
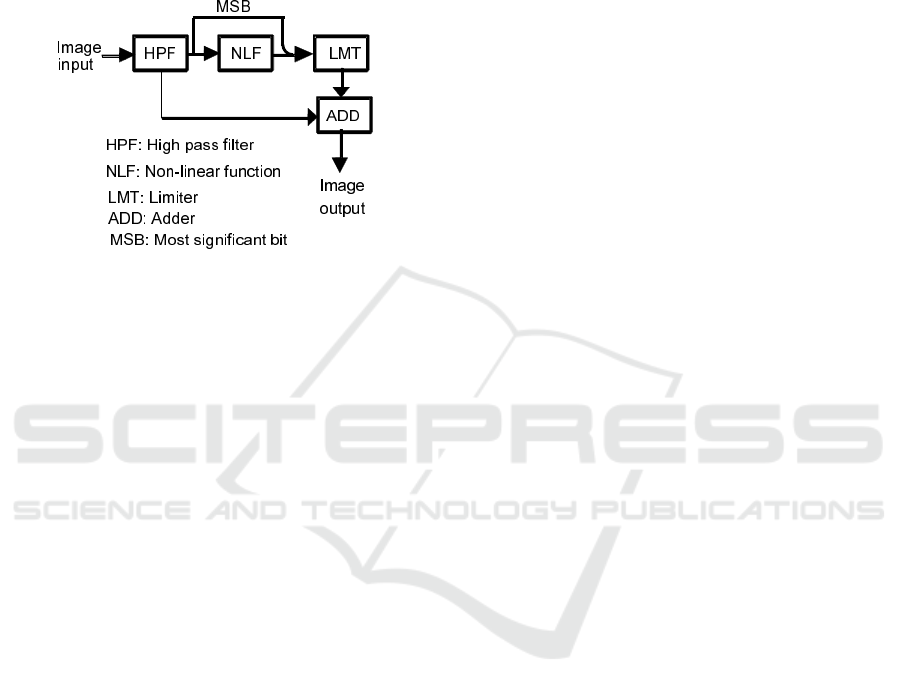
Figure 1: This caption has one line so it is centered.
3 NLSP
NLSP was originally proposed for up-converted im-
age from HDTV to 4KTV (Gohshi et al., 2017)
and works in real-time. Currently, most commercial
4KTV sets are equipped with SR functions. However,
the SR functions that are presently used are inferior to
NLSP (Mori et al., 2015). The basic idea of NLSP is
similar to that of one-dimensional signal processing
shown in Figure 1. The input is distributed into two
blocks. The upper path establishes high-frequency el-
ements that the original image does not have as fol-
lows: the original image is processed using i.e.,or mi-
nus) for each pixel. After the HPF, the edges are pro-
cessed with a nonlinear function (NLF). If an even
function (e.g., y = x
3
) is used as the NLF, then, the
sign is lost. To prevent information loss, the most
significant bit is obtained from the edge information
prior to the NLF and restored after the NLF. NLFs
generate harmonics that can develop frequency ele-
ments that are higher than that of the original image.
NLSP by using a number of NLFs should be able to
produce high-frequency elements. Here we propose a
cubic function, y = x
3
, as the NLF.
Generally, images are expanded in a Fourier series
(Mertz and Gray, 1934). Herein, we utilize the one-
dimensional image f (x):
f (x) =
+N
∑
n=−N
a
n
cos(nω
0
) + b
n
sin(nω
0
) (1)
ω
0
is the fundamental frequency and N means a pos-
itive integer. The HPF attenuates low-frequency ele-
ments including the zero frequency element (DC). We
denote the output of the HPF by g(x) and it becomes
as follows.
g(x) =
−M
∑
n=−N
a
n
cos(nω
0
) + b
n
sin(nω
0
)
+
N
∑
n=M
a
n
cos(nω
0
) + b
n
sin(nω
0
) (2)
where M is also a positive integer and N > M. The fre-
quency elements from −M to M are eliminated with
the HPF. DC has the largest energy in the images, and
it sometimes causes saturation whereby the images
become either all white or all black. The output of
NLF does not cause saturation by eliminating DC, and
it has the following effect. Edges are represented with
sin(nω
0
) and cos(nω
0
) functions. The cubic func-
tion y = x
3
generates sin
3
(nω
0
) and cos
3
(nω
0
) from
sin(nω
0
) and cos(nω
0
). sin
3
(nω
0
) and cos
3
(nω
0
)
generate sin3(nω
0
) and cos3(nω
0
). Theoretically it
can be explained as follows.
(g(x))
3
=
−M
∑
n=−3N
c
n
cos(nω
0
) + d
n
sin(nω
0
)
+
3N
∑
n=M
c
n
cos(nω
0
) + d
n
sin(nω
0
) (3)
where c
n
and d
n
are the expansion coefficients
of Equation 3. Although Equation 3 has the high-
frequency elements from (N +1)nω
0
to 3N, these ele-
ments do not exist in the input image, that is, Equation
1. Given that these high-frequency elements are pro-
duced with the NLF, some of them are too large and
should be processed with LMT. After the LMT pro-
cessing, the developed high-frequency elements are
added into the input by using the ADD function in
Figure 1. The high frequency elements, produced
by NLF, that are three times higher than the input,
and they can be used to double the size of the im-
ages horizontally and vertically, such as during the
up-conversion from 4K to 8K. Moreover, given that
images and videos are two-dimensional signals, ap-
plying NLSP horizontally and vertically is necessary.
NLSP is not a simple edge enhancement, such as the
enhancer. Aside from the enhancer, other technolo-
gies, such as blind deconvolution (Richardson, 1972)
(Lucy, 1974) and SR, are also available. However, be-
cause these technologies require iterations, they can-
not work in real-time for the 8K endoscope.
Real-time Nonlinear Signal Processing Super Resolution of 8K Endoscope Cameras
345

(a) Original image
(256 × 256 pixels)
(b) Enlarged image of (a)
with Lanczos2 filter
(512 × 512 pixels)
Figure 2: Example of image enlargement.
(a) 2D-FFT result of
Figure 2(a)
(b) 2D-FFT result of
Figure 2(b)
Figure 3: 2D-FFT result.
Figure 4: NLSP processed result of Figure2 (a).
Figure 5: 2D-FFT result of Figure4.
4 CAPABILITY OF THE NLSP
In this section, a simulation result is discussed to
prove the capability of the NLSP. Herein, we use an
Figure 6: Real time NLSP hardware.
image enlarged with the Lanczos-2 filter (Duchon,
1979) because the enlargement always causes blur.
Figure 2(a) shows a 256 × 256 pixel image, and Fig-
ure 2(b) illustrates the a 512 × 512 pixel image en-
larged of Figure 2(a). Compared with Figures 2(a)
and 2(b), Figure 2(b) has an enlargement blur. Figure
3 illustrates the two dimensional fast Fourier trans-
form (2D-FFT) results of Figure 2. In Figure 3(a) the
same spectrum is repeated every 2π, which is the sam-
pling frequency, horizontally and vertically. In Figure
3(b), the spectrum appears only in the center position
because the horizontal and vertical sampling frequen-
cies become double and the other spectrum appears
outside of the image. Figure 4 illustrates the NLSP-
processed image of Figure 2(b). By comparing Fig-
ures 2(b) and 4, Figure 4 is evidently better. Figure 5
shows the 2D-FFT of Figure 4. Figure 5 has the high-
frequency elements that Figure 2(b) does not possess
indicating that NLSP can produce high-frequency ele-
ments that the input image cannot possess. In section
2, we define SR first as a technology that can pro-
duce high-frequency elements that are not present in
the original LR, and then it also improves the image
quality. By comparing Figures 2(b) and 4, the former
condition of SR defined in Section 2, is satisfied. In
the case of Figures 3(b) and 5, the latter condition of
SR is also met. We also develop a real-time 4KTV
NLSP hardware shown in Figure 6. Although many
devices are present on the circuit board, most of them
are interface devices for the input and output. The
Figure 7: 2D-LPF characteristic.
SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications
346
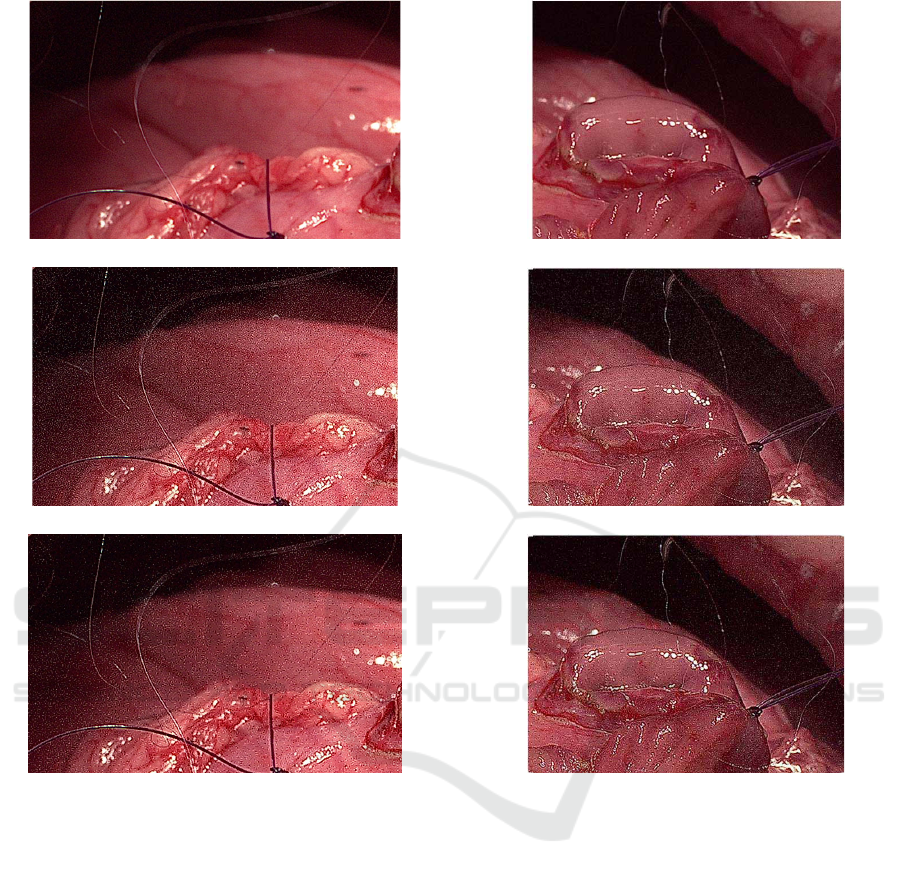
(a) 8K endoscope image 1
(b) NLSP processed image of Figure 8(a)
(c) NLSP and 2D-LPF processed image of Figure
8(a)
Figure 8: 8K endoscope image and processed images 1.
NLSP algorithm is written in a field-programmable
gate array (FPGA) under the heat sink at the center of
the circuit board.
5 EXPERIMENTAL RESULT OF
THE 8K ENDOSCOPE IMAGE
USING A REAL-TIME NLSP
HARDWARE
Because the input and output of the real-time hard-
ware is 4K, we need four parallel circuit boards when
we use the hardware to an 8K video in real-time. The
full 8K image cannot be illustrated in the paper ow-
ing to space limitations. Figures 8–10 show the ex-
(a) 8K endoscope image 2
(b) NLSP processed image of Figure 9(a)
(c) NLSP and 2D-LPF processed image of Figure
9(a)
Figure 9: 8K endoscope image and processed images 2.
perimental results. These areas are cropped from the
full 8K endoscope images and contain the 0.02 mm
threads. Figures 8(a), 9(a) and 10(a) show the ar-
eas of the original 8K endoscope images. Figures
8(b), 9(b) and 10(b) illustrate the NLSP-processed
images by using the real-time hardware shown in Fig-
ure 6. When comparing the original images (Figures
8(a), 9(a) and 10(a)) with the NLSP-processed images
(Figures 8(b), 9(b) and 10(b)), the threads become
more visible in the out-of-focus areas. However, the
NLSP processing creates an undesirable effect which
is noise. A two-dimensional low-pass filter (2D-LPF)
is introduced to reduce the noise. Figure 7 presents
the characteristic of 2D-LPF. The 2D-LPF decreases
only the number of diagonal high-frequency elements
to reduce the noise. Given that the 2D-LPF is pro-
Real-time Nonlinear Signal Processing Super Resolution of 8K Endoscope Cameras
347
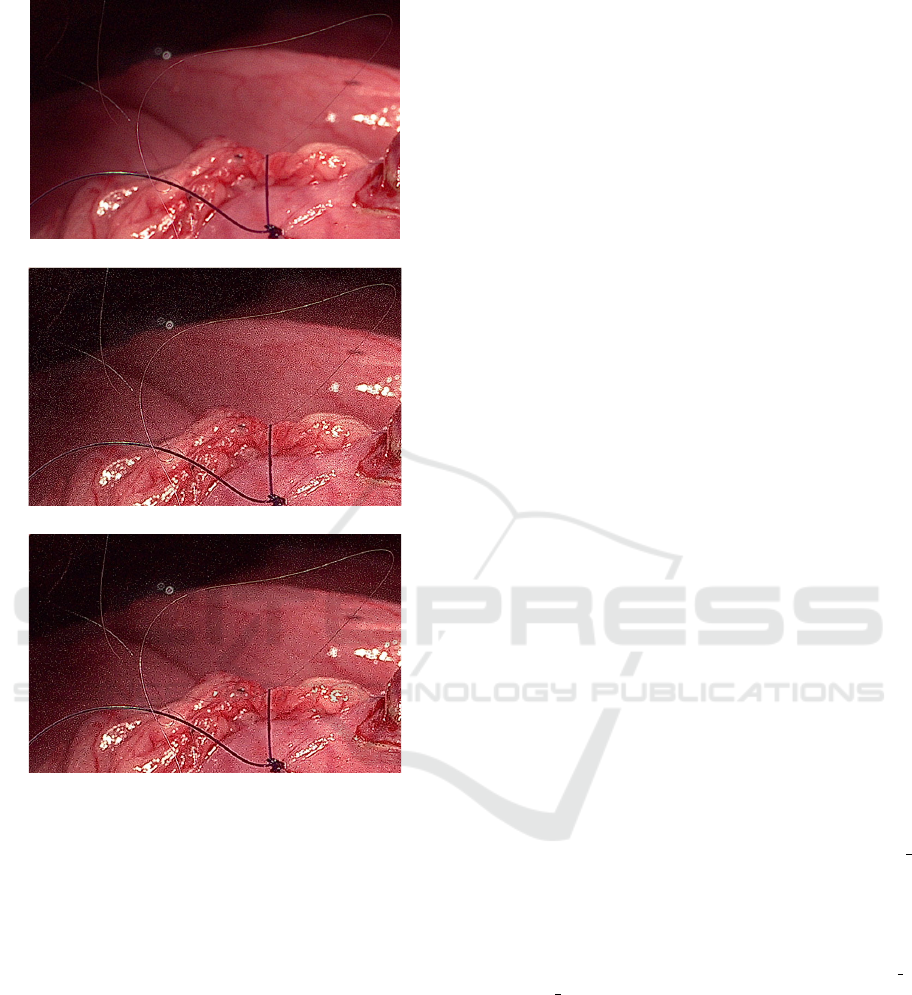
(a) 8K endoscope image 3
(b) NLSP processed image of Figure 10(a)
(c) NLSP and 2D-LPF processed image of Figure
10(a)
Figure 10: 8K endoscope image and processed images 3.
gramed in the FPGA illustrated in Figure 6, the 2D-
LPF can also work in real-time.
Figures 8(c), 9(c) and 10(c) show the NLSP-
and 2D-LPF-processed results of the original images
shown in Figures 8(a), 9(a) and 10(a), respectively.
When comparing Figures 8(c), 9(c) and 10(c) with
Figures 8(a), 9(a) and 10(a), the noise is reduced
and the 0.02 mm threads remain visible. However,
the noise level is not sufficiently low in the 2D-
LPF-processed images shown in Figures 8(c), 9(c)
and 10(c). Although an infinitive impulse response
filter-type noise reducer is a practical signal process-
ing for videos, it does not work well (Lee, 1980).
Three requirements necessary to completely reduce
the noise are : (1) sufficient lighting conditions, (2)
high-sensitivity photoelectric device, and (3) noise-
reducing signal processing. The improvement of the
lighting conditions seem to be easy. However, heat in-
creases in proportion to brightness. Bright lights emit
more heat that might hurt organs because the light is
used inside the body. Although high-sensitivity pho-
toelectric device is useful, it is time consuming. Cur-
rently, the new noise-reducing signal processing is be-
lieved to be practical.
6 CONCLUSION
In this study, a real-time SR system that consists of
NLSP and 2D-LPF is proposed. The SR system is
applied to the 8K endoscope video. It enhances the
image quality and the unfocused 0.02 mm thread be-
comes visible, indicating that the proposed real-time
SR system improves the focus depth. The future work
will be focused on the development of a novel noise-
reducing signal processing method for 8K endoscope.
REFERENCES
Bannore, V. (2010). Iterative-Interpolation Super-
Resolution Image Reconstruction.
Duchon, C. E. (1979). Lanczos filtering in one and two
dimensions. Journal of Applied Meteorology, Vol. 18,
pp. 1016-1022.
Funatsu, R., Yamashita, Y., Mitani, K., and Nojiri, Y.
(2013). Focus-aid signal for super hi-vision cameras.
Technical Report 53, NHK.
Gohshi, S., Nakamura, S., and Tabata, H. (2017). Devel-
opment of real-time hdtv-to-8k tv upconverter. VISI-
GRAPP 2017, VISAPP, 4:52–59.
Hitachi (2015). http://www.rbbtoday.com/article/2015/04/07
/130240.html.
Houa, X. and Liu, H. (2011). Super-resolution image re-
construction for video sequence. IEEE Transactions
on Image Processing.
Ikegami (2015). http://www.ikegami.co.jp/news/detail.html
/news id=907.
Ledig, C., Theis, L., Huszar, F., Caballero, J., Cunning-
ham, A., Acosta, A., Aitken, A., Tejani, A., Totz, J.,
Wang, Z., and Shi, W. (2017). Photo-realistic single
image super-resolution using a generative adversarial
network. IEEE CVPR.
Lee, J. S. (1980). Digital image enhancement and noise fil-
tering by use of local statistics. IEEE Trans. on Pattern
Analysis and Machine Intelligence,, pages 165–168.
Lucy, L. B. (1974). An iterative technique for the rectifica-
tion of observed distributions. THE ASTRONOMICAL
JOURNAL, 79(6):745–754.
SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications
348

Mertz, P. and Gray, F. (1934). A theory of scanning and its
relation to the characteristics of the transmitted signal
in telephotography and television. IEEE Transactions
on Image Processing.
Mori, C., Sugie, M., Takeshita, H., and Gohshi, S. (2015).
Subjective assessment of super-resolution: High-
resolution effect of nonlinear signal processing. AP-
SITT 2015.
Richardson, W. H. (1972). Bayesian-based iterative method
of image restoration. Journal of The Optical Society
of America, 62(1):55–59.
Shahar, O., Faktor, A., , and Irani, M. (2011). Space-time
superresolution from a single video. CVPR f11 Pro-
ceedings of the 2011 IEEE Conference on Computer
Vision and Pattern Recognition, 19(11):3353–3360.
van Eekeren, A. W. M., Schutte, K., and van Vliet, L. J.
(2010). Multiframe super-resolution reconstruction of
small moving objects. IEEE Transactions on Image
Processing.
Real-time Nonlinear Signal Processing Super Resolution of 8K Endoscope Cameras
349
