Asynchronous Control Design of Continuous-time Markovian Jump

Systems with Bounded Time-varying Transition Rates

Ngoc Hoai An Nguyen

and Sung Hyun Kim

School of Electrical Engineering, University of Ulsan, Daehak-ro 93, Nam-Gu, Ulsan, 680-749, South Korea

Keywords: Asynchronous Control, Dissipative Control, Markovian Jump Systems, Transition Rates.

Abstract:

The asynchronous control design of continuous-time Markovian jump systems with bounded time-varying

transition rates is addressed in this paper. According to the framework of parameterized linear matrix in-

equalities (PLMIs), essential stabilization conditions are established with consideration on dissipativity per-

formance and then transform to solvable sets of linear matrix inequalities (LMIs) under our proposed method.

Especially, our technique is derived from not only time-varying system modes but also asynchronous control

modes transition rates. The effectiveness of our method is then illustrated through our numerical example.

1 INTRODUCTION

Markovian jump systems (MJSs) is a prosperous re-

search area which have drawn energetic attraction

in both academic and industries communities due to

their advantages. Firstly, as a special class of hybrid

systems, MJSs involve both time and event-driven

mechanism to represent plants under abrupt changes

in structure and parameters, for examples, sudden

environment changes, component failures, package

dropout, subsystems interconnection adjustment. The

second advantageous aspect is that MJSs have been

devoted to the study of practically diverse application

such as communication networks, power systems, so-

lar receiver control, networked control aircraft ﬂight

systems, robotics (see (Zhou et al., 2017; Liu et al.,

2017; Mao et al., 2007; Zhai et al., 2016; Joo and

Kim, 2015; Nguyen and Kim, 2019; Shi and Yu,

2009), etc). To dominate the variations among those

systems, MJSs have been extended from Markov pro-

cess which follows a certain transition rates matrix.

Recently, to cover a wider range of practical appli-

cations systems, the term transition rates are deﬁned

as time-varying rather than ideally constant and time-

invariant. Rasing from this research trend, the an-

alyze technique emerged from bounded interval of

time-varying transition rates has been took advantage

to achieve many signiﬁcant results in control commu-

nity (refer to (Kim, 2014b; Kim, 2014a; Nguyen et al.,

https://orcid.org/0000-0001-7651-2537

https://orcid.org/0000-0003-2495-7117

2016; Yin et al., 2018)), etc).

As for control synthesis, in past few decades, a lot

of research pursues the mode-independent control

method. Up to now, research trend has adopted to the

mode-dependent Lyapunov method in designing con-

trollers, with strict synchronization between plants

and controllers. Nonetheless, with the growing in

large scale and complexity of modern industrial pro-

cess, the system dynamic and controller are quite

different to each other. Therefore, a strict synchro-

nization is likely to be hard in real time since some-

times controller can not access exact mode informa-

tion from system, especially when the systems are in-

sensitive to some amount of uncertainties, device fail-

ure or external perturbation. Under this circumstance,

the necessity to discuss asynchronous phenomenon

for control synthesis/ﬁlter of MJSs is desired to fur-

ther explore.

Among those research on asynchronization mat-

ter on MJSs, the asynchronous L

-L

∞

ﬁltering for

discrete-time MJSs with occurred sensor nonlinear-

ities satisfying the Bernoulli distribution are con-

cerned in (Wu et al., 2014). On another research

result, (see, for details, (Kim, 2019a) and (Kim,

2019b)) has discussed the issue of passivity-based

asynchronous controller, synchronous controller as

well as mode-independent controller for discrete-time

MJSs. Recently, asynchronous stabilization problem

for discrete-time MJSs was discussed at which both

synchronous case and asynchronous ones have been

surveyed to ﬁgure out sufﬁcient and necessary sta-

bilization conditions (Guan et al., 2019). However,

384

Nguyen, N. and Kim, S.

Asynchronous Control Design of Continuous-time Markovian Jump Systems with Bounded Time-varying Transition Rates.

DOI: 10.5220/0007952103840389

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 384-389

ISBN: 978-989-758-380-3

there is still much room left on the asynchronous sta-

bilization for continuous-time MJSs, which motivates

us to conduct this paper.

The purpose of our paper is to address asynchronous

control design for continuous-time Markovian jump

systems with bounded time-varying transition rates

since the difﬁculty emerged from both asynchronous

phenomenon and unavailable transition rates need to

be discussed and enhanced. The contribution of our

paper can be itemized as follows:

• Our control method can deal with asynchronous

controller, partially asynchronous controller, as

well as perfectly synchronous controller based on

the assumption of conditional probability matrix

between system modes and controller modes.

• The robustness of controller has been taken to deal

with external factors such as system uncertain-

ties, disturbance so that the closed-loop system

is stochastically stable with strictly (Q ,S,R )-γ-

dissipative performance.

• The result is meaningful in practically real time

application since this paper pursues to adapt time-

varying transition rates, where system randomly

switches from one mode to another at time-

dependent pace.

• To be promise in our future research with the ex-

tension of application in nonhomogenous MJSs

at which transition rates are not only ﬁxed or

bounded but also completely unknown.

Notations: The notations X ≥ Y and X > Y mean

that X −Y is positive semi-deﬁnite and positive def-

inite, respectively. In symmetric block matrices, the

asterisk (∗) is used as an ellipsis for terms induced

by symmetry. E{·} denotes the mathematical ex-

pectation; diag(·) stands for a block-diagonal ma-

trix; He{Q } = Q + Q

for any square matrix Q ;

and L

[0,∞) stands for the space of square summable

sequences over [0, ∞). For a

∈ {1,2,· · ·} such

that a

i+1

> a

, i ∈ {1, 2, ··· , n}, the following nota-

tions are used:





i∈{a

,···,a

}



··· Q







i∈{a

,···,a

}

= diag



,··· ,Q



, where Q

de-

notes real submatrix with appropriate dimensions or

scalar values.

2 SYSTEM DESCRIPTION AND

PRELIMINARIES

Let us consider the following continuous-time Marko-

vian jump system deﬁned on a complete probability

space (Ω,F ,P ):











˙x(t) =



A(φ(t)) + ∆A(φ(t)



x(t)



B(φ(t)) + ∆B(φ(t))



u(t) + E(φ(t))w(t),

z(t) = C(φ(t))x(t) + D(φ(t))u(t),

(1)

where x(t) ∈ R

, u(t) ∈ R

, w(t) ∈ R

, z(t) ∈ R

and φ(t) ∈ N

= {1, 2,...,n

} denote the state, the

saturated control input, the disturbance input belong-

ing to L

[0,∞), the performance output, and the plant

operation mode, respectively. Especially, the process

{φ(t),t ≥ 0} is characterized by a continuous-time

nonhomogeneous Markov process governed by the

following transition probabilities (TPs):



φ(t + δ) = h



φ(t) = g





(t)δ + o(δ) if h 6= g,

1 + π

(t)δ + o(δ) if h = g,

where δ > 0, lim

δ→0

(o(δ)/δ) = 0, and π

(t) denotes

the transition rate (TR) from mode g to mode h at time

t + δ, satisfying that

•

∑

h∈N

(t) ≡ 0, (2)

• π

(t) ≥ 0, ∀h ∈ N

\ {g}. (3)

Based on the property of TRs, this paper intends

to address the following two ﬁnite sets such that

= N

holds: for g ∈ N



(t) = π

is time-invariant and completely known

, (4)



(t)

is unknown but bounded as π

≤ π

(t) ≤ π

(5)

Then, from (2), (4), and (5), it is

•

∑

h∈

(t) + Π

≡ 0, (6)

• π

(t) ∈



,π



, ∀h ∈

, (7)

where Π

∑

h∈H

. Further, in (1), the

parameter uncertainties are represented as fol-

lows: ∆A(φ(t)) = G(φ(t))∆(φ(t),t)H

(φ(t))

and ∆B(φ(t)) = G(φ(t))∆(φ(t),t)H

(φ(t)),

where G(φ(t) = g) = G

, H

(φ(t) = g) = H

and H

(φ(t) = g) = H

are known constant

matrices with appropriate dimensions; and

∆(φ(t) = g,t) = ∆

(t) ∈ R

×n

is an unknown

matrix with Lebesgue measurable elements such that

Asynchronous Control Design of Continuous-time Markovian Jump Systems with Bounded Time-varying Transition Rates

385

k∆

(t)k ≤ 1 holds. In what follows, let us consider

an asynchronous mode-dependent control law of the

following form:

u(t) = F(ρ(t))x(t), (8)

where ρ(t) ∈ N

= {1,2,·· · ,n

} denotes the control

mode, and F(ρ(t) = `) = F

denotes the control gain

to be designed later. Further, since the control mode

ρ(t) is deﬁnitely associated with the plant mode φ(t),

it is supposed to be characterized by the following

conditional probability:



ρ(t) = `



φ(t) = g



= ϖ

, ∀g ∈ N

, ` ∈ N

, (9)

which satisﬁes

∑

`∈N

= 1 and 0 ≤ ϖ

≤ 1 for all

g and `. As a result, the closed-loop system with (1)

and (8) is described as follows:

(

˙x(t) =



+ ∆



x(t) + E

w(t),

z(t) =

x(t),

(10)

where

= A

+ B

= C

+ D

, ∆

∆

(t)

, and

= H

+ H

Remark 2.1. As reported in (Choi et al., 2017), the

strict (Q ,S,R )-γ-dissipativity performance can be re-

duced into two special performances: 1) H

∞

perfor-

mance by setting Q = −I, S = 0, and R = (γ

+ γ)I;

and 2) passivity performance by setting Q = 0, S = I,

and R = 2γI.

3 CONTROL DESIGN

Let us consider the following mode-dependent Lya-

punov function:

V (t,ρ(t)) = x

(t)P(ρ(t))x(t), (11)

where 0 < P(ρ(t) = `) = P

∈ R

×n

. Then the weak

inﬁnitesimal operator of the process {x(t),φ(t),ρ(t)}

acting on V (t) := V (t,ρ(t)) is given by

∇V (t) = lim

δ→0



t + δ, ρ(t + δ) = m



φ(t) = g



−V (t,ρ(t) = `|φ(t) = g)

= lim

δ→0

(

∑

m∈N

∑

h∈N

\{g}



(t)δ + o(δ)



×V (t + δ,m)

+ϖ



(t)δ + o(δ) + 1



×V (t + δ, m)

−

∑

`∈N

V (t, `)

)

∑

m∈N

∑

h∈N

(t)V (t,m) +

∑

`∈N

V (t,`)

∑

`∈N





∑

h∈N

∑

m∈N

(t)ϖ

V (t,m)+

V (t,`)





According to (10),

∇V (t) =

∑

`∈N

(t)





η(t), (12)

where

η(t) =



(t) w

(t)



∈ R

,(i.e.,n

= n

+ n

= P

+ He

(

+ ∆

)

∑

h∈N

∑

m∈N

(t)ϖ

The following lemma provides the robust stochastic

stability condition for (10) with w(t) ≡ 0.

Lemma 3.1. Suppose that there exist P

> 0 and F

such that the following condition holds:

0 > Ψ

, ∀g ∈ N

, ` ∈ N

. (13)

Then closed-loop system (10) with w(t) ≡ 0 can be

said to be robustly stochastically stable.

The following lemma provides the robust asyn-

chronous dissipative control synthesis conditions for

(10), formulated in terms of parameterized linear ma-

trix inequalities (PLMIs).

Lemma 3.2. For a prescribed scalar µ, suppose that

there exist matrices 0 <

∈ R

×n

, W

∈ R

×n

∈ R

×n

; and scalar variables γ,

> 0 such that the following conditions hold: for

g ∈ N

, ` ∈ N









+ B



+α

(∗) (∗) (∗)

− SC

− SD

−R +γI 0 0

+ Q

0 −I 0

+ H

0 0 −α







+ e

∑

h∈N

\{g}

(t)

(µ)

e, (14)

0 ≤



(∗)



, ∀m ∈ N

. (15)

where e =



I 0 0 0



∈ R

×(n

)

, and

(µ) =

∑

m∈N



− 2µϖ

+ µ



Then closed-loop system (10) is robustly stochasti-

cally stable and strictly (Q ,S , R )-γ-dissipative, and

the control gains are reconstructed as follows: F

−1

, ∀` ∈ N

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

386

The following theorem provides the relaxed robust

asynchronous control synthesis conditions for (10)

with strict (Q ,S,R )-γ-dissipativity performance, for-

mulated in terms of linear matrix inequalities (LMIs).

Theorem 3.1. For a prescribed scalar µ, suppose

that there exist symmetric matrix 0 <

∈ R

×n

∈ R

×n

; matrices

∈ R

m×n

, X

∈ R

×n

∈ R

×n

; and γ, α

> 0 such that the following

conditions hold: for g ∈ N

, ` ∈ N

0 >

(∗)

(µ)e

h∈

\{g}

(1,1)

(∗)

(2,1)

(2,2)

, (16)

0 ≤



(∗)



, ∀m ∈ N

, (17)

where







(1,1)

(∗) (∗) (∗)

− SC

− SD

−R + γI 0 0

+ Q

0 −I 0

+ H

0 0 −α







(1,1)

= He



+ B



+ α

∑

h∈H

\{g}

(µ),

(1,1)







e, if g ∈ H

0, otherwise

(1,1)

∑

h∈

\{g}





(2,1)







h∈

\{g}

, if g ∈ H

0, otherwise

(2,1)

(−π

−π

h∈

\{g}

(2,2)





h∈

\{g}

e =



I 0 0 0



∈ R

×(n

)

(µ) =

∑

m∈N



− 2µϖ

+ µ



Then closed-loop system (10) is robustly stochasti-

cally stable and strictly (Q ,S , R )-γ-dissipative, and

the control gains are reconstructed as follows:

−1

, ∀` ∈ N

. (18)

4 ILLUSTRATIVE EXAMPLE

Example 1: Let us consider the following

continuous-time nonhomogenous MJS with four

modes, used in (Zong et al., 2013):



2 2

1 −3



, A



1 2

0 −1





2 3

1 −1



, A



1 1

2 −3







, B





, B









, E





, E



0.5





0.3



, E



0.4



, C



1 2





1 1



, C



1 3



, C



0 1





0.1



, G



0.1



, G



0.1





0.2



, H



0.1 0.1





0.2 0.3



, H



0.2 0.3





0.2 0.4



, H

= 0.1,

= 0.2, H

= 0.3, H

= 0.4,

= 0.1, D

= 0.2, D

= 0.3, D

= 0.4. (19)

Further, the TR matrix is taken as follows:

(t)

g,h∈N







× 0.3 × 0.4

× −1 0.3 ×

0.8 × −1.3 ×

1.0 × × −1.5







, (20)

where all × denote the bounded TRs with upper and

lower bound values listed in Table 1.

Table 1: Interval of bounded transition rates.

(t) [-1.4, -0.7] π

(t) [0, 0.5]

(t) [0, 0.7] π

(t) [0, 0.5]

(t) [0, 0.7] π

(t) [0, 0.5]

(t) [0, 0.7] π

(t) [0, 0.5]

That is, it is given that H

= {2,4},

{1,3}, H

= {2,3},

= {1,4}, H

= {1,3},

{2,4}, H

= {1, 4},

= {2, 3}. Meanwhile, the

conditional probability matrix is taken as follows:

g∈N

,`∈N







0.4 0.2 0.3 0.1

0.1 0.5 0.3 0.1

0.2 0.3 0.4 0.1

0.1 0.3 0.4 0.2







. (21)

The goal of this example is to design an asynchronous

mode-dependent state-feedback control (8) such that

the closed-loop system is stochastically stable with

strict strictly (Q ,S , R )-γ-dissipativity performance.

Asynchronous Control Design of Continuous-time Markovian Jump Systems with Bounded Time-varying Transition Rates

387

To this end, by Theorem 1, the following feasible so-

lution is obtained: γ = 0.4470, and



−7.9921 −11.8143





−7.8669 −11.6618





−7.9062 −11.7685





−7.8386 −11.4010



Furthermore, to show the validity of the obtained con-

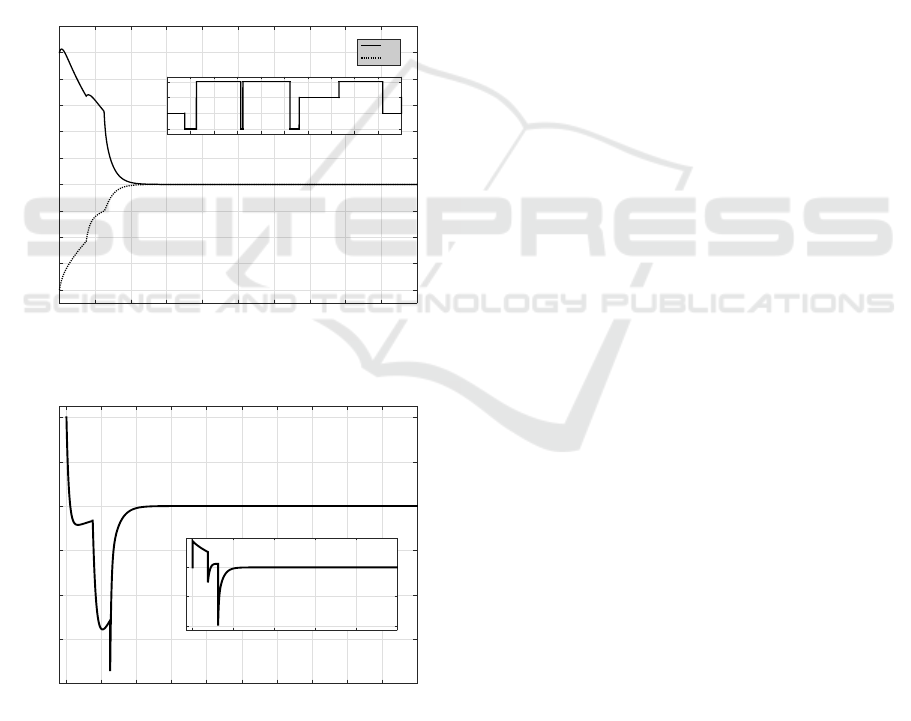
trol gains, Figure 1 demonstrates the state response

of the closed-loop system, where x

= [0.5 − 0.4]

w(t) = 0.1e

−0.3t

sin(0.2πt), and the applied control

input is plotted in Figure 2. Clearly, from Figure

1, it can be found that the state gradually converges

to zero as time increases despite the presence of the

asynchronous controller and incomplete knowledge

of transition rates.

Time (sec)

0 1 2 3 4 5 6 7 8 9 10

State x(t)

-0.4

-0.3

-0.2

-0.1

0.1

0.2

0.3

0.4

0.5

0.6

(t)

Time (sec)

0 1 2 3 4 5 6 7 8 9 10

Plant Mode φ(t)

Figure 1: State response x(t) and mode evolution ρ(t) used

in Example 1.

Time (sec)

0 1 2 3 4 5 6 7 8 9 10

Control Input u(t)

-0.8

-0.6

-0.4

-0.2

0.2

0.4

Time (sec)

0 2 4 6 8 10

Performance Output z(t)

# 10

-4

-2

Figure 2: Control input u(t) and performance output z(t).

5 CONCLUSIONS

This paper has investigated the problem of asyn-

chronous control for continuous-time MJSs with

bounded time-varying transition rates and system un-

certainties. In order to obtain a ﬁnite set of solvable

LMIs from mode-dependent PLMIs, our method has

been proposed to conduct the impact of both system

modes and controller modes on stabilization condi-

tions. Eventually, this paper has presented the LMIs-

based stabilization conditions to design an asyn-

chronous controller with dissipativity performance.

ACKNOWLEDGEMENTS

This work was supported by the National Research

Foundation of Korea Grant funded by the Korean

Government ( NRF- 2018R1D1A1B07041456 ).

REFERENCES

Choi, H. D., Ahn, C. K., Shi, P., Wu, L., and Lim, M. T.

(2017). Dynamic output-feedback dissipative control

for T–S fuzzy systems with time-varying input delay

and output constraints. IEEE Transactions on Fuzzy

Systems, 25(3), 511-526.

Guan, C., Fei, Z., and Yang, T. (2019). Necessary and

sufﬁcient criteria for asynchronous stabilization of

Markovian jump systems. Journal of the Franklin In-

stitute, 356(3), 1468-1483.

Joo, H. and Kim, S. H. (2015). LPV control with pole

placement constraints for synchronous buck convert-

ers with piecewise-constant loads. Mathematical

Problems in Engineering, Article ID 686857.

Kim, S. H. (2014a). Control synthesis of Markovian jump

fuzzy systems based on a relaxation scheme for in-

complete transition probability descriptions. Nonlin-

ear Dynamics, 78(1), 691-701.

Kim, S. H. (2014b). Less conservative stabilization con-

ditions for Markovian jump systems with partly un-

known transition probabilities. Journal of the Franklin

Institute, 351(5), 3042-3052.

Kim, S. H. (2019a). Asynchronous dissipative ﬁlter design

of nonhomogeneous Markovian jump fuzzy systems

via relaxation of triple-parameterized matrix inequali-

ties. Information Sciences, 478, 564-579.

Kim, S. H. (2019b). Dissipative control of Markovian jump

fuzzy systems under nonhomogeneity and asynchro-

nism. Nonlinear Dynamics, 1-18.

Liu, M., Zhang, L., Shi, P., and Zhao, Y. (2017). Slid-

ing mode control of continuous-time Markovian jump

systems with digital data transmission. Automatica,

80, 200-209.

Mao, Z., Jiang, B., and Shi, P. (2007). H

∞

fault detection ﬁl-

ter design for networked control systems modelled by

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

388

discrete Markovian jump systems. IET control theory

& applications, 1(5), 1336-1343.

Nguyen, N. H. A. and Kim, S. H. (2019). Relaxed

robust stabilization conditions for nonhomogeneous

Markovian jump systems with actuator saturation and

general switching policies. International Journal of

Control, Automation and Systems, 17(3), 586-596.

Nguyen, N. H. A., Kim, S. H., and Choi, J. (2016). Stabi-

lization of semi-Markovian jump systems with uncer-

tain probability intensities and its extension to quan-

tized control. Mathematical Problems in Engineering,

Volume 2016, Article ID 8417475.

Shi, Y. and Yu, B. (2009). Output feedback stabilization of

networked control systems with random delays mod-

eled by Markov chains. IEEE Transactions on Auto-

matic Control, 54(7), 1668-1674.

Wu, Z. G., Shi, P., Shu, Z., Su, H., and Lu, R. (2014). Asyn-

chronous L

-L

∞

ﬁltering for discrete-time stochastic

Markov jump systems with randomly occurred sensor

nonlinearities. Automatica, 50(1), 180-186.

Yin, Y., Zhu, L., Zeng, H., Liu, Y., and Liu, F.

(2018). Stochastic stability analysis of integral non-

homogeneous Markov jump systems. International

Journal of Systems Science, 49(3), 479-485.

Zhai, D., An, L., Li, J., and Zhang, Q. (2016). Fault detec-

tion for stochastic parameter-varying Markovian jump

systems with application to networked control sys-

tems. Applied Mathematical Modelling, 40(3), 2368-

2383.

Zhou, J., Dong, H., and Feng, J. (2017). Event-triggered

communication for synchronization of Markovian

jump delayed complex networks with partially un-

known transition rates. Applied Mathematics and

Computation, 293, 617-629.

Zong, G., Yang, D., Hou, L., and Wang, Q. (2013). Robust

ﬁnite-time H

∞

control for Markovian jump systems

with partially known transition probabilities. Journal

of the Franklin Institute, 350(6), 1562-1578.

Asynchronous Control Design of Continuous-time Markovian Jump Systems with Bounded Time-varying Transition Rates

389