
Time-based Countermeasures for Relay Attacks on PKES Systems
Yifan Xie, Hyung June Kim, Sa Yong Chong and Taek Lyul Song
Department of Electronic Systems Engineering, Hanyang University, Ansan, Republic of Korea
Keywords:
PKES, Relay Attack, Distance Bounding, TOA, Localization.
Abstract:
The development of passive keyless entry and start (PKES) systems in modern vehicles enables drivers to
access and control their vehicles remotely using smart keys, which improves the driving conveniences. The
PKES system verifies the smart key identity if the communication channel between the vehicle and the smart
key is established. When the message in the communication channel is relayed by other devices, it can be
manipulated by the attackers and the PKES systems become vulnerable. The distance bounding protocol,
which estimates the physical proximity between the vehicle and the smart key, is one of the countermeasures
against relay attacks. In this paper, the time-based distance bounding is studied. Since the effectiveness of
distance bounding protocol relies heavily on the estimation accuracy, various time-based estimation algorithms
are enumerated and compared in this paper.
1 INTRODUCTION
Traditional vehicles are usually accessed and au-
thorized to drive through physical keys and lock-
ing systems. In order to improve drivers’ experi-
ence and convenience, modern vehicles are embedded
with passive keyless entry and start (PKES) systems,
which allows the driver to open the door and start the
engine remotely by pressing the button on the smart
key (Francillon et al., 2011; Ahmad et al., 2018; Patel
et al., 2018).
However, the PKES systems are vulnerable if the
messages between the vehicle and the smart key are
relayed by some attack devices. When the attacker
places one attack device near the vehicle, fake signals
are seduced from the vehicle and sent to the smart key
to get open/start authorizations. Another attack de-
vice is then placed a few meters from the smart key
to establish the relay channel. The signals from the
vehicle are received by the attack device instead of
the smart key such that the messages are relayed and
can be manipulated. The possibility of the relay at-
tack is caused by the PKES system vulnerability. In
a PKES system, the vehicle periodically probes the
communication channel to search the short beacons
from the smart key. Once the short beacon is detected
by the vehicle, i.e. the smart key is located inside
the vehicle’s communication range, the PKES system
concludes that the smart key is in the proximity of the
vehicle and all commands from the smart key are au-
thorized. This verification procedure assumes that the
communication ability implies the physical proxim-
ity, which makes the relay attacks possible.
Numerous countermeasures are proposed in past
decades to prevent the relay attacks on PKES systems
(Francillon et al., 2011). For instances, (1) the smart
key can be put into a protective cage (made by metal-
lic) for signal shielding after parking the vehicle; (2)
design another button on the smart key to disable the
embedded battery after parking the vehicle; (3) use
the distance bounding protocol to estimate the phys-
ical proximity, etc. The first two countermeasures
are inconvenient and the vehicle could still be under
the relay attacks when the driver forgets to take ac-
tions. The distance bounding based countermeasure
is recommended and studied in this paper. The dis-
tance bounding protocol provides protections against
attacks on access control systems by verifying the
smart key location. The command from the smart key
will be authorized only if when it is transmitted from
the physical proximity of the vehicle. Therefore, the
accuracy of the estimated smart key location is critical
for the distance bounding protocol.
Among all distance bounding protocols, the smart
key location can be estimated by diverse methods ac-
cording to signal properties of phase change, ampli-
tude attenuation and traveling time, etc (Ranganathan
and Capkun, 2017). The signal traveling time in-
formation can be exploited by the time of arrival
(TOA) measurement and the time difference of ar-
Xie, Y., Kim, H., Chong, S. and Song, T.
Time-based Countermeasures for Relay Attacks on PKES Systems.
DOI: 10.5220/0007957407950801
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 795-801
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
795

rival (TDOA) measurement. The TOA measurement
has smaller sensor noise relative to the TDOA mea-
surement, which leads to its popularity. In this paper,
two least-square (LS) based methods called uncon-
strained squared-range-based LS (USR-LS) and con-
strained squared-range-based LS (CSR-LS) are intro-
duced for position estimation using the TOA measure-
ments. Both the USR-LS method and the CSR-LS
method minimize the residual using only one set of
the TOA measurements. Since the effectiveness of the
TOA-based countermeasure relies on estimation ac-
curacy, the authors propose to improve the estimation
accuracy by using multiple TOA measurement sets.
The first TOA measurement set is used for track ini-
tialization via the CSR-LS method and the other TOA
measurement sets are used serially by an extended
Kalman filter (EKF).
The rest of the paper is organized as follows. The
relay attack model and the distance bounding are in-
troduced in Section 2. Analyses for the TOA and the
TDOA measurement selection are discussed in Sec-
tion 3. Details for the USR-LS method, the CSR-LS
method and the multiple-transmission method are de-
scribed in Section 4. Simulations for the three meth-
ods are studied in Section 5, followed by the conclu-
sions in Section 6.
2 PROBLEM STATEMENTS
2.1 Relay Attack Model
The PKES system in modern vehicles verifies
whether the correct smart key is located around the
vehicle by verifying the communication ability, as-
suming that the communication ability implies the
physical proximity. This verifying procedure makes
the PKES system vulnerable to the relay attacks. In
typical relay attacks, two attack devices are deployed
near the vehicle and the smart key separately to estab-
lish the communication channel for relayed messages
as shown in Fig. 1.
When the driver parks his vehicle and leaves the
parking lot, the attacker approaches the door handle
with the first attack device to seduce a fake signal to
the smart key. The second attack device is deployed
near the exit of the parking lot. When driver passes
the exit with smart key inside his pocket, the second
attack device instead of the key receives the signal
from the vehicle and sends the open command to the
vehicle. Consequently the attacker succeeds to en-
ter the vehicle. Similar fake signals are created when
the attacker starts the engine button to seduce a fake
start command. This relay attack model enables the
attacker to steal even the smart key is physically re-
mote from the vehicle (Francillon et al., 2011).
2.2 Distance Bounding
For the purpose of preventing the relay attacks
on PKES systems, the distance bounding protocol
(Brands and Chaum, 1993) is proposed to measure
the upper-bound distance (physical proximity) be-
tween the verifier (the smart key) and the prover (the
vehicle). Various distance bounding protocols are
proposed in recent years, emphasizing aspects such
as location privacy, provable security, noise chan-
nels, nonce space size, etc (Rasmussen and
ˇ
Capkun,
2008; Boureanu et al., 2013; Hancke and Kuhn, 2005;
Mitrokotsa et al., 2013).
Apart from the distance bounding protocol types,
methods for estimating the physical distance between
the verifier and the prover can be classified into var-
ious categories regarding to measurement types: (1)
phase of radio frequency signal; (2) received sig-
nal strength (RSS); (3) signal arrival time, etc (Ran-
ganathan and Capkun, 2017).
When the signal arrival time in each sensor is
available, both the TOA measurement and the TDOA
measurement can be generated that there exists two
options for estimating the physical distance. In or-
der to select a more appropriate measurement type
for the distance bounding protocol, analyses includ-
ing the superiorities and the defects of the TDOA and
the TOA based localization methods are discussed in
Section 3.
2.3 State Vector and Distance
Measurement
Assume that N time-synchronized sensors are
mounted on the vehicle at predetermined positions
x
i
= [x
i
,y
i
]
T
(i = 1,...,N) and passively receive the
signals transmitted from the smart key. The smart
key at position x = [x,y]
T
not only broadcasts the
acknowledgement (ACK) request to the PKES sys-
tem but also the time-stamp of the signal transmit-
ting time. The TOA measurements can be obtained by
subtracting the signal transmitting time and receiving
time measured by each sensor. The radius vector from
sensor s
i
to the smart key is denoted by r
i
= x −x
i
.
By multiplying with the signal propagation speed c,
the TOA measurement in sensor s
i
can be converted
into the range measurement
z
i
= ||r
i
||+ ν
i
= h
i
(x
i
) + ν
i
, i = 1,...,N (1)
where ν
i
∼N
0,σ
2
is the range measurement noise.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
796
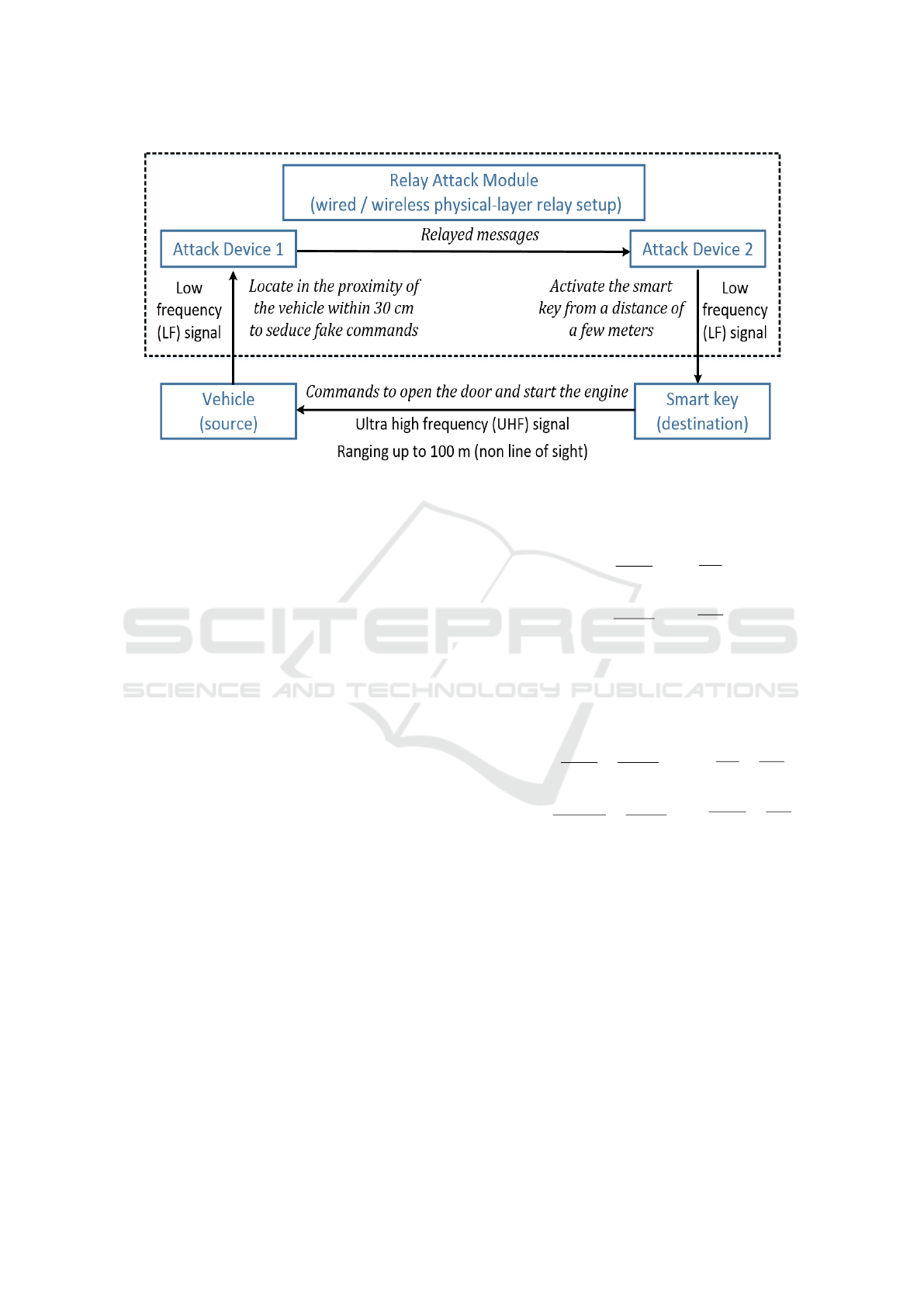
Figure 1: An example of relay attacks on PKES systems.
Let sensor s
N
be the common reference sensor in
the sensor network, the TDOA measurements in range
domain are given by
z
i,N
= (||r
i
||−||r
N
||) +(ν
i
−ν
N
)
= h
i
(x
i
) −h
N
(x
N
) +u
i,N
, i = 1,...,N −1 (2)
where u
i,N
∼N
0,2σ
2
is the range difference mea-
surement noise.
3 TIME-BASED MEASUREMENT
ANALYSIS
The superiority of the TDOA based localization
method (Gillette and Silverman, 2008; Ho and Chan,
1993) is that the clocks only need to synchronize with
the reference clock instead of the entire sensor net-
work. But the TDOA based methods inevitably suf-
fer from localization inaccuracy. A comparison be-
tween the measurement noises of TOA and TDOA by
eqs (1) and (2) suggests that the covariance of TDOA
is two times bigger than that of TOA. This can also
be numerically analyzed by comparing the measure-
ment uncertainty coverages of TOA and TDOA. The
measurement uncertainty coverage indicates an area
where the target can be at an arbitrary position inside,
which can be evaluated by the inverse of Fisher infor-
mation matrix (FIM) (Bar-Shalom et al., 2004; Bar-
Shalom et al., 2011)
P
k
=
H
T
k
R
k
H
k
−1
, (3)
where H
k
is the Jacobian matrix and R
k
is the mea-
surement noise covariance matrix. For TOA-based
methods, the Jacobian matrix and measurement noise
covariance matrix are given by
H
TOA
k
=
∂h
1
(x
1
)
x
1
.
.
.
∂h
N
(x
N
)
x
N
=
r
1
||r
1
||
.
.
.
r
N
||r
N
||
, (4)
R
TOA
k
= σ
2
I
N
, (5)
where I
n
indicates an n×n identity matrix. Similarly,
the Jacobian matrix and measurement noise covari-
ance matrix for TDOA based methods are given by
(Kaune et al., 2011; Xie et al., 2018)
H
T DOA
k
=
∂h
1
(x
1
)
x
1
−
∂h
N
(x
N
)
x
N
.
.
.
∂h
N
(x
N−1
)
x
N−1
−
∂h
N
(x
N
)
x
N
=
r
1
||r
1
||
−
r
N
||r
N
||
.
.
.
r
N−1
||r
N−1
||
−
r
N
||r
N
||
,
(6)
R
T DOA
k
= 2σ
2
1 0.5 ··· 0.5
0.5 1 ··· 0.5
.
.
.
.
.
.
.
.
.
.
.
.
0.5 0.5 ··· 1
(N−1)×(N−1)
.
(7)
Given a situation where N = 6 sensors are
mounted on a vehicle and the smart key transmits the
UHF signal 5 m away from the vehicle center(sensor
s
3
position), the measurement uncertainty coverages
for both TOA and TDOA are illustrated in Fig. 2.
The measurement uncertainty coverage of TDOA is
significantly larger than that of TOA and even larger
the vehicle size, which suggests the inappropriateness
of using the TDOA measurement for distance bound-
ing protocol.
Time-based Countermeasures for Relay Attacks on PKES Systems
797

Figure 2: An example of measurement uncertainty coverage
comparison(σ = 0.3 m).
Another problem of constraining the TDOA mea-
surement for distance bounding protocol is that the
sensors are closely spaced. The standard hyper-
bola equation indicating the transmitter position for
a TDOA measurement is given by
x
2
a
2
−
y
2
b
2
= 1, (8)
which subjects to constraints of c
2
= a
2
+ b
2
and
c > a. The distance between sensor s
1
and sensor
s
2
is 2c = 1.6 m in Fig. 2, and the corresponding
TDOA measurement is 2a = 1.48 m. Since the sen-
sors are not perfect, the TDOA measurement is usu-
ally corrupted by the sensor noise with a standard de-
viation
√
2σ. Therefore the noise-corrupted TDOA
measurement is (2a +
√
2σ) ≈ 1.9 m > 2c, which vi-
olates the hyperbola constraint. The TDOA based lo-
calization algorithms cannot be applied under such
circumstances, otherwise an inaccurate result can be
expected.
Therefore the TOA measurement is studied in this
paper. Various TOA based localization methods are
discussed detailedly in the following sections.
4 TOA-BASED ESTIMATION
The least square approach has been widely studied
in the TOA measurement-based target localization
(Smith and Abel, 1987; Cheung et al., 2004a; Che-
ung et al., 2004b; Cheung and So, 2005; Stoica and
Li, 2006; Beck et al., 2008). The methods in (Smith
and Abel, 1987; Stoica and Li, 2006) provide a simple
but efficient solution by neglecting the quadratic con-
straint, which is called unconstrained squared-range-
based LS estimate. The constrained squared-range-
based LS estimate in (Beck et al., 2008) improves the
localization accuracy by introducing a Lagrange mul-
tiplier and the solution is obtained through a bisection
algorithm, which makes it computationally expensive.
Both the USR-LS method and the CSR-LS method
require only one set of TOA measurements. The pro-
posed multiple-transmission method require the vehi-
cle owner pressing the smart key multiple times such
that multiple sets of TOA measurements are gener-
ated and used for improving the estimation accuracy.
Detailed descriptions for the above methods are pre-
sented in the following.
4.1 USR-LS Method
The essence of least square is to estimate the optimal
smart key position by minimizing the residual
min
N
∑
i=1
||x −x
i
||
2
−z
2
i
2
= min
N
∑
i=1
(x −x
i
)
2
+ (y −y
i
)
2
−z
2
i
2
= min
N
∑
i=1
−2x
i
x −2y
i
y + x
2
+ y
2
+ x
2
i
+ y
2
i
−z
2
i
2
,
(9)
which can be expressed by a matrix form as
L(ω) = (Aω −b)
T
(Aω −b), (10)
where
A =
−2x
1
−2y
1
1
.
.
.
.
.
.
.
.
.
−2x
N
−2y
N
1
,ω =
x
y
x
2
+ y
2
, (11)
b =
z
2
1
−(x
2
1
+ y
2
1
)
.
.
.
z
2
N
−(x
2
N
+ y
2
N
)
. (12)
The solution of L(ω) can be obtained by
∂L(ω)
∂ω
= 2A
T
Aω −2A
T
b = 0, (13)
and the corresponding optimal solution is
ˆ
ω =
A
T
A
−1
A
T
b. (14)
The solution
ˆ
ω does not follow the quadratic con-
straint. For instance, the estimated variable vector for
Fig. 2 is
ˆ
ω =
−3.99
3.78
25.67
, (15)
where (−3.99)
2
+ (3.78)
2
= 30.21 6= 25.67 and fails
to follow the quadratic constraint.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
798

4.2 CSR-LS Method
The CSR-LS method minimizes the quadratic func-
tion in eq (10) subjecting to a quadratic constraint
such that
L(ω) = {(Aω −b)
T
(Aω −b) : ||x||
2
= x
2
+ y
2
},
(16)
which is equivalent to minimize the Lagrangian
L(ω,λ) = (Aω −b)
T
(Aω −b) + λ(2f
T
ω + ω
T
Dω),
(17)
where
f =
0
0
−0.5
,D =
1 0 0
0 1 0
0 0 0
, (18)
and λ is the Lagrange multiplier.
Similarly, the solution of L(ω,λ) can be obtained
by
∂L(ω,λ)
∂ω
= 2(A
T
A+λD)ω−2A
T
b+2λf = 0, (19)
and the corresponding solution is
ˆ
ω(λ) = (A
T
A + λD)
−1
(A
T
b −λf). (20)
The solution
ˆ
ω(λ) subjects to the quadratic constraint
φ(λ) ≡ 2f
T
ˆ
ω(λ) +
ˆ
ω(λ)
T
D
ˆ
ω(λ) = 0. (21)
The method in (Cheung et al., 2004b) manipulates eq
(21) and transforms it into a five-root equation, and
λ is determined by a complicated root finding proce-
dure.
The optimization in eq (16) leads to a nonconvex
problem. There exists multiple local optima such that
a global optimum can be hardly obtained. The method
in (Beck et al., 2008) provides an efficiently and glob-
ally optimal solution by converting it into a general-
ized trust region subproblem (GTRS) (Mor
´
e, 1993).
According to GTRS, function φ(λ) is strictly decreas-
ing over interval
I
PD
=
−
1
λ
1
(D,A
T
A)
,∞
, (22)
where λ
i
(E,F) = λ
i
(F
−1/2
EF
−1/2
) indicates the ith
eigenvalue of F
−1/2
EF
−1/2
(ordered increasingly).
Therefore the solution for eq (21) can be obtained by
applying a bisection algorithm over interval I
PD
in-
stead of applying the complicated root finding proce-
dure. More details for the CSR-LS method are avail-
able in (Beck et al., 2008).
4.3 Multiple-transmission Method
The smart key in PKES systems is powered by an em-
bedded battery. In order to save the energy consump-
tion as well as prolong the service time of the bat-
tery, the vehicle owner is recommended to press the
smart key only once to activate the PKES system. The
USR-LS method and the CSR-LS method are desig-
nated to optimize the estimation accuracy under the
assumption of single signal transmission. For situ-
ations where the estimation accuracy dominates the
evaluation criteria, multiple signal transmissions from
the smart key contribute to improving the estimation
accuracy since more information is accumulated. In
these cases, the vehicle owner is recommended to
press the smart key M (M > 1) times. Each trans-
mission generates a set of TOA measurements and all
TOA measurement sets are mutually uncorrelated and
independent. The method for handling the multiple
signal transmissions is proposed and summarized in
the following:
1) The first TOA measurement set is used for the
CSR-LS method to obtained the state mean of an
initial track
ˆ
x. The FIM is calculated to obtain the
state covariance of the initial track
ˆ
P.
2) The other (M −1) TOA measurement sets are used
by EKF to serially update the track state
ˆ
x and
ˆ
P.
The TOA measurement generated by the j th sen-
sor in the ith transmission is denoted as z
i
j
. The
pseudo code for the serial EKF update is shown in
Algorithm 1.
Algorithm 1: Serial EKF update.
1: for i = 2 : M do
2: for j = 1 : N do
3:
¯
x =
ˆ
x,
¯
P =
ˆ
P
4: H
j
= ∂h
j
(
¯
x)/∂
¯
x
5: S
j
= H
j
¯
PH
T
j
+ σ
2
6: K
j
=
¯
PH
T
j
S
−1
j
7:
ˆ
x =
¯
x + K
j
(z
i
j
−h
j
(
¯
x))
8:
ˆ
P =
¯
P −K
j
H
j
¯
P
9: end for
10: end for
5 SIMULATION
The simulation settings of the sensor deployment and
sensor noise are identical to that of in Fig. 2, where
N = 6 sensors are mounted on the vehicle and the
smart key is located 5 m from the vehicle center. The
Time-based Countermeasures for Relay Attacks on PKES Systems
799

standard deviation of the TOA measurement noise is
σ = 0.3 m. The simulation includes 100 Monte Carlo
trials. In each trial, the USR-LS method, the CSR-LS
method and the multiple-transmission method (with
M = 2) are all applied to estimate the smart key po-
sition. The estimation accuracy is evaluated by root
mean square error (RMSE). In order to achieve a more
intuitive simulation result, the RMSE at every posi-
tion of the surveillance area is calculated. The simu-
lation results are shown in Figs. 3-5. As can be seen
that the numerical results are presented by RMSE dis-
tributions in which detailed RMSE values are distin-
guished by a color bar.
The smart key locates at position [−4,3]
T
. The
corresponding RMSE values for USR-LS, CSR-LS
and multiple-transmission are 1.11 m, 0.6331 m and
0.4348 m, respectively. The multiple-transmission
method delivers the most accurate estimation at the
costs of higher computational load and more energy
consumption. A summary for the three estimation
methods are listed in Table 1. According to Table
1, the comparison between the USR-LS method and
the CSR-LS method indicates a trade-off between
the computational load and estimation accuracy. The
comparison between the CSR-LS method and the
multiple-transmission method indicates a trade-off
between energy consumption and estimation accu-
racy.
s
1
s
2
s
3
s
4
s
5
s
6
-4 -2 0 2 4
x axis(m)
-3
-2
-1
0
1
2
3
y axis (m)
0.4
0.6
0.8
1
1.2
X: -4
Y: 3
Level: 1.11
Figure 3: RMSE distribution of the USR-LS method.
6 CONCLUSION
The distance bounding protocol was proposed to pro-
tect PKES systems from the relay attacks by esti-
mating the physical distance between the vehicle and
the smart key. The effectiveness of distance bound-
ing protocol relies heavily on the estimation accu-
racy. In this paper, three TOA based position estima-
tion methods such as USR-LS, CSR-LS and multiple-
transmission are reviewed and proposed to validate
s
1
s
2
s
3
s
4
s
5
s
6
-4 -2 0 2 4
x axis(m)
-3
-2
-1
0
1
2
3
y axis (m)
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
X: -4
Y: 3
Level: 0.6331
Figure 4: RMSE distribution of the CSR-LS method.
s
1
s
2
s
3
s
4
s
5
s
6
-4 -2 0 2 4
x axis(m)
-3
-2
-1
0
1
2
3
y axis (m)
0.2
0.4
0.6
0.8
1
X: -4
Y: 3
Level: 0.4348
Figure 5: RMSE distribution of the multiple-transmission
method.
the estimation accuracy. Simulation results show that
trade-offs can be made among computational load,
estimation accuracy and energy consumption when
different methods are applied. Additionally hybrid
schemes that use combinations of the discussed meth-
ods enable the PKES system to operate more flex-
ibly under diverse environmental conditions will be
explored in future studies.
ACKNOWLEDGEMENT
This work was supported by Hanwha Systems Com-
pany under the contract U-17-017.
REFERENCES
Ahmad, U., Song, H., Bilal, A., Alazab, M., and Jolfaei, A.
(2018). Secure passive keyless entry and start system
using machine learning. In International Conference
on Security, Privacy and Anonymity in Computation,
Communication and Storage, pages 304–313.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
800

Table 1: TOA-based estimation summary.
Method Computational load Estimation accuracy Energy consumption
USR-LS low low low
CSR-LS medium medium low
Multiple-transmission high high high
Bar-Shalom, Y., Li, X. R., and Kirubarajan, T. (2004). Esti-
mation with applications to tracking and navigation:
theory algorithms and software. John Wiley & Sons.
Bar-Shalom, Y., Willett, P. K., and Tian, X. (2011). Track-
ing and data fusion. YBS publishing.
Beck, A., Stoica, P., and Li, J. (2008). Exact and approxi-
mate solutions of source localization problems. IEEE
Transactions on signal processing, 56(5):1770–1778.
Boureanu, I., Mitrokotsa, A., and Vaudenay, S. (2013). Se-
cure and lightweight distance-bounding. In Interna-
tional Workshop on Lightweight Cryptography for Se-
curity and Privacy, pages 97–113. Springer.
Brands, S. and Chaum, D. (1993). Distance-bounding pro-
tocols. In Workshop on the Theory and Applica-
tion of of Cryptographic Techniques, pages 344–359.
Springer.
Cheung, K. W., Ma, W.-K., and So, H.-C. (2004a). Ac-
curate approximation algorithm for toa-based max-
imum likelihood mobile location using semidefinite
programming. In 2004 IEEE International Confer-
ence on Acoustics, Speech, and Signal Processing,
volume 2, pages ii–145. IEEE.
Cheung, K. W. and So, H.-C. (2005). A multidimensional
scaling framework for mobile location using time-of-
arrival measurements. IEEE transactions on signal
processing, 53(2):460–470.
Cheung, K. W., So, H.-C., Ma, W.-K., and Chan, Y.-T.
(2004b). Least squares algorithms for time-of-arrival-
based mobile location. IEEE Transactions on Signal
Processing, 52(4):1121–1130.
Francillon, A., Danev, B., and Capkun, S. (2011). Re-
lay attacks on passive keyless entry and start systems
in modern cars. In Proceedings of the Network and
Distributed System Security Symposium (NDSS). Ei-
dgen
¨
ossische Technische Hochschule Z
¨
urich, Depart-
ment of Computer Science.
Gillette, M. D. and Silverman, H. F. (2008). A linear
closed-form algorithm for source localization from
time-differences of arrival. IEEE Signal Processing
Letters, 15:1–4.
Hancke, G. P. and Kuhn, M. G. (2005). An rfid distance
bounding protocol. In First International Conference
on Security and Privacy for Emerging Areas in Com-
munications Networks (SECURECOMM’05), pages
67–73. IEEE.
Ho, K. and Chan, Y. (1993). Solution and performance anal-
ysis of geolocation by TDOA. IEEE Transactions on
Aerospace and Electronic Systems, 29(4):1311–1322.
Kaune, R., H
¨
orst, J., and Koch, W. (2011). Accuracy anal-
ysis for TDOA localization in sensor networks. In In-
formation Fusion (FUSION), 2011 Proceedings of the
14th International Conference on, pages 1–8. IEEE.
Mitrokotsa, A., Peris-Lopez, P., Dimitrakakis, C., and Vau-
denay, S. (2013). On selecting the nonce length in
distance-bounding protocols. The Computer Journal,
56(10):1216–1227.
Mor
´
e, J. J. (1993). Generalizations of the trust region prob-
lem. Optimization methods and Software, 2(3-4):189–
209.
Patel, J., Das, M. L., and Nandi, S. (2018). On the security
of remote key less entry for vehicles. In 2018 IEEE
International Conference on Advanced Networks and
Telecommunications Systems (ANTS), pages 1–6.
Ranganathan, A. and Capkun, S. (2017). Are we really
close? verifying proximity in wireless systems. IEEE
Security & Privacy.
Rasmussen, K. B. and
ˇ
Capkun, S. (2008). Location privacy
of distance bounding protocols. In Proceedings of the
15th ACM conference on Computer and communica-
tions security, pages 149–160. ACM.
Smith, J. and Abel, J. (1987). Closed-form least-squares
source location estimation from range-difference mea-
surements. IEEE Transactions on Acoustics, Speech,
and Signal Processing, 35(12):1661–1669.
Stoica, P. and Li, J. (2006). Lecture notes-source localiza-
tion from range-difference measurements. IEEE Sig-
nal Processing Magazine, 23(6):63–66.
Xie, Y., Lee, J. H., and Song, T. L. (2018). Analysis for
reference sensor selection in time difference of arrival-
based localisation. Electronics Letters, 54(25):1454–
1456.
Time-based Countermeasures for Relay Attacks on PKES Systems
801
