
Secret Verification Method Suitable for the Asymmetric Secret
Sharing Scheme
Takato Imai and Keiichi Iwamura
Faculty of Engineering, Tokyo University of Science, 6-3-1 Niijuku, Katsushika-ku, Tokyo, 125-8585, Japan
Keywords: Secret Sharing Scheme, Asymmetric, Verification, Cloud.
Abstract: Conventional secret sharing schemes, such as Shamir's secret sharing scheme, cannot prevent the leak of
shares when they are deposited on servers. In contrast, in an asymmetric secret sharing scheme, the owner of
the secret has a stronger authority than the server, and the number of servers storing the share can be set to
less than k. Therefore, even if all the shares stored in the server leak, the secret is not leaked. This can prevent
the leakage of secrets from attacks on servers. In the conventional secret sharing scheme, a correct secret
cannot be reconstructed if the attacker outputs a false share at the time of reconstruction by hijacking the
server. This problem cannot be addressed even if asymmetric secret sharing is used. Therefore, we extend the
asymmetric secret sharing scheme in a manner enabling the owner to detect a secret when an attacker outputs
a false share. In the proposed scheme, a server is not required to store information other than the share if n >
k. In other words, no burden is imposed on the server for verification. In addition, the hijacked servers can be
identified under certain conditions, realizing an efficient verification method for secrets that is suitable for the
asymmetric secret sharing scheme.
1 INTRODUCTION
In recent years, the utilization of big data using cloud
computing has garnered attention for the creation of
new businesses, including e-business. Cloud
computing can distribute and store a user's data in a
virtual mass storage consisting of multiple servers on
a network, called cloud, and access the data from
anywhere through the network as required by the
user. However, when data are deposited in the cloud,
the data must be encrypted to render it resistant to
information leakage. In addition to encrypting and
storing data, a function of the secret calculation
capable of performing arithmetic processing while
concealing individual data using concealed data
distributed and stored in the cloud is required. Use of
the secret sharing scheme as a method of realizing
such data concealment and concealment calculation
has garnered attention. In secret sharing, the original
secret is distributed into n pieces, called share, and
can be reconstructed by collecting k (k
≦
n) shares.
However, from the less than k shares, no secret. The
(k, n) threshold secret sharing scheme (hereinafter
called the Shamir scheme) by Shamir is well known
as one of these secret sharing schemes (Shamir,
1979). A conventional secret sharing system,
including the Shamir scheme, consists of n data
servers that store shares, a dealer that distributes a
secret, and a restorer that restores the secret. That is,
at the time of distribution, the owner of the secret
distributes it as a dealer or the distribution of the
secret is requested from a dealer who appears only at
the time of secret distribution. The dealer then
performs a secret distribution operation to calculate
the n shares. The shares are stored separately in n data
servers. The restorer can reconstruct the secret by
collecting k shares among the distributed n shares.
However, k servers are attacked without the secret
owner’s knowledge because the conventional secret
sharing systems cannot prevent k or more shares from
being collected; hence, the shares are leaked, and the
secret is reconstructed. A scheme, called asymmetric
secret sharing scheme (Takahashi and Iwamura.,
2014); (Takahashi and Iwamura, 2013); (Sarathi Roy
et al., 2014), was also proposed. In this scheme, the
owner can generate up to k − 1 shares from one key.
In the secret sharing schemes other than the
asymmetric secret sharing scheme, each server is
generally equal, and the owner cannot prevent the
secret from being leaked from the server. In contrast,
in the asymmetric secret sharing scheme, if the owner
172
Imai, T. and Iwamura, K.
Secret Verification Method Suitable for the Asymmetric Secret Sharing Scheme.
DOI: 10.5220/0007958201720179
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 172-179
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

has more authority than the server, and the number of
servers storing the share is less than k, the secret will
not leak even if all the shares stored in the server are
leaked. That is, k or more shares are not leaked unless
the owner generates the share from one key; hence,
the owner of the secret can prevent the share leakage
by managing the key safely.Therefore, the
asymmetric secret sharing scheme is secure against
secret leakage; however, a problem that occurs is that
an attacker can output a false share at the time of
reconstruction by hijacking the server. The restorer
cannot reconstruct the correct secret, and the secret
cannot be verified. This problem cannot be solved
even if the asymmetric secret sharing scheme is used.
Meanwhile, the verification method of the
reconstructed secret in the conventional secret
sharing scheme often contains extra information,
called authenticator, other than the share to verify the
reconstructed secret. Consequently, a problem arises
involving an increase in the amount of information
managed by the server (Cabelllo et al., 2002); (Ogata
and Araki, 2013); (Ogata and Satoshi, 2013);
(Hoshino and Obana, 2015); (Zhu, 2017).
In addition, these methods often cannot calculate
in any finite field; therefore, the convenience is low.
In many verification methods, servers exchange
shares and authenticators and calculate to verify the
secret using their information at the time of
reconstruction, thereby increasing the amount of
communication and number of calculations (Al
Mahmoud, 2016). Thus, as a verification method that
does not use the authenticator, the method with
tamper resistance using public key cryptography
exists (Takahashi and Iwamura., 2014). However,
attacks against this are limited to the chosen
ciphertext attack, and the attacker repeatedly sends
his/her own fake ciphertext to the server and analyzes
the message and timing returned by the server to
obtain the secret key and plaintext. Therefore, the
conventional verification method for secrets is not
efficient and often not applicable in any case.
We propose herein an efficient verification
method for secrets by extending the asymmetric
secret sharing scheme. The extension is realized by
enabling the owner to generate not only the shares,
but also the server ID from the key. This allows the
owner to verify the restored secret even if the attacker
outputs a false share. Additionally, if n > k, each
server is not required to store information other than
the shares; that is, no burden is imposed on the server
for verification. Furthermore, when k + u servers
exist, all the attacked servers can be identified if the
number of e servers that outputs a false share is u > e.
As mentioned earlier, our verification method for
secrets having less calculation and communication,
which can specify the fraudulent server is realized.
Section 2 describes various conventional methods
for verifying the recovered secret; Section 3 presents
the related works required to understand our proposed
scheme; Section 4 denotes the details of Proposed
Scheme 1, where no information other than the share
is required when n > k.
2 CONVENTIONAL METHOD
2.1 Authenticator Method by
Exponentiation of Secret (Cabelllo
et al., 2002); (Ogata and Araki,
2013)
(Cabelllo et al., 2002) or
(Ogata and
Araki, 2013) is generated as an authenticator.
However, they cannot be calculated in any finite field.
In particular, in the scheme described in (Cabelllo
et al., 2002), the probability of an attacker's success is
1 when
. For example, if an attacker uses false
shares for the secret and the authenticator, false secret
and false authenticator
are
reconstructed. In this case, the attacker must set
, such that the fraud is successful. However, the
attacker can always realize
when
.
Therefore, the probability of the attacker’s success is
1. This method is less convenient because the bit
string used by the computer is often an element of GF
(
). Another problem is that the storage capacity of
each server increases by storing the share of the
authenticator. Similarly, in the case of the method in
(Ogata and Araki, 2013), when
, the
convenience is increased compared to the method in
(Cabelllo et al., 2002) because the attacker's success
probability is 1; however, it also has a restriction on
the finite field in addition to storage capacity
increases.
2.2 First Section Authenticator Method
for Bit String Decomposition of
Secret (Ogata and Satoshi, 2013);
(Hoshino and Obana, 2015)
Split the secret s on GF (2
) in half, divide the bit
strings = (s
1
,s
2
) ∈ GF(2
n
) , and distribute secret s
and authenticator
= s
1
∙s
2
using the secret sharing
scheme. If the recovered secret
and the
authenticator
are
= s
1
∙s
2
, the information
restored is valid. If they do not match, the information
Secret Verification Method Suitable for the Asymmetric Secret Sharing Scheme
173

restored is invalid. This cannot be applied to arbitrary
bit sequences. In the scheme presented in (Ogata and
Satoshi, 2013), it is valid only when the bit length is
even, and the secret is
. In addition, the
method in (Hoshino and Obana, 2015) decomposes a
secret into N bits; however, it is effective only when
, and cannot set an arbitrary bit
sequence. Furthermore, the storage capacity increases
because each server required information other than
the shares of the secret.
2.3 Authenticator Method using
Functions and Random Numbers
on Share (Zhu, 2017)
The random number b and
are generated in
addition to the polynomial
of the k − 1-th
equation related to the secret s. The shares of
and
are distributed to each server. Additionally,
at the time of restoration, the restorer restores
and
using Lagrange's interpolation
formula. Subsequently, if a random number b exists
that satisfies
, the secret s is restored.
However, a secret can be found by most k − 2
attackers instead of k − 1. As mentioned in Section 1,
an authenticator exists in addition to the sharing of
and
. Therefore, the storage capacity of the
server is increased.
2.4 Method of Broadcasting
Authenticator (Al Mahmoud, 2016)
Each server divides the received share
. Each server stores
, and
is the information
for verification. Each server prepares
of the k
− 1 linear expression such that
.
Furthermore, each server uses the random numbers
such that
.
Additionally, expression
is prepared.
Subsequently,
is calculated, and
are calculated. Each server
broadcasts to each other. At the time of restoration,
from the
collected by each server,
this test verifies whether
holds. If it holds, then
is correct, and each server
restores the secret S.
2.5 Method using Public Key
Encryption (Takahashi and
Iwamura, 2014)
Assuming an attacker, called overlap-joint tampering,
the attacker can additionally obtain shares that are not
subject to tampering as input. In addition, the purpose
of the attacker is to use the decryption oracle, receive
a share of a certain message m, and generate a share
that can be reassembled into a message related to m.
It performs a selective ciphertext attack, but supports
it using a secure public key cryptosystem (IND-CCA
secure). It offers computational security; however, it
is limited to the selected ciphertext attack, and the
number of attackers is not concretely shown.
3 PRELIMINARIES
3.1 Shamir’s Secret Sharing Scheme
[Share Generation]
Calculate n shares from a secret s and distribute the
shares to n servers. Hereinafter, the calculation is
performed with the following prime number p as a
modulus:
Choose an arbitrary prime number p such that s <
p and n < p.
Select different n values from
and set server ID
.
From
, k −1 random numbers
are
generated, and the following k − 1-order polynomial
is created.
(1)
Substitute n server ID
for
and
calculate n shares
.
(2)
Distribute shares to each server. Server IDs
are public information.
[Reconstruction]
Let
be the share used for
reconstruction. Furthermore, let
be
the server ID corresponding to the share.
The restorer collects k
and obtains s using
the Lagrange's interpolation formula.
3.2 Lagrange's Interpolation Formula
Let
be the server ID. In general,
is public information, and
is a share output from
each server. Therefore, if the share
output from k
servers and its server ID
are known, the following
equation is obtained, and secret s can be obtained by
substituting.
ICE-B 2019 - 16th International Conference on e-Business
174

(3)
However, if an attacker sends a fake share
instead of
,
shown in (4) is calculated,
where
(4)
That is, not the secret , but the incorrect secret
is
reconstructed such as follows:
Furthermore, if the server ID
used in the
Lagrange's interpolation formula is known, the
attacker can continuously manipulate false secret
.
For example, if the server
transmits false share
for the first time, and the server
transmits false share
for the second time,
the secret is reconstructed as follows:
(5)
(6)
At this time, the attacker can adjust
according to Eqs. (7) and (8) such that the difference
between
becomes 0. In this case,
false secret
can be repeatedly restored.
(7)
(8)
3.3 Asymmetric Secret Sharing Scheme
The asymmetric secret sharing scheme is a secret
sharing scheme in which the owner of the secret uses
pseudorandom numbers generated using the key as
the shares. The asymmetric secret sharing scheme has
been proven to exhibit computational security
depending on the encryption method.
is
used.
[Asymmetric Secret Sharing Scheme].
Select t servers (t < k) from n servers, and call these a
key server. The key server contains no share, and
contains only a key to generate pseudorandom
numbers. The n − t servers other than the key server
are called data servers, and they store the calculated
shares. However, n − t < k. Furthermore, the owner
with a secret has one key, and all keys of the
key server are generated from. Additionally,
is assigned to m secrets
for data identification.
represents the encryption of using key .
(Takahashi and Iwamura, 2014).
[Share Generation]
The owner generates t keys
for t
key servers using as follows:
(9)
The owner generates a pseudorandom number
as
follows using the data identifier
of the secret
.
are shares
of
(10)
The owner determines coefficients
of Eq. (1).
The owner solves the following equations using
and
and
determines the remaining coefficients,
:
(11)
(12)
The owner calculates the remaining shares
using Eq. (1) with the determined
coefficients and sends
and
to the data
servers
.
[Reconstruction]
The restorer, who reconstructs the secret
, selects
any k − t server from the n − t data servers and sends
the data identifier
of the secret
to the
selected server.
The selected data server
sends share
corresponding to
to the restorer.
The restorer requests t shares to the owner.
When the owner permits the restorer to restore,
is generated from the using
Eq. (9), and the pseudorandom number
is
generated from Eq. (10) to be sent to the restorer.
The restorer who receives share and
pseudorandom numbers reconstructs secret
using
the Lagrange's interpolation formula.
Secret Verification Method Suitable for the Asymmetric Secret Sharing Scheme
175

4 PROPOSED SCHEME
The attacker can set the difference between the false
secrets shown in Eq. (7) to 0 because he can calculate
using public server ID
.
Therefore, we extend the asymmetric secret sharing
scheme in which the owner can generate and hide
only the share, to enable the owner to generate and
hide the server ID of the key server as well. However,
the server ID of the data server is public. Furthermore,
the extended asymmetric secret sharing scheme as the
proposed scheme 1 assumes .
4.1 Extended Asymmetric Secret
Sharing Scheme 1 (N > K)
4.1.1 [Share Generation]
1. The owner generates two sets of t key server’s
keys
and
using
as follows, where is a constant, and is a
concatenation of and .
(13)
2. The owner generates pseudorandom numbers
and
using the data identifier
of the
secret
.
(14)
3. The owner uses
generated in 2 as the server ID
for the key server and
as the
share
of
4. The owner performs processing 3–5 using
in
Share Generation, as shown in Section 3.3. The
owner sends
to the data server.
4.1.2 [Reconstruction and Verification]
1. Let ). The restorer who
reconstructs the secret
sends the data identifier
of the secret
to all data servers.
2. The data server
sends the shared
corresponding to
to the restorer.
3. The restorer requests t shares to the owner.
4. When the owner permits the restorer to restore,
are generated from
using Eq. (13), and
are
generated from Eq. (14).The owner then sends
them to the restorer.
5. The restorer changes the k − t combinations
received from the data server and reconstructs
secrets in addition to the t sets of
and
generated by the owner. Furthermore, he verifies
that the reconstructed results match each other. If
all results do not match, all recovered secrets are
not adopted. The matched reconstruction results
are adopted.
4.2 Security Verification
As shown in Section 3.3, the owner can control the
generation of shares in the asymmetric secret sharing
by securely managing their own key: hence, k shares
will not be leaked without the owner's knowledge.
Similarly, in the case of the extended asymmetric
secret sharing scheme 1 shown in Section 4.1, k
shares will not be leaked without the owner’s
knowledge because the owner must give permission
at the time of reconstruction. Therefore, the security
concerning share leakage can be regarded the same.
The feature of extended asymmetric secret sharing
scheme 1 is that the server ID
is created and
concealed by the owner. Consequently, an attacker
who is not permitted to reconstruct will not know the
server ID used to generate the share; therefore, he
cannot manipulate the difference between the
reconstructed secrets, as shown in Eq. (7).
Therefore, even if the attacker manipulates the
share from
to
, the difference between
all the reconstructed secrets cannot be made to match.
As a result, the unmatched secrets are not adopted as
incorrect values.
We will explain the principle of security for
verification using simple examples. For simplicity,
we assume herein that the owner is a restorer. For
example, in the case of, in
the Share Generation process, the owner generates
and hides server ID
and the
corresponding share from the key. The server ID of
the data server is
(publicly known). Consider a
case in which two data servers
and
are hijacked
by an attacker at the time of reconstruction, and false
shares
are the output.
In this case, the combination of the two shares
received from the data server is changed, and
restoration is performed twice. The first time, secret
is reconstructed by the combination of
, and
the second time is reconstructed by the combination
of
. Here,
are the server IDs
generated by the owner, which the attacker is unaware
of. In this case,
is reconstructed the first time,
ICE-B 2019 - 16th International Conference on e-Business
176
and is reconstructed the second time as
follows:
(15)
(16)
Here, even if
are hijacked by the same
attacker, the attacker does not know
and
cannot set
as
=.
(17)
That is, if
is the entropy for , then
(18)
However, the example above is the case of, and
although it is understood that a false share is the
output, the incorrect server cannot be identified.
Next, if , three
data servers exist, and three shares can be used for
verification. Here, when
is hijacked and outputs a
false share
, the secrets reconstructed using
other correct shares are identical because
, and the secret reconstructed using the share
of
is a different value from the others. In this case,
an invalid data server
can be identified.
As the second example, when two data servers are
hijacked, all the reconstructed secrets are invalid
because they do not match. Therefore, assuming that
is the number of data servers that output false
shares, if , an unauthorized server can be
identified, and if , an unauthorized server
cannot be identified, although it can verify fraud.
Furthermore, when the restorer is not the owner,
the restorer who is permitted to restore a certain secret
, knows the key server IDs
, but
the key server ID
is for each i, which is different.
Therefore, even if an attacker knows the key
server's ID and shares regarding a secret, it cannot be
applied to other secrets.
In addition, the extended asymmetric secret
sharing scheme 1 has no restrictions on the finite field
because the secret is used as it is and not divided.
5 EVALUATION
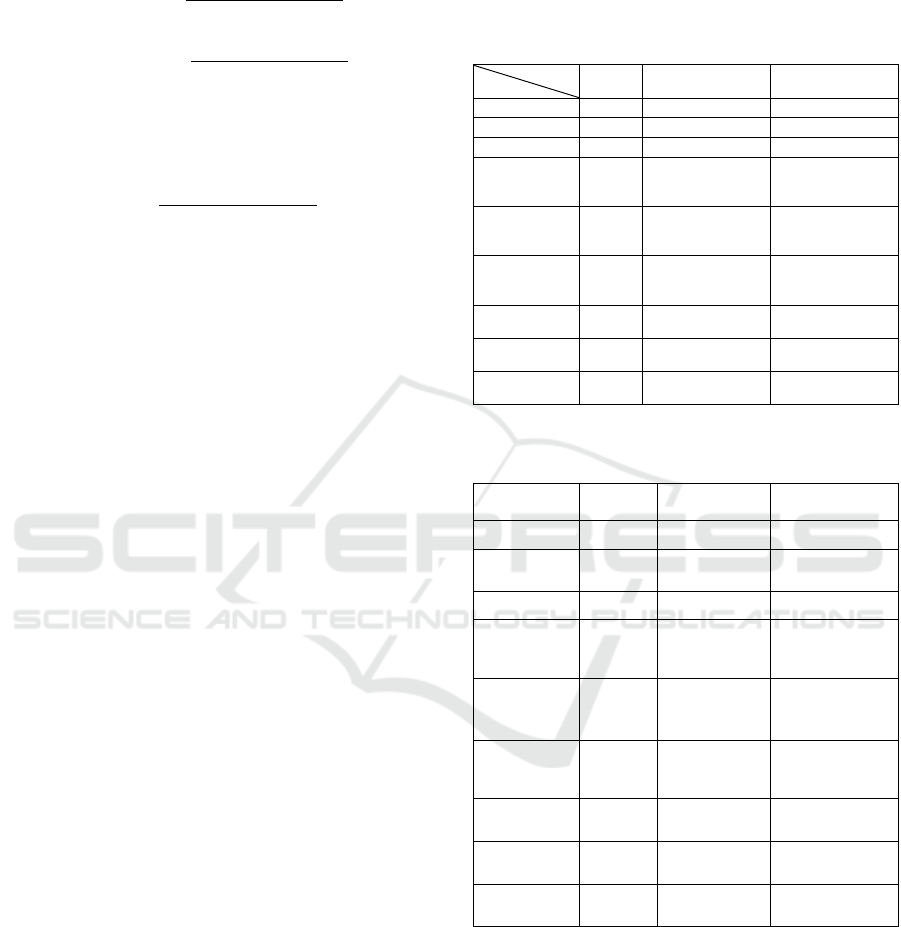
Tables 1 and 2 show the comparison between the
proposed scheme 1 and the conventional methods. In
Tables 1 and 2, “secret” implies the restriction on the
secret, and the maximum number of attackers implies
the maximum number of servers that can be hijacked.
In the proposed method 1, the maximum is
because .
Table 1: Comparison of the Proposed and Conventional
Methods.
Proposed
Conventional
(Cabello et al., 2002)
Conventional (Ogata
and Satoshi, 2013)
Condition
Secret
Any
Any
Any
Prime number
Any
Other than
Other than
Maximum
number of
attackers
Server's
memory
capacity
One share
of secret
Two shares of secret
and authenticator
Two shares of secret
and authenticator
Communication
amount
between servers
0
0
Server
complexity
0
0
Rogue server
detection
〇
×
×
Number of
reconstructions
u + 1
2
2
Table 2: Comparison of the Proposed and Conventional
Methods.
Proposed
Conventional
(Zhu, 2017)
Conventional (Al
Mahmoud., 2016)
Condition
Secret
Any
Only
Only
Prime number
Any
Any
Any
Maximum
number of
attackers
Server's
memory
capacity
One share
of secret
Two shares of
secret and
authenticator
One share+
One Authenticator
※5
Communication
amount
between servers
0
0
(※6)
Server
complexity
0
×
×
Rogue server
detection
〇
(※7)
Number of
reconstructions
u + 1
2
2
(※5)
(※6) Amount of communication that the server
sends
(※6)Amount of communication that the server receives
(※7)Calculation for processing to solve discrete logarithms
In evaluation, (Cabello et al., 2002) and (Ogata
and Satoshi, 2013) are representative in 2.1 and 2.2
and compared with the proposed scheme 1. The
method shown in 2.5 uses public key encryption;
hence, the amount of calculation is large, and the
assumed attack is different from those of other
Secret Verification Method Suitable for the Asymmetric Secret Sharing Scheme
177

methods. Therefore, the comparison is omitted
herein.
From Table 1, the proposed scheme has less data
stored by each server, and it is also possible to detect
unauthorized servers.
In addition, only the proposed method is not
limited as to the prime number that is the module in
calculation.
Tables 1 and 2 shows that the proposed scheme
only requires the share compared to the other method,
and the secret and prime number used are not restrics.
6 PRACTICALITY
Currently, individuals and companies are big data
societies with a lot of information. There are two
ways to save data: 1) using the on-premises type
servers owned by each individual, and 2) using the
cloud type servers deposited in a virtual environment
on the Internet.
Recently, individuals and many companies have
begun to use data storage systems such as
MicrosoftAzure, -Google Drive, and iCloud.
However, data on the cloud are the target of
malicious attackers and the leakage of customer
information has been in the news multiple times.
When a secret sharing scheme is used to protect
customer information, schemes other than
asymmetric secret sharing have no means of
preventing information leakage.
Therefore, as an example of application of our
proposed extended asymmetric secret sharing
scheme, we use it to protect customer information. In
this case, the customer, as the owner, distributes their
information using the extended asymmetric secret
sharing scheme, and manages keys securely. If the
number of shares deposited in the data server is k-1 or
less, the customer information is protected even if the
information stored in all the data servers leaks. In
addition, it is possible to efficiently confirm whether
the restored information has been falsified by our
extended asymmetric secret sharing scheme.
Therefore, the proposed scheme realizes safe and
low-cost customer service.
7 CONCLUSIONS
We proposed herein extended asymmetric secret
sharing schemes to verify secret reconstruction at
.
By concealing the server ID, we secured against
attack using the weak point of the Lagrange's
interpolation formula. Consequently, our schemes
can show the legitimacy of the reconstructed secret by
performing u + 1 times or 2 times the reconstruction
without using special functions, such as an
authenticator. Furthermore, the server held only the
share for which , and the secret and the finite
field used were not restricted.
REFERENCES
A. Shamir., 1979. How to share a secret, Communications
of the ACM, vol. 22, no. 11, pp. 612–613.
S. Cabello., C. Padró., G. Sáez., 2002. Secret sharing
schemes with detection of cheaters for a general access
structure, Designs, Codes and Cryptography, vol. 25,
pp. 175–188.
W. Ogata., T. Araki., 2013. Cheating detectable secret
sharing schemes for random bit strings, IEICE Trans.
Fundamentals, vol. E96-A, no. 11.
W. Ogata., T. Satoshi., 2013. Cheating detectable secret
sharing schemes for random bit strings, IEICE Trans.
Fundamentals, vol. E96-A, no. 11.
H. Hoshino., S. Obana., 2015. Almost optimum secret
sharing schemes with cheating detection for random bit
strings, Advances in Information and Computer
Security, Lecture Notes in Computer Science, vol. 9241,
Springer Verlag, pp. 213–222.
X. Zhu., 2017. Efficient (k, n) Secret sharing scheme secure
against k − 2 cheaters. International Conference on
Networking and Network Applications.
Q. Al Mahmoud., 2016. A novel verifiable secret
sharingwith detection and identification of cheaters’
group, I.J. Mathematical Sciences and Computing.
Narita Tasuku., KitagawaFuyuki., Yoshida Yusuke., Tanaka
Keisuke., 2019, Secret sharing satisfying computational
tamper resistance, SCIS.
S. Takahashi., K. Iwamura., 2014. Asymmetric
secretsharing scheme suitable for cloud systems, 2014
IEEE 11th Consumer Communications andNetworking
Conference, pp. 798–804, Las Vegas.
S. Takahashi., K. Iwamura, 2013. Secret sharing scheme
suitable for cloud computing, The 27th IEEE
International Conference on Advanced Information
Networking and Applications, pp. 530–537, Barcelona.
P. Sarathi Roy., A. Adhikari., R. Xu., K. Morozov., K.
Sakurai.,2014. An efficient t-cheater identifiable secret
sharing scheme with optimal cheater resiliency,
International Conference on Security, Privacy, and
Applied Cryptography, pp. 47–58.
Y. Liu., C. Yang., Y. Wang., L. Zhu., W. Ji., 2018.Cheating
identifiable secret sharing scheme using symmetric
bivariate polynomial, Information Sciences 453, pp.
21–29.
W. Ogata., T. Araki., 2017. Computationally secure
verifiable secret sharing scheme for distributing many
ICE-B 2019 - 16th International Conference on e-Business
178

secrets, IEICE Trans. Fundamentals, vol. E100–A, no.
1.
Y. Liu., Z. Wang., W. Yan., 2015. Linear (k, n) secret sharing
scheme with cheating detection, IEEE International
Conference on Computer and Information Technology;
Ubiquitous Computing and Communications;
Dependable, Autonomic and Secure Computing;
Pervasive Intelligence and Computing.
L. Harn., C. Lin., 2009. Detection and identification of
cheaters in (t, n) secret sharing scheme, Designs, Codes
and Cryptography, vol. 52, pp. 15–24.
H. Ghodosi., 2011. Comments on Harn-Lin’s cheating
detection scheme, Designs, Codes and Cryptography,
vol. 60, pp. 63–66.
T. Araki., 2007. Efficient (k, n) threshold secret sharing
schemes secure against cheating from n cheaters,
LectureNotes, In Computer Science, pp. 133–142.
Obana S., 2011. Almost optimum t-cheater identifiable
Secret sharing schemes. In Proceedings of
EUROCRYPT′11, LNCS, vol. 6632, pp. 284–302.
Springer-Verlag.
Backes M., Kate A., Patra A., 2011. Computational
verifiable secret sharing revisited. In: Proceedings of
ASIACRYPT′11, LNCS, vol. 7073, pp. 590–609.
Springer-Verlag.
Liu Y.X., Harn L., Yang Q.N., Zhang Y.Q., 2012. Efficient
(n, t, n) Secret sharing schemes. Journal of Systems and
Software,85(6), 1125–1132.
Kinnno Kazuhiro., 2012. Advantages and problems in the
use of cloud computing.
McDonald, K., 2010. Above the Clouds: Managing Risk in
the World of Cloud Computing, IT Governance
Publishing.
Mell, P., Grance T., 2011. The NIST Definition of Cloud
Computing (Draft), National Institute of Standards and
Technology (NIST) Special Publication 800-145
(Draft).
Weinman, J., 2011. Mathematical Proof of the Inevitability
of Cloud Computing, http://www.joeweinman.com/
Resources/Joe_Weinman_Inevitability_Of_Cloud.pdf.
Secret Verification Method Suitable for the Asymmetric Secret Sharing Scheme
179
