
Cooperative Energy Management Software for Networked Microgrids
Ilyes Naidji
1,2 a
, Olfa Mosbahi
2
, Mohamed Khalgui
2 b
and Abdelmalik Bachir
3
1
University of Tunis El Manar, Tunis, Tunisia
2
National Institute of Applied Sciences and Technology (INSAT), University of Carthage, Tunis 1080, Tunisia
3
LESIA Laboratory, University of Mohamed Khider, Biskra, Algeria
Keywords:
Energy Management Software, Microgrid, Coalition Formation, Stability, Energy Transfer.
Abstract:
Smart distribution systems are critical cyber-physical energy systems that consists of multiple networked mi-
crogrids (MGs) with a distributed architecture. The main problem behind these cyber-physical energy systems
is how to manage energy sources to have an efficient and economic energy supply. This paper proposes a
cooperative energy management software (EMS) for networked microgrids (MGs) by explicitly modeling the
cooperative behavior of MGs. The network of MGs is autonomously self-organized into multiple stable coali-
tions to achieve an efficient and economic energy exchange. The coalition consists of several MGs that ex-
change energy with a competitive energy prices to maximize their utility. We formulate the problem of energy
management in networked MGs by a coalition formation game between MGs. We develop a merge-and-split-
based coalition formation (MSCF) algorithm to ensure the stability of the formed coalitions and maximize the
profits of MGs. Then, we design an intra coalition energy transfer (ICET) algorithm for transferring energy
between MGs within the same coalition to minimize power loss. The simulation results demonstrate a satis-
factory performance in terms of profit maximization that exceeds 21% and in terms of power loss reduction
that exceeds 51%, thanks to the proposed cooperative energy management software.
1 INTRODUCTION
The architecture of smart distribution systems is be-
coming more and more complex after the appearance
of networked microgrids (MGs). Smart distribution
systems turn into several networked MGs that consists
of distributed energy resources (DERs). The smart
distribution system must operate in a reliable and safe
manner as in manufacturing systems (Gu et al., 2018),
(Khalgui et al., 2008) where the control system can
reconfigure the operation and adapt its behavior to
the related situation (Hafidi et al., 2018). Recently,
with the increasing integration of distributed energy
resources especially renewable energy, manifold MGs
may emerge within the distribution system, which
triggers the problem of energy management of multi-
ple networked MGs (Asarias and Pedrasa, 2017). The
most practical solution of this problem is to develop
an efficient energy management software (EMS) that
is responsible for the management of power sources
to provide a sufficient power supply to the end users
(Naidji et al., 2018).
a
https://orcid.org/0000-0001-8747-0766
b
https://orcid.org/0000-0001-6311-3588
The EMS has the objective to operate the power
generation efficiently and economically to supply the
end users and increase the reliability of the sys-
tem by proactively minimizing blackouts (Meskina
et al., 2017), (Meskina et al., 2018). At this point,
the energy management problem generates multiple
sub-problems such as operational cost optimization,
power loss reduction, energy consumption schedul-
ing or power supply availability (Abidi et al., 2017).
Thus, an intelligent distributed solution should be
looked for (Khalgui and Mosbahi, 2010) under energy
constraints (Aissa et al., 2019), (Ghribi et al., 2018)
which can be a multiobjective optimization (Lakhdhar
et al., 2019) in some situations. Several studies in the
literature addressed the energy management in net-
worked MGs by proposing different softwares with
different perspectives. The authors in (Wang et al.,
2015) propose a coordinated EMS of networked MGs.
The coordinated operation between MGs is formu-
lated as a stochastic bi-level problem with the objec-
tive to reduce the operational costs of both MGs and
DSO. In (Zamora and Srivastava, 2018), a voltage and
frequency control algorithm is designed using multi-
layer architecture in Networked MGs to regulate volt-
428
Naidji, I., Mosbahi, O., Khalgui, M. and Bachir, A.
Cooperative Energy Management Software for Networked Microgrids.
DOI: 10.5220/0007965604280438
In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 428-438
ISBN: 978-989-758-379-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

age magnitude and frequency, as well as output power
of the distributed generations (DGs). In (Nunna and
Doolla, 2013), a multi-agent system (MAS) based
EMS in networked MGs is proposed with the partic-
ipation of the different entities in the energy market.
In (Fathi and Bevrani, 2013), the energy consump-
tion scheduling in networked MGs is studied consid-
ering the uncertainty of load demand. In (Wu and
Guan, 2013), the energy management in networked
MGs is modeled by a decentralized partially observ-
able Markov decision process. A dynamic program-
ming solution is proposed to minimize the MG oper-
ational cost.
However, in most of the above existing research
efforts, the cooperative behavior of MGs has not been
explicitly modeled. Only interactions between MGs
and DSO have been considered which limits the gain
of MGs. The cooperation between MGs can be en-
sured by forming several coalitions. The coalition
consists of several MGs that exchange energy with a
competitive energy prices.
The studies in (Jadhav and Patne, 2017), (Gao
et al., 2018), (Cintuglu and Mohammed, 2017), (Ma
et al., 2018), (Du et al., 2018) demonstrate that the in-
terconnection of multiple MGs can improve the sys-
tem operation and control. In (Jadhav and Patne,
2017), a priority-based energy scheduling problem is
designed for multiple MGs. A non cooperative energy
competition game is designed to solve the problem. In
(Gao et al., 2018), a decentralized EMS is proposed to
control the operation of power exchange between the
DSO and MGs. The alternating direction method of
multipliers is used to solve the problem. In (Cintuglu
and Mohammed, 2017), a novel bidding behavior and
an auction architecture is proposed to enable compet-
itive negotiations between networked MGs and the
central aggregator. The authors in (Ma et al., 2018)
propose an online EMS for the DSO to control energy
scheduling of networked MGs using regret minimiza-
tion and online alternating direction method of mul-
tipliers. In (Du et al., 2018), a cooperative operation
model is proposed for multiple MGs where the whole
network is considered as a grand coalition to achieve
higher operation economy. However, even when the
cooperation is addressed, the stability of the formed
coalitions is not ensured. These limitations can re-
duce the gain of MGs and increase the cost including
power loss.
In this respect, the main contribution of this pa-
per is the proposal of a new cooperative energy man-
agement software in networked MGs using coali-
tional game theory to self-organize into multiple sta-
ble coalitions for maximizing the profits of MGs. We
develop a merge-and-split-based coalition formation
(MSCF) algorithm based on coalitional game theory
and merge and split rules to ensure the stability of the
formed coalitions. Then, we develop an intra coali-
tion energy transfer (ICET) algorithm to transfer en-
ergy between MGs that are in the same coalition. The
ICET algorithm aims to minimize power loss result-
ing from transferring energy in long distances. Sig-
nificant gains are obtained with the proposed energy
management software in terms of profit maximiza-
tion, thanks to the designed coalition formation algo-
rithm, and in terms of energy saving, thanks to the en-
ergy transfer algorithm. The originality of this paper
is threefold:
• The proposal of a cooperative energy manage-
ment software that ensures the cooperation be-
tween MGs by forming several stable coalitions.
• The maximization of the profits of MGs and re-
duction of power loss by the cooperation between
MGs.
• The control of complexity of the energy manage-
ment problem in networked MGs.
Section 2 presents the system model. Section 3
formulates the problem of energy management in net-
worked MGs with the proposed cooperative game
theoretic approach. Section 4 gives the proposed
methodology for solving the energy management
problem. Section 5 shows the simulation results and
finally Section 6 concludes this paper.
2 SYSTEM MODEL
This section describes the networked MGs system ar-
chitecture, the pricing scheme that allows to apply the
coalition formation, and the coalition formation pre-
liminaries.
2.1 Networked Microgrids Architecture
Consider a smart distribution system managed by the
distribution system operator (DSO). The system con-
sists of N networked MGs with distributed energy
resources (DERs) that are composed of: Distributed
generation (DG) units which can be conventional or
renewable generators, and energy storage systems
(ESSs). The distributed energy resources are respon-
sible for the power supply of the microgrid. We as-
sume that each microgrid has loads to serve. We also
assume that each microgrid has an energy manage-
ment software (EMS) that is responsible for the opti-
mization of power consumption and usage of DERs.
We organize MGs into groups (also called coali-
tions). Let Θ
j
i
denotes the i
th
MG belonging to the j
th
Cooperative Energy Management Software for Networked Microgrids
429

group (i.e., coalition). Let D(Θ
j
i
) be the total demand
of Θ
j
i
and S(Θ
j
i
) its total supply. The energy status
E(Θ
j
i
) of Θ
j
i
is given by the difference of total supply
and demand, i.e.,
E(Θ
j
i
) = S(Θ
j
i
) − D(Θ
j
i
) (1)
A positive value of energy status denotes that Θ
j
i
can
sell E(Θ
j
i
) amount of energy while a negative value
denotes that Θ
j
i
needs to purchase E(Θ
j
i
) amount of
energy from the distribution system. Therefore, the
set of all MGs can be grouped into three subsets that
are balanced MGs Λ = {λ
1
,...,λ
|Λ|
}, MGs with en-
ergy surplus Π = {π
1
,...,π
|Π|
} and MGs with energy
shortage Ψ = {ψ
1
,...,ψ
|Ψ|
}.
Conventionally, the energy transfer is carried out
between MGs and DSO. Consequently, this trans-
fer results in more power loss due to the existence
of transformers and the transmission loss due to the
Joule effect if the DSO is located within long dis-
tances to the microgrid. Furthermore, the energy
transfer between MGs and DSO is unprofitable to
MGs due to operator policy that imposes disadvan-
tageous energy prices (e.g., the operator buy in low
prices and sell in high prices).
An interesting alternative to achieve a cost effec-
tive energy management and minimize the power loss
is the cooperation between MGs by forming coali-
tions. The MGs inside the same coalition can ex-
change energy with a competitive energy price and
interact with the distribution system operator as a last
resort to minimize the power loss and reduce the en-
ergy cost. The networked MGs system is described
in Fig. 1. Each microgrid consists of distributed en-
ergy resources (DERs) such as distributed generation
(DG) units and energy storage systems (ESSs). Fur-
thermore, each microgrid is connected with the dis-
tribution system through a voltage transformer while
it is connected with the other MGs via a low volt-
age power line. With this architecture, a microgrid
can exchange power with another microgrid if there
is a transmission line between them, i.e., a low volt-
age power line. This energy exchange brings more
profit to both MGs since it is cheaper and more effi-
cient than exchanging with the distribution system.
2.2 Pricing Scheme for Coalition
Formation
The pricing scheme is an influential factor to perform
cooperation between MGs. Particularly, the coali-
tion formation process should justify the preference
of MGs over the DSO in energy exchange. The de-
sign of an inappropriate pricing scheme will result in
. . .
Voltage
transformer
Voltage
transformer
Voltage
transformer
Voltage
transformer
Voltage
transformer
Voltage
transformer
DSO
Medium voltagepower line
Communication line
Low voltage power line
DG
ESS
DG
ESS ESS
DG
DG DG DG
ESSESSESS
DGDistributed Generation
Energy Storage System ESS
Distribution System Operator DSO
Figure 1: Networked MGs system architecture.
disadvantageous outcome. The designed pricing
scheme must motivate a microgrid to cooperate with
other MGs by exchanging the energy surplus. Thus,
we have designed a motivating pricing scheme to en-
suring that forming coalitions between MGs is al-
ways more rewarding than exchanging with the DSO.
For instance, let us assume that α = 0.2$/kwh is
the energy selling price to the DSO, β = 0.4$/kwh
is the energy purchasing price from DSO and γ =
0.25$/kwh is the price of selling/purchasing energy
between MGs. Hence, a microgrid always prefers to
exchange energy with other MGs since it can save
0.05$/kwh in selling and 0.2$/kwh in purchasing by
exchanging energy to MGs instead of DSO. Thus, the
pricing scheme is designed as follows:
β > γ > α (2)
where we define σ as a threshold given by (γ−α) ≤ σ.
2.3 Coalition Formation Preliminaries
An interesting framework for coalition formation is
given in (Apt and Witzel, 2009) using merge-and-split
rules. To run the coalition formation game, the fol-
lowing preliminaries are required.
A coalition Ξ
k
j
is a set of players, i.e., MGs that
exchange energy in order to maximize their profits,
i.e.,
Ξ
k
j
= {Θ
j
1
,...,Θ
j
|Ξ
k
j
|
} (3)
where j is the coalition number and k is the collection
that the coalition belongs. A coalition is called the
grand coalition G if it is formed by all the set of pla-
ICSOFT 2019 - 14th International Conference on Software Technologies
430

yers N. A collection Ω
k
is any family of mutually
disjoint coalitions, i.e.,
Ω
k
= {Ξ
k
1
,...,Ξ
k
|Ω
k
|
} (4)
Various criteria exist in the literature to compare be-
tween collections or coalitions. In this paper, the
Pareto order is used for comparing collections. The
Pareto order is based on a preference operator which
is an order defined for comparing two collections Ω
k
and Ω
l
. We assume that we have a subset A ⊆ N. Let
us take two different partitions of the subset A as a
choice that are Ω
k
and Ω
l
. Therefore, Ω
k
Ω
l
denotes
that Ω
k
is preferred than Ω
l
in partitioning A.
In a collection Ω
k
, each player, i.e., MG Θ
j
i
∈ Ξ
k
j
has a utility function Φ(Θ
j
i
) which defines the payoff
of the player in a coalition Ξ
k
j
. Here in our case, as
more the MG Θ
j
i
exchanges energy in a coalition Ξ
k
j
,
the energy profit increases thus, the utility function
is at its best (max ) when the energy status of a MG
E(Θ
j
i
) in the coalition Ξ
k
j
approaches to zero, i.e.,
Φ(Θ
j
i
) =
(
max, if E(Θ
j
i
) = 0,
1
E(Θ
j
i
)
, otherwise
(5)
Ω
k
Ω
l
, i.e., Ω
k
is preferred than Ω
l
by Pareto
order, if
Φ(Θ
j
i
) ≥ Φ(Θ
g
i
) ∀ Θ
j
i
∈ Ξ
k
j
,Θ
g
i
∈ Ξ
l
g
(6)
with at least one strict inequality, i.e., a collection is
preferred by the players over another collection, if at
least one player is able to improve its utility without
decreasing the utility of the other players. Hence, the
merge and split rules for coalition formation can be
defined as follows:
Merge Rule: Merge any set of coalitions
{Ξ
k
1
,Ξ
k
2
,...,Ξ
k
|Ω
k
|
} if
|Ω
k
|
S
j=1
Ξ
k
j
{Ξ
k
1
,Ξ
k
2
,...,Ξ
k
|Ω
k
|
}
Split Rule: Split any coalition
|Ω
k
|
S
j=1
Ξ
k
j
if
{Ξ
k
1
,Ξ
k
2
,...,Ξ
k
|Ω
k
|
}
|Ω
k
|
S
j=1
Ξ
k
j
3 PROBLEM FORMULATION
This section gives the formulation of the energy man-
agement problem in networked MGs. Since the net-
worked MGs system is a cyber-physical one, the prob-
lem of energy management here needs to be solved
by an efficient software. The main problem here con-
sists of two sub-problems that are coalition formation
and energy transfer. The first sub-problem consists
of forming several stable coalitions between MGs to
optimize the power supply availability economically
and efficiently. A coalition formation game is formu-
lated for the cooperation between MGs to optimally
exchange the power surplus. The second sub-problem
consists of transferring energy in each formed coali-
tion. The energy transfer problem is formulated as a
power loss minimization problem to optimally trans-
fer energy in each coalition.
3.1 Coalition Formation Game
3.1.1 Challenge
Instead of sharing the power surplus with the DSO,
MGs can cooperate with others by forming several
coalitions to exchange their power surplus. Unbal-
anced power of each microgrid is purchased or sold
within coalition. After performing the energy transfer
within coalition, the rest of energy surplus or shortage
can be balanced by the DSO as a last resort.
3.1.2 Formalization
The coalitional game can be defined with the follow-
ing pair (N,v) that consists of a finite set of players
N (MGs in our case) and a characteristic function or
value v. The carachteristic function v : 2
N
→ R asso-
ciates a payoff v(Ξ
k
j
) for each coalition Ξ
k
j
, i.e.,
v(Ξ
k
j
) = min | S(Ξ
k
j
) − D(Ξ
k
j
) | (7)
The characteristic function v of a coalition Ξ
k
j
is de-
fined by the aggregated energy status in this coalition.
Thus, v(Ξ
k
j
) has its best value when the difference
between the total power demand and supply is mini-
mized. The members of the coalition Ξ
k
j
can distribute
this payoff among themselves. Here, as less as a mi-
crogrid exchanges energy with the distribution system
operator, it receives more payoff. A distributed coali-
tion formation game is given by specifying a value for
each coalition. The set of the formed coalitions form
the coalition structure CS, .i.e,
CS =
|Ω
k
|
[
j=1
Ξ
k
j
(8)
The coalition structure payoff ρ(CS) is the sum of the
local coalition payoffs, i.e.,
ρ(CS) =
|Ω
k
|
∑
j=1
v(Ξ
k
j
) (9)
Cooperative Energy Management Software for Networked Microgrids
431
3.2 Energy Transfer
The energy transfer (ET) among MGs in a coalition
should have a minimum power loss P
Ξ
k
j
L
. The overall
power loss P
Ξ
k
j
L
of a coalition Ξ
k
j
while transferring
power among MGs is given by
P
Ξ
k
j
L
= −
∑
i,e∈Ξ
k
j
P
L
(i,e) (10)
where P
L
(i,e) is the power loss resulting from trans-
ferring energy over transmission lines between Θ
j
i
and Θ
j
e
. Note that, the power loss is defined as a
characteristic function of a coalition Ξ
k
j
instead of a
microgrid Θ
j
i
, since loss occurs during power transfer
between MGs in the same coalition. Technically, the
power loss according to (Gao et al., 2018) is given by
P
L
(i,e) = I
2
R =
h
P(E)
V
i
2
. α . d(i,e) (11)
where P(E) is the power required for energy transfer,
V is the carrying voltage on the transmission line, α is
the line resistance and d(i,e) is the distance between
Θ
j
i
and Θ
j
e
. The characteristic function of the coali-
tion formation game is designed to consider a trade-
off between power supply and loss. Overall, the en-
ergy management problem of networked MGs can be
formulated with the following equations:
max ρ(CS) (12)
min
∑
Ξ
k
j
∈CS
P
Ξ
k
j
L
(13)
4 METHODOLOGY
This section gives the solution of the energy manage-
ment problem formulated in the previous section. The
originality of this work is the proposal of a coopera-
tive energy management software for networked MGs
which is based on two algorithms: the coalition for-
mation algorithm and energy transfer algorithm that
are detailed hereafter. The software ensures the coop-
eration between MGs by forming several stable coali-
tions which lead to a significant technical and eco-
nomical gains.
4.1 Coalition Formation
4.1.1 Motivation
As some MGs might fail to generate/consume the
predicted amount of energy, they are required to ex-
change energy with other MGs at more beneficial
prices than the DSO. For this reason, the energy man-
agement is executed in two consecutive steps that
are coalition formation and then energy transfer. A
coalition formation game is designed to form a stable
coalition structure in order to maximize the profits of
MGs. After that, the energy transfer process is exe-
cuted to exchange energy in each coalition with the
objective to minimize power loss. The proposed soft-
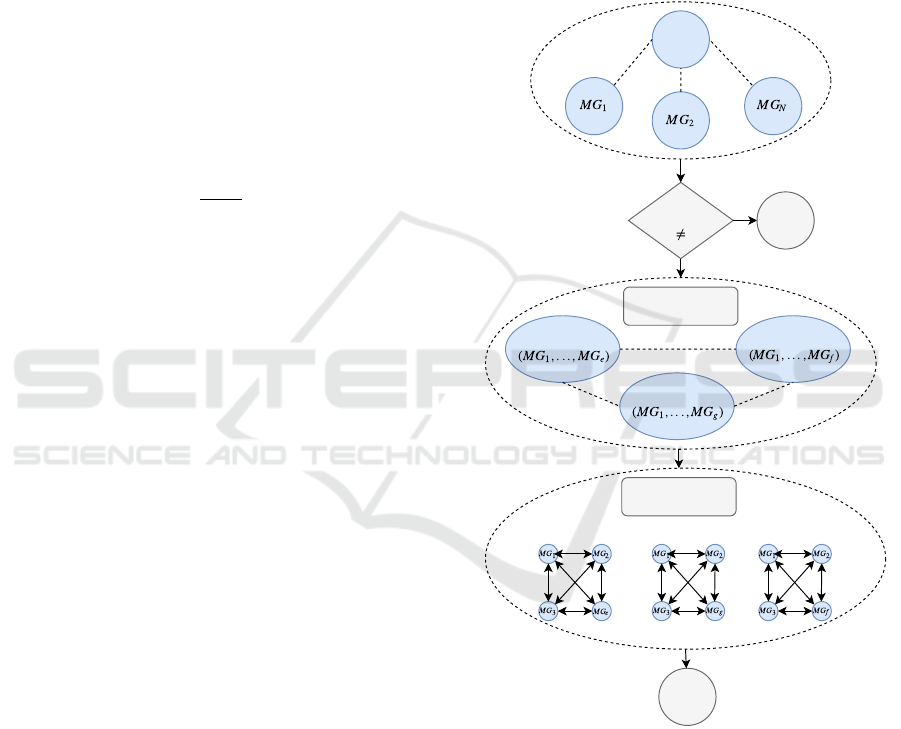
ware is globally illustrated in Fig. 2 and detailed in
the next subsections.
DSO
End
No
Yes
Coalition 1
Coalition j
End
if energy status
0
Coalition Formation
Coalition 2
Intra Coalition Energy
Transfer
Coalition 1 Coalition 2 Coalition j
Figure 2: Flowchart of the proposed cooperative EMS.
The software starts by checking the energy status
E of each microgrid in the network, if it is equal to
zero, then the microgrid does not participate in the
coalition formation game, else, the microgrid partic-
ipates. After that, the coalition formation process
starts forming several coalitions until the network is
stabilized. Then, the intra coalition energy transfer
starts transferring energy in each coalition in order to
minimize the power loss.
ICSOFT 2019 - 14th International Conference on Software Technologies
432

4.1.2 Formalization
The set of balanced MGs Λ will not participate in the
coalition formation game while MGs with energy sur-
plus Π and energy shortage Ψ participate in the coali-
tional game. If | Π |= 0, then all of the MGs with
energy shortage purchase power from the DSO, and
if | Ψ |= 0, then all of the MGs with energy surplus
sell power to the DSO. Thus, in such case, the MGs
cannot cooperate. Specifically, the required condition
for the coalition formation game is given by
| Π | . | Ψ |6= 0 (14)
The coalition formation game aims to find the best
coalitions that maximize the profit from energy ex-
change, i.e.,
Ω
k
= argmax
|Ω
k
|
∑
j=1
v(Ξ
k
j
) (15)
4.1.3 Implementation
Alg. 1 presents the proposed merge-and-split coali-
tion formation algorithm (MSCF). The algorithm can
be executed by a trusted third party that coordinates
between coalitions and MGs. It assumes that MGs
report their energy status to this party.
The first collection Ω
k
is initialized with every sin-
gleton microgrid Θ
j
i
as a coalition Ξ
k
j
∈ Ω
k
. A ma-
trix called visited is used to memorize all pairs of
the visited coalitions for merge process. The ma-
trix has the structure of an adjacency matrix. Ini-
tially, the visited matrix is set to false for all coali-
tions, after that, the merge process starts. The collec-
tion Ω
k
is submitted for merging, i.e., a random pair
of coalitions (Ξ
k
j
,Ξ
k
l
) is chosen from Ω
k
to check if
Ξ
k
j
S
Ξ
k
l
{{Ξ
k
j
},{Ξ
k
l
}}, then coalitions Ξ
k
j
and Ξ
k
l
decide to merge. Ξ
k
j
S
Ξ
k
l
is saved in Ξ
k
j
, and Ξ
k
l
is
removed from Ω
k
, then Ξ
k
j
enters in the next merge
step. So, the visited matrix is updated. Ω
k
continues
for merging by searching non-visited coalitions. After
the test of all the combinations, if there is no merge,
the merge process ends.
The resulted Ω
k
is then passed to split process.
Every coalition Ξ
k
j
∈ Ω
k
having more than one mem-
ber, i.e., microgrid, is subject to splitting. The al-
gorithm tries to split Ξ
k
j
into two disjoint coalitions
Ξ
k
l
and Ξ
k
m
where Ξ
k
l
S
Ξ
k
m
= Ξ
k
j
. The splitting oc-
curs only if one of the MGs belonging to the coalition
can improve its individual payoff, without hurting the
payoff of the other MGs.
If one or more split occurs, then merge process
starts again. Multiple successive merge-and-split pro-
cesses are repeated until the coalition formation game
Algorithm 1: Merge-and-Split Coalition Formation
(MSCF).
1 Input: Θ
0
1
,Θ
0
2
,...,Θ
0
N
(set of microgrids)
2 Output: CS{coalition structure}
3 for j ← 1 to N do
4 Ξ
k
j
= Θ
j
j
;
5 end
6 initialization Ω
k
= {Ξ
k
1
,Ξ
k
2
,...,Ξ
k
N
}
7 repeat
8 f inish= true;
9 forall Ξ
k
j
,Ξ
k
l
∈ Ω
k
, j 6= l do
10 visited [Ξ
k
j
][Ξ
k
l
] ← False
11 end
12 {Merge process}
13 repeat
14 Ω
k
= Merge(Ω
k
)
15 update visited matrix
16 until (no merge occurs);
17 {Split process}
18 repeat
19 Ω
k
= Split(Ω
k
)
20 until (no split occurs);
21 if (one or more split occurs) then
22 f inish = f alse;
23 end
24 until ( f inish == true);
25 CS = Ω
k
;
terminates. The termination criteria is that there are
no merge or split to execute for all existing coalitions
in Ω
k
.
4.1.4 Proof of Stability of the Proposed MSCF
Algorithm
We demonstrate the stability of the formed coali-
tions regardless the environmental changes of the net-
worked MGs system. We provide the concept of de-
fection function given in (Apt and Witzel, 2009), to
prove the stability of the formed coalitions.
Definition 4.1. A defection function ID assigns to
each partition P of the grand coalition G a group of
collections.
The players in P can only form the collections as-
signed by ID. If no group of players is interested in
leaving the partition P, then P is ID-stable. Apt and
Witzel proposed in (Apt and Witzel, 2009) a defection
function ID
P
that allows to form all partitions of P in
the grand coalition G, such that, ID
P
-stability is de-
fined based on this defection function. ID
P
allows any
group of players to leave P through merge-and-split
rules to form another partition. Thus, ID
P
-stability
Cooperative Energy Management Software for Networked Microgrids
433

means that no coalition has a motivation to merge or
split.
Running Example. In order to demonstrate the sta-
bility of the proposed algorithm, let us consider a
simple example with three MGs with the follow-
ing energy status E = {20,−5,−10}. Ω
k
is ini-
talized with every microgrid as a coalition Ξ
k
j
, i.e.,
Ω
k
= {Ξ
k
1
,Ξ
k
2
,Ξ
k
3
}. Ξ
k
2
and Ξ
k
3
cannot form coali-
tion because they cannot improve their payoff since
E is negative for both of them. Consider that Ξ
k
1
communicates with Ξ
k
2
in order to merge. Based
on the values of E, {Ξ
k
1
,Ξ
k
2
} {{Ξ
k
1
},{Ξ
k
2
}} since
{
1
15
,max} {{
1
20
},{−
1
5
}}, such that both of Ξ
k
1
and
Ξ
k
2
improve their payoff.
Now, there are two coalitions {Ξ
k
3
} and {Ξ
k
1
,Ξ
k
2
}.
{Ξ
k
3
} communicates with {Ξ
k
1
,Ξ
k
2
} in order to
merge. {Ξ
k
1
,Ξ
k
2
,Ξ
k
3
} {{Ξ
k
1
,Ξ
k
2
},{Ξ
k
3
}} since
{
1
5
,max,max} {{
1
15
,max},{−
1
10
}}, so the merge
occurs. This is because, Ξ
k
1
and Ξ
k
3
improve their
payoff while Ξ
k
2
keeps its previous payoff. Now
{Ξ
k
1
,Ξ
k
2
,Ξ
k
3
} tries to split. Ξ
k
1
will not split to from
a coalition with Ξ
k
2
or even with Ξ
k
3
. Thus, there
are no coalitions to be able to merge or split any
further. As a result, the final coalition structure
CS = Ω
k
= {Ξ
k
1
,Ξ
k
2
,Ξ
k
3
} is D
P
-stable.
The proposed algorithm is repeated periodically,
enabling the MGs to autonomously self-organize in
structured coalitions until no merge or split occurs,
i.e., until the stability of the network.
4.1.5 MSCF Algorithm Complexity
The complexity of the proposed MSCF algorithm
is determined by the number of merge-and-split at-
tempts. In the worst case of merge process, each
coalition attempts to merge with all the other coali-
tions in Ω
k
. Thus, the first merge process occurs af-
ter
N(N−1)
2
attempts, the second after
(N−1)(N−2)
2
at-
tempts and so on. In such case, the complexity is
O(N
3
). However, the merge process significantly re-
quires less number of attempts since a merge of two
coalitions occurs, it does not need to search for other
merge attempts.
Splitting a coalition Ξ
k
j
in the worst case is
O(2
|Ξ
k
j
|
) involving to find all the possible partitions of
the considered coalition. To avoid this scenario, one
of the two partitions of size | Ξ
k
j
− 1 | and 1, respec-
tively, should be feasible. If none of them is feasible,
the split process stops. So, the complexity of the split
process depends on the size of the formed coalitions
and not on the total number of MGs. As a result, in
some cases the complexity of the split process is re-
duced to O(| Ξ
k
j
|). Therefore, the complexity of the
proposed MSCF algorithm can be reduced by limit-
ing the size of the formed coalitions, thus allowing to
control the complexity of the proposed algorithm.
4.2 Energy Transfer
After the coalition formation process, the energy
transfer among coalitions members is executed.
Alg. 2 aims to find the optimal energy transfer be-
tween MGs in the same coalition by transferring en-
ergy between the closest MGs in order to minimize
the power loss.
Algorithm 2: Intra Coalition Energy Transfer
(ICET).
1 Input: Coalition Ξ
k
j
, distance matrix dist
2 Output: Energy transfer matrix ET
3 Π = set of energy seller within Ξ
k
j
;
4 Ψ = set of energy buyer within Ξ
k
j
in
decreasing order;
5 foreach ψ ∈ Ψ do
6 π = argmin dist(ψ, π) ; %nearest MG
seller %
7 if ψ is None then
8 ET (0, ψ) = ψ.energy;
9 break;
10 end
11 di f = π.energy− | ψ.energy |;
12 ψ.energy −= di f ;
13 π.energy −= di f ;
14 ET (π, ψ) = di f ;
15 end
16 foreach π ∈ Π do
17 if π.energy > 0 then
18 ET (π, 0) = π.energy;
19 end
20 end
Initially, for each MG buyer, we search for the
nearest MG seller. After that, we subtract the given
amount of energy from the energy buyer and seller
and the energy transfer matrix ET is filled with the
energy sellers in rows and with energy buyers in
columns and so on until we supply all the MGs that
have energy shortage. Finally, if an amount of energy
rests, it is saved in ET indexed with energy sellers in
rows and zero in columns.
5 SIMULATION RESULTS
In this section, the proposed cooperative energy man-
agement software is applied on a case study consist-
ICSOFT 2019 - 14th International Conference on Software Technologies
434

ing of multiple networked MGs and some simulation
results are given.
5.1 Case Study
The networked MGs system is modeled with a mesh
structure which ensures a high level of service. Fig. 3
shows the networked MGs system considered in our
case study. The figure shows the distribution of mi-
crogrids around the distribution system operator.
0 1 2 3 4 5 6 7 8 9 10
Distance (KM)
0
1
2
3
4
5
6
7
8
9
10
Distance (KM)
MG1
MG2
MG3
MG4
MG5
MG6
MG7
MG8
MG9
MG10
MG11
MG12
MG13
MG14
MG15
MG16
DSO
Figure 3: Networked MGs system.
We assume that the distribution network covers an
area of 100 km
2
and consists of N MGs. We assume
also that the MGs are randomly located around the
distribution system operator (DSO) which is located
in the center of the network. We have randomly scat-
ter 16 MGs which is a reasonable number of MGs in
real smart grids.
5.2 Coalition Structure
Fig. 4 shows the coalition structure of the proposed
MSCF algorithm which is applied on our case study.
Tab. 1 illustrates the coalition structure by specify-
ing the MGs that belong to each formed coalition.
We compare the performance of our merge-and-split
Coalition Formation (MSCF) algorithm, with that of
three other algorithms: 1) Grand Coalition Formation
(GCF) algorithm (Du et al., 2018), which consider the
grand coalition as an optimal solution for the coali-
tional game, 2) Random Coalition Formation (RCF)
algorithm (Ray and Vohra, 2015), (Okada, 2011),
which forms a random size of coalitions, where the
members of that coalitions are randomly selected,
3) Same-Size Coalition Formation (SSCF) algorithm
(Vatsikas et al., 2011), which forms coalitions with
0 1 2 3 4 5 6 7 8 9 10
Distance (KM)
0
1
2
3
4
5
6
7
8
9
10
Distance (KM)
MG1
MG2
MG3
MG4
MG5
MG6
MG7
MG8
MG9
MG10
MG11
MG12
MG13
MG14
MG15
MG16
DSO
C1
C2
C3
C4
Figure 4: Coalition structure.
Table 1: Stable coalitions.
Coalition Members
Exchanged energy
with DSO (kw/h)
Ξ
k
1
{Θ
1
1
,Θ
1
2
,Θ
1
3
,Θ
1
5
,Θ
1
6
} 13
Ξ
k
2
{Θ
2
7
,Θ
2
8
,Θ
1
10
} 21
Ξ
k
3
{Θ
3
9
,Θ
3
11
,Θ
3
13
} 2
Ξ
k
4
{θ
4
4
,Θ
4
12
,Θ
4
15
,Θ
4
16
} 18
the same size where the members of that coali-
tions are also randomly selected. In Fig. 5, we
show the performance of the coalition structures
(CS) payoff with different size of the networked
MGs. The figure shows that the MSCF gives the
highest global payoff for MGs compared with the
other algorithms. In fact, the less power exchange
with the DSO, the more profit from power ex-
change. The proposed MSCF algorithm creates a
stable coalitions that minimize the power exchange
with the DSO. The significant difference between the
MSCF and the SSCF is in the decision making in coa-
4 MGs 8MGs 16 MGs 24 MGs
Number of microgrids
0
20
40
60
80
100
120
140
160
180
CS payoff ($)
MGCF
GCF
RCF
SSCF
Figure 5: Coalition structure payoffs.
Cooperative Energy Management Software for Networked Microgrids
435
coalition formation process. The proposed MSCF
algorithm forms coalitions based on merge-and-split
rules. The decision making in SSCF and RCF is
random which yields to a very high standard devia-
tion. As a result, the formed coalitions are unable to
perform energy exchange efficiently and the coalition
members receive less payoff. On average, the global
CS payoff of MSCF exceeds the payoff of the RCF,
GCF and SSCF about 18.24%, 21.33% and 17.15%,
respectively.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Microgrids
0
2
4
6
8
10
12
14
16
Average Power Poss per Microgrid (kw)
Non cooperative approach
Grand Coalition Formation (GCF)
Merge and Split Coalition Formation (MSCF)
Figure 6: Power loss per microgrid.
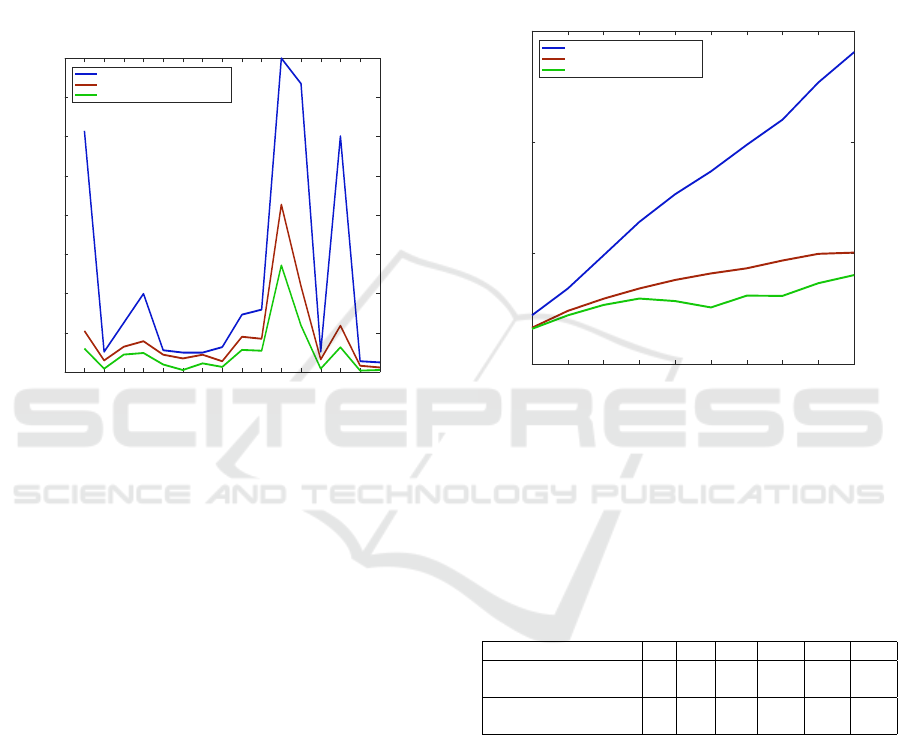
Fig. 6 shows the average power loss for individ-
ual MGs with non cooperative approach as in (Jadhav
and Patne, 2017), and with a cooperative approach.
In the cooperative approach, the GCF algorithm as
in (Du et al., 2018) and the proposed MSCF algo-
rithm are compared. In the non-cooperative approach,
a high level of power loss is observed due to the long
distances between MGs and DS and the existence of
power transformers resulting in more power loss. A
significant decrease in power loss is observed with
the cooperative approach in the case of GCF algo-
rithm where MGs inter-exchange power. The power
transfer between MGs reduces the power loss caused
by transporting power in long distances which is the
case of the non-cooperative approach. With the pro-
posed MSCF algorithm, the power loss is less than
the GCF algorithm. The proposed MSCF algorithm
forms many small size coalitions resulting in short
distances of power transfer which reduce the power
loss compared with the GCF algorithm that forms the
grand coalition resulting in long distances of power
transfer compared with the proposed MSCF algo-
rithm, so, more power loss.
In order to demonstrate the scalability of the pro-
posed cooperative approach, the total power loss of
MGs for different sized networked MGs systems is
compared in Fig. 7 where the number of MGs is up
to 100. The result is obtained after executing a non-
cooperative and cooperative energy exchange (GCF
and MSCF). The loss is significantly reduced with the
cooperative approach. As more as the network size
increases, the MSCF algorithm further reduces the
power loss (about 72%) and the reduction is signifi-
cantly high compared with the GCF algorithm (about
51%).
10 20 30 40 50 60 70 80 90 100
Number of microgrids
0
50
100
150
Total power loss (kw)
Non cooperative approach
Grand Coalition Formation (GCF)
Merge and Split Coalition Formation (MSCF)
Figure 7: Total power loss.
5.3 Discussion
Tab. 2 presents the execution time of the coalition
formation algorithm in two cases that are: 1) limiting
the size of the formed coalitions, 2) without limiting
the size. The proposed coalition formation method-
Table 2: Execution time of MSCF algorithm.
Number of microgrids 10 50 100 200 300 500
Execution time in
seconds (case 1)
2 2 2.3 2.3 2.7 2.9
Execution time in
seconds (case 2)
2 3.3 5.9 10.5 12.6 21.7
ology is quite inexpensive in terms of computational
burden, its heaviest task is the split process, which is
executed in few seconds even for large networks. As
expected, the execution time taken by the proposed
methodology is of the order of seconds regardless of
the number of existing microgrids in the distribution
system. Thus, the results confirms that the execution
time does not depend on the number of microgrids,
i.e., the network size but depends on the size of the
formed coalitions which is a controllable parameter.
ICSOFT 2019 - 14th International Conference on Software Technologies
436

6 CONCLUSION
An efficient cooperative energy management software
for networked MGs is proposed. A motivating pric-
ing scheme is designed to encourage the MGs for co-
operation by forming several stable coalitions. This
cooperation is beneficial from the economic and tech-
nic point of view. We develop a scalable merge-and-
split based coalition formation (MSCF) algorithm that
ensures the stability of the network. The proposed
MSCF algorithm performs better in over sized sys-
tems where the power loss reduction is greater and
the payoff is more. Furthermore, we control the com-
plexity of the proposed MSCF algorithm by limiting
the size of the formed coalitions. Finally, we design
an intra coalition energy transfer (ICET) algorithm to
transfer energy in each coalition. The ICET algorithm
gives the best results in terms of power loss reduc-
tion thanks to the stability of the coalitions formed
by MSCF algorithm. As a perspective, we will study
additional choices of decision-making models for net-
worked MGs and consider other behaviors of MGs in
energy management softwares.
REFERENCES
Abidi, M. G., Smida, M. B., Khalgui, M., Li, Z., and Wu, N.
(2017). Multi-agent oriented solution for forecasting-
based control strategy with load priority of microgrids
in an island mode–case study: Tunisian petroleum
platform. Electric Power Systems Research, 152:411–
423.
Aissa, Y. B., Bachir, A., Khalgui, M., Koubaa, A., Li, Z.,
and Qu, T. (2019). On feasibility of multichannel re-
configurable wireless sensor networks under real-time
and energy constraints. IEEE Transactions on Sys-
tems, Man, and Cybernetics: Systems, pages 1–16.
Apt, K. and Witzel, A. (2009). A generic approach to coali-
tion formation. International Game Theory Review,
11(03):347–367.
Asarias, F. N. and Pedrasa, M. A. A. (2017). Resilient dis-
tributed generation dispatch in multi-microgrid sys-
tems. In IEEE Innovative Smart Grid Technologies
- Asia (ISGT-Asia), pages 1–6.
Cintuglu, M. H. and Mohammed, O. A. (2017). Behavior
modeling and auction architecture of networked mi-
crogrids for frequency support. IEEE Transactions on
Industrial Informatics, 13(4):1772–1782.
Du, Y., Wang, Z., Liu, G., Chen, X., Yuan, H., Wei, Y., and
Li, F. (2018). A cooperative game approach for coor-
dinating multi-microgrid operation within distribution
systems. Applied Energy, 222:383–395.
Fathi, M. and Bevrani, H. (2013). Adaptive energy con-
sumption scheduling for connected microgrids under
demand uncertainty. IEEE Transactions on Power De-
livery, 28(3):1576–1583.
Gao, H., Liu, J., Wang, L., and Wei, Z. (2018). Decen-
tralized energy management for networked microgrids
in future distribution systems. IEEE Transactions on
Power Systems, 33(4):3599–3610.
Ghribi, I., Abdallah, R. B., Khalgui, M., Li, Z., Alnowi-
bet, K., and Platzner, M. (2018). R-codesign: Code-
sign methodology for real-time reconfigurable embed-
ded systems under energy constraints. IEEE Access,
6:14078–14092.
Gu, C., Li, Z., Wu, N., Khalgui, M., Qu, T., and Al-Ahmari,
A. (2018). Improved multi-step look-ahead control
policies for automated manufacturing systems. IEEE
Access, 6:68824–68838.
Hafidi, Y., Kahloul, L., Khalgui, M., Li, Z., Alnowibet, K.,
and Qu, T. (2018). On methodology for the verifica-
tion of reconfigurable timed net condition/event sys-
tems. IEEE Transactions on Systems, Man, and Cy-
bernetics: Systems, (99):1–15.
Jadhav, A. M. and Patne, N. R. (2017). Priority-based en-
ergy scheduling in a smart distributed network with
multiple microgrids. IEEE Transactions on Industrial
Informatics, 13(6):3134–3143.
Khalgui, M., Carpanzano, E., and Hanisch, H.-M. (2008).
An optimised simulation of component-based em-
bedded systems in manufacturing industry. Interna-
tional Journal of Simulation and Process Modelling,
4(2):148–162.
Khalgui, M. and Mosbahi, O. (2010). Intelligent distributed
control systems. Information and Software Technol-
ogy, 52(12):1259–1271.
Lakhdhar, W., Mzid, R., Khalgui, M., Li, Z., Frey, G., and
Al-Ahmari, A. (2019). Multiobjective optimization
approach for a portable development of reconfigurable
real-time systems: From specification to implementa-
tion. IEEE Transactions on Systems, Man, and Cyber-
netics: Systems, 49(3):623–637.
Ma, W.-J., Wang, J., Gupta, V., and Chen, C. (2018).
Distributed energy management for networked micro-
grids using online ADMM with regret. IEEE Trans-
actions on Smart Grid, 9(2):847–856.
Meskina, S. B., Doggaz, N., Khalgui, M., and Li, Z. (2017).
Multiagent framework for smart grids recovery. IEEE
Transactions on Systems, Man, and Cybernetics: Sys-
tems, 47(7):1284–1300.
Meskina, S. B., Doggaz, N., Khalgui, M., and Li, Z.
(2018). Reconfiguration-based methodology for im-
proving recovery performance of faults in smart grids.
Information Sciences, 454:73–95.
Naidji, I., Smida, M. B., Khalgui, M., and Bachir, A.
(2018). Non cooperative game theoretic approach
for residential energy management in smart grid. In
The 32nd Annual European Simulation and Modelling
Conference, pages 164–170, Ghent, Belgium.
Nunna, H. K. and Doolla, S. (2013). Multiagent-based
distributed-energy-resource management for intelli-
gent microgrids. IEEE Transactions on Industrial
Electronics, 60(4):1678–1687.
Okada, A. (2011). Coalitional bargaining games with ran-
dom proposers: Theory and application. Games and
Economic Behavior, 73(1):227–235.
Cooperative Energy Management Software for Networked Microgrids
437

Ray, D. and Vohra, R. (2015). Coalition formation. In
Handbook of game theory with economic applica-
tions, volume 4, pages 239–326. Elsevier.
Vatsikas, S., Armour, S., De Vos, M., and Lewis, T. (2011).
A distributed algorithm for wireless resource alloca-
tion using coalitions and the nash bargaining solution.
In 2011 IEEE 73rd Vehicular Technology Conference
(VTC Spring), pages 1–5. IEEE.
Wang, Z., Chen, B., Wang, J., Begovic, M. M., and Chen,
C. (2015). Coordinated energy management of net-
worked microgrids in distribution systems. IEEE
Transactions on Smart Grid, 6(1):45–53.
Wu, J. and Guan, X. (2013). Coordinated multi-microgrids
optimal control algorithm for smart distribution man-
agement system. IEEE Transactions on Smart Grid,
4(4):2174–2181.
Zamora, R. and Srivastava, A. K. (2018). Multi-layer ar-
chitecture for voltage and frequency control in net-
worked microgrids. IEEE Transactions on Smart
Grid, 9(3):2076–2085.
ICSOFT 2019 - 14th International Conference on Software Technologies
438
